Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Compressed Sensing Technique
2.2. Centroid Downshift Method
2.3. Envelope Detection from Fourier Transform Coefficients
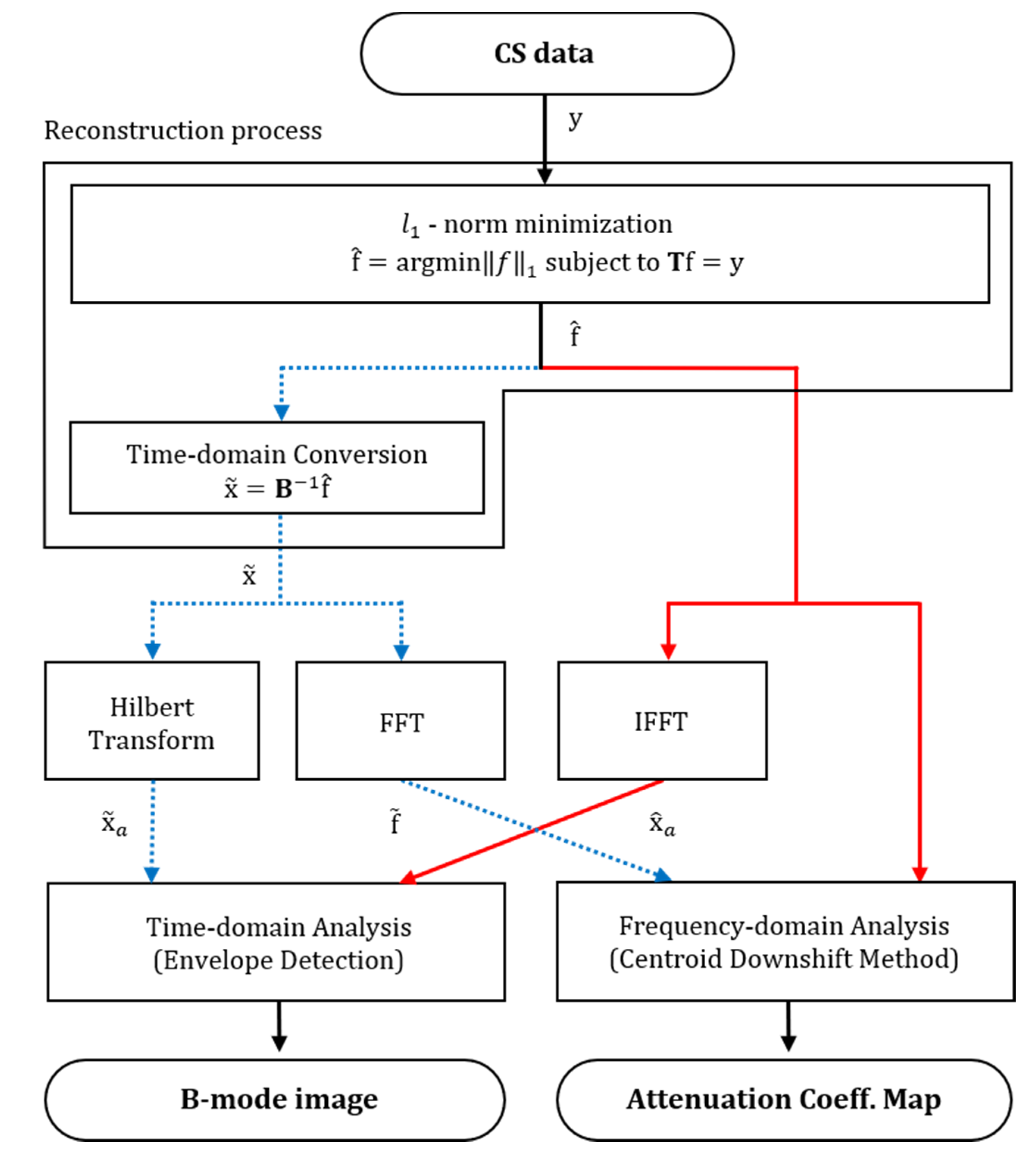
2.4. Signal-Processing Framework for Ultrasound Compressed Sensing Data
2.5. Numerical Phantoms
3. Results
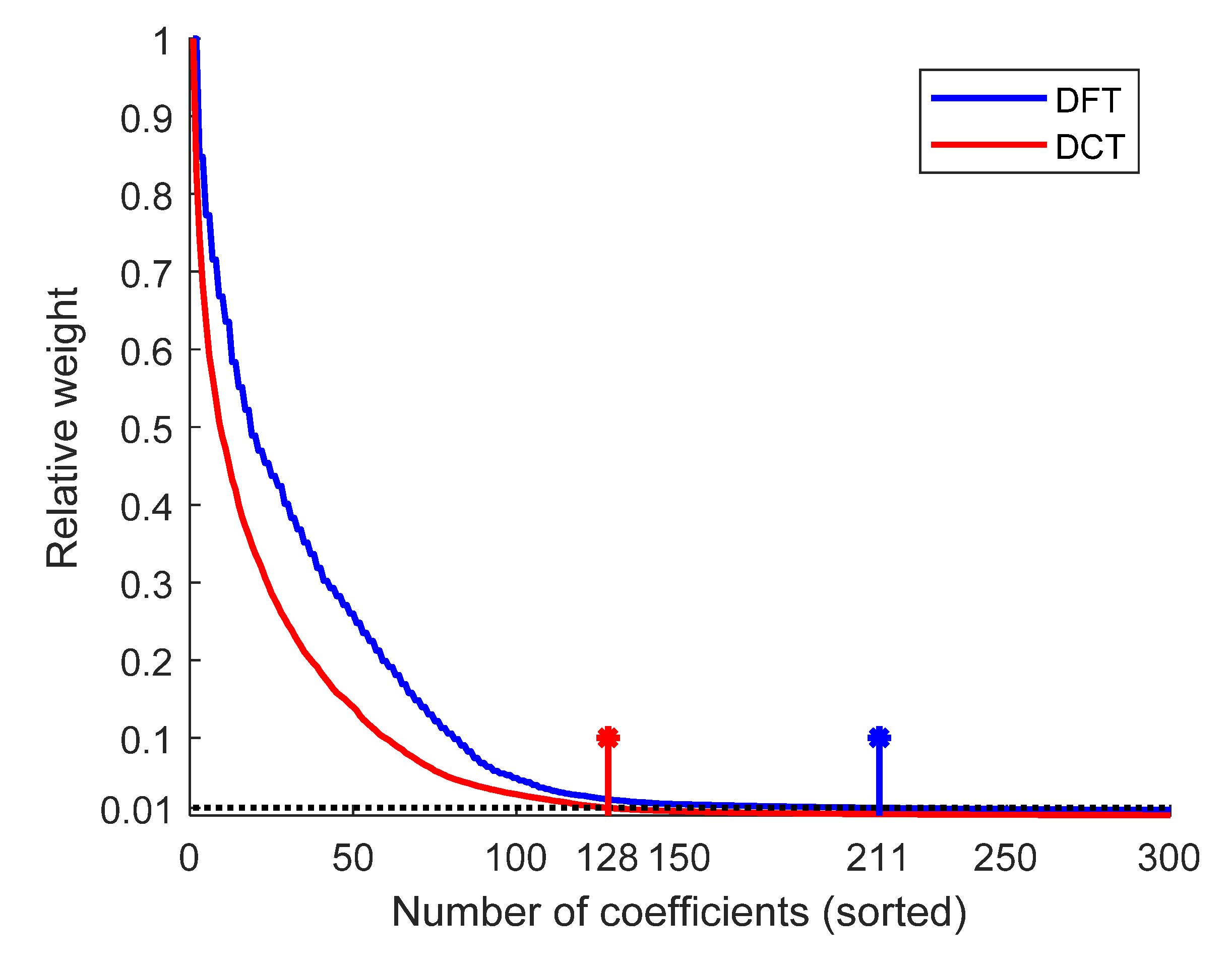
3.1. Comparison of the DFT and DCT Basis Matrices
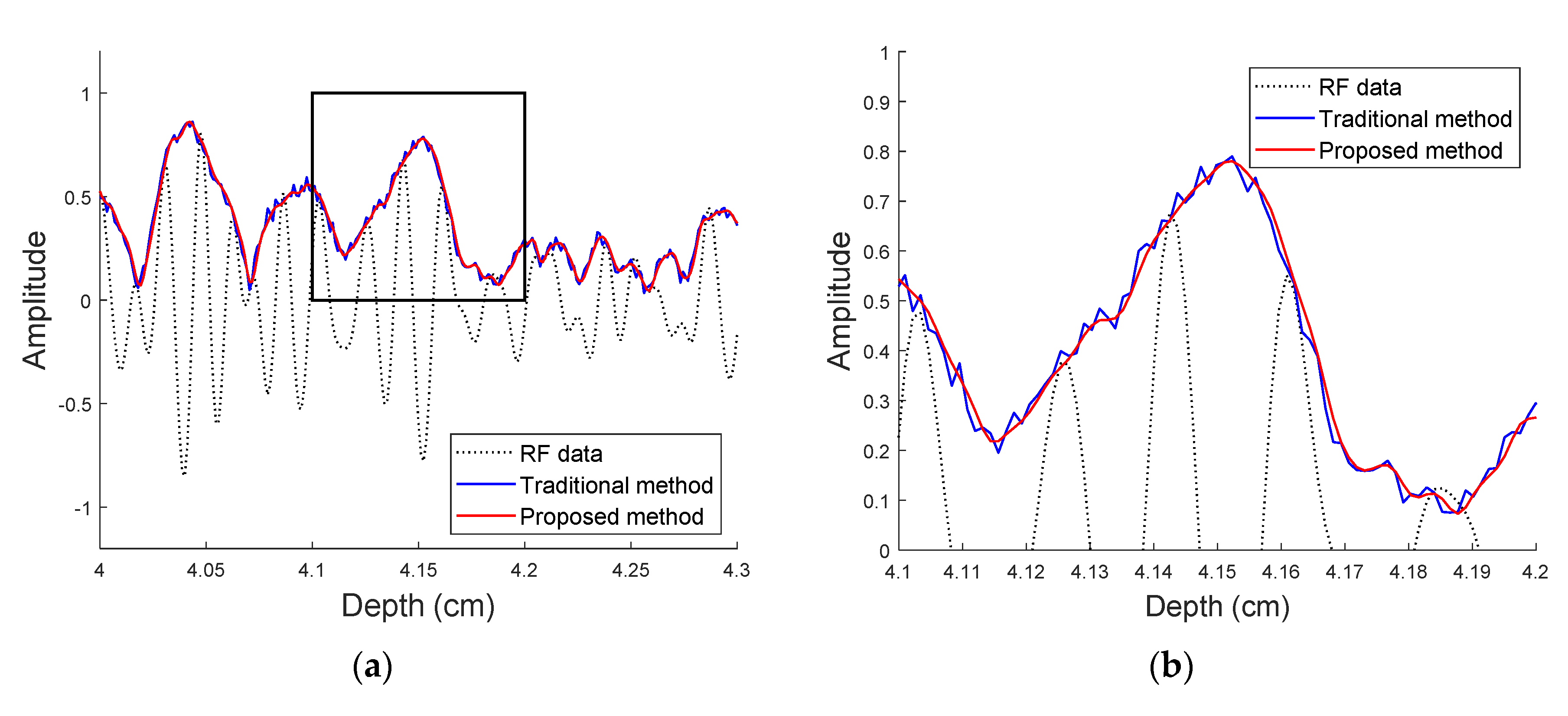
3.2. Envelope Detection
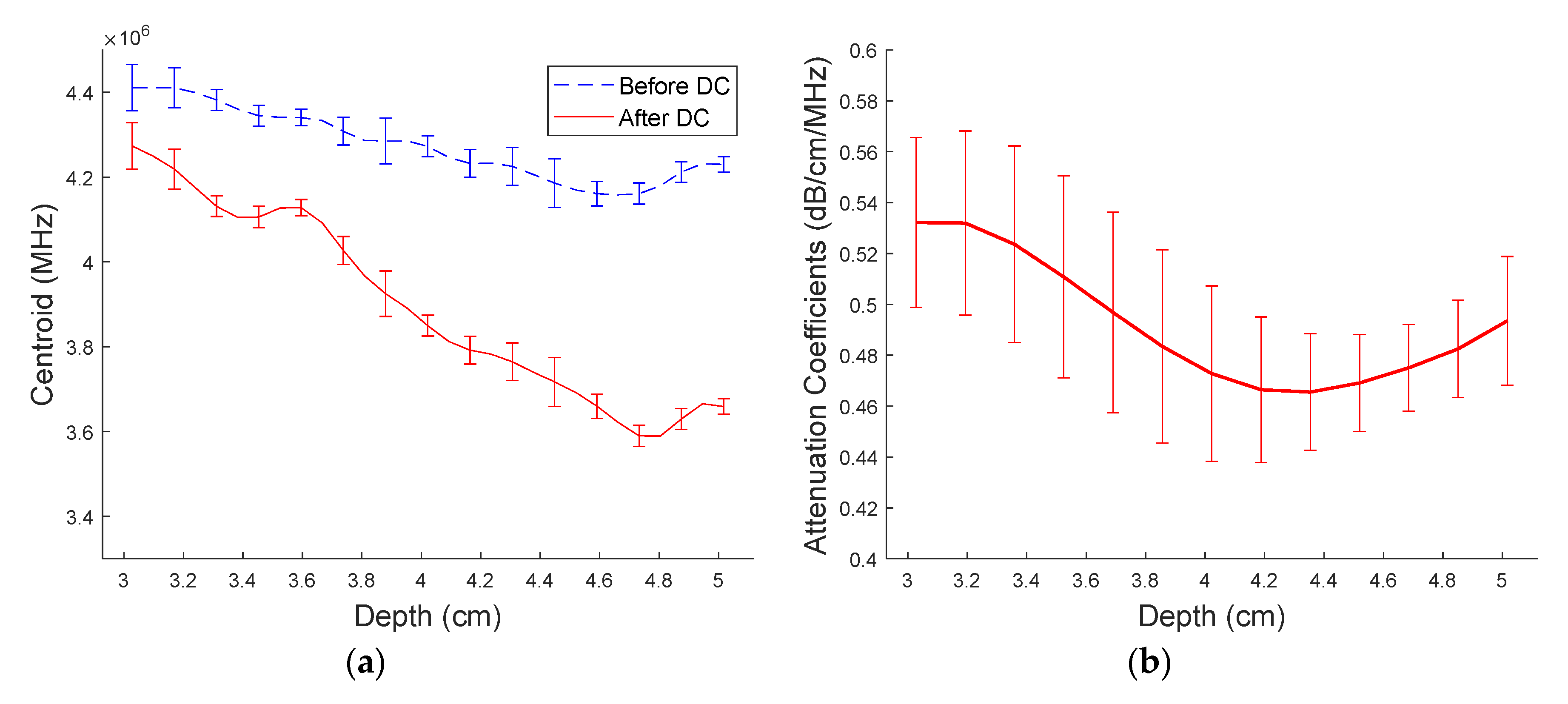
3.3. Attenuation Estimation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CDM | Centroid Downshift Method |
| CS | Compressed Sensing |
| DCT | Discrete Cosine Transform |
| DFT | Discrete Fourier Transform |
| FFT | Fast Fourier Transform |
| IFFT | Inverse Fast Fourier Transform |
| QUS | Quantitative UltraSound |
| RF | Radiofrequency |
| RMSE | Root Mean Square Error |
| ROI | Region of Interest |
| TGC | Time Gain Compensation |
| TM-phantom | Tissue-Mimicking Phantom |
References
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar]
- Nyquist, H. Certain topics in telegraph transmission theory. Proc. IEEE 2002, 90, 280–305. [Google Scholar] [CrossRef]
- Otazo, R.; Candès, E.; Sodickson, D.K. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med. 2015, 73, 1125–1136. [Google Scholar] [CrossRef]
- Metzler, C.A.; Maleki, A.; Baraniuk, R.G. From denoising to compressed sensing. IEEE Trans. Inf. Theory 2016, 62, 5117–5144. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhu, Y.; Kong, L.; Liu, C.; Gu, Y.; Vasilakos, A.V.; Wu, M.Y. CDC: Compressive data collection for wireless sensor networks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 2188–2197. [Google Scholar] [CrossRef]
- Liebgott, H.; Basarab, A.; Kouame, D.; Bernard, O.; Friboulet, D. Compressive sensing in medical ultrasound. In Proceedings of the IEEE International Ultrasonics Symposium, Dresden, Germany, 7–10 October 2012. [Google Scholar] [CrossRef]
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.S.; Yan, S. Sparse representation for computer vision and pattern recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Abrol, V.; Sharma, P.; Sao, A.K. Voiced/nonvoiced detection in compressively sensed speech signals. Speech Commun. 2015, 72, 194–207. [Google Scholar] [CrossRef]
- Do, T.T.; Chen, Y.; Nguyen, D.T.; Nguyen, N.; Gan, L.; Tran, T.D. Distributed compressed video sensing. In Proceedings of the 16th IEEE International Conference on Image Processing, Cairo, Egypt, 7–10 November 2009; pp. 1393–1396. [Google Scholar] [CrossRef]
- Schiffner, M.F.; Schmitz, G. Ultrafast image acquisition in pulse-echo ultrasound imaging using compressed sensing. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Liebgott, H.; Prost, R.; Friboulet, D. Pre-beamformed RF signal reconstruction in medical ultrasound using compressive sensing. Ultrasonics 2013, 53, 525–533. [Google Scholar] [CrossRef]
- Chernyakova, T.; Eldar, Y.C. Fourier-domain beamforming: The path to compressed ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1252–1267. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.M.; Mung, J.; Yen, J.T. Fresnel-based beamforming for low-cost portable ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 112–121. [Google Scholar] [CrossRef]
- Hiller, S.; Fiorito, F.; Wüthrich, K.; Wider, G. Automated projection spectroscopy (APSY). Natl. Acad. Sci. USA 2005, 102, 10876–10881. [Google Scholar]
- Gołowicz, D.; Kasprzak, P.; Kazimierczuk, K. Enhancing compression level for more efficient compressed sensing and other lessons from NMR spectroscopy. Sensors 2020, 20, 1325. [Google Scholar]
- Shim, J.; Hur, D.; Kim, H. Spectral analysis framework for compressed sensing ultrasound signals. J. Med. Ultrason. 2019, 46, 367–375. [Google Scholar] [CrossRef]
- Fink, M.; Hottier, F.; Cardoso, J.F. Ultrasonic signal processing for in vivo attenuation measurement: Short time Fourier analysis. Ultrason. Imaging 1983, 5, 117–135. [Google Scholar] [CrossRef]
- Knuth, D.E. Postscript about NP-hard problems. ACM SIGACT News 1974, 6, 15–16. [Google Scholar] [CrossRef]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Techavipoo, U.; Varghese, T.; Chen, Q.; Stiles, T.A.; Zagzebski, J.A.; Frank, G.R. Temperature dependence of ultrasonic propagation speed and attenuation in excised canine liver tissue measured using transmitted and reflected pulses. J. Acoust. Soc. Am. 2004, 115, 2859–2865. [Google Scholar] [CrossRef]
- Levy, Y.; Agnon, Y.; Azhari, H. Measurement of speed of sound dispersion in soft tissues using a double frequency continuous wave method. Ultrasound Med. Biol. 2006, 32, 1065–1071. [Google Scholar] [CrossRef] [PubMed]
- Wear, K.A.; Stiles, T.A.; Frank, G.R.; Madsen, E.L.; Cheng, F.; Feleppa, E.J.; Hall, C.S.; Kim, B.S.; Lee, P.; O’Brien, W.D.; et al. Interlaboratory comparison of ultrasonic backscatter coefficient measurements from 2 to 9 MHz. J. Ultrasound Med. 2005, 24, 1235–1250. [Google Scholar] [CrossRef] [PubMed]
- Taggart, L.R.; Baddour, R.E.; Giles, A.; Czarnota, G.J.; Kolios, M.C. Ultrasonic characterization of whole cells and isolated nuclei. Ultrasound Med. Biol. 2007, 33, 389–401. [Google Scholar] [CrossRef]
- Liu, W.; Zagzebski, J.A.; Varghese, T.; Gerig, A.L.; Hall, T.J. Spectral and scatterer-size correlation during angular compounding: Simulations and experimental studies. Ultrason. Imaging 2006, 28, 230–244. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Varghese, T. Attenuation estimation using spectral cross-correlation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 510–519. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Varghese, T. Hybrid spectral domain method for attenuation slope estimation. Ultrasound Med. Biol. 2008, 34, 1808–1819. [Google Scholar] [CrossRef]
- Wear, K.A. A Gaussian framework for modeling effects of frequency-dependent attenuation, frequency-dependent scattering, and gating. IEEE Trans. Ultrason. 2002, 49, 1572–1582. [Google Scholar] [CrossRef]
- Fink, M.A.; Cardoso, J. Diffraction effects in pulse-echo measurement. IEEE Trans. Ultrason. 1984, 31, 313–329. [Google Scholar] [CrossRef]
- Mohana Shankar, P. A general statistical model for ultrasonic backscattering from tissues. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 727–736. [Google Scholar] [CrossRef]
- Kuc, R. Bounds on estimating the acoustic attenuation of small tissue regions from reflected ultrasound. Proc. IEEE 1985, 73, 1159–1168. [Google Scholar] [CrossRef]
- Flax, S.W.; Pelc, N.J.; Glover, G.H.; Gutmann, F.D.; McLachlan, M. Spectral characterization and attenuation measurements in ultrasound. Ultrason. Imag. 1983, 5, 95–116. [Google Scholar] [CrossRef] [PubMed]
- Bridge, C.P. Introduction to the Monogenic Signal. arXiv 2017, arXiv:1703.09199. [Google Scholar]
- Marple, S.L. Computing the discrete-time “analytic” signal via FFT. In Proceedings of the Conference Record of the Thirty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 1997; pp. 1322–1325. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Li, Y.; Zagzebski, J.A. A frequency domain model for generating b-mode images with array transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 690–699. [Google Scholar] [CrossRef]
- Sassaroli, E.; Crake, C.; Scorza, A.; Kim, D.S.; Park, M.A. Image quality evaluation of ultrasound imaging systems: Advanced B-modes. J. Appl. Clin. Med. Phys. 2019, 20, 115–124. [Google Scholar] [CrossRef]
- Kundu, S.; Kolouri, S.; Erickson, K.I.; Kramer, A.F.; McAuley, E.; Rohde, G.K. Discovery and visualization of structural biomarkers from MRI using transport-based morphometry. NeuroImage 2018, 167, 256–275. [Google Scholar] [CrossRef] [PubMed]





| 50% | 60% | 70% | 80% | 90% | ||
|---|---|---|---|---|---|---|
| DFT | Traditional | 0.625 | 0.718 | 0.836 | 0.94 | 1 |
| Proposed | 0.63 | 0.73 | 0.839 | 0.946 | 1 | |
| DCT | Traditional | 0.197 | 0.411 | 0.612 | 0.825 | 0.982 |
| Proposed | 0.156 | 0.366 | 0.545 | 0.778 | 0.955 |
| 50% | 60% | 70% | 80% | 90% | |
|---|---|---|---|---|---|
| Traditional | 0.582 | 0.593 | 0.655 | 0.804 | 1 |
| Proposed | 0.108 | 0.254 | 0.464 | 0.714 | 0.914 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Park, J.; Kim, H. Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis. Appl. Sci. 2020, 10, 6956. https://doi.org/10.3390/app10196956
Kim Y, Park J, Kim H. Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis. Applied Sciences. 2020; 10(19):6956. https://doi.org/10.3390/app10196956
Chicago/Turabian StyleKim, Yisak, Juyoung Park, and Hyungsuk Kim. 2020. "Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis" Applied Sciences 10, no. 19: 6956. https://doi.org/10.3390/app10196956
APA StyleKim, Y., Park, J., & Kim, H. (2020). Signal-Processing Framework for Ultrasound Compressed Sensing Data: Envelope Detection and Spectral Analysis. Applied Sciences, 10(19), 6956. https://doi.org/10.3390/app10196956




