Featured Application
The proposed active sidewall panel with integrated structural actuators and sensors (smart lining module) is intended for application of cabin noise reduction in propeller driven regional aircraft like ATR 42, ATR 72, DHC-8 Q400 or in new energy efficient regional or short-range aircraft with counter rotation open rotor (CROR) or electric propeller engines. Since the smart lining modules are autonomous and geometrically compliant with their passive counterparts, they can be readily integrated into the aircraft.
Abstract
This work deals with the reduction of aircraft interior noise using active sidewall panels (linings). Research work done in the past showed that considerable reductions of the sound pressure level (SPL) in the cabin are possible using structural actuators mounted on the lining and error microphones distributed in front of the linings. However, microphones are undesirable for error sensing because they are not suitable for the realisation of an integrated and autonomous active lining (smart lining module). Therefore, the goal of the present work is the replacement of the microphones by structural sensors. Using the structural sensors as remote sensors in combination with an acoustic filter, virtual microphones can be defined. The present study relies on experimental data of a double-walled fuselage system which is mounted in a sound transmission loss facility. Simulation results based on measured time data and identified frequency response functions are provided. Different configurations of virtual microphones are investigated regarding the SPL reduction and the induced vibration of the lining panel.
1. Introduction
The problem of active noise control in propeller-driven aircraft has been thoroughly investigated in research during the last few decades. Several systems have been successfully implemented for example in the aircraft Saab 2000 or Bombardier DHC-8 Q400. One approach applies active noise control (ANC) using anti-sound generated by loudspeakers to reduce the sound pressure in the cabin. Early results of ANC in aircraft are published by Elliott et al. [1]. In this work, the interior sound pressure level (SPL) associated with the blade passing frequency (88 Hz) is reduced up to 13 dB. A different method to reduce interior SPL is the active structural acoustic control (ASAC). There, shakers or piezoelectric patch actuators are used to control the sound radiating structural vibration. Fuller and Jones [2] published early results on this topic. To implement an ASAC system in aircraft, the fuselage or the interior parts are augmented with structural actuators and sensors. One approach uses active sidewall panels (linings) to realize active noise control in aircraft. In Lyle and Silcox [3], experiments with active linings are documented. The active linings are mounted to a stiffened fuselage barrel. A loudspeaker is used for the acoustic excitation of the barrel. The SPL reduction achieved by the active linings is up to 5 dB. Ground tests in a McDonnell Douglas DC-9 aircraft are documented in Tran and Mathur [4]. The linings in the aft section are augmented with 16 piezoelectric patch actuators. The 32 error microphones are positioned at the headrests and in the aisle. The results of this approach are considered unsatisfactory by the authors because systems with loudspeakers and systems with actuators mounted on the fuselage implemented on the same aircraft showed a higher performance (see [4], Figure 4). Active linings using electrodynamic exciters as actuators are successfully realized by Misol et al. [5] and by Misol [6]. In [5], tests of an active lining in a sound transmission loss facility and, in [6], full-scale tests of two active lining modules mounted in the cabin of a Dornier Do728 aircraft, are reported. A loudspeaker array with 112 sources is used to mimic the acoustic excitation of the engine. A maximum SPL reduction of 11.3 dB and a mean SPL reduction of 6.8 dB are achieved in front of the active linings inside the Do728 cabin. The active noise control systems mentioned so far have in common that they use microphones for error sensing. However, the requirement of having distributed and closely adjacent microphones in the whole cabin is undesirable because it requires additional wiring and prevents flexible cabin layouts. The so-called smart lining concept pursued by Misol et al. tries to overcome these drawbacks by modular active linings with structurally integrated actuators, sensors and control. This concept requires a substitution of the physical error microphones by so-called virtual error microphones. Different methods are applicable to set up a noise reduction system with virtual microphones. In the work of Mazur and Pawelczyk [7], a virtual microphone control for an active noise-cancelling casing is realized. The active vibration control system is tuned in a two-stage approach to reduce the SPL at specific locations in the acoustic field solely based on vibration sensor data. A related approach is pursued in Haase and Unruh [8], where the locations of vibration sensors of an active vibration control system are optimized regarding the reduction of the radiated sound power of a fuselage structure. Another method is the remote microphone technique for active control proposed by Roure and Albarazzin [9]. In this technique, the error microphones are substituted by remote microphones and an observer filter. In a similar approach, Cheer and Daley [10] replace the remote microphones by accelerometers mounted on the radiating structure. This approach is adopted for the smart lining concept because it allows for getting rid of the undesirable error microphones.
The present contribution deals with the noise reduction of an active lining system which uses the integrated accelerometers in a remote sensing scheme as proposed by Cheer and Daley. The main contribution of this work is the evaluation of the sound reduction potential of different virtual microphone configurations under optimal laboratory conditions using measurement data. The influence of the active control system on the lining surface vibrations (actuator feedback) is also evaluated. Simulations are based on measurement data of an Airbus A350 lining formerly described in [5]. The lining used is an original component from the series production of the company DIEHL Aviation Laupheim. Initial results on the noise reduction performance of a smart lining with remote sensors and an observer are reported in Misol [11].
2. Methods
2.1. Experimental Setup
In Figure 1, a scheme of the laboratory setup in the sound transmission loss facility of the German Aerospace Center (DLR) is shown. The loudspeaker array (LSA) which is used for the disturbance excitation is positioned in front of the fuselage structure having an offset of approximately 0.15 m. Of the 112 loudspeakers of the LSA, 72 are used. The remaining loudspeakers are not used because they are beyond the fuselage panel surface. The 72 loudspeakers are arranged in an array of nine rows and eight columns. Two different acoustic load cases are considered. One acoustic load case is typical for a counter rotating open rotor (CROR) engine. It is characterized by multiple tones with frequencies 119.4 Hz, 149.2 HZ, 268.6 Hz, 388 Hz and 417.9 Hz [12]. The bandwidth is limited to the first five harmonics because these tones are most critical for the interior noise. The second acoustic load case is realized by driving the 72 loudspeakers with uncorrelated bandlimited white noise signals. The resulting broadband sound field is intended to roughly approximate the characteristics of a turbulent boundary layer. Both load cases are relevant for propeller-driven aircraft, but the tonal parts dominate. This can be attributed to the higher sound pressures and the higher spatial correlation of the CROR load case. It is assumed that the propeller induced pressure components are up to 30 dB higher than the TBL induced pressure components. This is especially true in or near the rotor plane, the part of the fuselage closest to the engines. Absolute measured auto-spectra of a TBL excitation can be taken from Klabes et al. ([13], Figure 11) and numerically determined absolute pressure values of a CROR engine are provided in Stürmer and Akkermans [14].
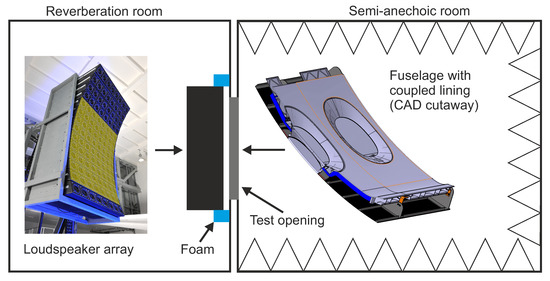
Figure 1.
Top view schematic of the experimental setup in the transmission loss facility. The loudspeaker array is located in the reverberation room and the fuselage with coupled lining is mounted in the test opening of the facility. The used loudspeakers are highlighted in yellow. The air gap between the fuselage structure and the loudspeaker array is proofed with foam to reduce acoustic feedback from the reverberation room.
The test specimen consists of a carbon fiber reinforced plastics (CFRP) fuselage structure with a coupled lining. Figure 2 shows the experimental setup seen from the semi-anechoic room. The fuselage structure (not visible) is supported by shock mounts placed in the corners of the outer frames (yellow boxes in Figure 2b). From a set of 19 evenly distributed accelerometers (indicated in blue), 16 are selected as potential remote sensors. The three discarded sensors are marked with an X. The reason for the exclusion of these three sensors is the low coherence due to the unfavourable position on the window pane or due to a sensor defect. The 20 microphones (indicated in green) are arranged in two vertical lines as shown in Figure 2b. It is assumed that the vertical locations of the passengers ears will usually be between these two lines. The 20 microphones are positioned at three distances m, m and m from the lining to capture SPL variations from the window to the aisle. The 60 locations of the virtual microphones are defined in Figure 3. All sensor signals plus an analog reference signal from the LSA and plus the two actuator control voltages are captured simultaneously with a sampling rate of 5 kHz and a time duration of 100 s. The reference signal is sampled from an analog output signal of the LSA containing the five CROR harmonics. Time data are sampled for both load cases. The data of the CROR load case are used for the identification of the observer filter and for the simulation of the active control system. Time data of the broadband load case are used for the selection of the remote sensors. The time data which are needed for the calculation of the frequency response functions (FRF) from the actuators to the remote sensors and to the microphones are obtained from a multi-reference test. For this purpose, the loudspeaker field is switched off and all actuators are driven simultaneously with uncorrelated band-limited white noise signals. Further details on how the time data are used will be provided in subsequent sections.
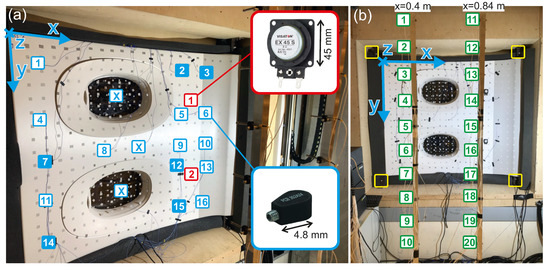
Figure 2.
Experimental setup in the transmission loss facility seen from the semi anechoic room. The locations of the actuators and the accelerometers are indicated in (a) and the microphone locations are indicated in (b). The accelerometers are indicated in blue, the actuators in red and the microphones in green. The accelerometers finally chosen as remote sensors are 2, 3, 7, 12, 14 and 15 (blue backed boxes). The microphones are positioned m, m or m in front of the lining along two vertical lines at and spanning two planes used for control performance evaluation.
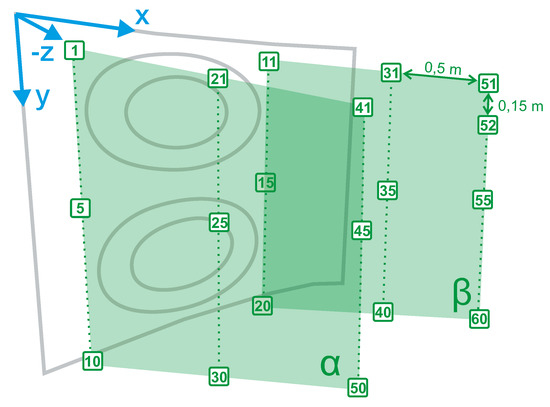
Figure 3.
Locations of the virtual microphones on the planes and .
2.2. Sensors and Actuators
The sensors and the actuators of the smart lining are defined using the measurement data of the two load cases. Since the CROR load case is deterministic, one remote sensor is sufficient to estimate the sound pressures at all microphone locations. However, the use of a single remote sensor is considered undesirable with regard to robustness because its failure would lock down the whole system. Furthermore, a larger number of remote sensors is needed to achieve a high signal coherence for the broadband load case. The multiple coherence function is used as a performance metric for the optimization of the number and the positions of the remote sensors. Equation (1) is applicable for systems with multiple inputs and a single output. Here we have up to 16 inputs from the remote sensors and one output from the 60 virtual microphones. The data from the broadband load case are taken for calculation. In Equation (1), is the vector of remote sensor (accelerometer) signals and y is the sound pressure at one of the 60 microphone positions. The spectra of these signals are denoted by and Y:
The multiple coherence function, which is a frequency dependent real number between zero and one, is averaged twice. The first average is taken over the discrete frequency k leading to as given by Equation (1) and the second average is taken over the 60 microphone positions leading to . Roozen et al. ([15], Equation (5)) propose a global coherence function that could be used for the calculation of a weighted average of the 60 multiple coherence values. The proposed scaling of the coherence with the corresponding autospectrum of the output signal implies that microphone locations associated with a higher autospectrum have a larger impact on the average coherence value. This means that locations closer to the lining surface generally would have a stronger influence on the optimization outcome. Here, the virtual microphone locations are not optimized and all signals are treated equally.
The considered frequency bandwidth for Equation (1) is 50–500 Hz. The power spectral density (PSD) estimates , and are calculated with 79 spectral averages. A threshold value of is considered a reasonable compromise between system complexity and prediction quality. At least six accelerometers are required to reach this value. This conclusion was drawn from initial calculation of for different heuristically chosen sensor combinations. The best combination of six sensors out of 16 is found by combinatorics. The complete optimization run requires calculations of . The best combination of six accelerometers has an average mean coherence of compared to the worst combination with .
According to Equation (2), the observer filter is defined as the FRF matrix of the remote sensor signals as inputs and the microphone signals as outputs. Measurement data of the CROR load case are taken for the calculation:
For the multi-tonal noise reduction problem, the observer matrix is evaluated at the five frequency lines corresponding to the CROR frequencies. Alternative forms of having a diagonal structure or being a fully populated matrix are mentioned in Roure and Albarazzin [9].
The smart lining is equipped with two electrodynamic actuators of the type Visaton EX 45 S (10 W, , , 0.06 kg) at the locations indicated in Figure 2a. The actuators are attached to the cabin-side surface of the lining with double-sided adhesive tape. This setup is suitable for the laboratory CROR excitation with 113 dB SPL in front of the fuselage panel, but it is not powerful enough for a real CROR load case with sound pressure levels of 130 dB [16]. The FRF from the actuators to the microphones and the sound pressures at the microphone locations for the laboratory CROR load case are used to estimate the required actuator number for the real case.
Equation (3) provides the control voltage that is required to counteract the sound pressures at the microphone locations. The exclamation mark above the equal sign means that both sides should be equal:
The inverse Fourier transform of the control voltage spectrum containing the values from Equation (3) at the five CROR frequency lines yields the control voltage . The peak amplitude of is 0.924 V, which is far below the maximum value of 8.9 V. Taking a safety factor of two, the actuator stroke margin is dB and a maximum CROR pressure level of dB could be handled by the two actuators. A doubling of the actuator number from two to four provides additional 6 dB stroke and, hence, four Visaton EX 45 S (or similar) exciters are sufficient to ensure control authority for realistic CROR pressure levels of 130 dB. The locations of the two actuators are not optimized. However, an optimization study described in Misol and Algermissen [17] suggests that the chosen actuator locations are highly suitable. Due to the high damping of the structural parts and the coupled air cavity, the modal behavior of the system is weakly pronounced and the actuator optimization has a rather flat objective function. Another aspect which makes the performance of the smart lining less dependent on the actuator locations is that, unlike, for example, in Mazur et al. [18], the system is tuned to reduce the SPL locally in the acoustic near field instead of globally in the whole cavity. For the mentioned reasons, it is considered appropriate to position the actuators in a straightforward manner. A more elaborate actuator placement based on genetic optimization is described in [19]. Such an optimization could be used for the final implementation of a smart lining to maximise the performance for a given cabin layout.
2.3. Simulation
Figure 4 shows the scheme of the adaptive controller. The observer from Equation (2) is located in the upper left and the adaptive controller with least mean squares (LMS) algorithm in the lower left part. The right part of Figure 4 defines the output signals used for control performance evaluation. Estimated systems or signals are marked by a hat above their symbol to distinguish them from the true values. The simulation inputs , x and (blocks highlighted in green) are measured in the laboratory with the CROR load case applied. The vector contains the signals of the remote sensors (accelerometers). The reference signal is denoted by x. The vector contains the signals of 20 microphones measured at three distances from the lining (60 time series in total). The block transforms the input signal of dimension N into an output signal of dimension . In this block, the input signals are filtered through R parallel bandpass filters. The center frequencies of the pass-band of the bandpass filters correspond to the CROR frequencies. Here, with , the input dimension is multiplied by five. Each output element of the block is a complex tonal signal (phasor). Hence, the scalar x is transformed to the vector which contains the five complex reference signals and the vector is mapped to the vector containing five sub-vectors of the complex structural disturbances . Further details of the block are published in Misol ([6], Figure 6). The error signal vector is obtained from subtracting the estimated secondary pressure (anti-sound) signals from the measured disturbance pressure signals . This is true under the assumption that the estimated FRF matrix matches the true (unknown) FRF matrix . describes the full FRF matrix from all actuators to all 60 virtual microphones and describes the reduced FRF matrix from all actuators to the virtual error microphones. Furthermore, the actuator feedback on the remote sensors described by is assumed to be perfectly compensated inside the adaptive controller by an ideal plant model (feedback compensation). Therefore, the blocks describing this feedback effect are omitted in the control scheme. Thus, the simulation results described in the next section must be considered as an upper limit for the SPL reduction which is possible for the system under consideration. In reality, the performance of the controller will be compromised due to imperfect plant models. A robustness study based on plant uncertainties and variances is required to assess the implications of the idealizing assumption. Such a study is beyond the scope of this work and remains a future task.
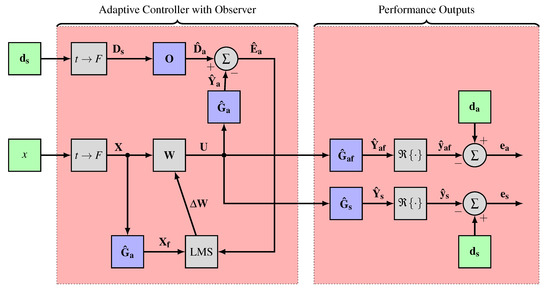
Figure 4.
Block diagram of the adaptive controller with observer filter and performance outputs.
The adaptive controller is implemented in the frequency domain. This is considered reasonable for a multi-tonal case. The applied complex filtered-x LMS algorithm is based on Johansson et al. [20]. In contrast to Johansson et al., the transformation of the input signals into the frequency domain is realized by the block as described above. By this kind of implementation, the signal delay associated with FFT analysis is avoided. This could be beneficial in case of non-stationary conditions as in climb or descent of an aircraft. It is beyond the scope of this paper to assess the benefits and drawbacks of the proposed method.
Each actuator is controlled by one complex filter weight per frequency which makes the implementation of the adaptive finite impulse response (FIR) filter very efficient. In the following, the time dependence is denoted by index n:
The adaptation of the weight vectors
is done using with and . contains the complex filter weights for harmonic r. Accordingly, the FRF matrix is split into five complex matrices . The cost function to be minimized is the sum of the squared estimated error signals . is the real part of a complex quantity.
3. Results and Discussion
The block diagram shown in Figure 4 is implemented in the MATLAB Simulink environment. The impact of the active control on the sound pressure in front of the lining and on the vibration of the lining is evaluated based on simulation results obtained with the implemented model. The sound pressure results are based on the acoustic residual , which is calculated from the measured acoustic disturbance and from the anti-sound from the active system . The vibration results are based on the vibratory residual that is calculated from the measured vibratory disturbance and from the actuator vibration feedback on the remote sensors (see Figure 4).
Figure 5 shows the SPL distribution in front of the lining evaluated on the two planes defined in Section 2.1. The y-axis is aligned with the longitudinal axis of the aircraft (in the laboratory it is rotated). The z-axis indicates the distance from the lining. In configuration 1, which is the uncontrolled case, the highest SPL occurs close to the lining surface at y-values from 0.4–0.7 m. In this y-range, the windows are located. The SPL decreases with increasing distances from the lining surface which is expected for an anechoic environment. In configuration 2, two virtual error microphones are placed in plane . This leads to strong SPL reductions close to the two microphone locations. Increased SPL are observed at locations further away from these so-called quiet zones. The mean SPL in plane is slightly reduced, whereas the mean SPL in plane is significantly increased. This behavior is expected for ANC systems with local error sensing schemes. It must be noted that configuration 2 realizes a square control system because it has two actuators and two error sensors. Therefore, the residual SPL at the two virtual microphone locations should vanish. Approximation errors in the block are responsible for the non-zero residual. These errors decrease with increasing sampling rates. In configuration 3, six virtual error microphones are placed in plane . The y-locations of these six microphones coincide with the y-locations of the maximum SPL in the uncontrolled case. Compared to configuration 2, the SPL reductions are less strong but more evenly distributed. In both planes, a reduction of the average SPL is achieved. In configuration 4, six additional virtual microphones are placed in plane at the same y- and z-locations as in configuration 3. This leads to a stronger SPL reduction in plane without compromising the control performance in plane . Finally, in configuration 5, virtual microphones are placed in all possible 60 locations. Compared to configuration 4, this leads to a further reduction of the mean SPL and a more homogeneous SPL distribution. It is concluded that a larger number of virtual microphones improves the homogeneity of the remaining sound field with regard to the SPL. This is mainly due to the higher harmonics and interaction tones of the CROR as can be seen in Figure 6. Increasing the number of error sensors is easily achieved for a remote sensing scheme because the number of physical sensors and the number of complex filter weights are not influenced. Only the row dimension of the observer and the actuator FRF matrix increase with the number of virtual sensors, which slightly increases the numerical computation effort of the real-time control system.
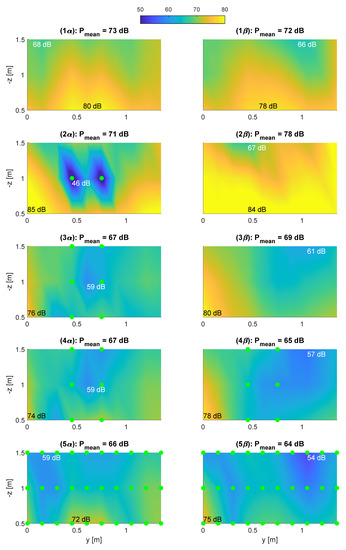
Figure 5.
SPL distribution in front of the lining evaluated on two planes and . Four different virtual microphone configurations (2–5) are compared to the uncontrolled case (1). The maximum, minimum and mean SPL are provided for each plot. The locations of the virtual error microphones are indicated by a green dot.
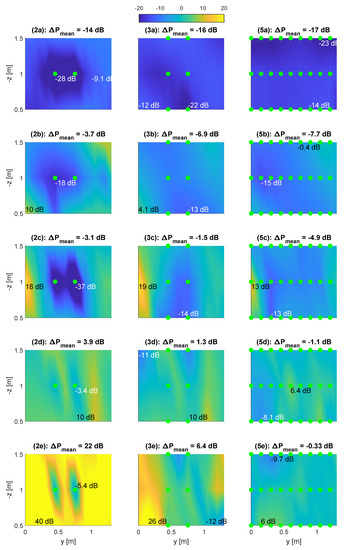
Figure 6.
Tonal SPL reduction in front of the lining averaged over two planes. The row designation (a) to (e) refers to the five CROR frequencies. Three different virtual microphone configurations (2, 3 and 5) are evaluated relative to the uncontrolled case (1). The maximum, minimum and mean SPL reductions are provided for each plot. The locations of the virtual error microphones are indicated by a green dot.
Figure 6 contrasts the tonal SPL reductions achieved by configurations 2, 3 and 5. For the sake of simplicity, the mean value of the SPL reductions in both planes is shown in each plot. The first row (a) of Figure 6 shows that the fundamental tone with the blade passing frequency 119.4 Hz is strongly suppressed in all three configurations. In configuration 2, the highest SPL reduction is achieved around the two virtual error microphones. As before, the mean SPL reduction is maximised for the maximum number of virtual error sensors. A similar behavior is observed for the second (149.2 HZ) and the third (268.6 Hz) frequency in rows two (b) and three (c). However, the mean SPL reductions are approximately 10 dB less than for the fundamental tone. A mean SPL reduction at the fourth (388 Hz) and fifth (417.9 Hz) frequency in rows four (d) and five (e) is only observed in configuration 5. All configurations achieve local SPL reductions with SPL increases elsewhere. A local error sensing scheme like in configuration 2 leads to strong tonal SPL increases up to 40 dB locally and 22 dB globally as can be seen in subfigure (2e). It is noted for configuration 2 that the strong local SPL reduction around the two virtual error microphones (quiet zones), which are located in plane , is less pronounced because the SPL reduction is averaged over both planes. From the results shown in Figure 5 and Figure 6, it is concluded that a local error sensing scheme is generally undesirable (apart from special localized application scenarios) because it leads to strong spatial variations of the SPL. Furthermore, as can be seen in Figure 7, the vibration levels of the lining structure increase for a local error sensing scheme.
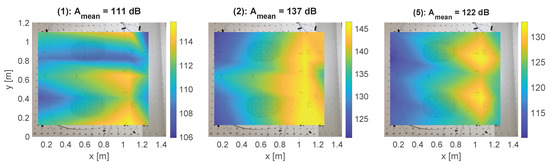
Figure 7.
Vibration level distribution on the lining surface. Two different virtual microphone configurations (2 and 5) are compared to the the uncontrolled case (1).
Table 1 lists the mean and the maximum reductions of the SPL for the investigated configurations. The assignment of the microphone numbers from column two of Table 1 to the microphone positions is possible with Figure 3. The two actuators indicated in Figure 2 are used in all configurations. The SPL values are calculated from the root mean square (rms) values of the virtual microphone signals. The mean/maximum SPL reduction equals the mean/maximum value of the difference between the SPL values of the uncontrolled and the controlled case.

Table 1.
Mean and maximum SPL reductions of the configurations averaged over all 60 microphones.
Figure 7 shows the vibration level distribution on the lining surface calculated from the signals of the sixteen accelerometers shown in Figure 2. It is noted that the vibration level of the window panes is not visualized correctly because the signals of the two corresponding sensors are not evaluated. However, it can be assumed that the vibration levels of the window panes are hardly changed due to the weak feedback of the actuators to the panes. A significant increase of the vibration levels is observed for both active control system configurations. The local error sensing scheme of configuration 2 leads to an increase in the mean vibration level by 26 dB and the global error sensing scheme of configuration 5 increases the mean vibration level by 11 dB. It is concluded that both configurations act as so-called active noise vibration control (ANVC) systems. In an ANVC system, the structure acts as a loudspeaker to produce anti-sound at the error sensor locations. The radiated sound power is not necessarily reduced in such a system which could be seen as a drawback. On the other hand, the ability of the ANVC system to simultaneously reduce the contribution of other vibrating interior parts to the SPL at the virtual error microphones can be considered an advantage. A combined structural and acoustic error sensing scheme could lead to a compromise between global sound power and local sound pressure reduction. The realization of such a scheme is beyond the scope of this work and remains a future task. Research work for an industry-compatible integration of the active components into the lining base structure is currently being carried out in the EU-project ACASIAS [21]. To test the performance of the smart lining under real aircraft conditions, flight tests in a propeller-driven aircraft are planned. Of special interest are the noise reduction performance and the robustness of the smart lining under varying temperature and pressure conditions. Initial robustness tests under variable temperature conditions in the laboratory will be done in the near future within the ACASIAS project.
Funding
The research work documented in this manuscript is part of the project Advanced Concepts for Aero-Structures with Integrated Antennas and Sensors (ACASIAS) funded by the European Union under Grant No. 723167.
Acknowledgments
The author gratefully acknowledges the support of Dietmar Völkle, Markus Klingseis, Florian Hesselbach and Alexander Rehmann from DIEHL Aviation Laupheim.
Conflicts of Interest
The author declares no conflict of interest.
References
- Elliott, S.J.; Nelson, P.A.; Stothers, I.M.; Boucher, C.C. In-flight experiments on the active control of propeller-induced cabin noise. J. Sound Vib. 1990, 140, 219–238. [Google Scholar] [CrossRef]
- Fuller, C.R.; Jones, J.D. Experiments on reduction of propeller induced interior noise by active control of cylinder vibration. J. Sound Vib. 1987, 112, 389–395. [Google Scholar] [CrossRef]
- Lyle, K.H.; Silcox, R.J. A Study of Active Trim Panels for Interior Noise Reduction in an Aircraft Fuselage; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1995. [Google Scholar] [CrossRef]
- Tran, B.N.; Mathur, G.P. Aircraft interior noise reduction tests using active trim panels. In Proceedings of the 1996 National Conference on Noise Control Engineering Noise-Con 96, Bellevue, Washington, USA, 29 September–2 October 1996; pp. 395–400. [Google Scholar]
- Misol, M.; Algermissen, S.; Rose, M.; Monner, H.P. Aircraft Lining Panels with Low-Cost Hardware for Active Noise Reduction. In Proceedings of the 2018 Joint Conference ACOUSTICS, Ustka, Poland, 11–14 September 2018. [Google Scholar] [CrossRef]
- Misol, M. Full-scale experiments on the reduction of propeller-induced aircraft interior noise with active trim panels. Appl. Acoust. 2020, 159, 107086. [Google Scholar] [CrossRef]
- Mazur, K.; Pawelczyk, M. Virtual Microphone Control for an Active Noise-Cancelling Casing. Active Noise and Vibration Control. In Solid State Phenomena; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2016; Volume 248, pp. 57–66. [Google Scholar] [CrossRef]
- Haase, T.; Unruh, O. Active Control of Counter-Rotating Open Rotor Interior Noise in a Dornier 728 Experimental Aircraft: Optimised Sensor Placement. Acta Acust. United Acust. 2016, 102, 361–372. [Google Scholar] [CrossRef]
- Roure, A.; Albarrazin, A. The remote microphone technique for active noise control. In Proceedings of the Active 99: The International Symposium on Active Control of Sound and Vibration, Fort Lauderdale, FL, USA, 2–4 December 1999; Douglas, S., Ed.; Volumes 1–2, pp. 1233–1244. [Google Scholar]
- Cheer, J.; Daley, S. Active structural acoustic control using the remote sensor method. J. Physics Conf. Ser. 2016, 744. [Google Scholar] [CrossRef]
- Misol, M. Active sidewall panels with remote microphone technique for aircraft interior noise reduction. In Proceedings of the 26th International Congress on Sound and Vibration, Canadian Acoustical Association, Montréal, QC, Canada, 7–11 July 2019; pp. 1–8. [Google Scholar]
- Algermissen, S.; Meyer, S.; Appel, C.; Monner, H.P. Experimental synthesis of sound pressure fields for active structural acoustic control testing. J. Intell. Mater. Syst. Struct. 2013. [Google Scholar] [CrossRef]
- Klabes, A.; Appel, C.; Herr, M.; Bouhaj, M. Fuselage Excitation During Cruise Flight Conditions: Measurement and Prediction of Pressure Point Spectra. In Proceedings of the AIAA Aviation, 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Stürmer, A.; Akkermans, R. Validation of Aerodynamic and Aeroacoustic Simulations of Contra-Rotating Open Rotors at Low-Speed Flight Conditions. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Roozen, N.B.; Leclere, Q.; Rychtáriková, M.; Glorieux, C. A global error estimator for the uncertainty of a multi-channel spectral analysis. Appl. Acoust. 2015, 87, 57–63. [Google Scholar] [CrossRef]
- Stürmer, A. DLR CROR & Propeller Noise Prediction: Numerical Approach Requirements & Limitations. In Proceedings of the 14th CEAS-ASC Workshop, Warsaw, Poland, 7–8 October 2010. [Google Scholar]
- Misol, M.; Algermissen, S. Remote Sensing for a Lining Integrated Active Structural Acoustic Control System. In European Conference on Multifunctional Structures (EMuS); Martinez, X., Schippers, H., Eds.; International Centre for Numerical Methods in Engineering (CIMNE): Barcelona, Spain, 11–12 June 2019; pp. 24–29. [Google Scholar]
- Mazur, K.; Wrona, S.; Pawelczyk, M. Performance evaluation of active noise control for a real device casing. Appl. Sci. 2020, 10, 377. [Google Scholar] [CrossRef]
- Misol, M.; Haase, T.; Algermissen, S.; Papantoni, V.; Monner, H.P. Lärmreduktion in Flugzeugen mit aktiven Linings. In Proceedings of the Smarte Strukturen und Systeme—Tagungsband des 4SMARTS-Symposiums, Braunschweig, Germany, 21–22 June 2017; pp. 329–339. [Google Scholar]
- Johansson, S.; Sjösten, P.; Nordebo, S.; Claesson, I. Comparison of multiple-and single-reference MIMO active noise control approaches using data measured in a Dornier 328 aircraft. Int. J. Acoust. Vib. 2000, 5, 77–88. [Google Scholar]
- Advanced Concepts for Aero-Structures with Integrated Antennas and Sensors (ACASIAS). Available online: http://www.acasias-project.eu/ (accessed on 9 September 2020).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).