Abstract
The penetration to geological shield occurs in many situations at various velocities and scales, for example, meteor-cratering, pile driving, falling of objects from high-rise building construction, and debris/fragments from failed components. The soil media is an efficient energy dissipation system and effective shock protection shield. Impact circumstances are currently getting widespread attention. A lot of research has been done on soil media for impact and penetration. The phenomenon of dynamic penetration in heterogeneous particulate soil medium is very complex and the target soil media under dynamic impact especially under high speed and deep penetration neither behave completely as solid nor as liquid. The topics of recent research interest in the field of penetration to soil media and their significant findings are critically reviewed in the present study. The dedicated review of analytical, empirical, experimental, and computational methods to predict the response of soils media-impacting objects to penetration is presented. The emerging challenges in fundamental research of penetration into soil media are outlined and it is an attempt to formulate the future research directions in the field of soil media penetration.
1. Introduction
Projectile penetration in soil media occurs in various circumstances at different velocities and scales, such as meteor-cratering [1], pile driving and dropping artifacts from high-rise building construction [2], debris/fragments from collapsed parts of construction [3], the digging of mining machineries [4], locomotion of legged robots over rough terrain [5], and raindrop impact to the soil surface [6]. The soil media can also be utilized as an efficient energy dissipation system [7]. The behavior of individual particles of granular materials under projectile impact such as translation, rotation and particle crushing, and collective behavior of granular material as well as dilation, rearrangement, formation of buckling of force chain, and strain localization are affected by the scale of impact-penetration study [8]. The basic problem of soil media response, which is subject to dynamic loading, and particularly to projectile effect, is a complex mechanical behavior i.e., behavior as solid-like or liquid-like materials, under different impact state conditions [9] and has long since been examined. The granular bed, having particles with density like projectile material, behaves like a solid material when impacted by projectiles at low initial velocity and resists the penetration of the projectile. However, when the projectile collides with the granular bed at a high impact velocity or even when the impact velocity is negligible but the density of the projectile material is much higher than that of the particles in the granular bed, the bed would behave like a liquid and the projectile can penetrate into the granular bed, similar to the penetration into a viscous liquid [10]. During the impact, several different mechanical phenomena can occur. Tension and shear failure, localized deformation, effects of adiabatic shear, and crack propagation are only some of the important phenomena that may occur individually or simultaneously. For many years, investigators have been trying to measure critical characteristics of impacts or penetrations on targets, like strain history, deflections, and forces occurring during impact, in the hope of validating existing or proposed theories of impact. Iskander et al. [11] and Omidvar et al. [12] proposed a state-of-the-art review on granular material under low and high velocity impact penetration. The review addressed the effects of soil and penetrator properties on the penetration process, especially on deep penetration. Backman and Goldsmith [13] identified terminal ballistics aspects and addressed penetration mechanics for various types of penetrators and targets media. Different physical mechanisms of deformation such as elastic, plastic, and thermal behaviors, as well as a decrease in compressibility, can be anticipated in the impact-penetration processes [14]. A number of researcher have dedicated their work to study the process of projectile penetration into different material targets, such as for soil [15], rocks [16], concrete [17], glass [18] aluminum [19], steel [20], multi-layered fabric composite plates [21], high-density polyethylene honeycomb protection structure [22], and thermal protection material [23], among many other materials. A comparative study of the penetration process in homogenous material will help to develop a suitable method to study the heterogeneous materials penetration process.
Projectile Penetration Process Parameters
The penetration process of projectile and soil target are classified into three groups, namely, non-penetrating projectile (impact of soft projectile into solid rocks), penetrating projectile (rigid projectile penetration into the softer soil by shearing, pulverizing, and compressing), and impact in water (penetration in highly saturated alluvial soils under effect of incompressibility of soil and the viscosity of water). The impacting objects on target media may be of free falling or rigid projectiles type. Target media may be naturally occurring media such as a geological shield or manufactured media such as concrete/metal shield. The static and kinematic properties of projectiles are characterized by the shape of tip, diameter of shank (D), and length (L) and velocity (v) of projectiles, which is classified as hypervelocity (v > 3 km/s), ultra-ordnance (1.5 < v < 3 km/s), ordnance (500 < v < 1500 m/s), and sub-ordnance (v < 500 m/s). They also defined the target materials and thicknesses of the target (h) as thin (h/D < 1), intermediate (1 < h/D < 10), and semi-infinite (h/D > 10) [13]. The mechanisms of penetration resistance are dependent on interactive characteristics of impacting objects and target media such as particle size of soil media [24], bulk packing fraction [25], penetration depth [17], intruder shape [2], and penetration velocity [26]. An enormous number of studies on projectile penetration area have been published in last 50 years dealing with different process parameters such as different target materials, various geometry and velocity of impacting objects, and different investigation procedures. Though many researchers have devoted their work to summarize the projectile penetration studies in general, dedicated reviews of recent publication dealing with projectile penetration into soil media are scarce. An extensive and dedicated literature survey for the response of soils media to penetration, categorizing the applied methodologies into the analytical, computational, and experimental methods, have been presented in the following paragraph. This review studies would provide updates on current and future research directions in the field of soil media penetration.
2. Analytical Methods
2.1. Classification of Methods
The authors have proposed several analytical models over the years to describe the process of penetration mechanism of impacting objects on target media with suitability to material, impact velocity, and geometric properties of both the impacting objects and target media [27]. Analytical models collect insight into the phenomenon and penetration mechanics and provide tools for design studies, optimization, and risk analysis in the impact of object–target media interactions. The execution of analytical models is faster than other approaches, namely, numerical or experimental methods. Omidvar et al. [12] presents the research summary of the analytical method applied to predict the response of granular media to projectile impact at the meso-scale and macro-scale. They outlined the research areas in the granular target media such as effect of saturation in soil media, role of particle crushing in impact energy dissipation, and rate of strain rate, that need further attention. The various proposed physics-based analytical approaches to analyze the response of targets to impacting objects are internal friction theory and cavity expansion theory (CET)-based models [28], model of orthogonal layers or discs [29], Poncelet Model [30], hydrodynamic and modified hydrodynamic-theory-based models [31], conservation of energy and momentum models [32,33], Tate–Alekseevskii model [34,35], dynamic plasticity and Ravid–Bodner models [36], and the Walker–Anderson model [37]. Many of the above-mentioned analytical models are applied to predict the impact penetration of ductile and homogenous targets with specific penetration problem and may be extended to study the projectile penetration process in soil media and non-homogenous media by developing them into a versatile model of projectile penetration of soil targets. The summary of underlying mathematical equations presenting the theoretical background of the analytical method is given in Appendix A. The analytical methods developed so far are basically based on “Newton’s second law of motion or conservation of momentum” to study projectile-penetration and have validity over a wide range of projectile velocity. The analytical method developed on the law of conservation of energy has limited applicability because energy dissipation changes with impact velocity [38]. The cavity expansion theory-based formulation is used for studying low, and low to high transition velocity impact problems (3 km/s > v > 0.3 km/s) [Yu 2013], the Tate–Alekseevskii formulation is used for studying medium velocity impact problems (v~3 km/s) [35], and the fluid-dynamics formulation is used for studying high velocity impact problems (v > 3 km/s) [31]. The categorization of impact penetration processes based on the physical mechanisms that describe the nature of the penetration process are elastic, plastic, and thermal behaviors, as well as a reduced compressibility [14]. The resistive force or resistance function of a rigid projectile to penetration in a projectile-penetration process has three components, namely, dissipative, static, and dynamic components. The first component has a negligible effect on resistive force for granular media [32]. The static aspect of resistance force depends on penetration depth. The dynamic component depends on the projectile’s velocity in the direction of penetration, cross-sectional area, and soil density. However, the first principle theory for explaining the role of granular resistance, i.e., predicting granular media’s rheological response, is still a challenge, mainly on the edge of solid–liquid-like transition [39] at high-velocity impact. To calculate resistive force, stress at the impactor nose must be integrated over the applicable area incorporating yield criterion in terms of yield stress, projectile geometry, and the velocity in direction of impact. Sabetamal et al. [40] found that the effects of strain rates and remolding on the shear strength of the soil could not be considered for predicting the soil behavior of cohesive soil using the modified cam-clay (MCC) model. O’Loughlin et al. [15] has found that the frictional bearing resistance is augmented during high-velocity penetration due to the combination of high strain rates and negative excess pore pressures. This is the most critical aspect to be implemented in modelling tools as mechanism by which the frictional bearing resistance contributes to the total penetration resistance is not well understood.
The cavity expansion theory (CET) model was developed for improvement over previous models, with the assumption that when an impactor penetrates the target medium it creates a cavity, which give rise to the stresses on the neighborhood of the cavity. The developed stress in vicinity of cavity depends on constitutive model of target media representing various characteristics such as compression, shear, dilation, fracture, and other relevant properties. This cavity expands under the action of stresses generated into the target medium. The CET models for the projectile-penetration process completely describe the instantaneous local interaction between a target material and a projectile [28,41,42,43]. The model proposes a relation between expansion of a cavity and projectile penetration in target material. CET model can be used to describe completely the projectile-penetration process, such as depth of penetration, deceleration-time history of projectile, time histories of velocity, stresses in the target material, stress variation with depth and radial distance, and forces at the projectile nose [44,45]. The cavity expansion theory models are classified into three types based on description of cavity surface dynamics. Static (or sometimes called “quasi-static”) models describe the stresses on a cavity’s surface in static state. “Quasi-dynamic models” evaluate cavity surface stresses because of the constant rate of increase in cavity radius. Dynamic models consider cavity surface acceleration. An extensive survey of the research on penetration cavity expansion theory is summarized in the monograph of Yu [28]. Yankelevsky and Adin [41] proposed a model of dynamic cylindrical cavity expansion (CCE) that assumes cavity expansion results in the formation of cracked, elastic, and comminuted response regions. In the CCE dynamic model, vertical penetration of a slender body of revolution (using cylindrical coordinates) is typically considered, and it is presumed that particles of the target material travel in the radial direction during projectile penetration. The target material is treated as a series of independent thin layers, and the cavity expansion induced by moving projectiles is modelled in each layer. This method enables the measurement of stress at the boundary of the hole in each layer and, thereby, the force acting on the projectile at every location on the projectile’s lateral surface. The theory model of “spherical cavity expansion (SCE)” is commonly used in quasi-dynamic projectile–target interactions when a spherically symmetrical cavity expansion from a zero initial radius is at continuous velocity. The expansion cavity problem of penetration considering spherical symmetry conditions in compressible material under dynamic conditions divides the target material into three regions: Undisturbed, elastic, and elasto-plastic. The response of target material into different behavior regions is depicted in Figure 1. The boundary conditions for this model are radial stress continuity and plastic yield at the elastic/plastic interface and continuous speed at the cavity wall. Guo et al. [42] compared the Forrestal model with the cylindrical cavity expansion penetration model [43] and concluded that gap between the prediction of these two models is minimal for impact velocity below 100 m/s and the discrepancy increases with the increase in impact velocities. Heuzé [16] concluded from the review of analytical and numerical method that CET give higher contact stresses on the projectiles than finite element models because of kinematic constraints, and lack of surface weakening of the soil media.
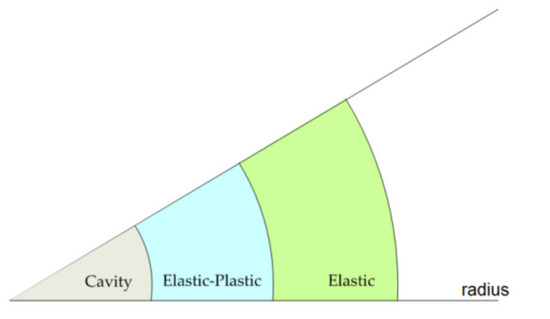
Figure 1.
Description of soil behavior regions during cavity expansion.
2.2. Granular Target Media
The one the important and most researched soil media in impact penetration is granular or non-cohesive materials. The granular material behavior is quite different than the other penetrating soil materials. The strength and stiffness of granular material is dependent on scale, confining pressure, and fluid pressure within the void spaces. These materials are characterized by rigid plastic deformation and dilatancy during shear loading. The loading behavior of granular material depends on loading history and initial arrangement of the particles. The densification of granular system during the penetration process is incorporated in analytical model densification by adjusting the density or locking density in terms of volumetric strain, which depends on initial (bulk) target density and locked density or maximum elastic density. Length scale of penetration problem in granular media is selected based on whether to resolve the bulk and grain scale behaviors of penetration process. An extensive review of impact mechanics of granular material is due to Bless et al. [46]. Kang et al. [47] developed a predictive model for the process of penetration under quasi-static conditions using macroscopic laws or Archimedes’ drag force theory, defining the drag force as a hybrid of viscous force and hydrostatic-like force. The viscous force emerges from the transfer of momentum between the grains and is proportional to the square of the projectile’s instantaneous speed with reference to the granular medium. The hydrostatic-like force stems from the frictional plasticity of the granular matter and relies on the depth of the penetration. The thermal effect on projectile drag force during impact in granular medium is evaluated by Seguin and Gondret [48]. Galanov et al. [18] presents an analytical approach-based analysis of the influence of the basic properties of target (brittle materials) and geometrical factors of target and projectile, on formation of penetration resistance. Alekseevskii [35] proposed a steady-state hydrodynamic theory for analysis of penetration process including the effects of the projectile and target material strengths. The analytical models are also developed to predict depth of penetration as a function of impact velocity, soil moisture, and essential geometric and material properties of projectiles. Khan [49] has carried out investigation of projectiles penetration phenomenon in non-cohesive soil (Sand) and non-cohesive targets under dry, saturated, and compacted conditions. The results for soil (Sand) targets under dry, saturated, and compacted conditions with conical nose projectile penetration are depicted in Figure 2. The saturated condition of soil media reduces the projectile penetration depth. The error in the prediction of penetration depth for the projectiles of different nose shapes in different soil targets using the proposed analytical models lie within 10% when compared with experimental results. In shallow penetration, the granular medium dissipates much of its energy in the initial phase of penetration, while in deep penetration, the compression and shear of the granular medium result in energy dissipation [50]. The absorption of energy in the shear is primarily due to friction and volume changes as the grains slip, roll, and climb over each other. The kinetic energy of impactor transferred to target during the penetration process is dissipated in form of tearing energy of strips or layers, total energy in soil volume change, frictional energy, motion energy of target media, and thermal energy. A projectile’s infinite penetration into light-weighted “expanded polystyrene particles (EPP)” is detected when the projectile’s weight exceeds a critical value. The role of initial velocity with various impact velocities in infinite penetration into a light granular material consist of EPP particles media is investigate by Huang et al. [50].
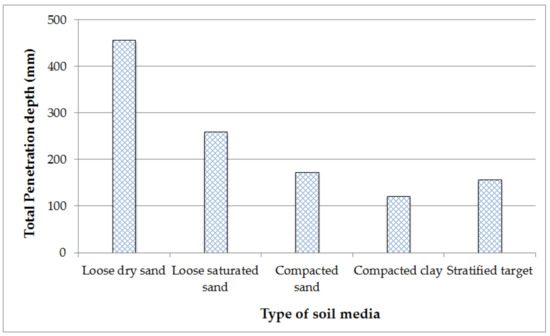
Figure 2.
Penetration depth of conical nose projectile in dry, saturated, and compacted soil targets.
In granular material, pore collapse, grain fracture, and the formation of force chains are some of the significant phenomena regulating sand behavior at grain scale, and dynamic target-projectile interactions on a bulk scale are further challenging. The penetration performance of granular materials at large scales is quite different. The issues of performance of dynamic impact in granular materials are investigated by Singh et al. [51], Huang et al. [52], and Vinutha and Sastry [53] for shear banding, sinking effect, and the jamming transition, respectively. Voorene et al. [54] “provides a simple analytical model for fundamental understanding of the development and transmission of dynamic force chains and the motion and fracture of individual sand grains as projectile moves”. The researchers have also paid attention to improve the existing cavity expansion approaches for target granular material behavior prediction capacity. The improved sand media behavior is obtained by Macek and Duffey [55] by employing finite spherical cavity expansion analysis studying the expansion of finite radii cavity. They adopted a “spherical cavity expansion forcing function” based on a finite-sized cavity to compensate for the near-surface effects of geological media penetration. Jiang and Sun [56] employ a constitutive model that considers the role of grains fracture to obtain improved behavior target under impact. The better prediction of the sand under complex shape projectile impact is obtained by Kotov et al. [57] by incorporating the local projectile–target interaction assuming each element of the projectile interacts independently in the sand media.
2.3. Projectile Non-Normal Impact and Stability
The obliquity of projectile and final penetration depth in target media affects the response of projectile penetration process. The obliquity introduces a non-axisymmetric resistance on the projectile surface. Non-normal impact is defined by “angle of attack” (AoA) and angle of obliquity. The angle of obliquity is the angle of the velocity vector and the vertical to the target surface, while AoA is the angle between instantaneous velocity vector and projectile axis of symmetry. A projectile can strike a target with oblique, pitch, and/or yaw angles and previous studies on the projectile trajectory in the soil target demonstrate that the projectile trajectory with an initial oblique angle could become curvilinear and could even travel towards the target surface [58]. The definitions of non-normal impact penetration are graphically shown in Figure 3. The study of non-normal penetration using the simplified analytical model of penetration with lateral loading (SAMPLL), which employs empirically based algorithms to treat the lateral loads resulting from angle of attack and trajectory angle of the projectile, is carried out by Young [59]. Ricochet phenomenon, associated with shallow penetration, occurs when the projectile’s final velocity vector is directed away from the target and there is a threshold angle of impact, critical impact angle, above which ricochet cannot occur. Ricochet takes place in three stages, i.e., the entry phase, plough phase, and exit phase, and is affected by geometry, obliquity angle, impact velocity, mass, and target properties [60]. The critical impact angles for aluminum and lead spheres striking sand media, predicted by analytical and experimental procedures, are 23 and 52°, respectively. Wen [61] developed the analytical models for the penetration of targets vertically struck by projectiles using the formulation that assumes the average resistance of the target material consisting of cohesive static resistive pressure resulting from the elastic-plastic deformation of the target materials and the dynamic resistive pressure resulting from the speed effects. Comprehensive information on non-normal effects is limited, generally as it involves additional parameters that go beyond those essential for vertical impacts. Goldsmith [62] has summarized the research work on analytical modelling of non-ideal projectile impact on various targets. The effect of projectile trajectory and yaw angle on penetration in soil target studied by Goldsmith [62] is portrayed in Figure 4. Under certain circumstances, free surface effects may become important, such as long-rod projectile penetration, brittle target medium, large oblique angles of impact, and shallow penetration [63]. The analysis of general penetration dynamics problem including the non-normal penetration is carried out by Ben-Dor et al. [64] considering the impact penetration as an inverse problem using semi-empirical relations that employ the dependencies between the initial velocity and the depth of penetration. The deep penetration study of hard projectile in soil target by Gao and Li [65] concluded that the trajectory instability occurs at critical impact velocity, and the projectile trajectory returns to a straight line (linear motion) from the curvilinear motion near the characteristic convergent velocity. The trajectory instability and convergence of the curvilinear motion of projectile is driven by increase in impact velocity, projectile geometry, uniformity of grain size distribution within the soil mass, increase in grain size and porosity, and other striking parameters [66]. Analytical model for rigid projectile dynamics is proposed by Simonov and Osipenko [67] to analyze the trajectory and stability of the projectile during deep penetration in an elasto-plastic medium. A “differential area force law (DAFL)”-based analytical method, proposed by the AVCO Corporation [16] in which the projectile surface resistance is written as a quadratic function of velocity, is most effective in studying the projectile’s curvilinear motion and stability during non-deformable projectile deep penetration into hard soil media [65].
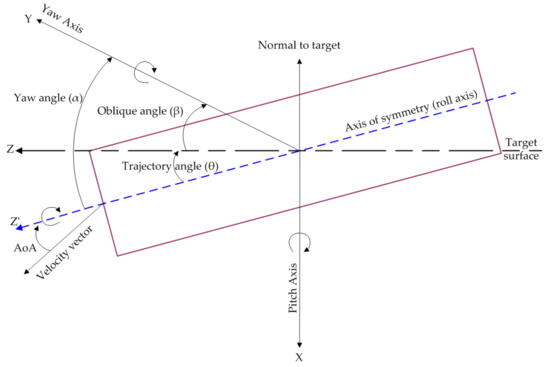
Figure 3.
Definition of angle of attack (AoA), oblique angle, yaw angle, and trajectory angle.
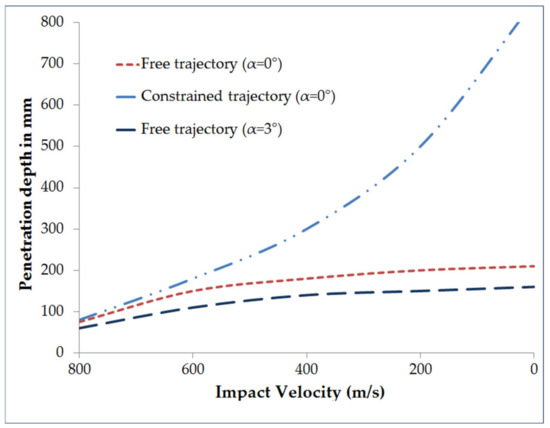
Figure 4.
Variation of penetration depth with projectile impact velocity in cohesionless soil, projectile trajectory (with and without rotation of projectile), and yaw angle (α).
2.4. Multi-Stage and Multi-layers Penetration Modelling
For better physical representation of soil-penetrator interaction, Yankelevisky [29] developed a model of orthogonal layers or discs as an update of the cylindrical cavity expansion approach by representing the soil medium by soil discs or independent layers of small thickness (Figure 5). The so-called disc models or method of plane sections deliver more improved results over the previous models results because existing models are established on simple mechanisms that do not properly represent the penetration phenomenon and the interaction between the surrounding soil and the projectile. However, the stress field precedes the penetration front, thus, the next layer will affect the rate of penetration. “Highly plastic volumetric deformations in the projectile nose vicinity are the principal mechanism that governs the penetration phenomenon”. The model is particularly useful to study the effect of projectile nose shape with projectile velocity. The disc models or model of orthogonal layers have not been further investigated by the researchers. The spherically symmetric cavity in granular media formed in response to the penetration of the projectile, from zero initial radius at constant low velocity, is assumed by Forrestal and Tzou [44] to have three regions, namely cracked, plastic, and elastic. However, with the increase of velocity, the cracked region will gradually reduce and finally diminish, leaving only the plastic and elastic regions. They proposed separate mechanical properties and constitutive models for elastic-plastic and elastic-cracked-plastic region responses. The elastoplastic field dynamic expansion of a pressurized spherical cavity is due to Forrestal and Luk [68] and Masri and Durban [69] for the compressible Mises solid.
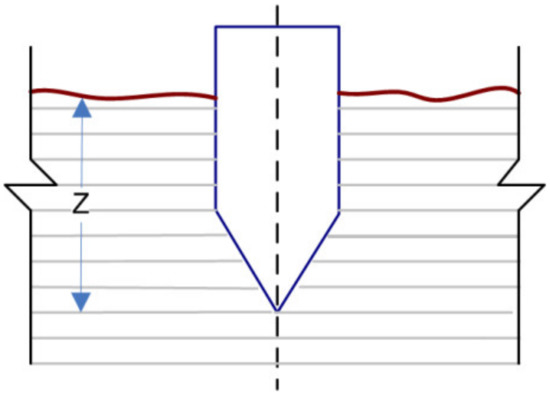
Figure 5.
Model of Orthogonal Layers or Discs.
The researchers basically adopted material strength models as Mohr, Tresca, Mohr-Coulomb, or combined Tresca and Mohr-Coulomb yield criterion for heterogeneous materials. Ravid and Bodner [36,70] introduce multi-stage penetration/perforation models as the major advance in impact penetration using analytical methods. They proposed five stages of penetration/perforation for a rigid projectile for ductile thin materials target, but the penetration model can be extended to semi-infinite soil media by considering three-stage penetrations, namely, near-surface penetration of projectile, bulge formation in target, and final penetration depth. “The penetration stage continues till the plastic flow field reaches the rear of the target, at which point a spherical bulge begins to form, the uplifting of target material at the surface stops, and all target movement is in the direction of penetration”. Radially, away from the projectile, there is a transition from downward movement to horizontal movement. Once the projectile passes a given depth, the target continues to move downward, as momentum is shifted to the target. The target geometry in final stage is identified by the plastic flow in compressibility condition. A two-stage process for projectile-penetration process, cratering stage, and tunneling stage, as shown in Figure 6, is proposed by Frew et al. [71] to analyze the impact response on hard target media. The cratering stage is usually approximately twice the depth of the projectile and the tunneling stage is approximately one projectile diameter in depth. Orphal [72] has viewed the impact penetration process as a two-stage process, transient state and quasi-steady state. The dynamics of the transient phase includes the initial impact with shallow penetration and is characterized by transient projectile-to-target interaction as crater is developed. In the second stage, i.e., “quasi-steady state, the force on the impactor varies fairly gradually over time, and at the end of the penetration there are new transient effects associated with the stopping of the projectile, that may include transition from dynamic to static friction, inertia effects attributed to target motion, and the target ‘s elastic rebound”. For several applications of projectile penetration for granular material, the first or second stage governs, depending on the impact speed [73]. Siddiqui and Abbas [74] devoted their work to improve the existing analytical models for the prediction of deceleration time history, penetration depth, and forces on different shape projectiles impacting geomaterial targets. They noticed proximity in the results with the experimental values.
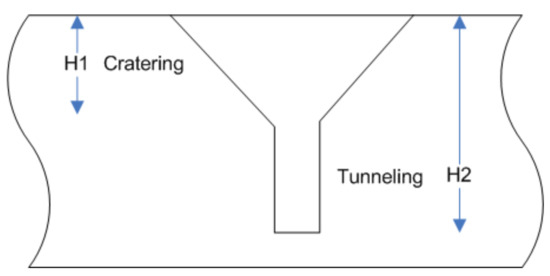
Figure 6.
Two-stage penetration model.
3. Computational Methods
Substantial advances in computing resources and numerical modeling capabilities require the implementation of complex numerical approximations to govern analytical models of penetration mechanics. Numerical approaches have many benefits over analytical methods and empirical methods based on experimental tests. The numerical methods are most suitable to model the frictional effect, influence of inhomogeneity on projectile instability, and target erosion during the penetration, which is not possible to incorporate in analytical methods [75]. The numerical simulation could offer the detailed description of the entire penetration process from all aspects and are cost effective. However, the accuracy of numerical solution depends on analytical models of inherent behavior and associated numerical approximations of penetration problem. This necessitates the development of in-situ experimental techniques to not only improve our observed understanding, but also to validate the simulated solutions. The experimental methods or even analytical methods quantify projectile velocity, stress, final penetration depth into the target, and the final target/projectile deformation [76]. Of these, only the stress may be measured with any temporal resolution given normally used methods, and none yield any information about target material behavior during the process beyond general bulk results. The numerical methods can predict the particle response along with the bulk response of the target. The numerical models can simulate the “non-uniform distribution of grains, material strength including strain hardening with time and temperature-independent properties” [77], mesoscale interactions, spall, phase change, void collapse, grain failure, and mode of contact building on the basic Hertzian philosophy, exploring different descriptions of penetration [77,78]. As a continuum modeling of the phase of projectile penetration in the soil target, numerical methods readily analyze complex target and projectile geometries, i.e., multi-layered materials, obliquity, by treating the soil media as a single component bulk material, where the removal of soil porosity is controlled by an additional constitutive relationship such as the P-α [79], P-λ [80], or P-ε [81] model. Borg et al. [82] and Bazhenov et al. [83] discusses many computational simulations of penetration mechanism and works with utilizing computer software to model penetration and other related behavior of soil media. Numerical modeling such as the use of constitutive granular media models are defined as a continuum, and particle methods are used to model granular media at the mesoscale. “Continuum constitutive models” can be computationally efficient compared to mesoscale particle models. However, experimental tests are typically needed to calibrate parameters of the constituent model. Mesoscale models are usually computationally expensive using particle methods. Owing to major developments in computational powers in recent years, mesoscale models are increasingly being used as an alternative to experimental tests.
The past investigators used three types of numerical methods to perform penetration analysis of missiles into geological targets, namely “Finite Differences method (FDM), Finite Elements method (FEM), and Discrete Elements method (DEM)”. The application of Finite Element Method to simulate the penetration in soil media is due to Paik et al. [84] and Ko et al. [85]. The Finite element simulation of ball drop test along with experimental study for clay material is presented by Rahbek [86]. The impact of the steel ball with the clay was monitored with a high-speed camera to study steel ball–clay interaction. The simulations showed that linear yield stress curve model was not adequate to model the penetration dynamics of clay and showed too-heavy oscillations after impact in the simulations with this model. The simulations results reproduced the experimental results satisfactorily with the visco-plastic material model with a damping term introduced. The arbitrary Lagrangian–Eulerian (ALE) method-based finite element solution of dynamic penetration of large deformation problems in inhomogeneous clay layers media is carried out by Carter and Mazen [87]. The rate-dependent non-linear soil behavior with moving boundaries and contacts are implemented in the solution approach. The differential area force law (DAFL) approach-based 2-D and 3-D software is developed by Danielson and Adley [88] to simulate the motion of a projectile penetrating into a solid target.
Cundall and Strack [89] developed discrete modeling of the penetration of granular matter. The discrete modelling identifies the energy dissipating mechanisms of particle-penetrator friction, inter-particle friction, as well as collisional energy dissipation during penetration [90] and allows to simulate the behavior of several penetration conditions in granular media [91]. Discrete particle modelling (DPM) typically disregards physical phenomena such as particle crushing and granular media thermal effects. While numerical modeling depending on a discrete element approach is increasingly applied in penetration analysis, it needs extensive material parameters at large strain, high strain-rates, high temperature, and high pressure. Immense resources are required for these parameters, and considerable uncertainties are inevitable. Using a simple analytical model is a viable alternative to these analyses at a fraction of experimental and computational expenses. Holmen et al. [92] presented numerical simulations of low-velocity sand penetration using the discrete particle method (DPM). The DPM was implemented in IMPETUS Afea Solver [93], a commercially explicit nonlinear finite element code. The key advantages of proposed DPM are lower computation costs because the approach neglects the rotational degrees of freedom and can be applied to considerably large-scale technical issues, robust contact formulation, and coupling for nonlinear finite element solver. The simulation results are validated by the experimental results of dropped-object-rig tests at low impact velocities for resisting force of the sand and final penetration depth in the sand. Numerical simulations are generally able to explain the sand’s behavior during penetration. The predicted peak forces in numerical study are underestimated while the predicted penetration depths are slightly overestimated. The experimental results showed that the resistance force–penetration–depth curves are very sensitive to the shape of the projectile nose. Børvik et al. [94] showed that the particle diameters to be used in the discrete modelling of granular matter should be marginally larger than the median grain diameter in the real sand for good results. The physical properties and mechanical performance of soils, especially when loading is dynamic, are affected by water saturation (or water content) due to a complex interaction between pore water and pore air, solid grains, and the diameter and shape of a crater created by a rigid spherical impactor with a given impact velocity, and diameter depends largely on water saturation [95].
Hybrid and Coupled Numerical Methods
The hybrid methods are developed to take advantage of and overcome the shortcoming of the individual methods. The numerical simulation of the high-speed projectile penetrating soil target event using the “Finite Element Method-Smoothed Particle Hydrodynamic Method (FEM-SPH)” coupled algorithm is proposed by Yang et al. [96]. They observed that the “FEM-SPH algorithm” not only overcomes the defect of smooth particle tensile instability, but also overcomes the problem of low computational efficiency of the finite element method and can naturally simulate large deformation problems such as super-high-speed projectile–soil collision. The accuracy of the coupled FEM-SPH method depends on the algorithm suitable to the numerical calculation of the dynamic numerical calculation. The DAFL and semi-empirical resistance function-based formulation is applied via Finite Element Code ABACUS by Li and Flores-Johnson [97] to predict the projectile trajectory under different oblique and yaw angles in the soil medium. They found that the projectile’s relative mass center location had a strong influence on the projectile’s rotation control. Fang et al. [98] developed the analytical method, which implements DAFL and semi-empirical resistance function in ABAQUS explicit solver, for predictions of projectile penetration and perforation. The solution of a dynamically expanding spherical cavity in a finite sphere of incompressible “Mohr-Coulomb target material” accounts for variations in target resistance acting on the projectile’s top and bottom sides due to the free surface impact. The numerical predictions are in good agreement with the normal and oblique penetration/perforation. “Abelev et al. [99,100] investigated the penetration behavior of the STING penetrometer numerically through the use of finite element and finite difference approaches. Shear strength is derived from the numerical experiments using cone factors and by application of a strain-rate correction [100]”. A three-dimensional finite element investigation of penetration into targets consisted of concrete layer and its semi-infinite foundation is due to Yongxiang and Shunshan [101]. They reached the conclusion that the penetration depth, the residual velocity, and the projectile deceleration amplitude increases with the projectile’s initial velocity. “Three-dimensional dynamic FEM and DEM simulations” of behaviors of penetration into granular target is performed by Ogawa et al. [102] considering the impact of cylindrical projectiles on randomly distributed identical spheres. They noticed that this highly densified area was created just before the projectile and began to spherically propagate at a much higher speed than that of the projectile leaving a fairly rare area. Mechanical impedance of projectile and the mechanical properties of target materials play a predominant role on dynamic penetration phenomena.
Flores-Johnson et al. [103] simulates the dynamic behavior of partially saturated sand under low-velocity impact loading by the hybrid approach using discrete element method (DEM) and the finite element method (FEM). The influence of capillary forces on the dynamic behavior of sand under high-pressure loading conditions is integrated in the simulation based on the capillary bridge model [104]. Experiments are also performed to examine the effect of water saturation on the height and shape of sand piles after impact, and to validate simulations. The simulations obtained experimental patterns of ejecta and height of the sand pile. They found that increasing water saturation (between 10 and 30 per cent) had an impact on the height of the sand pile at a drop height due to an increase in the cohesion between the particles. Mechanics of projectile penetration requires proper modelling and specifying constitutive equations for complex target materials, for example the heterogenous material soil. Thus, many models have been developed for the modelling of soil targets [105,106], and analyses involving experimental evaluation of undefined coefficients in standard equations of motion, or development of empirical equations for different soil types from experimental data are carried out [107,108]. Teland and Moxnes [109] have carried out a comparative study of numerical simulations results to analytical model results for projectiles impacting into soil media.
4. Experimental Methods
Considerable progress has been made in impact experimental studies of geological shield. With the emergence of new in-situ experimental measuring techniques, highly determined quantitative observations of dynamic events can be made within soil media. However, the impact experimental procedures are complex and costly in nature. The analytical and numerical solution approaches are needed as a supplement to high-precision testing of penetration process. The influence of the basic properties of target materials, velocity of projectiles, and geometrical factors of targets and projectiles, on the formation of penetration resistance, has been assessed in experiments and various empirical methods to formulate the resistance against penetration relations that have been developed. Empirical methods are mostly used when the penetration depth and terminal parameters are intended during the penetration process and when the penetrator is assumed to be a rigid body. Nonetheless, the analytical methods are restricted to a specific range of velocity because they are based on curve fitting data and most of them are unit-dependent and constrained by the validity scale, only appropriate within the set of tests from which the data are acquired. Additionally, the response of the particle based on empirical methods is distinct from the bulk response of the projectile-soil impact process, and the bulk response may have an impact on the response of the particle due to low-speed impact. A projectile can impact a target normally or with pitch, oblique, and/or yaw angles. For vertical impact penetration tests, the impact velocity, size, weight, and geometry of the projectile, the final depth, and the axial deceleration record are important. Additional parameters such as the moment of “inertia and CG of the projectile, the lateral components of the impact velocity, the 2-or 3-D trajectory (including projectile orientation) and the lateral components of the deceleration record are also involved in non-normal tests”. The experimental study often investigates the influence of the relationships between impactor density, diameter, drop-height, soil properties, and boundary configurations on the penetration depth. The variation of terminal penetration of projectile at various impact speed is shown in Figure 7. Figure 7 also mentions the post-impact condition of project and target with increasing speed of projectile. Thompson [110]) has conducted the most comprehensive experimental study of vertical penetration phenomena of a projectile into homogeneous granular material. Detailed information concerning non-normal impact effects on penetration performance can be obtained by conducting a reverse ballistic test [111]. The experimental methods, high-speed imaging, and digital analysis [112] investigated soil media’s ballistic behavior, not only over several velocities of the projectile penetration phenomenon, but over several length scales. To study the in-situ behavior of soil materials under impact penetration, other sophisticated experimental techniques such as photo-elasticity [113] and grain-scale particle tracking [114] have been developed. The results of impact penetration tests may also be used with greater accuracy and reliability for sub-surface investigations [115] and may replace the conventional cone penetration test. Other impact penetration applications include remote soil exploration (including extra-terrestrial), seismic monitoring and surveying, and post-construction exploration of the soil properties of large earth structures [116].
Figure 7.
Variation of depth of projectile penetration with projectile velocity [92].
The numbers of works related to penetration tests are conducted basically to tackle the issue of determining the resistance to penetration [117,118] and final penetration depth [119,120] under specified kinematic characteristics of projectile. The direct measurement of resistance during penetration is due to Bazhenov et al. [121] and indirect measurement i.e., empirical formulations for the resistance versus penetration relations based on the experimental data, is proposed by Backman and Goldsmith [13]. Forces that resist penetration in soil media are calculated using the inverse experiment method, in which a sand container impacts the end of a measuring bar with hemispheric and conic heads [122]. Experimentally, Savvateev et al. [123] studied the “high-speed penetration of hard projectiles into dry and wet sand, the penetration depth increased with an increase in impact speed in the range of relatively low velocities impact”. However, at impact speeds of approximately 1.3 km/s, the depth of penetration began to decrease due to increasing levels of stress and temperature caused by friction between projectile and the target material. A review of past research indicates that considerable experimental work has been done on the impact of projectiles on non-cohesive soil or granular material targets [14,124]. However, there are scant experimental studies available on the impact of projectiles on cohesive targets [125,126].
4.1. Natural Soil/Synthetic Soil Models and Prototypes
Large-scale field experiments in which full-scale projectiles penetrate natural soil deposits are performed to deduce the extent of terminal penetration, time history of deceleration, and resistant forces, but these cannot be used to derive the empirical models due to soil profile variability [127]. The small-scale laboratory tests investigating the penetration process allow to attain more controlled soil conditions. However, the extrapolation to field behavior of relatively small laboratory tests requires consideration of several experimental design parameters such as relative density and over-consolidation, soil ageing, diameter ratio (ratio of diameter of projectile and diameter of test container), particle size, and gravity stress [12,128]. In order to achieve complete similitude between the model and the prototype of a large geo-medium event, the model must be constructed and tested in such a way as to satisfy the conditions of geometric similarity (constant ratio of all corresponding lengths in the model and prototype), kinematic similarity (proportionality of the two systems in regards to all corresponding time and time intervals), mechanical similarity (proportionality of the weight and density between the two systems), and dynamic similarity (proportionality of all the forces in the system) [129]. It is reasonable to start a study with the simplest system after considering such limitations for the model tests. Once a satisfactory model design method has been developed, a more complex and physically realistic system may be investigated with a slight modification. Awoshika and Cox [130] use similitude or dimensional analysis to simulate a space capsule landing on soils using a model design. A series of cone model tests on “Ottawa Sand and Colorado River Sand” and with modified models on clay soils are conducted to examine the validity of the model design for cohesionless and cohesive soils. Anandarajah et al. [131] found that in typical 1-g laboratory model research, there is a major scaling discrepancy due to the self-weight dependence of stress and the resulting strength distribution in granular soil. Taylor et al. [132] describes a combined 1-g and centrifuge penetration model test of projectile penetration into granular soils of a full-scale projectile penetration process that overcomes both scaling difficulties and the problem of quantification of sample properties. Test results are compared with Young’s equation-based predictions and penetration depth modification. O’Loughlin et al. [125] and “Richardson et al. [126] present 1:200 model centrifuge experiments in kaolin clay and compare the results (particularly penetration features) with True [133] and Freeman and Burdett [134] approaches”. Hossain et al. [135] uses centrifugal experiments and numerical modelling to present a study on the performance of anchor penetration in clay and calcareous silt and discusses the difference in the output of the penetration event in clay targets. Figure 8 shows the variation of terminal penetration depth found from the large-scale prototype experiment-based empirical methods at various impact velocities of a rod-like projectile on different soil target media. The penetration depth varies as square of impact velocity, except in the case of Robins [136] and Resal [137] in which penetration depth predicts logarithmic variation with impact velocity [138]. The projectile geometry has a significant effect on peak resistance force on projectiles penetrating soil media. Figure 9, depicting penetration resistance forces on projectiles using model tests at various impact velocities, infers that blunt-shape projectiles experience higher peak resistance force than ogive-shaped projectiles, and decreasing nose sharpness decreases the resistance force on projectile.
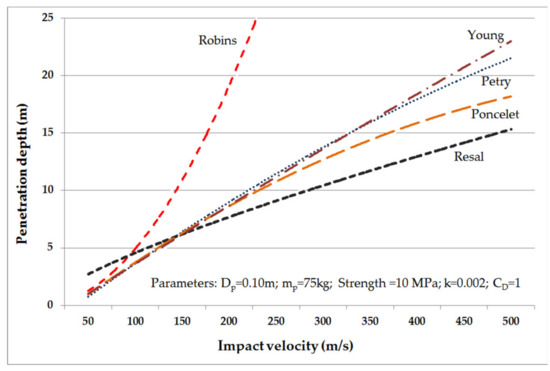
Figure 8.
Comparison of penetration depth using the different methods.
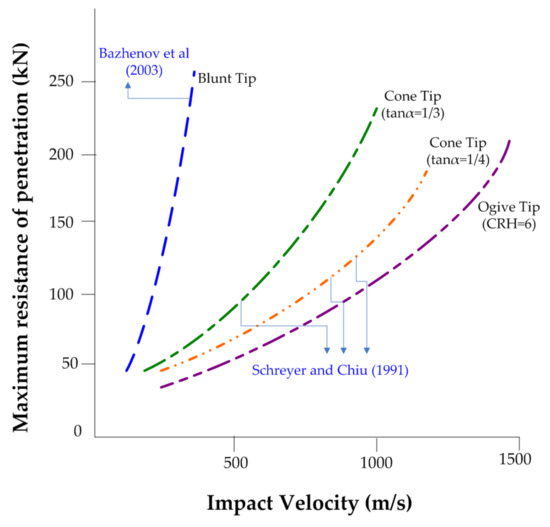
Figure 9.
Maximum penetration resistance force on projectiles using laboratory model tests.
Recent work uses transparent soils to determine in detail the particle–structure interactions during impact penetration in cohesion-less soil [139] and cohssive soil [140]. Omidvar et al. [141] conducted penetration tests using “refractive index-matched granular media” with macroscopic physical and mechanical properties replicating the behavior of natural soils to visualize, non-intrusively, in-situ granular kinematics under impact penetration in granular media. Using digital image correlations, they extract soil displacements and corresponding granular kinematics from the acquired images, and the measured deformations present different soil-projectile interaction characteristics during penetration. “From the comparison of dynamic and quasi-static penetration into transparent soils, they concluded that the magnitude of cumulative lateral displacements in both cases is comparable, whereas significantly larger cumulative vertical displacements occur during dynamic penetration”. They highlighted the fact of shear-induced dilation near the terminal penetration velocity, pointing to the dominance of frictional bearing resistance at the terminal penetration depth. The granular material under dynamic condition behave as shear-thickening fluid such as under high velocity impact and penetration behavior of target materials should be investigated considering the fluidic aspect of the granular media. Brown et al. [142] investigates the shear-thickening or the fluidic aspect of the granular media and the inherent effects on characteristics such as viscosity. Bi et al. [143] investigate the idea of dynamic jamming that appears in shear-thickening fluids due to the propagation of stress throughout the medium building up as particle resistance to disturbance from its neighbors increases as propagation radiates. Albert et al. [144] calculated the drag resistance during projectile penetration in granular material induced by jamming and develops a boundary-layer-like description for the force propagation, which was, surprisingly, minimally dependent on velocity. The exploration of other mechanisms, especially granular media under dynamic conditions and the propagation of force during penetration process through chains of grains, is due to Borg et al. [82]. Collins et al. [63] conducts the measurement of the internal flow fields in long-rod projectile penetration of the sand using digital speckle radiography (DSR). They concluded that processes such as reorganization, sliding, and void filling occur, allowing the grains to move in directions other than the force being applied. As a result, it is impossible to model sand either as a fluid or as conventional solids. The numerically simulated distribution of the velocity has a strong resemblance to the displacement fields experimentally measured.
4.2. Impact Penetration Based Soil Investigation
Conventional Techniques for soil investigations, particularly for large civil projects in remote areas, are quite expensive in both time and money. In recent years, interest has been developed to explore the feasibility to use the high-speed earth-penetrating projectiles for application to soil investigations. Caudle et al. [145] have suggested that if the impact velocity and properties of the soil medium are known, the decelerations and depth of a given projectile can be predicted. This also means that if the decelerations and depth are known for a given projectile and impact velocity, it is possible to determine the properties of the soil media (unrealistic material) being penetrated with more reliability and to provide the comparative evaluation of the earth subsurface. In-situ testing methods, such as static velocity “Cone Penetration Testing (CPT)”, have been developed to determine the geotechnical properties of soils where the main parameters, sleeve friction, cone resistance, and pore pressure at (or behind) the cone are measured during the penetration of a conical tip into the soil. The interpretation of CPT data is well supported by a theoretical and empirical background [146]. The dynamic penetration-based impact penetrometer (lance insertion retardation meter, LIR meter) with lower handling requirements than CPT, and ballistic penetrator and deep penetrating anchors (DPA) have been recently developed for assessing the geotechnical properties. The impact penetrometer only uses acceleration sensors to determine the geotechnical properties based on the acceleration data measured. There are two types of impact penetrometers available, i.e., lightweight devices for near-surface investigations [147] and huge penetrometers [148] for anchor performance evaluation. From field testing and laboratory observations, Lunne et al. [146] and Stephan [149] show that quantitative measures, such as cone resistance, bearing capacity, shear strength, or void ratio, can be extracted through further processing of qualitative penetrometer data. “Chow and Airey [150] present an empirical model based on model penetrometer tests and reference triaxial tests to determine undrained shear strength of clayey soil targets and the influence of penetrator mass, penetrator tip shape, impact velocity, and the strain rate on undrained shear strength”. The authors conclude that projectile mass and tip shape have a negligible influence on the strain rate effects during the tests. The experimental methods are used to assess the effect of projectile shape on penetration depth [151,152,153] and curve fitting of experimental results to existing theoretical models [153,154]. Such methods avoid study of the physical properties/processes of the phenomena of penetration. In shallow penetration, the granular medium loses most of its energy in the initial stage of penetration with transient interaction of the projectile with the target medium while in deep penetration, the compression and shear of the granular medium result in energy dissipation [41]. The energy absorption in the shear is primarily due to friction and changes in volume as grains “slip, roll and climb” over each other [Collins et al., 2011]. Ben-Dor et al. [155] provide a summary of the recommendations for approximate empirical models and penetration depth relationships suggested for the description of high-speed penetration into geological shields. The summary also includes the empirical studies not available in the English language. The penetration depth in the projectile impact into the soil media reaches its maximum value at critical speed, i.e., velocity at which the maximum value of the penetration depth is reached [156]. The study by Savvateev et al. [123] inferred that the maximum achievable depth of penetration in granular media appeared proportional to the density of the projectile material. They also concluded that the critical velocity of the projectile material could be calculated based on the melting temperature and fusion heat. The influence of material properties of the projectile on the terminal penetration depth is portrayed in Figure 10. Appendix B lists the maximum projectile penetration depth formulae in dynamic penetration derived by various authors
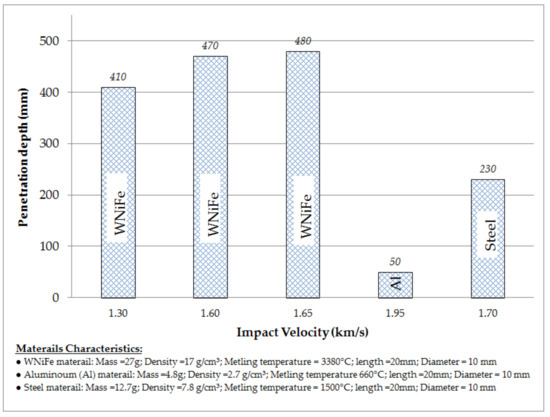
Figure 10.
Effect of material properties of projectile on penetration depth.
4.3. Local and Bulk Behavior of Soil Media
The bulk behavior for homogeneous material derives directly from the microstructure of the material but behaviors local to the grain scale of material, such as of granular materials, may cause significant deviation from the expected bulk response [157]. Some of the investigators have explored single-grain interactions utilizing radiography to view grain fracture in-situ with the help of a Split-Hopkinson bar configuration [158]. Vooren et al. [54] present a novel experiment to illustrate the fundamental mechanism of dynamic force chains, as well as the movement and fracture of individual grains in granular material penetration. Two separate experiments have been carried out, one for fractures of individual sand grains and the other for force chain phenomena within the granular system. A “quasi-static experiment” has been used to estimate the fracture strength of individual sand grains at a projectile speed of more than 35 m/s. In dynamic experiments, a two-wave structure propagated through the sand system has been observed, consisting of a compaction wave and a damage wave. The compaction wave removes porosity and grains in the region near the projectile nose are fractured by the damage wave. This is achieved by launching a projectile along a view window, backed up by sand, and directly viewing and photographing projectile/sand interactions. Depending on the “shape of the projectile nose, the impact velocity and the mechanical properties of the target”, the target may be removed from the surface of the projectile body (usually the shank or the aft body of the projectile) during penetration, which is referred to as a wake separation [159]. Erosion processes on captured projectiles also indicate that the target medium may reattach to the projectile surface [160]. Despite the suggestion of a simplified model to consider such issues in penetration analysis, the comparison between calculated and experimental results is not convincing [58] and less interest is shown in further investigating the grain ejection or wake-up phenomenon in granular media during projectile impact. Deboeuf et al. [161] studied grain ejection dynamics by sphere impacting on a granular material. Boudet et al. [162] proposed a model for ejection from the growth of craters in a small layer of thickness relative to the size of both projectile and target grains at low impact speeds, while Cintala et al. [163] measured ejection velocities of grains during high velocity impact.
5. Conclusions
The study presents a dedicated summary of the analytical, computational, experimental, and empirical methods to predict the response of dynamic impact on soils media covering the novel works on impact penetration. It is established from the projectile–target interactions, understanding that the target soil media under dynamic impact, especially under high speed and deep penetration, neither behave completely as solid nor as liquid. It is observed from the current state of the art that the robust and range of impact velocities applicable soil penetration models are based on the law of motion and conservation of momentum and the models based on conservation of energy have not found much interest due to the change in energy dissipation with impact velocity complexity. It is observed that employing appropriate material strength model for soil media, equation-of-state, contact algorithm, and yield criteria plays a significant role in the simulation of dynamic impact penetration process. The analytical models are the most economical models for the study of penetration phenomenon. It is observed that responses local to the grain scale of soil material may cause significant deviation from the expected bulk response, and focused local as well as bulk behavior including fracture of soil media provide the complete understanding of the penetration phenomenon. The application of artificial soils that have macroscopic physical and mechanical properties replicating the behavior of natural soils, in experimental investigation of penetration, could provide a complete picture of dynamic projectile penetration phenomenon. It is observed from the existing literature that recent development in penetration research is focused on modeling the target media into numerous thin layers and complete penetration process into multiple stages. It is also observed that dynamic penetration in soil can be applied to soil investigations.
Despite numerous efforts up to the recent studies, the understanding of the soil media impact penetration mechanisms remains insufficient as the phenomenon of dynamic penetration in heterogeneous particulate soil medium is very complex. The projectile–target interactions clearly necessitates coupled and hybrid theoretical-experimental investigations based on a variety of projectile-target configurations, material characteristics of projectile, as well as target medium including porosity/saturation and range of initial velocities. There appears to be a need for thermal coupling and numerical error estimation coupling for accurate simulation of penetration process. Further research is also clearly needed in the coupling of the modelling of the target media as multi-material/multi-layered targets and modelling of bulk penetration process as a multi-stages process. Further, there is scope to employ new development in experimental technologies and new/hybrid computational methodologies, especially recent development in finite element methods, to study the soil penetration mechanism. There appears to be a need of further investigation in the detachment of soil from the projectile body surface area during projectile penetration into soil, that is termed as wake separation, and reattachment of the target medium to the projectile surface. The important area that also requires further work is soil investigation through the projectile penetration in soil targets specially for large projects and remote area soil investigations.
Author Contributions
Conceptualization, M.A. and S.A.; methodology, M.A. and M.N.D.; resources, M.A., J.M., and H.T.H.; writing—original draft preparation, M.A., S.A., and H.T.H.; writing—review and editing, J.M. and M.N.D.; project administration, M.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for this research was given under award numbers R.G.P2/73/41 by the Deanship of Scientific Research; King Khalid University, Ministry of Education, Kingdom of Saudi Arabia.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under grant number (R.G.P2/73/41).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | Description |
| A, B and C | Model Constant (A/Cv is static target resistance term, Bv2 is drag term), |
| A | Projectile Area |
| Bmax | Maximum hardness at crater bottom |
| D10* | effective grain size of soil, |
| E, | Material Elastic modulus, |
| F | net resistant force |
| F1, F2, F3 | respectively dissipative, dynamic, and static components of resistant force |
| & | Normal and tangential forces acting on particle i by contacting particle j, respectively; |
| and | Resultant force and moment on the projectile, |
| G | gravity acceleration |
| Ii, and ωi (ω) | Moment of inertia and angular velocity of particle i |
| Kϕ | coefficient (>1) |
| L, D | Projectile length, Diameter |
| Rolling moment; | |
| Twisting moment | |
| P (=ρs g h) | hydrostatic-like pressure |
| Pr | Pressure |
| Pst | term of static resistance; |
| Rt | Target resistance to penetration |
| R(t), (t), (t) | Disc internal boundary radial values of displacement, velocity, and acceleration |
| S | Soil penetrability number representing soil properties, |
| Yp | dynamic flow stress of projectile, |
| a | Hole radius, |
| c | cohesion of soil c, |
| d | Penetration depth of a cone, |
| dS | Infinitesimal area element pointing normal to the intruder surface, |
| h | Heaviside function, |
| l1, l2 | first and second characteristic length |
| kϕ | coefficient (>1) α to the internal friction coefficient φ, |
| m (mi) and v (vi) | mass and velocity of projectile (particle), |
| p(t) | Interaction pressure, positive in compression; |
| s | Extent of plastic zone in projectile, |
| t | Rise time of impact, |
| z | unit vector in z-direction, |
| σy | yield stress |
| α and β | nose geometry factors |
| ρs | packing density of the granular matter |
| η | a parameter dependent on grain properties; |
| ρp | Density of projectile, |
| αc | [1+ (h/Rc)] |
| τo | principal stress difference at failure; |
| λ | Projectile aspect ratio |
| εL. | volumetric locking strain; |
| ρo | initial density; |
| ρL | current locking density; |
| ρ, | Initial or current |
| ρ* | max. density reached during loading. |
| σr, σθ | radial and hoop components of the Cauchy stress |
| Angular momentum vector about the mass centre of projectile frame, | |
| Normal stress, | |
| ) | shear stress on projectile surface, |
| μ | coefficient of kinetic friction, or Factor of friction between projectile and soil, or Tangent of angle of repose of granular material, |
| vector from the center of particle i to the contact point with particle j; | |
| θ | apex angle of a wedge or a cone, |
| φ | angle of internal friction of soil, |
| ρ (ρt), s | density of soil (or target) and, degree of saturation of soil |
| θ | Semi-vertex angle of cone-nose projectile in degrees” |
| ν | Poisson’s ratio |
Appendix A

Table A1.
Analytical Methods and Basic Equations.
Table A1.
Analytical Methods and Basic Equations.
| General Formulations (Newton’s 2nd Law of motion) | |
| Forrestal and Luk [45] | ) |
| Poncelet [164] | |
| Resal [137] | |
| Local friction force model (LFFM) [38] | dFd = Kϕ P. dS = μ P dS |
| Ambroso et al. [165] | |
| DEM (Rolling spring-dashpot-slider model) [166] | |
| General Formulations (conservation of momentum) | |
| Walker-Anderson model [37] | |
| Hydro-dynamic theory steady state, incompressible model [30] |

Table A2.
Analytical Methods and Basic Equations (contd.).
Table A2.
Analytical Methods and Basic Equations (contd.).
| Modified Hydro-dynamic theory model [31] | |
| Tate-Alekseevskii model (Modified Bernoulli’s Equation) [34,35] | |
| Grigoryan [167] | |
| Spherical Cavity Expansion (SCE) [168] | |
| Cylindrical Cavity Expansion (CCE) or Disc or Orthogonal layers model [42] | , |
| Modified Archimedes’ law [46] | |
| Non-linear differential area force law (DAFL) [65] | ,
, |
| Dimensional Similitude Analysis [169] |
Appendix B

Table A3.
Penetration depth Formulae by different Authors.
Table A3.
Penetration depth Formulae by different Authors.
| Author Reference | Penetration Depth Formulae |
|---|---|
| General Formula | |
| Euler [169] | |
| Poncelet [164] | |
| Bless et al. [120] | |
| Resal [137] | |
| Petry [170] | |
| Patterson [171] | |
| Ambroso et al. [165] | |
| Lohse et al. [157] | |
| Charters and Summers [172] | |
| Christman and Gehring [31] | |
| Young [173] |

Table A4.
Penetration depth Formulae by different Authors (contd.).
Table A4.
Penetration depth Formulae by different Authors (contd.).
| Author Reference | Penetration Depth Formulae |
|---|---|
| Bernard and Creighton [159] | |
| Taylor et al. [132] | |
| Forrestal and Luk [45] | |
| Adeli et al. [174] | |
| Crull [175] | |
| Pensky [176] | |
| Richmond [177] | |
| Savvateev et al. [123] | |
| Nechitailo [156] |
References
- Öhman, T.; Aittola, M.; Kostama, V.-P.; Raitala, J. The Preliminary Analysis of Polygonal Impact Craters within Greater Hellas Region, Mars. In Impact Tectonics; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Lobo-Guerrero, S.; Vallejo, L.E. Influence of pile shape and pile interaction on the crushable behavior of granular materials around driven piles: DEM analyses. Granul. Matter 2007, 9, 241. [Google Scholar] [CrossRef]
- Ng, K.; Ksaibati, R. Understanding the Responses of Surrounding Soils to Pile Setup from Medium-Scale Experiments and Cone Penetration Tests. Transp. Infrastruct. Geotechnol. 2018, 5, 129–145. [Google Scholar] [CrossRef]
- Maciejewski, J.; Jarzȩbowski, A.; Tra̧mpczyński, W. Study on the efficiency of the digging process using the model of excavator bucket. J. Terramechanics 2003, 40, 221–233. [Google Scholar] [CrossRef]
- Aguilar, J.; Goldman, D.I. Robophysical study of jumping dynamics on granular media. Nat. Phys. 2016, 12, 278–283. [Google Scholar] [CrossRef]
- Van der Meer, D. Impact on Granular Beds. Annu. Rev. Fluid Mech. 2017, 49, 463–484. [Google Scholar] [CrossRef]
- Hou, M.; Peng, Z.; Liu, R.; Wu, Y.; Tian, Y.; Lu, K.; Chan, C.K. Projectile impact and penetration in loose granular bed. Sci. Technol. Adv. Mater. 2005, 6, 855. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Alsaleh, M.I.; Alshibli, K.A. Evolving internal length scales in plastic strain localization for granular materials. Int. J. Plast. 2005, 21, 2000–2024. [Google Scholar] [CrossRef]
- Kadanoff, L.P. Built upon sand: Theoretical ideas inspired by granular flows. Rev. Mod. Phys. 1999, 71, 435. [Google Scholar] [CrossRef]
- Goey, C.H.; Pei, C.; Wu, C.-Y. DEM Modelling of Subsidence of a Solid Particle in Granular Media. In Discrete Element Modelling of Particulate Media; Royal Society of Chemistry: London, UK, 2012. [Google Scholar]
- Iskander, M.; Bless, S.; Omidvar, M. Rapid Penetration into Granular Media: Visualizing the Fundamental Physics of Rapid Earth Penetration; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 9780128011553. [Google Scholar]
- Omidvar, M.; Iskander, M.; Bless, S. Response of granular media to rapid penetration. Int. J. Impact Eng. 2014, 66, 60–82. [Google Scholar] [CrossRef]
- Backman, M.E.; Goldsmith, W. The mechanics of penetration of projectiles into targets. Int. J. Eng. Sci. 1978, 16, 1–99. [Google Scholar] [CrossRef]
- Hopkins, H.G. Dynamic expansion of spherical cavities in metals. Prog. Solid Mech. 1960, 1, 85–164. [Google Scholar]
- O’Loughlin, C.D.; Nazem, M.; Chow, S.H.; Randolph, M.F.; Gaudin, C.; White, D.J. Dynamic embedment of projectiles in clay. Aust. Geomech. J. 2014, 49, 133–145. [Google Scholar]
- Heuzé, F.E. An overview of projectile penetration into geological materials, with emphasis on rocks. Int. J. Rock Mech. Min. Sci. 1990, 27, 1–14. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, H.; Fang, Q.; Kong, X.Z. Modified spherical cavity expansion model for projectile penetration into concrete targets. Acta Mech. Sin. 2019, 35, 518–534. [Google Scholar] [CrossRef]
- Galanov, B.A.; Kartuzov, V.V.; Ivanov, S.M. A Model for Penetration Resistance in Brittle Materials Taking Into Account Strain Hardening of Solid Phase in Mescal-Zone Powder Material. Procedia Eng. 2015, 103, 135–142. [Google Scholar] [CrossRef][Green Version]
- Liu, W.H.; Hu, Z.J.; Ye, L.Y.; Liu, Y.F. The Study of Projectile Penetration into Aluminum Armor Plate. Adv. Mater. Res. 2011, 284–286, 2517–2520. [Google Scholar] [CrossRef]
- Cheon, J.; Choi, Y. Influence of Projectile Velocity on Penetration into a Steel Plate. Int. J. Precis. Eng. Manuf. 2020, 21, 137–144. [Google Scholar] [CrossRef]
- Manes, A.; Bresciani, L.M.; Giglio, M. Ballistic performance of multi-layered fabric composite plates impacted by different 7.62 mm caliber projectiles. Procedia Eng. 2014, 88, 208–215. [Google Scholar] [CrossRef]
- Chen, S. Anti-penetration simulation for HDPE honeycomb protection structure. Chem. Eng. Trans. 2017, 62, 49–54. [Google Scholar]
- Miller, J.E.; Christiansen, E.L.; Davis, B.A.; Deighton, K.D. Ballistic performance model of crater formation in monolithic, porous thermal protection systems. Procedia Eng. 2015, 103, 398–404. [Google Scholar] [CrossRef][Green Version]
- Feng, Y.; Blumenfeld, R.; Liu, C. Support of modified Archimedes’ law theory in granular media. Soft Matter 2019, 15, 3008–3017. [Google Scholar] [CrossRef] [PubMed]
- Tapia, F.; Espíndola, D.; Hamm, E.; Melo, F. Effect of packing fraction on shear band formation in a granular material forced by a penetrometer. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 014201. [Google Scholar] [CrossRef] [PubMed]
- Nazhat, Y.; Airey, D. The kinematics of granular soils subjected to rapid impact loading. Granul. Matter 2015, 17, 1–20. [Google Scholar] [CrossRef]
- Anderson, C.E., Jr. Analytical models for penetration mechanics: A Review. Int. J. Impact Eng. 2017, 108, 3–26. [Google Scholar] [CrossRef]
- Yu, H.S. Cavity Expansion Methods in Geomechanics; Springer Science & Busines Media: Berlin, Germany, 2013. [Google Scholar]
- Yankelevsky, D.Z. Effect of Soil Parameters on High Velocity Projectile Penetration. In Proceedings of the International Conferences on Recent Advances in Geotechnical Earthquake Engineering and Soil Dynamics. 10, St. Louis, MO, USA, 29 April 1981; Available online: http://scholarsmine.mst.edu/icrageesd/01icrageesd/session04b/10 (accessed on 21 August 2020).
- Stilp, A.J.; Hohler, V. Long rod penetration mechanics Chapter 5. In High Velocity Impact Dynamics; Zukas, J.A., Ed.; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Christman, D.R.; Gehring, J.W. Analysis of high-velocity projectile penetration mechanics. J. Appl. Phys. 1966, 37, 1579–1587. [Google Scholar] [CrossRef]
- Recht, R.F.; Ipson, T.W. Ballistic perforation dynamics. J. Appl. Mech. 1963, 30, 384–390. [Google Scholar] [CrossRef]
- Walker, J.D. Hypervelocity penetration modeling: Momentum vs. energy and energy transfer mechanisms. Int. J. Impact Eng. 2001, 26, 809–822. [Google Scholar] [CrossRef]
- Tate, A. Long rod penetration models—Part II. Extensions to the hydro-dynamic theory of penetration. Int. J. Mech. Sci. 1986, 28, 599–612. [Google Scholar] [CrossRef]
- Alekseevskii, V.P. Penetration of a Rod into a Target at High Velocity. Combust. Explos. Shock Waves 1993, 2, 63–66. [Google Scholar] [CrossRef]
- Ravid, M.; Bodner, S.R.; Holcman, I. Analysis of very high-speed impact. Int. J. Eng. Sci. 1987, 25, 473–482. [Google Scholar] [CrossRef]
- Walker, J.D.; Anderson, C.E., Jr. A time-dependent model for long-rod penetration. Int. J. Impact Eng. 1995, 16, 19–48. [Google Scholar] [CrossRef]
- Brzinski, T.; Mayor, P.; Durian, D. Depth-dependent resistance of granular media to vertical penetration. Phys. Rev. Lett. 2013, 111, 168002. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.M.; Nagel, S.R. Physics of the granular state. Science 1992, 255, 1523–1531. [Google Scholar] [CrossRef] [PubMed]
- Sabetamal, H.; Nazem, M.; Carter, J.P.; Sloan, S.W. Large deformation dynamic analysis of saturated porous media with applications to penetration problems. Comput. Geotech. 2014, 55, 117–131. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z.; Adin, M.A. A simplified analytical method for soil penetration analysis. Int. J. Numer. Anal. Methods Geomech. 1980, 4, 233–254. [Google Scholar] [CrossRef]
- Guo, X.J.; He, T.; Wen, H.M. Cylindrical cavity expansion penetration model for concrete targets with shear dilatancy. J. Eng. Mech. 2013, 139, 1260–1267. [Google Scholar] [CrossRef]
- Forrestal, M.J. Penetration into dry porous rock. Int. J. Solids Struct. 1986, 22, 1485–1500. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Tzou, D.Y. Spherical cavity-expansion penetration model for concrete targets. Int. J. Solids Struct. 1997, 34, 4127–4146. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Luk, V.K. Penetration into Soil Targets. Int. J. Impact Eng. 1992, 12, 427–444. [Google Scholar] [CrossRef]
- Bless, S.; Omidvar, M.; Iskander, M. High-Speed Penetration of Granular Geomaterials; Elsevier: Amsterdam, The Netherlands, 2015; p. 93. [Google Scholar]
- Kang, W.; Feng, Y.; Liu, C.; Blumenfeld, R. Archimedes’ law explains penetration of solids into granular media. Nat. Commun. 2018, 9, 1101. [Google Scholar] [CrossRef]
- Seguin, A.; Gondret, P. Drag force in a cold or hot granular medium. Phys. Rev. E 2017, 96, 032905. [Google Scholar] [CrossRef]
- Khan, M.A. Mechanics of projectile penetration into non-cohesive soil targets. Int. J. Civ. Eng. 2015, 13, 28–39. [Google Scholar]
- Huang, K.; Delfin, D.H.; Rech, F.; Dichtl, V.; Hidalgo, R.C. The role of initial speed in projectile impacts into light granular media. Sci. Rep. 2020, 10, 3207. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Magnanimo, V.; Saitoh, K.; Luding, S. Effect of cohesion on shear banding in quasi-static granular materials. Phys. Rev. E 2014, 90, 022202. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Ran, X.; Blumenfeld, R. Vertical dynamics of a horizontally oscillating active object in a two-dimensional granular medium. Phys. Rev. E 2016, 94, 062906. [Google Scholar] [CrossRef]
- Vinutha, H.; Sastry, S. Disentangling the role of structure and friction in shear jamming. Nat. Phys. 2016, 12, 578–583. [Google Scholar] [CrossRef]
- Voorena, V.; Borga, J.; Sandusky, H.; Felts, J. Sand Penetration: A Near Nose Investigation of a Sand Penetration Event Andrew. Procedia Eng. 2013, 58, 601–607. [Google Scholar] [CrossRef]
- Macek, R.W.; Duffey, T.A. Finite cavity expansion method for nearsurface effects and layering during earth penetration. Int. J. Impact Eng. 2000, 24, 239–258. [Google Scholar] [CrossRef]
- Jiang, M.J.; Sun, Y.G. Cavity expansion analyses of crushable granular materials with state-dependent dilatancy. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 723–742. [Google Scholar] [CrossRef]
- Kotov, V.L.; Balandin, V.V.; Bragov, A.M.; Linnik, E.Y.; Balandin, V.V. Using a local interaction model to determine the resistance to penetration of projectiles into sandy soil. J. Appl. Mech. Tech. Phys. 2013, 54, 612–621. [Google Scholar] [CrossRef]
- Bernard, R.S.; Creighton, D. Projectile Penetration in Soil and rock: Analysis for Non-Normal Impact, Technical Report; SL-79-15AD-A081044; US Army Waterways Experiment Station: Vieksburg, MS, USA, 1979. [Google Scholar]
- Young, C.W. Simplified Analytical Model of Penetration with Lateral Loading e User’s Guide; Report No. SAND98-0978; Sandia National Laboratories: Albuquerque, NM, USA, 1998; p. 61. [Google Scholar]
- Rosenberg, Z.; Dekel, E. Terminal Ballistics; Springer: Berlin/Heidelberg, Germany, 2012; p. 395. [Google Scholar]
- Wen, H.M. Predicting the Penetration and Perforation of Targets Struck by Projectiles at Normal Incidence. Mech. Struct. Mach. 2002, 30, 543–577. [Google Scholar] [CrossRef]
- Goldsmith, W. Non-ideal projectile impact on targets. Int. J. Impact Eng. 1999, 22, 95–395. [Google Scholar] [CrossRef]
- Collins, A.L.; Addiss, J.W.; Walley, S.M.; Promratana, K.; Bobaru, F.; Proud, W.G.; Williamson, D.M. The effect of nose shape on the internal flow fields during ballistic penetration of sand. Int. J. Impact Eng. 2011, 38, 951–963. [Google Scholar] [CrossRef]
- Ben-Dor, G.; Dubinsky, A.; Elperin, T. Some inverse problems in penetration mechanics. Mech. Based Des. Struct. Mach. 2010, 38, 468–480. [Google Scholar] [CrossRef]
- Gao, X.; Li, Q.M. Trajectory instability and convergence of the curvilinear motion of a hard projectile in deep penetration. Int. J. Mech. Sci. 2017, 121, 123–142. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Teeter, R.D.; Felice, C.W.; Gupta, Y.M. Two dimensional mesoscale simulations of projectile instability during penetration in dry sand. J. Appl. Phys. 2008, 104, 083502. [Google Scholar] [CrossRef]
- Simonov, I.V.; Osipenko, K.Y. Stability, paths, and dynamic bending of a blunt body of revolution penetrating an elastoplastic medium. J. Appl. Mech. Tech. Phys. 2004, 45, 428–439. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Luk, V.K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid. J. Appl. Mech. 1988, 55, 275–279. [Google Scholar] [CrossRef]
- Masri, R.; Durban, D. Dynamic spherical cavity expansion in an elasloplastic compressible mises solid. J. Appl. Mech. Trans. ASME 2005, 72, 887–898. [Google Scholar] [CrossRef]
- Ravid, M.; Bodner, S.R. Dynamic perforation of viscoplastic plates by rigid projectiles. Int. J. Eng. Sci. 1983, 21, 577–591. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Hanchak, S.J. Penetration Experiments with Limestone Targets and Ogive-Nose Steel Projectiles. J. Appl. Mech. 2000, 67, 841–845. [Google Scholar] [CrossRef]
- Orphal, D.L. Phase three penetration. Int. J. Impact Eng. 1997, 20, 601–616. [Google Scholar] [CrossRef]
- Goldman, D.I.; Umbanhowar, P. Scaling and dynamics of sphere and disk impact into granular media. Phys. Rev. E 2008, 77, 021308-1–021308-14. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, N.A.; Abbas, H. Mechanics of missile penetration into geo-materials. Struct. Eng. Mech. 2002, 13, 639–652. [Google Scholar] [CrossRef]
- Kondic, L.; Fang, X.; Losert, W.; O’Hern, C.S.; Behringer, R.P. Microstructure evolution during impact on granular matter. Phys. Rev. E 2012, 85, 011305–1–011305-17. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Shi, C.; Liu, Z.; Wen, D. Theoretical Research Progress in High-Velocity/Hypervelocity Impact on Semi-Infinite Targets. Shock Vib. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modelling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Borg, J.P.; Vogler, T.J. Mesoscale simulations of a dart penetrating sand. Int. J. Impact Eng. 2008, 35, 1435–1440. [Google Scholar] [CrossRef]
- Herrmann, W. Constitutive equation for the dynamic compaction of ductile porous materials. J. Appl. Phys. 1969, 40, 2490–2499. [Google Scholar] [CrossRef]
- Grady, D.E.; Winfree, N.A.; Kerley, G.I.; Wilson, L.T.; Kuhns, L.D. Computational modeling and wave propagation in media with inelastic deforming microstructure. J. Phys. IV Fr. 2000, 10, 15–20. [Google Scholar] [CrossRef]
- Wunnemann, K.; Collins, G.S.; Melosh, H.J. A strain-based porosity model for use in hydrocode simulations of impacts and implications for transient crater growth in porous targets. Icarus 2006, 180, 514–527. [Google Scholar] [CrossRef]
- Borg, J.P.; Morrissey, M.P.; Perich, C.A.; Vogler, T.J.; Chhabildas, L.C. In situ velocity and stress characterization of a projectile penetrating a sand target: Experimental measurements and continuum simulations. Int. J. Impact Eng. 2013, 51, 23–35. [Google Scholar] [CrossRef]
- Bazhenov, V.G.; Bragov, A.M.; Konstantinov, A.Y.; Kotov, V.L. Comparative analysis of methods for modeling the penetration and plane-parallel motion of conical projectiles in soil. J. Appl. Mech. Tech. Phys. 2015, 56, 381–390. [Google Scholar] [CrossRef]
- Paik, K.; Salgado, R.; Lee, J.; Kim, B. Behaviorofopen-and closed-ended piles driven into sands. J. Geotech. Geoenviron. Eng. 2003, 129, 296–306. [Google Scholar] [CrossRef]
- Ko, J.; Jeong, S.; Lee, J.K. Large deformation FE analysis of driven steel pipe piles with soil plugging. Comput. Geotech. 2016, 71, 82–97. [Google Scholar] [CrossRef]
- Rahbek, D.B. Finite Element Simulations of Drop Indentations into Oily Clay; FFI-rapport 2014/02221; Norwegian Defense Research Establishment (FFI): Kjeller, Norway, 2015; Available online: http://hdl.handle.net/20.500.12242/1118 (accessed on 26 August 2020).
- Carter, J.P.; Mazem, M. Analysis of dynamic penetration of soils. In Proceedings of the From Materials to Structures: Advancement through Innovation-Proceedings of the 22nd Australasian Conference on the Mechanics of Structures and Materials, ACMSM, Sydney, Australia, 11–14 December 2012. [Google Scholar]
- Danielson, K.T.; Adley, M.D. A meshless treatment of three-dimensional penetrator targets for parallel computation. Comput. Mech. 2000, 25, 267–273. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Seguin, A.; Bertho, Y.; Gondret, P.; Crassous, J. Sphere penetration by impact in a granular medium: A collisional process. Europhys. Lett. 2009, 88, 44002–1–44002-6. [Google Scholar] [CrossRef]
- Tran, Q.A.; Chevalier, B.; Breul, P. Discrete modeling of penetration tests in constant velocity and impact conditions. Comput. Geotech. 2016, 71, 12–18. [Google Scholar] [CrossRef]
- Holmen, J.K.; Olovsson, L.; Børvik, T. Discrete modelling of low-velocity penetration in sand. Comput. Geotech. 2017, 86, 21–32. [Google Scholar] [CrossRef]
- IMPETUS Afea, A.S. IMPETUS Afea Solver. 2016. Available online: http://www.impetusafea.com (accessed on 21 August 2020).
- Børvik, T.; Dey, S.; Olovsson, L. Penetration of granular materials by small-arms bullets. Int. J. Impact Eng. 2015, 75, 123–139. [Google Scholar] [CrossRef]
- Takita, H.; Sumita, I. Low-velocity impact cratering experiments in a wet sand target. Phys. Rev. E 2013, 88, 022203. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.; Li, J.; Qu, H.; Pan, Y.; Kang, Y.; Zhang, Y. Numerical Simulation of Hypervelocity Impact FEM-SPH Algorithm Based on Large Deformation of Material. Preprints 2016. [Google Scholar] [CrossRef][Green Version]
- Li, Q.M.; Flores-Johnson, E.A. Hard projectile penetration and trajectory stability. Int. J. Impact Eng. 2011, 38, 815–823. [Google Scholar] [CrossRef][Green Version]
- Fang, Q.; Kong, X.; Wu, H.; Yan, H. Predictions of projectile penetration and perforation by DAFL with the free surface effect. Struct. Shock Impact XII 2012, 126, 249. [Google Scholar] [CrossRef]
- Abelev, A.; Simeonov, J.; Valent, P. Numerical investigation of dynamic free-fall penetrometers in soft cohesive marine sediments using a finite element approach. In Proceedings of the OCEANS 2009, MTS/IEEE Biloxi—Marine Technology for Our Future: Global and Local Challenges, Biloxi, MS, USA, 26–29 October 2009; pp. 2626–2633. [Google Scholar]
- Abelev, A.; Tubbs, K.; Valent, P. Numerical investigation of dynamic free-fall penetrometers in soft cohesive marine sediments using a finite difference approach. In Proceedings of the OCEANS 2009, MTS/IEEE Biloxi—Marine Technology for Our Future: Global and Local Challenges, Biloxi, MS, USA, 26–29 October 2009; pp. 2616–2625. [Google Scholar]
- Yongxiang, D.; Shunshan, F. Numerical simulation of flat-nose projectile penetrating concrete and soil target. In Proceedings of the 3rd WSEAS International Conference on Applied and Theoretical Mechanics, Tenerife, Canary Islands, Spain, 14–16 December 2007. [Google Scholar]
- Ogawa, K.; Takeda, S.; Kobayashi, H.; Tanigaki, K. Simulation of dynamic response of projectile and granular target. In EPJ Web of Conferences; EDP Sciences: Les Ulis, France, 2015; Volume 94, p. 0404. [Google Scholar]
- Flores-Johnson, E.A.; Wang, S.; Maggi, F.; El Zein, A.; Gan, Y.; Nguyen, G.D.; Shen, L. Discrete element simulation of dynamic behaviour of partially saturated sand. Int. J. Mech. Mater. Des. 2016, 12, 495–507. [Google Scholar] [CrossRef]
- Rabinovich, Y.I.; Esayanur, M.S.; Moudgil, B.M. Capillary forces between two spheres with a fixed volume liquid bridge: Theory and experiment. Langmuir 2005, 21, 10992–10997. [Google Scholar] [CrossRef]
- Yankelevsky, D.Z. Projectile penetration through a narrow drill in soil. Int. J. Impact Eng. 1983, 1, 377–391. [Google Scholar] [CrossRef]
- Yu, H.S.; Mictchell, J.K. Analysis of cone resistance: Review of methods. J. Geotech. Geoenviron. Eng. ASCE 1998, 124, 140–149. [Google Scholar] [CrossRef]
- Thigpen, L. Projectile penetration of elastic-plastic earth media. J. Geotech. Eng. ASCE 1974, 100, 279–294. [Google Scholar] [CrossRef]
- True, D.G. Penetration of Projectiles into Seafloor Soils; Final Report No. CEL-TR-822; Naval. Civil Engineering Lab.: Port Hueneme, CA, USA, 1975. [Google Scholar]
- Teland, J.A.; Moxnes, J.F. Analytical Cavity Expansion Penetration Models Compared with Numerical Simulations; Technical Report; Norwegian Defence Research Establishment: Kjeller, Norway, 2003. [Google Scholar]
- Thompson, J.B. Low-Velocity Impact Penetration of Low-Cohesion Soil Deposits. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1975. [Google Scholar]
- Liu, J.; Huang, F.; Xu, K.; Liu, L.; Zuo, T.; Pi, A. Influence of Mass Ratio on Forward and Reverse Ballistic Impact Equivalence: Experiments, Simulations, and Mechanism Analysis. Exp. Mech. 2017, 57, 387–404. [Google Scholar] [CrossRef]
- Uehara, J.S.; Ambroso, M.A.; Ojha, R.P.; Durian, D.J. Low-speed impact craters in loose granular media. Phys. Rev. Lett. 2003, 90, 194301. [Google Scholar] [CrossRef] [PubMed]
- Clark, A.H.; Kondic, L.; Behringer, R.P. Particle scale dynamics in granular impact. Phys. Rev. Lett. 2012, 109, 238302–1–238302–5. [Google Scholar] [CrossRef] [PubMed]
- Nordstrom, K.N.; Lim, E.; Harrington, M.; Losert, W. Granular dynamics during impact. Phys. Rev. Lett. 2014, 112, 228002–1–228002–5. [Google Scholar] [CrossRef]
- Zacny, K.; Bualat, M.; Lee, P.; Alvarez, L.; Fong, T.; Deans, M.; VanGundy, L.; Lees, D. Using percussive, dynamic, and static soil penetrometers to assess geotechnical properties and the depth to ground ice of the mars and lunar analog terrains on the Devon Island, Canadian Arctic. In Earth and Space 2012: Engineering, Science, Construction, and Operations in Challenging Environments; Zacny, K., Mall, R.B., Binienda, W., Eds.; ASCE: Pasadena, CA, USA, 2012; pp. 284–294. [Google Scholar]
- Melzer, K.-J. Measuring Soil Properties in Vehicle Mobility Research: Cone Penetration Resistance and Relative Density; Technical Report; U.S. Army Engineer Waterways Experiment Station, CE: Vicksburg, MS, USA, 1970. [Google Scholar]
- Braslau, D. Partitioning of energy in hypervelocity impact against loose sand target. J. Geophys. Res. 1970, 75, 3987–3999. [Google Scholar] [CrossRef]
- Pournaghiazar, M.; Russell, A.; Khalili, N. Linking cone penetration resistances measured in calibration chambers and the field. Géotech. Lett. 2012, 2, 29–35. [Google Scholar] [CrossRef]
- Bivin, Y.K.; Simonov, I.V. Mechanics of dynamic penetration into soil medium. Mech. Solids 2010, 45, 892–920. [Google Scholar] [CrossRef]
- Bless, S.; Peden, B.; Guzman, I.; Omidvar, M.; Iskander, M. Poncelet coefficients of granular media. In Dynamic Behavior of Materials; Song, B., Casem, D., Kimberley, J., Eds.; Proceedings of the Society for Experimental Mechanics Series, 1; Springer: Lombard, IL, USA, 2014; pp. 373–380. [Google Scholar]
- Bazhenov, V.G.; Bragov, A.M.; Kotov, V.L. Experimental-theoretical study of the penetration of rigid projectiles and identification of soil properties. J. App. Mech. Tech. Phys. 2009, 50, 1011. [Google Scholar] [CrossRef]
- Bragova, А.М.; Balandina, V.V.; Igumnova, L.А.; Кotova, V.L.; Kruszkab, L.; Lomunova, А.K. Impact and penetration of cylindrical bodies into dry and water-saturated sand. Int. J. Impact Eng. 2018, 122, 197–208. [Google Scholar] [CrossRef]
- Savvateev, A.F.; Budin, A.V.; Kolikov, V.A.; Rutberg, P.G. High-Seed Penetration into Sand. Int. J. Impact Eng. 2001, 26, 675–681. [Google Scholar] [CrossRef]
- Miyai, S.; Kobayakawa, M.; Tsuji, T.; Tanaka, T. Influence of particle size on vertical plate penetration into dense cohesion-less granular materials (large-scale DEM simulation using real particle size). Granul. Matter 2019, 21, 105. [Google Scholar] [CrossRef]
- O’Loughlin, C.D.; Nazem, S.H.; Chow, M.F.; Randolph, C.; Gaudin, D.J.W. Dynamic Embedment of Projectiles in Clay. Aust. Geomech. 2009, 49, 133–145. [Google Scholar]
- Richardson, M.D.; O’Loughlin, C.D.; Randolph, M.F.; Gaudin, C. Setup following installation of dynamic anchors in normally consolidated clay. J. Geotech. Geoenviron. Eng. 2009, 135, 487–496. [Google Scholar] [CrossRef]
- Christensen, B.K. Twenty Five Years of Penetration Records at Sandia National Laboratories-PENTDB: A Relational Database; Report SAND 88-1402; Sandia National Laboratories: Albuquerque, NM, USA, 1989; p. 53. [Google Scholar]
- Cooper, W.L. Communication of Stresses by Chains of Grains in High-Speed Particulate Media Impacts; Proulx, T., Ed.; Dynamic Behavior of Materials, Conference Proceedings of the Society for Experimental Mechanics Series; Springer: New York, NY, USA, 2011; Volume 1. [Google Scholar] [CrossRef]
- Baker, W.E.; Westine, P.S.; Dodge, F.T. Similarity Methods in Engineering Dynamics: Theory and Practice of Scale Modeling; Spartan Books: Rochell Park, NJ, USA, 1973. [Google Scholar]
- Awoshika, K.; Cox, W.R. An Application of Similitude to Model Design of a Soil-Projectile System; NASA Contractor Report CR-1210; Department of Civil Engineering, The University of Texas at Austin, to National Aeronautics and Space Administration, Langley Research Centre: Hampton, VA, USA, November 1968. [Google Scholar]
- Anandarajah, A.; Kim, Y.S.; Thompson, P.Y.; Rosengren, P. Progress in Geotechnical Dynamic Centrifuge Modeling; Final Report No. ESL-TR-8462; Air Force Engrg. Services Ctr.: Tyndall Air Force Base, FL, USA, 1985. [Google Scholar]
- Taylor, T.; Fragaszy, R.J.; Ho, C.L. Projectile Penetration in Granular Soils. J. Geotech. Eng. 1991, 117, 658–672. [Google Scholar] [CrossRef]
- True, D.G. Undrained Vertical Penetration into Ocean Bottom Soils. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1976. Available online: http://search.proquest.com/docview/302795036 (accessed on 26 May 2020).
- Freeman, T.J.; Burdett, J.R.F. Deep Ocean Model Penetrator Experiments. Report CD-NA-10-502, 1986-EN-C; Directorate-General for Science, Research and Development: Brussels, Belgium. Available online: http://bookshop.europa.eu/en/deep-ocean-model-penetrator-experiments.-report-pbCDNA10502/ (accessed on 26 May 2020).
- Hossain, M.S.; O’Loughlin, C.D.; Kim, Y. Dynamic installation and monotonic pullout of a torpedo anchor in calcareous silt. Géotechnique 2015, 65, 77–90. [Google Scholar] [CrossRef]
- Robins, B. New Principles of Gunnery (Originially published in 1742). In Mathematical Tracts of the Late Benjamin Ribins; James, W., Ed.; Wright Printer, St. John’s Square: London, UK, 1761; Volume 1, p. 341. [Google Scholar]
- Resal, H. Sur la penetration d’un projectile dans les semi-fluides et les solides. Compte Rendus 1895, 120, 397–401. [Google Scholar]
- Faulstich, A.J.; Herring, H.J. Two Aspects of Earth Penetration: Measurement of Resistance to Burial and Theoretical Prediction of Penetration in Stratiform Soil; Report No. NOLTR 69-116; United States Naval Ordnance Laboratory: White Oak, MD, USA, 1969; p. 48. [Google Scholar]
- Ezzein, F.M.; Bathurst, R.J. A transparent sand for geotechnical laboratory modeling. Geotech. Test. J. 2011, 34, 590–601. [Google Scholar] [CrossRef]
- Ads, A.; Iskander, M.; Bless, S. Soil–projectile interaction during penetration of a transparent clay simulant. Acta Geotech. 2020, 15, 815–826. [Google Scholar] [CrossRef]
- Omidvar, M.; Iskander, M.; Bless, S. Soil–projectile interactions during low velocity penetration. Int. J. Impact Eng. 2016, 93, 211–221. [Google Scholar] [CrossRef]
- Brown, E.; Zhang, H.; Forman, N.A.; Maynor, B.W.; Betts, D.E.; DeSimone, J.M.; Jaeger, H.M. Shear thickening and jamming in densely packed suspensions of different particle shapes. Phys. Rev. E 2011, 84, 031408. [Google Scholar] [CrossRef]
- Bi, D.; Zhang, J.; Chakraborty, B.; Behringer, R.P. Jamming by shear. Nature 2011, 480, 355–358. [Google Scholar] [CrossRef] [PubMed]
- Albert, I.; Sample, J.G.; Morss, A.J.; Rajagopalan, S.; Barabási, A.L.; Schiffer, P. Granular drag on a discrete object: Shape effects on jamming. Phys. Rev. E 2001, 64, 061303. [Google Scholar] [CrossRef]
- Caudle, W.N.; Pope, A.Y.; McNeill, R.L.; Margason, B.E. The Feasibility of Rapid Soil Investigations using High-Speed, Earth-Penetrating Projectiles. In Proceedings of the International Symposium on Wave Propagation and Dynamic Properties of Earth Materials, Albuquerque, NM, USA, 23–25 August 1967. [Google Scholar]
- Lunne, T.; Robertson, P.K.; Powell, J.J.M. Cone Penetration Testing in Geotechnical Practice; Taylor & Francis: London, UK, 1997. [Google Scholar]
- Stark, N.; Hanff, H.; Kopf, A. Nimrod: A tool for rapid geotechnical characterization of surface sediments. Sea Technol. 2009, 50, 10–14. [Google Scholar]
- Lieng, J.T.; Tjelta, T.I.; Skaugset, K. Installation of two prototype deep penetrating anchors at the Gjøa Field in the North Sea. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2010; pp. 1999–2007. [Google Scholar] [CrossRef]
- Stephan, S.; Kaul, N.; Villinger, H. Validation of impact penetrometer data by cone penetration testing and shallow seismic data within the regional geology of the Southern North Sea. Geo-Mar. Lett. 2015, 35, 203–219. [Google Scholar] [CrossRef]
- Chow, S.H.; Airey, D.W. Free-falling penetrometers: A laboratory investigation in clay. J. Geotech. Geo-Environ. Eng. 2014, 140, 201–214. [Google Scholar] [CrossRef]
- Chian, S.C.; Tan, B.C.V.; Sarma, A. Projectile penetration into sand: Relative density of sand and projectile nose shape and mass. Int. J. Impact Eng. 2017, 103, 29–37. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Lee, L.M.; Jenrette, L.M. Laboratory-scale penetration experiments into geological targets to impact velocities of 2.1 km/s. J. Appl. Mech. ASME 1986, 53, 317–320. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Hanchak, S.J. Penetration limits velocity for ogive nose projectiles and limestone targets. J. Appl. Mech. ASME 2002, 69, 853–864. [Google Scholar] [CrossRef]
- Hearst, J.R.; Lynch, C.S. Measurement of in-situ strength using projectile penetration. Int. J. Rock Mech. Min. Sci. Geomech. 1994, 31, 243–251. [Google Scholar] [CrossRef]
- Ben-Dor, G.; Dubinsky, A.; Elperin, T. Engineering models of high-speed penetration into geological shields. Central Eur. J. Eng. 2014, 4, 1–19. [Google Scholar] [CrossRef]
- Nechitailo, N. Hypervelocity Penetration into Soil. Procedia Eng. 2015, 103, 427–435. [Google Scholar] [CrossRef][Green Version]
- Lohse, D.; van der Meer, D. Structures in sand streams. Nature 2009, 459, 1064–1065. [Google Scholar] [CrossRef]
- Parab, N.D.; Claus, B.; Hudspeth, M.C.; Black, J.T.; Mondal, A.; Sun, J.; Fezzaa, K.; Xiao, X.; Luo, S.N.; Chen, W. Experimental assessment of fracture of individual sand particles at different loading rates. Int. J. Impact Eng. 2014, 68, 8–14. [Google Scholar] [CrossRef]
- Bernard, R.S.; Creighton, D.C. Non-Normal Impact and Penetration: Analysis for Hard Targets and Small Angles of Attack; Technical Report S-78-14; U.S. Army Engineer Waterways Experiment Station Soils and Pavements Laboratory: Vieksburg, MS, USA, 1978. [Google Scholar]
- Byers, R.K.; Yarrington, P.; Chabai, A.J. Dynamic penetration of soil media by slender projectiles. Int. J. Eng. Sci. 1978, 16, 835–844. [Google Scholar] [CrossRef]
- Deboeuf, S.; Gondret, P.; Rabaud, M. Dynamics of grain ejection by sphere impact on a granular bed. arXiv 2008, arXiv:0808.2295. [Google Scholar] [CrossRef] [PubMed]
- Boudet, J.F.; Amarouchene, Y.; Kellay, H. Dynamics of impact cratering in shallow sand layers. Phys. Rev. Lett. 2006, 96, 158001. [Google Scholar] [CrossRef]
- Cintala, M.J.; Berthoud, L.; Horz, F. Ejection-velocity distribution from impact into coarse-grained sand. Meteor. Planet. Sci. 1999, 34, 605–623. [Google Scholar] [CrossRef]
- Poncelet, J.V. Introduction Ii la Mecanique Industrielle. Brussels, Belgium, 2nd ed.; Meline, Cans et Compagnie: Brussels, Belgium, 1839; p. 271. [Google Scholar]
- Ambroso, M.A.; Santore, C.R.; Abate, A.R.; Durian, D.J. Penetration depth for shallow impact cratering. Phys. Rev. E 2002, 71, 051305. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Shen, Z.; Wang, J. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances. Comput. Geotech. 2015, 65, 147–163. [Google Scholar] [CrossRef]
- Grigoryan, S.S. On basic concepts of soil dynamics. J. Appl. Math. Mech. 1960, 24, 1604–1627. [Google Scholar] [CrossRef]
- Buchely, M.; Maranon, A. Spherical Cavity Expansion Approach for the Study of Rigid-Penetrator’s Impact Problems. Appl. Mech. 2020, 1, 3. [Google Scholar] [CrossRef]
- Euler, L. Neue Grundsatze der Artillerie, 1st ed.; Reprinted in Euler’s Opera Omnia; Druck und Verlag Von B. G. Teubner: Berlin, Germany, 1922; p. 484. [Google Scholar]
- Petry, L. Monographies de Systemes D’artillerie; Meline, Cans et Compagnie: Brussels, Belgium, 1910. [Google Scholar]
- Patterson, W.J.; Albuquerque, N.M.; Sandia Laboratories. Untitled Letter Report to: Bernard, R.S. oil Dynamics Division; U.S. Army Engineer Waterways Experiment Station, CE: Vicksburg, MS, USA, 26 August 1976. [Google Scholar]
- Charters, A.C.; Summers, J.L. Comments on the Phenomena of High-Speed Impact; NOLR1238, U.S. Naval Ordance Lab.: White Oak, MD, USA, 1959; pp. 200–221. [Google Scholar]
- Young, C.W. Depth Prediction for Earth-Penetrating Projectiles. J. Soil Mech. Found. Div. Am. Soc. Civ. Eng. 1969, 95, 803–817. [Google Scholar]
- Adeli, H.; Amin, A.M.; Sierakowski, R.L. Earth penetration by solid impactors. Shock Vib. Dig. 1986, 18, 14–22. [Google Scholar] [CrossRef]
- Crull, M.; Taylor, L.; Tipton, J. Estimating ordnance penetration into earth. In Proceedings of the UXO Forum’99, Atlanta, GA, USA, 25–27 May 1999. [Google Scholar]
- Pensky, O.G. Mathematical Modelling of Dynamics of Driving Rigid Bodies into Continuous Medium using Heat Impulse Machines. Ph.D. Thesis, Perm State University, Perm, Russian, 2007. (In Russian). [Google Scholar]
- Richmond, P.W. Influence of Nose Shape and L/D Ratio on Projectile Penetration in Frozen Soil; Special Report No. 80-17; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1981. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).