World-Models for Bitrate Streaming
Abstract
1. Introduction
2. Background
2.1. Bitrate Streaming
2.2. Reinforcement Learning
- is the set of possible states;
- is the set of possible actions available to an agent;
- is the transition kernel for states and actions, the probability that an action a at state s leads to state ; and,
- is the reward function, the immediate reward from transitioning to state from s due to action a.
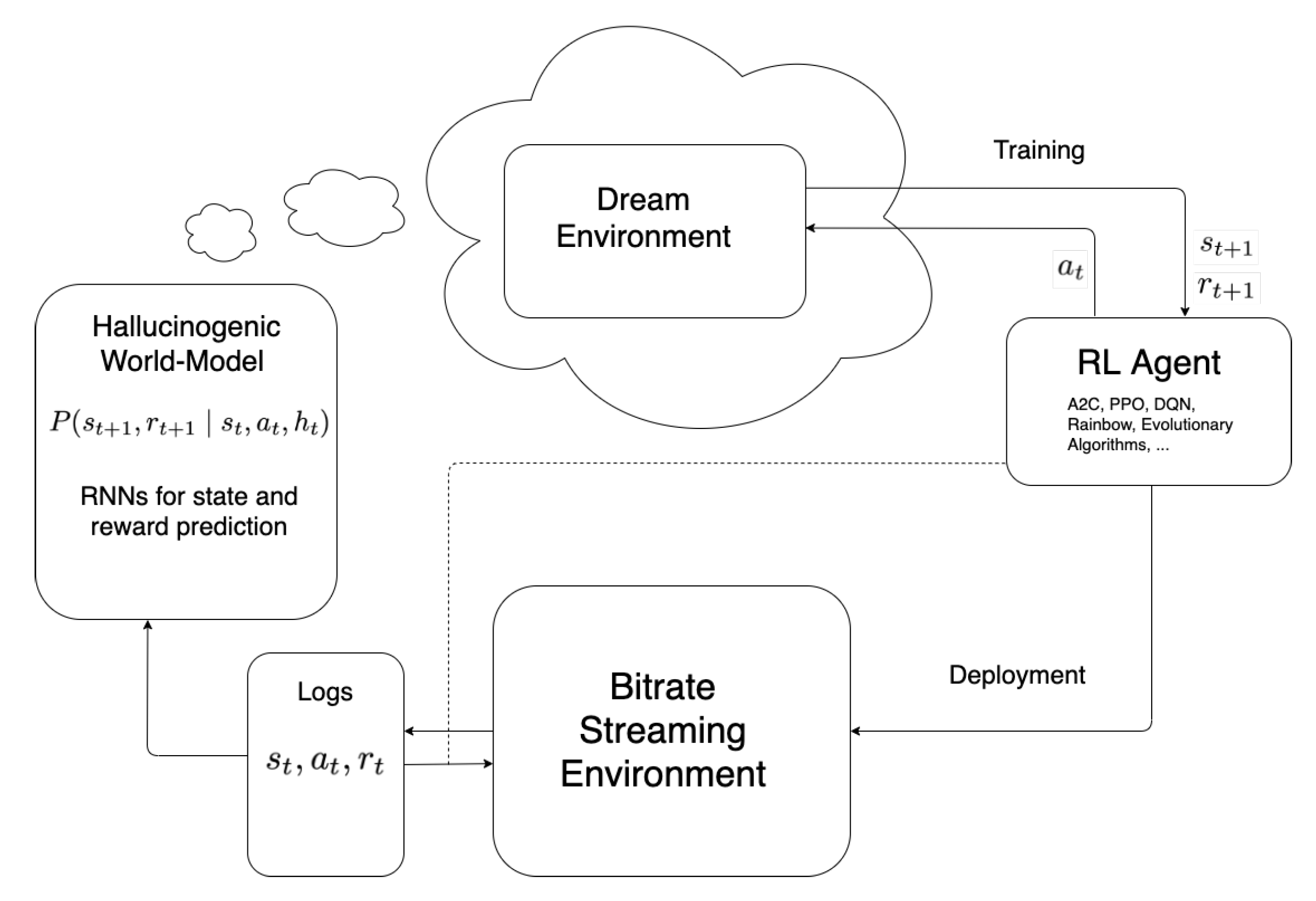
2.3. Motivation for World-Models
3. World-Models
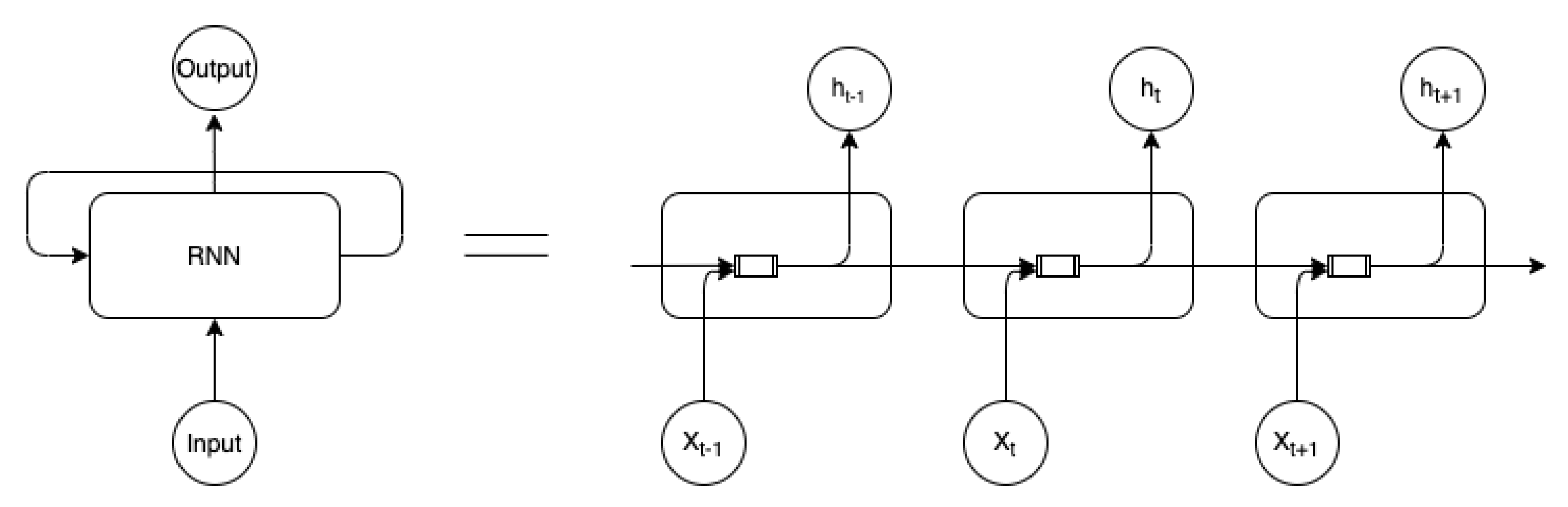
3.1. Generative Models
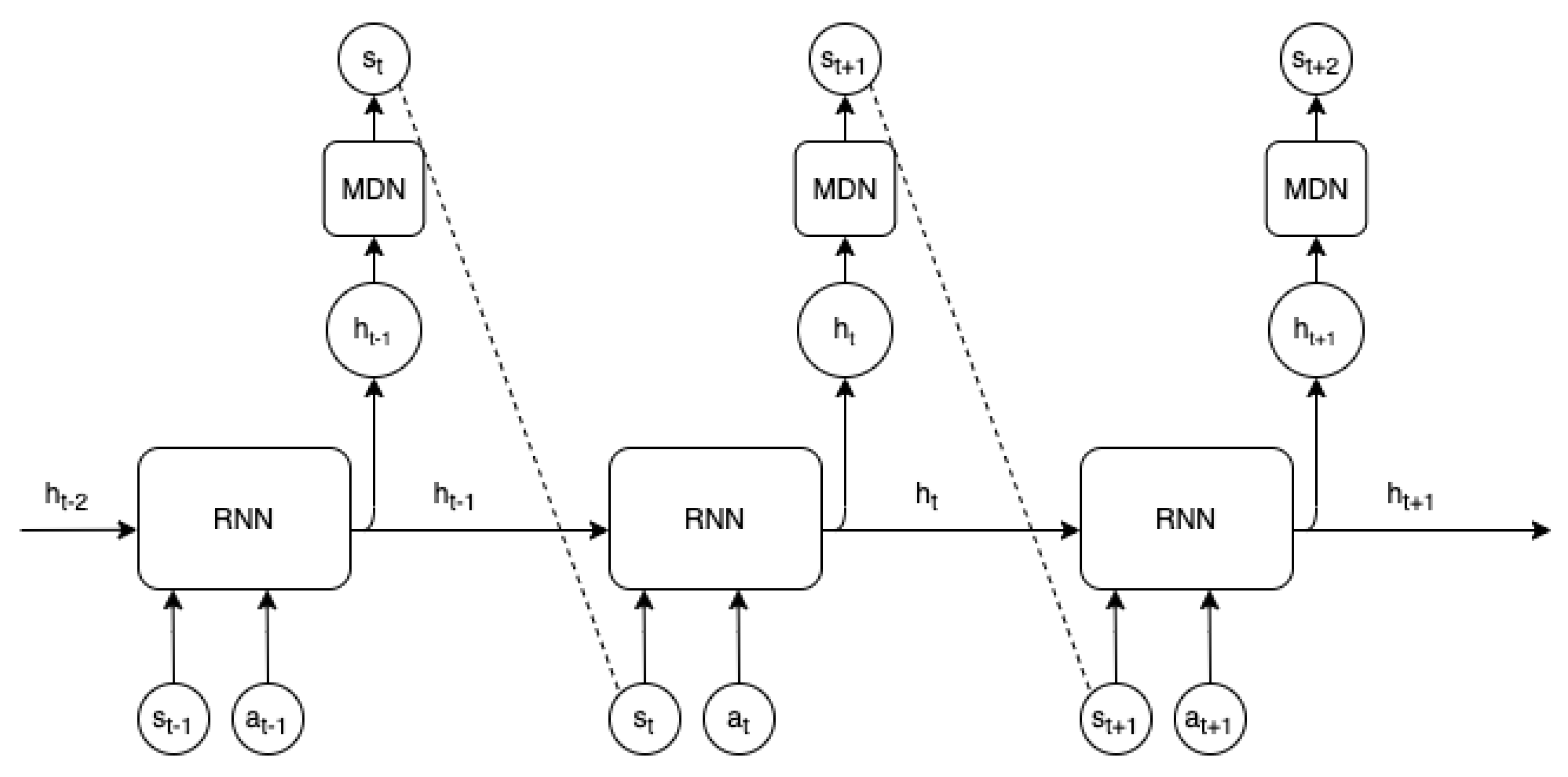
3.2. MDN-RNN World-Model
4. Design
4.1. World-Model Design
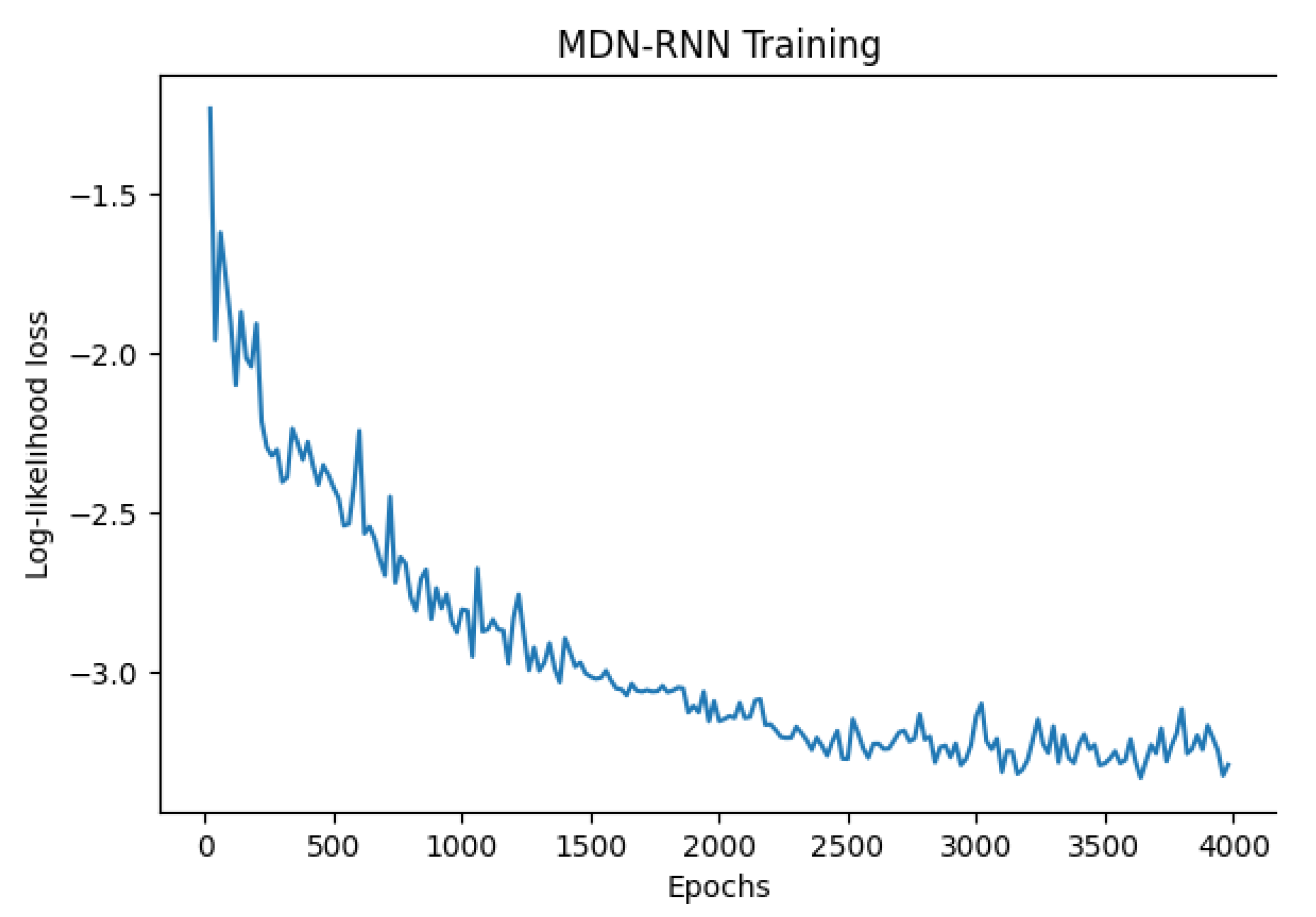
4.2. Training Methodology
5. Results and Discussion
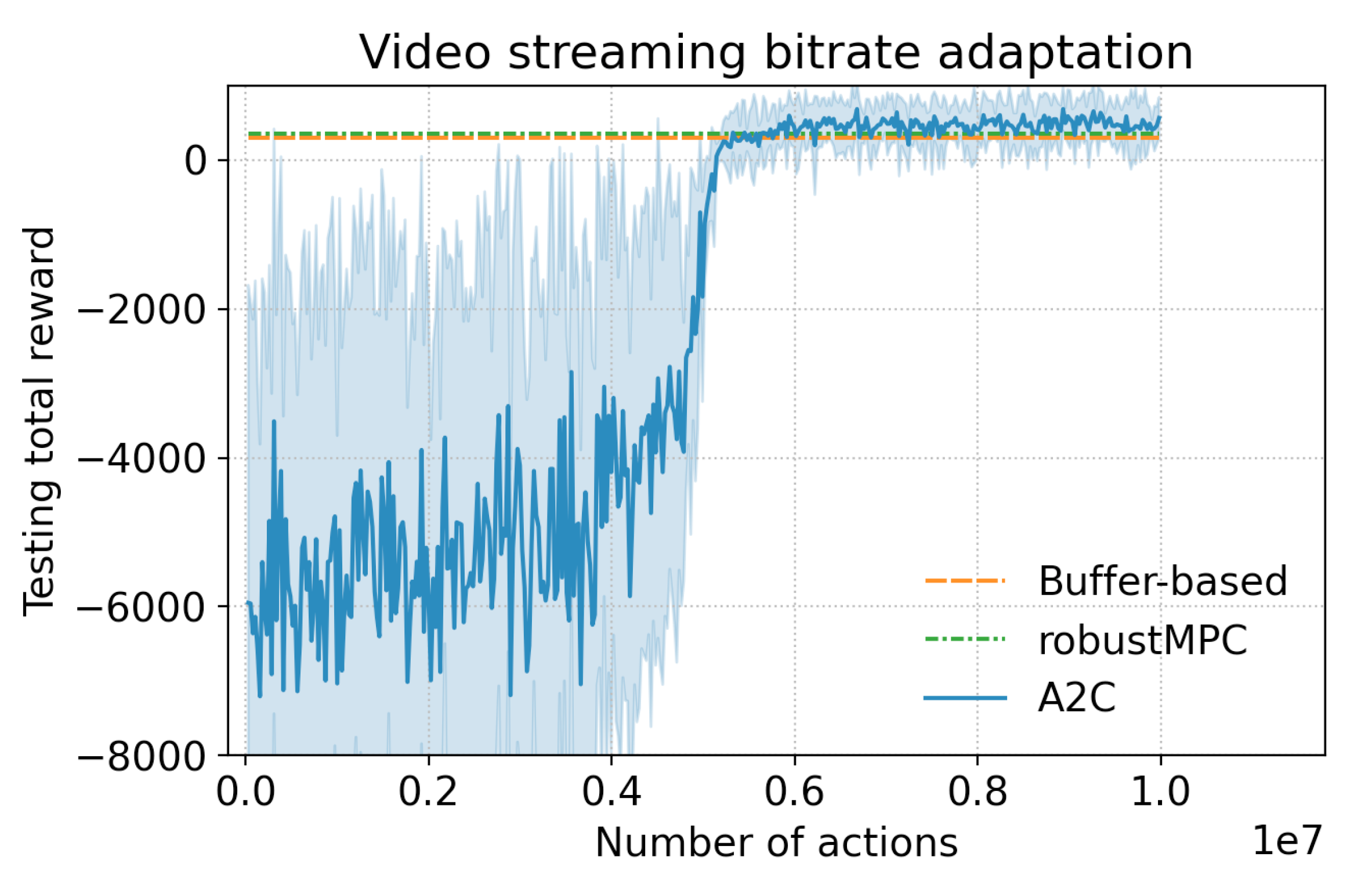
5.1. Baselines
5.2. Training in a Dream
5.3. Sample Complexity Bounds
5.3.1. Rainbow
5.3.2. World-Model Comparisons
5.4. Summary
5.5. Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ALE | Arcade Learning Environment |
| A2C | Advantage Actor-Critic |
| A3C | Asynchronous Advantage Actor-Critic |
| GMM | Gaussian Mixture Model |
| LSTM | Long Short-Term Memory |
| MDN-RNN | Mixture Density Network - Recurrent Neural Network |
| MDP | Markov Decision Process |
| MPC | Model Predictive Control |
| MSE | Mean Squared Error |
| Mbps | Megabits per second |
| POMDP | Partially Observable Markov Decision Process |
| RL | Reinforcement Learning |
| RNN | Recurrent Neural Network |
| TPE | Tree-structured Parzen Estimator |
| QoE | Quality-of-Experience |
Appendix A. Bitrate Streaming MDN-RNN
| Num Steps | 4000 |
| Input Sequence Length | 12 |
| Output Sequence Length | 11 |
| Batch Size | 100 |
| RNN Hidden State Size | 0.00005 |
| Number of Gaussians | 5 |
| Learning Rate | 0.005 |
| Grad Clip | 1.0 |
| Use Dropout | False |
| Learning Rate Decay | 0 |
Appendix B. Rainbow Hyperparameter Search
Appendix B.1. Grid Search
- Target Update Period: {50, 100, 1000, 4000, 8000}
- Update Horizon: {1, 3}
- Update Period: {1, 4}
- Min Replay History: {500, 5000, 20,000}
Appendix B.2. Autotuner
- Learning Rate: (0.01, 0.15)
- Target Update Period: (50, 20,000)
- Update Horizon: (1, 8)
- Update Period: (1, 8)
- Min Replay History: (100, 40,000)
References
- Mao, H.; Netravali, R.; Alizadeh, M. Neural Adaptive Video Streaming with Pensieve. In Proceedings of the Conference of the ACM Special Interest Group on Data Communication, Los Angeles, CA, USA, 21–25 August 2017; pp. 197–210. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. A Brief Survey of Deep Reinforcement Learning. arXiv 2017, arXiv:1708.05866. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement Learning: A Survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Schmidhuber, J. On Learning to Think: Algorithmic Information Theory for Novel Combinations of Reinforcement Learning Controllers and Recurrent Neural World Models. arXiv 2015, arXiv:1511.09249. [Google Scholar]
- Ha, D.; Schmidhuber, J. Recurrent World Models Facilitate Policy Evolution. In Advances in Neural Information Processing Systems 31; Curran Associates, Inc.: New York, NY, USA, 2018; pp. 2451–2463. Available online: https://worldmodels.github.io (accessed on 18 August 2020).
- Kaiser, L.; Babaeizadeh, M.; Milos, P.; Osinski, B.; Campbell, R.H.; Czechowski, K.; Erhan, D.; Finn, C.; Kozakowski, P.; Levine, S.; et al. Model-Based Reinforcement Learning for Atari. arXiv 2019, arXiv:1903.00374. [Google Scholar]
- Mao, H.; Negi, P.; Narayan, A.; Wang, H.; Yang, J.; Wang, H.; Marcus, R.; Shirkoohi, M.K.; He, S.; Nathan, V.; et al. Park: An Open Platform for Learning-Augmented Computer Systems. In Advances in Neural Information Processing Systems; Curran Associates Inc.: New York, NY, USA, 2019; pp. 2490–2502. [Google Scholar]
- Akamai. dash.js. Available online: https://github.com/Dash-Industry-Forum/dash.js/ (accessed on 18 August 2016).
- Huang, T.Y.; Handigol, N.; Heller, B.; McKeown, N.; Johari, R. Confused, Timid, and Unstable: Picking a Video Streaming Rate is Hard. In Proceedings of the 2012 Internet Measurement Conference, Boston, MA, USA, 14–16 November 2012; pp. 225–238. [Google Scholar]
- Bemporad, A.; Morari, M. Robust Model Predictive Control: A Survey. In Robustness in Identification and Control; Springer: Berlin/Heidelberg, Germany, 1999; pp. 207–226. [Google Scholar]
- Spiteri, K.; Urgaonkar, R.; Sitaraman, R.K. BOLA: Near-Optimal Bitrate Adaptation for Online Videos. In Proceedings of the IEEE INFOCOM 2016—The 35th Annual IEEE International Conference on Computer Communications, San Francisco, CA, USA, 10–15 April 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 1–9. [Google Scholar]
- Huang, T.Y.; Johari, R.; McKeown, N.; Trunnell, M.; Watson, M. A Buffer-Based Approach to Rate Adaptation: Evidence from a Large Video Streaming Service. In Proceedings of the 2014 ACM Conference on SIGCOMM, Chicago, IL, USA, 17–22 August 2014; pp. 187–198. [Google Scholar]
- Chebotar, Y.; Hausman, K.; Zhang, M.; Sukhatme, G.; Schaal, S.; Levine, S. Combining Model-Based and Model-Free Updates for Trajectory-Centric Reinforcement Learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 703–711. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Vinyals, O.; Ewalds, T.; Bartunov, S.; Georgiev, P.; Vezhnevets, A.S.; Yeo, M.; Makhzani, A.; Küttler, H.; Agapiou, J.; Schrittwieser, J.; et al. StarCraft II: A New Challenge for Reinforcement Learning. arXiv 2017, arXiv:1708.04782. [Google Scholar]
- Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A.; Fei-Fei, L.; Farhadi, A. Target-driven Visual Navigation in Indoor Scenes using Deep Reinforcement Learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3357–3364. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-Critic Algorithms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 1008–1014. [Google Scholar]
- Hessel, M.; Modayil, J.; Van Hasselt, H.; Schaul, T.; Ostrovski, G.; Dabney, W.; Horgan, D.; Piot, B.; Azar, M.; Silver, D. Rainbow: Combining Improvements in Deep Reinforcement Learning. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Dulac-Arnold, G.; Mankowitz, D.; Hester, T. Challenges of Real-World Reinforcement Learning. arXiv 2019, arXiv:1904.12901. [Google Scholar]
- Haj-Ali, A.; Ahmed, N.K.; Willke, T.; Gonzalez, J.; Asanovic, K.; Stoica, I. Deep Reinforcement Learning in System Optimization. arXiv 2019, arXiv:1908.01275. [Google Scholar]
- Buesing, L.; Weber, T.; Racaniere, S.; Eslami, S.; Rezende, D.; Reichert, D.P.; Viola, F.; Besse, F.; Gregor, K.; Hassabis, D.; et al. Learning and Querying Fast Generative Models for Reinforcement Learning. arXiv 2018, arXiv:1802.03006. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Generating Sequences With Recurrent Neural Networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- Bishop, C.M. Mixture Density Networks. 1994. Available online: http://publications.aston.ac.uk/id/eprint/373/ (accessed on 18 August 2020).
- Bellemare, M.G.; Naddaf, Y.; Veness, J.; Bowling, M. The Arcade Learning Environment: An Evaluation Platform for General Agents. J. Artif. Intell. Res. 2013, 47, 253–279. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, X.; Houthooft, R.; Schulman, J.; Abbeel, P. Benchmarking Deep Reinforcement Learning for Continuous Control. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1329–1338. [Google Scholar]
- Brockman, G.; Cheung, V.; Pettersson, L.; Schneider, J.; Schulman, J.; Tang, J.; Zaremba, W. OpenAI Gym. arXiv 2016, arXiv:1606.01540. [Google Scholar]
- Riiser, H.; Vigmostad, P.; Griwodz, C.; Halvorsen, P. Commute Path Bandwidth Traces from 3G Networks: Analysis and Applications. In Proceedings of the 4th ACM Multimedia Systems Conference, Oslo, Norway, 28 February–1 March 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 114–118. [Google Scholar]
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. Available online: https://github.com/hill-a/stable-baselines. (accessed on 18 August 2018).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2011; pp. 2546–2554. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
| Temperature | Dream Score | Real Score | Test Score | Real (Single Sweep) |
|---|---|---|---|---|
| 0.1 | 2064.1 ± 1.7 | −22,010.7 ± 694.1 | −18,215.6 ± 632.6 | −22,010.75 ± 10,986.6 |
| 0.5 | 1036.9 ± 253.1 | −3801.2 ± 2115.6 | −2304.6 ± 1978.1 | −4965.1 ± 4222.8 |
| 0.75 | 649.5 ± 136.8 | −2461.0 ± 2165.7 | −1696.4 ± 1695.5 | −1159.8 ± 1754.6 |
| 1 | 726.1 ± 177.4 | −437.6 ± 776.2 | −13.4 ± 535.9 | −1317.7 ± 1781.3 |
| 1.1 | 770.0 ± 32.0 | 159.1 ± 189.7 | 370.5 ± 80.8 | 61.2 ± 810.6 |
| 1.2 | 569.7 ± 242.2 | 220.3 ± 92.9 | 339.4 ± 100.5 | 192.3 ± 365.1 |
| 1.3 | 594.0 ± 19.5 | 175.6 ± 101.2 | 367.1 ± 29.4 | 290.1 ± 367.2 |
| 1.4 | 406.8 ± 34.0 | 235.6 ± 120.4 | 370.6 ± 60.0 | 316.7 ± 274.6 |
| 1.5 | 305.5 ± 69.1 | 309.0 ± 64.5 | 449.3 ± 32.3 | 315.3 ± 349.0 |
| 1.75 | −177.7 ± 36.4 | 362.4 ± 30.2 | 444.7 ± 17.6 | 396.3 ± 279.9 |
| 2 | −952.0 ± 39.2 | 402.3 ± 8.8 | 476.2 ± 24.0 | 392.2 ± 193.5 |
| 2.25 | −5686.5 ± 5295.1 | −1595.8 ± 3052.8 | −1178.3 ± 2381.2 | 132.0 ± 46.1 |
| 2.5 | −7753.0 ± 5860.0 | −1585.1 ± 3039.7 | −1267.3 ± 2488.4 | 202.6 ± 383.1 |
| 3 | −17,087.6 ± 5885.9 | −3390.0 ± 3106.3 | −2570.8 ± 2434.8 | −5021.2 ± 4105.5 |
| Temperature | Dream Score | Real Score | Test Score | Max Average Real Score |
|---|---|---|---|---|
| 1 | −3532.04 ± 2848.57 | −1525.94 ± 88.95 | 195.52 ± 100.36 | 282.45 ± 109.67 |
| 1.25 | −5666.19 ± 7003.71 | −4158.25 ± 2865.73 | −1205.58 ± 2329.62 | 132.80 ± 38.21 |
| 1.5 | −13,128.57 ± 10942.65 | −437.6 ± 6462.24 | −3375.84 ± 5514.53 | 320.92 ± 113.37 |
| 2 | −235.71 ± 13.72 | 369.18 ± 9.25 | 478.96 ± 3.26 | 378.79 ± 309.28 |
| 2.25 | −1628.17 ± 7.91 | 429.08 ± 11.65 | 557.84 ± 5.87 | 441.09 ± 316.88 |
| Temperature | Dream Score | Real Score | Test Score | Max Average Real Score |
|---|---|---|---|---|
| 0.75 | 550.04 ± 22.86 | −813.62 ± 764.66 | −403.87 ± 659.83 | 68.85 ± 826.89 |
| 1 | 453.31 ± 12.76 | 96.09 ± 50.03 | 382.93 ± 30.09 | 151.88 ± 826.91 |
| 1.25 | 291.33 ± 61.87 | −37.10 ± 132.88 | 247.92 ± 87.29 | 82.31 ± 648.22 |
| 1.5 | 158.27 ± 126.67 | 280.53 ± 182.38 | 428.88 ± 83.72 | 399.79 ± 245.12 |
| Num. Actions | Agent | Mean Episode Score | STDEV |
|---|---|---|---|
| - | Random Agent | −5729.3 | −4250.1 |
| - | Buffer-based Agent | 237.7 | 435.4 |
| - | RobustMPC Agent | 286.2 | 502.5 |
| 5 M | A2C Model-free Agent | 500.5 | 358.8 |
| 5 M | Best World-model Agent | 408.71 | 280.5 |
| 1 M | Best World-model Agent | 441.0 | 316.8 |
| 1 M | Best Rainbow Agent | 306.3 | 316.3 |
| 500 k | Best World-model Agent | 399.7 | 245.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, H.; Fricke, K.; Yoneki, E. World-Models for Bitrate Streaming. Appl. Sci. 2020, 10, 6685. https://doi.org/10.3390/app10196685
Brown H, Fricke K, Yoneki E. World-Models for Bitrate Streaming. Applied Sciences. 2020; 10(19):6685. https://doi.org/10.3390/app10196685
Chicago/Turabian StyleBrown, Harrison, Kai Fricke, and Eiko Yoneki. 2020. "World-Models for Bitrate Streaming" Applied Sciences 10, no. 19: 6685. https://doi.org/10.3390/app10196685
APA StyleBrown, H., Fricke, K., & Yoneki, E. (2020). World-Models for Bitrate Streaming. Applied Sciences, 10(19), 6685. https://doi.org/10.3390/app10196685





