Next Article in Journal
Effect of Carbonation Curing on Physical and Durability Properties of Cementitious Materials Containing AOD Slag
Previous Article in Journal
Variable Guide Vane Scheduling Method Based on the Kinematic Model and Dual Schedule Curves
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 10
Issue 19
10.3390/app10196644
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Migration of the 3T3 Cell with a Lamellipodium on Various Stiffness Substrates—Tensegrity Model

by
Arkady Voloshin
Department of Mechanical Engineering and Mechanics and Bioengineering, Lehigh University, Bethlehem, PA 18017, USA
Appl. Sci. 2020, 10(19), 6644; https://doi.org/10.3390/app10196644
Submission received: 30 August 2020 / Revised: 17 September 2020 / Accepted: 18 September 2020 / Published: 23 September 2020
(This article belongs to the Special Issue Cell Motility and Collective Cell Migration Modelling)
Browse Figures
Versions Notes

Abstract

:
Changes in mechanical stimuli and the physiological environment are sensed by the cell. Thesechanges influence the cell’s motility patterns. The cell’s directional migration is dependent on the substrate stiffness. To describe such behavior of a cell, a tensegrity model was used. Cells with an extended lamellipodium were modeled. The internal elastic strain energy of a cell attached to the substrates with different stiffnesses was evaluated. The obtained results show that on the stiffer substrate, the elastic strain energy of the cell adherent to this substrate decreases. Therefore, the substrate stiffness is one of the parameters that govern the cell’s directional movement.

1. Introduction

A single cell migration is an important component of many biological events. It may be initiated by number of various factors, such as mechanical [1] (mechanotaxis), electrical [2] (galvanotaxis), thermal [3] (thermotaxis), topological [4,5] (topotaxis) and chemical [6] (chemotaxis). Cell migration is dependent on many factors, among these the mechanical interaction between the adherent cell and the substrate. The particular mechanisms that govern how the various environmental factors influence the cell’s biological responses are not well known. However, it is obvious that physical environmental changes in the cell’s motility and morphology are influenced by the cell’s internal mechanical balance [7]. It was shown that an adherent cell senses mechanical stimulus [8,9,10] and responds to it by keeping the cell’s intracellular and extracellular forces in balance [11,12].
Many studies have focused on developing a mechanism called “mechanotransduction”. It is a process that allows a cell to sense mechanical loads and to transduce them into a biochemical signal. It has been shown that the motility of a cell is dependent on the substrate’s stiffness [13,14,15]. Lo [13] called this process a “durotaxis”. This process is dependent on the assumption that a cell is capable of probing the stiffness of the substrate it is adherent to and respond to it by applying contractile forces. A number of theoretical [16] and numerical [17,18,19] models were developed to describe and understand the mechanical cellular responses. Numerical mechanical models based on the finite element analysis of tensegrity structures [20,21] are often utilized to describe the cell’s response to environmental mechanical stimuli.
Modifications in the morphology and structure of the cell due to the external loads are important for various cell functions, as growth, proliferation, differentiation and motility [22,23]. It was shown that the directional motility of a cell is a significant part of tumor metastasis and wound healing [24,25].
The formation of focal adhesion and cell migration [26,27] is dependent on the forces generated within the actin cytoskeleton, as these forces are dependent on the cell’s interaction with the extracellular matrix.
Through probing the environment, i.e., the substrate’s stiffness, cells can guide their activities that will lead to changes in the morphologies and direction of migration.
A recent study [28] showed that cells are capable of sensing and reacting to the substrate’s stiffness. Conversely, the opposite results were obtained [29] for epithelial cells. They were more often extending into branches while on a low stiffness substrate than on a stiffer substrate.
Models have been introduced to understand and describe cell behavior on the substrates with different stiffnesses [30,31,32,33,34,35,36,37,38]. These models provide an understanding of the effects of the substrate’s physical properties on adherent cell morphologies and motility.
Two main approaches are used to investigate the reaction of the cells to environmental changes: continuum [31,32,33,34] and discrete approaches [31,36,37,38].
In continuum mechanical models, the cells are treated as a continuum material. The continuum approach was successfully utilized to present a blood cell as a viscous liquid, while the cortex as a membrane [32]. It was used to study the small deformation characteristics of leukocytes [34]. It was also used to model the interaction of a single chondrocytes with the extracellular matrix [33].
The discrete models are based on the micro and nano-structural approach. They comprise a tensegrity model, an open-cell foam model, tensed cable network model, or a spectrin network model, to name a few. A cytoskeleton is a main structural component in micro and nano structural approaches when modeling the adherent cell [31]. A prestressed tensegrity network model was successfully used to describe the deformation of the adherent cell and compared with the values measured on cells in vivo and on isolated actin filaments [31].
The tensegrity-based architecture was introduced by Buckminster Fuller in 1961 [35]. The approach of tensegrity is often used to describe how tissues and cells are constructed and respond to external excitation [36].
The tissues may act as a continuous structure at the macroscopic scale, however, they should be treated as discrete structural entities when viewed at the microscale [37]. Cells form attachments to the substrate and neighboring cells that distribute over the cell’s surfaces discretely [38]. A tensegrity structure can easily represent these features.
As it was mentioned above [1,2,3,4,5,6], there are number of factors influencing a cell migration, the current work only examines the effect of the substrate’s mechanical properties (stiffness) on cell migration.
In this paper, a tensegrity structure was used to model the cell–substrate interaction to explain the dependency of the cell’s motility on the stiffness of the substrate. During the cell’s attachment to a substrate, the geometry of the cell changes similarly to the effect of the application of external loads to the cell membrane. The movement of the cell along a substrate is dependent on its internal elastic strain and interfacial energies.
It is hypothesized here that a cell probes its environment and guides its directional movement depending on the underlying substrate stiffness. It is also hypothesized that a cell senses the stiffness of the substrate in a number of directions by extending the lamellipodium. When the cell finds a direction that would decrease its internal elastic strain energy, it chooses it as the preferred direction of the movement. It is also hypothesized that this direction corresponds to the direction of the higher stiffness of the substrate. Since the cell prefers to stay in the lowest possible energetic state [39,40], it will select the migration direction that will lower its internal elastic energy. In other words, giving the choice of substrate stiffness, the cell will move and adhere to the stiffer area of the substrate since its internal elastic energy would be lower.
One of the mechanisms that allows a cell to migrate is to use lamellipodia. The lamellipodia and filopodia are the structures extending from the leading edge of a cell (Figure 1). A thin protrusion filled with a network of actin is a lamellipodium. Filopodia may be described as ‘sensors’ that cells use to probe their environment [41]. When a cell probes any substrate, the lamellipodia expands. When a cell encounters a soft substrate, the lamellipodia retracts causing the cell to change directions [1].
The experimental observation of the cell–substrate interaction was used to develop a tensegrity-based model. This allows to model the cell probing of the stiffness of a substrate. During this process, the internal elastic strain energy of the cell is changed. The cytoskeleton and lamellipodium of a cell were represented as a tensegrity structure with the prestress. Its internal elastic strain energy was evaluated by a finite element method for an array of the substrate’s stiffness value.

2. Materials and Methods

2.1. Tensegrity Model

A tensegrity structure comprises of a network of connected elements each supporting compression or tension. They are arranged to provide a stable volume and shape in the space while loaded by external loads. The tensegrity structure (Figure 2) is a useful tool to describe the cell motion and morphology changes because it is based on the mechanical integrity and equilibrium through the coordination of the tensile actin filaments and compressive microtubules [42,43]. The tensegrity model is constructed from the set of compression components inside of a net of tension components that keep the compressed members from each other. The tensile elements provide a load-supporting capability to the structure. Tensegrity models were used to describe the mechanical responses of various cells, like viruses and erythrocytes [36].
The basic tensegrity model (Figure 2) consists of 30 elements. Six pre-compressed struts represent microtubule members and 24 pre-tensed cables represent the microfilaments.
The current tensegrity structure (Figure 3) represents the cytoskeleton of a 3T3 cell, its nucleus, and lamellipodia. 3T3 cells are mouse fibroblast cells [43]. The 3T3 cells originated from a 1962 cell line [44]. In this model, a spring element is added between node 46 and 49 that will simulate the connection of a cell to the substrate. The spring element’s stiffness varies to simulate the substrate stiffness so that the strain energy of the model can be found at each stiffness value.
The intermediate filaments have been ignored since their influence on the cell’s mechanical behavior becomes significant only at the high deformations of the cell (over 20%) [45,46], but at the small deformation of the cell, there is only a slight increase in the reaction force when the intermediate filaments are added.
A recent study found that the elastic energy of the cytoskeleton of a 3T3 cell is a dependent on the substrate stiffness it is attached to [47]. The current study aims to find the internal elastic strain energy of a cytoskeleton, its nucleus, and the lamellipodium of a 3T3 cell for a range of the substrate stiffness values.
Node 3 is located at the coordinate system’s origin and represents the point of focal adhesion. This links the substrate and cell and it is fixed in the current model. All other nodes can move in any direction to simulate the cell spreading; however, no rotation is allowed. The length of the cables and struts of this model are able to change due to the response to the applied prestress and deformation.
The distance between the “superior plane” (the top X–Y plane) and the “inferior plane” (the bottom X–Y plane) represents the initial cell height of 8.7 μm. The superior and interior planes were set to be parallel to the X–Y plane before the application of deformation.
Three tensegrity structures are shown in Figure 3. The furthest to the left with the largest structure is the tensegrity model of the cytoskeleton and the nucleus of a 3T3 cell. The two smaller structures to the right represent the lamellipodium of the 3T3 cell. The spring element connecting nodes 46 and 49 represent substrate stiffness.

2.2. Material Properties of the Elements

Link 180, Beam 188 and Combine 14 from the ANSYS (Canonsburg, PA, USA) elements library were used to model the microtubules, microfilaments and substrate stiffness. Link 180 and Beam 188 are three-dimensional truss elements. The Link 180 element represents elements of the cable system, and the Beam 188 element represents the compressive elements of the strut system. The Combine 14 element was used to represent the substrate’s stiffness. All the elements of the model were treated as linear elastic members. The mechanical properties used in the current analysis are summarized in the Table 1. The cross-sectional area of the microtubules was 45.2 × 10−17 m2 and of the microfilaments 45.2 × 10−17 m2 [48]. It was hypothesized earlier that the microtubules cannot be extended [49], but for the purpose of this investigation the microtubules and microfilaments are assumed to be completely elastic. The length of the microtubule elements was selected to be 2.4 × 10−5 m and the microfilaments 1.467 × 10−5 m [50]. These values are summarized in Table 1.
The attachment of the cell to the surface was modeled via focal adhesion. The migration of various types of cells on different substrates were experimentally studied. A recent study used a flat PDMS substrate to study REF52 fibroblast cell migration as a function of the substrate’s stiffness gradients. In this study, the stiffness was in the range from 0.003 N/m to 1.4 N/m [51]. Gray [52] evaluated acrylamide and PDMS substrates. The Young’s moduli were 2.5 ± 0.2 MPa for acrylamide and 12 ± 1 kPa for PDMS. The cross-section area of the substrate was about 10 mm × 50 mm with the height of 1 mm. Stiffness is evaluated as function of the Young’s modulus and the dimensions of the substrate: K = (AE)/L, where A = cross sectional area, L = length, and E is Young’s modulus. The PDMS’s stiffness was calculated to be between 2.6 N/m and 540 N/m. The substrate was made from PDMS, however, by using range of PDMS concentrations the substrates with different rigidities could be generated. The stiffness range of the substrate in this study was selected to be from 10−3 to 1000 N/m.

2.3. Prestress

A cellular prestress allows resisting extracellular forces and maintaining cell morphology [53]. It was suggested [54] that the prestress and the cells’ mechanical properties impact the deformation of a cell. The prestress is needed to make the model behave comparable to the behavior of the cell in-vivo since the amount of prestress affects the cells’ stiffness and allows to the model keep its original shape. Thus, prestress was applied to the current cytoskeleton model. It was found that the prestress has small effect on the cell directional movement due to the changes in the substrate stiffness [47]. In this study, the prestress tension of 0.8 × 10−14 N was applied to microfilaments and a compressive force of −1.92 × 10−14 N was applied to the microtubule elements of the model.

2.4. Simulation Procedure

The cell model can sense and evaluate the stiffness of the substrate by extending one of its nodes. To probe the substrate stiffness, the cell extends and attaches one of the nodes to the substrate. Due to this process, the cell’s internal elastic strain energy changes. The stiffness of the substrate was modeled by a spring element between nodes 46 and 49 (Figure 3). The internal cell strain energy is then calculated for the corresponding stiffness value. Since a cell prefers to stay in a low energy state, it is assumed that the lower the internal strain energy, the likelier it is that the cell will move towards that stiffness value.
To begin the simulation, prestress forces were applied to all elements. This causes a change in the nodes’ locations because the length of the microfilaments and microtubules was changed. The new node positions are calculated. The next step is to apply the same displacement to nodes 46 and 49. The displacement of the spring element between node 46 and node 49 is 1 × 10−6 m in the X direction. This displacement, however, creates a reaction force at the nodes. The new nodes’ locations and reaction forces are calculated from this step to be used in the next steps. In the third step, node 49 is fixed. The reaction forces from node 46 are then applied to find the total strain energy of the cell.

2.5. Cell Movement Mapping

After the relationship between the cell’s internal strain energy and substrate stiffness is developed, the mapping of the anticipated cell movement on a substrate with a variable stiffness can show the cell’s tendency to move towards the higher stiffness value. This is done by the conduction of Monte Carlo simulations in MATLAB. A plane simulating the substrate was created by assuming a diagonal with increasing stiffness values. Based on these values and the use of a random number generator, one can simulate a surface with quasi-random varying stiffness. The sample of such a generated surface is shown in Figure 4. This surface stiffness distribution will be used to predict the movement of the cell utilizing the principle of searching for a minimum internal elastic energy.
The algorithm to model cell migration on the substrate was built. From a given starting position, the cell probes the surrounding substrate and moves towards the location with the locally highest stiffness value. This process is repeated until the cell cannot find any position with the local stiffness higher than at its current position.

3. Results

Simulations were performed while the cell was placed on the flat substrate with no topological preference, thus only the substrate stiffness was a guiding factor for the cell motion. To analyze the effect of the stiffness on the cell’s favored direction of motion, the model was solved for an array of the substrate stiffness values.

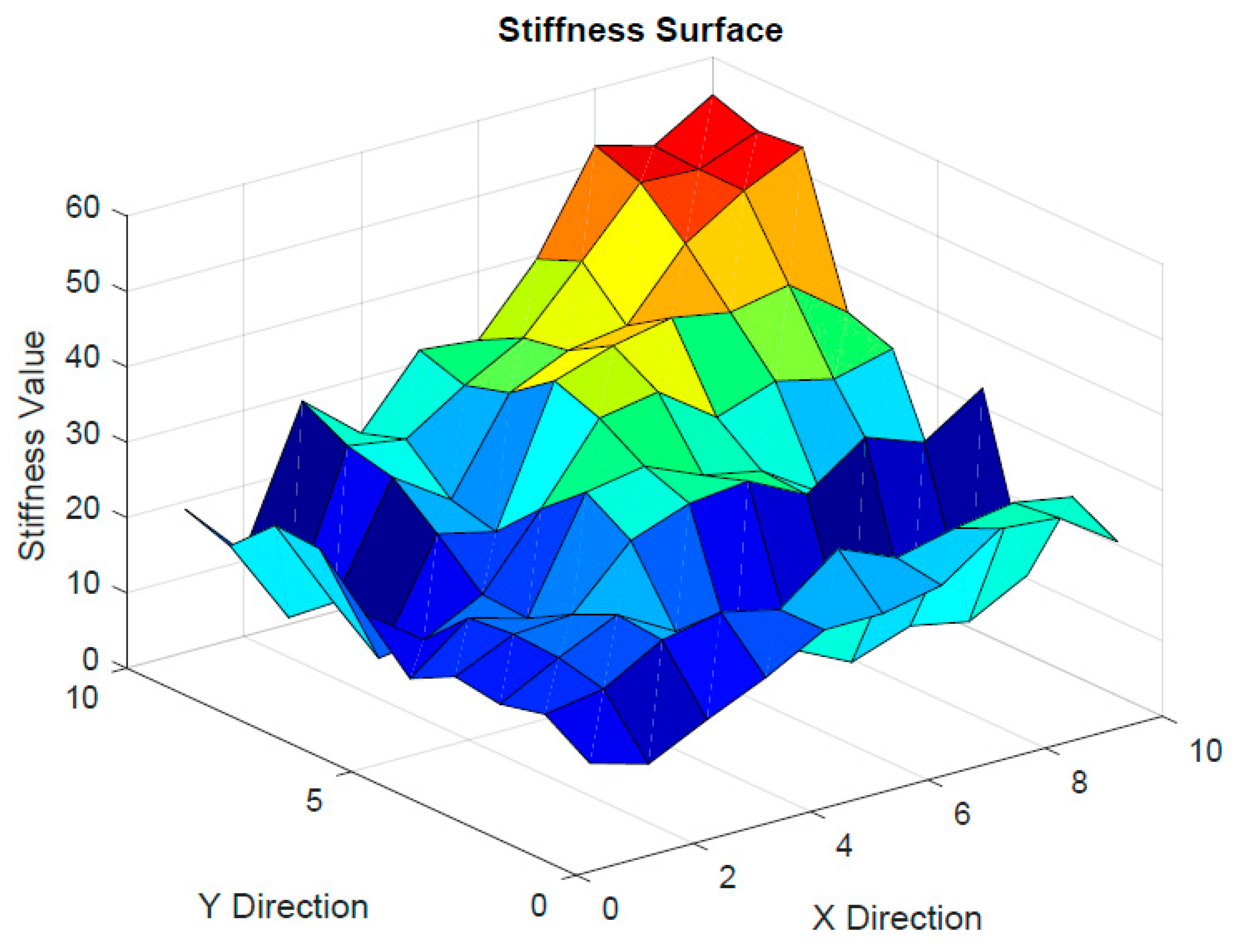
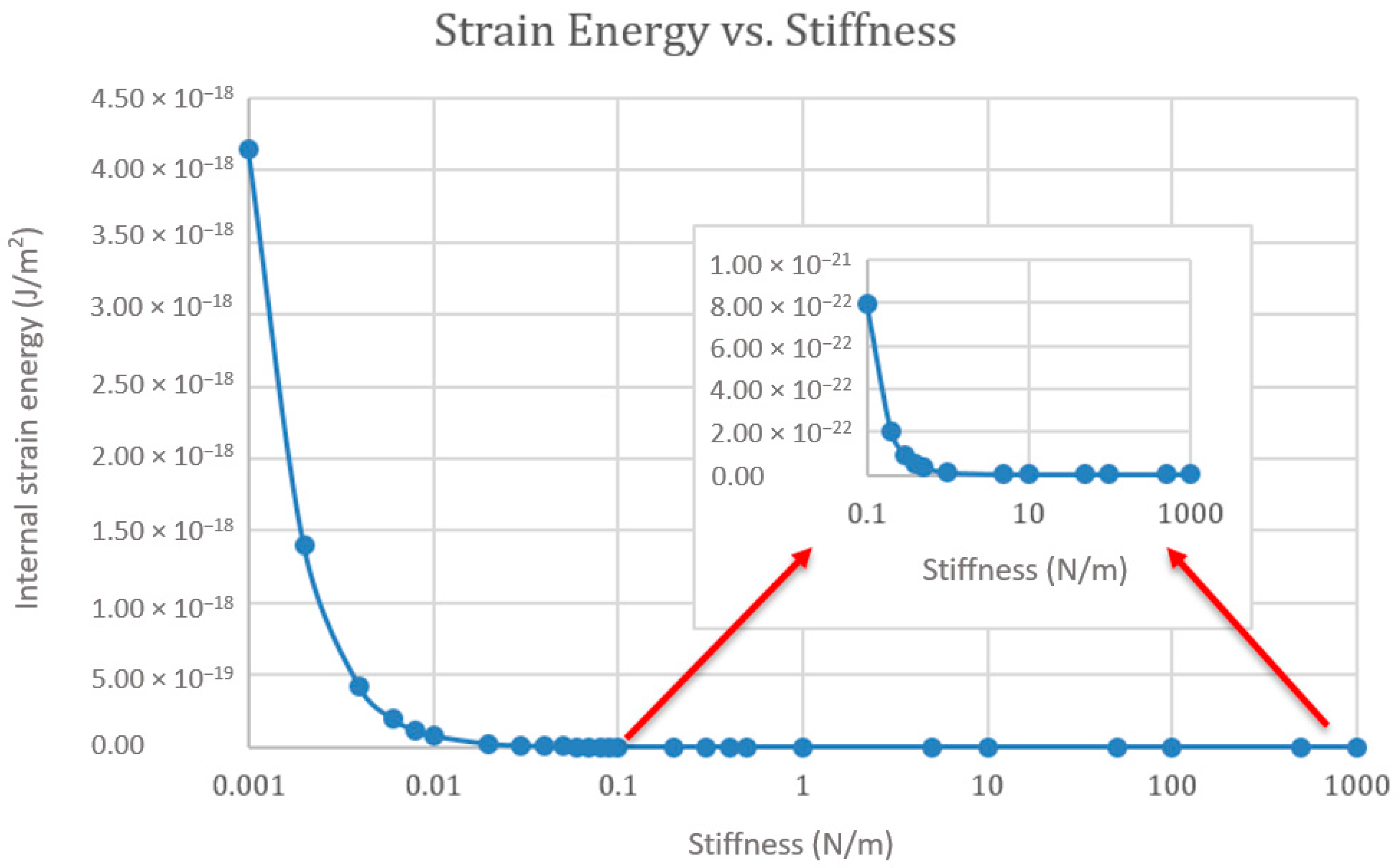
Effect of the Substrate Stiffness on the Cell’s Strain Energy

ANSYS Mechanical APDL solver was utilized to calculate the internal strain energy of the cell adherent to the substrates with changed stiffnesses. The effect of the substrate stiffness can be visually seen on the image of the cell’s geometry while the cell is on a substrate with a low stiffness (Figure 5) and a high stiffness (Figure 6).
One can see that the cell in Figure 5 is more deformed than the cell in Figure 6. This makes sense since the larger deformation of a soft substrate causes the larger deformation of the cell. Conversely, the more rigid the substrate is, the less deformation of the cell is observed.
The relationship between the cell’s internal strain energy and the substrate’s stiffness is shown in Figure 7.
Running the algorithm to model the cell’s motion on the simulated substrate (Figure 4) results in the predicted path as shown in Figure 8. Starting from the initial location at the point (0,0) with the lowest local stiffness, the cell eventually arrives to the location at the point (8,10) that had the highest stiffness value. The general path is towards the area with the highest local stiffness.

4. Discussion

It was hypothesized here that the cell’s motion is guided by the cell’s probing of the substrate’s stiffness and the selection of the direction that will lead to the region of the higher substrate stiffness. From the principle of conservation of energy, the cell preferred to be in the lowest possible energetic state. Experiments revealed that the cells usually probe their environment by lamellipodial extensions [55,56]. This action guides their movement to accord to the substrate stiffness [57]. The results of the current analysis, utilizing the tensegrity model for the cytoskeleton with a lamellipodia, show that with the substrate stiffness increase, the adherent cell internal elastic strain energy decreases. This is the reason for the cell’s movement to the more rigid area of the substrate. It was shown [14,27] that the mechanical interaction between the substrate and cell adjusts the morphology and migration of the cell. Ni and Chiang [39] modeled the influence of the substrate stiffness on a cell’s morphology and migration. The model showed that the internal elastic strain energy of the cell was affected by intracellular and extracellular forces and led to changes in the cell’s morphology and migration activity. The result being that the increase in the substrate’s stiffness leads to the lower internal elastic energy state of cell. The experiments presented here confirm the results of the possible cell’s movement utilizing the tensegrity model. The similar experimental results were presented in the study of 3T3 cells while culturing them on flexible polyacrylamide sheets [13]. By controlling the material concentrations, the regions with different stiffness on the same substrate sheet were created. It was shown that the cell’s migration rate increased when the cell crossed the boundary between the low and higher stiffness area. Thus, the cells preferred to migrate in the direction of the stiffer region. This experiment supports the results calculated on the basis of the tensegrity model of the cell.
Mapping the migration of a cell on a substrate with the varying stiffness (Figure 4) can help in predicting the cell’s movement along the surface with varying stiffness (Figure 8). The proposed procedure may be useful in the prediction of the directional movement of the cell. Since it has been verified that a cell’s movement is the function of internal strain energy, mapping the cell’s movement should be possible as long as the substrate’s stiffness is known.
The simulation results support the evidence that the cell migration is guided by the substrate stiffness since it leads to the minimization of the internal elastic energy of a cell. The cell’s migration is guided by a multifaceted interplay of physical and chemical signals, including substrate stiffness.

5. Conclusions

The tensegrity model of a cell adherent to various substrates was studied here. The obtained results supported the hypothesis that the stiffer the substrate is where the cell is located, the lower the internal cell elastic strain energy is. Since the attachment of the cells with lower internal elastic strain energy and substrates are more stable, it would increase the cells’ focal adhesions and functional efficiencies [58]. Such attachments could result in a cell migration from the region with lower stiffness to the stiffer part of the substrate.
The substrate’s stiffness plays an imperative role in the cell’s directional movement. It was established that the cell’s elastic strain energy will decrease with the increase in the substrate’s stiffness. This relationship explains the fact that on a substrate with gradient stiffness, the cells move towards stiffer regions as it was experimentally observed.
The obtained results confirm that the internal elastic strain energy of a cell is dependent on the mechanical properties of the extracellular environment. By studying the cell’s response to the various substrate rigidities it was shown that the cells will migrate to the location that will lower their internal elastic energy which supports the available experimental data.

Funding

This research received no external funding.

Acknowledgments

I would like to acknowledge Alan Wopperer’s help in creating and running the ANSYS code.

Conflicts of Interest

The author declares that there is no conflict of interest.

References

  1. Lo, C.M.; Wang, H.B.; Dembo, M.; Wang, Y.L. Cell movement is guided by the rigidity of the substrate. Biophys. J. 2000, 79, 144–152. [Google Scholar] [CrossRef] [Green Version]
  2. Curtze, S.; Dembo, M.; Miron, M.; Jones, D.B. Dynamic changes in traction forces with DC electric field in osteoblast-like cells. J. Cell Sci. 2004, 117 Pt 13, 2721–2729. [Google Scholar] [CrossRef] [Green Version]
  3. Umemura, K.; Miyabayashi, T.; Taira, H.; Suzuki, A.; Kumashiro, Y.; Okano, T.; Mayama, S. Use of a microchamber for analysis of thermal variation of the gliding phenomenon of single Navicula pavillardii cells. Eur. Biophys. J. 2015, 44, 113–119. [Google Scholar] [CrossRef] [PubMed]
  4. Yalcintas, E.P.; Hu, J.; Liu, Y.; Voloshin, A. Modeling cell spreading and alignment on micro-wavy surfaces. Comput. Modeling Eng. Sci. 2014, 98, 151–180. [Google Scholar] [CrossRef]
  5. Park, J.S.; Kim, D.-H.; Levchenko, A. Topotaxis: A new mechanism of directed cell migration in topographic ecm gradients. Biophys. J. 2018, 114, 1257–1263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Walsh, D.I., 3rd; Lalli, M.L.; Kassas, J.M.; Asthagiri, A.R.; Murthy, S.K. Cell chemotaxis on paper for diagnostics. Anal. Chem. 2015, 87, 5505–5510. [Google Scholar] [CrossRef]
  7. Stamenović, D.; Ingber, D.E. Tensegrity-guided self assembly: From molecules to living cells. Soft Matter 2009, 5, 1137–1145. [Google Scholar] [CrossRef]
  8. Discher, D.E.; Janmey, P.; Wang, Y.L. Tissue cells feel and respond to the stiffness of their substrate. Science 2005, 310, 1139–1143. [Google Scholar] [CrossRef] [Green Version]
  9. Georges, P.C.; Janmey, P.A. Cell type-specific response to growth on soft materials. J. Appl. Physiol. 2005, 98, 1547–1553. [Google Scholar] [CrossRef] [Green Version]
  10. Wang, N.; Butler, J.P.; Ingber, D.E. Mechanotransduction across the cell surface and through the cytoskeleton. Science 1993, 260, 1124–1127. [Google Scholar] [CrossRef]
  11. Chicurel, M.E.; Chen, C.S.; Ingber, D.E. Cellular control lies in the balance of forces. Curr. Opin. Cell Biol. 1998, 10, 232–239. [Google Scholar] [CrossRef]
  12. Ghosh, K.; Pan, Z.; Guan, E.; Ge, S.; Liu, Y.; Nakamura, T.; Ren, X.D.; Rafailovich, M.; Clark, R.A. Cell adaptation to a physiologically relevant ECM mimic with different viscoelastic properties. Biomaterials 2007, 28, 671–679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Wong, S.; Guo, W.H.; Wang, Y.L. Fibroblasts probe substrate rigidity with filopodia extensions before occupying an area. PNAS 2014, 111, 17176–17181. [Google Scholar] [CrossRef] [Green Version]
  14. Sochol, R.D.; Higa, A.T.; Janairo, R.R.; Li, S.; Lin, L. Unidirectional mechanical cellular stimuli via micropost array gradients. Soft Matter 2011, 7, 4606–4609. [Google Scholar] [CrossRef]
  15. Zhang, H.; Lin, F.; Huang, J.; Xiong, C. Anisotropic stiffness gradient-regulated mechanical guidance drives directional migration of cancer cells. Acta Biomater. 2020, 106, 181–192. [Google Scholar] [CrossRef] [PubMed]
  16. Flaherty, B.; McGarry, J.P.; McHugh, P.E. Mathematical models of cell motility. Cell Biochem. Biophys. 2007, 49, 14–28. [Google Scholar] [CrossRef] [PubMed]
  17. McGarry, J.G.; Prendergast, P.J. A three-dimensional finite element model of an adherent eukaryotic cell. Eur. Cell Mater. 2004, 7, 27–33. [Google Scholar] [CrossRef]
  18. Chen, T.J.; Wu, C.C.; Tang, M.J.; Huang, J.S.; Su, F.C. Complexity of the tensegrity structure for dynamic energy and force distribution of cytoskeleton during cell spreading. PLoS ONE 2010, 5, e14392. [Google Scholar] [CrossRef] [Green Version]
  19. Parameswaran, H.; Lutchen, K.R.; Suki, B. A computational model of the response of adherent cells to stretch and changes in substrate stiffness. J. Appl. Physiol. 2014, 116, 825–834. [Google Scholar] [CrossRef] [Green Version]
  20. Wendling, S.; Oddou, C.; Isabey, D. Stiffening response of a cellular tensegrity model. J. Theor. Biol. 1999, 196, 309–325. [Google Scholar] [CrossRef]
  21. Coughlin, M.F.; Stamenovic, D. A tensegrity model of the cytoskeleton in spread and round cells. J. Biomech. Eng. 1998, 120, 770–777. [Google Scholar] [CrossRef] [PubMed]
  22. Chen, C.S.; Mrksich, M.; Huang, S.; Whitesides, G.M.; Ingber, D.E. Geometric control of cell life and death. Science 1997, 276, 1425–1428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Bernstein, L.R.; Liotta, L.A. Molecular mediators of interactions with extracellular matrix components in metastasis and angiogenesis. Curr. Opin. Oncol. 1994, 6, 106. [Google Scholar] [CrossRef] [PubMed]
  24. Garcia-Gonzalez, D.; Muñoz-Barrutia, A. Computational insights into the influence of substrate stiffness on collective cell migration. Extrem. Mech. Lett. 2020, 40, 100928. [Google Scholar] [CrossRef]
  25. Yeung, T.; Georges, P.C.; Flanagan, L.A.; Marg, B.; Ortiz, M.; Funaki, M.; Zahir, N.; Ming, W.Y.; Weaver, V.; Janmey, P.A. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil. Cytoskelet. 2005, 60, 24–34. [Google Scholar] [CrossRef]
  26. Li, S.; Guan, J.L.; Chien, S. Biochemistry and biomechanics of cell motility. Annu. Rev. Biomed. Eng. 2005, 7, 105–150. [Google Scholar] [CrossRef]
  27. Sheetz, M.P.; Felsenfeld, D.P.; Galbraith, C.G. Cell migration: Regulation of force on extracellular-matrix-integrin complexes. Trends Cell Biol. 1998, 8, 51–54. [Google Scholar] [CrossRef]
  28. Canver, A.C.; Ngo, O.; Urbano, R.L.; Clyne, A.M. Endothelial directed collective migration depends on substrate stiffness via localized myosin contractility and cell-matrix interactions. J. Biomech. 2016, 49, 1369–1380. [Google Scholar] [CrossRef]
  29. Saez, A.; Ghibaudo, M.; Buguin, A.; Silberzan, P.; Ladoux, B. Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates. Proc. Natl. Acad. Sci. USA 2007, 104, 8281–8286. [Google Scholar] [CrossRef] [Green Version]
  30. Yeung, A.; Evans, E. Cortical shell-liquid core model for passive flow of liquid-like spherical cells into micropipets. Biophys. J. 1989, 56, 139–149. [Google Scholar] [CrossRef] [Green Version]
  31. Coughlin, M.F.; Stamenović, D. A prestressed cable network model of the adherent cell cytoskeleton. Biophys. J. 2003, 84, 1328–1336. [Google Scholar] [CrossRef] [Green Version]
  32. Karcher, H.; Lammerding, J.; Huang, H.; Lee, R.T.; Kamm, R.D.; Kaazempur-Mofrad, M.R. A three-dimensional viscoelastic model for cell deformation with experimental verification. Biophys. J. 2003, 85, 3336–3349. [Google Scholar] [CrossRef] [Green Version]
  33. Lim, C.T.; Zhou, E.H.; Quek, S.T. Mechanical models for living cells—A review. J. Biomech. 2006, 39, 195–216. [Google Scholar] [CrossRef] [PubMed]
  34. Shieh, A.C.; Athanasiou, K.A. Principles of cell mechanics for cartilage tissue engineering. Ann. Biomed. Eng. 2003, 31, 1–11. [Google Scholar] [CrossRef] [PubMed]
  35. Fuller, B. Tensegrity. Portf. Artnews Annu. 1961, 4, 112–127. [Google Scholar]
  36. Ingber, D.E. Cellular tensegrity: Defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 1993, 104, 613–627. [Google Scholar]
  37. Sander, E.A.; Stylianopoulos, T.; Tranquillo, R.T.; Barocas, V.H. Image-based multiscale modeling predicts tissue-level and network-level fiber reorganization in stretched cell-compacted collagen gels. Proc. Natl. Acad. Sci. USA 2009, 106, 17675–17680. [Google Scholar] [CrossRef] [Green Version]
  38. Cukierman, E.; Pankov, R.; Stevens, D.R.; Yamada, K.M. Taking cell-matrix adhesions to the third dimension. Science 2001, 294, 1708–1712. [Google Scholar] [CrossRef]
  39. Ni, Y.; Chiang, M.Y. Cell morphology and migration linked to substrate rigidity. Soft Matter 2007, 3, 1285–1292. [Google Scholar] [CrossRef]
  40. Zanotelli, M.R.; Rahman-Zaman, A.; VanderBurgh, J.A.; Taufalele, P.V.; Jain, A.; Erickson, D.; Bordeleau, F.; Reinhart-King, C.A. Energetic costs regulated by cell mechanics and confinement are predictive of migration path during decision-making. Nat. Commun. 2019, 10, 4185. [Google Scholar] [CrossRef] [Green Version]
  41. Mattila, P.K.; Lappalainen, P. Filopodia: Molecular architecture and cellular functions. Nature 2008, 9, 446–454. [Google Scholar] [CrossRef] [PubMed]
  42. Ingber, D.E.; Tensegrity, I. Cell structure and hierarchical systems biology. J. Cell Sci. 2003, 116, 1157–1173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Ingber, D.E. Tensegrity and mechanotransduction. J. Bodyw. Mov. Ther. 2008, 12, 198–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Todaro, G.J.; Green, H. Quantitative studies of the growth of mouse embryo cells in culture and their development into established lines. J. Cell Biol. 1963, 17, 299–313. [Google Scholar] [CrossRef]
  45. Mousavi, S.J.; Doweidar, M.H.; Doblaré, M. Computational modelling and analysis of mechanical conditions on cell locomotion and cell-cell interaction. Computer Methods in Biomechanics and Biomedical Engineering 2012, 17, 678–693. [Google Scholar] [CrossRef]
  46. Wang, N.; Stamenovic, D. Contribution of intermediate filaments to cell stiffness, stiffening, and growth. Am. J. Physiol. Cell Physiol. 2000, 279, C188–C194. [Google Scholar] [CrossRef] [Green Version]
  47. Voloshin, A. Modeling cell movement on a substrate with variable rigidity. Int. J. Biomed. Eng. Sci. 2016, 3, 19–36. [Google Scholar] [CrossRef]
  48. Gittes, F.; Mickey, B.; Nettleton, J.; Howard, J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993, 120, 923–934. [Google Scholar] [CrossRef]
  49. Ingber, D.E. Tensegrity II. How structural networks influence cellular information processing networks. J. Cell Sci. 2003, 116, 1397–1408. [Google Scholar] [CrossRef] [Green Version]
  50. Mehrbod, M.; Mofrad, M.R.K. On the significance of microtubule flexural behavior in cytoskeletal mechanics. PLoS ONE 2011, 6, e25627. [Google Scholar] [CrossRef]
  51. Trichet, L.; Le Digabel, J.; Hawkins, R.J.; Vedula, S.R.K.; Gupta, M.; Ribrault, C.; Hersen, P.; Voituriez, R.; Ladoux, B. Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness. Proc. Natl. Acad. Sci. USA 2012, 109, 6933–6938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  52. Gray, D.S.; Tien, J.; Chen, C.S. Repositioning of cells by mechanotaxis on surfaces with micropatterned Young’s modulus. J. Biomed. Mater. Res. Part A 2003, 66, 605–614. [Google Scholar] [CrossRef] [PubMed]
  53. Stamenovic, D.; Liang, Z.; Chen, J.; Wang, N. Effect of the cytoskeletal prestress on the mechanical impedance of cultured airway smooth muscle cells. J. Appl. Physiol. 2002, 92, 1443–1450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Gardel, M.L.; Nakamura, F.; Hartwig, J.H.; Crocker, J.C.; Stossel, T.P.; Weitz, D.A. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA 2006, 103, 1762–1767. [Google Scholar] [CrossRef] [Green Version]
  55. Pelham, R.J.; Wang, Y.L. High resolution detection of mechanical forces exerted by locomoting fibroblasts on the substrate. Mol. Biol. Cell 1999, 10, 935–945. [Google Scholar] [CrossRef] [Green Version]
  56. Galbraith, C.G.; Yamada, K.M.; Galbraith, J.A. Polymerizing actin fibers position integrins primed to probe for adhesion sites. Science 2007, 315, 992–995. [Google Scholar] [CrossRef] [Green Version]
  57. Hadjipanayi, E.; Mudera, V.; Brown, R.A. Guiding cell migration in 3D: A collagen matrix with graded directional stiffness. Cell Motil. Cytoskelet. 2009, 66, 121–128. [Google Scholar] [CrossRef]
  58. Lazopoulos, K.A.; Stamenović, D. Durotaxis as an elastic stability phenomenon. J. Biomech. 2008, 41, 1289–1294. [Google Scholar] [CrossRef]
Applsci 10 06644 g001 550
Figure 1. Lamellipodia and filopodia at the cell’s leading edge. [41]. The green line shows the cell’s adherent area, while the red lines represent a network of actin filaments.
Figure 1. Lamellipodia and filopodia at the cell’s leading edge. [41]. The green line shows the cell’s adherent area, while the red lines represent a network of actin filaments.
Applsci 10 06644 g001
Applsci 10 06644 g002 550
Figure 2. Cytoskeleton tensegrity model. (Solid bars represent pre-compressed microtubules; thin lines represent pre-tensed microfilaments).
Figure 2. Cytoskeleton tensegrity model. (Solid bars represent pre-compressed microtubules; thin lines represent pre-tensed microfilaments).
Applsci 10 06644 g002
Applsci 10 06644 g003 550
Figure 3. Tensegrity model of the cell with the lamellipodium. The spring element connecting nodes 46 and 49 represents the substrate stiffness.
Figure 3. Tensegrity model of the cell with the lamellipodium. The spring element connecting nodes 46 and 49 represents the substrate stiffness.
Applsci 10 06644 g003
Applsci 10 06644 g004 550
Figure 4. Simulated substrate stiffness.
Figure 4. Simulated substrate stiffness.
Applsci 10 06644 g004
Applsci 10 06644 g005 550
Figure 5. Cell original (white lines) and deformed geometry (blue lines) at the substrate with a stiffness of 0.001 N/m.
Figure 5. Cell original (white lines) and deformed geometry (blue lines) at the substrate with a stiffness of 0.001 N/m.
Applsci 10 06644 g005
Applsci 10 06644 g006 550
Figure 6. Cell original (white lines) and deformed geometry (blue lines) at the substrate with a stiffness of 1000 N/m.
Figure 6. Cell original (white lines) and deformed geometry (blue lines) at the substrate with a stiffness of 1000 N/m.
Applsci 10 06644 g006
Applsci 10 06644 g007 550
Figure 7. Elastic energy of the cell adherent to the substrate as a function of the stiffness. Inset shows a stiffness range between 0.1 and 1000 N/m.
Figure 7. Elastic energy of the cell adherent to the substrate as a function of the stiffness. Inset shows a stiffness range between 0.1 and 1000 N/m.
Applsci 10 06644 g007
Applsci 10 06644 g008 550
Figure 8. Predicted movement of a cell along the substrate with the stiffness distribution as shown in Figure 4.
Figure 8. Predicted movement of a cell along the substrate with the stiffness distribution as shown in Figure 4.
Applsci 10 06644 g008
Table
Table 1. Mechanical properties of microtubules, microfilaments and substrate.
Table 1. Mechanical properties of microtubules, microfilaments and substrate.
MicrotubulesMicrofilamentsSubstrate
ANSYS ElementLink180Beam188Combin14
Cross Sectional Area (m2) 45.2 × 10−1745.2 × 10−17N/A
Length (m)2.40 × 10−51.467 × 10−52.26 × 10−5
Young’s Modulus (Pa)1.20 × 1092.6 × 109 N/A
v0.30.3N/A
Stiffness Range (N/m)N/AN/A10−3–1000

Share and Cite

MDPI and ACS Style

Voloshin, A. Migration of the 3T3 Cell with a Lamellipodium on Various Stiffness Substrates—Tensegrity Model. Appl. Sci. 2020, 10, 6644. https://doi.org/10.3390/app10196644

AMA Style

Voloshin A. Migration of the 3T3 Cell with a Lamellipodium on Various Stiffness Substrates—Tensegrity Model. Applied Sciences. 2020; 10(19):6644. https://doi.org/10.3390/app10196644

Chicago/Turabian Style

Voloshin, Arkady. 2020. "Migration of the 3T3 Cell with a Lamellipodium on Various Stiffness Substrates—Tensegrity Model" Applied Sciences 10, no. 19: 6644. https://doi.org/10.3390/app10196644

APA Style

Voloshin, A. (2020). Migration of the 3T3 Cell with a Lamellipodium on Various Stiffness Substrates—Tensegrity Model. Applied Sciences, 10(19), 6644. https://doi.org/10.3390/app10196644

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop