Analysis of University Students’ Behavior Based on a Fusion K-Means Clustering Algorithm

Abstract

With the development of big data technology, creating the ‘Digital Campus’ is a hot issue. For an increasing amount of data, traditional data mining algorithms are not suitable. The clustering algorithm is becoming more and more important in the field of data mining, but the traditional clustering algorithm does not take the clustering efficiency and clustering effect into consideration. In this paper, the algorithm based on K-Means and clustering by fast search and find of density peaks (K-CFSFDP) is proposed, which improves on the distance and density of data points. This method is used to cluster students from four universities. The experiment shows that K-CFSFDP algorithm has better clustering results and running efficiency than the traditional K-Means clustering algorithm, and it performs well in large scale campus data. Additionally, the results of the cluster analysis show that the students of different categories in four universities had different performances in living habits and learning performance, so the university can learn about the students’ behavior of different categories and provide corresponding personalized services, which have certain practical significance.

1. Introduction

With the continuous development of information technology, the data accumulated in the campus information environment is gradually expanding, and a complete campus big data environment has been formed. Traditional campus management concepts and data analysis methods have been unable to meet the growing data processing needs. How to effectively manage and share campus data, use big data mining ideas to optimize student management, and provide clearer, more detailed data services for students is a problem faced by today’s campus service system.

At present, there is much research on university students’ behavior, involving multiple aspects of behavior. Some researchers analyzed the college students’ physical activities (PA) to find PA patterns and their determinants, which will help college students to notice their health conditions [1]. Belingheri examined the prevalence of smoking, binge drinking, physical inactivity, and excessive bodyweight in a population of healthcare students attending an Italian university [2]. SY Park studied the university students’ behavioral intention to use mobile learning [3]. J Kormos investigated the influence of motivational factors and self-regulatory strategies on autonomous learning behavior [4]. Most of the above studies mainly used traditional mathematical statistical methods to obtain data information, but did not further explore the laws behind the data. Besides, it can be seen from these studies that the learning behavior and life behavior of university students are the main concerns of the school. Therefore, we mainly focus on the learning performance and living habits of university students, and classify them accordingly.

Educational data mining (EDM) can discover hidden patterns and knowledge from a large amount of data. Many scholars have applied data mining to the analysis of university students’ behaviors to find the laws behind their behaviors. For example, Man Wai Lee used data mining techniques to analyze learner preferences. The study found that field independent learners frequently use backward/forward buttons and spent less time for navigation, while field dependent learners often use main menu and have more repeated visiting. [5]. Jingyi Luo used the free comments written by students at the end of each class to continuously track students’ learning and improve the prediction of students’ final grades [6]. Arat G. analyzed the relationship between risk behaviors and resilience among South Asian minority youth. They discussed the resilience-based research, practical, and social policy implications [7]. Zullig K.J. examined the association between prescription opioid misuse and suicidal ideation, suicide plan, and suicide attempt among adolescents. The research demonstrated the harmful effects of prescription opioid misuse and its association with suicidal behaviors among adolescents [8]. Natek analyzed the course scores of 106 undergraduates and used the decision tree algorithm to discover the factors that affect the grades of the undergraduates’ course [9]. S.K. Yadav applied decision tree algorithms on students’ past performance data to generate the model that can be used to predict the students’ performance. It helps earlier in identifying the dropouts and students who need special attention [10]. Some of the above studies used supervised machine learning methods. For the classification method of supervised machine learning, the “label” of university students is determined, that is, the types of university students are defined in advance, and the work done is only to “classify” by analyzing the behavior data of university students. However, in most cases, the number of types of students in a university cannot be known in advance, so unsupervised machine learning methods are needed for clustering.

Clustering algorithm is a very important technology in data mining. Clustering is the process of assigning samples to different classes. In general, in the clustering results, samples in the same category tend to have greater similarities, while samples in different classes have greater dissimilarities. The goal of clustering is to divide the data based on a specific similarity measure. Clustering algorithm is suitable for the description of students’ behaviors. Based on a cluster analysis of 320,000 students, Saenz V.B. found that there is a huge difference in the utilization rate of support services among different student groups [11]. Rapp K. performed cluster analysis on German nurse students quitting smoking [12]. OR Battaglia investigated students’ behavior by using cluster analysis as an unsupervised methodology in the field of education [13]. Some researchers have also conducted other student behavior cluster studies [14,15,16].

The above literature analysis shows that there are many papers that use data mining techniques to analyze student behavior analysis. However, there are not many papers on the analysis of college students’ behavior using clustering methods. Some papers used the clustering algorithm, which did not take into account the clustering effect and efficiency to analyze the students’ behaviors. Currently, commonly used clustering methods include: partition clustering [17], density clustering, hierarchy-based [18], model-based [19], and density-based [20]. K-Means clustering algorithm is a traditional clustering algorithm proposed by Macqueen, which is simple and efficient [21]. At the same time, it has the advantages of scalability and high efficiency for processing large data sets. The K-Means clustering algorithm has a wide range of applications [22,23,24,25,26]. Some scholars also apply K-Means to the behavior analysis of university students. For example, P.D. Antonenko illustrated the use of K-Means clustering to analyze characteristics of learning behavior while learners engage in a problem-solving activity in an online learning environment [27]. C.Y. Yang analyzed the characteristics of big data in university campus and adopted K-Means algorithm to propose an early warning system of college students’ behavior based on the Internet of Things and big data environment [28]. SE Sorour proposed a new approach based on text mining techniques for predicting student performance using latent semantic analysis and K-means clustering methods [29].

Although the K-Means algorithm has many advantages, it still has fatal flaws. These defects will greatly limit the application of K-Means. It has two major drawbacks. (1) The value of k needs to be specified in advance. The number of manually assigned clusters is inaccurate. Each type of data has its own characteristics. Randomly specifying k for unknown data does not reflect the clustering effect of the data itself. So, the clustering result has a great deal of randomness. (2) The K-Means algorithm starts randomly assigning cluster centers. Different cluster centers often result in different final clustering results. The K-Means algorithm is heavily dependent on the initial cluster center, and the final iterated cluster center is not necessarily the global optimal cluster center. At the same time, there are many improvements to the K-Means algorithm, but these two problems cannot be solved effectively. There are some algorithms to optimize the value of k. The main approach to this point improvement is to assign a number of values to k by guessing in advance and determine the best value of k by measuring the sum of the squared clustering errors. This approach has made great progress compared to before, but it is inefficient. Under certain k values, the initial clustering may exist without solutions. Therefore, multiple clusters are required to obtain the clustering result. Although it is possible to obtain better k-values, it takes a lot of time to work in the early stage and is unrealistic for dealing with large amounts of data. The common algorithm in this class is K-Means++. There is also an optimization algorithm for clustering centers. Wang W proposed a way to optimal cluster centers for detecting images [30]. The clustering by fast search and find of density peaks (CFSFDP) clustering algorithm was proposed in 2014 [31]. The clustering algorithm takes into account the characteristics of clustering centers and data. The algorithm is simple in logic, but the clustering result is much better than the traditional clustering algorithm. However, the efficiency of the algorithm is low. It is unable to meet the requirement of a large amount of data clustering time. There are also some other clustering algorithms [32,33,34,35,36,37]. Minaei-Bidgoli B. considered the effects of resampling and adaptive methods on the clustering effect [38]. Alizadeh H. selected categories based on a new cluster stability measure [39]. Parvin H. combined the ant colony algorithm and clustering algorithm [40]. Some studies of clustering algorithms considered the weight [41,42,43]. The application of fuzzy clustering is also becoming more and more widespread [44,45,46,47].

The algorithms above can get better clustering results, however, based on the recommendation system to select cluster centers, the efficiency is very low. Aiming to improve the disadvantages of both K-Means and CFSFDP in application, we proposed a new algorithm to describe the students’ behavior.

The innovations and contributions of this research are as follows:

• We applied the relevant theories and knowledge of data mining and machine learning to the analysis of university students’ behavior. This is an application innovation in the field of machine learning and education.
• Compared with the traditional behavior analysis model of college students, this study used data for analysis, which reduces the subjectivity of human judgment and avoids prejudice caused by preconceptions. Therefore, the analysis results of this study are more objective.
• Most current research used the K-Means algorithm, but the number of student categories and cluster centers are difficult to determine. The K-Means and clustering by fast search and find of density peaks (K-CFSFDP) proposed in this study can automatically determine the number of student behavior types and typical representatives based on data. Therefore, K-CFSFDP has high flexibility and wide applicability, and it also avoids human intervention in the clustering process.
• The K-CFSFDP proposed in this research did not completely rely on the CFSFDP framework, instead, it improved CFSFDP in some aspects. Therefore, the running time is shorter and the running efficiency is higher, which has application advantages in the environment of campus big data.

2. Materials and Methods

2.1. Students’ Behavior Data from Four Universities

2.1.1. Behavior Analysis Indicators

The data is obtained from 4 universities in China. For convenience, S1, S2, S3, and S4 represent 4 different universities. We mainly described the university students’ behavior on two aspects: living habit and learning performance.

The evaluation indexes of living habit are as

Table 1. Evaluation indexes of living habit.

Index	Type	Note
Regular diet	Numerical value	The number of days per month
Physical Exercise	Numerical value	The number of days per month
Regular rest	Numerical value	The number of days per month
Normal consumption	Numerical value	The number of days per month

:

The evaluation indexes of learning performance are as

Table 2. Evaluation indexes of learning performance.

Index	Type	Note
Average score	Numerical value	The number of scores per month
Attendance rate	Numerical value	The number of attendances per month
study-time	Numerical value	The hours of studying per month
Book reading	Numerical value	The number of books per month

:

2.1.2. Data Normalization

As the dimensions of various behavior indicators are not uniform, this study used maximum and minimum standardization to normalize the data. This is a linear transformation of the original data, which can map the data values on the [0, 10] interval. The transformation function is as follows:

$$x^{*}=\frac{10\left(x-min\right)}{max-min}$$

(1)

where max is the maximum value of the data and min is the minimum value of the data.

After normalization, the average values of the data were calculated. Then the evaluation indexes of the living habit and learning performance were obtained, and the value range was from 1 to 10. When the value is higher, the performance is much better.

The data in 4 different universities is as

Table 3. Students’ data from 4 universities (partial data).

Number	S1		S2		S3		S4
1	6.07368	5.55742	7.66723	6.00785	7.55621	7.50524	6.67336	7.32494
2	6.14057	5.66159	6.55764	1.74391	8.17891	7.65729	6.00577	6.74123
3	7.22919	5.99426	5.68571	3.41523	8.11347	8.21814	5.87413	6.55677
4	6.12385	5.81432	5.55817	2.78966	7.60752	8.22783	6.97421	7.36017
1997	8.69287	1.67829	6.11535	3.34144	9.66132	4.19352	4.55479	5.19746
1998	7.48125	2.52936	5.78211	2.66147	7.88631	4.75178	8.56978	3.67127
1999	8.36386	1.64275	5.66985	2.40725	7.25812	4.99851	3.33214	4.87413
2000	8.45574	4.23727	7.61459	3.42789	7.33275	4.63247	6.11267	3.39741

:

2.1.3. Data Visualization

In order to provide more details of the data, this study used violin plots, box plots, scatter plots and scatter plot matrices to visualize the data. From the data visualization chart, we could get the distribution law and aggregation degree of the data.

The violin plot can display the distribution status and probability density of multiple sets of data. The violin chart of the data is shown in Figure 1. Green represents the living performance score, blue represents the learning performance score, and the abscissa corresponds to 4 different universities. It can be seen from the violin chart that the distribution of student behavior data in different schools is different. The living data and learning data of students in the same school are not the same. In addition, it can be intuitively seen from the figure that the student behavior data does not meet the common normal distribution, and the data is concentrated near certain values, so there is a possibility of clustering.

A box plot is a statistical chart that can display data dispersion. It can display the maximum, minimum, median, outlier, and upper and lower quartiles of a set of data. It can provide key information about the location and dispersion of data, especially when comparing different university student behavior data. The box diagram of the data is shown in Figure 2. Green represents the living performance score, blue represents the learning performance score, and the abscissa corresponds to 4 different universities. The horizontal line in the middle of the box is the median of the data, and the upper and lower ranges of the box correspond to the upper and lower quartiles of the data. The horizontal line above the box is the maximum value, and the horizontal line below the box is the minimum value. The solid points are outliers. It can be seen from the figure that, overall, the learning scores of college students in most schools were lower than living scores. In addition, the center points of most data were between 4 and 7.

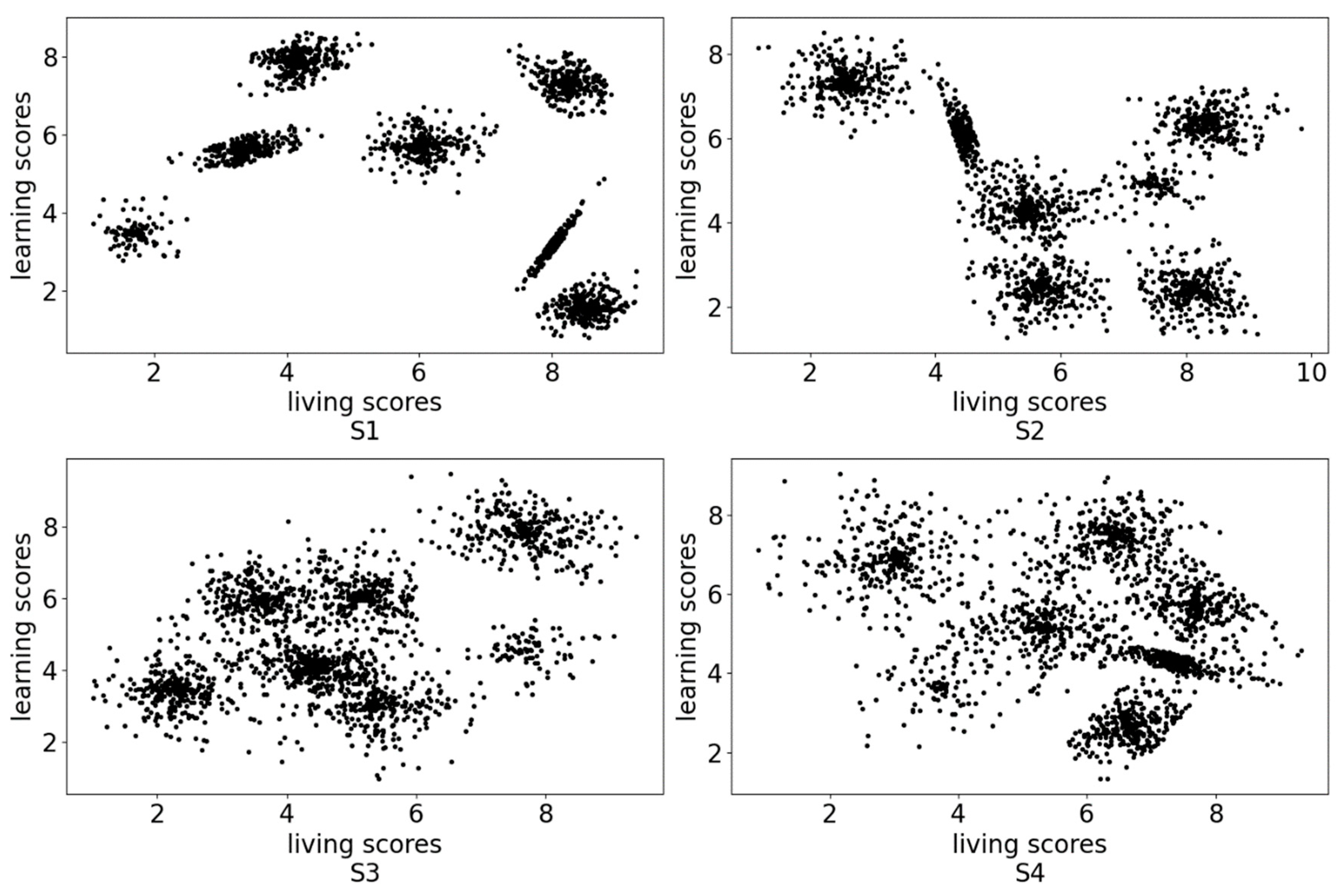
The data distribution scatter diagram is shown in Figure 3. It can be seen intuitively from the figure that the data points show the phenomenon of aggregation. Some data points are very densely distributed, while others are relatively sparsely distributed. We can see very intuitively from the data distribution map of the first university that these data points were clustered into 7 categories. This shows that many students had similar living habits and learning performance and could be divided into a certain number of categories.

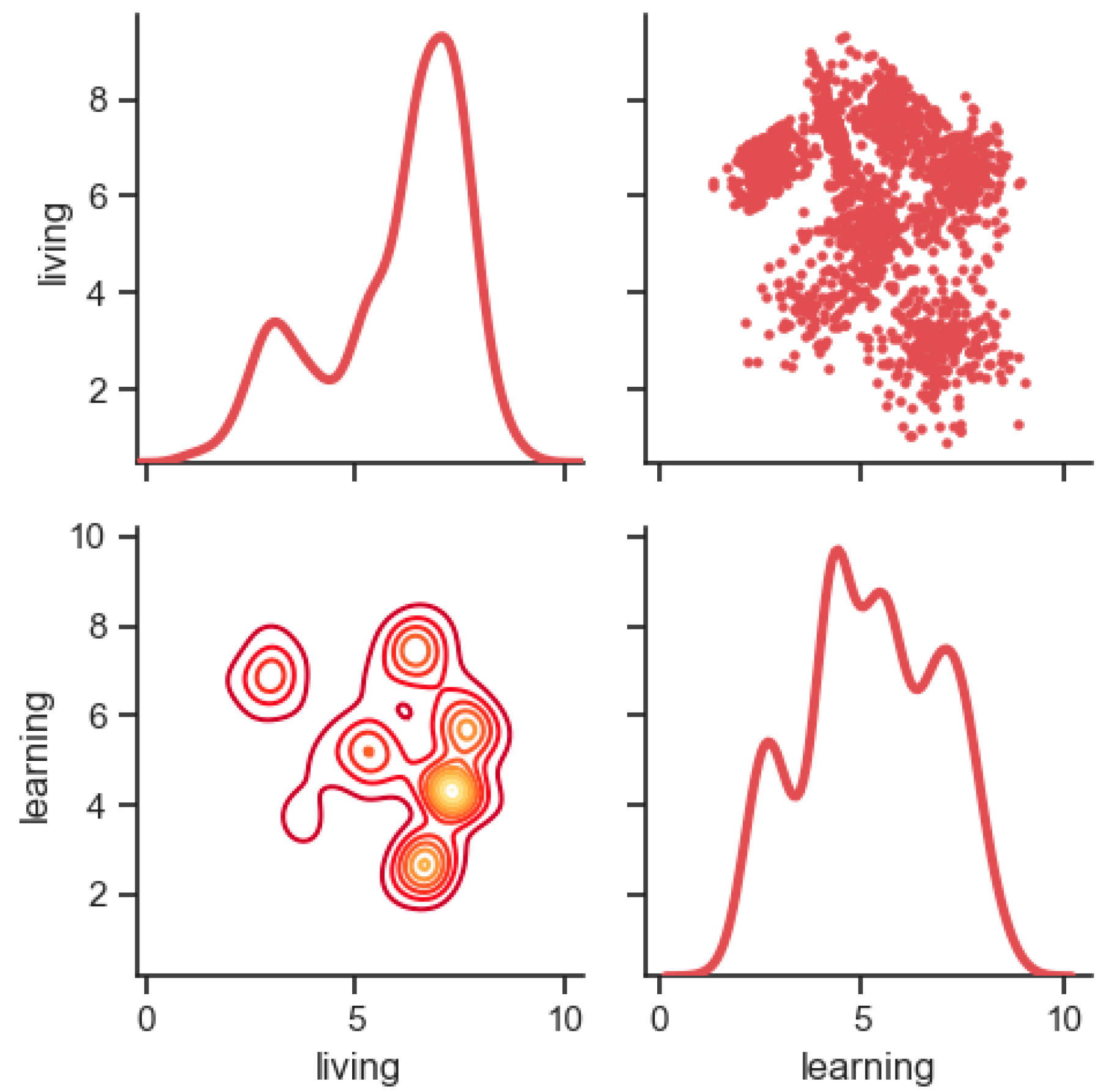
Further, we draw scatter plot matrices to comprehensively show the distribution of data and the shape of aggregation. The scatter plot matrix can reflect the correlation between learning scores and living scores. The matrix includes three types of charts. The upper triangle represents the scatter plot of the data, the diagonal line represents the probability density distribution map, and the lower triangle represents the contour map (the denser the data, the more concentrated the line, and the brighter the color).

The scatter plot matrices of the four universities are shown in Figure 4, Figure 5, Figure 6 and Figure 7 respectively. It can be seen from these scatter plot matrices that some data points were very densely distributed. This proves that some university students had similarities in living and study, and they gathered into a certain number of clusters. In addition, it can be seen from the figure that the number of distribution groups, the characteristics of study and life, and the degree of aggregation of student behavior in different universities were different. Therefore, the task of this research was to divide these categories using cluster analysis, so as to make a scientific and targeted classification of university student behavior. This helps school administrators to provide corresponding guidance for university students’ improvement in living and learning according to different categories.

2.1.4. Data Analysis and Algorithm Tools

The above data analysis and visualization show that the categories and distribution of student behaviors in different schools were different, so it is impossible to use a unified baseline to classify student behaviors. That is, there is no universal student classification method to label each student’s category. In other words, the existing classification methods based on expert evaluation and educational standards are not objective and accurate enough and do not consider the diversity of student categories. Therefore, this is an unsupervised machine learning problem. Clustering is an effective method to solve unsupervised learning problems. We mainly used the K-CFSFDP algorithm to analyze the students’ behaviors and compared with K-Means and CFSFDP clustering algorithms.

The K-Means clustering algorithm is a classical algorithm that is widely used in fields such as data mining and knowledge discovery. The principle of K-Means clustering algorithm is simple with high efficiency, and it is adapted to big data sets. However, it has two major drawbacks. First, the k value needs to be set in advance, in most cases, the optimal number of categories for a dataset can not be determined in advance, so it is difficult to choose a reasonable value. For example, in this study, the number of student groups in each school may not be the same. Second, in the K-Means algorithm, it is necessary to determine an initial partition based on the initial cluster center and then optimize the initial partition, and the choice of this initial cluster center has a greater impact on the clustering result. Once the initial value is not selected well, it may not be able to obtain effective clustering results. For example, we cannot find a representative from each student category, especially when the number of student categories is unknown.

We proposed the K-CFSFDP algorithm to determine the k value and cluster center based on the characters of the data set.

2.2. Clustering by K-Means

The principle of the K-Means clustering algorithm is simple. Given a data set $X_i(i=1,2,3\dots n)$. K value and the cluster centers are specified. Sum of the squared errors (SSE) is the objective function of the K-Means clustering algorithm

$$SSE={\displaystyle \sum }_{i=1}^k{\displaystyle \sum }_{x\in C_i}{\left|x-{\overline{x}}_i\right|}^2$$

(2)

$C$ represents one class of the cluster result, k represents the number of categories, and ${\overline{x}}_i$ is the average of one class. When the objective function obtains the minimum value, the clustering effect is optimal.

The step of K-Means clustering algorithm is divided into the following three steps:

Step 1: Assign samples to their nearest center vector and reduce the value of the objective function

$${\displaystyle \sum }_{i=1}^n\underset{j\in \left\{i=1,2,3\dots k\right\}}{min}|\left|x_i-p_j\right|{|}^2$$

(3)

Distance formula between points and points adopts Euclidean distance:

$$d\left(x_i,x_j\right)=\sqrt{{\displaystyle \sum }_{k=1}^d{\left(x_{ik}-x_{jk}\right)}^2}$$

(4)

p represents k cluster centers. d represents the attribute of x.

Step 2: Update cluster average

$${\overline{x}}_i=\frac{1}{\left|C_i\right|}{\displaystyle \sum }_{x\in C_i}X$$

(5)

Step 3: Calculate the objective function

When the value of the objective function is the lowest, the cluster effect is optimal.

2.3. Determining the K Value and Cluster Center

In order to correct the two drawbacks in the K-Means clustering algorithm. The paper uses the way of determining the cluster centers proposed by Alex Rodriguez and Alessandro Laio in the “CFSFDP” cluster algorithm, which is novel, simple, and fast, and it can find the right number of classifications and the global optimal clustering center according to the data. The core of the algorithm is the description of its cluster center [31].

There are two basic assumptions in the clustering algorithm:

• Cluster centers are surrounded by neighbors with lower local density.
• Cluster centers are at a relatively large distance from any points with a higher local density.

This clustering algorithm can be divided into four steps, which are introduced as follows.

Step 1: Calculate the local density

The dataset for clustering is$\mathrm{S}=\left\{x_i\right\}\begin{array}{c}N\\ i=1\end{array}$. $I_S=\left\{1,2,\dots ,N\right\}$ is the corresponding indicator set. $d_{ij}=d\left(x_i,x_j\right)$ represents a certain distance between points $x_i$ and $x_j$. According to Cut-off kernel, the local density ${\rho }_i$ of data point $i$ is defined as follows:

$${\rho }_i={\displaystyle \sum }_{j\in I_{s\backslash \left[i\right]}}\chi \left(d_{ij}-d_c\right)$$

(6)

where $\chi \left(x\right)$ is defined as follows:

$$\chi \left(x\right)=\{\begin{array}{c}1,x<0;\\ 0,x\ge 0.\end{array}$$

(7)

Additionally, $d_c$ is a cutoff distance that needs to be specified in advance. Based on formula (6), ${\rho }_i$ is the number of data points whose distance is less than $d_c$, without regard to the number of $x_i$ itself. To some extent, the parameter $d_c$ determines the effect of this clustering algorithm. If $d_c$ is too large, the local density value of each data point will be large, resulting in low discrimination. The extreme case is that the value of $d_c$ is greater than the maximum distance of all points, so the end result of the algorithm is that all points belong to the same cluster center. If the value of $d_c$ is too small, the same group may be split into multiples. The extreme case is that $d_c$ has a smaller distance than all points, which will result in each point being a cluster center. The reference method is to select a $d_c$ so that the average number of neighbors per data point is about 1–2% of the total number of data points.

Step 2: Calculate the distance

A descending sequence of subscripts ${\left\{q_i\right\}}_{i=1}^N$ was generated.

$${\rho }_{q_1}\ge {\rho }_{q_2}\ge \dots \ge {\rho }_{q_N}$$

(8)

The distance formula is as follows:

$${\delta }_i=\{\begin{array}{c}\underset{q_j}{min}\left\{d_{q_i}{}_{q_j}\right\},i\ge 2;\\ \underset{j\ge 2}{max}\left\{{\delta }_{q_j}\right\},i=1.\end{array}$$

(9)

For the above formula, when$i=1$, ${\delta }_i$ is the distance between the data point with the largest distance from $x_i$ in S. If$i>2$, ${\delta }_i$ represents the distance between $x_i$ and the data point (or those points) with the smallest distance from $x_i$ for all data points with a local density greater than $x_i$.

Step 3: Select the clustering center

So far, we could get the $\left({\rho }_i,{\delta }_i\right),i\in I_S$ of every data point. When considering comprehension, the following formula is used to select the clustering center:

$${\gamma }_i={\rho }_i{\delta }_i,i\in I_S,$$

(10)

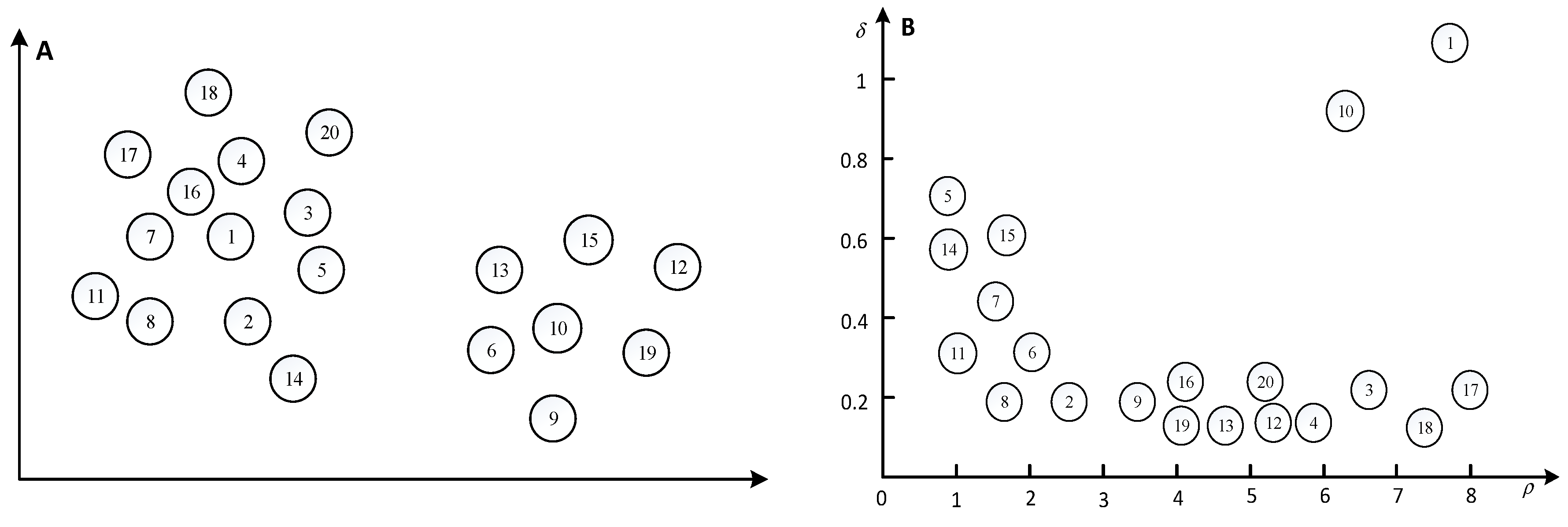
For example, Figure 8 contained 20 data points, and the ${\gamma }_i={\rho }_i{\delta }_i,i\in I_S$ of every data point could be obtained.

Next, $\gamma$ was calculated to select the cluster center. Figure 9 shows the $\gamma$ curve.

According to Figure 9, it can be found that for the non-cluster centers, the curve is smoother. Besides this, there is a clear jump between the cluster centers and non-cluster centers.

Step 4: Categorize other data points

After the cluster center was determined, the category labels of the remaining points were specified according to the following principles: the category label of the current point was equal to the label of the nearest point higher than the current point density, which will take much time.

The CFSFDP proposed by Alex Rodriguez and Alessandro Laio has the following defects:

1.

The density calculation adopts the cut-off kernel function, and the clustering result is very dependent on $d_c$.

2.

The author did not provide a specific distance calculation formula. The distance measurement of different problems is not the same, the specific distance measurement formula should be determined according to the actual problem.

3.

The method of categorizing other data points is inefficient. After the cluster centers have been found, each remaining point is assigned to the same cluster as its nearest neighbor of higher density, which will cause unnecessary multiple iterations and repeated calculations. Besides, as the amount of data increases, the amount of calculation will increase sharply, resulting in a long running time of the algorithm, and it is difficult to meet the operational needs of campus big data. In addition, this classification method does not take full advantage of the determined number of clusters and cluster centers.

This study improved the above problems in the K-CFSFDP algorithm, especially the data point classification problem, so as to improve the operating efficiency of the CFSFDP algorithm.

2.4. K-CFSFDP Algorithm

Based on the way of determining the k value and cluster center, the K-CFSFDP algorithm was proposed, which mainly includes the following steps:

Step 1: Data process: data normalization:

We first used formula (1) to standardize the data. This step was implemented in the data preprocessing section.

Step 2: Calculate the density of each point:

The clustering set was$\mathrm{S}=\left\{x_i\right\}\begin{array}{c}N\\ i=1\end{array}$. We adopted the Gaussian kernel function to calculate the density. The formula is as follows:

$${\rho }_i={\displaystyle \sum }_{j\in I_{s\backslash \left[i\right]}}{e}^{-{\left(\frac{d_{ij}}{d_c}\right)}^2}$$

(11)

$I_S=\left\{1,2,\dots ,N\right\}$ is an indicator set. d_ij = dist(x_i, x_j) represents the Euclidean distance between points $x_i$ and $x_j$.

Step 3: Calculate the distance value for each point:

• Distance formula between points and points adopted the Euclidean distance as shown in formula (4). The $d_{ij}$ was calculated and was $d_{ij}=d_{ji},i<j,i,j\in I_S$.
• According to ${\left\{{\rho }_i\right\}}_{i=1}^N$, we generated its descending order subscript ${\left\{q_i\right\}}_{i=1}^N$.
• We calculated the distance value ${\left\{{\delta }_i\right\}}_{i=1}^N$.

Step 4: Calculate the γ value:

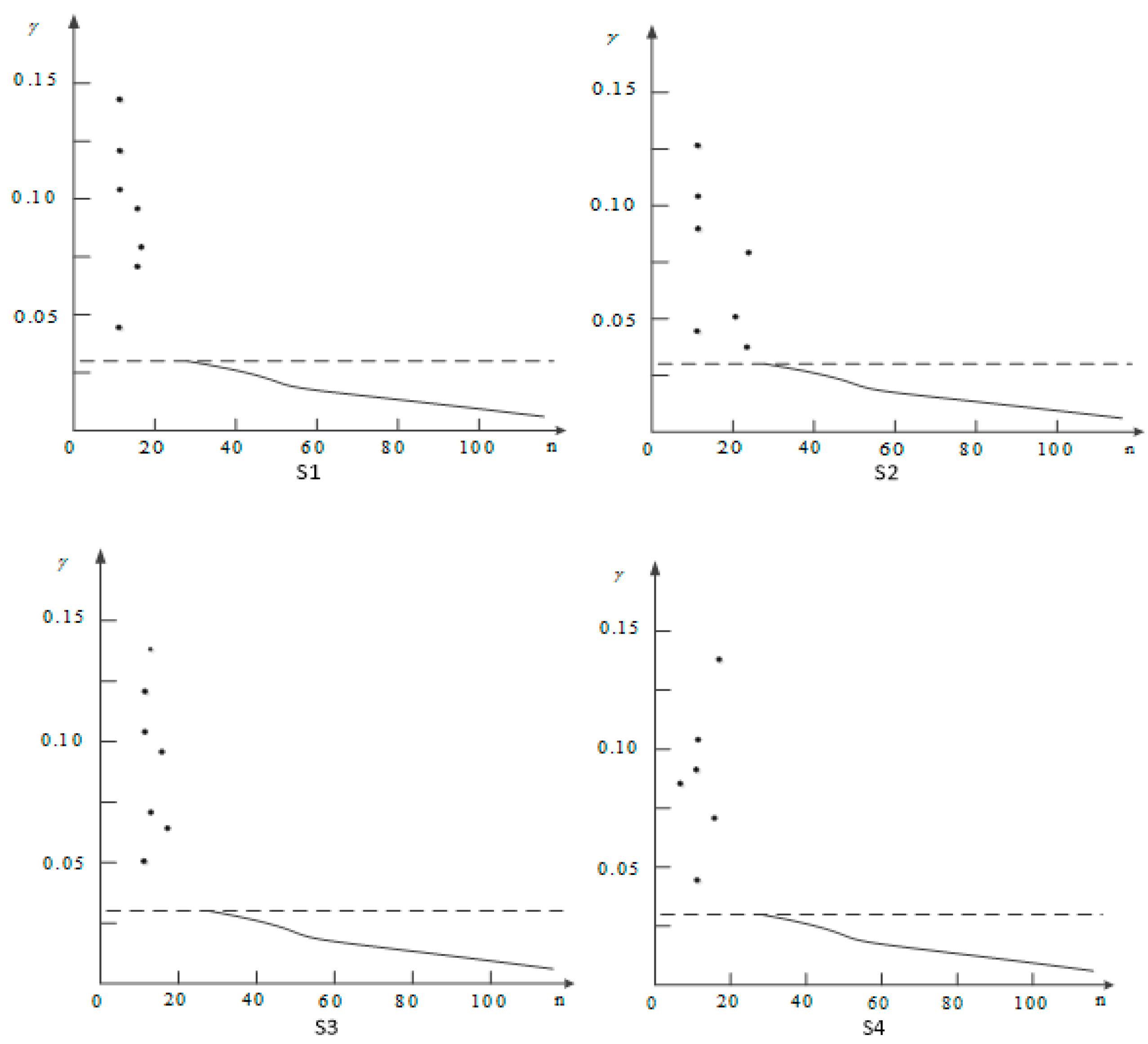
Based on ${\left\{{\rho }_i\right\}}_{i=1}^N$ and ${\left\{{\delta }_i\right\}}_{i=1}^N$, ${\left\{{\gamma }_i\right\}}_{i=1}^N$ was calculated. The magnitude of ${\left\{{\rho }_i\right\}}_{i=1}^N$ and ${\left\{{\delta }_i\right\}}_{i=1}^N$ might be different. If the difference is too large, it’s necessary to perform a normalization process.

Step 5: Determine the k value and the cluster center:

We selected the number of cluster (k value) and cluster center according to the decision graph and initialized the data point classification attribute tag ${\left\{c_i\right\}}_{i=1}^N$, as follows:

$$c_i=\{\begin{array}{c}t,tϵ\left[1,k\right],if{x}_i\mathit{is}\mathit{the}\mathit{cluster}\mathit{center}\mathit{and}\mathit{belongs}\mathit{to}\mathit{the}\mathit{first}k\mathit{cluster}\\ -1,\mathit{other}\hfill \end{array}$$

(12)

Step 6: Use Euclidean distances to classify other points (formula 4):

For data points that were not cluster centers ($c_i=-1$), we calculated the Euclidean distance between the data point and each cluster center, selected the cluster center with the shortest distance, and classified the data point into the category to which the cluster center belongs.

Compared with CFSFDP, K-CFSFDP has achieved improvements in the following aspects:

1.

K-CFSFDP used Gaussian kernel instead of the original cut-off kernel in CFSFDP. Cut-off kernel is a discrete value while Gaussian kernel is a continuous value. Therefore, the Gaussian kernel has a smaller probability of conflict (i.e., different data points have the same local density value). In addition, the Gaussian kernel still satisfies that the more data points whose distance from $x_i$ is less than $d_c$, the greater the value of ${\rho }_i$.

2.

We clarified the measurement method of data point distance in K-CFSFDP.

2.

Using the determined number of clusters and cluster centers, this study optimized the classification of other data points. Each data point only needs to traverse the Euclidean distance to each cluster center to find the nearest cluster, without additional calculations to the distance of other non-cluster center data points. This greatly reduces the computational complexity of the algorithm. Assigning data points to the cluster center closest to it can spend less time to improve efficiency.

Compared to the original K-Means algorithm, the advantages of the K-CFSFDP algorithm is that the algorithm can automatically select the appropriate number of classes and initial cluster center based on the characteristics of the data. This can reduce human involvement in clustering.

2.5. Model Performance Metrics

In order to evaluate the performance of the clustering model, in addition to SSE and running time, we also adopted the following evaluation criteria: silhouette coefficient (SC) [48], Calinski–Harabasz index (CHI) [49], and Davies–Bouldin index (DBI) [50]. These are commonly used evaluation criteria for clustering performance measurement.

2.5.1. Silhouette Coefficient (SC)

For a good cluster, the distance between samples of the same category is very small, and the distance between samples of different categories is very large. The silhouette coefficient (SC) can evaluate both characteristics at the same time. A higher silhouette coefficient score relates to a model with better clusters.

The silhouette coefficient $s$ for a single sample is given as:

$$s=\frac{b-a}{max\left(a,b\right)}$$

(13)

where $a$ is the mean distance between a sample and all other points in the same class and $b$ is the mean distance between a sample and all other points in the next nearest cluster.

The silhouette coefficient for a set of samples is given as the mean of the silhouette coefficient for each sample [48].

2.5.2. Calinski–Harabasz Index (CHI)

A higher Calinski–Harabasz score relates to a model with better clusters. For a set of data $E$ of size $n_E$, which has been clustered into $k$ clusters, the Calinski–Harabasz score $s$ is defined as the ratio of the between-clusters dispersion mean and the within-cluster dispersion [49]:

$$s=\frac{\mathrm{tr}\left(B_k\right)}{\mathrm{tr}\left(W_k\right)}\times \frac{n_E-k}{k-1}$$

(14)

where $\mathrm{tr}\left(B_k\right)$ is trace of the between group dispersion matrix and $\mathrm{tr}\left(W_k\right)$ is the trace of the within-cluster dispersion matrix defined by:

$$W_k={\displaystyle \sum }_{q=1}^k{\displaystyle \sum }_{x\in C_q}\left(x-c_q\right){(x-c_q)}^T$$

(15)

$$B_k={\displaystyle \sum }_{q=1}^k{n}_q\left(c_q-c_E\right){(c_q-c_E)}^T$$

(16)

With $C_q$ the set of points in cluster $q$, $c_q$ the center of cluster $q$, $c_E$ the center of $E$, and $n_q$ the number of points in cluster $q$.

2.5.3. Davies–Bouldin Index (DBI)

A lower Davies–Bouldin index relates to a model with better separation between the clusters. The index is defined as the average similarity between each cluster $C_i$ for $i=1,\dots ,k$ and its most similar one $C_j$ [50]. In the context of this index, similarity is defined as a measure $R_{ij}$ that trades off:

$s_i$,

the average distance between each point of cluster $i$ and the centroid of that cluster—also known as the cluster diameter.

$d_{ij}$,

the distance between cluster centroids $i$ and $j$.

A simple choice to construct $R_{i}j$ so that it is nonnegative and symmetric is:

$$R_{ij}=\frac{s_i+s_j}{d_{ij}}$$

(17)

Then the Davies–Bouldin index is defined as:

$$DBI=\frac{1}{k}{\displaystyle \sum }_{i=1}^k\underset{i\ne j}{max}{R}_{ij}$$

(18)

3. Results

3.1. The Results of K-CFSFDP

First, we used the K-CFSFDP clustering algorithms to process the four kinds of data. According to this algorithm, the k value and the cluster centers can be determined. Figure 10 is the density, distance decision graph, where the colored points represent the selected cluster center points.

γ value is shown as Figure 11. According to the γ value, the γ values of the seven scattered points were relatively large, so the four kinds of data were divided into seven cluster centers. The cluster centers are shown as

Table 4. The cluster centers of K-Means and clustering by fast search and find of density peaks (K-CFSFDP).

Center	S1		S2		S3		S4
1	6.03289	5.74414	8.32161	6.38682	5.16315	6.04157	6.48546	7.47637
2	8.01669	3.18551	5.64966	2.47307	5.33499	2.75543	3.03581	6.96716
3	4.15422	7.85831	2.56964	7.40917	2.28359	3.47640	7.31236	4.29811
4	8.21340	7.33396	5.42544	2.32415	4.40999	4.06838	6.68811	7.70098
5	8.54662	1.66175	8.11425	2.41816	7.64964	7.92441	5.33691	5.16572
6	3.37340	5.61049	4.44462	6.11261	3.62245	5.93139	6.67577	2.67338
7	1.66517	3.49263	7.41792	4.91789	7.59799	4.57699	3.72421	3.66076

, and the clustering results are shown in the Figure 12.

3.2. K-Means Clustering Algorithm

According to the traditional K-Means clustering algorithm, k value needs to be specified in advance. We in turn specified the value of k, drew the sum of squares due to error (SSE) curve, and then determined the specific value of k.

Due to the possibility of no solution in the traditional K-Means clustering algorithm, when the K-Means algorithm was initialized, the clustering centers were randomly selected. In order to ensure the validity of the results of the K-Means clustering algorithm. We conducted 10 experiments for each k value of the K-Means algorithm, and took the average of each cluster center in 10 experiments as the final cluster center for each k, then calculated the SSE, and the SSE curve is shown as Figure 13.

According to Figure 13, it can be found that as the value of k increased, the SSE value decreased. When the value of k was 7, the SSE reached the minimum value, as the value of k continued to increase, the SSE gradually increased, so the best number of clusters was 7. The traditional K-Means algorithm clustering effect is shown in Figure 14.

According to the SSE curve, the best value of k was 7. So, we used the traditional K-Means clustering algorithm to cluster and chose 7 as the value of k.

Table 5. Cluster centers of the K-Means cluster algorithm.

Center	S1		S2		S3		S4
1	8.27400	2.39930	2.59326	7.40172	4.46283	4.08395	7.54576	4.89052
2	4.13315	7.68235	5.44932	4.33228	5.46431	2.86967	6.65832	2.67032
3	7.77590	7.66245	8.36084	6.38125	7.68175	4.50673	5.54568	5.14083
4	1.71074	3.49110	5.67678	2.42658	7.68820	7.87882	4.08892	5.44782
5	3.37812	5.62245	4.44752	6.11293	3.49562	5.95816	3.76442	3.64857
6	6.06610	5.73412	7.41603	4.88391	2.30457	3.41682	2.82903	7.02875
7	8.03260	3.21768	8.08883	2.36514	5.15896	6.10679	6.45891	7.35572

is the mean value of the cluster centers under multiple clustering.

3.3. CFSFDP Cluster Algorithm

In addition to the traditional K-Means clustering algorithm, we also used the CFSFDP algorithm for clustering. Since the clustering center and the CFSFDP algorithm were consistent in this paper, the improved K-Means clustering algorithm was the same as the clustering center of the algorithm.

The clustering results are shown in Figure 15.

3.4. Evaluation and Comparison of Three Algorithms

The comparison results of each model under different evaluation criteria are shown in

Table 6. Silhouette coefficient (SC) and Calinski–Harabasz index (CHI) value of the three algorithms.

Criteria	SC			CHI
University	K-Means	CFSFDP	K-CFSFDP	K-Means	CFSFDP	K-CFSFDP
S1	0.720163	0.773615	0.78262114	18654.66	17171.17	20351.42166
S2	0.629851	0.653892	0.67294505	8548.027	7939.654	9330.545438
S3	0.511018	0.551514	0.56356586	4042.819	4053.911	4316.641802
S4	0.516445	0.526225	0.56055753	3389.293	3115.909	3572.915619

and

Table 7. Davies–Bouldin index (DBI) and sum of the squared errors (SSE) value of the three algorithms.

Criteria	DBI			SSE
University	K-Means	CFSFDP	K-CFSFDP	K-Means	CFSFDP	K-CFSFDP
S1	0.47214	0.283085	0.27428561	168.6821	169.2103	168.5100431
S2	0.573574	0.427371	0.41893048	159.0415	157.6216	158.5206654
S3	0.723378	0.581062	0.56537985	149.0415	148.9562	142.2402269
S4	0.751687	0.611766	0.56924453	165.5415	156.224	163.5586647

. The running time of the three algorithms is shown in

Table 8. Running time(s) of the three algorithms.

Type Algorithm	S1	S2	S3	S4
K-CFSFDP	8.667326	7.011259	9.043949	8.7854173
K-Means	0.435833	1.091194	0.831946	0.823445
CFSFDP	12.740592	10.269540	13.293498	12.880990

.

In order to more clearly reflect the comparison results of the three models, we standardized the results in Table 6, Table 7 and Table 8 and set the value range to [0–5]. Then we visualized the results, as shown in Figure 16, Figure 17, Figure 18 and Figure 19. They show more intuitively the performance scores of three models under five performance metrics in different universities.

4. Discussion

Now we could analyze university students’ behavior based on the results shown in Table 4 and Figure 12. From Table 4, it can be found the students’ behaviors were different among four universities. S1 was taken as an example to analyze the students’ behaviors. The center point of the first category was (6.0389, 5.47474), 6.0389 was the score of living habit, and 5.47474 was the score of learning performance, the center point indicates that the living habits and learning performance of students in this category were moderate. The center point of the second category was (8.01667, 3.18542), which indicates that students in this category had good living habits but poor learning performance. The fact was adverse in the third type, the center point of the third category was (4.15417, 7.85827), which shows these students performed well in learning performance and badly in living habit.

Figure 12 shows that students in these four schools could be divided into seven categories, but the distribution of student behavior categories in different schools was different. From Figure 12, the distribution of most S1 students was located in the top right of the figure. Compared with the three other universities, it could be found that the students performed very differently between each category. Most of the S2 categories were in the lower right of the picture, which indicates that the learning performance was better, but the living habits were poor. S3 and S4 students performed moderately in living habit and learning performance.

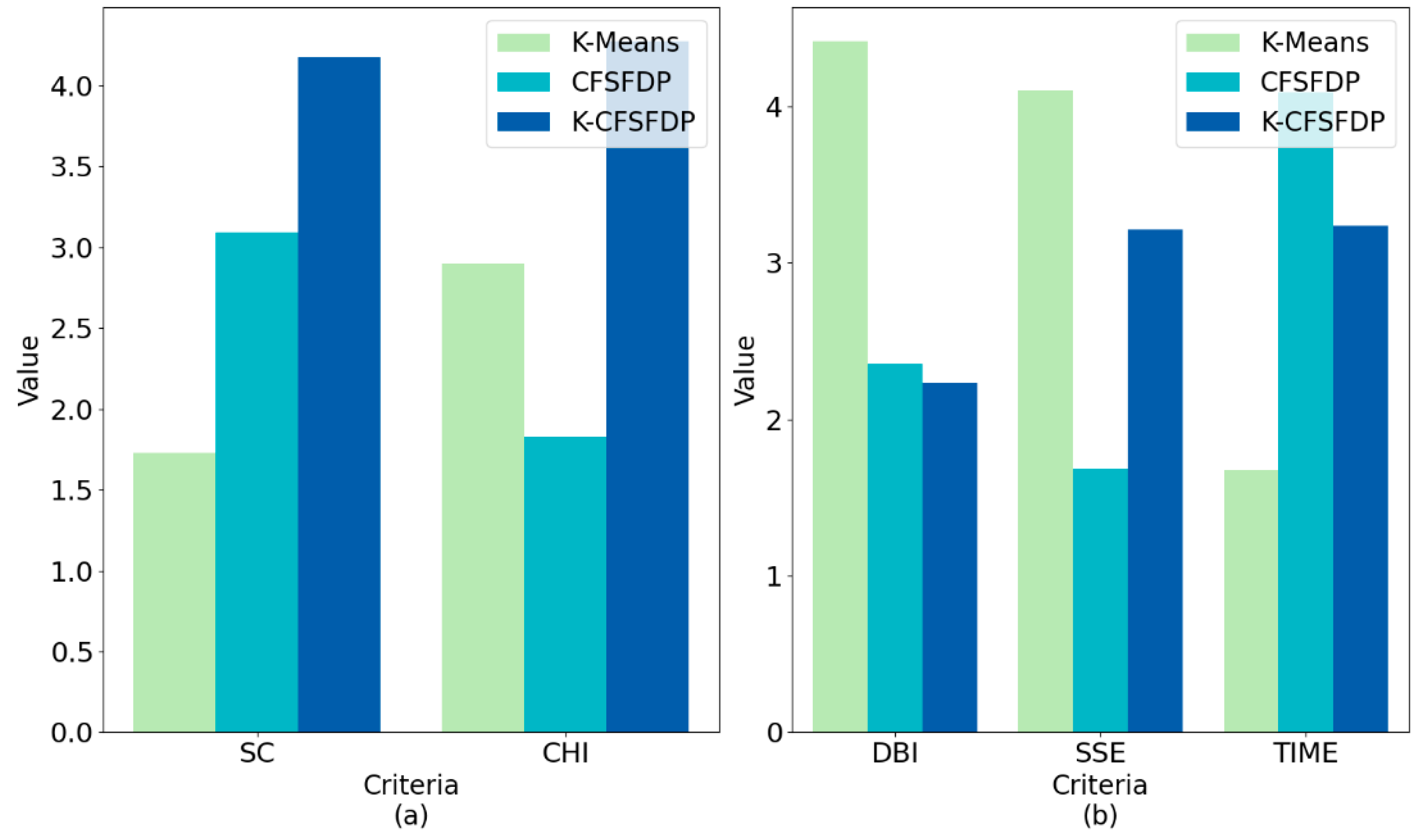
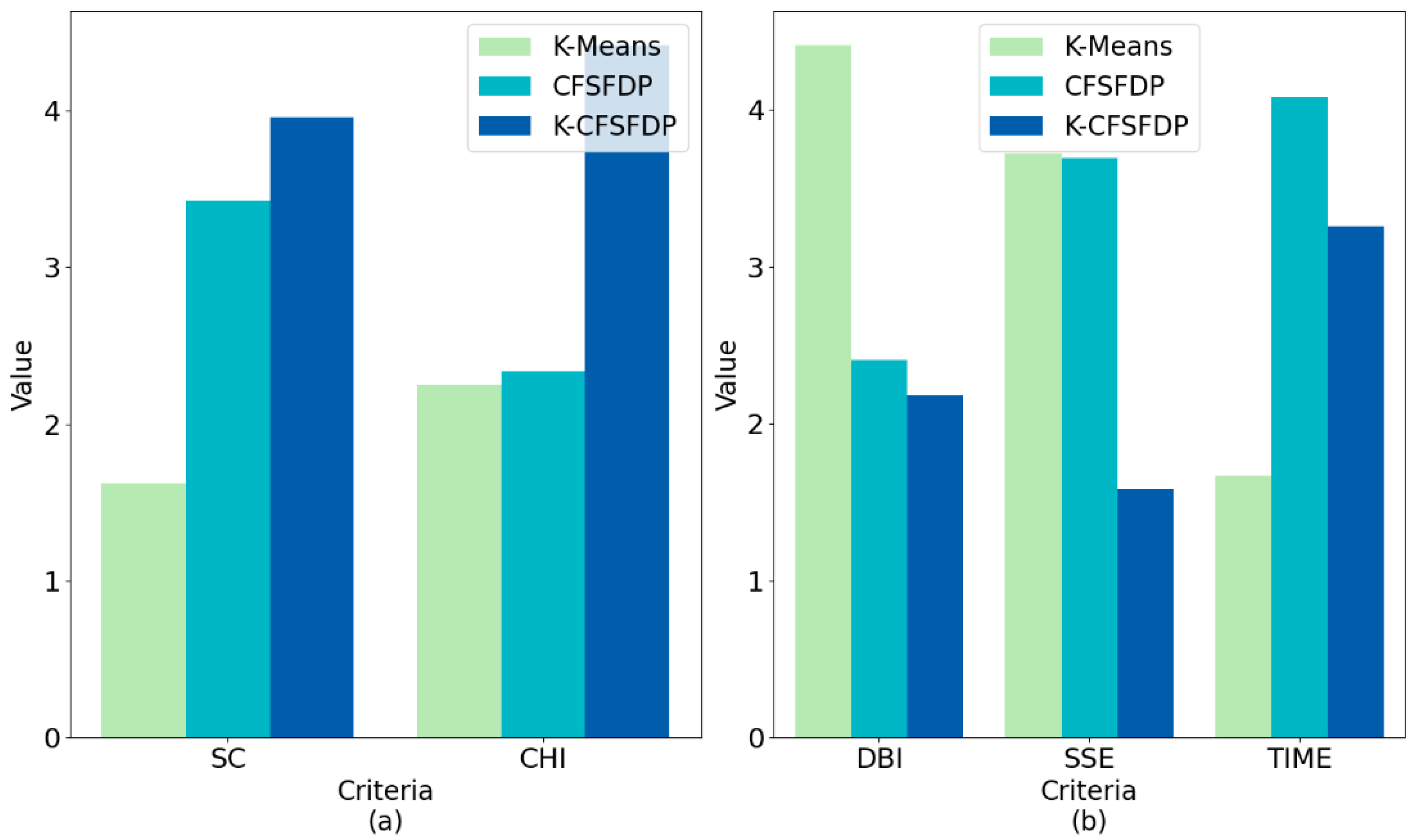
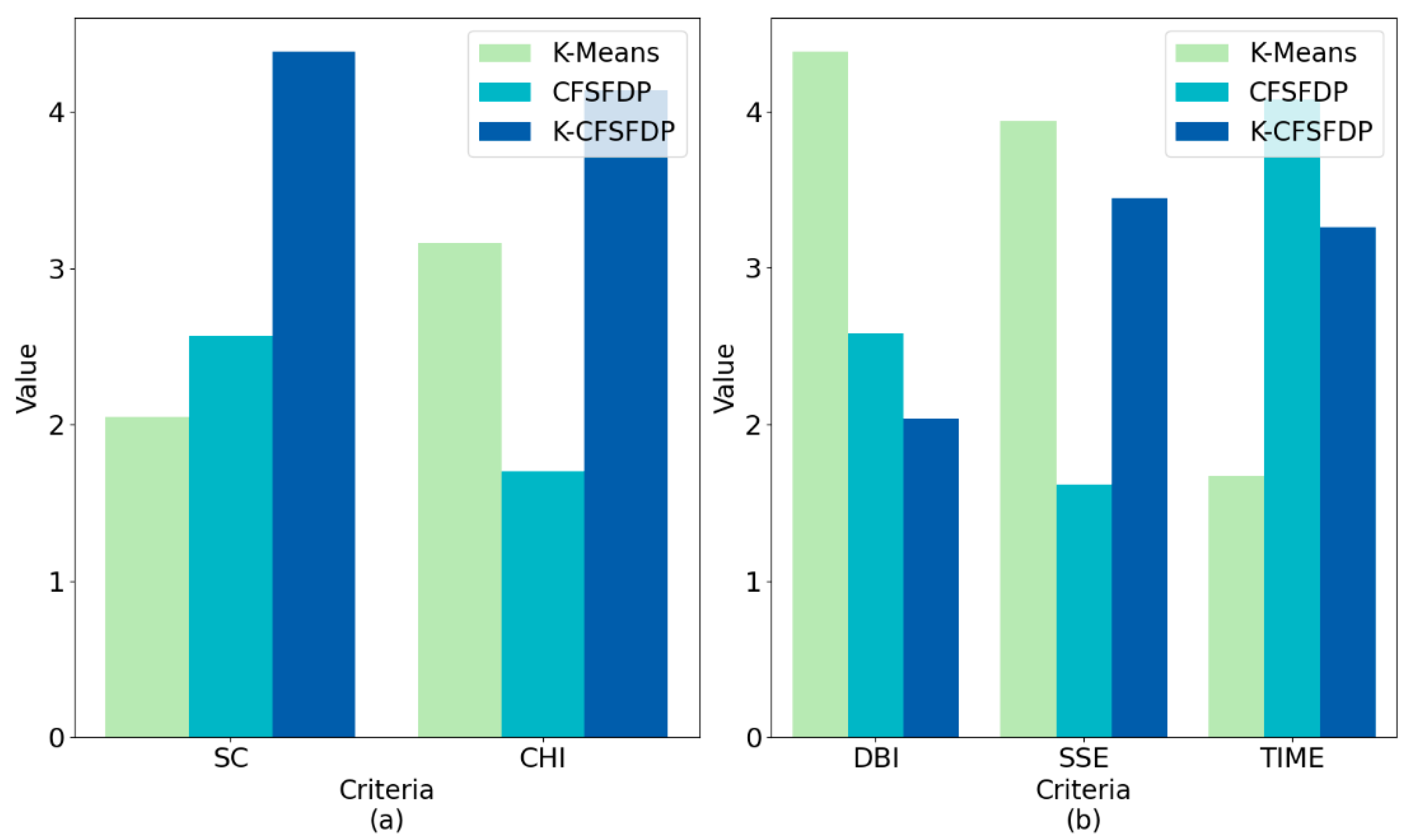
We measured and compared the effects of the three algorithms on the behavior clustering of university students by calculating SC, CHI, DBI, and SSE. It can be seen from Table 6 and Figure 16a, Figure 17a, Figure 18a and Figure 19a that the SC and CHI of K-CFSFDP were higher than those of K-Means and CFSFDP on the four university data sets. It can be seen from Table 7 and Figure 16b, Figure 17b, Figure 18b and Figure 19b that the DBI of K-CFSFDP was lower than that of K-Means and CFSFDP on the four university data sets. According to the SSE value, it could be clearly found that the K-CFSFDP algorithm was obviously better than the traditional K-Means clustering algorithm, and the partial SSE of the K-CFSFDP algorithm was less than CFSFDP algorithm. This shows that the clustering effect of K-CFSFDP was better than that of K-Means and CFSFDP, and could better cluster the behavior of university students. The experimental results in Table 6 and Table 7 confirmed that because K-CFSFDP could determine the number of student categories (number of clusters) and student representatives (cluster centers), and used the Gaussian kernel function to calculate the point density, it has greater advantages. Therefore, compared with the other two algorithms, K-CFSFDP could better gather students with similar learning behaviors and living habits.

We compared the running time of the three algorithms based on the same data. From Table 8 and Figure 16b, Figure 17b, Figure 18b and Figure 19b, it could be found that the traditional K-Means algorithm ran faster than the other two algorithms. However, the time spent in its early stage was much longer than the other two algorithms. The running time of K-CFSFDP algorithm was shorter than CFSFDP. Therefore, K-CFSFDP could perform clustering faster and reduced the computing time of large-scale campus data.

Compared with the current studies and methods on the behavior analysis of university students, the method proposed in this paper had considerable advantages in the following aspects:

(1)

Traditional data mining and supervised machine learning methods often set labels in advance when classifying student behaviors. University student behavior data is often only used to analyze the relationship between behavior characteristics and labels. This does not take into account the diversity of student behavior and the knowledge contained in the data itself, and the evaluation criteria for labels are often subjective. For example, in accordance with the traditional supervised machine learning algorithm (such as decision trees, random forests, etc.), students with a score greater than 60 can be labeled as “good students”, and those with scores less than 60 can be labeled as “bad students”. Student behavior data and label data are input into a supervised machine learning model for training and analysis. After the training is completed, when the behavior data of a new student is input, the model will output which category the student belongs to. Obviously, this method has two problems. First, it is difficult to quantify the evaluation criteria of the label. People can question: “Why is the label threshold of good students 60 instead of 50 or 70?” Therefore, the judgment of labels is often vague, and the classification results of students are not objective. Second, the environmental conditions of different schools are different. It is possible that the difficulty of the exam of school B is greater than that of school A, and a student with a score of 50 may be defined as a “good student”. Therefore, the judgment of student labels is often more complicated and the model is difficult to adjust flexibly. The method proposed in this paper does not need to determine in advance how many types of university students there are, nor does it need to determine in advance which type a student belongs to. This method uses unsupervised clustering to automatically classify students’ behavior data based on the similarity, so the result is more objective and accurate, and it can reflect the impact of the university’s own characteristics on students’ behavior.

(2)

The traditional K-Means clustering algorithm can select the number of clusters according to the SSE value, but the number of possible classes of the data needs to be estimated in advance. This is unrealistic for unfamiliar large data sets because it is impossible to determine the number of student behavior categories in advance. Additionally, the K-Means clustering algorithm may not find the cluster center. As for CFSFDP, its computing time is relatively long, which cannot be applied to large-scale campus data. The method proposed in this paper combines the advantages of the two algorithms, which can accurately determine the number of student behavior categories and cluster centers, and can also process large-scale university student behavior data at a reasonable speed.

5. Conclusions

In this paper, the K-CFSFDP algorithm based on K-Means and CFSFDP was proposed to analyze different university students’ behaviors. We first introduced the relevant research on the behavior analysis of university students, and clarified that educational data mining was the current development trend. We noticed that clustering was an effective tool for behavior analysis of university students. We found that K-Means clustering algorithm had the disadvantage of not specifying K value and its clustering effect depended on the initial clustering center. Although CFSFDP clustering algorithm had good clustering results, its operation efficiency was low. Under the background of big data, the CFSFDP algorithm will be greatly restricted. Considering the clustering effect and running time, we constructed the K-CFSFDP algorithm as an effective tool to analyze the behavior of university students. In order to verify the effectiveness of the model, we collected data on the learning performance and living habits of 8000 students from four universities, and used K-Means, CFSFDP, and K-CFSFDP to cluster these data. We judged the clustering effect and operating efficiency through the value of SC, CHI, DBI, SSE, and the running time. Comparing and analyzing the experimental results, we could draw the following conclusions:

• University students with similar learning performance and living habits in each university gathered into a certain number of sets.
• Clustering centers could reflect the behavioral characteristics of a certain category of students in the areas of learning performance and living habits.
• The distribution of behavior categories of university students in different schools was not the same.
• The K-CFSFDP algorithm could directly specify the appropriate k value and the optimal clustering center. That is, the algorithm could determine the number of student behavior types and behavior scores of each university.
• K-CFSFDP had a better clustering effect than K-Means algorithm, and had a shorter running time than CFSFDP algorithm, so it could be applied to the analysis of university students’ behavior.

This study had certain practical significance in education and the pedagogical aspect. Teachers or school administrators could better obtain the categories and characteristics of student behavior. The practical value and significance of this study are as follows:

First, this study could achieve a scientific and reasonable classification of university students’ behavior and was simple to operate. For university decision makers and student administrators, they do not need to judge in advance which category a student belongs to. They only need to collect students’ behavioral data, and then input them into the model for clustering and analysis. This facilitates the management process of decision makers and avoids preconceived judgments about student behavior types. Since it is based on the data clustering, the result is more objective and accurate.

Second, this study can help school administrators provide targeted assistance to different student groups. The clustering results can show the differences between each type students, which can help schools better understand student behavior. Schools can analyze and summarize the behavior characteristics of different types of students, and take targeted measures for different types of students to help them have good living habits and perform well in learning.

Third, the results of this research can provide feedback on the management effects of school administrators. For example, if a university has a small number of student groups, it means there exists a high similarity and concentrated distribution of students’ behavior. This indicates that student life on campus may be tedious. As a result, school administrators should take measures to enrich students’ campus life. If a university’s student clusters are more distributed near certain values, or less distributed near certain values, education administrators can rethink what caused the imbalance in student distribution and take targeted improvement measures. For another example, if there are a large number of students in a certain group and a small number of students in another group, education administrators can think about what caused this difference, so as to provide corresponding assistance to the minority student groups. This can avoid ignoring the need of minority student groups.

Fourth, the results of this research can help educators to further analyze what factors can affect and determine the behavior characteristics of students, such as using correlation analysis methods to study the relationship between students’ personal characteristics (such as gender, height, weight, etc.) and student behavior.

Fifth, this study provides a benchmark for the behavior classification of university students. Since K-CFSFDP determines the student behavior category, it is equivalent to providing a classification baseline about sample label. Therefore, we can use supervised machine learning methods to analyze university student behavior.

This research was an application innovation of university student behavior analysis. There were application scope and applicable conditions. The application circumstances and data requirements of the algorithm proposed in this study were as follows:

1.

University student behavior data was structured data.

Structured data refers to data that can be represented and stored in a relational database, and is represented in a two-dimensional form. The general characteristics are: the unit of data is “row”, a row of data represents the information of an entity, and the attributes of each row of data are the same. In this study, each row of the data represented each student, and each column was the student’s behavioral attributes (such as learning habits and living habits).

2.

The behavior classification of college students was an unsupervised learning problem.

Machine learning can be divided into supervised learning and unsupervised learning. There are data and labels in supervised learning, and machine learning can learn a function that maps data to labels. There are many forms of label definition, such as classifying students as “good students” or “bad students” based on the threshold of test scores. The data for unsupervised learning has no labels. In this study, we obtained student behavior data through statistics without any labels. That is, we did not define in advance which categories the students belong to, nor did we define the characteristics of each category, so it was an unsupervised learning problem. This means that from the distribution map of student behavior data (the abscissa is the learning score, the ordinate is the living score), we could not intuitively judge how many categories these data could be divided into, nor could we judge the typical representative data points of each category. We used K-CFSFDP to automatically classify students based on the similarity of data.

3.

The scale of college students’ behavior data was relatively large.

First, the collection, calculation, and storage of big data are huge. Second, the dimensionality of the data is higher. Third, the data growth rate is very fast, and the data acquisition and processing speed is required to be fast. Fourth, the data value density is relatively low. In this study, the number of students in each university was often very large, reaching tens of thousands. This study counted data of a total of 8000 students, which had a certain number scale. In addition, we counted the data of each student’s study and living habits. There were eight evaluation indicators (as shown in Table 1 and Table 2), and the data had a certain dimension.

The study in this paper had the following indications for further research. First, this paper only analyzed student behavior from two dimensions of living habits and learning performance. The behavior of university students has multiple dimensions, such as social behavior, network behavior, etc. Future research will expand the dimensions of student behavior and test the clustering effect of K-CFSFDP on high-dimensional student behavior data. Second, this study only used data from four universities, so the number of data sets was small. In future research, we will investigate more universities to expand the number of data sets, so that we can use a statistical test to analyze and compare the clustering results of different methods. Third, each clustering algorithm has its own distance metric function. Each distance metric function is not suitable for all data. The K-CFSFDP algorithm in this paper is still using Euclidean distance. Different distance metrics should be adopted for different data characteristics. Fourth, the cutoff distance $d_c$ in CFSFDP has a significant impact on the clustering results. The K-CFSFDP did not further optimize the $d_c$. Future study will explore how to choose the best $d_c$ in K-CFSFDP.