Thermodynamics of Plutonium Monocarbide from Anharmonic and Relativistic Theory
Abstract
1. Introduction
2. Computational Methods
2.1. Electronic-Structure Methods
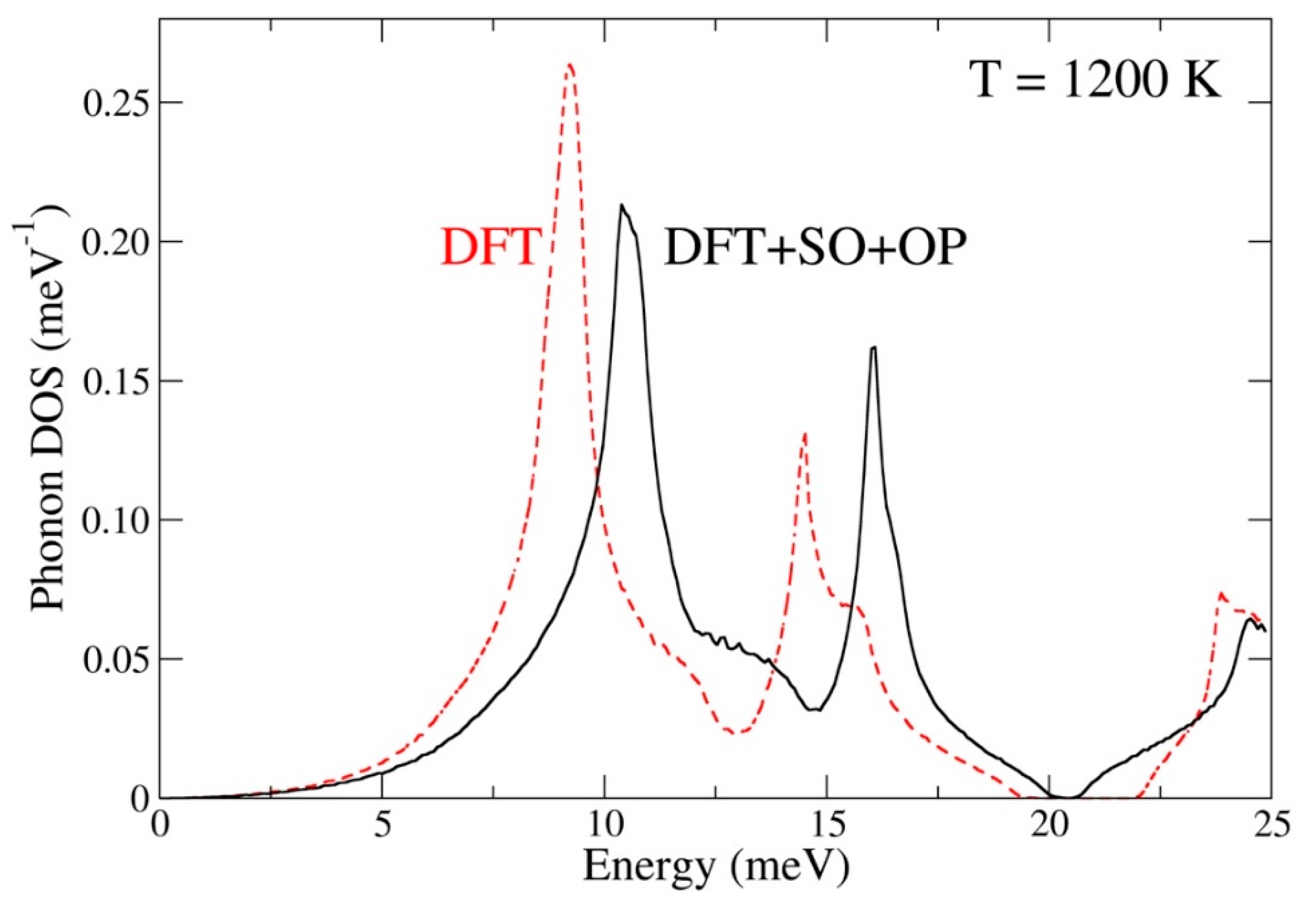
2.2. Lattice-Dynamics Methods
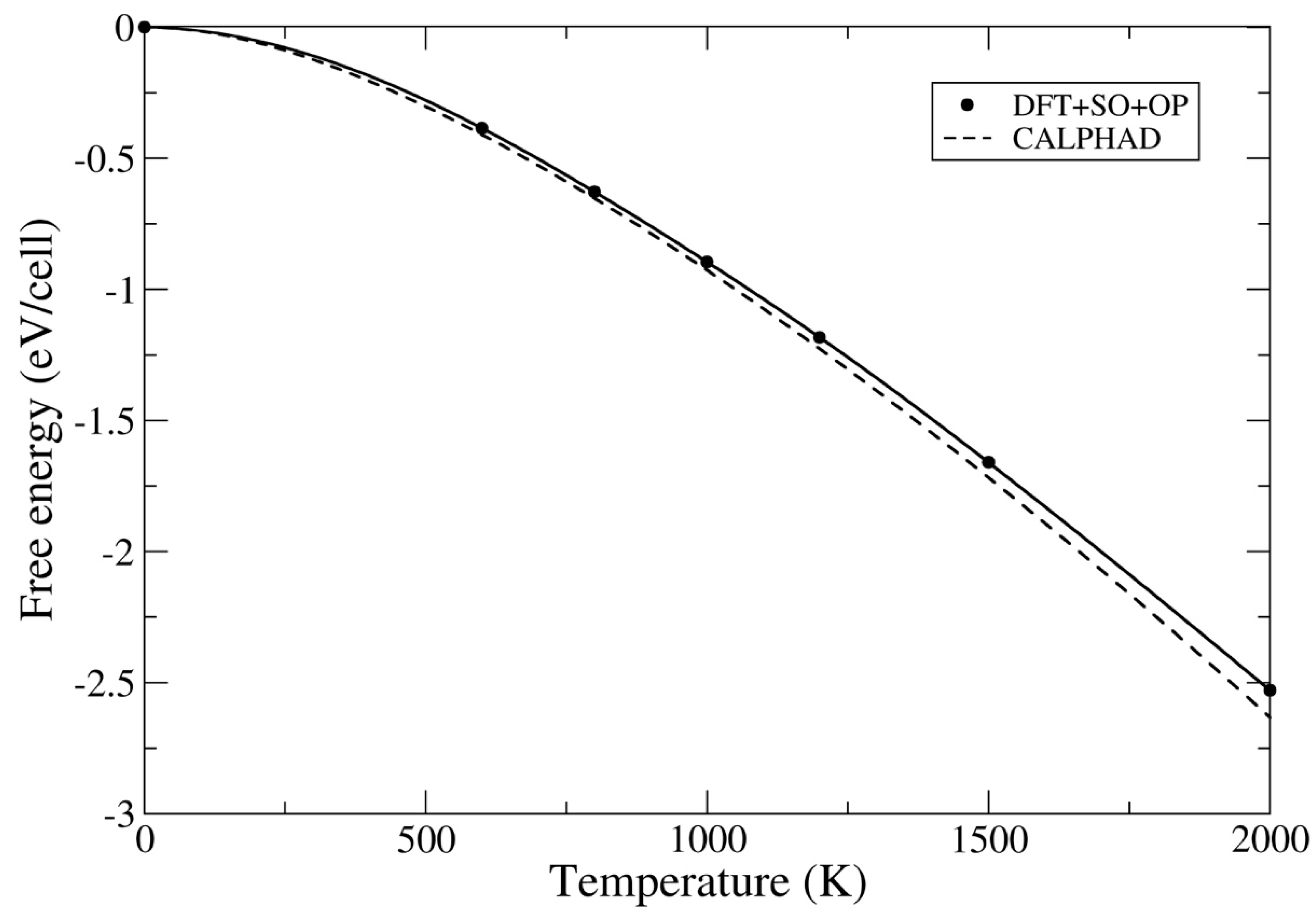
2.3. CALPHAD Method
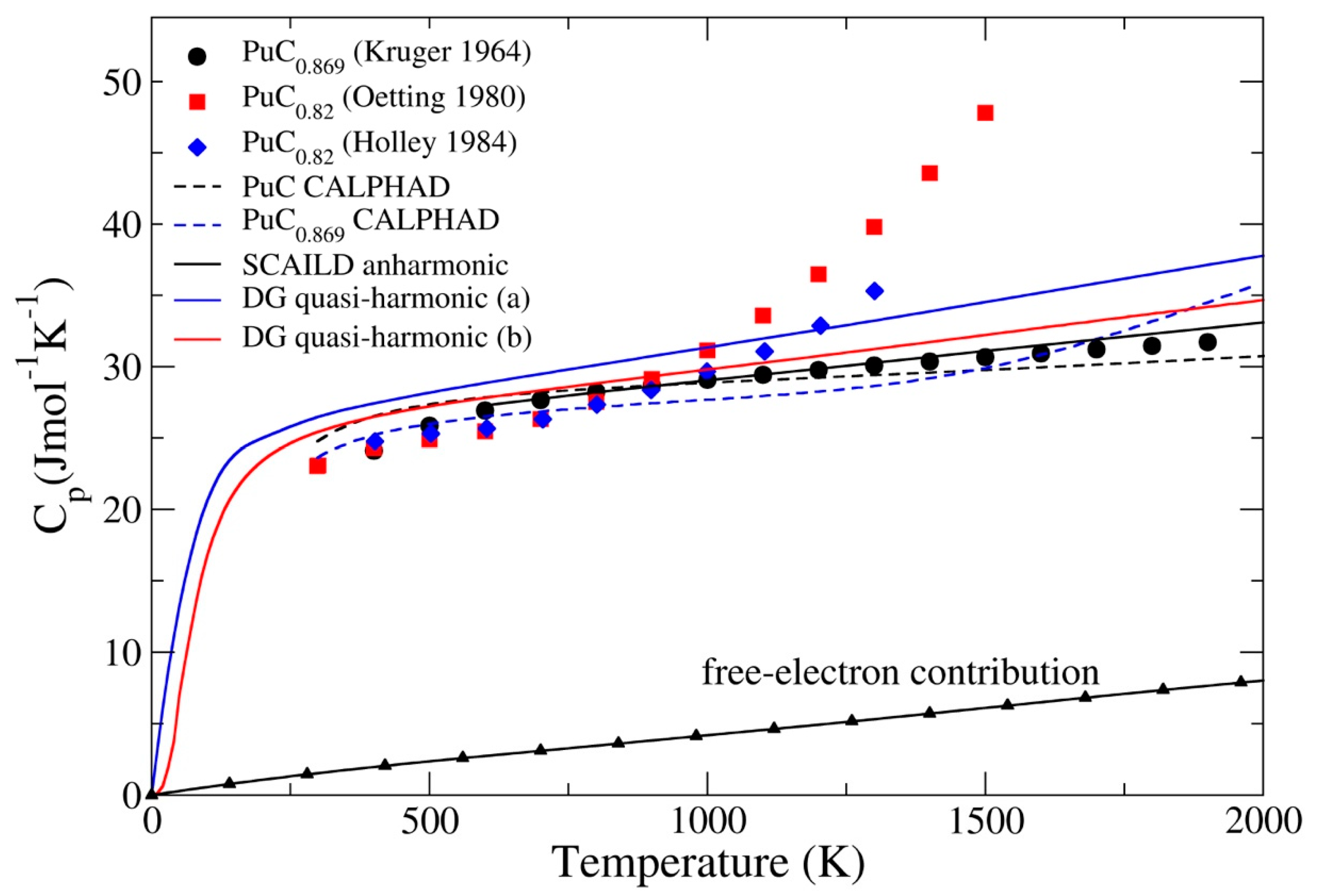
3. Results
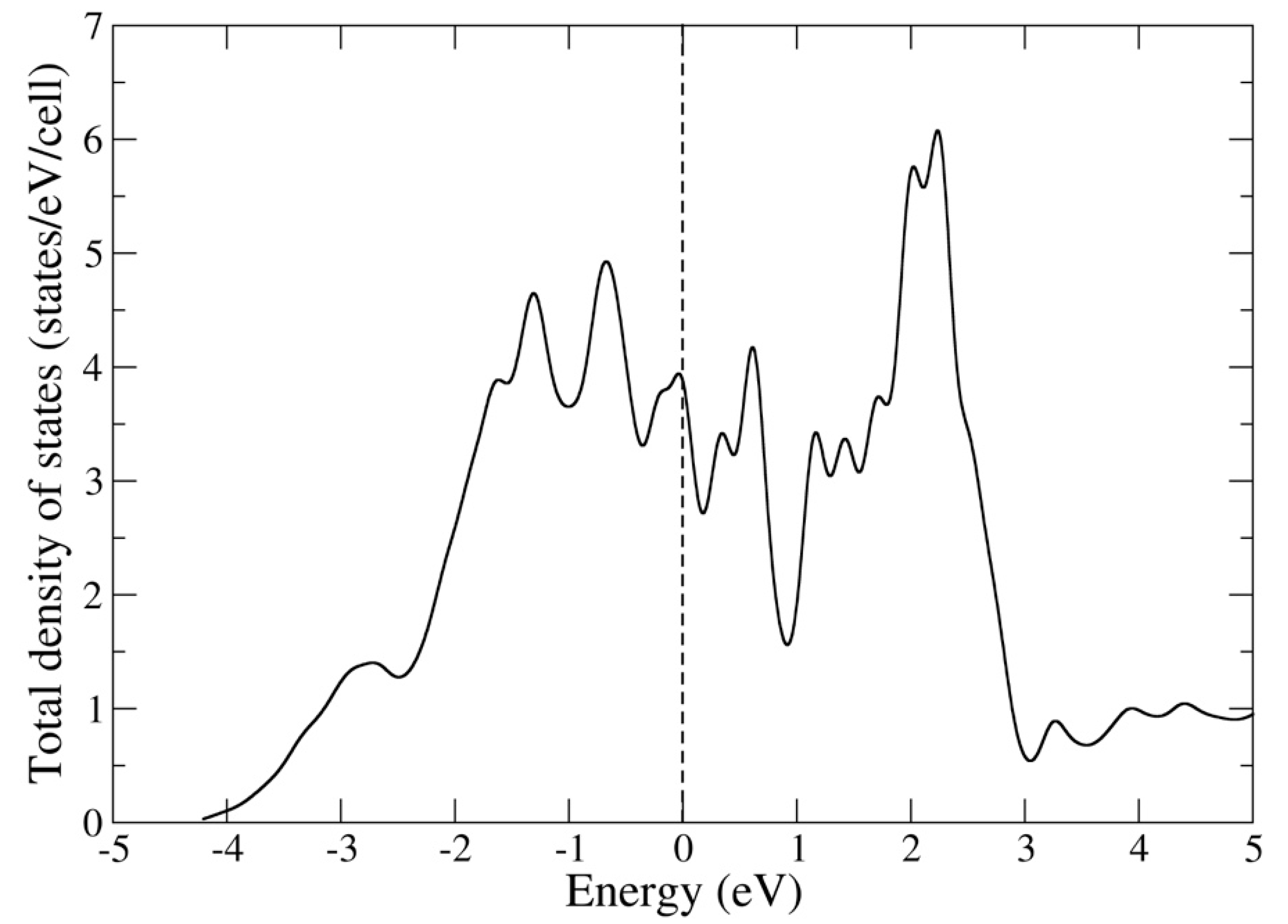
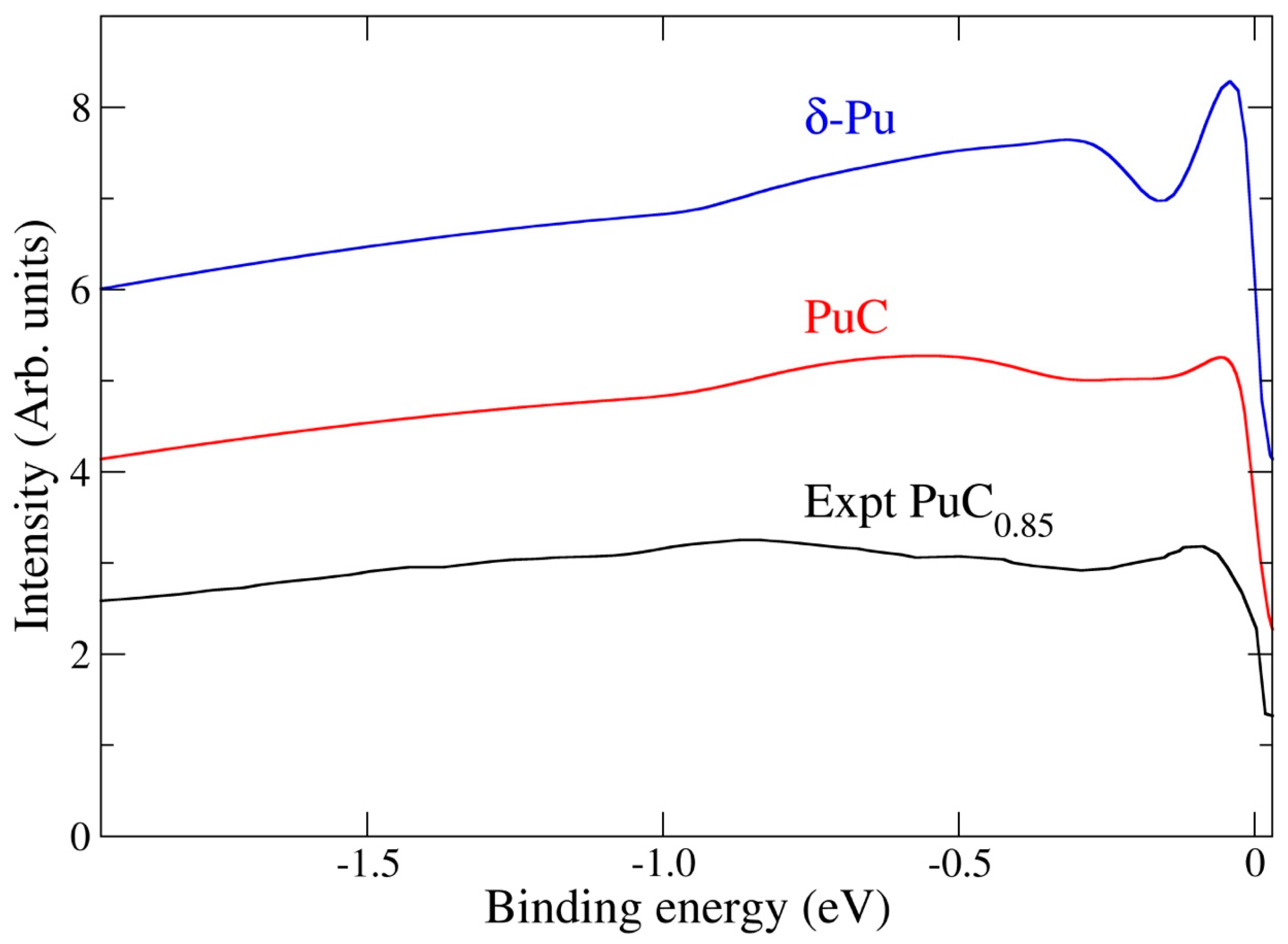
3.1. Electronic Structure
3.2. Ground-State Properties and Thermodynamics
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Petit, L.; Svane, A.; Szotek, Z.; Temmerman, W.M.; Stocks, G. Electronic structure and ionicity of actinide oxides from first principles. Phys. Rev. B 2010, 81, 045108. [Google Scholar] [CrossRef]
- Wen, X.-D.; Martin, R.L.; Henderson, T.M.; Scuseria, G.E. Density functional theory studies of the electronic structure of solid state actinide oxides. Chem. Rev. 2012, 113, 1063–1096. [Google Scholar] [CrossRef] [PubMed]
- Moore, K.T.; Van Der Laan, G. Nature of the 5f states in actinide metals. Rev. Mod. Phys. 2009, 81, 235–298. [Google Scholar] [CrossRef]
- Söderlind, P. First-principles phase stability, bonding, and electronic structure of actinide metals. J. Electron. Spectrosc. Relat. Phenom. 2014, 194, 2–7. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Sadigh, B. Density-functional theory for plutonium. Adv. Phys. 2019, 68, 1–47. [Google Scholar] [CrossRef]
- Sadigh, B.; Kutepov, A.; Landa, A.; Söderlind, P. Assessing relativistic effects and electron correlation in the actinide metals Th to Pu. Appl. Sci. 2019, 9, 5020. [Google Scholar] [CrossRef]
- Amadon, B. First-principles DFT + DMFT calculations of structural properties of actinides: Role of Hund’s exchange, spin-orbit coupling, and crystal structure. Phys. Rev. B 2016, 94, 115148. [Google Scholar] [CrossRef]
- Savrasov, S.Y.; Kotliar, G. Ground state theory of δ-Pu. Phys. Rev. Lett. 2000, 84, 3670–3673. [Google Scholar] [CrossRef]
- Marianetti, C.A.; Haule, K.; Kotliar, G.; Fluss, M.J. Electronic Coherence in δ-Pu: A dynamical mean-field theory study. Phys. Rev. Lett. 2008, 101, 056403. [Google Scholar] [CrossRef]
- Söderlind, P.; Zhou, F.; Landa, A.; Klepeis, J.E. Phonon and magnetic structure in δ-plutonium from density-functional theory. Sci. Rep. 2015, 5, 15958. [Google Scholar] [CrossRef]
- Wen, X.-D.; Martin, R.L.; Scuseria, G.E.; Rudin, S.P.; Batista, E.R. A screened hybrid DFT study of actinide oxides, nitrides, and carbides. J. Phys. Chem. C 2013, 117, 13122–13128. [Google Scholar] [CrossRef]
- Pogany, P.; Kovács, A.; Visscher, L.; Konings, R.J.M. Theoretical study of actinide monocarbides (ThC, UC, PuC, and AmC). J. Chem. Phys. 2016, 145, 244310. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, D.; Garg, S.; Goswami, G. Thermodynamic analysis of mixed carbide, carbonitride and nitride fuels for fast breeder reactors. J. Nucl. Mater. 1989, 161, 44–56. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Perron, A.; Sadigh, B.; Heo, T.W. Ground-state and thermodynamical properties of uranium mononitride from anharmonic first-principles Theory. Appl. Sci. 2019, 9, 3914. [Google Scholar] [CrossRef]
- Söderlind, P. Quantifying the importance of orbital over spin correlations in δ-Pu within density-functional theory. Phys. Rev. B 2008, 77, 085101. [Google Scholar] [CrossRef]
- Guéneau, C.; Dupin, N.; Sundman, B.; Martial, C.; Dumas, J.-C.; Gossé, S.; Chatain, S.; De Bruycker, F.; Manara, D.; Konings, R.J. Thermodynamic modelling of advanced oxide and carbide nuclear fuels: Description of the U-Pu-O-C systems. J. Nucl. Mater. 2011, 419, 145–167. [Google Scholar] [CrossRef]
- Sundman, B.; Jansson, B.; Andersson, J.-O. The Thermo-Calc databank system. Calphad 1985, 9, 153–190. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Wills, J.M.; Eriksson, O.; Andersson, P.; Delin, A.; Grechnyev, O.; Alouani, M. Full-Potential Electronic Structure Method; Springer Science and Business Media LLC: Berlin, Germany, 2010. [Google Scholar]
- Eriksson, O.; Brooks, M.S.S.; Johansson, B. Orbital polarization in narrow-band systems: Application to volume collapses in light lanthanides. Phys. Rev. B 1990, 41, 7311–7314. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.; Rudin, S. The self-consistent ab initio lattice dynamical method. Comput. Mater. Sci. 2009, 44, 888–894. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Faulkner, J. The modern theory of alloys. Prog. Mater. Sci. 1982, 27, 1–187. [Google Scholar] [CrossRef]
- Vitos, L. Total-energy method based on the exact muffin-tin orbitals theory. Phys. Rev. B 2001, 64, 014107. [Google Scholar] [CrossRef]
- Vitos, L.; Abrikosov, I.; Johansson, B. Anisotropic lattice distortions in random alloys from first-principles theory. Phys. Rev. Lett. 2001, 87, 156401. [Google Scholar] [CrossRef]
- Söderlind, P.; Grabowski, B.; Yang, L.H.; Landa, A.; Björkman, T.; Souvatzis, P.; Eriksson, O. High-temperature phonon stabilization of γ-uranium from relativistic first-principles theory. Phys. Rev. B 2012, 85, 060301(R). [Google Scholar] [CrossRef]
- Söderlind, P. Lattice dynamics and elasticity for ε-plutonium. Sci. Rep. 2017, 7, 1116. [Google Scholar] [CrossRef]
- Moruzzi, V.L.; Janak, J.F.; Schwarz, K. Calculated thermal properties of metals. Phys. Rev. B 1988, 37, 790–799. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C. Introduction to Chemical Physics; McGraw-Hill: New York, NY, USA, 1939. [Google Scholar]
- Dugdale, J.S.; Macdonald, D.K.C. The thermal expansion of solids. Phys. Rev. 1953, 89, 832–834. [Google Scholar] [CrossRef]
- Morse, P.M. Diatomic molecules according to the wave mechanics. II. vibrational levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
- Otero-De-La-Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Söderlind, P.; Nordström, L.; Yongming, L.; Johansson, B. Relativistic effects on the thermal expansion of the actinide elements. Phys. Rev. B 1990, 42, 4544–4552. [Google Scholar] [CrossRef]
- Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams with Special Reference to Refractory Metals; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Saunders, N.; Miodownik, A. CALPHAD Calculation of Phase Diagrams: A Comprehensive Guide; Elsevier Science: Oxford, UK, 1998. [Google Scholar]
- Lukas, H.; Fries, S.; Sundman, B. Computational Thermodynamics: The CALPHAD Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bajaj, S.; Landa, A.; Söderlind, P.; Turchi, P.E.; Arroyave, R. The U–Ti system: Strengths and weaknesses of the CALPHAD method. J. Nucl. Mater. 2011, 419, 177–185. [Google Scholar] [CrossRef]
- Ravat, B.; Oudot, B.; Perron, A.; Lalire, F.; Delaunay, F. Phase transformations in PuGa 1at.% alloy: Study of whole reversion process following martensitic transformation. J. Alloys Compd. 2013, 580, 298–309. [Google Scholar] [CrossRef]
- Perron, A.; Ravat, B.; Oudot, B.; Lalire, F.; Mouturat, K.; Delaunay, F. Phase transformations in Pu-Ga alloy: Synergy between simulations and experiments to elucidate direct and indirect reversion competition. Acta Mater. 2013, 61, 7109–7120. [Google Scholar] [CrossRef]
- Perron, A.; Turchi, P.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F.; Kurata, M. Thermodynamic re-assessment of the Pu-U system and its application to the ternary Pu-U-Ga system. J. Nucl. Mater. 2014, 454, 81–95. [Google Scholar] [CrossRef]
- Perron, A.; Turchi, P.; Landa, A.; Söderlind, P.; Ravat, B.; Oudot, B.; Delaunay, F. The Pu-U-Am system: An ab initio informed CALPHAD thermodynamic study. J. Nucl. Mater. 2015, 458, 425–441. [Google Scholar] [CrossRef]
- Moore, E.E.; Turchi, P.E.; Landa, A.; Söderlind, P.; Oudot, B.; Belof, J.L.; Stout, S.A.; Perron, A. Development of a CALPHAD thermodynamic database for Pu-U-Fe-Ga alloys. Appl. Sci. 2019, 9, 5040. [Google Scholar] [CrossRef]
- Perron, A.; Turchi, P.; Landa, A.; Oudot, B.; Ravat, B.; Delaunay, F. Thermodynamic assessments and inter-relationships between systems involving Al, Am, Ga, Pu, and U. J. Nucl. Mater. 2016, 482, 187–200. [Google Scholar] [CrossRef]
- Gouder, T.; Havela, L.; Shick, A.B.; Huber, F.; Wastin, F.; Rebizant, J. Variability of 5f states in plutonium carbides. J. Phys. Condens. Matter 2007, 19, 476201. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Sadigh, B. Density-functional investigation of magnetism in δ-Pu. Phys. Rev. B 2002, 66, 205109. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Tobin, J.; Allen, P.; Medling, S.; Booth, C.; Bauer, E.D.; Cooley, J.C.; Sokaras, D.; Weng, T.-C.; et al. On the valence fluctuation in the early actinide metals. J. Electron. Spectrosc. Relat. Phenom. 2016, 207, 14–18. [Google Scholar] [CrossRef][Green Version]
- Green, J.; Arnold, G.; Leary, J.; Nereson, N. Crystallographic and magnetic ordering studies of plutonium carbides using neutron diffraction. J. Nucl. Mater. 1970, 34, 281–289. [Google Scholar] [CrossRef]
- Yang, R.; Tang, B.; Tao, G.; Ao, B. Structural, magnetic, electronic and optical properties of PuC and PuC0.75: A hybrid density functional study. J. Nucl. Mater. 2016, 473, 54–60. [Google Scholar] [CrossRef]
- Zachariasen, W.H. Crystal chemical studies of the 5f-series of elements. XII. New compounds representing known structure types. Acta Crystallogr. 1949, 2, 388–390. [Google Scholar] [CrossRef]
- Storms, E.K. The Refractory Carbides; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Söderlind, P.; Eriksson, O.; Johansson, B.; Wills, J.M. Electronic properties off-electron metals using the generalized gradient approximation. Phys. Rev. B 1994, 50, 7291–7294. [Google Scholar] [CrossRef]
- Söderlind, P.; Gonis, A. Assessing a solids-biased density-gradient functional for actinide metals. Phys. Rev. B 2010, 82, 033102. [Google Scholar] [CrossRef]
- Mounet, N.; Marzari, N. First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives. Phys. Rev. B 2005, 71, 205214. [Google Scholar] [CrossRef]
- Verma, A.K.; Kaushik, S.; Singh, D.; Yadav, R.R. Elastic and thermal properties of carbides of U, Pu, and Am. J. Phys. Chem. Solids 2019, 133, 21–27. [Google Scholar] [CrossRef]
- Söderlind, P.; Landa, A.; Klepeis, J.E.; Suzuki, Y.; Migliori, A. Elastic properties of Pu metal and Pu-Ga alloys. Phys. Rev. B 2010, 81, 224110. [Google Scholar] [CrossRef]
- Krajewski, A.; D’Alessio, L.; De Maria, G. Physio-chemical and thermophysical properties of cubic binary alloys. Cryst. Res. Technol. 1998, 33, 341–374. [Google Scholar] [CrossRef]
- Grimvall, G. Spin disorder in paramagnetic fcc iron. Phys. Rev. B 1989, 39, 12300–12301. [Google Scholar] [CrossRef]
- Wang, Y. Classical mean-field approach for thermodynamics: Ab initio thermophysical properties of cerium. Phys. Rev. B 2000, 61, R11863–R11866. [Google Scholar] [CrossRef]
- Kruger, O.L.; Savage, H. Heat capacity of plutonium monocarbide from 400° to 1300° K. J. Chem. Phys. 1964, 40, 3324. [Google Scholar] [CrossRef]
- Oetting, F.L. The chemical thermodynamics of nuclear materials. J. Nucl. Mater. 1980, 88, 265–272. [Google Scholar] [CrossRef]
- Holley, C.E.; Rand, M.H.; Storms, E.K. The Chemical Thermodynamics of Actinide Elements and Compounds. Part 6: The Actinide Carbides; IAEA: Vienna, Austria, 1984; pp. 53–72. [Google Scholar]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier BV: Amsterdam, The Netherlands, 1999; pp. 157–172. [Google Scholar]
- Haines, H.; Hall, R.; Lee, J.; Mortimer, M.; McElroy, D. The low temperature specific heats of three plutonium carbides. J. Nucl. Mater. 1980, 88, 261–264. [Google Scholar] [CrossRef]
- Hill, H.H. Plutonium 1970 and Other Actinides; Miner, W.D., Ed.; The metallurgical society of the AIME: New York, NY, USA, 1970; pp. 2–19. [Google Scholar]
- Lai, C.; Hu, Y.; Qiu, R. Thermodynamical stability of substoichiometric plutonium monocarbide from first-principles calculations. Phys. Chem. Chem. Phys. 2020, 22, 9009–9013. [Google Scholar] [CrossRef] [PubMed]


| Method | V | B | B′ | C11 | C12 | C44 | G | ν |
|---|---|---|---|---|---|---|---|---|
| DFT+SO+OP | 16.2 | 125 | 2.7 | 218 | 78.0 | 75.0 | 73.0 | 0.256 |
| DFT | 15.6 | 141 | 0.65 | 177 | 123 | 141 | 73.9 | 0.277 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Söderlind, P.; Landa, A.; Perron, A.; Moore, E.E.; Wu, C. Thermodynamics of Plutonium Monocarbide from Anharmonic and Relativistic Theory. Appl. Sci. 2020, 10, 6524. https://doi.org/10.3390/app10186524
Söderlind P, Landa A, Perron A, Moore EE, Wu C. Thermodynamics of Plutonium Monocarbide from Anharmonic and Relativistic Theory. Applied Sciences. 2020; 10(18):6524. https://doi.org/10.3390/app10186524
Chicago/Turabian StyleSöderlind, Per, Alexander Landa, Aurélien Perron, Emily E. Moore, and Christine Wu. 2020. "Thermodynamics of Plutonium Monocarbide from Anharmonic and Relativistic Theory" Applied Sciences 10, no. 18: 6524. https://doi.org/10.3390/app10186524
APA StyleSöderlind, P., Landa, A., Perron, A., Moore, E. E., & Wu, C. (2020). Thermodynamics of Plutonium Monocarbide from Anharmonic and Relativistic Theory. Applied Sciences, 10(18), 6524. https://doi.org/10.3390/app10186524







