Abstract
Forecasting domestic and foreign power demand is crucial for planning the operation and expansion of facilities. Power demand patterns are very complex owing to energy market deregulation. Therefore, developing an appropriate power forecasting model for an electrical grid is challenging. In particular, when consumers use power irregularly, the utility cannot accurately predict short- and long-term power consumption. Utilities that experience short- and long-term power demands cannot operate power supplies reliably; in worst-case scenarios, blackouts occur. Therefore, the utility must predict the power demands by analyzing the customers’ power consumption patterns for power supply stabilization. For this, a medium- and long-term power forecasting is proposed. The electricity demand forecast was divided into medium-term and long-term load forecast for customers with different power consumption patterns. Among various deep learning methods, deep neural networks (DNNs) and long short-term memory (LSTM) were employed for the time series prediction. The DNN and LSTM performances were compared to verify the proposed model. The two models were tested, and the results were examined with the accuracies of the six most commonly used evaluation measures in the medium- and long-term electric power load forecasting. The DNN outperformed the LSTM, regardless of the customer’s power pattern.
1. Introduction
Accurately predicting the power demand is very important for the stable operation of power systems with fluctuating power demands. The scale of the electric grid industry has grown with the shift of the social environment to a highly industrialized and information-oriented society. The amount of air-conditioning and heating equipment used by general consumers has rapidly increased. Accordingly, electricity consumption patterns change with changes in weather and specific days (e.g., regular holidays and temporary holidays). These changes require accurate and stable predictions, and an accurate analysis of the power load patterns is essential. The power load pattern has similar characteristics for all days of the week, but may vary for special days. For example, the power load pattern on a Wednesday is affected by the working day or a holiday on the previous day. Therefore, simply classifying the power load patterns by the day of the week is not appropriate; hence, prediction methods that can classify patterns according to power consumption data characteristics are necessary [1,2,3].
Power consumption patterns are periodically assessed by analyzing customer usage. These patterns are considered almost hourly, daily, weekly, monthly, and yearly. Electric power load forecasting is classified according to the duration of the planning period of the utility: short-term load forecasting (STLF), medium-term load forecasting (MTLF), and long-term load forecasting (LTLF) [4,5,6]. The LTLF predicts the power demand for more than one year and is applicable to power systems and long-term network planning. Essentially, two approaches are available for this purpose:
- (1)
- The peak load approach is used to find the trend curve obtained by plotting the past values of the annual peaks against the years of operation.
- (2)
- The energy approach aims to forecast annual sales, including annual energy sales, to different classes of customers (e.g., residential, commercial, industrial), which can then be converted to the annual peak demand using the annual load factors.
MTLF predicts the electricity demand for one month to one year, between the LTLF and STLF. Meanwhile, STLF estimates the power demand for one hour to one week. It has a scheduling function that determines the highest economic commitment of the power generation source. STLF also provides the system dispatcher with up-to-date weather forecasts to ensure that the system can be operated both economically and stably.
The electricity forecasting for building energy consumption is affected by weather (temperature, dew point, humidity, wind speed, wind direction, sky cover, and sunshine), time factors (the day of the week, the hour of the day holidays), and customer classes (residential, commercial, and industrial). Existing studies on building energy consumption can be divided into three categories [7,8]:
- (1)
- White box-based approaches, also named “physics-based models” require detailed physical information of complex buildings [9,10]. Owing to these characteristics, although the forecasting accuracy is high, a high computational cost is required for the simulation. Recently, there have been a series of attempts to simplify white box-based approaches. However, this simplification is prone to errors and generally overestimates the energy savings of buildings [11,12,13]. There are several tools, such as DOE-2, EnergyPlus, BLAST, TRYSYS, and ESP-r, which aid white box-based approach [14].
- (2)
- Black box-based approaches are also commonly referred to as “data-driven models”. These approaches rely on time-series statistical analyses and machine learning to assess and forecast electricity consumption [15,16,17]. Data-driven models are divided into three categories:
- Conventional models refer to exponential smoothing (ES) [18], moving average (MA) [19], statistical regressions [20], auto-regressive (AR) models [21], genetic algorithms (GA) [22], and fuzzy-based models [23,24]. They provide a good balance between forecasting accuracy and implementation simplicity. However, they have shown significant limitations in their ability to model nonlinear data patterns and the forecasting horizon.
- Classification-based models applied to electric power load forecasting are k-nearest neighbors (k-NN) [25] and decision trees (DT) [26]. Although both are intuitive models with high predictive accuracy, they are limited owing to their need for a comprehensive set of input data.
- Artificial intelligence models have been studied for many years and are generally referred to as machine learning and deep learning [27]. Some of the most popular artificial intelligence models are support vector machine (SVM) [28], artificial neural networks (ANN) [29], deep neural network (DNN) [30], and long short-term memory (LSTM) [31]. These models-based forecasting algorithms lead to less operator-dependent and more versatile methods in terms of data usage, with much higher forecasting accuracy.
- (3)
- Grey-box-based approaches have also been named “hybrid-based models” which are a combination of white box and black box models [32,33,34,35]. These models have the advantage of using improved single data-driven models with optimization, or a combination of several machine learning algorithms. However, these approaches have the shortcoming of computational inefficiency because these approaches involve uncertain inputs and complex interactions among elements and stochastic occupant behaviors [36,37,38].
The power consumption pattern may vary depending on the customer class as electric utilities usually serve different types of customers (i.e., residential, commercial, and industrial customers). The power consumption of residential buildings is low compared to those of commercial and industrial buildings and is not significantly affected by holidays, specific days, and seasons. The power consumption patterns in most industrial and commercial sectors are high on weekdays and low on holidays. However, some industrial buildings have irregular power consumption patterns, regardless of season and holiday. Industrial buildings with irregular power consumption cannot accurately predict medium- to long-term power forecasting. Consequently, the utility is unable to manage power supply in response to power demand. Therefore, in this study, two industrial buildings (i.e., companies T and B) with different power consumption patterns were selected to evaluate the medium- and long-term power forecasting performance accuracies of the proposed models. Company B is a two-shift manufacturer and Company T is a three-shift livestock processing firm. The two industrial buildings are located in Naju-si, Jeonnam, South Korea, and their electricity consumption data (per day) are collected monthly. The hourly power usage data comprised three years’ worth of data from 2017 to 2019. In addition, we measured the performance of the proposed models by adopting mean absolute error (MAE), root mean squared error (RMSE), coefficient of variation RMSE (CVRMSE), mean absolute error (MAPE), coefficient of determination (R2), and computation time.
The remainder of this study is organized as follows: Section 2 analyzes the power consumption of two buildings with different power consumption patterns and explains the deep learning techniques, DNN and LSTM. Section 3 describes the multivariate, DNN, and LSTM models proposed herein; Section 4 describes the test environment, including the test data set, and analyzes the test results; and Section 5 concludes the study and discusses future research.
2. Preliminaries and Problem Definition
2.1. Load Forecasting
Load forecasting predicts the power needed to meet short-, medium-, and long-term demands.
- (1)
- The advantages of load forecasting are as follows:
- It helps utility companies to better operate and manage supplies for their customers;
- It is an important process that can increase the efficiency and profit of power generation and distribution companies.
- It helps plan capacity and operation to provide a stable energy supply to all consumers [39,40,41]
- (2)
- The challenges of load forecasting are as follows:
- The power load series is complex and shows various seasonality levels; hence, a given time load can be accommodated at the same time in a specific weekday for the same time load and the previous week as well as the previous time load;
- Many important exogenous variables must be considered when forecasting power, especially those related to weather, making it difficult to achieve an accurate prediction [42,43].
Several load forecasting studies have analyzed weather factors and power consumption patterns in various ways [44,45,46,47,48]
The present study proposed that power demand forecasting includes special days (e.g., special holidays and official holidays) during the week and accounts for buildings with different power consumption patterns. In the former, the power consumption of on special day during the week is estimated to approximate that of the weekend. Table 1 shows the dates and days of the week for a special day of January, April, July, and October in Korea in the last three years (2017–2019). For the latter, we forecast medium- and long-term power demands for the B and T companies with different power consumption patterns based on Table 1.

Table 1.
The holidays in Korea for three years.
Figure 1 shows the average electricity usage for each day of the week for January (winter), April (spring), July (summer), and October (autumn) for company B for three years. The following observations are made from Figure 1:
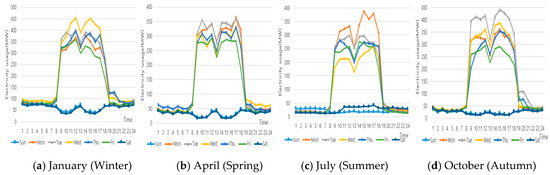
Figure 1.
An average weekly power consumption pattern of Company B for three years.
- (1)
- The electricity usage of company B for three years is in the order of summer (121 MW) < spring (154 MW) < autumn (159 MW) < winter (197 MW). It is less affected by weather than summer and winter, where air-conditioning usage is the highest.
- (2)
- It showed the highest electricity usage occurs during working hours (8 a.m. to 7 p.m.) from Monday to Friday (weekdays). Saturdays and Sundays (weekends) show that there is almost no electricity usage (below 50 MW). In addition, there was almost no power consumption during lunchtime from 12:00 to 1:00 p.m. compared with other hours on weekdays.
- (3)
- As a result of comparing the electricity usage for special days of company B for three years, the power consumption pattern is regular in April and July because there are no special holidays. In addition, in October, as special holidays are mostly from Monday to Friday, power consumption patterns are regular, similar to those of April and July. However, January had high electricity usage on Wednesdays and Thursdays, excluding special holidays (Monday, Tuesday, and Friday).
Figure 2 shows the average electricity usage for each day of the week for January (winter), April (spring), July (summer), and October (autumn) for company T over three years. The following observations are made from Figure 2:
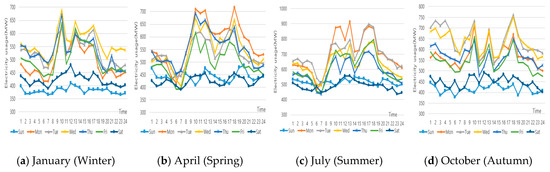
Figure 2.
An average weekly power consumption pattern company T for three years.
- (1)
- The electricity usage of T company for three years is in the order of winter (488 MW) < spring (511 MW) < autumn (546 MW) < summer (605 MW). As company T is a livestock meat processing company, cooling is more important than heating, so it uses more electricity in spring, autumn, and summer than in winter.
- (2)
- The power consumption pattern of company T’s weekend (Saturday to Sunday) is smaller than on weekdays, but fluctuations in electricity usage are more flexible at each time than those of company B. In particular, the power consumption pattern during the week largely fluctuates regardless of the time of day and day of the week.
- (3)
- As a result of comparing the electricity power for special days at company T for three years, it can be seen that the electricity usage of company T differs depending on the amount of supply, regardless of the special days.
In conclusion, we can see that the power consumption pattern of company T is different from that of company B, and the power consumption pattern depends on the amount of supply regardless of special days, time zones, days of the week, and seasons.
2.2. DNN
The multilayer perceptron (MLP) is a class of artificial neural network (ANN) that consists of at least three layers (input, hidden, and output layers) of nodes [49]. Except for input nodes, each node is a neuron that uses an activation function (i.e., step, sigmoid, tanh, ReLU: Rectified Linear Unit), which determines whether to output the received data to the next layer. The MLP is a machine learning solution and has been applied to various applications such as speech recognition, image recognition, and machine translation software. However, the MLP faces the problems of vanishing gradient, the reasoning of new facts, and the inability to process new data. These problems were solved by the development of deep learning [50].
DNNs have recently become a hot topic for image processing technology, reduced computational cost due to graphics processing unit development, and new machine learning techniques. DNNs have been actively studied to help solve the problem of complex and nonlinear functions. In addition, DNNs exhibit excellent learning performance on unclassified data; thus, they are used in various fields, such as artificial intelligence, graphic modeling, optimization, pattern recognition, and signal processing [51,52,53].
DNNs have a structure in which several hidden layers are added to an MLP, which has only one or two hidden layers. Figure 3 shows the DNN structure. The left side of the DNN has an input layer. The center has L − 1 hidden layers. The right side has an output layer. Hence, there are a total of L layers. is input to the input layer, and the output layer outputs . Therefore, there are nodes, except for the bias node in the input layer and c nodes in the output layer. The number of nodes, excluding the bias node, in layer l is denoted as . The 0th layer corresponds to the input layer, and is equal to d. The Lth layer corresponds to the output layer, and is equal to c.
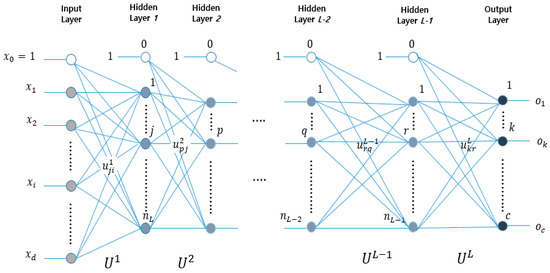
Figure 3.
Deep neural network structure.
The weights connecting layers l − 1 and l are computed as . The total weight may be represented by the matrix in Equation (1).
2.3. LSTM
The algorithms most commonly used for time series forecasting among deep learning methods are the recurrent neural network (RNN) [54], LSTM [31], and gated recurrent unit (GRU) [55]. The RNN has many advantages concerning the processing of sequence data but has more disadvantages in the problems of long-term dependency, gradient disappearance, and gradient explosion. In 1997, Hochreiter proposed the LSTM to solve the long-term dependence problem of RNN [56]. Figure 4 shows the structure of LSTM, which consists of four gates: forget, input, update, and output gates.
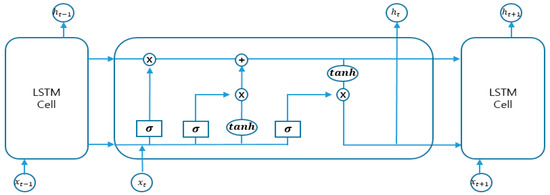
Figure 4.
Structure of the long short-term memory.
The forget gate determines which information to delete, the input gate determines whether new information is stored in the cell state, the update gate updates the cell state, and the output gate determines which output value to output. Equation (2) is the calculation formula for each state, as follows:
where and are the previous and current input values, respectively; and are the previous and current hidden gates, respectively; and are the previous and current cell states, respectively; , , , and are the weight values connecting the input to the forget, input, update, and output gates, respectively; , , , and are the bias values for the forget, input, update, and output gate’s calculation, respectively; is a sigmoid function; and is a hyperbolic tangent function.
3. Proposed Electric Power Load Forecasting Methodology
Section 3 describes the proposed medium- to long-term power prediction methodology. Figure 5 shows the simulation flow chart proposed in this study. First, for the data reading process, the original data from years 2017 to 2019 are read for medium- to long-term power prediction. Second, the original data are divided into data partitioning processes for training and testing. Finally, after the proposed DNN and LSTM function are performed, they are evaluated using the prediction error calculation formula. Section 3.1 describes the multivariate model collected over three years (2017–2019) for medium- and long-term electric load forecasting. Section 3.2 and Section 3.3, respectively, describe the proposed DNN and LSTM, which are the most commonly used methods for time series prediction during deep learning.
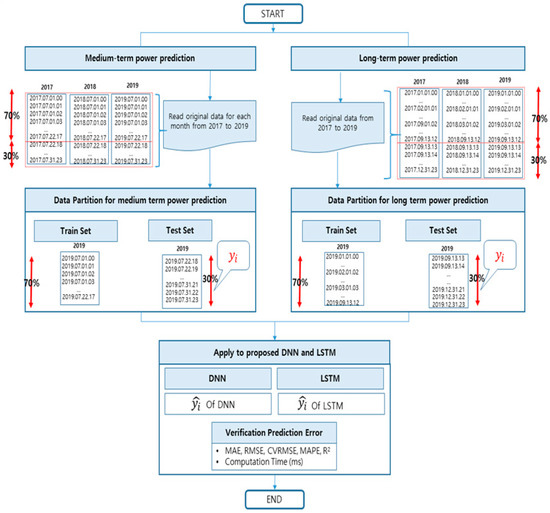
Figure 5.
Proposed simulation flow chart.
3.1. Proposed Multivariate Model
Figure 6 shows the seasonal consumption patterns of the B and T companies over three years (2017–2019). The Korean weather has four distinct seasons with large differences in temperature over the course of the year, and features a large amount of rain in the summer. Considering the seasonal characteristics of Korea, we chose April in spring, July in summer, October in autumn, and January in winter. Figure 6a–d show the power loads of company B in spring, summer, autumn, and winter, respectively. Figure 6e–h illustrate the power loads of company T in spring, summer, autumn, and winter, respectively.
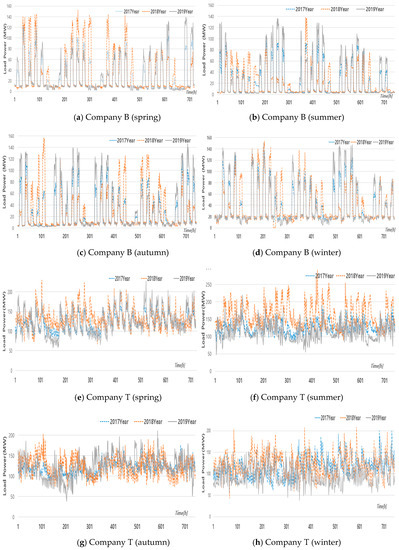
Figure 6.
Power consumption patterns of companies B and T for three years (2017–2019).
Figure 6a–d show that company B has similar power consumption patterns for three years because it is not significantly affected by season and time. However, in Figure 6e–h, the power consumption pattern is irregular because company T’s power consumption is independent of season and time.
A multivariate model was proposed, as shown in Figure 7, and was designed from the input to the output layer. The input layer has three layers for each year. An artificial neural network is defined as the first input layer (input_1: InputLayer), the second (input_2: InputLayer), and the third (input_3: InputLayer) which denote the power load in 2017, 2018, and 2019, respectively. The three input layers are each composed of one dense layer (dense_1: dense, dense_2: dense, dense_3: dense). The three dense layers concatenate to form one concatenate layer (concatenate_1: Concatenate). Finally, the dense layer (dense_4: Dense) is an input layer for use in the DNN.
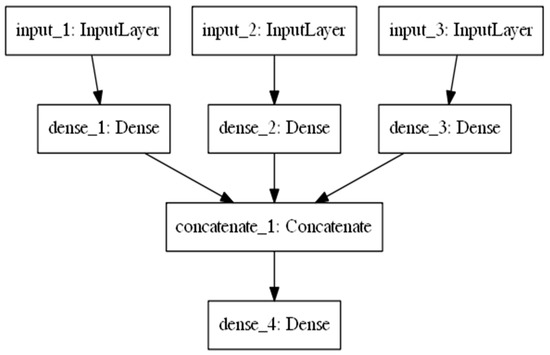
Figure 7.
Proposed multivariate model.
Figure 8 shows a schematic of the proposed model, including the shape of the inputs and outputs of each layer. Keras’ sequential API (Application Programming Interface) was adopted to implement the DNN model [57]. Keras’ sequential API is a function that simply defines and uses complex models (e.g., sharing multiple layers or using various types of input and output). In Figure 8, the step size of the input and output of the InputLayer is set to three, Dense is set to three inputs, and output is set to 100 to have connectivity with the InputLayer. Three InputLayers are concatenated into one concatenate. Finally, the dense data are forecast as the final DNN structure. In future work, we will study whether forecasting performance varies depending on the step size.
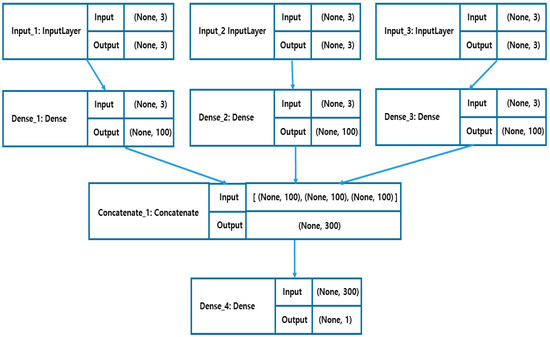
Figure 8.
Schematic of the multivariate model for load forecasting.
3.2. Proposed DNN Model
The proposed DNN model comprises three layers (Figure 9), namely the input, hidden, and output layers. The input layer () is composed of one node. The hidden layer is composed of 100 nodes. The output layer () is composed of one node for load forecasting. As described in Section 3.1, the input layer () is the final dense layer with a value of dense_4: Dense. The proposed DNN was implemented using four hidden layers (H1–H4).
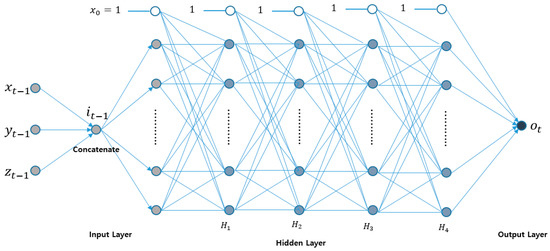
Figure 9.
Proposed deep neural network (DNN) model.
3.3. Proposed LSTM Model
Among the several deep learning technologies, LSTMs are widely used for time series prediction problems. Considering these observations, the LSTM network shown in Figure 10 was constructed for load forecasting. The input data (that is, , , and predicted the power using the load data for 3 years. , , and were the input data to be learned using the LSTM in the years 2017, 2018, and 2019, respectively.
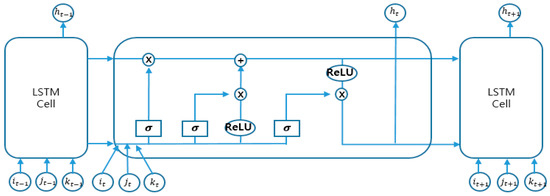
Figure 10.
Proposed long short-term memory (LSTM) model.
3.4. Simulation Parameters of the DNN and LSTM
Table 2 summarizes the simulation parameters used in this study, verifying that for the DNN and LSTM, the learning rate (=0.05), loss function (MSE: Mean Square Error), optimizer (ADAM) [58], and activation function (ReLU) [59] were the same.

Table 2.
Simulation parameters of the DNN and the LSTM.
4. Case Studies and Discussion
This section describes the test dataset and evaluation metrics for the two companies used for applying the proposed method. The experimental environment and results are also analyzed herein.
4.1. Test Environment and Test Data Set
To verify the proposed method, experiments were performed on a personal computer equipped with an Intel® Xeon® W-2133, 3.60 GHz CPU (Intel, Santa Clara, CA, USA), and 32 GB RAM. The test operating system was Windows 10 (64 bit) (Microsoft, Redmond, WA, USA). All the proposed methods were implemented using deep learning libraries provided by TensorFlow [60] and Keras [57].
The dataset used in this study selected two industrial buildings (i.e., Company T and B) with different power consumption patterns. The two industrial buildings are located in Naju, Jeollanam-do, Korea. Their electricity usage data (per day) are collected monthly at one-hour intervals, and hourly electricity usage data is composed of three-year data from years 2017 to 2019. For MTLF, as illustrated in Figure 5, data for the first three weeks of each month were used for training and tested for the last week. For the LTLF, data from January to September were used for training and the last three months were tested. Table 3 shows that the proposed methods for MTLF and LTLF were applied by dividing training data (70%) and test data (30%), respectively.

Table 3.
Training and testing data for electric power load forecasting.
4.2. Performance Evaluation Metrics
Four widely used performance metrics (i.e., MAE, RMSE, CVRMSE [61], R2, and MAPE) were adopted to assess the prediction accuracy of the proposed methods.
In Equations (3)–(7), identifies the actual value of sample i, identifies the predicted value of sample i, n is the testing data, indicates the mean of the predicted values, SSE denotes the residual sum of squares, and SST represents the total sum of squares.
Finally, the calculation time required to perform the computation process for the proposed method was also adopted to evaluate the proposed methods.
4.3. Comparison and Analysis of Medium-Term Electric Power Load Forecasting
Table 4 shows the comparison of the proposed DNN and LSTM for medium-term electric power load forecasting. Lower values of MAE (MW), RMSE (MW), CVRMSE (%), and MAPE (%) denote higher model accuracy. The R2 values approaching one and the score values of approximately 100% show that the predictive value approximates the actual value. To compare the performances of the proposed DNN and LSTM, the difference between the DNN and LSTM of company B with similar power consumption patterns is expressed by ΔB, and the difference between the DNN and LSTM of company T having irregular power consumption patterns is expressed by ΔT. Meanwhile, to compare the performances of companies B and T with irregular power consumption patterns, the differences between the proposed DNN and LSTM are represented by ΔDNN and ΔLSTM, respectively.

Table 4.
Comparison of the DNN and LSTM performances for medium-term electric power load forecasting.
In the medium-term power prediction, the MAE, RMSE, CVRMSE (%), and MAPE of company B with a constant power consumption pattern indicated better performance than the proposed LSTM, with an average DNN of 0.55 MW, 1.56 MW, 5.32%, and 3.34%, respectively. The calculation time for company B was better than the proposed LSTM by an average of 2.75 ms. The R2 for company B was approached 0.99 for the proposed DNN and LSTM, except for the proposed LSTM for April (R2 = 0.97). The MAE, RMSE, CVRMSE (%), and MAPE of company T with irregular power consumption patterns outperformed the proposed LSTM with an average of 1.67 MW, 2.5 MW, 1.24% and 1.29%, respectively. The calculation time of company T was better than the proposed LSTM by 2.92 ms on average. The R2 for company T approached 0.99 for the proposed DNN and LSTM, except for the LSTM of the months of May (R2 = 0.88) and September (R2 = 0.95).
The comparison results of MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time for the proposed DNN and LSTM showed that the DNN and LSTM of company B with a better power consumption pattern outperformed those of company T with an irregular power consumption pattern. The comparison of MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time of the proposed DNN illustrated that company B outperformed company T by 0.1 MW, 0.07 MW, 0.6%, 1.24%, 0, and 0.29 ms, respectively. Meanwhile, the comparison results of MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time for the proposed LSTM showed that company B outperformed company T by 2.62 MW, 4.81 MW, 8.36%, 6.23%, 1.97, and 8.7 ms, respectively. In addition, Δ is the difference between ΔDNN and ΔLSTM. The MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time of ΔDNN’s were better than those of ΔLSTM by −2.22 MW, −4.06 MW, −6.56%, −4.63%, 0.01, and −5.67 ms, respectively.
In conclusion, on average, the DNN showed a better performance in terms of prediction error and calculation time compared to the LSTM, regardless of the power consumption pattern. The DNN, of the company with a regular power consumption pattern exhibited the best performance.
Figure 11 shows the error between the actual and predicted values for the proposed DNN and LSTM for company B in April 2019. April in Korea is the representative month of spring. Figure 11a shows the error between the actual and predicted values using the proposed DNN. Figure 11b depicts the error between the actual and predicted values using the proposed LSTM. The error range in Figure 11a is within −8 to 8, while that in Figure 11b is −10 to 70. The proposed DNN method was superior to the proposed LSTM (Table 4).
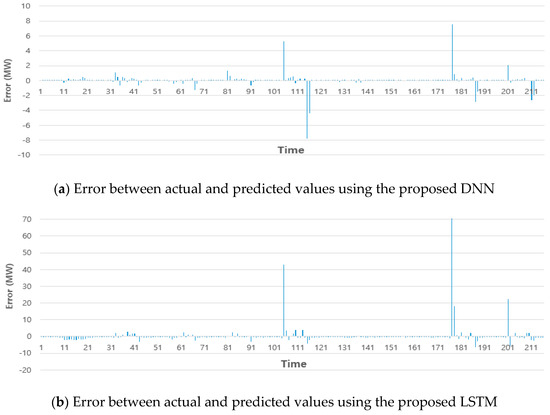
Figure 11.
Error between the actual and predicted values using the proposed DNN and LSTM (company B).
Figure 12 shows the error between the actual and predicted values of the DNN and the LSTM proposed for company T in May 2019. In Korea, May is also the representative month of spring. Figure 12a shows the error between the actual and predicted values using the proposed DNN. Figure 12b depicts the error between the actual and predicted values using the proposed LSTM. The error range in Figure 12a is −2 to 2, while that in Figure 12b is −15 to 35. The proposed DNN method had an excellent performance because the error range was much smaller than that of the proposed LSTM.
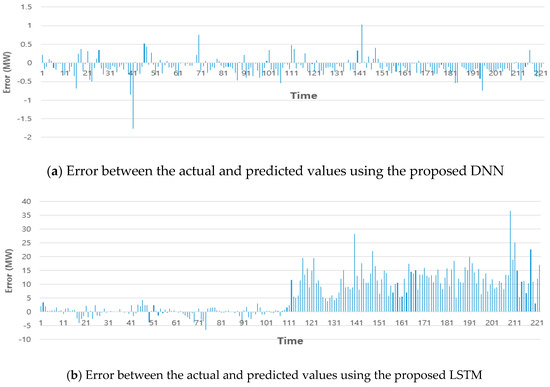
Figure 12.
Error between the actual and predicted values using the proposed DNN and LSTM (company T).
4.4. Comparison and Analysis of Long-Term Electric Power Load Forecasting
Table 5 shows the proposed DNN and LSTM comparisons for long-term power load forecasting. For the prediction error, the MAE (MW), RMSE (MW), CVRMSE (%), MAPE (%), R2, and calculation time (ms) were adopted for the long-term electric power load forecasting. For long-term electric power forecasting, the MAE, RMSE, CVRMSE (%), and MAPE of company B (ΔB) with a constant power consumption pattern indicated better performance than the proposed LSTM, with values of 0.03 MW, 0.04 MW, 0.15%, and 0.27%, respectively. The calculation time for company B was better than that of the proposed LSTM by an average of 29.8 ms. The R2 for company B implied that the DNN and LSTM approached approximately 0.99. The MAE, RMSE, CVRMSE (%), and MAPE of company T (ΔT) with irregular power consumption patterns showed a better performance than the proposed LSTM, with the proposed DNN being 0.05 MW, 0.21 MW, 0.16%, and 0.07%, respectively. The calculation time of company T was better than that for the proposed LSTM. The proposed DNN was 29.81 ms on average. The R2 of company T for DNN and LSTM was approached approximately 0.99. The comparison results of MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time for the proposed DNN and LSTM illustrated that the DNN and LSTM of company B (better power consumption pattern) outperformed that of company T (an irregular power consumption pattern). The comparison of the MAE, RMSE, CVRMSE (%), MAPE, R2, and the calculation time of the proposed DNN (ΔDNN) indicated that company B outperformed company T by 0.05 MW, 0.04 MW, 0.08%, 0.15%, 0, and 0.84 ms, respectively. Moreover, the comparison of the MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time of the proposed LSTM (ΔLSTM) showed that company B outperformed company T by 0.07 MW, 0.21 MW, 0.06%, 0.35%, 0, and 0.85 ms, respectively. In addition, MAE, RMSE, CVRMSE (%), MAPE, R2, and calculation time of ΔDNN were higher than those of ΔLSTM by 0.08 MW, 0.25 MW, 0.31%, 0.34%, 0 and 59.61 ms, respectively.

Table 5.
Comparison of the DNN and LSTM performances for long-term electric power load forecasting.
Figure 13a,b show the errors between the actual and predicted values of the proposed DNN and LSTM, respectively, for company B in 2019. The error range in Figure 13a is from −0.4 to 0.5, while that in Figure 13b is from −1 to 0.8. As described in Table 4, the proposed DNN method outperformed the proposed LSTM.
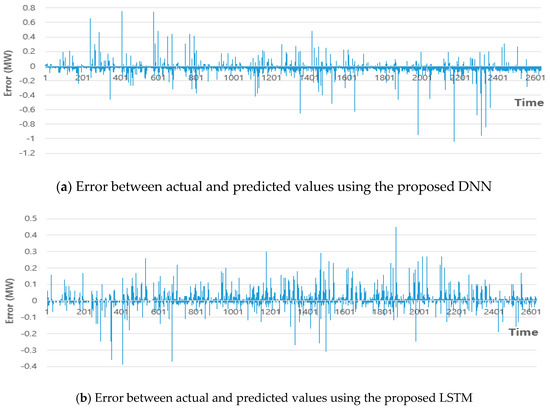
Figure 13.
Error between the actual and predicted values using the proposed DNN and LSTM (company B).
Figure 14a,b show the errors between the actual and predicted values of the proposed DNN and LSTM, respectively, for company T in 2019. The error range in Figure 14a is from −0.8 to 1, while that in Figure 14b is from −5 to 3.
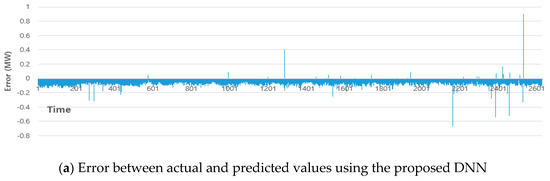
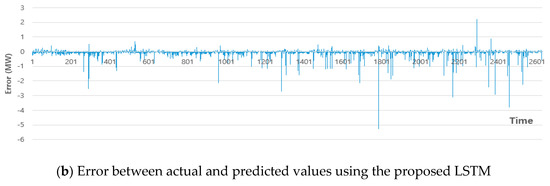
Figure 14.
Error between the actual and predicted values using the proposed DNN and LSTM (company T).
5. Conclusions and Future Work
Power demand forecasting is an essential process for planning periodic operations and facility expansion in the power sector. The electricity demand pattern is very complex because of energy market deregulation. Electric utilities employ electric power load forecasting to determine future inventory, costs, capacities, and interest rate changes. Therefore, finding a suitable prediction model for a specific power network is not an easy task.
In this study, two companies with different power consumption patterns were selected. Medium- and long-term power forecasting was predicted using a DNN and LSTM during deep learning. The experimental results showed that the proposed DNN outperformed the LSTM, regardless of the power consumption pattern. Furthermore, the performance of the proposed DNN was better than that of the proposed LSTM in terms of the prediction error (MAE, RMSE, CVRMSE, MAPE, and R2) and the calculation time.
However, the data used in this study have a limitation in that it does not consider weather data related to seasonality. Therefore, future research will expand medium- to long-term electric power forecasting by adding weather data to consider seasonality. In addition, our proposed method will be compared and evaluated against other methods for deep learning (GRU, Convolution-LSTM, Convolution Neural Network–LSTM, encoder-decoder LSTM) and machine learning (Adaptive Neuro Fuzzy Inference System-Subtractive Clustering, Adaptive Neuro Fuzzy Inference System-Fuzzy Clustering Means).
Author Contributions
S.Y. supervised and supported this study. N.S. wrote and implemented the algorithm. J.N. conducted related research and data collection. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This article was supported by the Korean Institute of Energy Technology Evaluation & Planning under the financial resources of the government in 2018 (20182410105210, Development and demonstration of multi-use application technology of consumer ESS).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Almeshaiei, A.; Soltan, H. A methodology for electric power load forecasting. Alex. Eng. J. 2011, 50, 137–144. [Google Scholar] [CrossRef]
- Yu, C.-N.; Mirowski, P.; Ho, T.K. A sparse coding approach to household electricity demand forecasting in smart grids. IEEE Trans. Smart Grid 2017, 8, 738–748. [Google Scholar] [CrossRef]
- Zheng, S.; Zhong, Q.; Peng, L.; Chai, X. A simple method of residential electricity load forecasting by improved Bayesian neural networks. Hindawi Math. Probl. Eng. 2018, 2018, 4276176. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, A. Long-term/mid-term electric load forecasting based on short-term correlation and annual growth. Electr. Power Syst. Res. 2005, 74, 353–361. [Google Scholar] [CrossRef]
- Feng, Y. Study on Medium and Long Term Power Load Forecasting Based on Combination Forecasting Model. Chem. Eng. Trans. 2015, 51, 859–864. [Google Scholar]
- Xue, B.; Keng, J. Dynamic transverse correction method of middle and long term energy forecasting based on statistic of forecasting errors. In Proceedings of the Conference on Power and Energy IPEC, Ho Chi Minh City, Vietnam, 12–14 December 2012; pp. 253–256. [Google Scholar]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Boris, D.; Milan, V.; Milos, Z.J.; Milija, S. White-Box or Black-Box Decision Tree Algorithms: Which to Use in Education? IEEE Trans. Educ. 2013, 56, 287–291. [Google Scholar] [CrossRef]
- Cavalheiro, J.; Carreira, P. A multidimensional data model design for building energy management. Adv. Eng. Inform. 2016, 30, 619–632. [Google Scholar] [CrossRef]
- Al-Homoud, M.S. Computer-aided building energy analysis techniques. Build. Environ. 2001, 36, 421–433. [Google Scholar] [CrossRef]
- Barnaby, C.S.; Spitler, J.D. Development of the residential load factor method for heating and cooling load calculations. ASHRAE Trans. 2005, 111, 291–307. [Google Scholar]
- Building Energy Software Tool. Available online: https://www.buildingenergysoftwaretools.com/ (accessed on 7 March 2020).
- Zhao, H.X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Williams, S.; Short, M. Electricity demand forecasting for decentralised energy management. Energy Build. Environ. 2020, 1, 178–186. [Google Scholar] [CrossRef]
- González-Vidal, A.; Ramallo-González, A.P.; Terroso-Sáenz, F.; Skarmeta, A. Data driven modeling for energy consumption prediction in smart building. In Proceedings of the 2017 IEEE International Conference on Big Data, Boston, MA, USA, 11–14 December 2017; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Brown, R.G. Smoothing Forecasting and Prediction of Discrete Time Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
- Simple Moving Average. Available online: https://www.investopedia.com/terms/s/sma.asp (accessed on 7 March 2020).
- Holt, C.E. Forecasting Seasonal and Trends by Exponentially Weighted Average (O.N.R. Memorandum No. 52); Carnegie Institute of Technology: Pittsburgh, PA, USA, 1957. [Google Scholar]
- Ohtsuka, Y.; Oga, T.; Kakamu, K. Forecasting electricity demand in Japan: A Bayesian spatial autoregressive ARMA approach. Comp. Stat. Data Anal. 2010, 54, 2721–2735. [Google Scholar] [CrossRef]
- Kubota, N.; Hashimoto, S.; Kojima, F.; Taniguchi, K. GP-preprocessed fuzzy inference for the energy load prediction. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; IEEE: New York, NY, USA, 2000; Volume 1, pp. 1–6. [Google Scholar]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Jallala, M.A.; González-Vidal, A.; Skarmeta, A.F.; Chabaa, S.; Zeroual, A. A hybrid neuro-fuzzy inference system-based algorithm for time series forecasting is applied to energy consumption prediction. Appl. Energy 2020, 268, 114977. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L., Jr. Discriminatory Analysis—Nonparametric Discrimination: Consistency Properties; International Statistical Institute: Voorburg, The Netherlands, 1989; Volume 57, pp. 238–247. [Google Scholar]
- Yu, Z.; Haghighat, F.; Fung, B.C.M.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build. 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
- Liu, T.; Tan, Z.; Xu, C.; Chen, H.; Li, Z. Study on deep reinforcement learning techniques for building energy consumption forecasting. Energy Build. 2020, 208, 109675. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Neocleous, C.C.; Schizas, C.N. Building heating load estimation using artificial neural networks. In Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques, San Francisco, CA, USA, 10–14 November 1997; Association for Computing Machinery: Toronto, ON, Canada, 1997. [Google Scholar]
- Bagnasco, A.; Fresi, F.; Saviozzi, M.; Silvestro, F.; Vinci, A. Electrical consumption forecasting in hospital facilities: An application case. Energy Build. 2015, 103, 261–270. [Google Scholar] [CrossRef]
- Gers, F.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks, ICANN’99, Edinburgh, UK, 7–10 September 1999; pp. 850–855. [Google Scholar]
- Foucquier, A.; Robert, S.; Suard, F.; Stéphan, L.; Jay, A. State of the art in building modelling and energy performances prediction: A review. Renew. Sustain. Energy Rev. 2013, 23, 272–288. [Google Scholar] [CrossRef]
- Tardioli, G.; Kerrigan, R.; Oates, M.; O’Donnell, J.; Finn, D. Data driven approaches for prediction of building energy consumption at urban level. Energy Proc. 2015, 78, 3378–3383. [Google Scholar] [CrossRef]
- Chalal, M.L.; Benachir, M.; White, M.; Shrahily, R. Energy planning and forecasting approaches for supporting physical improvement strategies in the building sector: A review. Renew. Sustain. Energy Rev. 2016, 64, 761–776. [Google Scholar] [CrossRef]
- Mat Daut, M.A.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Paudel, S.; Nguyen, P.H.; Kling, W.L.; Elmitri, M.; Lacarrière, B.; Corre, O.L. Support vector machine in prediction of building energy demand using pseudo dynamic approach. In Proceedings of the ECOS 2015—The 28th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Pau, France, 30 June 2015. [Google Scholar]
- Li, Z.; Han, Y.; Xu, P. Methods for benchmarking building energy consumption against its past or intended performance: An overview. Appl. Energy 2014, 124, 325–334. [Google Scholar] [CrossRef]
- Diamantoulakis, P.D.; Kapinas, V.M.; Karagiannidis, G.K. Big data analytics for dynamic energy management in smart grids. Big Data Res. 2015, 5, 94–101. [Google Scholar] [CrossRef]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Wang, Z.; Jun, L.; Zhu, S.; Zhao, J.; Deng, S.; Zhong, S.; Yin, H.; Li, H.; Qi, Y.; Gan, Z. A review of load forecasting of the distributed energy system. IOP Conf. Ser. Earth Environ. Sci. 2019, 237, 042019. [Google Scholar] [CrossRef]
- Shao, Z.; Gao, F.; Zhang, Q.; Yang, S.L. Multivariate statistical and similarity measure based semiparametric modeling of the probability distribution: A novel approach to the case study of mid-long term electricity consumption forecasting in China. Appl. Energy 2015, 156, 502–518. [Google Scholar] [CrossRef]
- Clements, A.E.; Hurn, A.S.; Li, Z. Forecasting dayahead electricity load using a multiple equation time series approach. Eur. J. Oper. Res. 2016, 251, 522–530. [Google Scholar] [CrossRef]
- De Felice, M.; Alessandri, A.; Catalano, F. Seasonal weather forecasts for medium-term electricity demand forecasting. Appl. Energy 2015, 137, 435–444. [Google Scholar] [CrossRef]
- Khatoon, S.; Sing, A.K. Effects of various factors on electric load forecasting: An overview. In Proceedings of the IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014; pp. 1–5. [Google Scholar]
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Andersen, F.M.; Larsen, H.V.; Boomsma, T.K. Long-term forecasting of hourly electricity load: Identification of consumption profiles and segmentation of customers. Energy Convers. Manag. 2013, 68, 244–252. [Google Scholar] [CrossRef]
- Sobhani, M.; Campbell, A.; Sangamwar, S.; Li, C.; Hong, T. Combining weather stations for electric load forecasting. Energies 2019, 12, 1510. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Yu, D. Deep learning: Methods and applications. Found. Trends Signal. Process. 2014, 30, 197–387. [Google Scholar]
- Lecun, Y. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Sainath, T.; Mohamed, A.R.; Kingsbury, B.; Ramabhadran, B. Convolutional neural networks for LVCSR. IEEE ICASSP 2013. [Google Scholar] [CrossRef]
- Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kling, W.L. Deep learning for estimating building energy consumption. Sustain. Energy Grids Netw. 2016, 6, 91–99. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder–Decoder for Statistical Machine Translation. EMNLP 2014. [Google Scholar] [CrossRef]
- Hochreiter, S.; Bengio, Y.; Paolo, F.; Schmidhuber, J. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies; IEEE Press: Los Alamitos, CA, USA, 2001; pp. 237–243. [Google Scholar]
- Keras.io: The Python Deep Learning Library. Available online: https://keras.io/ (accessed on 7 March 2020).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Nair, V.; Hinton, G. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the International Conference on Machine Learning, ICML, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Tensorflow.org: Deep Learning Library Developed by Google. Available online: https://www.tensorflow.org/ (accessed on 7 March 2020).
- Hong, T.; Kim, J.; Koo, C. LCC and LCCO2 analysis of green roofs in elementary schools with energy saving measures. Energy Build. 2012, 45, 229–239. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).