Abstract
This paper develops a finite-time path following control scheme for an underactuated marine surface vessel (MSV) with external disturbances, model parametric uncertainties, position constraint and input saturation. Initially, based on the time-varying barrier Lyapunov function (BLF), the finite-time line-of-sight (FT-LOS) guidance law is proposed to obtain the desired yaw angle and simultaneously constrain the position error of the underactuated MSV. Furthermore, the finite-time path following constraint controllers are designed to achieve tracking control in finite time. Additionally, considering the model parametric uncertainties and external disturbances, the finite-time disturbance observers are proposed to estimate the compound disturbance. For the sake of avoiding the input saturation and satisfying the requirements of finite-time convergence, the finite-time input saturation compensators were designed. The stability analysis shows that the proposed finite-time path following control scheme can strictly guarantee the constraint requirements of the position, and all error signals of the whole control system can converge into a small neighborhood around zero in finite time. Finally, comparative simulation results show the effectiveness and superiority of the proposed finite-time path following control scheme.
1. Introduction
The marine surface vessel (MSV) mainly relies on the guidance system to perform the required control scheme, such as path following, target tracking and path tracking, in which the influences of wind, currents and waves on the ship, which are simply considered in [1,2,3,4]. The path following control aims to control the ship to reach and track a predetermined parameterized curve at a certain velocity without time constraints [5]. In the last few years, the control problem of path following for the underactuated MSV has attracted extensive attention in the control field [6,7,8].
The guidance law is an important component of the path following problem, which aims to compute the desired heading angle for the subsequent controller design by processing path information. The classical guidance laws consist of the line-of-sight (LOS) guidance, constant bearing guidance, and pure pursuit guidance [9]. Especially, because the LOS guidance law has simple and intuitive characteristics, it has been widely used in the path following control of MSV. At an early stage, the classical LOS guidance law for reducing the cross-track error was presented in [10]. However, although the classical LOS guidance laws are simple and effective, they have limitations for the vessel, subject to external disturbances. Then, the integral line-of-sight (ILOS) guidance law was developed by introducing the integral actions into the LOS guidance law, which can eliminate the drifting effect [11,12]. Due to the complexity of the environment and the requirement of the operation accuracy, it is necessary to not only consider the tracking performance of the desired path, but also to ensure that the position errors of the ship during navigation does not have large jitter, otherwise it is not conducive to the accurate path tracking of the ship. In addition, in order to navigate safely, the actuator saturation of the underactuated MSV should be limited. Otherwise, the control performance of the system will deteriorate and lead to the instability of the control system [13]. For the problem of position error constraint and actuator saturation, in [14], a path-following controller based on the error-constrained line-of-sight (EC-LOS) guidance law was presented for an MSV. An asymmetric time-varying barrier Lyapunov function (BLF) and a smooth hyperbolic tangent function were proposed for a fully actuated MSV to address the asymmetrical input and output constraint in [15]. In the case of actuator saturation and external disturbance, a path following control scheme for a MSV with a prescribed performance was presented in [16]. In [17], a control scheme was presented for the underactuated MSV, which considers not only the position error constraint, input saturation, external disturbance and model uncertainties, but also time-varying sideslip. However, the convergence time of the above literature is asymptotically convergent, which implies that exact convergence cannot be guaranteed in finite time, and the influence of the convergence time is not considered. In order to obtain a high-performance solution, this paper proposes an FT-LOS guidance law, which can ensure that the position errors will not exceed the error constraint, and converge into a small neighborhood around zero in finite time.
In addition to the requirements of the error constraints and input saturation, it is also important to consider the effect of convergence time on system performance. The finite-time controller makes the system errors converge in finite time, thereby obtaining faster convergence rate and better disturbance rejection properties. The research on the finite-time control of the underactuated MSV focuses on trajectory tracking control problem. In [18], a finite-time disturbance observer was presented to reduce the environment disturbances, which has the advantages of fast convergence speed and strong robustness. In order to precisely estimate completely external disturbances and unknown dynamics, a finite-time tracking controller was presented for trajectory tracking in [19]. In addition, it improves the robustness and tracking accuracy of the control system. A finite-time sliding mode controller for an USV with model parametric uncertainties and external disturbances was presented in [20]. A path following controller based on a finite-time observer was proposed in [21], which only considers the large sideslip angle and external disturbances. However, the influence of position error constraints on vessel path following control are not considered. In [22], a fuzzy finite-time controller was proposed for the underactuated MSV, subject to external disturbances, parametric uncertainties, sideslip angle and actuator saturation in finite-time, but the position error constraint was not considered in the controller design. Therefore, considering the influence of position error constraint on path following controller, an FT-LOS guidance law was designed by introducing time-varying BLF into the design process of LOS guidance law.
Based on the above observations, this paper presents a finite-time path following control scheme for the underactuated MSV under the conditions of position constraint, external disturbances, model parameter uncertainties, and actuator saturation. The main contributions and superiority of this paper are summarized as follows:
- (1)
- A finite-time line-of-sight (FT-LOS) guidance law is designed by integrating a time-varying BLF into the classical LOS guidance law design process. The proposed FT-LOS guidance law can ensure that the position errors will not exceed the error constraints, and converge into a small neighborhood around zero in finite time.
- (2)
- The finite-time attitude constraint controller and the finite-time velocity constraint controller are designed to achieve tracking control in finite time. A command filter is designed to eliminate the complex calculation of the virtual control law.
- (3)
- The finite-time disturbance observers are proposed to reduce the compound disturbance. In addition the finite-time input saturation compensators are designed to avoid the actuator saturation and satisfy the finite-time convergence requirement.
- (4)
- The stability analysis shows that the proposed finite-time path following control algorithm can strictly guarantee the constraint requirement of the position, and all error signals of the whole closed-loop control system can converge into a small neighborhood around zero in finite time. Comparative simulation results illustrate the effectiveness and superiority of the proposed finite-time control scheme.
The rest of this paper is arranged as follows. Section 2 presents the preliminaries and problem formulation. The finite-time path following control algorithm is proposed in Section 3, consisting of the FT-LOS guidance law design, the finite-time attitude constraint controller design, and the finite-time velocity constraint controller design. Section 4 analyses the stability of the whole closed-loop control system. Comparative simulation results are shown and analyzed in Section 5 to demonstrate the effectiveness and superiority of the proposed finite-time path following control algorithm. Finally, the conclusions are shown in Section 6.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
Notation 1.
In this paper, stands for the absolute value of a scalar; stands for the estimate of ; defines the estimation error.
Definition 1.
([23]) A barrier Lyapunov function is a scalar function defined with respect to the system on an open region D containing the origin. The is continuous, is positive definite, has continuous first-order partial derivatives at every point of D, has the property as x approaches the boundary of D, and satisfies along the solution of for and some positive constant b.
Definition 2.
([24]) Consider the following system:
where is continuous on an open neighborhood of the origin and . The origin is said to be a finite-time-stable equilibrium of (1) if there exists an open neighborhood of the origin and a function , called the settling-time function, such that the following statements hold:
- (i)
- Finite-time convergence: For every , is defined on , for all , and .
- (ii)
- Lyapunov stability: For every open neighborhood of 0 there exists an open subset of N containing 0 such that, for every , for all .
The origin is said to be a globally finite-time-stable equilibrium if it is a finite-time-stable equilibrium with .
Lemma 1.
([25]) Suppose that there is a positive definite continuous Lyapunov function defined on of the origin, and
where , and . Then the origin of system (1) is locally finite-time stable and the settling time can be given by .
Lemma 2.
([26]) For any , , and a real number , then
2.2. Model of Underactuated Marine Surface Vessel
The dynamics and kinematics equations for the underactuated MSV are defined by [9]. The kinematics model of the underactuated MSV can be written as follows:
where represents the surge position, the sway position and the heading angle of the MSV in the earth-fixed inertial frame; represents the surge velocity, the sway velocity, and the yaw rate of the MSV in the body-fixed frame.
In order to simplify the dynamics model, it is necessary to make reasonable assumption as follows:
Assumption A1.
[21]
- (1).
- The heave, pitch and roll motions are neglected in path following on the horizontal plane.
- (2).
- The vehicle is rigid body and its mass distribution is homogeneous, and the vehicle is port/starboard symmetric.
- (3).
- The origin of body-fixed is located at the center of gravity of the vehicle.
The dynamics model of the underactuated MSV can be written as follows:
where the positive constant terms , , represent the vessel inertia including added mass. The positive constant terms , , represent the hydrodynamic damping, which can be obtained by using system identification. Therefore, have the model parametric uncertainties. are the time-varying environment disturbances. The surge force and the yaw moment are the control inputs. In practical engineering, because of the physical constraints of the vessel’s actuators, the control force and moment can be expressed as follows:
Assumption A2.
The compound disturbances and their respective derivatives are bounded, which satisfy the following inequalities: , , where and are positive constants.
2.3. Path Following Error Dynamic
In order to converge to the desired path, a general and effective guidance law for the path following control problem is a look-ahead LOS guidance law. Figure 1 shows the geometrical illustration of the LOS guidance law for the MSV.
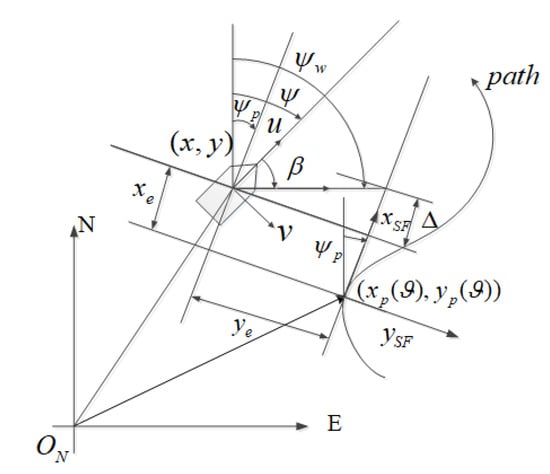
Figure 1.
The geometrical illustration of LOS guidance for a MSV.
The desired path is defined as , where represents the path variable. The path tangent angle is calculated by
where and . The along-track error and the cross-track error can be written as follows:
The differentiation of can be obtained:
Then, substituting (4) into (9) yields
where denotes the speed of the vessel and is the vessel’s sideslip angle.
Similarly, the differentiation of can be obtained:
and substituting (4) into (11) results in,
Finally, similar to [27], the derivatives of errors become
Considering the mathematical model of an underactuated MSV with the external disturbances, model parametric uncertainties, position constraint and input saturation, the control objectives of this paper are as follows: (1) Design the FT-LOS guidance law to ensure that the position error will not exceed the error constraint, and converge into a small neighborhood around zero in finite time. (2) The finite-time attitude constraint controller and the finite-time velocity constraint controller are designed to make the underactuated MSV track the desired path at the desired speed in finite time. In addition, it has faster convergence speed and better disturbance rejection performance. (3) All error signals of the whole closed-loop control system can converge into a small neighborhood around zero in finite time, and position errors meet the constraint requirements, that is to say, , , where are differentiable time-varying error constrains.
To facilitate the controller design, we make the assumption as follows:
Assumption A3.
The initial position errors satisfy the prescribed constraints , .
3. Finite-Time Path Following Control Algorithm Design
In this section, the finite-time path following control scheme is proposed to realize the control objectives. The finite-time path following control scheme for the underactuated MSV includes three parts: (1) FT-LOS guidance law design; (2) the finite-time attitude constraint controller design; (3) the finite-time velocity constraint controller design. The schematic diagram of the whole close-loop control system is shown in Figure 2. The specific design process of the finite-time path following control algorithm will be introduced in the following subsections.
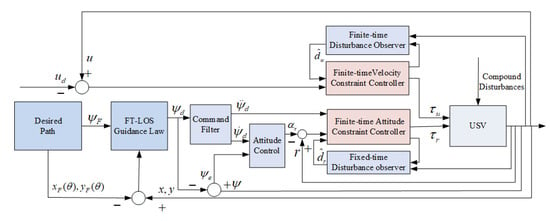
Figure 2.
The block diagram of path following control.
3.1. Ft-Los Guidance Law Design
The FT-LOS guidance law is proposed to obtain the update law and the desired heading angle.
The time-varying BLF will be integrated into the FT-LOS guidance to ensure the position error constraints. Define the time-varying BLF as follows:
where and .
Taking the derivative of , we obtain
Substituting (13) into (15), we obtain
Taking the time derivative of yields
Invoking (17) into (16), we have
with .
The update law and the desired heading angle are designed as
where , , and are positive design parameters; denotes the look-ahead distance; To avoid , we can take when , where is a small positive parameter.
Substituting (19)–(22) into (18) results in
where
and .
Remark 1.
In (24), we have , , and . Therefore, is bounded.
3.2. The Finite-Time Attitude Constraint Controller Design
Step 1. (Kinematics controller). Define the yaw tracking error as follows:
Define the Lyapunov function as follows:
Taking the time derivative of , we obtain
Step 2. (Dynamics controller). Define the yaw angle rate error as follows:
where is the virtual control law.
Substituting (28) into (27) yields
In order to avoid the complicated calculation of the derivative of , the proposed command filter is shown in Figure 3. Furthermore, an auxiliary system is presented to compensate for the estimation error.
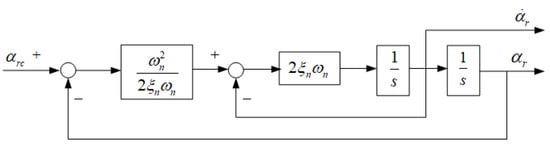
Figure 3.
Configuration of the command filter.
A second-order command filter is expressed as follows:
where and are positive design parameters; is the input signal of the second-order command filter; and denote the estimations of and , respectively.
Define the estimation error as follow:
Substituting (31) into (29) yields
Therefore, design a nominal virtual yaw rate for (32) as follows:
where , and denote the positive design constants. To compensate the estimation error of the virtual yaw rate, the auxiliary system is presented as follows:
where , and ; is a positive parameter.
The Lyapunov function is defined as follows:
Invoking (33) and (34), the time derivative of is given by
Based on the Young’s inequality, we can obtain
Substituting (37) and (38) into (36), we have
Taking the time derivative of along (5), we have
The Lyapunov function is defined as follows:
Taking the time derivative of along (39) and (40), we have
Next, a finite-time disturbance observer is designed in order to estimate the compound disturbance :
where is the observation value of the disturbance, , , are positive design constants and define the estimation error as . Then, taking the time derivative of results in
Theorem 1.
For the mathematical model of an underactuated MSV (4) and (5), considering the compound disturbance , a finite-time disturbance observer is designed as (43), then the disturbance observation error can converge to 0 in finite time.
Proof.
Consider a Lyapunov function as follows:
Taking the time derivative of results in
where and . According to the Lemma 1, the estimation error converges to 0 in finite time, and the convergence time is: .
The observation error of the compound disturbance is
Because it is proven that the estimation error converges to zero in finite time, the disturbance observation error can converge to 0 in finite time, that is , . The Theorem 1 has been proven. ☐
To handle the actuator saturation (6), a finite-time attitude input saturation compensator is designed as follows:
where is the output of the finite-time attitude input saturation compensator, , , . is designed as follows:
The finite-time attitude tracking constraint controller can be designed as follows:
where , and are positive parameters.
The Lyapunov function is defined as follows:
Taking the time derivative of along (48)–(50), we have
According to the Theorem 1, for , the disturbance observation error . Therefore, for , there are
Based on the Young’s inequality, we can obtain
Substituting (54)–(56) into (53), we have
3.3. The Finite-Time Velocity Constraint Controller Design
Define the surge velocity tracking error as follows:
where is the desired surge velocity.
Consider a Lyapunov function as follows:
Taking the time derivative of along (5) and (58), we have
Next, a finite-time disturbance observer is designed to estimate the compound disturbance :
where is the observation value of the disturbance, , , are positive design constants and define the estimation error as . Then, taking the time derivative of results in
Theorem 2.
For the mathematical model of an underactuated MSV (4) and (5), considering the compound disturbance , a finite-time disturbance observer is designed as (61), then the disturbance observation error can converge to 0 in finite time.
Proof
Define the Lyapunov function as follows:
Taking the time derivative of results in
where and . According to the Lemma 1, the estimation error converges to 0 in finite time, and the convergence time is: .
The observation error of the compound disturbance is
Because it is proven that the estimation error converges to zero in finite time, the disturbance observation error converges to 0 in finite time, that is , . Theorem 2 has been proven. ☐
To handle the actuator saturation (6), a finite-time velocity input saturation compensator is designed as follows:
where is the output of the finite-time velocity input saturation compensator, , , . is designed as follows:
Then, the finite-time surge velocity constraint controller is designed as follows:
where , and are control parameters.
Consider a Lyapunov function as follows:
Taking the time derivative of along (66)–(68), we have
According to the Theorem 2, for , the disturbance observation error . Therefore, for , there are
Based on the Young’s inequality, we can obtain
Substituting (72)–(74) into (71), we have
4. Stability Analysis
Theorem 3.
Consider the whole control system of the mathematical model (4) and (5) with external disturbances, model parametric uncertainties, and input saturation, and suppose that Assumptions 1 and 2 are satisfied. The update law and the desired heading angle are presented as (19) and (20), the auxiliary system is developed as (34), the finite-time disturbance observers are designed as (43) and (61), the finite-time tracking constraint controllers are designed as (50) and (68), and the finite-time input saturation compensators are designed as (48) and (66). Select the appropriate controller parameters: , , and , then the following conclusions are valid:
- (i)
- All the error signals of the whole control system are uniformly ultimately bounded. Additionally, position errors meet the constraint requirements, that is and .
- (ii)
- The tracking error of an underactuated MSV can converge into a small neighborhood around zero in finite time.
Proof
Construct the Lyapunov function of the whole control system as follows:
By virtue of (23), (57), (75) and Lemma 2, the differentiation of V can be obtained:
where , and .
- (i)
- According to (77), we have
Because , , similar to [15] and [20], solving the inequality (78) yields
Obviously, the BLF (14) is bounded. Therefore, it can be seen intuitively obtained that , , , , , , and are uniformly ultimately bounded. In addition, the BLF (14) satisfies the following inequalities:
Then, by solving [80], we obtain:
Therefore, this means that the position errors of the underactuated MSV meet the constraint requirements—i.e., , .
- (ii)
- When , , where . Therefore, from (77), we can see:
From Lemma 1, we can infer that V can converge to region in finite time. The convergence time is: . This means that the position tracking errors , in T. Similarly, the yaw tracking error , the yaw angle rate tracking error , the surge velocity tracking error , and the states , of the input saturation compensators converge into a small neighborhood around zero in T. According to Theorems 1 and 2, the observation errors , of disturbance observers converge to 0 in and , respectively. ☐
5. Simulation
In this section, the effectiveness and superiority of the proposed finite-time control scheme are verified by comparative simulation. The model parameters of the underactuated MSV are given as: , , , , , . The desired path is chosen as . The initial position is chosen as . The initial surge velocity is chosen as , and the desired surge velocity is chosen as . The initial value of other states is set as zero. The time-varying external disturbances are simulated as: , , .
The position error constraints are selected as , , and the input saturation limitations are set as , , and . The control parameters are selected as , , , , , , , , , , , , , , , , , , , , , , , , .
To better show the effectiveness and superiority of the proposed finite-time path following control scheme, the comparison is constructed with the EC-LOS guidance law [14] and backstepping controller. The EC-LOS guidance law is given as follows:
where and . In addition, the EC- LOS controller parameters are given as follows: , , , , .
The simulation results are described in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. Figure 4 shows the desired path and the actual path of the underactuated MSV under two guidance laws. It is shown that the proposed control scheme can control the vessel to follow the desired path quickly, which converges faster than the control scheme based on the EC-LOS guidance law. Figure 5 illustrates the velocities u, v and r of the underactuated MSV under two guidance laws, in which the vessel can quickly reach the desired surge velocity under the proposed control scheme. Figure 6 and Figure 7 show the along-track error and the cross-track error of the underactuated MSV under two guidance laws. As shown in the Figure 6 and Figure 7, both the along-track error and the cross-track error can quickly converge into a small neighborhood around zero under two guidance laws, and they will not exceed the position error constraints. However, the convergence rate of the along-track error and the cross-track error under the FT-LOS guidance law is faster than that under the EC-LOS guidance law. The comparison between the observation error of the finite-time disturbance observer and that of the disturbance observer is depicted in Figure 8. From Figure 8, we can see that the observation errors , of the disturbance observer converge to 0 in about 25 s and 27 s, respectively, and the observation errors , of the finite-time disturbance observer converge to 0 in about 15 s and 10 s, respectively, which are shorter than the convergence times of the observation errors of the disturbance observer. The surge force and the yaw moment of the underactuated MSV under input saturation are shown in Figure 9 and Figure 10, respectively. Under the finite-time input saturation compensator, the surge force and yaw moment of the underactuated MSV are all within the ranges of the input saturation constraint. Consequently, from the simulation results, it can be concluded that the proposed finite-time path following control scheme is more efficient and provides a better dynamic performance.
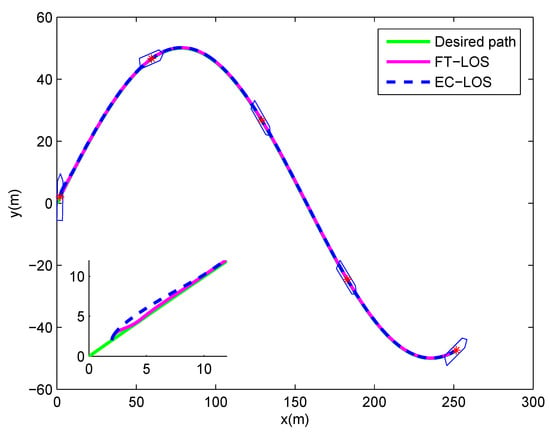
Figure 4.
Desired path and actual path of the underactuated MSV.
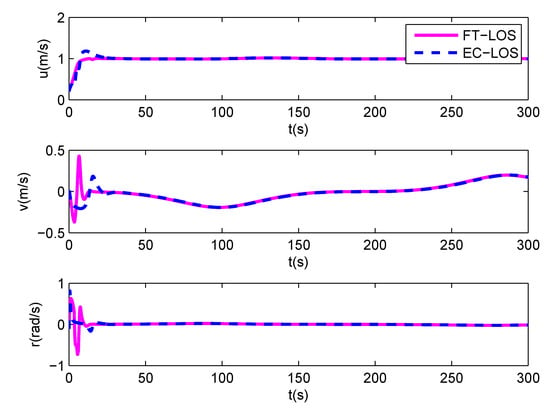
Figure 5.
The surge velocity, sway velocity and yaw angle velocity of the underactuated MSV.
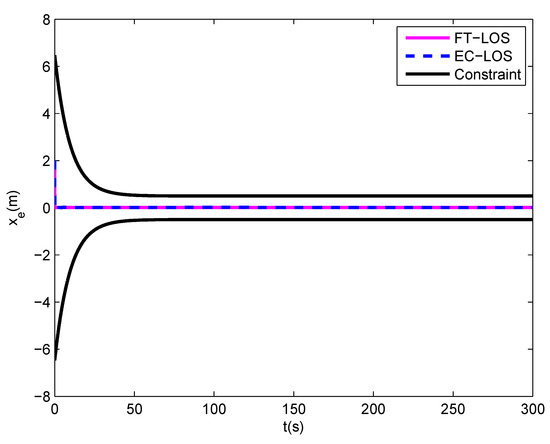
Figure 6.
Along-track error of the underactuated MSV by different guidance laws.
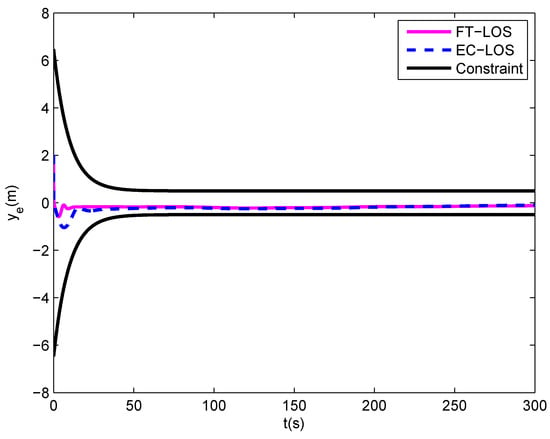
Figure 7.
Cross-track error of the underactuated MSV by different guidance laws.
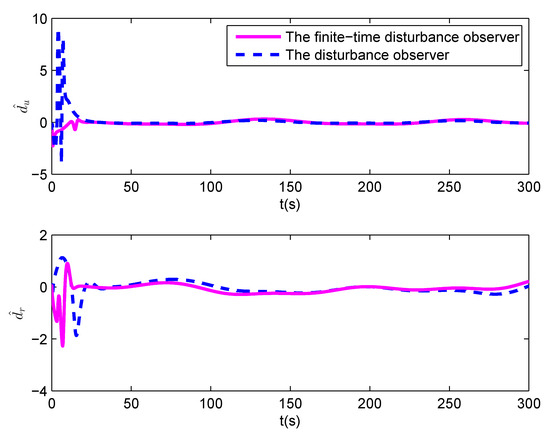
Figure 8.
The estimation errors by different disturbance observers.
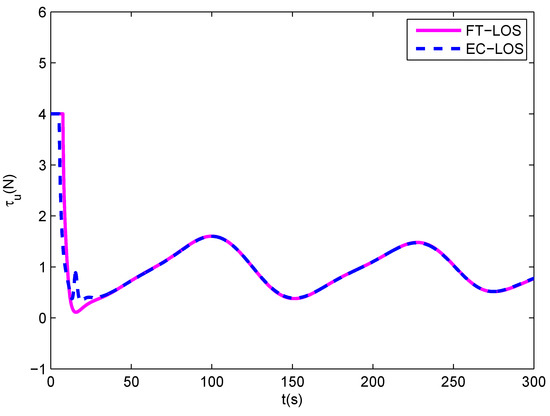
Figure 9.
The surge force under the input saturation.
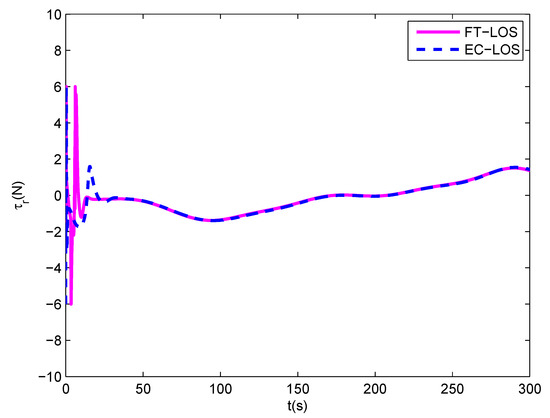
Figure 10.
The yaw moment under the input saturation.
6. Conclusions
In this paper, a finite-time path following control algorithm has been presented for the underactuated MSV with external disturbances, model parametric uncertainties, position constraint and input saturation. Different from the existing literature, position error constraints, input saturation and finite convergence time are simultaneously considered in the control design. The FT-LOS guidance law is designed to obtain the desired yaw angle and simultaneously constrain the position error of the underactuated MSV. The finite-time constraint controllers are designed to achieve tracking control in finite time. Then, the finite-time disturbance observers are proposed to estimate the compound disturbance including the external disturbances and model parametric uncertainties. Additionally, the finite-time input saturation compensators are designed to avoid the actuator saturation and satisfy the requirement of finite-time convergence. The stability analysis shows that the proposed finite-time control algorithm can strictly guarantee the constraint requirement of the position, and all error signals of the whole control system can converge into a small neighborhood around zero in finite time. Eventually, comparative simulation results illustrate the effectiveness and superiority of the proposed finite-time control algorithm. In future work, we will consider the unknown sideslip angle and time delays in the underactuated MSV.
Author Contributions
Methodology, L.W.; Software, L.W.; Supervision, M.F.; Writing—original draft, L.W.; Writing—review and editing, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Nature Science Foundation of China under Grant 51879049.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MSV | Marine surface vessel |
| LOS | Line-of-sight |
| BLF | Barrier Lyapunov function |
| FT-LOS | Finite-time line-of-sight |
| PLOS | Proportional line-of-sight |
| ILOS | Integral line-of-sight |
| EC-LOS | Error-constrained line-of-sight |
References
- Børhaug, E.; Pavlov, A.; Pettersen, K.Y. Straight line path following for formations of underactuated underwater vehicles. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2905–2912. [Google Scholar]
- Breivik, M.; Fossen, T.I. Guidance Laws for Autonomous Underwater Vehicles; In Tech: Vienna, Austria, 2009; pp. 51–76. [Google Scholar]
- Breivik, M.; Hovstein, V.E.; Fossen, T.I. Straight-line target tracking for unmanned surface vehicles. Model. Ident. Control 2009, 29, 131–149. [Google Scholar] [CrossRef]
- Muresan, M.P.; Giosan, I.; Nedevschi, S. Stabilization and validation of 3D object position using multimodal sensor fusion and semantic segmentation. Sensors 2020, 20, 1110. [Google Scholar] [CrossRef] [PubMed]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Breivik, M.; Fossen, T.I. Path following for marine surface vessels. In Proceedings of the Oceans MTS/IEEE Technology-Ocean, Kobe, Japan, 9–12 November 2004; Volume 4, pp. 2282–2289. [Google Scholar]
- Børhaug, E.; Pavlov, A.; Panteley, E.; Pettersen, K.Y. Straight line path following for formations of underactuated marine surface vessels. IEEE Trans. Contr. Syst. Technol. 2011, 19, 493–506. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]
- Fossen, T.I. Marine Control System: Guidance, Navigation and Control of Ship; Rigs and Underwater Vehicles: Trondheim, Norway, 2002. [Google Scholar]
- Fossen, T.I.; Breivik, M.; Skjetne, R. Line-of-sight path following of underactuated marine craft. IFAC Proc. (MCMC) 2003, 36, 211–216. [Google Scholar] [CrossRef]
- Børhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents. In Proceedings of the 47th IEEE Conference on Decision and Control, Caucun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar]
- Caharija, W.; Pettersen, K.Y.; Bibuli, M.; Calado, P.; Zereik, E.; Braga, J.; Bruzzone, G. Integral line-of-sight guidance and control of underactuated marine vehicles: Theory, simulations, and experiments. IEEE Trans. Control Syst. Technol. 2016, 24, 1623–1642. [Google Scholar] [CrossRef]
- Fu, M.; Wang, T.; Wang, C. Barrier Lyapunov function-based adaptive control of an uncertain hovercraft with position and velocity constraints. Math. Probl. Eng. 2019, 2019, 1940784. [Google Scholar] [CrossRef]
- Zheng, Z.; Sun, L.; Xie, L. Error-constrained LOS path following of a surface vessel with actuator saturation and faults. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1794–1805. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, Y.; Xie, L.; Zhu, B. Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output. IEEE Trans. Control Syst. Technol. 2018, 26, 1851–1859. [Google Scholar] [CrossRef]
- Zheng, Z.; Feroskhan, M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances. IEEE/ASME Trans. Mechatron. 2017, 22, 2564–2575. [Google Scholar] [CrossRef]
- Nie, J.; Lin, X. Robust nonlinear path following control of underactuated MSV with time-varying sideslip compensation in the presence of actuator saturation and error constraint. IEEE Access 2018, 36, 71906–71917. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, H.; Wang, C. High-gain observer-based line-of-sight guidance for adaptive neural path following control of underactuated marine surface vessels. IEEE Access 2019, 7, 26088–26101. [Google Scholar] [CrossRef]
- Wang, C.; Wu, Y.; Yu, J. Barrier Lyapunov functions-based dynamic surface control for pure-feedback systems with full state constraints. IET Control Theory Appl. 2017, 11, 524–530. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liu, Y.C.; Wang, N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Wang, N.; Sun, Z.; Yin, J.; Su, S.F.; Sharma, S. Finite-time observer based guidance and control of underactuated surface vehicles with unknown sideslip angles and disturbances. IEEE Access 2018, 6, 14059–14070. [Google Scholar] [CrossRef]
- Nie, J.; Lin, X. FAILOS guidance law based adaptive fuzzy finite-time path following control for underactuated MSV. Ocean Eng. 2019, 195, 106726. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S.; Tay, E.H. Barrier Lyapunov functions for the control of output-constrained nonlinear systems. Automatica 2009, 45, 918–927. [Google Scholar] [CrossRef]
- Bhat, S.P. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Xia, J.; Zhang, J.; Sun, W.; Zhang, B.; Wang, Z. Finite-time adaptive fuzzy control for nonlinear systems with full state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1541–1548. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, F. Finite-time consensus problems for networks of dynamic agents. IEEE Trans. Autom. Control 2010, 55, 950–955. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y.; Galeazzi, R. Line-Of-Sight path following for dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).