Abstract
Cellular structures consist of foams, honeycombs, and lattices. Lattices have many outstanding properties over foams and honeycombs, such as lightweight, high strength, absorbing energy, and reducing vibration, which has been extensively studied and concerned. Because of excellent properties, lattice structures have been widely used in aviation, bio-engineering, automation, and other industrial fields. In particular, the application of additive manufacturing (AM) technology used for fabricating lattice structures has pushed the development of designing lattice structures to a new stage and made a breakthrough progress. By searching a large number of research literature, the primary work of this paper reviews the lattice structures. First, based on the introductions about lattices of literature, the definition and classification of lattice structures are concluded. Lattice structures are divided into two general categories in this paper: uniform and non-uniform. Second, the performance and application of lattice structures are introduced in detail. In addition, the fabricating methods of lattice structures, i.e., traditional processing and additive manufacturing, are evaluated. Third, for uniform lattice structures, the main concern during design is to develop highly functional unit cells, which in this paper is summarized as three different methods, i.e., geometric unit cell based, mathematical algorithm generated, and topology optimization. Forth, non-uniform lattice structures are reviewed from two aspects of gradient and topology optimization. These methods include Voronoi-tessellation, size gradient method (SGM), size matching and scaling (SMS), and homogenization, optimization, and construction (HOC). Finally, the future development of lattice structures is prospected from different aspects.
1. Introduction
Lattice structure is an attractive material for many design applications (aerospace, biological engineering, mechanical engineering, etc.) because of the excellent properties including the light-weighting, high specific strength and stiffness, dissipate heat, and so on. As porous materials, before the lattice structure appeared, the name of cellular structure was more widely spread. The concept of “cellular structure” was originally proposed by Gibson and Ashby Evans, Hutchinson, et al. [1,2,3]. Gibson and Ashby deemed that cellular structure included foams (open-cell and closed-cell foams), honeycombs [1,2]. However, lattice structure as another type of cellular material is different from foams and honeycombs, and the difference of structure mainly lies in unit cell topology and scale, and properties [4,5].
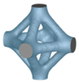
In order to classify more clearly the types of cellular structures, Dhruv Bhate [6], Tao and Leu [7] classified cellular structures into three categories, i.e., foams (open-cell and closed-cell foams), honeycombs, and lattice structures. The shape of unit cells in the foam structures are randomly generated (as shown in Figure 1a), and the cell walls have random orientations in space [2]. In the book of Metal Foams: A Design Guide, Ashby, Evans and Fleck, et al. had introduced in detail the properties, applications, and manufacturing methods of metallic foam structures [8]. Davies and Zhen indicated clearly that metallic foam structures had high porosity ranging from 40% to 98% [9]. Foams are the common cellular structures. Like cork, cancellous bone and wood show various foams. Honeycomb structures have regular shape, and unit cells have the same shape and size (Figure 1b) [2,10]. There are many cell shapes in honeycombs such as tetrahedron, triangular prism, square prism, hexagonal prism, and so on [2,11]. At present, re-entrant honeycomb auxetic structures [12,13,14,15,16] and chiral honeycomb structures [17,18,19] are attractive, which improve the performance and extend the application of honeycombs. Lattice structures are the kind of architecture that are formed by the array of spatial unit cells with edges and faces (as shown in Figure 1c) [7,20]. Cellular shape and size can be uniform or non-uniform. In some academic studies, cellular structures are often equivalent to lattice structures because of neglecting the differences between lattices and foams and honeycombs [21,22]. In their research literatures, the foam structures are actually the lattice structures. In fact, compared with foams and honeycombs, lattice structures have better mechanical properties [3,23]. Queheillalt, et al. [24,25] and Clough et al. [26] demonstrated that lattice structures have the potential to improve compressive and shear strength over foams and honeycomb structures when designed to suppress buckling. Otherwise, lattice structures have many superior properties that foams and honeycombs do not get because of the unique property of tailoring. In other words, each unit cell, and even each strut in the lattice structure can be set as the design variable and be optimized to satisfy specific customized requirements functionally, which means mechanical properties of lattices are more flexible to be controlled than foams and honeycombs [23,27]. Therefore, it can be concluded that lattice structures have better performance than foam structures and honeycomb structures.

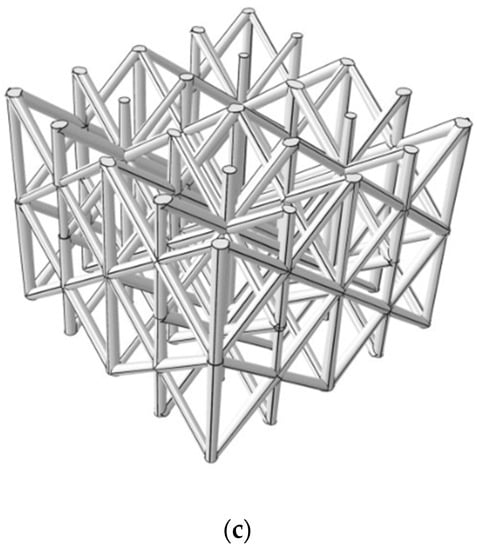
Figure 1.
Different types of cellular structures: (a) foam [2]; (b) honeycomb; (c) lattice structure [20].
In fact, in early industrial structure design, the solid material structure is mainly used because of its sufficient and other material properties. Although the solid material structure to a large extent meets the design requirements, there are still many defects, such as waste of materials, inflexible design, huge structure volume, and manufacturing difficulties. Besides, with the development of science and technology, the requirements for structural properties are higher than before. At present, structure design in industrial field pays more attention to lightweight and high performance. For example, in the field of aerospace, structural design not only requires excellent mechanical properties, but also meets the requirements of lightweight materials. In this way, scientific materials with low cost and high performance can be realized and achieved. With the application of cellular structure, it reduces the weight of structure, and realizes the design application of lightweight and high strength. Taking truss structure as an example, the hollow truss structure designed by filling the truss with cellular material has higher second-order moment of inertia. Compared with the solid truss structure, the cellular structure can improve the bearing capacity of the truss [28]. However, in terms of application, foams, honeycombs and lattices are not exactly the same (as listed in Table 1). Although these three structures have common applications such as aerospace, automotive, marine, and biomedical engineering, and so on, lattice structures are more widely used because of satisfying specific functional requirements.

Table 1.
Applications of cellular structures.
In view of the excellent properties, various unit cells and wide applications of lattice structures among cellular structures (including foams, honeycombs and lattices), lattice structures are becoming the research hot topic in academia and worthy to be reported. Compared with the review literature [33,48,66,67,68] of cellular structures, this manuscript has the following innovative perspectives about lattice structures.
- (1)
- The manuscript especially distinguishes the differences between lattices and foams and honeycombs from aspects of structure and properties. Additionally, the manuscript divides lattice structures into cellular structures.
- (2)
- The manuscript reviews the definition and classification, properties and applications, and manufacturing methods of lattice structures. Especially, there are some shortcomings in the definition of lattice structures in some literature. Therefore, based on the understanding of lattice structures, the definition is given new content, which makes the definition more perfect.
- (3)
- The most excellent work is to reclassify the lattice structures, which is divided into uniform lattice structure and non-uniform lattice structure. The design and optimization methods of lattice structure are reviewed comprehensively over existing literature.
- (4)
- The manuscript also emphasizes the lattice structure of non-uniform Poisson’s ratio, which is rarely involved in other literature. The lattice structures with different Poisson’s ratios are discussed in detail.
Consequently, in the second part of the manuscript, the definition and classification, properties and applications, and manufacturing methods of lattice structures are introduced. In the third part, different methods of designing and optimizing uniform lattice structures are reviewed. Similarly, different methods of designing and optimizing non-uniform lattice structures are reviewed in the fourth part of this paper. Finally, in the fifth part of this paper, the review of lattice structures is summarized, and the future design trend of lattice structures is prospected.
In addition, in order to facilitate researchers to retrieve the literature of lattice structures, the manuscript provides the retrieval method of literature cited by this paper. The keywords refer to cellular structure, foam, honeycomb, lattice structure when retrieving. For example, when retrieving the properties of lattice structure, you should use keywords such as lattice structure, strength, and stiffness on Google Scholar. Otherwise, literature cited by this manuscript have a long time span (about 40 years) and cover a wide range of contents, which support the review of lattice structures.
2. Lattice Structures
2.1. The Definition and Classification of Lattice Structure
As for the definition of lattice structures, Gibson and Ashby defined early the structures in which the cell walls have a common generator as two-dimensional cellular structures like honeycombs, and defined the structures in which cell walls have random orientations in space as three-dimensional cellular structures like foams [2]. However, there is still no unified concept about the definition of lattice structures, because the topology structures of lattices are not limited to only changing size of struts and connection mode of cells. Many scholars have their own understanding of lattice structures based on Gibson and Ashby’s definition of lattice structures. Generally speaking, lattice structures are defined as the three-dimensional structures composed of consecutively and repeatedly arranged interconnected cells, which can also be understood as a porous material structure composed of interconnected struts and nodes in three-dimensional space [69,70,71,72]. Tao et al. defined lattice structure as an architecture formed by an array of spatial periodic unit cells with edges and faces [7]. Dong et al. defined lattice structure as the truss-like structure with interconnected struts and nodes in three-dimensional space [23]. Seharing et al. defined lattice structure as the porous and hollow structure formed by arranging unit cells in three-dimensional space [73]. Helou et al. defined lattice structure as the space-filling unit cell that is able to be tessellated along any axis with no gaps between the cells [74]. There is a common point in the above definitions of lattice structure, that is, lattice structure is a three-dimensional space structure. For all that, there are still shortcomings in the above definition of lattice structure. For example, Tao’s definition of lattice structure [7] only emphasizes the periodic unit cells arrangement but ignores the aperiodic unit cells. Moreover, the gradient lattice structure appears in the structural design, which cannot be defined by distinguishing periodic and aperiodic unit cells arrangement.
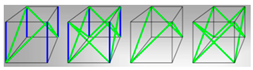
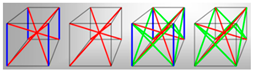
As for the classification of lattice structures, according to the arrangement of unit cells in lattice structures, lattice structures are generally divided into random lattice structures and periodic lattice structures [2,4,7,10]. With the design and optimization of topology structures, Wang and Rosen proposed the conformal lattice structures originally [75]. Compared with periodic lattice structures, conformal lattice structures can strengthen or consolidate complex surfaces. Dong et al. [23] described the classification of lattice structures in detail. They divided lattice structures into three categories, the first category is random lattice structures or disordered lattice structures (as shown in Figure 2a). The unit cells of random lattice structures are randomly distributed in the design space, and have different topological structures and sizes. The second category is periodic lattice structures. This kind of lattice structures can be regarded as the structure formed by periodic repeated arrangement of lattice cells with certain shape, topology, and size in three-dimensional Euclidean space (as shown in Figure 2b). The third kind is pseudo periodic lattice structures (also called conformal lattice structures). In pseudo lattice structures (i.e., conformal lattice structures proposed by Wang and Rosen), each unit cell only has the same topology, but its size is different (as shown in Figure 2c). Although lattice structures are divided into random, periodic, and pseudo, they can represent the unit cells arrangement in space, it is difficult to represent the unit cells arrangement form for gradient lattice structure. For example, the step-wise gradient lattice structure includes three floors (as shown in Figure 3) [76], each step of lattice structure has the same cell topology and regular arrangement, but the cell topology and arrangement between steps are different. In this way, it is difficult to classify the lattice structure as periodic or aperiodic cellular structure. In addition, with the research of positive Poisson’s ratio (PPR) and negative Poisson’s ratio (NPR) materials, many scholars have begun to study lattice structures with different Poisson’s ratio, which is usually named as non-uniform lattice structures [77,78,79,80,81]. In short, lattice structures with gradient and non-uniform PR unit cells should be referred to as non-uniform structures.
Figure 2.
Classification of lattice structures: (a) random lattice structures; (b) periodic lattice structures; (c) periodic lattice structures [23].
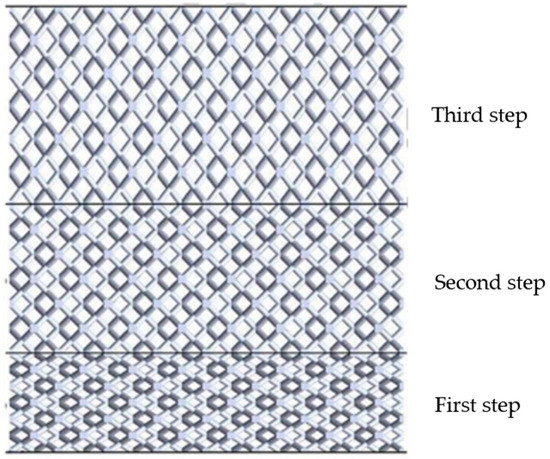
Figure 3.
Gradient lattice structures [76].
For the purpose of this paper, based on the research of lattice structure in the cited literature, the following is the definition and classification of lattice structure in this paper. Lattice structure is a porous three-dimensional spatial structure formed and tessellated by unit cells with different topological geometries, and belongs to cellular structures (including foam structure, honeycomb structure and lattice structure). According to the uniformity of cells distribution, the lattice structures are classified into uniform lattice structures and non-uniform lattice structures. Uniform lattice structures refer to the porous structures with uniform distribution of unit cells, which are formed by the same topological shapes and geometric sizes of unit cells repeatedly arranged in space. The non-uniform lattice structures refer to the porous structures in which unit cells have different topological shapes or geometric sizes and the unit cells are not arranged repeatedly, i.e., in the uneven distribution of materials.
2.2. Properties and Applications of Lattice Structures
2.2.1. Properties
Lattice structure is usually used in lightweight structure design to minimize material loss and energy consumption in the manufacturing process. Energy, material, and time of manufacturing process can be saved effectively by designing and optimizing the lattice structure [71]. It is common knowledge that lattice structure has good mechanical properties. In Section 2.2, the properties of lattice structure are described in detail.
(1) High stiffness and strength [25,72,82,83,84,85,86,87,88]. Bauer et al. [82] fabricated and characterized micro-truss and -shell structures made form cellular ceramic composites. They observed a size dependent strengthening of the alumina shell, especially when the characteristic thickness was less than 100 nm. The compressive strength of the artificial porous material was 280 MPa and the density was less than 1000 kg/m3. Mahshid et al. [88] fabricated structure samples including solid, hollow, and lattice structure, and compared the strength of structures by compression test. The deformation of samples after compression test is shown in Figure 4. The result indicated that though the strength of lattice structure was lower than that of solid structure, it can still meet the application requirements, and reduced the use of materials, and achieve lightweight design.

Figure 4.
Deformation of samples in compression test [88]: (a) solid; (b) hollow; (c) lattice.
(2) High energy absorption [40,41,42,89,90,91]. Ozdemir et al. [42] carried out quasi-static test analysis on lattice structures with cubic cells, diamond cells, and re-entrant cells respectively. They studied the dynamic load deformation behavior of lattice structures, including failure process and stress–strain response. Under the condition of low-speed and high-speed collision, the lattice structures showed obvious difference in deformation behavior and energy absorption effect. Al-Saedi et al. [90] investigated that the energy absorption capability of graded and uniform lattice structures (as shown in Figure 5). The result indicated that the total cumulative energy absorbed by the graded lattice structure was 3.2 ± 0.1 MJ/m3, and by the uniform lattice structure was 2.6 ± 0.2 MJ/m3. The total cumulative energy absorption per unit volume was higher in functionally graded lattice than in uniform lattice (as shown in Figure 6).

Figure 5.
Lattice structures [90]: (a) grade; (b) uniform.
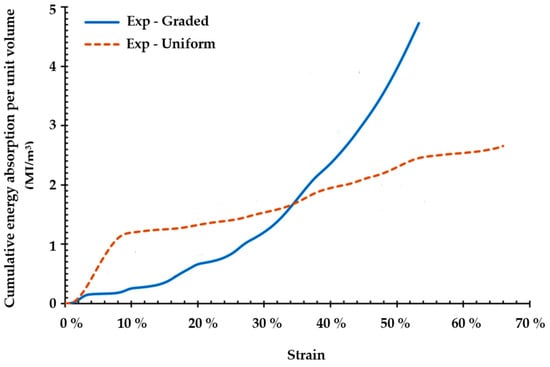
Figure 6.
Cumulative energy absorption per unit volume vs. compressive strain curves of uniform and graded structures [90].
(3) High damping [58,59,60,61]. Yin et al. [60] studied the damping performance of Hollow composite pyramidal lattice (CPL) through vibration test. The experimental results showed that the CPL structure increased the damping property of the material and had a tremendous damping effect. Yin pointed put that the damping ratios of space-filled CPL structures increased about two times that of hollow CPL structures for first three orders and four times for the fourth order.
Bandgap is the most promising feature for lattice structure when it comes to vibration isolation and damping. Syam, Elmadih, and D’Alessandro et al. [92,93,94,95,96], carried out many studies on bandgaps. Syam et al. designed six different lattice structures to investigate the vibration damping and isolation [92]. They used finite element simulation to analyze the displacement of six lattice structures under the same load condition. The results showed that the lattice structures of model 2, model 3, and model 5 had strong damping and vibration isolation effect (as shown Figure 7). As for vibration amplitude, model 3 can reduce vibration more than model 2 and model 5 for all damping factors. But model 1, 4, and 6 were too weak to sustain the predefined load. These studies provide a good theoretical basis for the application of lattice structures in vibration damping and isolation.
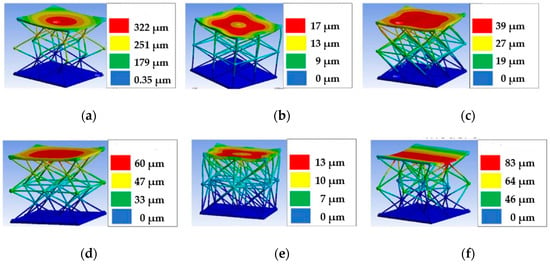
Figure 7.
FEA simulations to estimate displacement of six lattice structures [92]: (a) model 1; (b) model 2; (c) model 3; (d) model 4; (e) model 5; (f) model 6.
(4) Dissipate heat [27,44,45,46,78,97,98,99,100]. Wadley and Queheillalt [45] compared copper textile-based lattice structures with selected heat dissipation media including stochastic open-cell metal foams, periodic Kagome and lattice frame materials, corrugated ducts and louvered fins. Wadley and Queheillalt [45] pointed out that although the copper textile-based lattice structures performed as well as the stochastic open-cell metal foams (aluminum and copper based), the pumping power required was significantly lower for the textile-based structures, because of the periodic topology. Therefore, their overall thermal efficiency was about three times greater than that of comparable weight open-cell copper foams. In addition. Catchpole-Smith et al. also investigated the thermal conductivity of lattice structures [98]. Results showed that thermal conductivity was primarily a function of the material properties and volume fraction of the sample. The Schwarz primitive unit cell consistently gave the highest conductivity, with diamond and gyroid unit cells being marginally lower (as shown in Figure 8). On heat exchange and heat transfer properties of lattice structures, Fink et al. [99] and Do et al. [100] studied fluid dynamics of flow through microscale lattice structures, and verified the heat exchange and heat transfer performance of lattice structure.
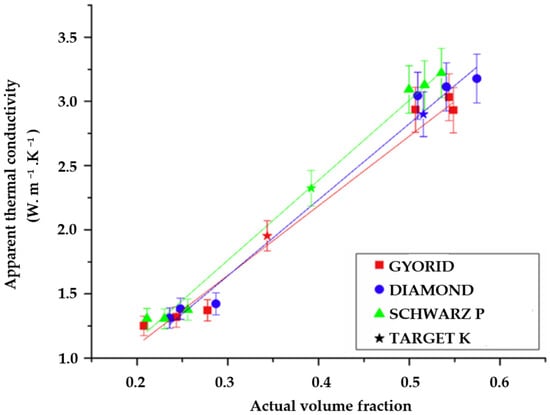
Figure 8.
Apparent thermal conductivity against actual volume fraction [98].
The mechanical properties of lattice structure are the fundamental aspects for the design of lattices. Only when the lattice structure with good mechanical properties is designed, it will be more widely used in various industries. For example, the fatigue behavior of lattice structure, is frequently investigated [101,102,103,104,105,106,107]. By controlling and designing the unit cell shape, surface properties, post treatment and graded porosity, the fatigue behavior can be significantly improved, which may guarantee the long-term application [104]. Therefore, the premise of designing lattice structure is to consider its application field and performance, which is the basis of designing lattice structure and determines the application period of lattice structure.
2.2.2. Applications
The excellent properties of lattice structures fill in the blank of manufacturing industry and provide unprecedented opportunities for structures with better manufacturing performance. The properties of lattice structures determine their wide application fields. Because of lightweight and high strength, lattice structures are often used in the structural design of aircraft, rocket, and other aerospace fields [63,64,65,108,109,110], automotive fields [47,56,57]. In addition, lattice structures have bio-compatibility and high strength, which can be designed into the shape of human tissue and bone to replace the diseased organs. Lattice structures have been tremendously used in the medical field because of flexible mechanical properties and structural characteristics, which can meet specific requirements [48,49,50,51,52,53,54,55,111,112,113,114,115,116,117,118,119,120]. The specific applications of lattice structures are shown in Figure 9.
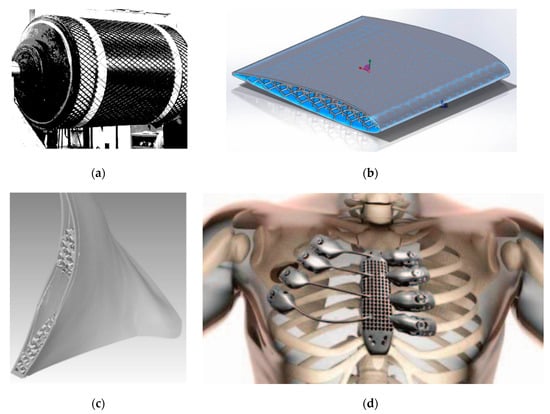
Figure 9.
Applications of lattice structures: (a) winding of helical rib [63]; (b) aerial vehicle wing structure [56]; (c) fan blade [57]; (d) biomedical implant [7,121].
2.3. Manufacturing Methods of Lattice Structures
At present, there are two kinds of methods of fabricating lattice structures, i.e., traditional machining processes and additive manufacturing. Helou and Kara [74] summarized the traditional processing and manufacturing methods, such as water jet cutting, investment casting, electroless plating, electrodeposition, and various processing methods in additive manufacturing including fused deposition modeling (FDM), selective laser melting (SLM), selective laser sintering (SLS), electron beam melting (EBM), binder jetting (BJ), etc.
There are advantages and disadvantages in the fabrication of lattice structure by traditional processing methods. In terms of advantages, the lattice structures with large-scale structure can be fabricated by traditional processing method. Adversely, using traditional processing methods to fabricate the lattice structures will be time-consuming and cumbersome post processing and cause more energy consumption and produce waste material. For instance, the investment casting method proposed by Deshpande [21,24] has high requirements for the fluidity of melt-liquid metal, resulting in being limited to nonferrous casting alloys with high fluidity. Additionally, the process of investment casting is very complex and easy to produce defects. Figure 10 is principle of 3D lattice structure of metal prepared by investment casting. The cell size of octahedral lattice materials fabricated by this process can only reach millimeter scale, which is difficult to meet the requirements of micro-nano-scale lattice structure. In addition, the extrusion and electro-discharge machining method (as shown in Figure 11) proposed by Queheillalt [122] still needs special mold, and the fabricating process is particularly complex and increases the generation cost. It is difficult to fabricate lattice structures with thin ribs and panels. Besides, stretching net folding method and punched hole mesh drawing method are proposed by Kooistra [123,124]. The biggest advantage of stretching net folding is that the plate mesh is made of the original sheet metal, which wastes less raw materials in the production process and saves the raw materials greatly. However, it still needs severe deformation in the manufacturing process and can only be used for materials with high ductility, resulting in low structural strength and complex processing technology [125,126]. Additionally, stamping forming method caused most of the material wastes. The splicing technology proposed by Wadley [126] still has the defects such as unstable lattice structures and limited performance.
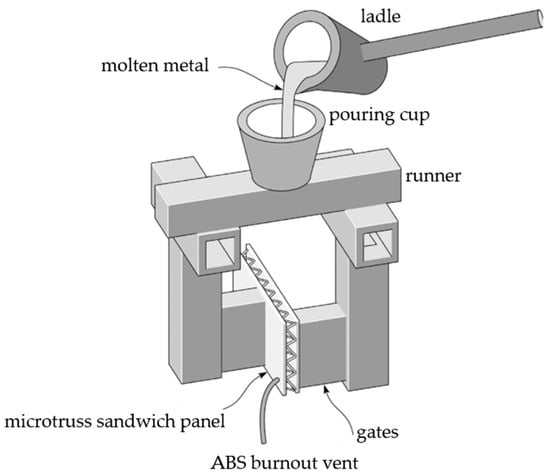
Figure 10.
Investment casting fabricating lattice structure [21,24].
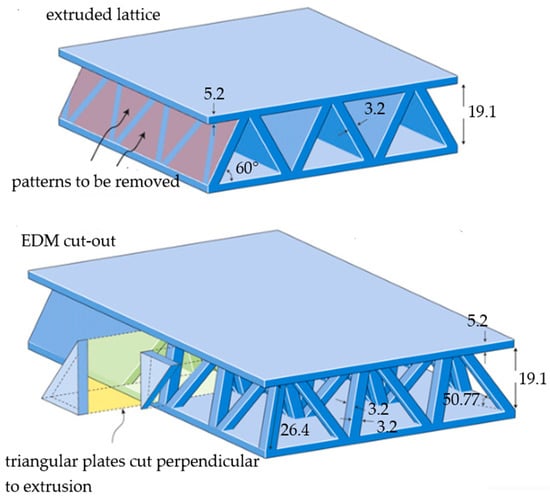
Figure 11.
Extrusion and electro-discharge machining method [122].
Additive manufacturing (AM) technology, as a new processing method, adopting the method of adding materials layer by layer, provides promising opportunities to automatically and flexibly fabricate structures with complicated shapes and architectures that could not be fabricated by conventional manufacturing processes. The combination of lattice structure and additive manufacturing technology is an unprecedented breakthrough in the field of industrial design. The fabrication of lattice structures by AM technology has the following advantages: (1) design flexibility; (2) fabricate lattice structure with wide range of sizes; (3) many kinds of materials (rubber, metal, alloy, ceramic, fiber, etc.); (4) set up program for automatic processing; (5) save energy and reduce cost, etc. There are also some shortcomings in AM technology, i.e., when designing lattice structures with suspended geometry, support materials need to be added, which also causes certain material waste and increases post-processing time. However, based on AM technology, the lattice structures have high design flexibility and can be fabricated into structural materials with complex internal geometry and small geometric size. Scientific researchers have designed different forms of lattice structures by AM, which promotes the development and wide application of lattice structures [48,127,128,129]. In this paper, the fabrication of lattice structures by AM technology is summarized, as shown in Table 2 (Table 2 is written with reference to Dong et al. [23]). In this paper, the index of relevant research literature is limited, it cannot summarize lattice structures by AM, and only lists some references published from 2018 to 2020 year in Google Scholar.

Table 2.
A summary of lattice structures fabricated by AM.
3. Design and Optimization of Uniform Lattice Structures
According to Section 2.1, the lattice structures are classified into uniform lattice structures and non-uniform lattice structures in this paper. In this section, the design and optimization of uniform lattice structures are mainly described from three aspects: (1) unit cell structure design, (2) mathematical algorithm, and (3) unit cell topology optimization. For the definition of lattice structure, lattice structure is formed by arrangement of unit cells in space. Different types of unit cells have their unique characteristics, which can reflect and determine the performance of the whole lattice structures. Therefore, design and optimization of unit cells are the basic research elements. In the third section of the paper, the design and optimization of uniform lattice structures are mainly realized and achieved through the design and optimization of single unit cells. Three aspects are described: (1) Uniform lattice structures formed based on the design of unit cell shape; (2) uniform lattice structures formed based on mathematical algorithm; (3) uniform lattice structures formed based on the optimization of unit cell topology.
3.1. Unit Cell Design Based on Geometric Wireframe
Lattice structures are a kind of porous material formed by repeated arrangement of unit cells. The properties of lattice structures are directly related to the geometric size, shape, structure, and spatial arrangement of unit cells. Most of academic work on the properties of lattice structures are based on the design of unit cell structures, the change of unit cells arrangement, and the optimization. With the application of various modeling software, it is easy to design different unit cell structures. Designers can freely use CAD software to design the geometric structure of unit cells, and then analyze the performance of the unit cells by finite element or experimental methods, and finally form a uniform lattice structure according to a certain arrangement of unit cells. Many literatures have studied the design of unit cells [154,155,156,157,158,159,160,161,162,163,164,165], the structures of unit cells in literature are shown in Appendix A.
For the design of unit cell shape, Chen [157] proposed a 3D texture mapping method, which enabled designers to select the unit cell structure that satisfied the design requirements from cell structure library (as shown in Figure 12), and then the internal structure was generated and defined in the Extensible Markup Language (XML) file combined with the selected unit cell structure. System can automatically convert the unit cell structure file into a CAD model. Finally, all the unit cells formed a lattice structure. The basic idea of 3D texture mapping is shown in Figure 13. For example, the designer knows in advance the stress state of solid cube structure on the left of plus sign, and then selects the lattice structure on the right side of the plus sign to map into the cube, forming a lattice structure by Boolean on the right side of the equal sign that can be made by additive manufacturing. The 3D texture mapping method proposed by Chen is based on mapping a unit cell structure into a design space to generate a customized lattice structure, which makes the design of lattice structure easy.

Figure 12.
3D unit cell structure library [157]: tetrahedron, octahedron, cube, vector (top row, from left to right); icosahedron, dodecahedron, tetrakaidecahedron, triacontahedron (bottom row, from left to right).
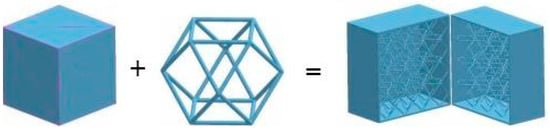
Figure 13.
3D texture mapping method [157].
3.2. Unit Cell Design Based on Mathematical Algorithm
It is an accurate method to describe lattice structures by using mathematical algorithm to design unit cell. Triply periodic minimal surface (TPMS) is one of the mathematical methods that can successfully transform the theoretical mathematical model into the actual lattice structures. TPMS can be generated in multiple ways including Weistreass formula evaluations, nodal approximations of the Weistreass formula, and numerical generation [74]. TPMS is a smooth infinite minimal surface, the minimal surface is defined as a surface in hyperbolic space which possesses a mean curvature or zero. TMPS divides the space into two mazes without self-intersection and has periodicity in three independent directions [166,167]. It can also be considered that an important subclass of TPMS is to divide the space into two disjoint but continuous interlaced regions. TPMS has two key features: (1) The average curvature on the surface is zero everywhere; (2) they are perimeter in all three coordinate directions (i.e., they extend infinitely in all directions and have the symmetry of one of the crystal-space groups).
Yang et al. [167] designed Schoen Gyroid unit cell to form lattice structure based on TPMS. The experimental results showed that Schoen Gyroid lattice structure had the characteristics of self-supporting and high manufacturability. Schoen Gyroid lattice structure made of titanium alloy showed good strength. Maskery et al. [168] pointed out that lattice structure designed by TPMS has a good combination of specific stiffness and axisymmetric stiffness, high surface volume ratio, and pore connectivity. TPMS method reduced the need for surface skin. Therefore, scholars use TPMS method to design the uniform lattice structures [98,169,170,171,172,173,174,175,176,177,178]. Al-Ketan et al. [178] reviewed multifunctional mechanical-metamaterials lattice structures based on TPMS. They summarized the TPMS mathematical formulas for generating different unit cell shapes. Figure 14 shows the different unit cell based on TMPS.
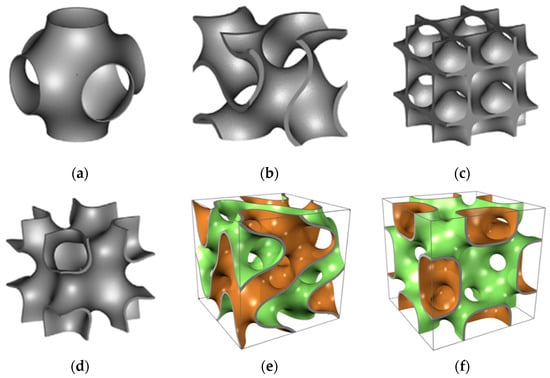
Figure 14.
Unit cell based on TPMS: (a) Schwartz P [176]; (b) Schoen G [176]; (c) Schwarz D [176]; (d) Schoen IWP [176]; (e) Fischer - Koch S [172]; (f) Schoen FRD [172].
Schwarz Primitive Φp:
cosx + cosy + cosz = c
Schoen-Gyroid ΦG:
sinx × cosy + siny × cosz + sinz × cosx = c
Schwarz-Diamond ΦD:
cosx × cosy × cosz − sinx × siny × sinz = c
Schoen-I-WP ΦIWP:
2(cosx × cosy + cosy × cosz + cosz × cosx) − (cos2x + cos2y + cos2z) = c
Fischer-Koch S ΦS:
cos2x × siny × cosz + cosx × cos2y × sinz + sinx × cosy cos2z = c
Schoen-FRD ΦFRD:
where x = 2πX/Lx, y = 2πY/Ly, z = 2πZ/Lz, and Lx, Ly and Lz are the unit cell sizes in the X, Y, and Z directions.
4(cosx × cosy × cosz) − (cos2x × cos2y + cos2y × cos2z + cos2z × cos2x) = c
Based on TPMS, Hao and Hussein [175] used implicit surfaces with unit cells of Diamond and Gyroid. Implicit surfaces provide a compact representation for potentially complex surfaces, and also offer a number of advantages such as flexibility and well-defined Boolean operation. First, the implicit surface was defined as an iso-surface of some function f. In three dimensions, the surface consists of a set of points P Є R3, and satisfies the Equation (7):
f (x, y, z) = 0 (f: R3R)
Therefore, when the points produced in CAD meet the conditions in Table 3, it could be determined whether the points were on the surface, outside the surface, or inside the surface.

Table 3.
Implicit surface in/out convention.
In the two lattice structures designed, each unit cell structure included an empty sphere and an annular connecting rod, which were surrounded by the annular connecting rod to form an empty sphere, as shown in Figure 15. Therefore, the implicit formulation of a unit sphere is given:

Figure 15.
Two types of unit cells [175]: (a) Schoen Gyroid; (b) Schwartz Diamond.
After generating the surface, using the trigonometric function Formula (9) to generate the periodic surface:
In a word, TPMS is suitable for the design of uniform lattice structure. A TPMS surface is infinite and periodic in three independent directions in space, which provides convenience for the uniform distribution of cell structure in space. The lattice structures based on TPMS not only have similar excellent performance compared with the lattice structures designed by other methods, such as light weight, high strength ratio, energy absorption, heat insulation, and sound insulation performance, but also inherits the smooth surface of TPMS, uniform curvature radius, and other characteristics [172].
3.3. Unit Cell Design Based on Topology Optimization
Academic literatures show that topology optimization is one of the methods to obtain uniform lattice structures [86,108,140,151,176,179,180]. By optimizing unit-cell struts’ sizes (i.e., thickness, length and diameter, etc.) and geometries, topology optimization effectively obtains lattice structures with specific performance, that is under condition of the specific constraints, the unit cells can be optimized to obtain specific performance requirements, and then unit cells can be arranged periodically to get the uniform lattice structures. Clausen et al. [180] created a new kind of programmable uniform lattice structure material with Poisson’s ratio between −0.8 and 0.8 by optimizing the unit cells. In large deformation up to 20% even more, the Poisson’s ratio of lattice structure was almost constant.
Homogenization method is one of the methods of topology optimization, and refers to a way to replace the composite with a kind of equivalent material model. Using homogenization to optimize lattice structures can be divided into two steps [23]. First, the local problem based on a unit cell is solved to get the effective material properties. Second, periodic materials are used to replace homogeneous materials with equivalent properties to solve the overall problem. Rodrigues [181] used homogenization method to optimize the topology structures of unit cells, and obtained uniform lattice structure. Rodrigues applied constraint load to the structure within the design domain, and optimized the topology structure of unit cells under the constraint conditions. Finally, the uniform lattice structure was formed, as shown in Figure 16. Although there were load constraints in different directions in the design domain, the uniform lattice structure had almost the same isotropic equivalent behavior as expected.
Figure 16.
Design and optimal material [181]: (a) optimal unit cell; (b) lattice structure.
Wang and Sigmund have made valuable research on topology optimization of unit cells [182,183]. The team carried out a detailed experimental study on the lattice structure with uniform negative Poisson’s ratio. Through the tensile test, the unit cell structure with negative Poisson’s ratio could be obtained by topology optimization. Figure 9 was one of topology structures of unit cells with negative Poisson ratio (Figure 17a), and the uniform lattice structure formed by arranging the unit cell (Figure 17b).
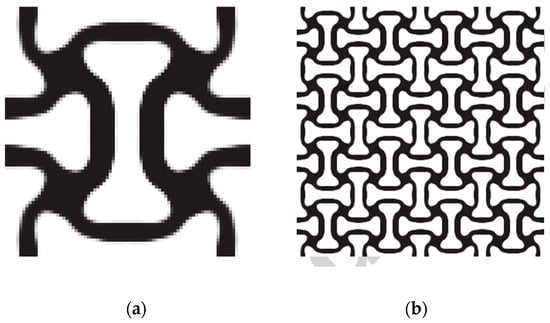
Figure 17.
Topology optimization of uniform lattice structure [183]: (a) unit cell; (b) lattice structure.
4. Design and Optimization of Non-Uniform Lattices
In this part of the paper, the design and optimization of non-uniform lattice structures are mainly discussed from two aspects: gradient lattice structures design, and structure optimization. Compared with uniform lattice structures, non-uniform lattice structures make the designer realize more free design. Through the design of non-uniform lattice structures, it can meet the needs of practical application. For example, in the bio-medicine field, irregular lattice structures are similar to human bone tissue, which is more suitable for the growth of bone tissue than regular lattice structures. Therefore, scholars use Voronoi-tessellation method to design non-uniform lattice structures replacing human bone tissue [184,185,186,187]. Consequently, it is an urgent need for clinical application to design non-uniform lattice structures to replace diseased bones. By optimizing the distribution, shape, and size of materials, the non-uniform lattice structures can reduce the material loss and processing time, and reduce the cost. More importantly, the non-uniform lattice structures are more excellent in performance. With the combination of Voronoi and additive manufacturing technology, fabricating non-uniform lattice structures with different gradients are achieved [76,90,131,137,188,189,190]. In the fourth part of this paper, the design and optimization of non-uniform lattice structures are mainly discussed from two aspects: gradient method and structure optimization.
4.1. Non-Uniform Lattice Structures Based on Functional Gradient Design
Gradient structures are very common in nature, which have variable density and porosity, and can combine a variety of unit cells with different topological structures. Compared with uniform lattice structures, gradient structures show different mechanical properties. Various gradient properties can be obtained to achieve different levels of functionalities and characteristics, by varying the design parameters such as cell size, strut length, and strut diameter of the unit cells in lattice structures [73]. Additionally, Voronoi-tessellation is also one of the important methods to form gradient lattice structures. Because Voronoi-tessellation is a method of space division, many points are distributed in a specific Euclidean space. Using Voronoi-tessellation to design non-uniform lattice structure can realize lightweight anisotropic lattice structure with gradient.
Wang [186] and team proposed a top-down design method based on Voronoi-tessellation, which successfully obtained a special, multi-functional, gradient non-uniform lattice structure. Through the quasi-static compression test, they showed that porosity and irregularity had huge influence on the mechanical properties of materials. Figure 18 showed the gradient lattice structure formed by the top-down Voronoi-tessellation method.
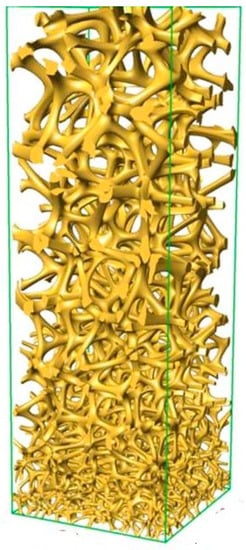
Figure 18.
Gradient lattice structure generated by top-down Voronoi-tessellation method [186].
Sienkiewicz et al. [190] investigated the mechanical response of gradient lattice structures manufactured via SLM. They designed and manufactured gradient discrete lattice structure, gradient increasing lattice structure, and gradient decreasing lattice structure respectively (as shown in Figure 19). By comparing with regular lattice structure, they pointed out that the special mechanical behaviors of lattice structures with gradient topologies made them attractive for energy absorption applications.
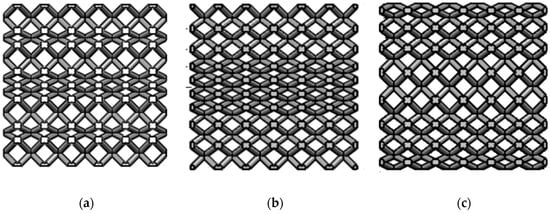
Figure 19.
The gradient lattice structure topologies [190]: (a) gradient discrete; (b) gradient increasing; (c) gradient decreasing.
4.2. Non-Uniform Lattice Structure Based on Structural Optimization
The optimization method of non-uniform lattice structure usually includes two main steps: (1) defining an infrastructure in the design domain in advance; (2) optimizing single or multiple parameters of each unit cell according to the results of topology optimization, then the non-uniform lattice structure can be obtained. Structural optimization includes size optimization, shape optimization, and topology optimization [183]. By using the structure optimization method, a large number of scholars have optimized the lattice structure. Scholars optimize the strength of the lattice structures by imposing specific constraints such as stress, strain, or load on the lattice structures. Or the researchers optimize the size and shape of the unit cell structure, and obtain the lattice structures with specific performance by studying the elasticity, heat dissipation, and other properties of the lattice structures [191,192,193,194,195,196,197,198,199,200,201,202,203,204,205].
For gradient design of non-uniform lattice structures, Han and Lu [27] proposed a novel method of designing non-uniform lattice structure based on additive manufacturing technology, namely size gradient method (SGM). Different from the relative density method, Han et al. took the distribution of unit cell structure of different size as the optimization objective. The specific way was to locate the unit cells in the area with similar unit Young’s modulus, replacing the “relative density model” of topology optimization with the distribution of cells of different sizes. Then, by using the young’s modulus as the transfer medium instead of the “relative density,” the mechanical properties of the lattice structure were closer to the topological optimization results. In addition, in order to ensure that the design domain was completely covered by the unit cell, each cell size needed to be discretized into several gradients, and all the size gradients should be integral times of the minimum gradient. Figure 20 is a non-uniform lattice structure generated based on the SGM.
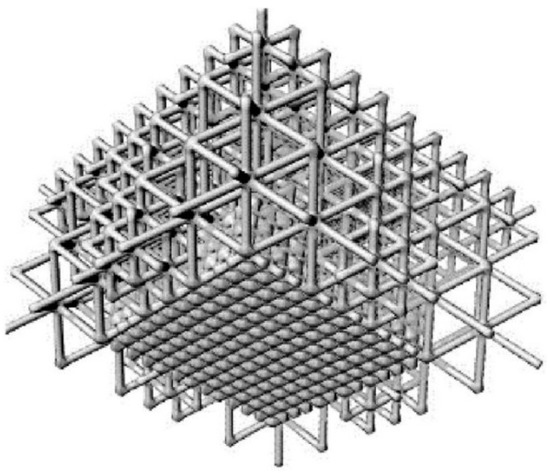
Figure 20.
Non-uniform lattice structure based on SGM method [27].
Nguyen et al. [191] proposed a heuristic method of lattice structure size optimization, i.e., size matching and scaling (SMS) method. In this optimization method, the optimization process was simplified into two variables, i.e., the maximum and minimum diameter of the connecting rod. In this method, first, the stress distribution of the lattice structure with intermediate scale similar to the stress distribution of the solid structure was observed, and then based on the local stress state, the cell structure was selected from the predefined cell library to complete the pre-designed lattice cell structure. Then, by optimizing the element of the support structure, the size of the lattice structure was adjusted to support the stress state. However, the load constraints of the lattice structure prepared by this method were limited, i.e., there was only one load. Figure 21 was the fuselage of the micro air vehicle with high strength, high rigidity and light weight designed by SMS method.
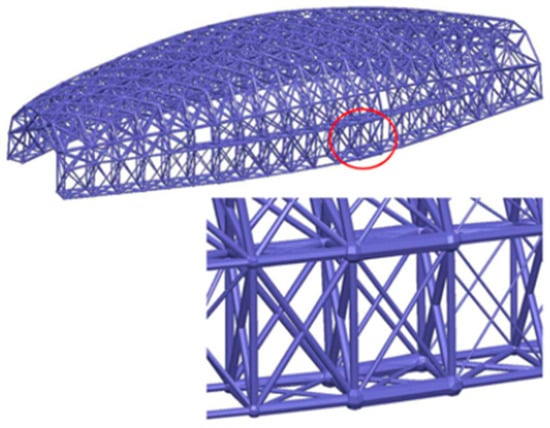
Figure 21.
Non-uniform lattice structure based on SMS method [191].
Toman and Zhang [205] proposed a topology optimization method of variable density non-uniform lattice structure. This method mainly adopted three key technologies: homogenization, optimization, and construction (HOC). By introducing the constitutive law of homogenized material, the equivalent continuous solid was used to represent the lattice structure. The constitutive law of homogenized material was a function of the characteristic parameters of the lattice microstructure, such as the relative density and the orientation of the lattice. The direct result was to get a continuous solid model, whose geometry can be optimized quickly by using the continuous topology optimization theory. Therefore, the optimized distribution of characteristic parameters (such as average density) of lattice microstructure was obtained. Finally, mapping the obtained characteristic parameters of microstructure to a single unit cell could construct a non-uniform lattice structure, as shown in Figure 22. The HOC method avoided the topology optimization of the explicit lattice structure, but it could still maintain the accuracy and reliability by establishing the appropriate micro-mechanical model.

Figure 22.
Non-uniform lattice structure based on HOC method [205].
5. Summary and Overview
This paper reviews the lattice structures by retrieving a lot of appropriate literature. First, the lattice structures are distinguished and compared with foams and honeycombs, and the definition and classification of lattice structures are explained. Second, the properties of lattice structures are analyzed in detail, and the wide applications of lattice structures are introduced. The primary work of this paper is to review methods of designing and optimizing of uniform lattice structures and non-uniform lattice structures. It is clear in the article that the outstanding properties of lattice structures are closely related to the topology structures of unit cells. As for the design of lattice structures, it is mainly based on the design of unit cells.
Through the review of lattice structure literature, some problems in the design of lattice structures are found. If these problems are not solved in time, the development of lattice structures will be limited as following:
- (1)
- In the current researches of lattice structures, the design of cell topological shape is insufficient, and most of the literature are still studying the existing cell structures. The performance of cell structure is directly related to lattice structure, so it is necessary to design cell topology with special performance. Leonardi et al. [206] made a preliminary exploration of the potentialities of H-C and H-C+D lattice structures.
- (2)
- In the topology optimization of lattice structures, most researcher are still focused on the strut’s sizes. The single optimization is not conducive to the design of lattice structures. Only from the point of view of optimizing struts, the lattice structures cannot meet the specific requirements. Kazemi et al. [179] proposed the geometry projection method, to optimizing the multi-material lattice structures. This is a new method to optimize lattice structure, which enriches the method of lattice topology optimization.
However, as the applications of lattice structures are more and more extensive, the design methods are more and more diverse. At present, the investigations of lattice structures are not limited to regular, and irregular structures. The application of materials with uniform Poisson’s ratio and non-uniform Poisson’s ratio enriches the lattice structures. Moreover, the performance requirements of lattice structures are different in various fields. In addition to lightweight, high strength, and other perfect properties, lattice structures with multiple properties are the most popular material in the future. It has become the basic requirements of the application field to develop lattice structures to meet specific requirements. Additionally, the materials used in lattice structures are more and more diverse. Metal materials, ceramic materials, rubber materials, composite materials and other materials are widely used to design lattice structure.
In a word, lattice structures are hot materials in the future development of various industries. Because of the outstanding performance and different characteristics, lattice structures will be widely used in biological tissue engineering, aerospace, automation manufacturing, and other fields that need lightweight and high-strength structure in the future. With the development of processing technology, such as additive manufacturing technology, the processing methods of lattice structures have also made a breakthrough. Additive manufacturing technology not only provides good opportunities for researchers to design lattice structure, but also brings great challenges. Therefore, with the development of multi-disciplinary interaction and based on the advantages of additive manufacturing technology, the development trend of lattice structure is predicted in the following directions:
- (1)
- Multi-material lattice structures. Because additive manufacturing technology adopts the manufacturing method of material layer printing, different materials can be used to manufacture lattice structure in order to meet the demand of using performance. For example, with the wide application of composite materials, a variety of composite materials can be mixed for designing lattice structures.
- (2)
- Multi-structure lattice structures. At present, the research of Poisson’s ratio structure has changed from uniform Poisson’s ratio to non-uniform Poisson’s ratio. From the former positive Poisson’s ratio structure to the present negative Poisson’s ratio structure, the design and optimization of multiple structures in lattice structures are bound to be the future research trend.
- (3)
- Multi-method to design the lattice structures. With the development of CAD technology and programming language, the design of lattice structures in the future will rely heavily on computer technology to develop lattice structure databases with different topology of unit cells. At the same time, equipped with detailed performance parameters using standards for various industries.
- (4)
- Micro-scale lattice structures. Because of different design methods and fabricating methods (such as additive manufacturing technology) of lattice structures, the scales of lattice structures are divided into macro size (>0.5 mm), micro size (0.1 mm–5 mm), micro size (micron level: 100 nm–100 um; nano level: <100 nm) [74,207]. Micro-nano scale lattice structures can be realized in the future, and will be a hot spot in research field.
In brief, lattice structures will become a kind of material with special properties, which combines multi-material, multi-structure, multi-method, and micro-scale. In the future work, scientists should establish a huge lattice structure database, which contains various forms of unit cell topology, and has performance standards for researchers to choose.
Author Contributions
C.P. searched and classified the literature, wrote the original draft preparation, and wrote the manuscript; Y.H. edited and polished the manuscript, made the project administration and funding acquisition; J.L. made the project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant from the “General program of Natural Science Foundation of Guangdong Province” (NO. 2019A1515011964).
Acknowledgments
The authors would like to thank the School of Mechanical Engineering of Beijing Institute of Technology (BIT), and Institute of Engineering Medicine of Beijing Institute of Technology (BIT).
Conflicts of Interest
The authors declare that they have no competing/financial conflict of interests in this paper.
Appendix A
Figure A1.
(a) Octet-truss [24]; (b) Kagomé [142].
Figure A2.
(a) Diagonal; (b) Octahedral [143].

Figure A3.
Unit cells [144].

Figure A4.
(a) Cross 1; (b) G6; (c) G7; (d) Dode Thin [146].
Figure A5.
(a) Body centered cubic (BCC); (b) reinforced body centered cubic (RBCC) [147].
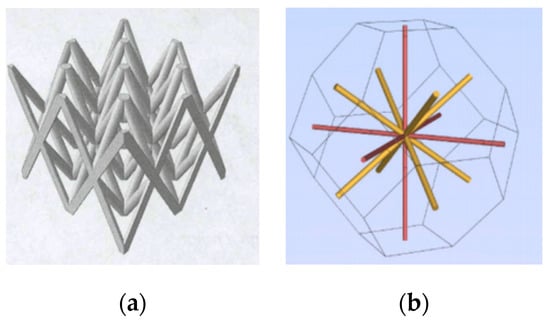
Figure A6.
(a) Pyramidai cell [148]; (b) Kelvin cell [149].
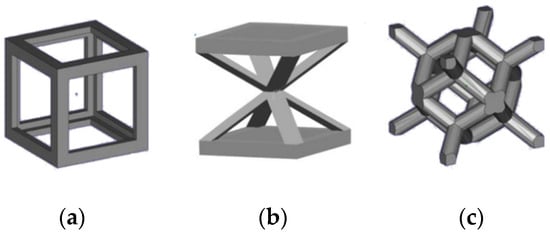
Figure A7.
(a) Cubic.; (b) G7; (c) Rhombic dodecahedron [150].
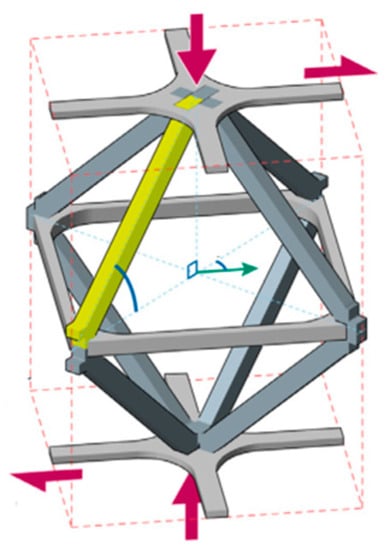
Figure A8.
Octet-truss cell [151].
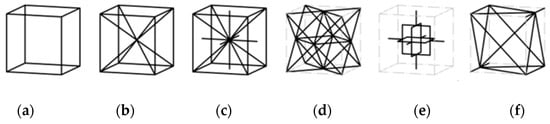
Figure A9.
(a) SC; (b) BCC; (c) RBCC; (d) OT; (e) GAM; (f) WG [152].

Figure A10.
Rectangular prism: (a) C01; (b) C02; (c) C03; (d) C04; hexagonal structures: (e) H01; (f) H02; (g) H03; (h) H04 [153].
References
- Gibson, L.J. Modelling the mechanical behavior of cellular materials. Mater.Sci. Eng. A 1989, 110, 1–36. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; pp. 16–21. [Google Scholar]
- Evans, A.G.; Hutchinson, J.W.; Ashby, M.F. Multifunctionality of cellular metal systems. Prog. Mater. Sci. 1998, 43, 171–221. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Bubb, S.L.; Young, P.; Raymont, D. Evaluation of light-weight AlSi10Mg periodic cellular lattice structures fabricated via direct metal laser sintering. J. Mater. Process. Technol. 2014, 214, 856–864. [Google Scholar] [CrossRef]
- Ashby, M. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 364, 15–30. [Google Scholar] [CrossRef]
- Bhate, D. Four Questions in Cellular Material Design. Materials 2019, 12, 1060. [Google Scholar] [CrossRef]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation Cleveland (ISFA 2016), Cleveland, OH, USA, 1–3 August 2016; pp. 326–332. [Google Scholar]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.W.; Wadley, H.N.G.; Gibson, L.J. Metal Foams: A Design Guide; Butterworth-Heinemann: Oxford, UK, 2000; pp. 1–3. [Google Scholar]
- Davies, G.J.; Zhen, S. Metallic foams: Their production, properties and applications. J. Mater. Sci. 1983, 18, 1899–1911. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, Y.F. A survey of the design methods for additive manufacturing to improve functional performance. Rapid Prototyp. J. 2016, 22, 569–590. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N.M.; Zhao, K.; Li, Z. Mechanical properties of a hollow-cylindrical-joint honeycomb. Compos. Struct. 2014, 109, 68–74. [Google Scholar] [CrossRef]
- Boldrin, L.; Hummel, S.; Scarpa, F.; Di Maio, D.; Lira, C.; Ruzzene, M.; Remillat, C.; Lim, T.-C.; Rajasekaran, R.; Patsias, S. Dynamic behaviour of auxetic gradient composite hexagonal honeycombs. Compos. Struct. 2016, 149, 114–124. [Google Scholar] [CrossRef]
- Ingrole, A.; Hao, A.; Liang, R. Design and modeling of auxetic and hybrid honeycomb structures for in-plane property enhancement. Mater. Des. 2017, 117, 72–83. [Google Scholar] [CrossRef]
- Wang, T.; Li, Z.; Wang, L.; Ma, Z.-D.; Hulbert, G.M. Dynamic Crushing Analysis of a Three-Dimensional Re-Entrant Auxetic Cellular Structure. Materials 2019, 12, 460. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69, 475–490. [Google Scholar] [CrossRef]
- Lira, C.; Innocenti, P.; Scarpa, F. Transverse elastic shear of auxetic multi re-entrant honeycombs. Compos. Struct. 2009, 90, 314–322. [Google Scholar] [CrossRef]
- Qi, D.; Lu, Q.; He, C.; Li, Y.; Wu, W.; Xiao, D. Impact energy absorption of functionally graded chiral honeycomb structures. Extreme Mech. Lett. 2019, 32, 100568. [Google Scholar] [CrossRef]
- X, L.; By, C.; Vbc, T.; Te, T. A New Chiral Beam Element for Modelling Chiral Honeycombs. J. Appl. Mech. Eng. 2017, 6. [Google Scholar] [CrossRef]
- Scarpa, F.; Blain, S.; Lew, T.; Perrott, D.; Ruzzene, M.; Yates, J.R. Elastic buckling of hexagonal chiral cell honeycombs. Compos. Part A Appl. Sci. Manuf. 2007, 38, 280–289. [Google Scholar] [CrossRef]
- Rezaei, R.; Karamooz-Ravari, M.R.; Badrossamay, M.; Kadkhodaei, M. Mechanical characterization and finite element modeling of polylactic acid BCC-Z cellular lattice structures fabricated by fused deposition modeling. Proc. IMECHE Part. C J. Mech. Eng. Sci. 2016, 203–210, 1989–1996. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam topology: Bending versus stretching dominated architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Yang, L.; Cormier, D.; West, H.; Harrysson, O.; Knowlson, K. Non-stochastic Ti–6Al–4V foam structures with negative Poisson’s ratio. Mater. Sci. Eng. A Struct. 2012, 558, 579–585. [Google Scholar] [CrossRef]
- Dong, G.; Tang, Y.; Zhao, Y.F. A Survey of Modeling of Lattice Structures Fabricated by Additive Manufacturing. J. Mech. Des. Trans. ASME 2017, 139, 100906. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids. 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Queheillalt, D.T.; Wadley, H.N.G. Cellular metal lattices with hollow trusses. Acta Mater. 2005, 53, 303–313. [Google Scholar] [CrossRef]
- Clough, E.C.; Ensberg, J.; Eckel, Z.C.; Ro, C.J.; Schaedler, T.A. Mechanical performance of hollow tetrahedral truss cores. Int. J. Solids Struct. 2016, 91, 115–126. [Google Scholar] [CrossRef]
- Han, Y.F.; Lu, W.F. A novel design method for nonuniform lattice structures based on topology optimization. J. Mech. Des. Trans. ASME 2018, 140, 091403. [Google Scholar] [CrossRef]
- Wadley, H.N.G. Cellular Metals Manufacturing. Adv. Eng. Mater. 2002, 40, 726–733. [Google Scholar] [CrossRef]
- Bienvenu, Y. Application and future of solid foams. C. R. Phys. 2014, 15, 719–730. [Google Scholar] [CrossRef]
- Hassan, M.R.; Scarpa, F.; Ruzzene, M.; Mohammed, N. Smart shape memory alloy chiral honeycomb. Mater. Sci. Eng. A Struct. 2008, 481, 654–657. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Haghpanah, B.; Ghosh, R.; Hamouda, A.; Nayeb-Hashemi, H.; Vaziri, A. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theor. Appl. Mech. Lett. 2016, 6, 81–96. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, J.; Fan, H. Plastic analyses of thin-walled steel honeycombs with re-entrant deformation style. Mater. Sci. Eng. A Struct. 2017, 688, 123–133. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.; Chirima, G.; Ravirala, N.; Zied, K. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of Mechanics and Applications of Auxetic Structures. Adv. Mater. Sci. Eng. 2014. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Cottam, R. Mechanical properties in tensile loading of H13 re-entrant honeycomb auxetic structure manufactured by direct metal deposition. MATEC Web Conf. 2015, 34, 01004. [Google Scholar] [CrossRef]
- Murray, G.; Gandhi, F.; Hayden, E. Polymer Filled Honeycombs to Achieve a Structural Material with Appreciable Damping. J. Intell. Mater. Syst. Struct. 2013, 23, 703–718. [Google Scholar] [CrossRef]
- Vaidya, U.K.; Ulven, C.; Pillay, S.; Ricks, H. Impact Damage of Partially Foam-filled Co-injected Honeycomb Core Sandwich Composites. J. Compos. Mater. 2003, 37, 611–626. [Google Scholar] [CrossRef]
- Takemiya, H. Field vibration mitigation by honeycomb WIB for pile foundations of a high-speed train viaduct. Soil. Dyn. Earthq. Eng. 2004, 24, 69–87. [Google Scholar] [CrossRef]
- Murray, G.J.; Gandhi, F. Auxetic honeycombs with lossy polymeric infills for high damping structural materials. J. Intell. Mater. Syst. Struct. 2013, 24, 1090–1104. [Google Scholar] [CrossRef]
- Evans, A.; He, M.; Deshpande, V.; Hutchinson, J.; Jacobsen, A.; Carter, W. Concepts for enhanced energy absorption using hollow micro-lattices. Int. J. Impact Eng. 2010, 37, 947–959. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Ro, C.J.; Sorensen, A.E.; Eckel, Z.; Yang, S.S.; Carter, W.B.; Jacobsen, A.J. Designing metallic microlattices for energy absorber applications. Adv. Eng. Mater. 2014, 16, 276–283. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy absorption in lattice structures in dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Maloney, K.; Fink, K.D.; Schaedler, T.A.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Multifunctional heat exchangers derived from three-dimensional micro-lattice structures. Int. J. Heat Mass Trans. 2012, 55, 2486–2493. [Google Scholar] [CrossRef]
- Lu, T.J.; Valdevit, L.; Evans, A.G. Active cooling by metallic sandwich structures with periodic cores. Prog. Mater. Sci. 2005, 50, 798–815. [Google Scholar] [CrossRef]
- Wadley, H.N.G.; Queheillalt, D.T. Thermal Applications of Cellular Lattice Structures. Mater. Sci. Forum 2007, 539, 242–247. [Google Scholar] [CrossRef]
- Valdevit, L.; Pantano, A.; Stone, H.; Evans, A. Optimal active cooling performance of metallic sandwich panels with prismatic cores. Int. J. Heat Mass Transf. 2006, 49, 3819–3830. [Google Scholar] [CrossRef]
- Yin, S.; Chen, H.; Wu, Y.; Li, Y.; Xu, J. Introducing composite lattice core sandwich structure as an alternative proposal for engine hood. Compos. Struct. 2018, 201, 131–140. [Google Scholar] [CrossRef]
- Melchels, F.P.W.; Feijen, J.; Grijpma, D.W. A review on stereolithography and its applications in biomedical engineering. Biomaterials 2010, 31, 6121–6130. [Google Scholar] [CrossRef]
- Jetté, B.; Brailovski, V.; Dumas, M.; Simoneau, C.; Terriault, P. Femoral stem incorporating a diamond cubic lattice structure: Design, manufacture and testing. J. Mech. Behav. Biomed. 2018, 77, 58–72. [Google Scholar] [CrossRef]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and characterization of a porosity graded lattice structure for additively manufactured biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- Heinl, P.; Müller, L.; Körner, C.; Singer, R.F.; Müller, F.A. Cellular Ti–6Al–4V structures with interconnected macro porosity for bone implants fabricated by selective electron beam melting. Acta Biomater. 2008, 4, 1536–1544. [Google Scholar] [CrossRef]
- Chen, W.M.; Lee, S.J.; Lee, P.V.S. Failure analysis of an additive manufactured porous titanium structure for orthopedic implant applications. Mater. Sci. Forum 2016, 863, 45–49. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Choi, S.K.; Saldana, C.J. Uncertainty quantification and validation of 3D lattice scaffolds for computer-aided biomedical applications. J. Mech. Behav. Biomed. 2017, 71, 428–440. [Google Scholar] [CrossRef]
- Soro, N.; Attar, H.; Brodie, E.; Veidt, M.; Molotnikov, A.; Dargusch, M.S. Evaluation of the mechanical compatibility of additively manufactured porous Ti-25Ta alloy for load-bearing implant applications. J. Mech. Behav. Biomed. 2019, 97, 149–158. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, R.; Antonov, M.; Kollo, L.; Holovenko, Y.; Prashanth, K.G. Mechanical behavior of Ti6Al4V scaffolds filled with CaSiO3 for implant applications. Appl. Sci. 2019, 9, 3844. [Google Scholar] [CrossRef]
- Moon, S.K.; Tan, Y.E.; Hwang, J.; Yoon, Y.-J. Application of 3D printing technology for designing light-weight unmanned aerial vehicle wing structures. Int. J. Precis. Eng. Manuf. Technol. 2014, 1, 223–228. [Google Scholar] [CrossRef]
- Magerramova, L.; Volkov, M.; Afonin, A.; Svinareva, M.; Kalinin, D. Application of light lattice structures for gas turbine engine fan blades. In Proceedings of the 31st congress of the international council of the aeronautical sciences (ICAS), Belo Horizonte, Brazil, 9–14 September 2018; pp. 1–10. [Google Scholar]
- Lou, J.; Ma, L.; Wu, L.Z. Free vibration analysis of simply supported sandwich beams with lattice truss core. Mater. Sci. Eng. B Solid-State Mater. Adv. Technol. 2012, 177, 1712–1716. [Google Scholar] [CrossRef]
- Xu, M.; Qiu, Z. Free vibration analysis and optimization of composite lattice truss core sandwich beams with interval parameters. Compos. Struct. 2013, 106, 85–95. [Google Scholar] [CrossRef]
- Yin, S.; Wu, L.; Yang, J.; Ma, L.; Nutt, S. Damping and low-velocity impact behavior of filled composite pyramidal lattice structures. J. Compos. Mater. 2014, 48, 1789–1800. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Belski, E.; Wang, X.; Sietins, J.M.; Ludwick, S.; To, A.C.; Ludwick, S.J. Natural frequency optimization of variable-density additive manufactured lattice structure: Theory and experimental validation. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 100502. [Google Scholar] [CrossRef]
- Horn, T.J.; Harrysson, O.L.A. Overview of current additive manufacturing technologies and selected applications. Sci. Prog. 2012, 95, 255–282. [Google Scholar] [CrossRef]
- Barynin, V.A.; Bunakov, V.A.; Rasin, A.F.; Vasiliev, V.V. Aerospace composite lattice structures. In Proceedings of the 120th International Conference on Composite Materials, Paris, France, 5–9 July 1999. [Google Scholar]
- Vasiliev, V.V.; Razin, A.F. Anisogrid composite lattice structures for spacecraft and aircraft applications. Compos. Struct. 2006, 76, 182–189. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Barynin, V.A.; Razin, A.F. Anisogrid composite lattice structures-Development and aerospace applications. Compos. Struct. 2012, 94, 1117–1127. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Gianpaolo, S.; Stefano, R.; Roberto, M.; Conchen, G. Geometric Modeling of Cellular Materials for Additive Manufacturing in Biomedical Field: A Review. Appl. Bionics Biomech. 2018. [Google Scholar] [CrossRef]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The Design Process of Additively Manufactured Mesoscale Lattice Structures: A Review. J. Comput. Inf. Sci. Eng. 2018, 18, 040801. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Gorguluarslan, R.M.; Gandhi, U.; Mandapati, R.; Choi, S.-K. Design and fabrication of periodic lattice-based cellular structures. Comput. Aided. Des. Appl. 2015, 13, 50–62. [Google Scholar] [CrossRef]
- Zok, F.W.; Latture, R.M.; Begley, M.R. Periodic truss structures. J. Mech. Phys. Solids 2016, 96, 184–203. [Google Scholar] [CrossRef]
- Helou, M.; Vongbunyong, S.; Kara, S. Finite Element Analysis and Validation of Cellular Structures. Procedia CIRP 2016, 50, 94–99. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. A review on integration of lightweight gradient lattice structures in additive manufacturing parts. Adv. Mech. Eng. 2020, 12, 1–21. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, analysis and manufacturing of lattice structures: An overview. Int. J. Comput. Integr. Manuf. 2017, 31, 243–261. [Google Scholar] [CrossRef]
- Wang, H.; Rosen, D.W. Parametric Modeling Method for Truss Structures. In Proceedings of the DETC’02 ASME 2002 Design Engineering Technical Conferences and Computer and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2002; pp. 759–767. [Google Scholar]
- Xiao, L.; Song, W. Additively-manufactured functionally graded Ti-6Al-4V lattice structures with high strength under static and dynamic loading: Experiments. Int. J. Impact Eng. 2018, 111, 255–272. [Google Scholar] [CrossRef]
- Han, Y.; Lu, W. Evolutionary design of nonuniform cellular structures with optimized Poisson’s ratio distribution. Mater. Des. 2017, 141, 384–394. [Google Scholar] [CrossRef]
- Han, Y.; Lu, W. Optimization design of nonuniform cellular structures for additive manufacturing. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference MSEC2018 College Station, College Station, TX, USA, 18–22 June 2018. V001T01A033. [Google Scholar]
- Radman, A.; Huang, X.; Xie, Y.M. Topology optimization of functionally graded cellular materials. J. Mater. Sci. 2013, 48, 1503–1510. [Google Scholar] [CrossRef]
- Daynes, S.; Feih, S.; Lu, W.F.; Wei, J. Optimization of functionally graded lattice structures using isostatic lines. Mater. Des. 2017, 127, 215–223. [Google Scholar] [CrossRef]
- Lira, C.; Scarpa, F.; Rajasekaran, R. A Gradient Cellular Core for Aeroengine Fan Blades Based on Auxetic Configurations. J. Intell. Mater. Syst. Struct. 2011, 22, 907–917. [Google Scholar] [CrossRef]
- Bauer, J.; Hengsbach, S.; Tesari, I.; Schwaiger, R.; Kraft, O. High-strength cellular ceramic composites with 3D microarchitecture. Proc. Natl. Acad. Sci. USA 2014, 111, 2453–2458. [Google Scholar] [CrossRef]
- Wendy, X.; Greer, J.R. Ultra-strong architected Cu meso-lattices. Extrem. Mech. Lett. 2015, 2, 7–14. [Google Scholar] [CrossRef]
- Messner, M.C. Optimal lattice-structured materials. J. Mech. Phys. Solids 2016, 96, 162–183. [Google Scholar] [CrossRef]
- Hou, A.; Gramoll, K. Compressive Strength of Composite Lattice Structures. J. Reinf. Plast. Comp. 2016, 17, 462–493. [Google Scholar] [CrossRef]
- Takezawa, A.; Koizumi, Y.; Kobashi, M. High-stiffness and strength porous maraging steel via topology optimization and selective laser melting. Addit. Manuf. 2017, 18, 194–202. [Google Scholar] [CrossRef]
- Parthasarathy, J.; Starly, B.; Raman, S.; Christensen, A. Mechanical Evaluation of Porous Titanium (Ti6Al4V) Structures with Electron Beam Melting (EBM). J. Mech. Behav. Biomed. Mater. 2010, 3, 249–259. [Google Scholar] [CrossRef]
- Mahshid, R.; Hansen, H.N.; Hojbjerre, K.L. Strength analysis and modeling of cellular lattice structures manufactured using selective laser melting for tooling applications. Mater. Des. 2016, 104, 276–283. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Al-Saedi, D.S.; Masood, S.H.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.; Tuck, C.; Ashcroft, I. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Syam, W.P.; Jianwei, W.; Zhao, B.; Maskery, I.; Elmadih, W.; Leach, R.K. Design and analysis of strut-based lattice structures for vibration isolation. Precis. Eng. 2018, 52, 494–506. [Google Scholar] [CrossRef]
- Elmadih, W.; Syam, W.P.; Maskery, I.; Chronopoulos, D.; Leach, R.K. Mechanical vibration bandgaps in surface-based lattices. Addit. Manuf. 2019, 25, 421–429. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Zega, V.; Ardito, R.; Corigliano, A. 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep.-UK 2018, 8, 2262. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Braghin, F.; Corigliano, A. Mechanical low-frequency filter via modes separation in 3D periodic structures. Appl. Phys. Lett. 2017, 111, 231902. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Belloni, E.; Ardito, R.; Corigliano, A.; Braghin, F. Modeling and experimental verification of an ultra-wide bandgap in 3D phononic crystal. Appl. Phys. Lett. 2016, 109, 221907. [Google Scholar] [CrossRef]
- Cheng, X.; Wei, K.; He, R.; Pei, Y.; Fang, D. The equivalent thermal conductivity of lattice core sandwich structure: A predictive model. Appl. Therm. Eng. 2016, 93, 236–243. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Sélo, R.; Davis, A.; Ashcroft, I.; Tuck, C.; Clare, A. Thermal Conductivity of TPMS Lattice Structures Manufactured via Laser Powder Bed Fusion. Addit. Manuf. 2019, 30, 100846. [Google Scholar] [CrossRef]
- Fink, K.D.; Kolodziejska, J.A.; Jacobsen, A.J.; Roper, C.S. Fluid dynamics of flow through microscale lattice structures formed from self-propagating photopolymer waveguides. Aiche. J. 2011, 57, 2636–2646. [Google Scholar] [CrossRef]
- Do, G.; Geißelbrecht, M.; Schwieger, W.; Freund, H. Additive manufacturing of interpenetrating periodic open cellular structures (interPOCS) with in operando adjustable flow characteristics. Chem. Eng. Process. 2019, 148, 107786. [Google Scholar] [CrossRef]
- Jamshidinia, M.; Wang, L.; Tong, W.; Ajlouni, R.; Kovacevic, R. Fatigue properties of a dental implant produced by electron beam melting® (EBM). J. Mater. Process. Tech. 2015, 226, 255–263. [Google Scholar] [CrossRef]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S. Numerical simulation of the fatigue behavior of additive manufactured titanium porous lattice structures. Mater. Sci. Eng. C Mater. 2016, 60, 339–347. [Google Scholar] [CrossRef]
- Zargarian, A.; Esfahanian, M.; Kadkhodapour, J.; Ziaei-Rad, S.; Zamani, D. On the fatigue behavior of additive manufactured lattice structures. Theor. Appl. Fract. Mech. 2019, 100, 225–232. [Google Scholar] [CrossRef]
- Ren, D.; Li, S.; Wang, H.; Hou, W.; Hao, Y.; Jin, W.; Yang, R.; Misra, R.D.K.; Murr, L.E.; Zhao, S. Fatigue behavior of Ti-6Al-4V cellular structures fabricated by additive manufacturing technique. J. Mater. Sci. Technol. 2018, 35, 285–294. [Google Scholar] [CrossRef]
- Köhnen, P.; Haase, C.; Bültmann, J.; Ziegler, S.; Schleifenbaum, J.H.; Bleck, W. Mechanical properties and deformation behavior of additively manufactured lattice structures of stainless steel. Mater. Des. 2018, 145, 205–217. [Google Scholar] [CrossRef]
- Zhao, S.; Li, S.; Hou, W.; Hao, Y.; Yang, R.; Misra, R. The influence of cell morphology on the compressive fatigue behavior of Ti-6Al-4V meshes fabricated by electron beam melting. J. Mech. Behav. Biomed. 2016, 59, 251–264. [Google Scholar] [CrossRef]
- Zhao, S.; Li, S.; Wang, S.; Hou, W.; Li, Y.; Zhang, L.-C.; Hao, Y.; Yang, R.; Misra, R.; Murr, L. Compressive and fatigue behavior of functionally graded Ti-6Al-4V meshes fabricated by electron beam melting. Acta Mater. 2018, 150, 1–15. [Google Scholar] [CrossRef]
- Totaro, G.; Gürdal, Z. Optimal design of composite lattice shell structures for aerospace applications. Aerosp. Sci. Technol. 2009, 13, 157–164. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Podshivalov, L.; Gomes, C.M.; Zocca, A.; Guenster, J.; Bar-Yoseph, P.; Fischer, A. Design, analysis and additive manufacturing of porous structures for biocompatible micro-scale scaffolds. Procedia CIRP 2013, 5, 247–252. [Google Scholar] [CrossRef]
- Arabnejad, S.; Johnston, R.B.; Pura, J.A.; Singh, B.; Tanzer, M.; Pasini, D. High-strength porous biomaterials for bone replacement: A strategy to assess the interplay between cell morphology, mechanical properties, bone ingrowth and manufacturing constraints. Acta Biomater. 2016, 30, 345–356. [Google Scholar] [CrossRef] [PubMed]
- Dantas, A.C.; Scalabrin, D.H.; De Farias, R.; Barbosa, A.A.; Ferraz, A.V.; Wirth, C. Design of Highly Porous Hydroxyapatite Scaffolds by Conversion of 3D Printed Gypsum Structures—A Comparison Study. Procedia CIRP 2015, 49, 55–60. [Google Scholar] [CrossRef]
- Du Plessis, A.; Yadroitsava, I.; Yadroitsev, I.; Le Roux, S.; Blaine, D. Numerical comparison of lattice unit cell designs for medical implants by additive manufacturing. Virtual Phys. Prototyp. 2018, 13, 1–16. [Google Scholar] [CrossRef]
- Zhang, D.Z.; Zhang, D.Z.; Zhang, P.; Zhao, M.; Jafar, S. Mechanical properties of optimized diamond lattice structure for bone scaffolds fabricated via selective laser melting. Materials 2018, 11, 374. [Google Scholar]
- Wu, J.; Aage, N.; Westermann, R.; Sigmund, O.; Westermann, R. Infill Optimization for Additive Manufacturing-Approaching Bone-Like Porous Structures. IEEE Trans. Vis. Comput. Graph. 2018, 24, 1127–1140. [Google Scholar] [CrossRef]
- Zhang, B.; Pei, X.; Zhou, C.; Fan, Y.; Jiang, Q.; Ronca, A.; D’Amora, U.; Chen, Y.; Li, H.; Sun, Y.; et al. The biomimetic design and 3D printing of customized mechanical properties porous Ti6Al4V scaffold for load-bearing bone reconstruction. Mater. Des. 2018, 152, 30–39. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Meta-biomaterials. Biomater. Sci.-UK 2020, 8, 18–38. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A. Additively manufactured porous metallic biomaterials. J. Mater. Chem. B 2019, 7, 4088–4117. [Google Scholar] [CrossRef] [PubMed]
- Du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Cancer Patient Receives 3D Printed Ribs in World-First Surgery. Available online: http://blog.csiro.au/cancer-patient-receives-3d-printed-ribs-in-world-first-surgery/ (accessed on 11 September 2015).
- Queheillalt, D.T.; Murty, Y.; Wadley, H.N.G. Mechanical properties of an extruded pyramidal lattice truss sandwich structure. Scr. Mater. 2008, 58, 76–79. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Wadley, H.N.G. Lattice truss structures from expanded metal sheet. Mater. Des. 2007, 28, 507–514. [Google Scholar] [CrossRef]
- Kooistra, G.W.; Deshpande, V.S.; Wadley, H.N.G. Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminum. Acta Mater. 2004, 52, 4229–4237. [Google Scholar] [CrossRef]
- Zhao, B.; Li, Z.Q.; Hou, H.L.; Han, X.; Liao, J.; Tan, Z.; Bai, B.; Bai, L. Research Progress on Fabrication Methods of Metal Three Dimensional Lattice. Rare Met. Mater. Eng. 2016, 45, 2189–2220. [Google Scholar]
- Wadley, H.N.G. Multifunctional periodic cellular metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef]
- Yan, C.; Hao, L.; Hussein, A.; Raymont, D. Evaluations of cellular lattice structures manufactured using selective laser melting. Int. J. Mach. Tools Manuf. 2012, 62, 32–38. [Google Scholar] [CrossRef]
- Cerardi, A.; Caneri, M.; Meneghello, R.; Concheri, G.; Ricotta, M. Mechanical characterization of polyamide cellular structures fabricated using selective laser sintering technologies. Mater. Des. 2013, 46, 910–915. [Google Scholar] [CrossRef]
- Tang, Y.; Zhou, Y.; Hoff, T.; Garon, M.; Zhao, Y.F. Elastic modulus of 316 stainless steel lattice structure fabricated via binder jetting process. Mater. Sci. Technol. 2016, 32, 648–656. [Google Scholar] [CrossRef]
- Xiao, L.; Song, W.-D.; Hu, M.; Li, P. Compressive properties and micro-structural characteristics of Ti–6Al–4V fabricated by electron beam melting and selective laser melting. Mater. Sci. Eng. A Struct. 2019, 764, 138204. [Google Scholar] [CrossRef]
- Wally, Z.J.; Haque, A.M.; Feteira, A.; Claeyssens, F.; Goodall, R.; Reilly, G.C. Selective laser melting processed Ti6Al4V lattices with graded porosities for dental applications. J. Mech. Behave. Biomed. 2018, 90, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Gangireddy, S.; Komarasamy, M.; Faierson, E.J.; Mishra, R.S. High strain rate mechanical behavior of Ti-6A1-4V octet lattice structures additively manufactured by selective laser melting (SLM). Mater. Sci. Eng. A-Struct. 2019, 745, 231–239. [Google Scholar] [CrossRef]
- Yan, X.; Li, Q.; Yin, S.; Chen, Z.; Jenkins, R.; Chen, C.; Wang, J.; Ma, W.; Bolot, R.; Lupoi, R.; et al. Mechanical and invitro study of an isotropic Ti6Al4V lattice structure fabricated using selective laser melting. J. Alloys Compd. 2019, 782, 209–223. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Chen, X.; Yi, C.; Chen, R.; Zhang, Z. Configuration Optimization Design of Ti6Al4V Lattice Structure Formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Xiong, Y.; Chen, X.; Sun, Y.; Gong, C.; Pu, H.; Wu, X.; Luo, J. Influence of unit cell pose on the mechanical properties of Ti6Al4V lattice structures manufactured by selective laser melting. Addit. Manuf. 2020, 34, 101222. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Li, W.; Liang, J. Orientation dependency for microstructure, geometric accuracy and mechanical properties of selective laser melting AlSi10Mg lattices. J. Alloys Compd. 2019, 791, 490–500. [Google Scholar] [CrossRef]
- Liu, M.; Takata, N.; Suzuki, A.; Kobashi, M. Development of gradient microstructure in the lattice structure of AlSi10Mg alloy fabricated by selective laser melting. J. Mater. Sci. Technol. 2020, 36, 106–117. [Google Scholar] [CrossRef]
- Yu, T.; Hyer, H.; Sohn, Y.; Bai, Y.; Wu, D. Structure-property relationship in high strength and lightweight AlSi10Mg microlattices fabricated by selective laser melting. Mater. Des. 2019, 182, 108062. [Google Scholar] [CrossRef]
- Caravaggi, P.; Liverani, E.; Leardini, A.; Fortunato, A.; Belvedere, C.; Baruffaldi, F.; Fini, M.; Parrilli, A.; Mattioli-Belmonte, M.; Tomesani, L.; et al. CoCr porous scaffolds manufactured via selective laser melting in orthopedics: Topographical, mechanical, and biological characterization. J. Biomed. Mater. Res. Part B 2019, 107, 2343–2353. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, Y.; Xiao, R.; Bai, Y.; Song, C.; Wang, D. Evaluation of topology-optimized lattice structures manufactured via selective laser melting. Mater. Des. 2018, 143, 27–37. [Google Scholar] [CrossRef]
- Zhong, T.; He, K.; Li, H.; Yang, L. Mechanical properties of lightweight 316L stainless steel lattice structures fabricated by selective laser melting. Mater. Des. 2019, 181, 108076. [Google Scholar] [CrossRef]
- Schneider, J.; Kumar, S. Multiscale characterization and constitutive parameters identification of polyamide (PA12) processed via selective laser sintering. Polym. Test. 2020, 86, 106357. [Google Scholar] [CrossRef]
- Xin, J.; Xi, L.G.; Meng, Z. Optimal design of three-dimensional non-uniform nylon lattice structures for selective laser sintering manufacturing. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Fina, F.; Goyanes, A.; Madla, C.M.; Awad, A.; Trenfield, S.J.; Kuek, J.M.; Patel, P.; Gaisford, S.; Basit, A.W. 3D printing of drug-loaded gyroid lattices using selective laser sintering. Int. J. Pharm. 2018, 547, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Gao, L.; Hu, X.; Cao, K.; Zhou, W.; Wang, W.; Lu, Y. Stereolithographic 3D Printing-Based Hierarchically Cellular Lattices for High-Performance Quasi-Solid Supercapacitor. Nano-Micro Lett. 2019, 11. [Google Scholar] [CrossRef]
- Yang, W.; An, J.; Chua, C.K.; Zhou, K. Acoustic absorptions of multifunctional polymeric cellular structures based on triply periodic minimal surfaces fabricated by stereolithography. Virtual Phys. Prototyp. 2020, 15, 242–249. [Google Scholar] [CrossRef]
- Dar, U.A.; Mian, H.H.; Abid, M.; Topa, A.; Sheikh, M.Z.; Bilal, M. Experimental and numerical investigation of compressive behavior of lattice structures manufactured through projection micro stereolithography. Mater. Today Commun. 2020. [Google Scholar] [CrossRef]
- Dong, G.; Wijaya, G.; Tang, Y.; Zhao, Y.F. Optimizing process parameters of fused deposition modeling by Taguchi method for the fabrication of lattice structures. Addit. Manuf. 2018, 19, 62–72. [Google Scholar] [CrossRef]
- Tao, Y.; Pan, L.; Liu, D.; Li, P. A Case Study: Mechanical Modeling Optimization of Cellular Structure Fabricated Using Wood Flour-Filled Polylactic Acid Composites with Fused Deposition Modeling. Compos. Struct. 2019, 216, 360–365. [Google Scholar] [CrossRef]
- Khan, S.Z.; Masood, S.H.; Ibrahim, E.; Ahmad, Z. Compressive behaviour of Neovius Triply Periodic Minimal Surface cellular structure manufactured by fused deposition modelling. Virtual Phys. Prototyp. 2019, 14, 360–370. [Google Scholar] [CrossRef]
- Akihiro, T.; Kazuo, Y.; Yuichiro, K.; Zhang, X.P.; Mitsuru, K. Isotropic Ti–6Al–4V Lattice via Topology Optimization and Electron-Beam Melting. Addit. Manuf. 2018, 22, 629–642. [Google Scholar]
- Ataee, A.; Li, Y.; Fraser, D.; Song, G.F.; Wen, C. Anisotropic Ti-6Al-4V gyroid scaffolds manufactured by electron beam melting (EBM) for bone implant applications. Mater. Des. 2018, 137, 45–354. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J.; Jia, L.; Yang, G.Y.; Tang, H.P.; Li, Y.Y. Additive manufacturing of Ti-6Al-4V lattice structures with high structural integrity under large compressive deformation. J. Mater. Sci. Technol. 2018, 35, 305–308. [Google Scholar] [CrossRef]
- Hyun, S.; Karlsson, A.M.; Torquato, S.; Evans, A.G. Simulated properties of Kagomé and tetragonal truss core panels. Int. J. Solids Struct. 2003, 40, 6989–6998. [Google Scholar] [CrossRef]
- Brooks, W.; Sutcliffe, C.; Cantwell, W.; Fox, P.; Todd, J. Rapid Design and Manufacture of Ultralight Cellular Materials. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 1–3 August 2005; pp. 231–241. [Google Scholar]
- Wettergreen, M.A.; Bucklen, B.S.; Starly, B.; Yuksel, E.; Sun, W.; Liebschner, M.A.K. Creation of a unit block library of architectures for use in assembled scaffold engineering. Cad Comput. Aided Des. 2005, 37, 1141–1149. [Google Scholar] [CrossRef]
- Chen, Y. 3D Texture Mapping for Rapid Manufacturing. Comput. Aided Des. Appl. 2007, 4, 761–771. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Medina, F.; Lopez, H.; Martinez, E.; Machado, B.I.; Hermandz, D.H.; Martinez, L.; Lopez, M.I.; Wicken, R.B.; et al. Next-generation biomedical implants using additive manufacturing of complex, cellular and functional mesh arrays. Philos. Trans. 2010, 368, 1999–2032. [Google Scholar] [CrossRef]
- Pettermann, H.E.; Hüsing, J. Modeling and simulation of relaxation in viscoelastic open cell materials and structures. Int. J. Solids Struct. 2012, 49, 2848–2853. [Google Scholar] [CrossRef]
- Hammetter, C.I.; Rinaldi, R.G.; Zok, F.W. Pyramidal lattice structures for high strength and energy absorption. J. Appl. Mech. Trans. Asme 2013, 80, 041015. [Google Scholar] [CrossRef]
- Gurtner, G.; Durand, M. Stiffest elastic networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014. [Google Scholar] [CrossRef]
- Li, S.J.; Xu, Q.S.; Wang, Z.; Hou, W.T.; Hao, Y.L.; Yang, R.; Murr, L.E. Influence of cell shape on mechanical properties of Ti-6Al-4V meshes fabricated by electron beam melting method. Acta Biomater. 2014, 10, 4537–4547. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Deshpande, V.; Wadley, H. Mechanical response of Ti-6Al-4V octet-truss lattice structures. Int. J. Solids Struct. 2015, 60, 107–124. [Google Scholar] [CrossRef]
- Savio, G.; Meneghell, R.; Concheri, G. Optimization of lattice structures for Additive Manufacturing Technologies. In Proceedings of the International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing (JCM 2016), Catania, Italy, 14–16 September 2016; pp. 213–222. [Google Scholar]
- Beyer, C.; Figueroa, D. Design and Analysis of Lattice Structures for Additive Manufacturing. J. Manuf. Sci. Eng. Trans. Asme 2016, 138, 121014. [Google Scholar] [CrossRef]
- Lord, E.A.; Mackay, A.L. Periodic minimal surfaces of cubic symmetry. Curr. Sci. 2003, 85, 346–362. [Google Scholar]
- Yang, L.; Yan, C.; Han, C.J.; Chen, P.; Yang, S.F.; Shi, Y.S. Mechanical response of a triply periodic minimal surface cellular structures manufactured by selective laser melting. Int. J. Mech. Sci. 2018, 148, 149–157. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2017, 152, 62–71. [Google Scholar] [CrossRef]
- Jung, Y.; Chu, K.T.; Torquato, S. A variational level set approach for surface area minimization of triply-periodic surfaces. J. Comput. Phys. 2007, 223, 711–730. [Google Scholar] [CrossRef][Green Version]
- Gandy, P.J.F.; Bardhan, S.; Mackay, A.L.; Klinowski, J. Nodal surface approximations to the P, G, D and I-WP triply periodic minimal surfaces. Chem. Phys. Lett. 2001, 336, 187–195. [Google Scholar] [CrossRef]
- Wang, Y. Periodic surface modeling for computer aided nano design. Cad Comput. Aided Des. 2007, 39, 179–189. [Google Scholar] [CrossRef]
- Kapfer, S.C.; Hyde, S.T.; Mecke, K.; Arns, C.H.; Schröder-Turk, G.E. Minimal surface scaffold designs for tissue engineering. Biomaterials 2011, 32, 6875–6882. [Google Scholar] [CrossRef] [PubMed]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R.; Young, P. Advanced lattice support structures for metal additive manufacturing. J. Mater. Process. Technol. 2013, 213, 1019–1026. [Google Scholar] [CrossRef]
- Montazerian, H.; Davoodi, E.; Asadi-Eydivand, M.; Kadkhodapour, J.; Solati-Hashjin, M. Porous scaffold internal architecture design based on minimal surfaces: A compromise between permeability and elastic properties. Mater. Des. 2017, 126, 98–114. [Google Scholar] [CrossRef]
- Hao, L.; Raymont, D.; Yan, C.; Hussein, A.; Young, P. Design and additive manufacturing of cellular lattice structures. In Proceedings of the 5th International Conference on Advanced Research and Rapid Prototyping (VRAP), Leiria, Portugal, 28 September–1 October 2011; pp. 249–254. [Google Scholar]
- Abu Al-Rub, R.K.; Rowshan, R.; Abu Al-Rub, R.K. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar]
- Savio, G.; Meneghello, R.; Concheri, G. Design of variable thickness triply periodic surfaces for additive manufacturing. Prog. Addit. Manuf. 2019, 4, 290–291. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Abu Al-Rub, R.K. Multifunctional mechanical-metamaterials based on triply periodic minimal surface lattices: A review. Adv. Eng. Mater. 2019, 21, 1900524. [Google Scholar] [CrossRef]
- Kazemi, H.; Vaziri, A.; Julián, A. Norato. Multi-material topology optimization of lattice structures using geometry projection. Comput. Methods Appl. Mech. 2020, 363, 112895. [Google Scholar] [CrossRef]
- Clausen, A.; Wang, F.; Jensen, J.S.; Sigmund, O.; Lewis, J. Topology Optimized Architectures with Programmable Poisson’s Ratio over Large Deformations. Adv. Mater. 2015, 27, 5523–5527. [Google Scholar] [CrossRef]
- Rodrigues, H.C. Topology Optimization of Structures: Applications in the Simulation and Design of Cellular Materials. In Proceedings of the “Enhancement and Promotion of Computational Methods in Engineering and Science X”, Sanya, China, 21–23 August 2006; pp. 125–136. [Google Scholar]
- Wang, F.; Sigmund, O.; Jensen, J.S. Design of materials with prescribed nonlinear properties. J. Mech. Phys. Solids 2014, 69, 156–174. [Google Scholar] [CrossRef]
- Sigmund, O.; Trans, P.; Lond, R.S. Topology optimization: A tool for the tailoring of structures and materials Topology optimization: A tool for the tailoring of structures and materials. Philos. Trans. R. Soc. Lond. A 2000, 358, 211–227. [Google Scholar] [CrossRef]
- Fantini, M.; Curto, M.; De Crescenzio, F. A method to design biomimetic scaffolds for bone tissue engineering based on Voronoi lattices. Virtual Phys. Prototyp. 2016, 11, 77–90. [Google Scholar] [CrossRef]
- Gómez, S.; Vlad, M.D.; López, J.; Fernández, E. Design and properties of 3D scaffolds for bone tissue engineering. Acta Biomater. 2016, 42, 341–350. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Shen, L.; Zhao, J.; Liang, H.; Wang, C. Design and Compressive Behavior of Controllable Irregular Porous Scaffolds: Based on Voronoi-Tessellation and for Additive Manufacturing. Acs Biomater. Sci. Eng. 2018, 4, 719–727. [Google Scholar] [CrossRef]
- Du, Y.; Liang, H.; Xie, D.; Mao, N.; Zhao, J.F.; Tian, Z.J.; Wang, C.J.; Shen, L.D. Design and statistical analysis of irregular porous scaffolds for orthopedic reconstruction based on voronoi tessellation and fabricated via selective laser melting (SLM). Mater. Chem. Phys. 2020, 239, 1–9. [Google Scholar] [CrossRef]
- Lu, L.; Sharf, A.; Zhao, H.S.; Wei, Y.; Fan, Q.N.; Chen, X.L.; Savoye, Y.; Tu, C.H.; CohenOr, D.; Chen, B.Q. Build-to-last: Strength to weight 3D printed objects. Acm Trans. Graph. 2014, 3, 1–10. [Google Scholar] [CrossRef]
- Ying, J.; Lu, L.; Tian, L.; Yan, X.; Chen, B.Q. Anisotropic porous structure modeling for 3D printed objects. Comput. Graph. 2018, 70, 157–164. [Google Scholar] [CrossRef]
- Sienkiewicz, J.A.; Płatek, P.; Jiang, F.; Sun, X.; Rusinek, A. Investigations on the Mechanical Response of Gradient Lattice Structures Manufactured via SLM. Metals 2020, 10, 213. [Google Scholar] [CrossRef]
- Nguyen, J.; Park, S.; Rosen, D. Heuristic optimization method for cellular structure design of light weight components. Int. J. Precis. Eng. Manuf. 2013, 14, 1071–1078. [Google Scholar] [CrossRef]
- Tang, Y.; Kurtz, A.; Zhao, Y.F. Bidirectional Evolutionary Structural Optimization (BESO) based design method for lattice structure to be fabricated by additive manufacturing. Cad Comput. Aided Des. 2015, 69, 91–101. [Google Scholar] [CrossRef]
- Salonitis, K.; Chantzis, D.; Kappatos, V. A hybrid finite element analysis and evolutionary computation method for the design of lightweight lattice components with optimized strut diameter. Int. J. Adv. Manuf. Technol. 2017, 90, 2689–2701. [Google Scholar] [CrossRef]
- Tang, Y.; Dong, G.; Zhou, Q.; Zhao, Y.F. Lattice Structure Design and Optimization with Additive Manufacturing Constraints. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1546–1562. [Google Scholar] [CrossRef]
- Pantz, O.; Trabelsi, K. A post-trement of the homogenization method for shape optimization. Siam J. Control Optim. 2008, 47, 1380–1398. [Google Scholar] [CrossRef]
- Pantz, O.; Trabelsi, K. Construction of minimization sequences for shape optimization. In Proceedings of the 15th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 23–26 August 2010; pp. 278–283. [Google Scholar]
- Verners, O.; Dobelis, M. Shape Optimization of a Superelement of Hexagonal Lattice Structure. Constr. Sci. 2010, 11, 66–76. [Google Scholar]
- Reinhart, G.; Teufelhart, S. Load-adapted design of generative manufactured lattice structures. Phys. Procedia 2011, 12, 385–392. [Google Scholar] [CrossRef]
- Reinhart, G.; Teufelhart, S. Optimization of mechanical loaded lattice structures by orientating their struts along the flux of force. Procedia CIRP 2013, 12, 175–180. [Google Scholar] [CrossRef]
- Janushevskis, A.; Melnikovs, A.; Boyko, A. Shape optimization of 3D mechanical systems using metamodels. Adv. Mater. Res. 2013, 705, 429–435. [Google Scholar] [CrossRef]
- Koizumi, Y.; Okazaki, A.; Chiba, A.; Kato, T.; Takezawa, A. Cellular lattices of biomedical Co-Cr-Mo-alloy fabricated by electron beam melting with the aid of shape optimization. Addit. Manuf. 2016, 12, 305–313. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Wang, Y.Q.; Michael, Y.; Wei, J.; Lu, W.F. Buckling optimization of Kagome lattice cores with free-form trusses. Mater. Des. 2018, 145, 144–155. [Google Scholar] [CrossRef]
- Wang, H.; Wu, M. Study on the Shape Optimization of Cable-Stiffened Single-Layer Latticed Shells. Int. J. Steel Struct. 2018, 18, 924–934. [Google Scholar] [CrossRef]
- Dapogny, C.; Estevez, R.; Faure, A.; Michailidis, G. Shape and topology optimization considering anisotropic features induced by additive manufacturing processes. Comput. Methods Appl. Mech. Eng. 2019, 344, 626–665. [Google Scholar] [CrossRef]
- Zhang, P.; Toman, J.; Yu, Y.Q.; Biyikli, E.; Tu, A.C. Efficient design-optimization of variable-density hexagonal cellular structure by additive manufacturing: Theory and validation. J. Manuf. Sci. Eng. Trans. Asme. 2015, 137, 41–45. [Google Scholar] [CrossRef]
- Leonardi, F.; Graziosi, S.; Casati, R.; Tamburrino, F.; Bordegoni, M. Additive Manufacturing of Heterogeneous Lattice Structures: An Experimental Exploration. In Proceedings of the 22nd International Conference on Engineering Design (ICED19), Delft, The Netherlands, 5–8 August 2019; pp. 669–678. [Google Scholar]
- Vyatskikh, A.; Delalande, S.; Kudo, A.; Zhang, X.; Greer, J.R. Additive manufacturing of 3D nano-architected metals. Nat. Commun. 2018, 9, 3864–3870. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).