Hyperbolic Asynchronous Method of a Radio Navigation Technique

Abstract

Humans have always wanted to determine positions in an unknown environment. At the beginning, methods were simple. They were based on the observation of characteristic points—in the case of shipping, additional observations of the coastline. Then came navigation based on astronomical methods (astronavigation). At the beginning of the XX-th century, a new way of determining the current location was developed. It used radio wave signals. First came radio beacons, then ground-based systems. Currently, satellite systems are being used. At present, the most popular one is the Global Positioning System (GPS). This system is fully controlled by the Department of Defense, and only the U.S. forces and their closest allies have been guaranteed the accuracy offered by the system. Armies of other countries can only use the civilian version. This situation has engendered the need for an independent radiolocation system. This article describes the construction and operation of such a technology demonstrator that was developed at Gdansk University of Technology. The main advantage of the system is the ability to manage it without the chain organization of the reference stations, which currently work with each other asynchronously. This article demonstrates the functionality of such a system. It also presents results and analysis of its effectiveness.

1. Introduction

The movement of people and things is one of the basic activities that commonly accompanies our existence and forces us to navigate efficiently, i.e., to guide a moving object along a certain trajectory to a designated destination. This process requires locating and determining the position of successive places along which the navigated object moves. This is important in all circumstances, especially in relation to public and private security and also in defense situations. It is also worth noting at this point that there would be no great geographical discoveries without the ability to navigate in endless water or desert areas.

In the past, different methods based on observation of the star system have been used in the navigation process. Astronavigation used especially in desert areas or at sea is a great example. In coastal areas, navigation was based on observations of the coastline and objects of known position on land, an example of which are lighthouses—the so-called terraced navigation [1].

An important breakthrough in this area occurred at the beginning of the last century when radio technology was used to determine the current location of objects. In this way, a new field of knowledge and technology was created, called radionavigation [2]. Generally speaking, the location of objects started to be determined with the use of the so-called radioneters cooperating with radio beacons, an example of which is the Consol system [3]. The next step in the development of radionavigation was to develop hyperbolic systems. Examples of such systems used in practice include the GEE system [2], OMEGA system [4], DECCA system [5] and the currently switched off LORAN system [6,7,8,9].

However, in the second half of the last century, with satellite technology, the era of radiolocation of objects based on radio signals transmitted from satellites and then received in the user’s terminal began. This represented a major breakthrough in radionavigation, allowing universal access to the radiolocation service. Currently, the most widespread satellite radionavigation system is the American GPS (Global Positioning System) [10,11]. The second most popular is the Russian GLONASS (GLobalnaya NAvigationalnaya Sputnikovaya Sistema) [12]. Besides, the following satellite navigation systems operate to a limited extent in practice in other countries: the Chinese COMPASS or, under another name, BeiDou-2 [13], European GALILEO [14] and Indian IRNSS [15].

The operation of the satellite navigation systems listed above is based on a hyperbolic way of determining the position of an object. As it is known, the basic structure of such a system is formed by a set (the so-called chain) of four stations, one main and three subordinates, which have to work together in synchronous mode. However, the requirement of synchronous cooperation of these stations is a weak point in the operation of such a system. This is due to the fact that in case of damage or intentional destruction of the main station, access to the location service disappears in the area covered by this chain. Moreover, the weakness of all satellite systems is their high susceptibility to interference, especially intentional spoofing or electromagnetic curtains.

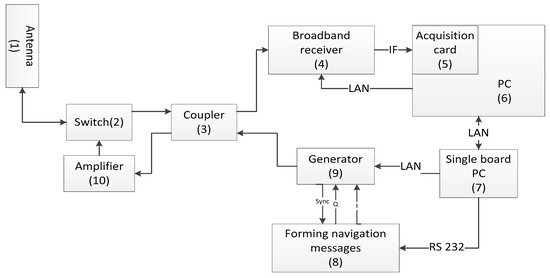
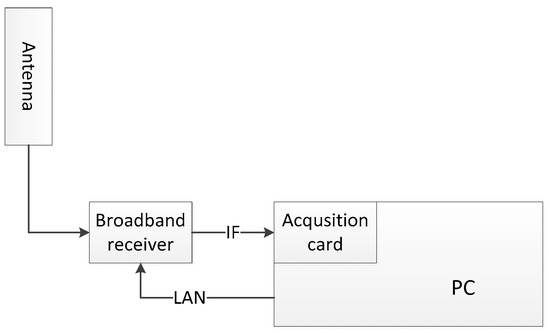
With the above in mind, at the faculty of Radiocommunication Systems and Networks of the Gdańsk University of Technology, on the initiative of the Polish Navy, research was undertaken to develop an asynchronous and self-organizing hyperbolic system for ground navigation as an alternative to the GPS satellite navigation system. Based on the results of these studies, a technological demonstrator of this new system was designed and built, the operation of which was tested in the measurement tests at sea [16].

In this article, the introduction refers to the basics of operation of the classical synchronous hyperbolic system, operating on the basis of the TDOA (Time Difference of Arrival) method. Next, selected algorithms for determining the position of an object in such a system are characterized in terms of their utility. In turn, the concept of asynchronous hyperbolic system operation and the algorithm of object positioning using such a system are presented in Section 3. Its protocol-system layer is also described. On this basis, a simulator for theoretical research was developed. Its assumptions are presented in Section 4, together with the results and conclusions from this research. On the basis of these conclusions, a demonstrator of asynchronous localization technology was designed and built for measurement tests, whose hardware and software layers are presented in Section 5, while Section 6 describes the results of tests of this demonstrator’s operation in real-life conditions at sea.

Finally, practical usefulness of the hyperbolic asynchronous system as an alternative navigation solution to GPS service has been summarized.

2. Basic of the Hyperbolic Technique

2.1. TDOA Method

As it is known, the operation of a hyperbolic radio navigation system, operating in synchronous mode based on the TDOA method, consists of determining the differences in the time $\Delta t$ of impulse signals coming to the user terminal from individual reference stations. The equivalent of these time differences may be the phase differences $\Delta \phi$ of these signals at the antenna of this terminal. They are the starting point for determining the hyperbolic lines, at the intersection of which the terminal is located. This means that in practice the position of the user terminal is determined by measuring the phase differences $\Delta \phi$ of the signals received in the user terminal from the main station and three sub-stations forming the structure of the same chain. By converting the differences $\Delta \phi$ into differences in the distance $\Delta d$ of the localized terminal from individual reference stations, individual hyperboles can be determined as sets of fixed points of difference of these distances, at the intersection of which the user terminal is located.

An example of creating such a hyperbolic in two-dimensional form for ground navigation applications is illustrated below in Figure 1 for a single set of two reference stations, i.e., main station G $\left(x_G,y_G\right)$ and subordinate station P $\left(x_P,y_P\right)$, where $\left(x_G,y_G\right)$ and $\left(x_P,y_P\right)$ are the known coordinates of their positions and are described in a two-dimensional rectangular coordinate system at this stage of consideration.

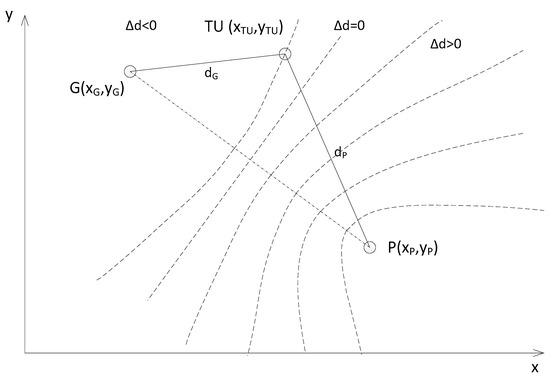
Figure 1. A method of determining hyperbolic positional lines for one pair of reference stations.

Using the markings from Figure 1, it is possible to describe the constant difference in distance $\Delta d\left(\Delta \phi \right)$, which is the basis for determining individual positional hyperbolts, as follows:

$$\Delta d\left(\Delta \phi \right)=d_G-d_P=c·\Delta t=\sqrt{{\left(x_G-x_{UT}\right)}^2+{\left(y_G-y_{UT}\right)}^2}-\sqrt{{\left(x_P-x_{UT}\right)}^2+{\left(y_P-y_{UT}\right)}^2}.$$

(1)

where

−

$d_G$ distance of the localized terminal from the main reference station,

−

$d_P$ distance of this terminal from a subordinate reference station,

−

$\left(x_{UT},y_{UT}\right)$ desired coordinates of the location of the user terminal (UT) to be located.

In practice, the TDOA method is based on the determination of three differences in the distance of the user terminal from the main reference station and from three individual subordinate reference stations. The differences $\Delta d_1\left(\Delta {\phi }_1\right)$, $\Delta d_2\left(\Delta {\phi }_2\right)$ and $\Delta d_3\left(\Delta {\phi }_3\right)$ can be written down in general terms as $\Delta d_i\left(\Delta {\phi }_i\right)$ for $i\in ⟨1,2,3⟩$. Then, based on (1), the above distance differences can be described by the following dependencies:

$$\begin{array}{ll}\hfill \Delta d_i\left(\Delta {\phi }_i\right)=d_G-d_{Pi}& =c·\Delta t_i=\\ & =\sqrt{{\left(x_G-x_{UT}\right)}^2+{\left(y_G-y_{UT}\right)}^2}-\sqrt{{\left(x_{Pi}-x_{UT}\right)}^2+{\left(y_{Pi}-y_{UT}\right)}^2} for i\in ⟨1,2,3⟩\end{array}$$

(2)

The scenario of locating a user terminal using a set of three positional hyperbolts from three pairs of reference stations, at the intersection of which the hyperbol is located, is illustrated in Figure 2.

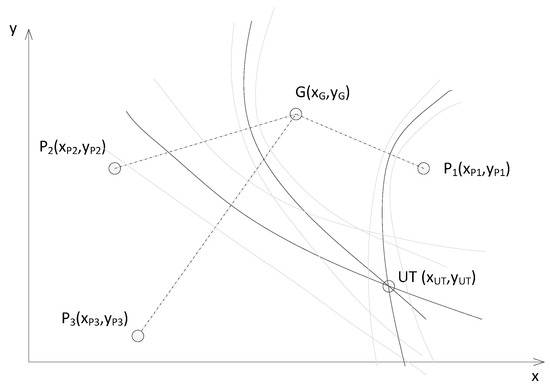
Figure 2. Determining the position of the user terminal (UT) using three pairs of reference stations.

In Figure 3, the time relationships of synchronized impulse signals transmitted from individual reference stations and their exemplary time shift $\Delta t_1$, $\Delta t_2$ and $\Delta t_3$ are shown at the location of the localized terminal.

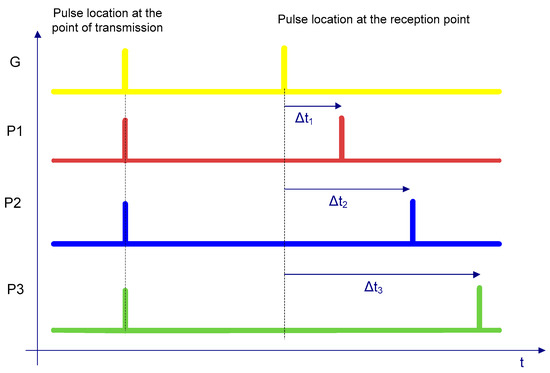
Figure 3. Example of time distribution of pulses transmitted by reference stations in a synchronous hyperbolic system.

The arrangement of non-linear Equation (2) can be solved by their linearization, i.e., it will support their development in the Taylor series [17], and then the use of the iterative approach. Another way may be to transform these equations into the form written as follows [18]:

$$d_{Pi}^2={\left(\Delta d_i+d_G\right)}^2 for i\in ⟨1,2,3⟩$$

(3)

In this case, Equation (3) can be converted to the form described below:

$$\Delta d_i^2+2\Delta d_i·d_G=x_{Pi}^2+y_{Pi}^2-2\left(x_{Pi}-x_G\right)x_{UT}-2\left(y_{Pi}-y_G\right)y_{UT}-x_G^2-y_G^2 for i\in ⟨1,2,3⟩$$

(4)

As you can see, Equation (4) is linear in relation to the values $\left(x_{UT},y_{UT}\right)$. However, their solution requires knowledge of the distance value. This can be omitted by using an appropriate positioning algorithm, as described below.

2.2. Selected Localization Algorithms for Hyperbolic Solution

On the basis of the literature studies and previous professional practice, and taking into account the adopted system features of the asynchronous navigation system being developed, for the purpose of solving Equation (4), the usefulness of the following locating algorithms was compared:

-

Chan algorithm [19],

-

Foy’s algorithm [20],

-

Fang algorithm [21],

whose names result from the names of the authors of these algorithms.

However, due to the limitation of the Fang algorithm, which can only be used for a maximum of three reference stations, the performance of the above algorithms has been tested for such a case. However, this does not limit the conclusions of such an analysis, which also apply to a larger number of reference stations.

The first one, the Chan algorithm, is one of the non-iterational methods of high utility importance, which provides satisfactory results regardless of the distance from the localized terminal to the reference stations. The basis for the operation of this algorithm is the following matrix, dependent on the user terminal coordinates $\left(x_{UT},y_{UT}\right)$ [19]:

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\end{array}\right]=-{\left[\begin{array}{l}\left(x_G-x_{P1}\right)\left(y_G-y_{P1}\right)\\ \left(x_G-x_{P2}\right)\left(y_G-y_{P2}\right)\end{array}\right]}^{-1}\cdot \left\{\left[\begin{array}{l}\Delta d_1\\ \Delta d_2\end{array}\right]\cdot d_G+\frac{1}{2}\cdot \left[\begin{array}{l}\Delta d_1^2+K_{P1}-K_G\\ \Delta d_2^2+K_{P2}-K_G\end{array}\right]\right\}.$$

(5a)

where

$$\begin{array}{l}{K}_G=x_G^2+y_G^2,\\ K_{P1}=x_{P1}^2+y_{P1}^2,\\ K_{P2}=x_{P2}^2+y_{P2}^2.\end{array}$$

(5b)

Equation (5a) can be written in a simpler form:

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\end{array}\right]=-\left[W\right]\cdot d_G-\left[Z\right],$$

(6a)

in which under (5a):

$$\left[W\right]=\left[\begin{array}{l}{w}_1\\ w_2\end{array}\right]=-{\left[\begin{array}{l}\left(x_G-x_{P1}\right)\left(y_G-y_{P1}\right)\\ \left(x_G-x_{P2}\right)\left(y_G-y_{P2}\right)\end{array}\right]}^{-1}\cdot \left[\begin{array}{l}\Delta d_1\\ \Delta d_2\end{array}\right],$$

(6b)

and

$$\left[Z\right]=\left[\begin{array}{l}{z}_1\\ z_2\end{array}\right]=\frac{1}{2}{\left[\begin{array}{l}\left(x_G-x_{P1}\right)\left(y_G-y_{P1}\right)\\ \left(x_G-x_{P2}\right)\left(y_G-y_{P2}\right)\end{array}\right]}^{-1}\cdot \left[\begin{array}{l}\Delta d_1^2+K_{P1}-K_G\\ \Delta d_2^2+K_{P2}-K_G\end{array}\right].$$

(6c)

As a result, a simple square equation of form must be solved to calculate the distance:

$$a{d}_G^2+b{d}_G+c=0,$$

(7a)

whereby

$$\begin{array}{l}a=w_1^2+w_2^2-1,\\ b=-2\cdot \left(w_1\cdot x_G+w_2\cdot y_G+w_1\cdot z_1+w_2\cdot z_2\right),\\ c=x_G^2+y_G^2+2\cdot x_G\cdot z_1+2\cdot y_G\cdot z_2+z_1^2+z_2^2.\end{array}$$

(7b)

As known, Equation (7a) has two solutions, the solution being defined by a relationship:

$$d_{G1}=\frac{-b-\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a},$$

(7c)

should be used when the localized terminal is located inside the area covered by reference station locations. The solution is determined by a relationship:

$$d_{G1}=\frac{-b+\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a},$$

(7d)

and should be applied outside the area defined above. The distance calculated in this way $d_G$ should be inserted into relation (5a) and then used to calculate the desired coordinates $\left(x_{UT},y_{UT}\right)$ of the localized user terminal (UT) [19].

The Foy algorithm is based on the linearization of the system of equations expressed by dependency (2), which—as already written above—should be developed in the Taylor series and then applied in an iterative approach. The result is an approximate solution, whose accuracy results from the number of iterative steps adopted. In the first step, rough initial values of the location of the localized terminal (UT) are defined by $\left(x_{UT},y_{UT}\right)$. Then, in each subsequent iterative step, a so-called correction vector is determined $\left[\Delta x_{UTi},\Delta y_{UTi}\right]$, which is added to the estimate of the position determined in the previous step, which can be recorded as follows [20]:

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\end{array}\right]=\left[\begin{array}{l}{x}_{UT}^{’}\\ y_{UT}^{’}\end{array}\right]+\left[\begin{array}{l}\Delta x_{UTi}\\ \Delta y_{UTi}\end{array}\right]+....,for i\in <1,2,\dots i_{\max }.$$

(8)

The correction vector $\left[\Delta x_{UTi},\Delta y_{UTi}\right]$ should be determined using the following formula:

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\end{array}\right]={\left({[\Delta ]}^T\cdot [\Delta ]\right)}^{-1}\cdot {[\Delta ]}^T\cdot \left[\epsilon \right],$$

(9a)

whereby

$$[\Delta ]=\left[\begin{array}{l}\left(\frac{\Delta x_G}{d_G}-\frac{\Delta x_{P1}}{d_{P1}}\right)\left(\frac{\Delta y_G}{d_G}-\frac{\Delta y_{P1}}{d_{P1}}\right)\\ \left(\frac{\Delta x_G}{d_G}-\frac{\Delta x_{P2}}{d_{P2}}\right)\left(\frac{\Delta y_G}{d_G}-\frac{\Delta y_{P2}}{d_{P2}}\right)\end{array}\right],$$

(9b)

and

$$\left[\epsilon \right]=\left[\begin{array}{l}{\epsilon }_1\\ {\epsilon }_2\end{array}\right]=\left[\begin{array}{l}\Delta d_{1(P)}-\Delta d_{1(e)}\\ \Delta d_{2(P)}-\Delta d_{2(e)}\end{array}\right],$$

(9c)

whereby

$$\begin{array}{l}\Delta x_G=x_G-x_{UT},\\ \Delta x_{P1}=x_{P1}-x_{UT},\\ \Delta x_{P2}=x_{P2}-x_{UT},\end{array}$$

(9d)

and

$$\begin{array}{l}\Delta y_G=y_G-y_{UT},\\ \Delta y_{P1}=y_{P1}-y_{UT},\\ \Delta y_{P2}=y_{P2}-y_{UT},\end{array}$$

(9e)

However, $\Delta d_{i(P)}$ and $\Delta d_{i(e)}$ mean values are determined on the basis of respectively measured differences $\Delta \phi \left(\Delta t\right)$ and estimated in subsequent iteration steps, in which the error vector $\left[\epsilon \right]$ is sought to minimize, which can be expressed as follows:

$${\epsilon }_1=\Delta d_{1(P)}-\Delta d_{1(e)}\Rightarrow 0\cap {\epsilon }_2=\Delta d_{2(P)}-\Delta d_{2(e)}\Rightarrow 0.$$

(9f)

As usual, the accuracy of the solution depends on the number of iteration steps. In the present case, practice shows that satisfactory accuracy is obtained after only five iteration steps [20].

The last of the listed algorithms, Fang’s algorithm, is based on a non-iterative approach. However, its significant limitation is the rigid geometry of the spacing of reference stations, which should be placed at strictly defined points of the local rectangular system, which are expressed by the following relationships [21]:

$$\begin{array}{l}{x}_G\cap y_G=0,\\ x_{P1}\ne 0\cap y_{P1}=0,\\ x_{P2}\ne 0\cap y_{P2}\ne 0.\end{array}$$

(10)

With assumptions (10), it can be shown that a simple linear relationship of a known form is correct [21]:

$$y_{UT}=a\cdot x_{UT}+b,$$

(11a)

in which

$$a=\frac{\left(\frac{\Delta d_{P2}}{\Delta d_{P1}}\cdot x_{P1}-x_{P2}\right)}{y_{P2}},$$

(11b)

and

$$b=\frac{x_{P2}^2+y_{P2}^2-\Delta d_{P1}\cdot \Delta d_{P2}\cdot \left(1-{\left(\frac{x_{P1}}{\Delta d_{P1}}\right)}^2\right)}{2y_{P2}}.$$

(11c)

However, before this, a square equation of the following form should be solved, in which one of the coordinates in Equation (11a) is unknown—e.g., $x_{UT}$:

$$a_x\cdot x_{UT}^2+b_x\cdot x_{UT}+c_x=0,$$

(11d)

in which

$$a_x=-\left(1-{\left(\frac{x_{P1}}{\Delta d_{P1}}\right)}^2+g^2\right),$$

(11e)

$$b_x=x_{P1}\left(1-{\left(\frac{x_{P1}}{\Delta d_{P1}}\right)}^2-2\cdot g\cdot h\right),$$

(11f)

$$c_x=\left(\frac{\Delta d_{P1}^2}{4}\right)\cdot \left(1-{\left(\frac{x_{P1}}{\Delta d_{P1}}\right)}^2-h^2\right),$$

(11g)

whereby

$$g=\frac{\Delta d_{P2}\cdot \left(\frac{x_{P1}}{\Delta d_{P1}}-x_{P2}\right)}{y_{P2}},$$

(11h)

while

$$h=\frac{x_{P2}^2+y_{P2}^2-\Delta d_{P2}^2+\Delta d_{P2}\cdot \Delta d_{P1}\cdot \left(1-{\left(\frac{x_{P1}}{\Delta d_{P1}}\right)}^2\right)}{2y_{P2}}.$$

(11i)

Solving Equation (11d), two solutions are obtained, in this case the coordinates $x_{UT}$ to which the comment expressed in the description of the solution of Equation (7a) refers. Then, by substituting the calculated value of one of the search coordinates appearing in relation (11a), the other is simply calculated. The result is the location of the localized terminal.

The algorithms described above are characterized by different usability, as described below:

• The Chan algorithm can be applied to any number of reference stations. Therefore, from the point of view of the asynchronous system that is being developed, it is the most useful method in practice.
• The Foy algorithm can also be applied to any number of reference stations. However, it is an iterative method, which entails specific requirements, especially for the time necessary to obtain a solution with the required accuracy. If an unfavorable starting point is adopted, there may be difficulties in achieving convergence of the solution. In addition, it must also be taken into account that the navigation system under development will operate in real time rigor.
• The Fang algorithm, on the other hand, is a simplified version of the Chan algorithm which can be used in a clearly limited range of only three reference stations.

3. An Idea of the Asynchronous Radio Localization

The method of determining the position in a hyperbolic navigation system as described in Section 2.1 requires the synchronous operation of reference stations, which is a significant limitation in terms of its use, as stated in the introduction. The method of determining the position of the user’s localized terminal in the hyperbolic system, developed at the Gdansk University of Technology, without the need to ensure synchronization of reference stations, is presented below. In this solution, the necessary synchronization of these stations is ensured by appropriate real-time recalculation of the data supplied to the user terminal from all reference stations within the operating range of the terminal [22].

3.1. Asynchronous Algorithm

The operation of this algorithm is illustrated by the example of three equivalent reference stations with known positions $S_1\left(x_{S1},y_{S1}\right)$, $S_2\left(x_{S2},y_{S2}\right)$ and $S_3\left(x_{S3},y_{S3}\right)$ where $\left(x_{S1},y_{S1}\right)$, $\left(x_{S2},y_{S2}\right)$ and $\left(x_{S3},y_{S3}\right)$ express the position of these stations in a two-dimensional rectangular coordinate system. The exemplary arrangement of these stations together with the user localized terminal (UT) is illustrated in Figure 4.

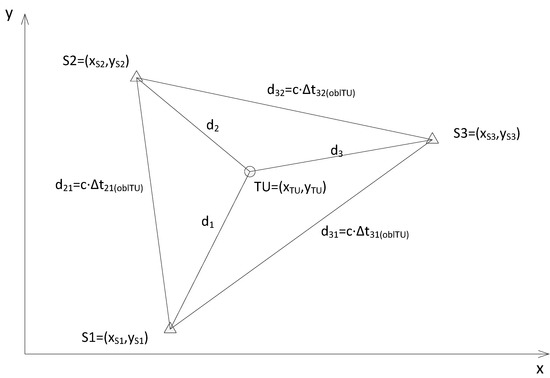
Figure 4. Example of the arrangement of reference stations with a user terminal (UT) in an asynchronous location system.

Each reference station is equipped with a transmitter-receiver radio system with an antenna with omnidirectional characteristics. This makes it possible to send signals to the other reference stations and to the local terminal, also equipped with an omnidirectional antenna. This also allows the terminal to receive signals transmitted by these stations. In addition, each reference station is equipped with a system for measuring the time difference between its reference time and that of receiving signals from other reference stations. These signals contain information about the measured time differences, which allows you to determine the degree of synchronization between the reference stations. In addition, the information received at the reference stations is updated and sent out to all stations, including the localized terminal. This issue is described in the next section, in the protocol description of the proposed solution.

In Figure 5, there is a sample time description of signals sent from all three reference stations, signals received at the station and signals received at the local user terminal (UT), together with measured time differences. These signals are presented in the form of impulses located on the time axis in places where the maximum autocorrelation function of pilot sequences located in the signals sent and received is present. This allows for an accepted way of accessing the electromagnetic spectrum in the form of DS-CDMA (Direct Sequence Code Division Multiple Access [22]).

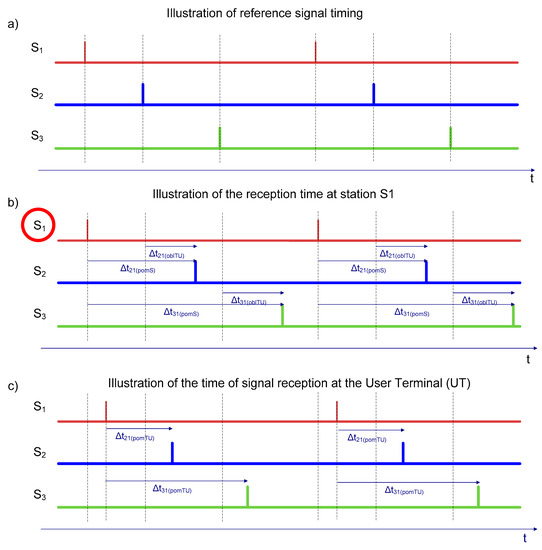
Figure 5. Example of the time status of signals sent by individual reference stations, received by the station $S_1$ and in the user terminal, together with measured time differences.

As shown in Figure 5a, reference stations operate in asynchronous mode. In this case, it is impossible to directly measure the time difference between the stations $S_1$ and $S_2$ ($\Delta t_{21}$) and between the stations $S_1$ and $S_3$ ($\Delta t_{31}$). It must be calculated based on the data provided, measured and calculated in the localized terminal (UT). Then the position can be calculated $\left(x_{UT},y_{UT}\right)$ using the following matrix equation based on the Chan algorithm [19], formulated for the sample set of reference stations—see relation (5a):

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\\ d_1\end{array}\right]=\left\{{[\Delta ]}^T\cdot {\left[Q\right]}^{-1}{[\Delta ]}^{-1}\right\}\cdot {[\Delta ]}^T\cdot {\left[Q\right]}^{-1}\cdot \left[{\Delta }_{prim}\right],$$

(12)

where

$$[\Delta ]=-\left[\begin{array}{l}\Delta x_{21}\Delta y_{21}\left(c\cdot \Delta t_{21}\right)\\ \Delta x_{31}\Delta y_{31}\left(c\cdot \Delta t_{31}\right)\end{array}\right],$$

(13a)

$$\left[Q\right]=\left[\begin{array}{l}1\frac{1}{2}\\ \frac{1}{2}1\end{array}\right],$$

(13b)

$$\left[{\Delta }_{prim}\right]=\frac{1}{2}\left[\begin{array}{l}{\left(c\cdot \Delta t_{21}\right)}^2-\left(x_{S2}^2+y_{S2}^2\right)+\left(x_{S1}^2+y_{S1}^2\right)\\ {\left(c\cdot \Delta t_{31}\right)}^2-\left(x_{S3}^2+y_{S3}^2\right)+\left(x_{S1}^2+y_{S1}^2\right)\end{array}\right],$$

(13c)

and

$$\begin{array}{l}\Delta x_{21}=x_{S2}-x_{S1},\\ \Delta y_{21}=y_{S2}-y_{S1},\\ \Delta x_{31}=x_{S3}-x_{S1},\\ \Delta y_{31}=y_{S3}-y_{S1},\end{array}$$

(13d)

The asynchronism ($\Delta t_{21}$, $\Delta t_{31}$) is calculated in the localized UT terminal in the following way—see Figure 5:

$$\begin{array}{l}\Delta t_{21}=\Delta t_{21(pomS1)}-\Delta t_{21(pomUT)}-\Delta t_{21(oblUT)},\\ \Delta t_{31}=\Delta t_{31(pomS1)}-\Delta t_{31(pomUT)}-\Delta t_{31(oblUT)},\end{array}$$

(14)

where

• $\Delta t_{21(pomS1)}$ and $\Delta t_{31(pomS1)}$ means the difference in time measured at the station $S_1$ between the reference time of that station and the reception times at that station from the station $S_2$ and from the station $S_3$, respectively,
• $\Delta t_{21(pomUT)}$ and $\Delta t_{31(pomUT)}$ means the difference in time measured in the localized UT terminal, between the time of reception in that terminal from the station $S_1$ and, respectively, from the station $S_2$ and from the station $S_3$,
• $\Delta t_{21(oblUT)}$ and $\Delta t_{31(oblUT)}$ means the propagation times of radio signals from station $S_1$ to stations $S_2$ and $S_3$, respectively, calculated in the localized UT terminal on the basis of the position coordinates of those stations, in this case based on $\left(x_{S1},y_{S1}\right)$, $\left(x_{S2},y_{S2}\right)$ and $\left(x_{S3},y_{S3}\right)$.

Then, in the localized UT using the Chan algorithm, Equation (12) is solved due to distance and Equation (5a) takes form:

$$\left[\begin{array}{l}{x}_{UT}\\ y_{UT}\end{array}\right]=-{\left[\begin{array}{l}\left(\Delta x_{21}\right)\left(\Delta y_{21}\right)\\ \left(\Delta x_{31}\right)\left(\Delta y_{31}\right)\end{array}\right]}^{-1}\cdot \left\{\left[\begin{array}{l}c\cdot \Delta t_{21}\\ c\cdot {\Delta }_{31}\end{array}\right]\cdot d_1+\frac{1}{2}\cdot \left[\begin{array}{l}{\left(c\cdot \Delta t_{21}\right)}^2+K_1-K_2\\ {\left(c\cdot \Delta t_{31}\right)}^2+K_1-K_3\end{array}\right]\right\},$$

(15a)

in which

$$\begin{array}{l}{K}_1=x_{S1}^2+y_{S1}^2,\\ K_2=x_{S2}^2+y_{S2}^2,\\ K_3=x_{S3}^2+y_{S3}^2.\end{array}$$

(15b)

3.2. Protocol Layer Description

The protocol layer of the asynchronous radionavigation system results from the way it works as described above. The key issue is the organization work and measurement activity of reference stations. These stations send out signals in a spreading way, containing so-called location messages, which contain two types of location data used to perform location calculations described by dependencies (12)–(15). The location data are divided into two groups. These are:

• Basic location data placed in the basic location telegram containing:

  ○

  identification number, longitude and latitude of the reference station,

  ○

  EIRP (dBm) of the signal radiated from the reference station antenna,

  ○

  position height (m a.s.l.) of the reference station antenna;

• Additional location data to be included in the additional location message, including:

  ○

  identification numbers of the reference stations from which radio signals containing measured time differences were received;

  ○

  current time differences between themselves and other reference stations, which is measured between the broadcasted signal by itself and signals received from neighboring stations.

As a reminder, the localized UT terminal receives all the signals with the messages from the reference stations within reach of where the terminal is located. This way of organizing the work of the reference stations and the UT location terminal makes the system work in self-organizing mode, provided that UT receives a signal from at least three reference stations.

In addition, all reference station transmitters are assumed to operate at the same power and carrier frequency, which facilitates the construction and operation of these stations’ receivers. However, it forces the cyclic (intermittent) character of these transmitters’ work. The random suspension (switching off) mode of the transmitters is based on Poisson’s layout, in which the duration of transmitting a navigation message consisting of the two abovementioned location messages was assumed as a random variable X, which can be expressed as follows:

$$p\left(X=k\right)=\frac{{\lambda }^k}{k!}\cdot e^{-\lambda },fork\in <0,1,\dots ),$$

(16)

where $\lambda$ indicates the average time of transmission of the navigational telegram. The generator of pseudo-random numbers with such a distribution was performed using the algorithm developed by Donald E. Knut [23]. As a result, the total time of switching off each of the transmitters was assumed to be 8 s. The time necessary to stabilize the operating conditions of the transmission track during the transmitter reclosure was taken into account. Moreover, on the basis of the performed tests, it was assumed that the average time of transmitting the navigation wire should be 30 s. With this in mind, using Poisson’s distributed timetable, the time of data acquisition in receivers of reference stations and the UT terminal was assumed to be 40 s.

3.3. Logical Layer Description

The following is a logical description of the transmission and reception paths used in reference stations, from the point of view of creating a signal with a navigation message as a data stream. It results from the proposed concept of the operation of a hyperbolic asynchronous system, based on access technology with direct DS-CDMA (Direct Sequence Code Division Multiple Access) [22].

From this point of view, the most important functionalities of the transmission track are:

• encryption, due to the purpose of this system,
• authentication,
• weave coding,
• packing, and
• a generation of distraction strings.

The resulting logical scheme of the transmission path is shown in Figure 6.

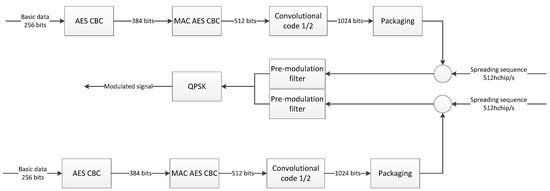
Figure 6. Logical diagram of the reference station’s transmission path.

The operation of the transmitting part starts with entering basic and additional data into independent encryption blocks working with the AES (Advanced Encryption Standard) algorithm in CBC (Cipher Block Chaining) mode with a key length of 256 bits. Then, after encryption, the data is fed to the MAC AES CBS (Message Authentication Code AES CBS) block, which is a shortcut function for further authentication and for checking during transmission that the data has not been disturbed (changed) during transmission or due to intentional external interference. Further, in order to correct errors that may also occur during transmission in the radio channel, convolutional coding (2,1,9) with an efficiency of half has been used. In the next block of the broadcasting part, the packaging process is carried out, which consists of separating the encrypted navigation data, using pilot strings, and adding the beginning and end of the created frame at the beginning and end sequence as start and end markers of the transmission. In the next step, data are spread with a spreading sequence and, after passing through a pre-modulation filter, are fed on a QPSK modulator.

The most important functionalities of the receiver are:

• decoded weave codes
• depacking
• decryption

In turn, the resulting logical scheme of the receiving track is shown in Figure 7.

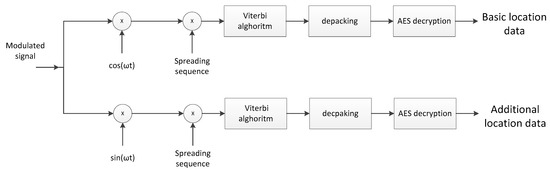
Figure 7. Logical diagram of the receiving path.

The receiver part is the opposite to a transmitter part. First, a modulated signal is divided into two branches. They are both put in a detecting unit (using Viterbi’s algorithm). Next, depacking takes place. The last step is the decryption of data (using AES).

4. Theoretical Investigations

The first stage of the verification study of the proposed method of asynchronous object localization is described, whose algorithm and protocol and system assumptions are presented above. At the beginning, the software simulator developed for these tests is characterized, along with the software environment with the user interface and the algorithm of its operation. Next, the adopted way of performing the tests is described, and the results obtained are discussed. In the final part, the conclusions are presented, on which the project of the technological demonstrator was based, in the form of a set of devices used to verify the experimental effectiveness of the proposed asynchronous object localization method.

4.1. Simulation Software for Theoretical Investigations

The algorithm of this simulator, based on the proposed method of object localization, was implemented in the Embarcadero XE Builder environment using proprietary software written in C++ language. Taking into account the subject of the research, a form of the main user interface window of this simulator was designed.

The absolute error ${\delta }_d\left[m\right]$ between the actual position of the user terminal (UT) is described by the coordinates $(x_{UT},y_{UT})$ and its position is determined by simulation calculations described by the coordinates $(x_{UT,cal},y_{UT,cal})$. This is expressed by the following well-known relationship:

$${\delta }_d=\sqrt{{\left(x_{UT}-x_{UT,cal}\right)}^2+{\left(y_{UT}-y_{UT,cal}\right)}^2}.$$

(17a)

In addition, for selected sets of results of simulation calculations, commonly used accuracy measures have also been used in the form:

the mean absolute error value $M{E}_{\delta }$:

$$M{E}_{\delta }=\frac{{\displaystyle \sum _{i=1}^N{\delta }_{di}}}{N-1},$$

(17b)

medium square error $MS{E}_{\delta }$:

$$MS{E}_{\delta }=\frac{{\displaystyle \sum _{i=1}^N{\delta }_{di}^2}}{N-1},$$

(17c)

root of a mean square error $RM{S}_{\delta }$:

$$RM{S}_{\delta }=\sqrt{MS{E}_{\delta }},$$

(17d)

where N is the number of crops tested.

The course of simulation calculations can be presented in an algorithmic form consisting of individual functional blocks, the general form of which is shown in Figure 8, while the part showing the calculation of the position of the localized terminal (UT) is shown in Figure 9.

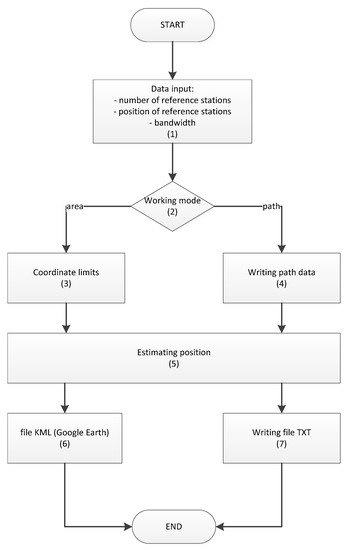
Figure 8. Algorithm of a computational simulator—general form.

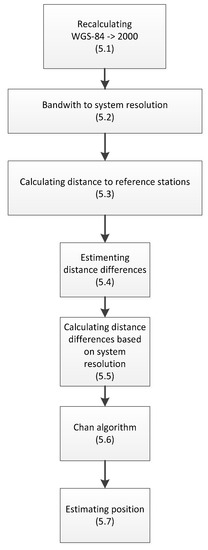
Figure 9. Algorithm of the simulator operation—UT position calculation.

The details of the functions of the individual blocks of this algorithm are as follows:

(1)

geographical coordinates of the position of the reference stations shall be entered in WGS-84 [24],

(2)

selection of one of the two modes of operation of the simulator is made by pressing one of the two buttons described in the graphical user interface as the set area and the set route,

(3)

when the setpoint mode is selected, the position of this area is determined by the entered coordinates of the extreme reference stations, i.e., the minimum and maximum values of their coordinates, which, together with the resolution, are used to determine the rectangular grid nodes which are the locations of the calculated positions of the localized terminal (UT). The resolution is calculated according to the following relation:

$$\Delta d_{min}\left[m\right]=\frac{v_{EM}\left[\frac{m}{s}\right]}{4B\left[Hz\right]}.$$

(18)

where B is the bandwidth of the operating band and $v_{EM}=c$ is the speed of radio wave propagation in a propagation environment.

(4)

If the mode is selected, the specified route will appear as a sub-window for loading a text file with the coordinates of successive user terminal (UT) locations $(x_{UT},y_{UT})$, which are the reference values calculated during simulation tests.

(5)

The calculation of location coordinates $(x_{UT,cal},y_{UT,cal})$ is carried out according to the description expressed in relation (12)–(15), which illustrates in more detail the form of the algorithm presented in Figure 9.

(6)

Then, in area mode, the calculated results are saved to files with the KML extension, in accordance with the Google Earth specification, for further analysis using map images.

(7)

In route mode, the calculated results are saved to a file with the txt extension for further analysis using a spreadsheet.

The algorithm of estimating position from part (5) is presented in Figure 9.

4.2. Analysis of Theoretical Investigation Results

Due to the planned comparative analyses, the scenarios of the planned computational tests have been adjusted to the possible measurement tests in practice. For organizational reasons it was assumed that the measurement tests would take place in the open water of the Gulf of Gdańsk. Therefore, the scenarios for computational research were based on this basis, assuming the use of three or four reference stations for cost reasons.

Bearing in mind what has been written above, the calculation of the effect of the frequency bandwidth of the asynchronous locating system and the position of the localized terminal (UT) on the efficiency of determining the position of that terminal was performed. The plan of these studies included:

• in the preset mode, the absolute error ${\delta }_d\left[m\right]$ distribution for different bandwidths of the B[MHz] system was investigated, which allowed for the assessment of the operational capabilities of this system,
• in the set route mode, the distribution of absolute error was examined, also for different bandwidths of the system, which in turn allowed for the assessment of its performance for specific trajectories,
• development of histograms of the absolute error of the tests was performed, and
• development of a stabularized comparison of the efficiency of the examined system was performed.

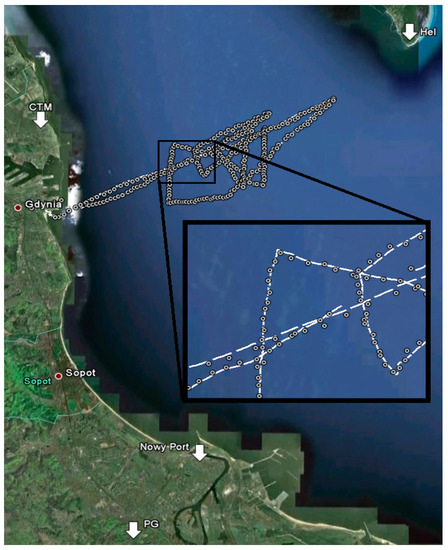
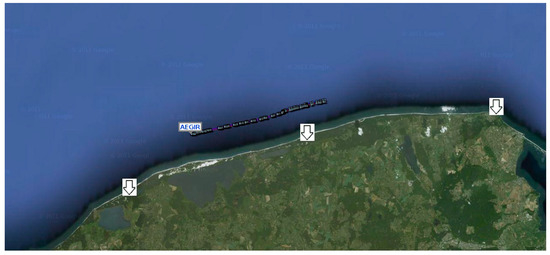
The simulation and measuring test area with the location of three reference stations is shown in Figure 10.

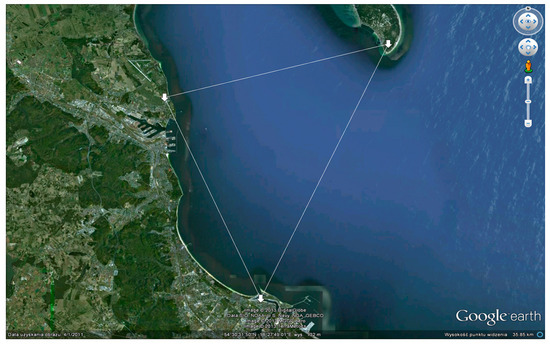
Figure 10. Illustration of a simulation and measuring test ground with marked locations of the three reference stations.

The results of absolute error ${\delta }_d\left[m\right]$. distribution tests carried out in the area mode for the location of reference stations shown in Figure 10 and for different B-bandwidths of the system are shown in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.

Figure 11. The absolute error ${\delta }_d\left[m\right]$ area distribution for 3 reference stations and for B = 1 MHz.

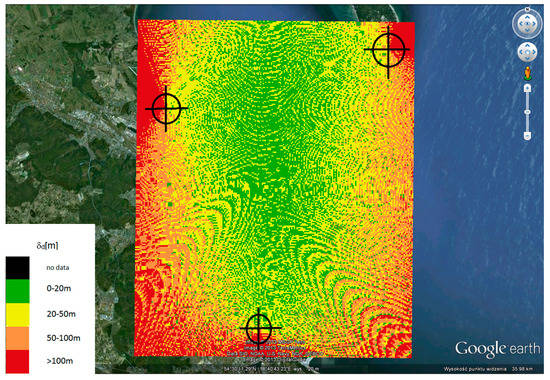
Figure 12. The absolute error ${\delta }_d\left[m\right]$ area distribution for 3 reference stations and for B = 2 MHz.

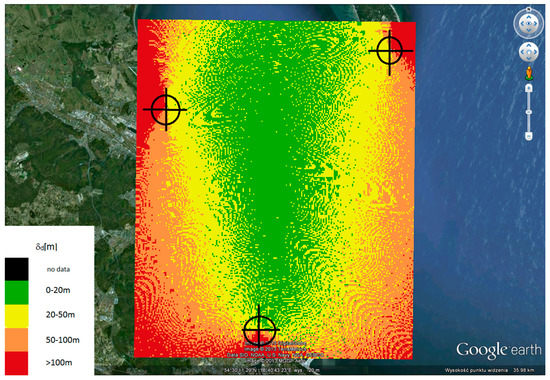
Figure 13. The absolute error area ${\delta }_d\left[m\right]$ distribution for 3 reference stations and for B = 4 MHz.

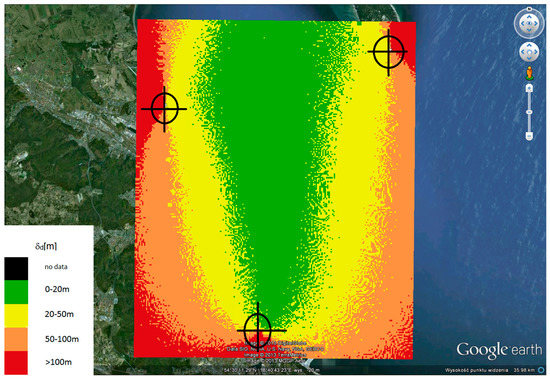
Figure 14. The absolute error ${\delta }_d\left[m\right]$ area distribution for 3 reference stations and for B = 8 MHz.

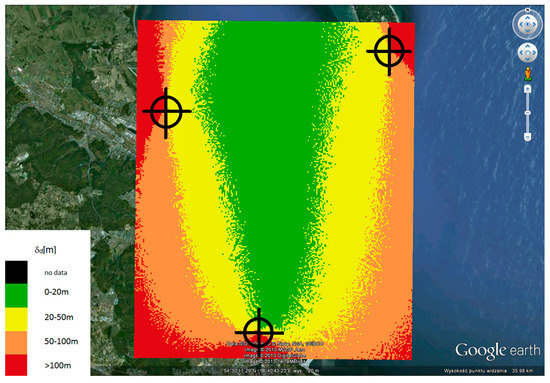
Figure 15. The absolute error ${\delta }_d\left[m\right]$ area distribution for 3 reference stations and for B = 10 MHz.

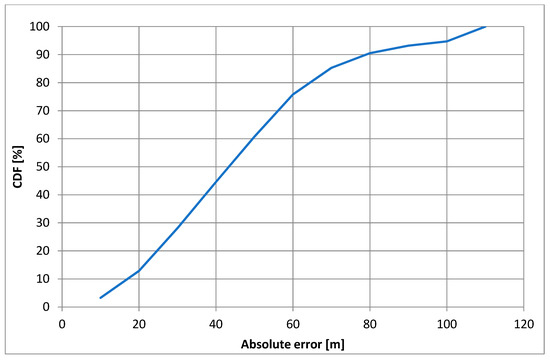
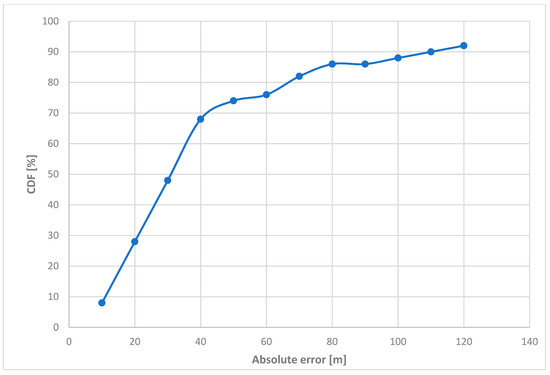
Analyzing the results presented in Figure 16, it can be concluded that the system provides access to a location service throughout the entire internal area covered by reference station locations, but with different accuracy depending on the location of the localized terminal. The absolute efficiency of the system, determined by error, is better the more central to the reference stations the location of the localized terminal is. This corresponds to the performance characteristics of synchronous navigation systems. However, an important conclusion that should be taken into account in further research is that an important factor affecting the accuracy of terminal localization (UT) in a system with a spread spectrum is the bandwidth of that system—the greater the bandwidth, the better the localization efficiency.

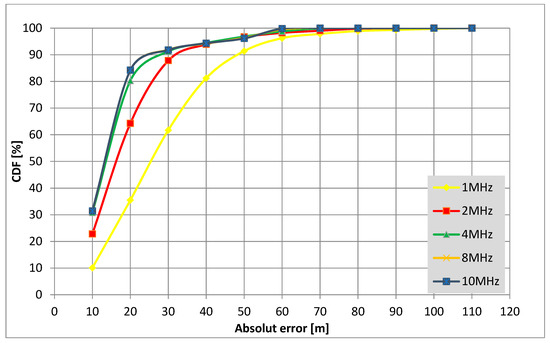
Figure 16. CDF (Cumulative Distribution Function) related to absolute error ${\delta }_d\left[m\right]$ for three reference stations and for different B-band widths.

In turn, the results of absolute error distribution tests carried out in the mode on a given route for three reference stations are shown in Figure 16 for different bandwidths of the system.

Analyzing the results of CDF (Cumulative Distribution Function) related to the absolute error distributions shown in Figure 16, it can be concluded that the accuracy of the performance of an asynchronous locating system working with the spread spectrum is better the larger its operating band. This corresponds to the previous conclusion.

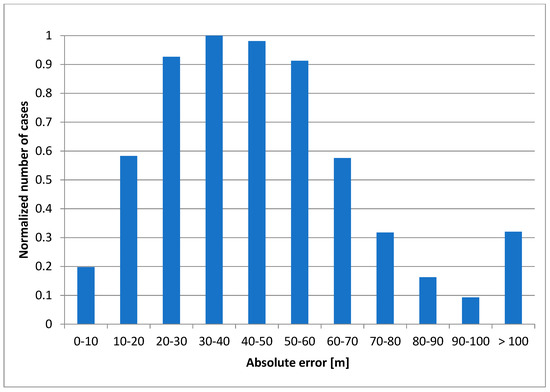
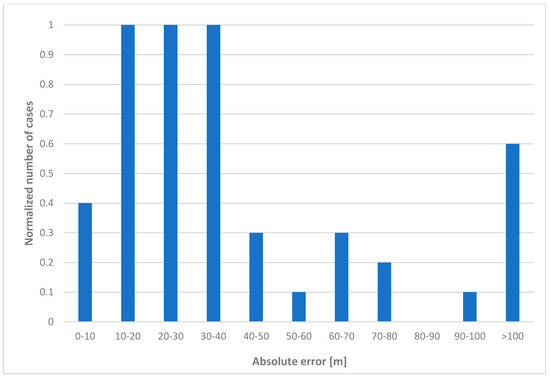
In the next step, absolute error histograms of the performed tests were developed. The resulting images are shown in the following Figure 17.

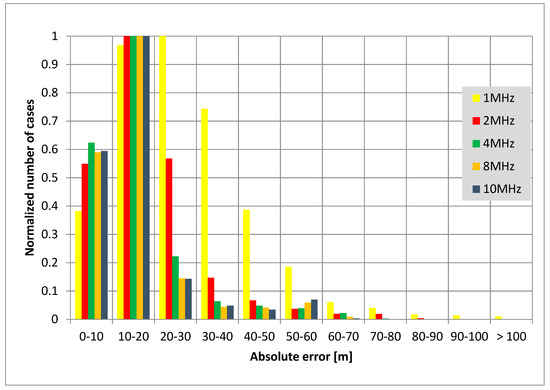
Figure 17. Absolute error ${\delta }_d\left[m\right]$ histogram for three reference stations and for different bandwidths.

The results of the studies presented in the histograms also confirm previous conclusions. This is especially true for the significant influence of the bandwidth on the quality of the tested asynchronous mode of the hyperbolic localization system.

Summarized here are the results of the theoretical research carried out. Table 1 summarizes the calculated error values $M{E}_{\delta }$, $MS{E}_{\delta }$ and $RM{S}_{\delta }$ for three reference stations and for different bandwidths.

Table 1. Comparison of errors $M{E}_{\delta }$ $MS{E}_{\delta }$ and $RM{S}_{\delta }$ for three reference stations and for different bandwidths.

	1 MHz	2 MHz	4 MHz	8 MHz	10 MHz
MEδ	27.86	18.78	15.75	15.14	15.09
MSEδ	1035.39	510.20	378.02	345.61	342.95
RMSδ	32.18	22.59	19.44	18.59	18.52

The comparison of errors in Table 1 also confirms the previous conclusions that the use of an increased number of reference stations in a locating system using the hyperbolic asynchronous method—for this purpose, using radio signals with the highest possible spread spectrum width—results in a clear improvement in the efficiency of such a system.

5. Measurement’s Verification of the Asynchronous Method of Radio Navigation

In this part of the article, the designed and built locating technology demonstrator, which is a tool for measuring tests, is described at the beginning. This demonstrator consists of four reference stations and a locator acting as a user terminal (UT). An important element of this set is its software layer, which is described very concisely. Next, the results of measurement tests performed according to the described scenarios of computational tests in the Gulf of Gdańsk and additionally in the coastal zone from the open seaside were described and analyzed.

5.1. Technological Localization Demonstrator for Measurement Verification

The two main components of the asynchronous locating technology demonstrator are described below, the construction and operation of the reference station and locating device (User Terminal). Both of these devices have been designed on the basis of the concept described in Section 3. The devices are built using ready-made components in the form of generators, receivers, amplifiers, computing units and data acquisition cards. The software layer covering signal processing as well as control and the control of the whole system is original [16].

Functional block diagrams of the reference station and the locator (User Terminal) are shown in Figure 18 and Figure 19, respectively.

Figure 18. Functional reference station block diagram.

Figure 19. Functional locator (User Terminal) block diagram.

As it can be seen in Figure 18, a reference station is a receiving and transmitting system equipped with an omnidirectional antenna (1). The radio signals containing location messages received by such an antenna, potentially from all directions, pass through the switch (transmit/receive) (2) and then through the coupler (3) to reach the broadband receiver (high frequency). (4) This takes place during a cyclic 8-s break forced by the switch (2), during which the transmission track, namely the power amplifier (10), is disconnected, as described in Section 3.2. In contrast, the received radio signal, still in the HF band, is amplified in the receiver (4) and then transferred (converted) to the IF band (intermediate frequency). This signal is then fed to the input of the data acquisition card (5) located in the computer (6), which controls the operation of the reference station (using LAN (Local Area Network) connection to a receiver (6)) and the implementation of time difference measurement procedures occurring in dependencies (14). Another function of the reference station is the creation of location messages, which takes place in the module (8) under the supervision of a single-board computer (7) which is connected with an RS-232 interface. These messages are placed in the radio signal, whose source is a generator (9) which is connected with (7) using LAN connection. This signal is fed to the power amplifier (10), where it is subject to the amplification necessary to ensure a certain range of operation of the reference station. When the transmission track is unlocked, the signal passes through switch (2) to the antenna (1), from which it is radiated to the propagation environment.

Taking into account the necessary high accuracy of time measurement, the reference stations of the described demonstrator used external frequency standards based on the rubidium standard by Stanford Research Systems, which ensured the generated frequency stability at the level 10⁻¹¹ [25]. For comparison, commonly used external frequency standards are characterized by a stability of 10⁻⁷.

The locator (User Terminal) shown in Figure 19 is a receiving system only, which receives signals transmitted by reference stations. These signals, after being received by the antenna and also omnidirectional, are fed to the broadband receiver where they are amplified and converted to the IF band. These signals from the receiver’s output go to the data acquisition card located in the control computer, where they are used to decode the location messages described in Section 3.2. On the basis of the information contained in these messages and the calculations performed in the control computer, the current position of the locator (User Terminal) is determined by the relationship (15).

Reference station and locator (User Terminal) software was written in C++ language using the Borland Builder application, but for visualization of the results, an application written in the Java environment was made.

The control computer software at the reference station carries out time difference measurement procedures and configures and controls the receiver and data acquisition card. This is functionally presented in the following brief manner by necessity:

• loading text-based configuration files,
• connecting to the receiver using the TCP/IP protocol and configuring the receiver in the carrier and intermediate frequency range and its operating band,
• verifying connection to the receiver,
• verifying if this is the first time the program starts and if so, the program starts the first single data acquisition,
• if this is the next work cycle of the program, it starts multithreaded work by starting the next data acquisition, and in parallel it starts performing data processing procedures from the previous acquisition,
• support of data card acquisition, i.e., their activation and configuration and then 40 s execution of the data acquisition procedure in the form of samples of the received signal,
• reading a data file from a previous acquisition, determining the size of this file and, on this basis, creating a dynamic array to write this data,
• parallel calculation of the degree of correlation between the received data (received signal sequence) and the bit strings of the pilot signal sequence characteristic of individual reference stations,
• recording of the abovementioned received data, i.e., sample numbers indicating the position of the first bit of the pilot string in location messages into a two-dimensional array, in which successive sequences of data received from individual reference stations are recorded in subsequent columns,
• visualization of the data received in the previous step to illustrate the current operating status of the station,
• determination (measurement) of time differences between signals received from other reference stations, the first component in relation (14),
• placing designated time differences in the location message,
• transmitting the location report to a single-board computer, where it is formatted and forwarded to a radio signal generator.

The software of the control computer in the locator (User Terminal) is functionally similar to that of the reference station and is presented as follows:

• loading text-based configuration files,
• connecting to the receiver using TCP/IP and configuring the receiver in the carrier and intermediate frequency range and its operating band,
• checking the connection to the receiver,
• checking if this is the first time the program starts and if so, the program starts the first single data acquisition,
• if this is the next work cycle of the program, it starts multithreaded work, i.e., it starts the next data acquisition and in parallel it starts performing data processing procedures from the previous acquisition,
• support of data card acquisition, their activation and configuration and then 40 s execution of the data acquisition procedure in the form of samples of the received signal at the output,
• reading a data file from a previous acquisition, determining the size of this file and, on this basis, creating a dynamic array to write this data,
• parallel calculation of the degree of correlation between the received data (received signal sequence) and the bit strings of the pilot signal sequence characteristic of individual reference stations,
• recording of the abovementioned received data, including sample numbers indicating the position of the first bit of the pilot string in location messages into a two-dimensional array, in which successive sequences of data received from individual reference stations are recorded in subsequent columns,
• visualization of the data received in the previous step to illustrate the current operating status of the locator (User Terminal),
• measurement of time differences between the received signals, the second component in relation (14),
• reading of location messages and decoding the data stored in them,
• entering the coordinates of the reference stations into the file station.txt,
• calculation of time differences based on coordinates stored in the file station.txt, the third component in dependencies (14),
• entering time differences into the patch_TDOA.txt file, the first component in dependencies (14),
• calculation of locator (User Terminal) position coordinates using dependency (15),
• reading and recording the locator’s (User Terminal) position coordinates as reference values, measured with a JAVAD GPS/GLONASS receiver [26] and ALPHA model [27], to perform calculations verifying the quality of operation of the tested asynchronous locating system.

5.2. Analysis of Measurement’s Investigation Results

The demonstrator of the technology of asynchronous object localization, which was used in the measurement tests, is characterized by the following system parameters, resulting from the obtained permissions to access the electromagnetic spectrum:

• the 431.5 MHz operating frequency,
• operating band width adjustable from 1 MHz to 4 MHz,
• the power of the signals transmitted 30 W.

A scenario of measurement tests carried out in the waters of the Gulf of Gdańsk is shown in Figure 20, where the measurement route of the floating laboratory and the location of the reference stations are marked, which is the same as in the case of the computational tests described on page 2. In this scenario, a bandwidth of 1 MHz was used.

Figure 20. Measurement scenario of tests carried out in the Gulf of Gdańsk.

A total of seven thousand measurement cases were collected. The results of these studies were used to verify computational (theoretical) tests. They are presented in the following way. Figure 21 presents graphs of absolute error ${\delta }_d\left[m\right]$ distribution for both configurations of reference stations. An absolute error (Equation (17a)) has been calculated as a difference between the position given by the asynchronous system and the position provided by an GNSS receiver which uses both GPS and GLONASS satellite systems to calculate its position [26,27]. On the other hand, Figure 22 presents a histogram of this error, also for both configurations of reference stations.

Figure 21. CDF related to absolute error ${\delta }_d\left[m\right]$ of results of measurements made in the Gulf of Gdańsk.

Figure 22. Histogram of the absolute error ${\delta }_d\left[m\right]$ of the results of measurements made in the Gulf of Gdańsk.

In addition, Table 2 lists errors $M{E}_{\delta }$, $MS{E}_{\delta }$ and $RM{S}_{\delta }$, calculated on the basis of obtained measurement results.

Table 2. Comparison of errors $M{E}_{\delta }$, $MS{E}_{\delta }$ and $RM{S}_{\delta }$ for three reference stations and 1 MHz bandwidth.

Bandwidth	MEδ [m]	MSEδ [m2]	RMSδ [m]
1 MHz	46.5	50671	225.3

As can be seen in these figures, the absolute error ${\delta }_d\left[m\right]$. value results from system limitations, especially from limited bandwidth of the tested system. The tone of the analysis of errors listed in Table 2 is slightly better. On the other hand, the measurement tests confirmed the possibility of asynchronous operation of the hyperbolic locating system.

As already written, such tests were also carried out for a significantly different configuration of reference stations located in the coastal zone on the open seaside for three reference stations. The configuration of these studies is illustrated in Figure 23, while Figure 24 shows the distribution of the absolute error ${\delta }_d\left[m\right]$. and Figure 25 shows the histogram of this error. In this scenario, a 4 MHz bandwidth was used.

Figure 23. Measurement scenario of tests performed on the coastal sea. Distance between two reference stations from the left is 32.5 km.

Figure 24. CDF related to absolute error ${\delta }_d\left[m\right]$ of the results of measurements made on the coastal sea.

Figure 25. Histogram of the absolute error ${\delta }_d\left[m\right]$ of the results of measurements made on the coastal sea.

In addition, Table 3 lists errors $M{E}_{\delta }$, $MS{E}_{\delta }$ and $RM{S}_{\delta }$, calculated on the basis of the obtained results of measurement tests carried out in the coastal sea area.

Table 3. Comparison of errors $M{E}_{\delta }$, $MS{E}_{\delta }$ and $RM{S}_{\delta }$ the results of measurement tests carried out in the coastal marine area for three reference stations and 4 MHz bandwidth.

MEδ [m]	MSEδ [m2]	RMSδ [m]
46.5	4132	64.3

6. Conclusions

The article presents the concept of an asynchronous method of determining position in a hyperbolic radionavigation system (radiolocation). It describes algorithmically the way of determining the position using an asynchronous approach. Its functional properties have been characterized on the basis of the results of simulation and measurement tests carried out in real operating conditions at sea. The results obtained in this way confirm the practical suitability of the proposed method and its functional properties for special purposes, e.g., defense, because Global Navigation Satellite Systems (GNSS) are seen by terrorists or hostile countries as a high value target. The Volpe Center report contains the following statement [28]: “During the course of its development for military use and more recent extension to many civilian uses, vulnerabilities of Global Navigation Satellite Systems (GNSS)—in the United States the Global Positioning System (GPS)—have become apparent. The vulnerabilities arise from natural, intentional, and unintentional sources. Increasing civilian and military reliance on GNSS brings with it a vital need to identify the critical vulnerabilities to civilian users, and to develop a plan to mitigate these vulnerabilities.”

The presented system is a contribution to the development of independent ground radiolocation systems. It is fully asynchronous. In case of damage or shutdown of one of the stations, the system is fully functional, the only condition is to receive signals from at least three ground stations. It has been developed to be very flexible. It allows the use of more than three ground stations. Placing them in areas of known positions allows for the creation of a grid which will provide readings of coordinates independent from satellite systems. Using more than three reference stations will also increase the precision of calculating the position. It works in both kinds of ground station configurations (triangle deployment and along the coastline as well).

In the course of designing and building the system, the adequacy of the system for water bodies was focused on. However, the versatility of the proposed solution suggests that the system would work on land as well.