Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading
Abstract
1. Introduction
2. Nonlinear Simulation Analysis of a Single-Keyed Dry Joint
2.1. Overview of the Simulation Example
2.2. Constitutive Relationship of Materials
2.2.1. Concrete Uniaxial Stress-Strain Relationship
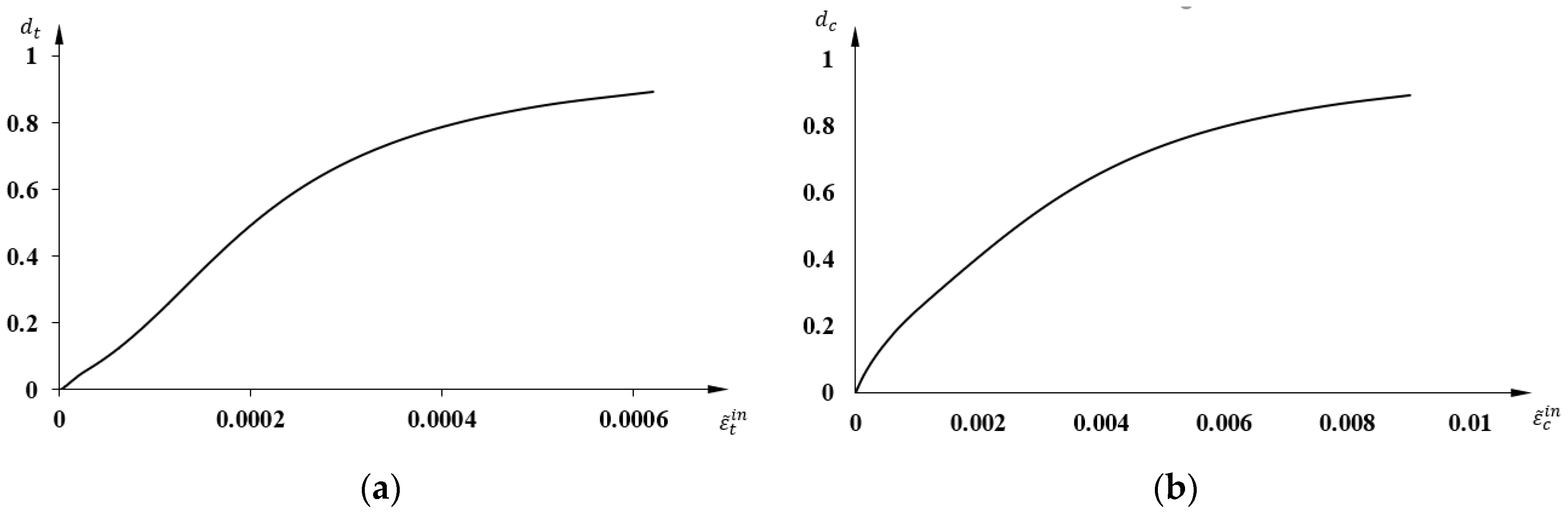
2.2.2. Plastic Damage Model of Concrete
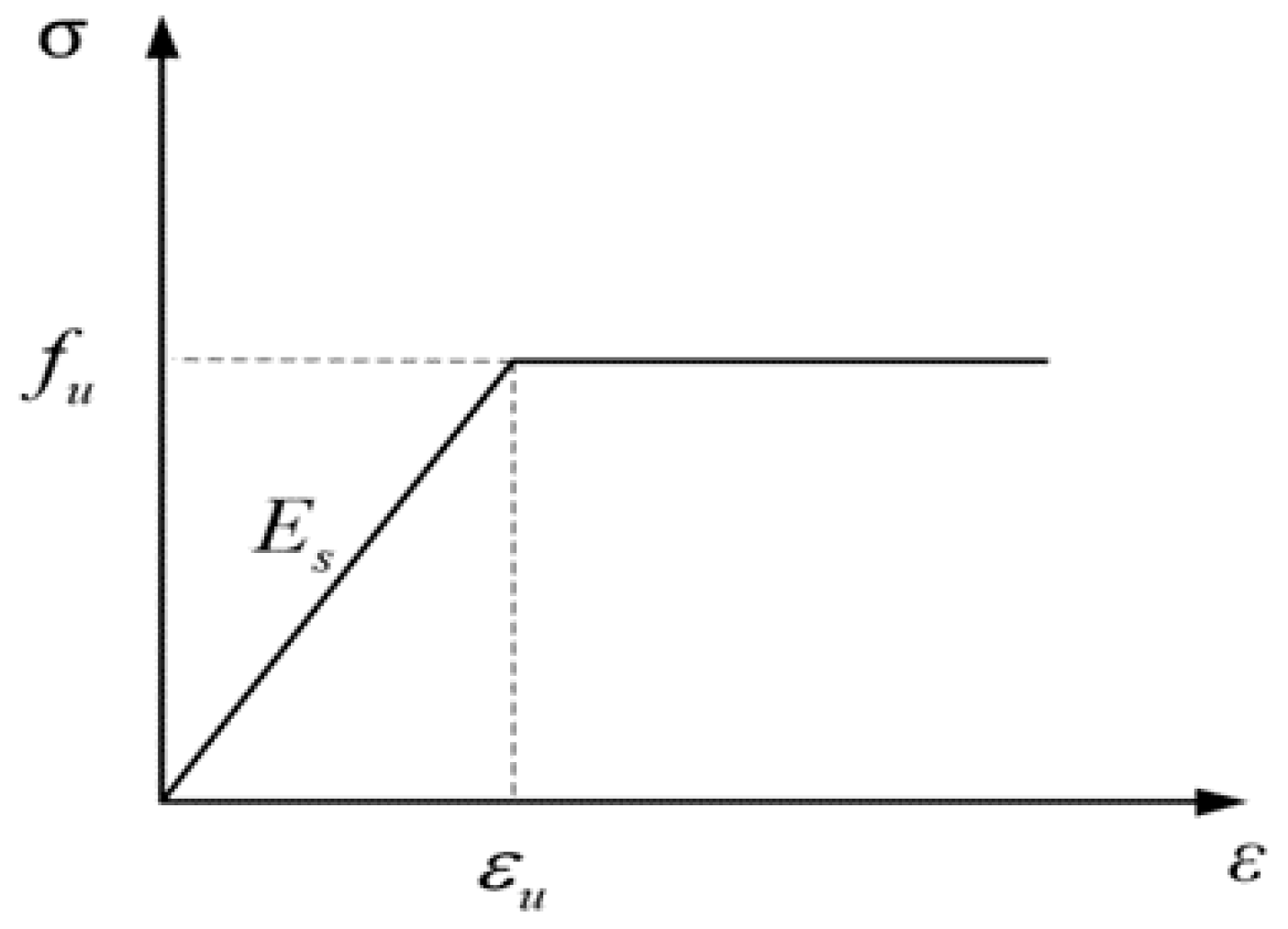
2.2.3. Stress-Strain Relationship of Rebar
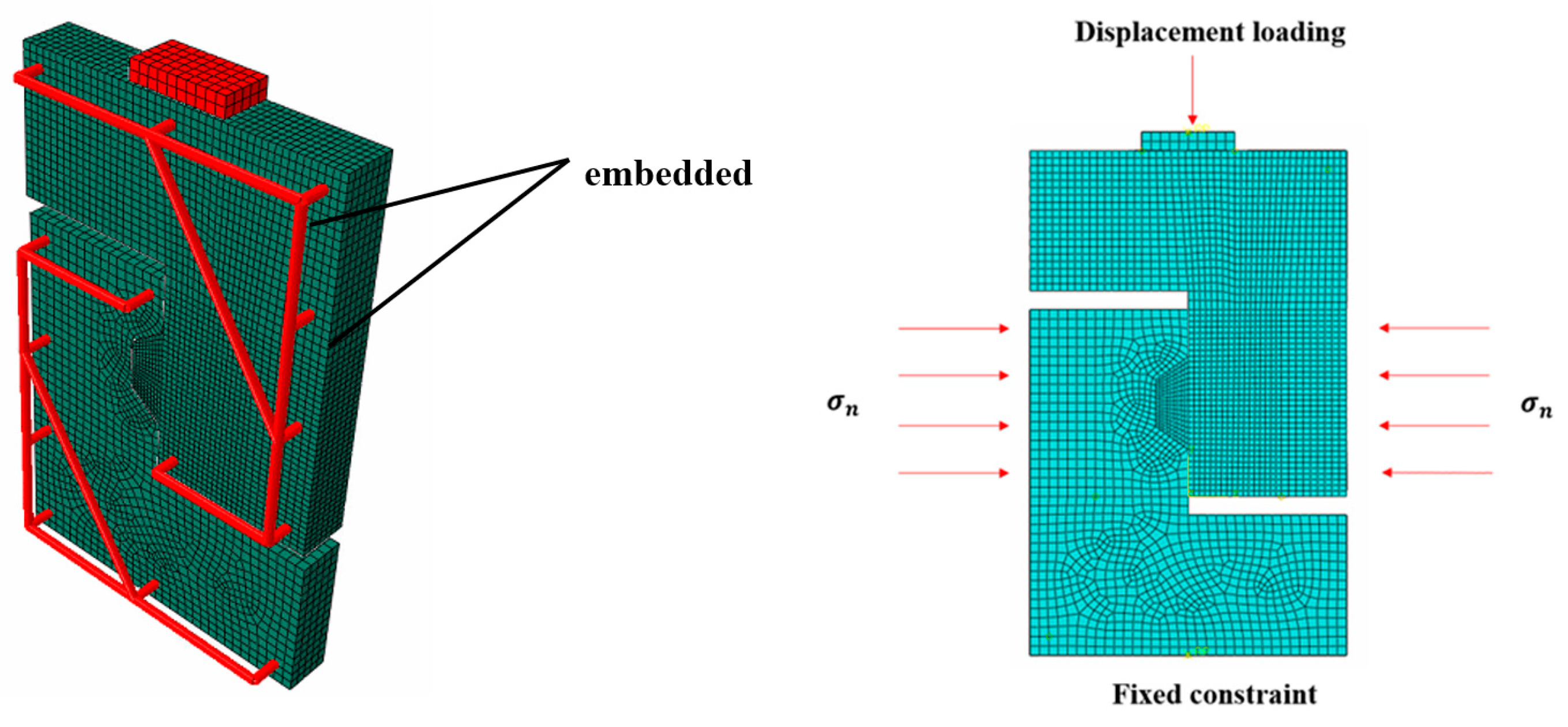
2.3. Finite Element Model
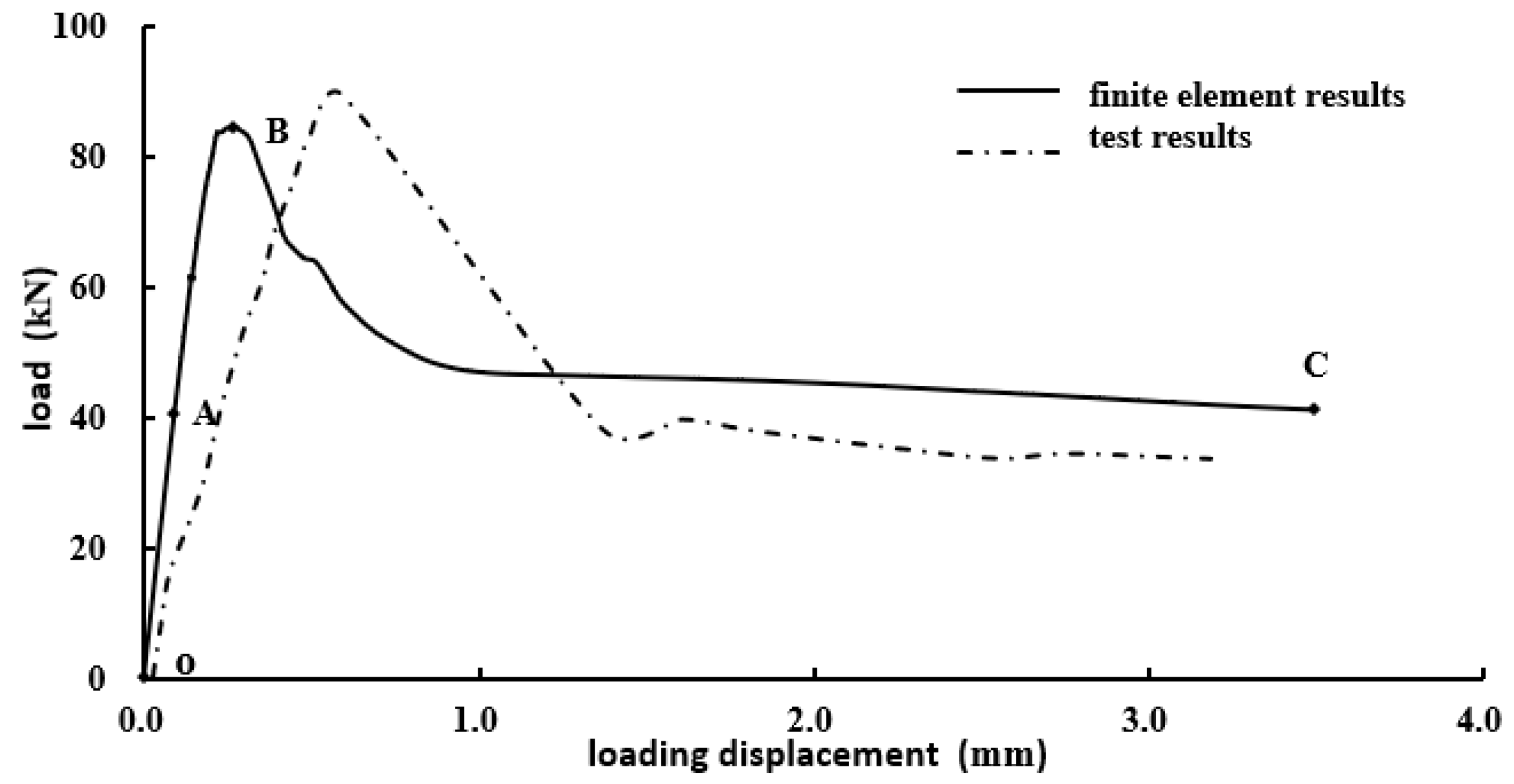
2.4. Verification of the Simulation Method
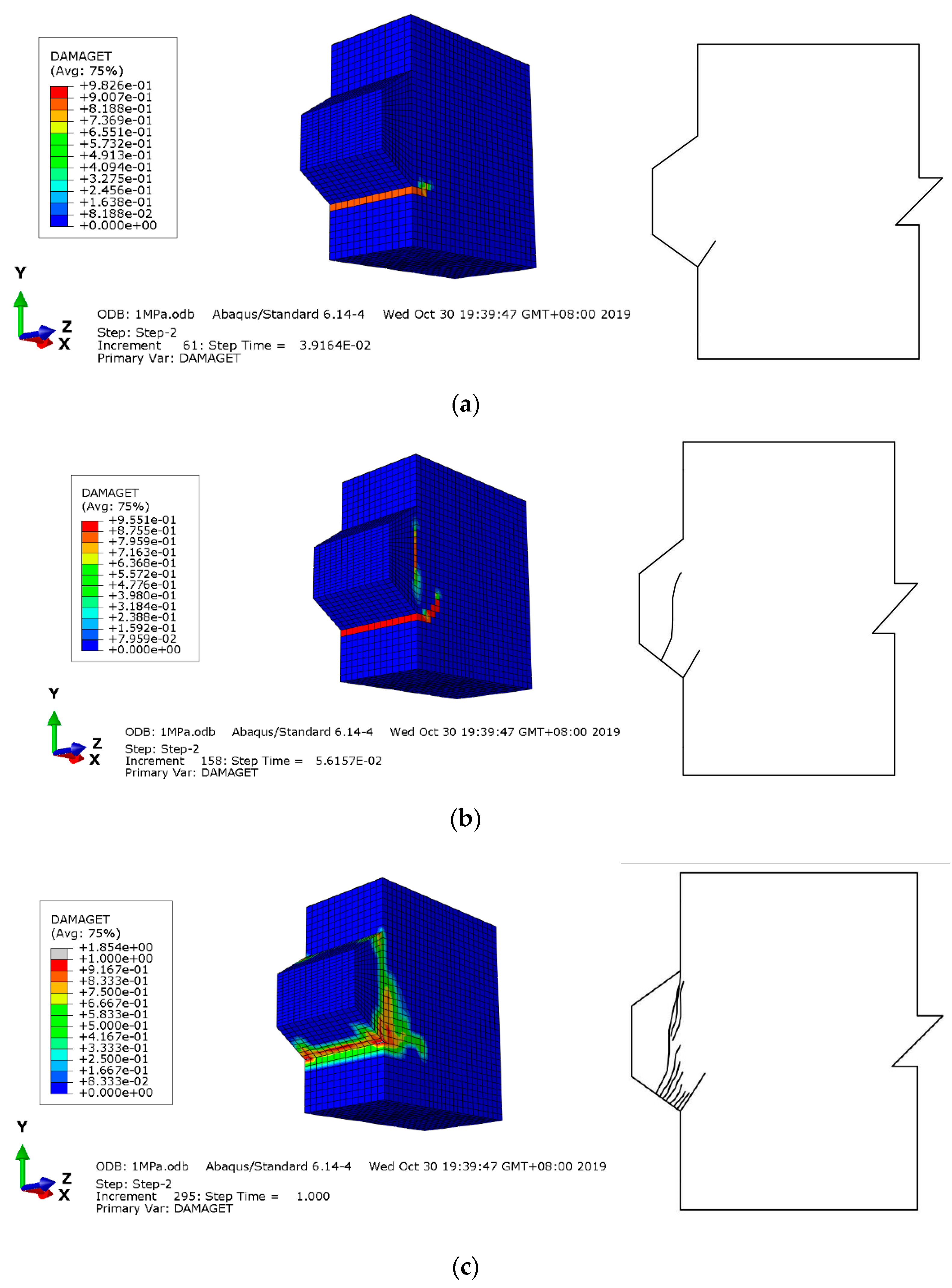
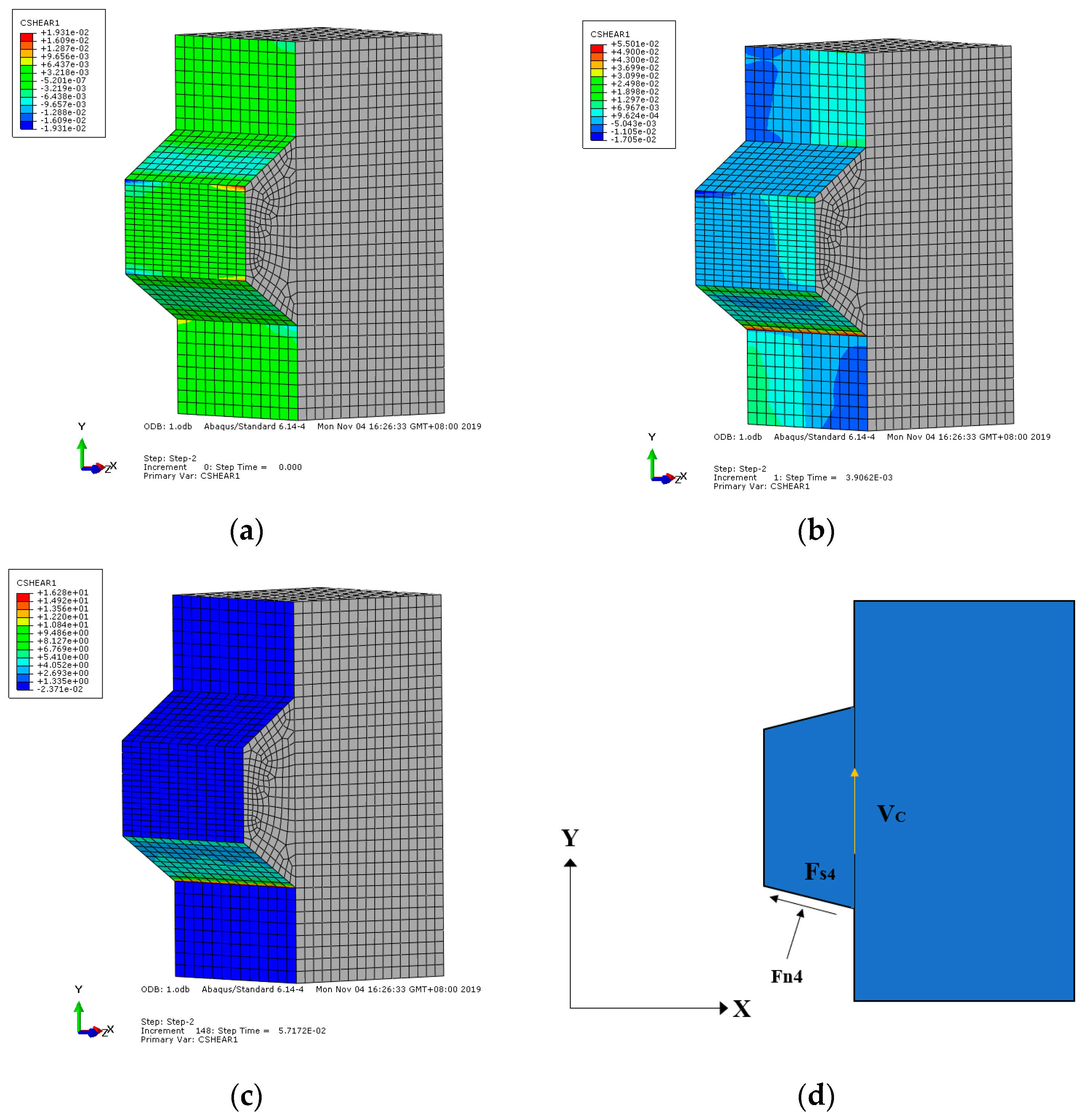
2.5. Nonlinear Behavior under Direct Shear
3. Discussion on the Existing Shear Capacity Formula
3.1. Existing Shear Capacity Formula
- (1)
- Buyukozturk’s formula [22]
- (2)
- AASHTO (2003) provisions [15]
- (3)
- ATEP provisions [25]
- (4)
- Rombach’s formula [23]
- (5)
- Turmo’s formula [17]
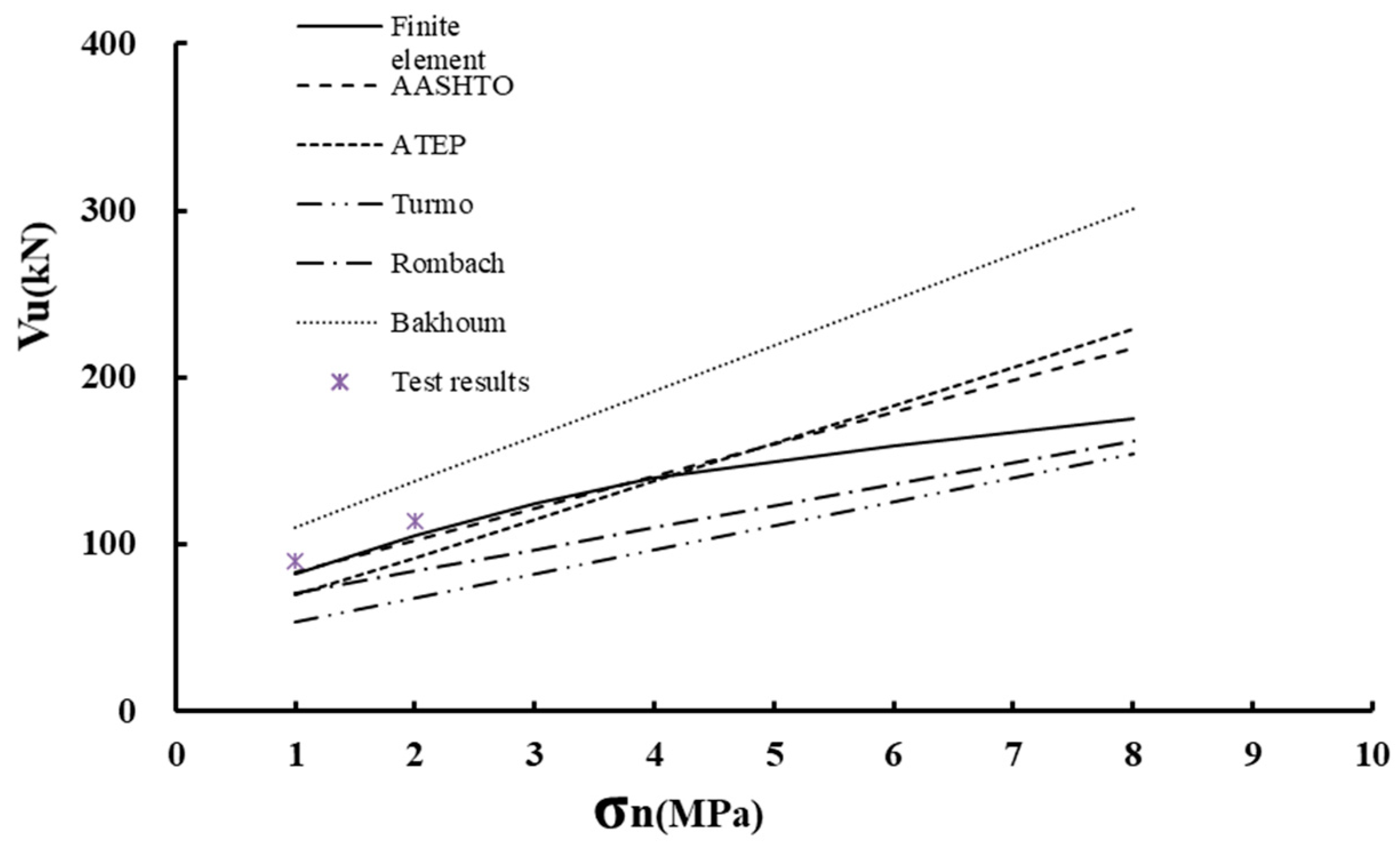
3.2. Comparison of the Existing Formulas
3.3. Force Transmission Mechanism
4. Influencing Factors Analysis
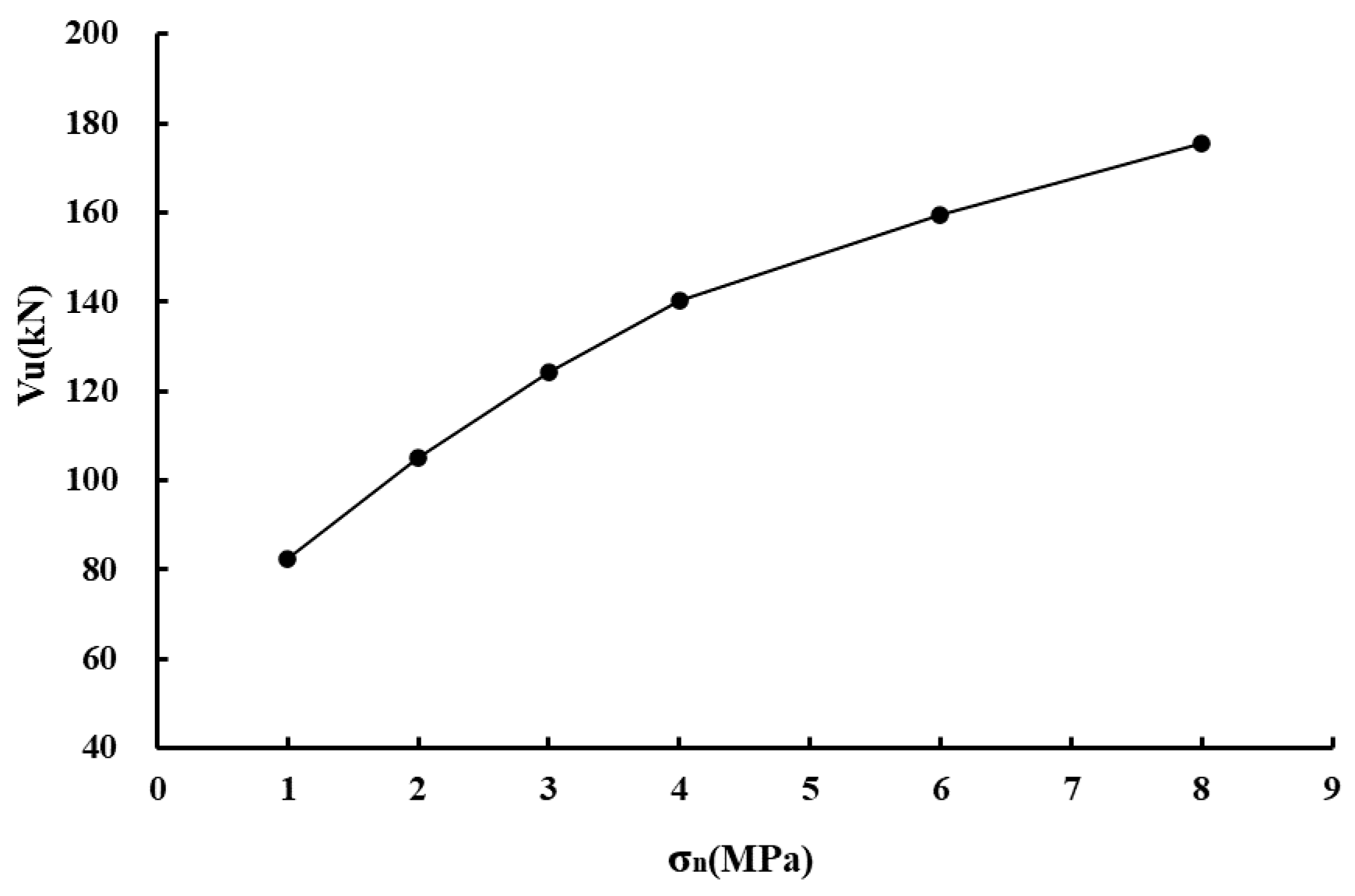
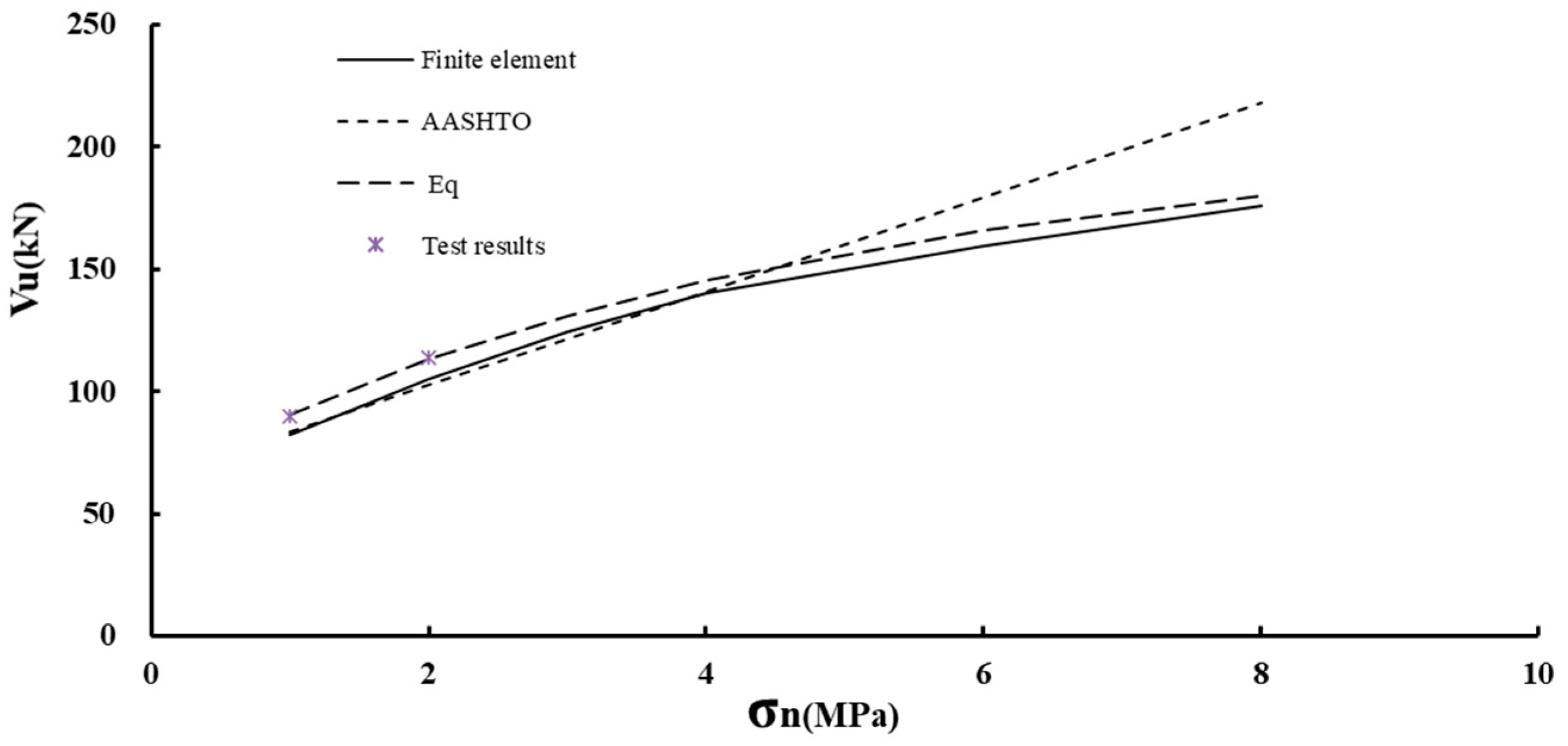
4.1. Lateral Prestress
4.2. Concrete Tensile Strength
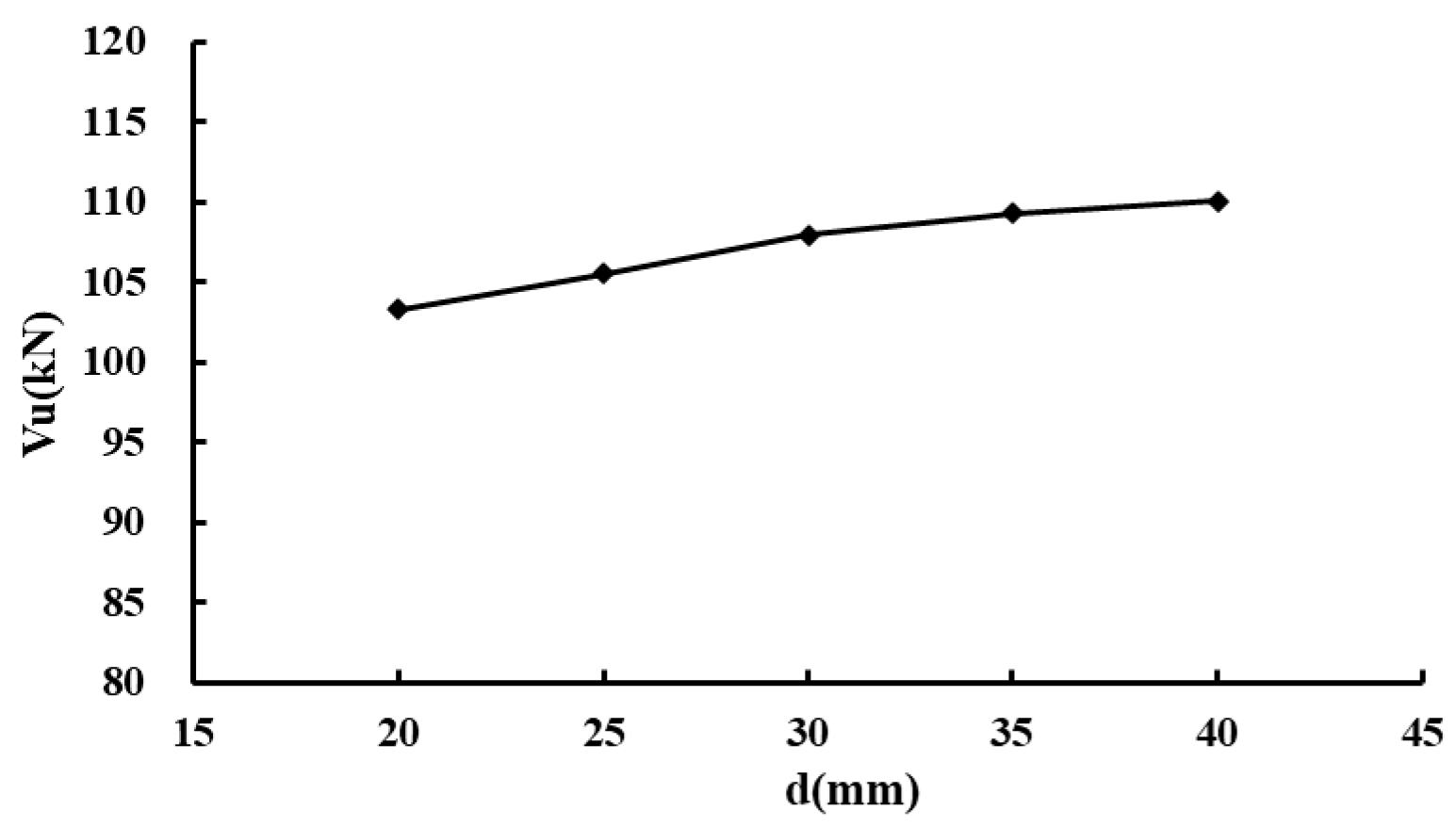
4.3. Dimension Parameters of the Key
- (1)
- Key depth
- (2)
- Key inclination
- (3)
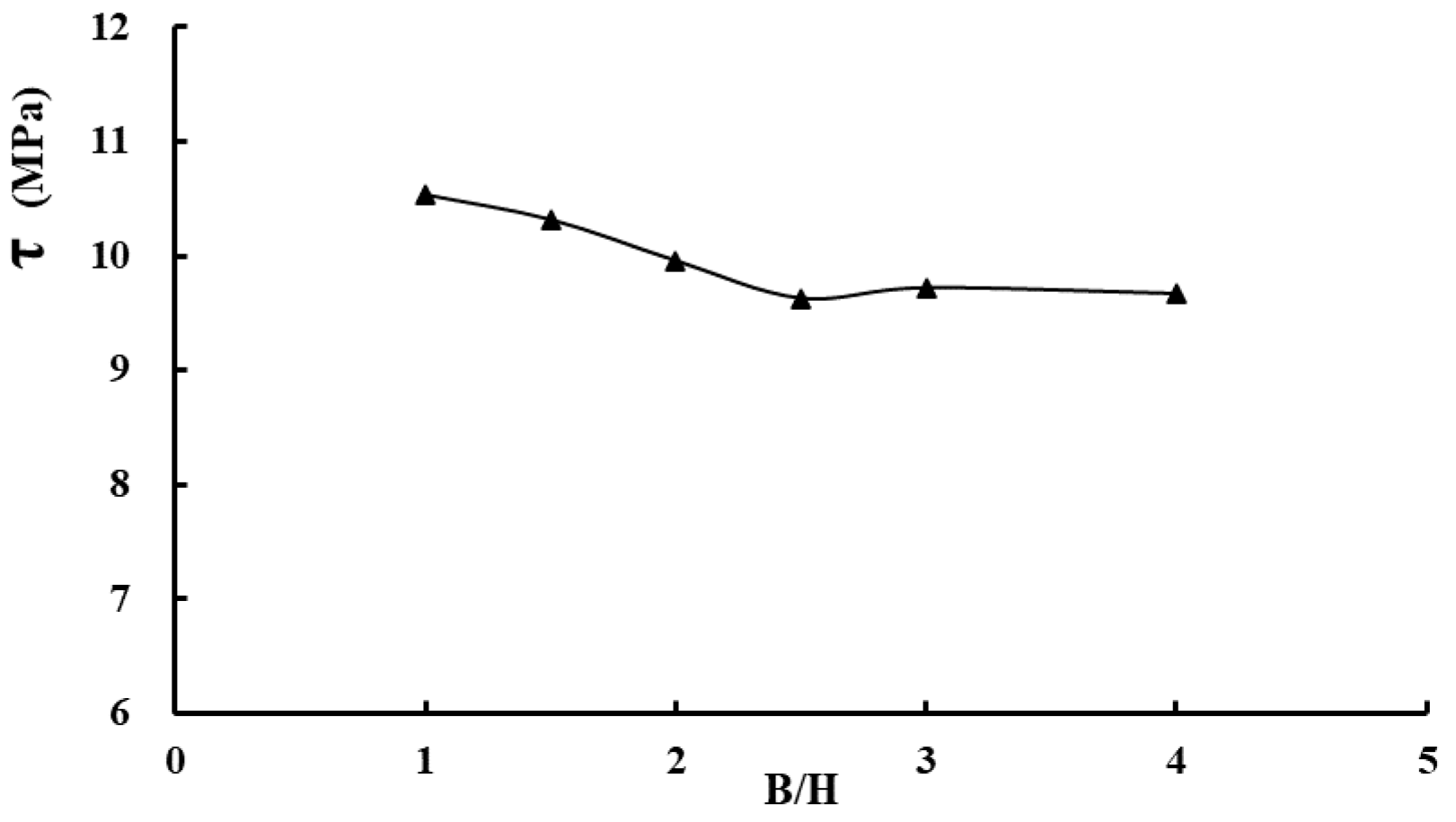
- Key aspect ratio (B/H)
5. Proposal and Evaluation of New Shear Capacity Formula
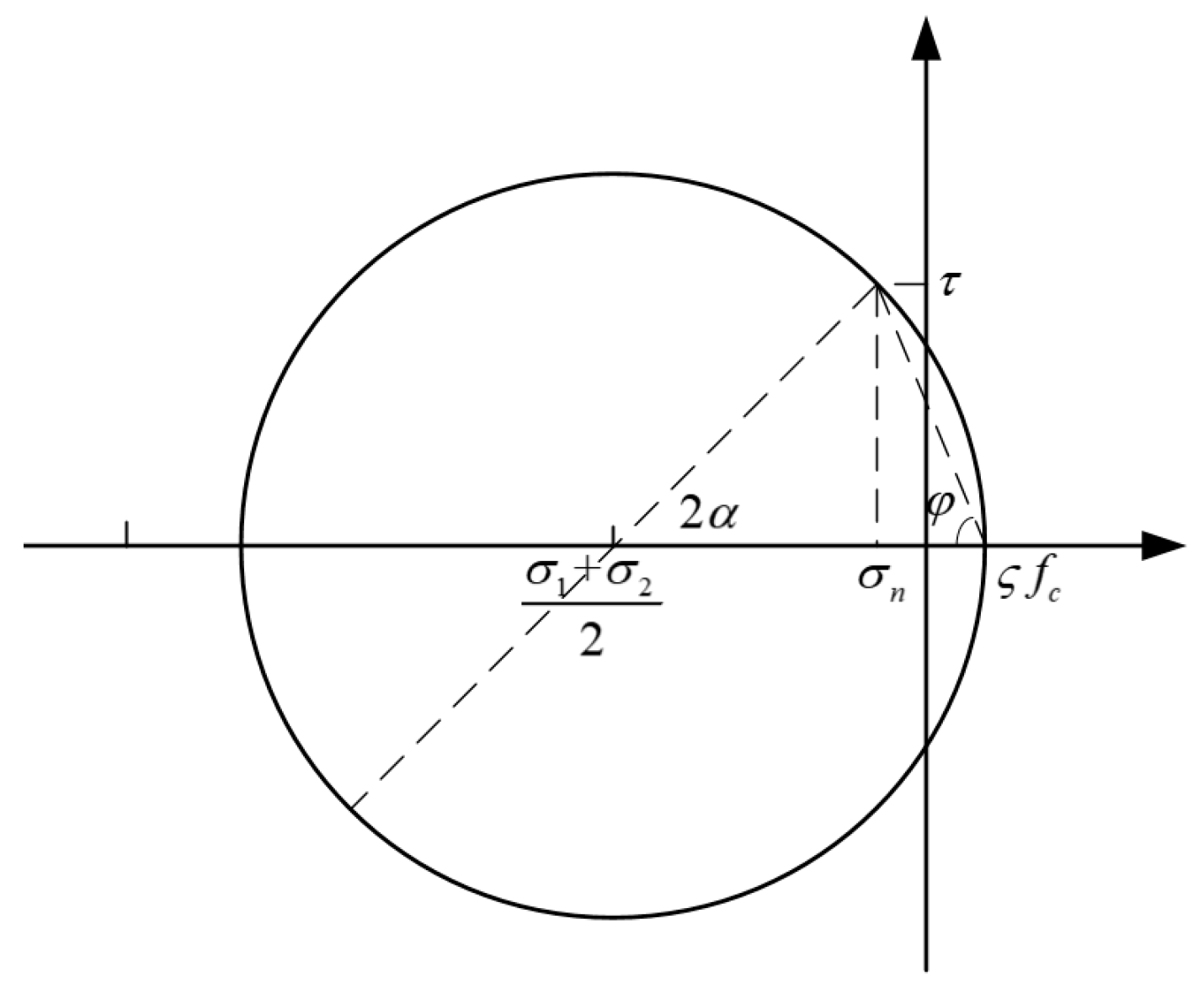
5.1. New Shear Capacity Formula
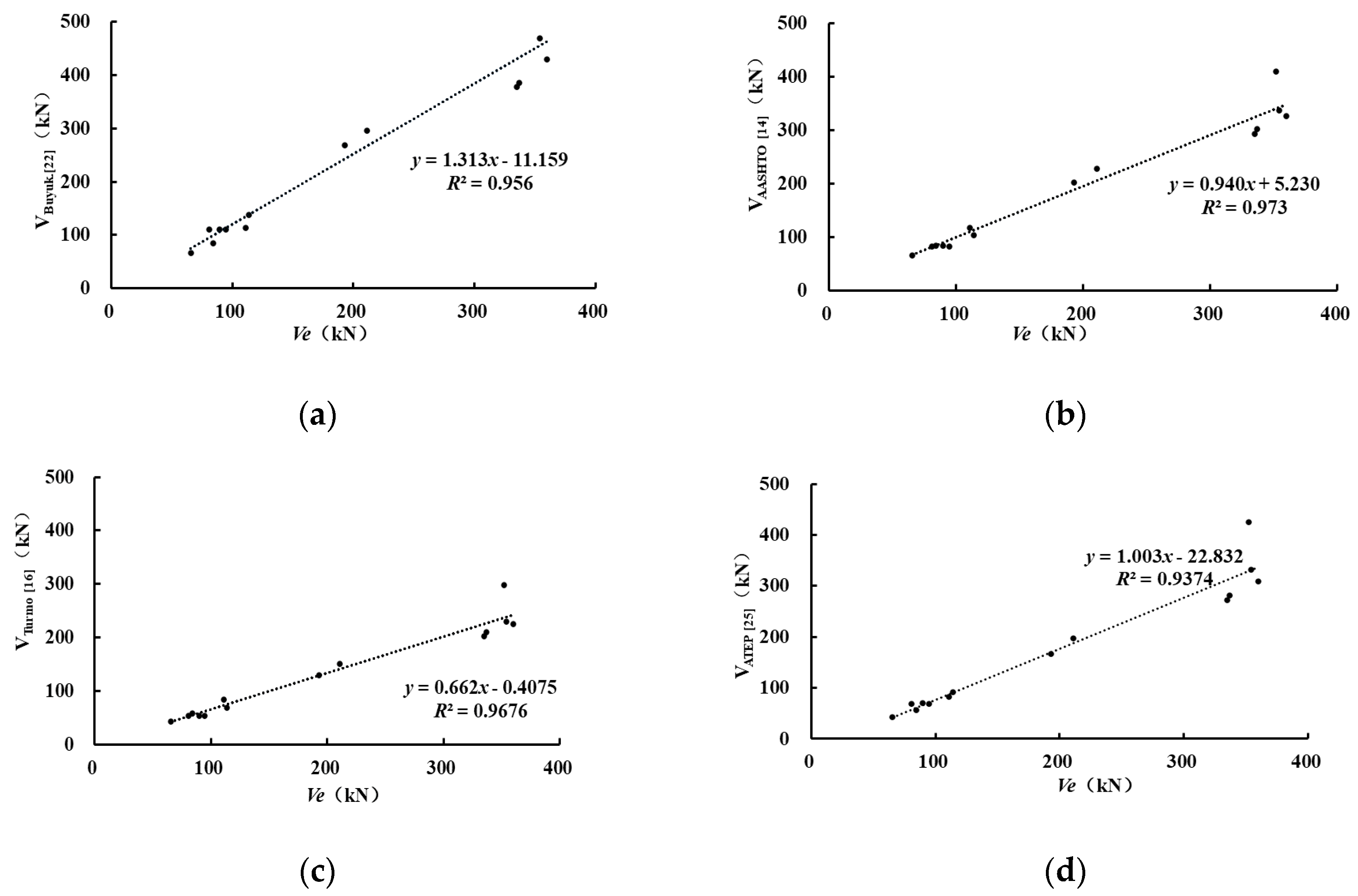
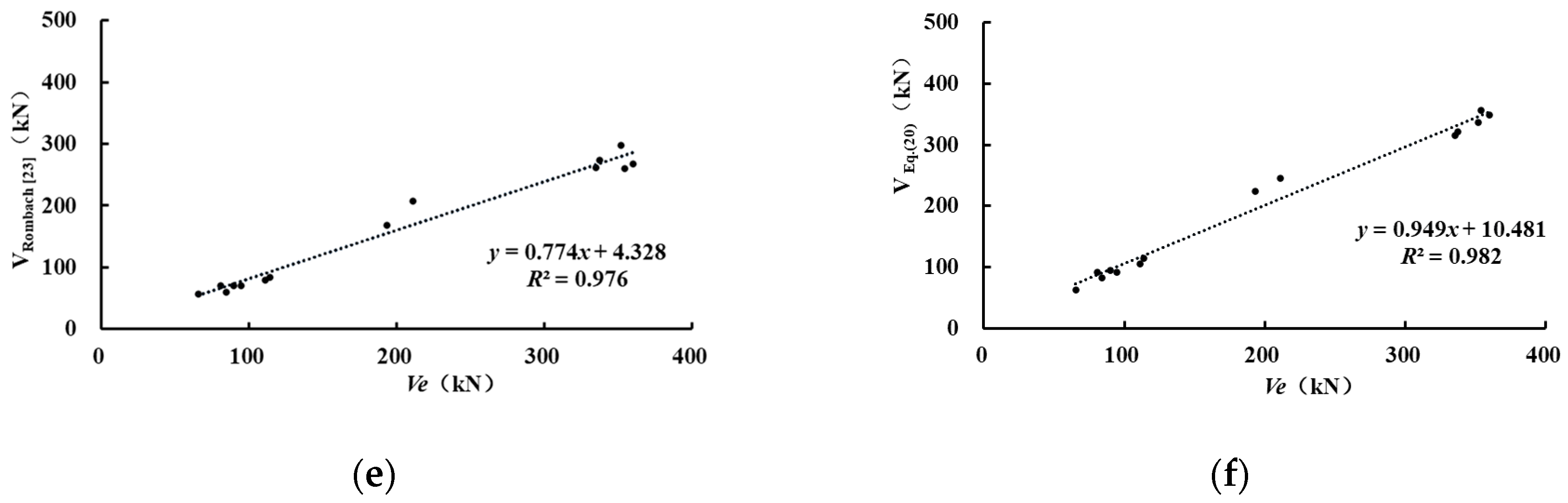
5.2. Evaluation of New Formula
6. Conclusions
- (1)
- Considering the plastic damage of concrete, the nonlinear FE model of the single-keyed dry joint was established, the ultimate shear capacity analysis under the direct shear loading was carried out on existed test specimen. Results demonstrated that the simulated results are in good agreement with the existing experimental results. Thus, the feasibility and correctness of the finite element simulation method were verified.
- (2)
- Both simulated and experimental results indicated that tensile damage occurred in on the underside of the key root even in the linear stage, which was then developed 45° upwards or vertically along the key root section. Concrete tensile strength at the key root is critical to the ultimate bearing capacity of the single-keyed dry joint under the direct shear loading.
- (3)
- The shear resistance of the concrete key root, related to lateral prestress and concrete tensile strength, is the only contributor to the ultimate shear capacity of the keyed dry joints. Friction on the joint interface was demonstrated to be only transferring force between the adjacent joints, does not increase with the increase of friction coefficient. Neither do dimension parameters of the key (such as key depth, key inclination and key aspect ratio) have much effect on . Meanwhile, a reasonable range of key inclination () would be suggested as 0.7~0.9 to obtain comparatively higher value of .
- (4)
- According to the above investigation and supposing the shear stress distributed evenly along key root width, a new formula of the shear capacity of the single-keyed dry joints was proposed based on the maximum principal stress strength criterion. In comparison with the predicted results obtained by other existed formulas, the proposed formula is demonstrated to be in perfect consistency with both tests and the FE simulation results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Wang, J.; Zhao, G.; Zhang, J. Design criterion for the self-centering capacity of precast segmental UHPC bridge columns with unbonded post-tensioning tendons. Eng. Struct. 2019, 200, 109706. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear strength of joints in precast posttensioned segmental bridges during 1959–2019, review and analysis. Structures 2019, 20, 527–542. [Google Scholar] [CrossRef]
- Podolny, W. An overview of precast prestressed segmental bridges. PCI J. 1979, 24, 56–87. [Google Scholar] [CrossRef]
- Prakhya, G.; Hopkin, I.; Hansford, B. Construction of a concrete segmental arch bridge over a railway. In Proceedings of the Institution of Civil Engineers—Bridge Engineering; Thomas Telford Ltd.: Westminster, London, 2019; Volume 172, pp. 226–240. [Google Scholar] [CrossRef]
- Li, G.; Hu, H.; Zhao, S. Axial–shear–flexure interaction behavior of joints in precast concrete segmental bridge columns. J. Bridg. Eng. 2018, 23, 04018071. [Google Scholar] [CrossRef]
- Figg, L.; Pate, W.D. Precast concrete segmental bridges—America’s beautiful and affordable icons. Pci. J. 2004, 49, 26. [Google Scholar]
- National Academies of Sciences and Medicine. Recommended AASHTO Guide Specifications for ABC Design and Construction; Culmo, M.P., Marsh, L., Stanton, J., Eds.; National Academies Press: Washington, DC, USA, 2018; p. 219. [Google Scholar] [CrossRef]
- Hou, W.; Li, Y.; Zheng, Y.; Guo, W. Multi-frequency energy harvesting method for vehicle induced vibration of rail transit continuous rigid bridges. J. Clean. Prod. 2020, 254, 119981. [Google Scholar] [CrossRef]
- Hou, W.; Li, Y.; Guo, W.; Li, J.; Chen, Y.; Duan, X. Railway vehicle induced vibration energy harvesting and saving of rail transit segmental prefabricated and assembling bridges. J. Clean. Prod. 2018, 182, 946–959. [Google Scholar] [CrossRef]
- Song, S. Experimental Study and Theoretical Analysis in Bending and Joint Shear of High-Speed Railway Precast Segmental Concrete Box Biudges. Ph.D. Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Anagnostopoulou, M.; Andre, F.; Amjad, A. Seismic Design and Analysis of a Precast Segmental Concrete Bridge Model; Technical report MCEER-11-0002, Sep.15, 2011; FHWA. NY 14261; University of New York: New York, NY, USA, 2011. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 7th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- Watts, R.; Mills, R.W.; Fish, R. The highway coalition revisited: Using the advocacy coalition framework to explore the content of the American Association of State Highway and Transportation Officials’ Daily Transportation Update. Public Voices 2016, 13, 79. [Google Scholar] [CrossRef]
- AASHTO. Interim Rivisions to the Guide Specifications for Design and Construction of Segmental Concrete Bridges, 2nd ed.; American Association of Hwy and Transportation Officials: Washington, DC, USA, 2003. [Google Scholar]
- Saibabu, S.; Srinivas, V.; Sasmal, S.; Lakshmanan, N.; Iyer, N.R. Performance evaluation of dry and epoxy jointed segmental prestressed box girders under monotonic and cyclic loading. Constr. Build. Mater. 2013, 38, 931–940. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Shear strength of match cast dry joints of precast concrete segmental bridges_ proposal for Eurocode 2. Mater. Constr. 2006, 56, 45–52. [Google Scholar]
- Turmo, J.; Ramos, G.; Aparicio, A. Shear strength of dry joints of concrete panels with and without steel fibres. Eng. Struct. 2006, 28, 23–33. [Google Scholar] [CrossRef]
- Bu, Z.-Y.; Wu, W.-Y. Inter shear transfer of unbonded prestressing precast segmental bridge column dry joints. Eng. Struct. 2018, 154, 52–65. [Google Scholar] [CrossRef]
- Leung, C.C.Y.; Au, F.T.K. Performance of in situ stitches in precast segmental bridges. Mag. Concr. Res. 2016, 68, 1–10. [Google Scholar] [CrossRef]
- Koseki, K.; Breen, J. Exploratory Study of Shear Strength of Joints for Precast Segmntal Bridges; FHWA/TX-84/32+248-l, September, 1983; Center for Transportation Research, The University of Texas at Austin: Austin, TX, USA, 1983. [Google Scholar]
- Büyüköztürk, O.; Bakhoum, M.M.; Beattie, S.M. Shear behavior of joints in precast concrete segmental bridges. J. Struct. Eng. 1990, 116, 3380–3401. [Google Scholar] [CrossRef]
- Rombach, I.G. Precast segmental box girder bridges with external prestressing—Design and construction. In Proceedings of Segmental Bridges; INSA: Rennes, India, 2002; pp. 1–15. [Google Scholar]
- Rombach, G.; Specker, A. Design of joints in segmental hollow box girder bridges. In Proceedings of the 1st FIB Kongress, Osaka, Japan, 13–19 October 2002. [Google Scholar]
- Alcalde, M.; Cifuentes, H.; Medina, F. Shear strength of dry keyed joints and comparison with different formulations. In Proceedings of the VIII International Conference on Fracture Mechanics of Concrete and Concrete Structures, Univ. of Castilla-La Mancha, Ciudad Real, Spain, 10–14 March 2014. [Google Scholar]
- Liu, T.; Wang, Z.; Guo, J.; Wang, J. Shear strength of dry joints in precast UHPC segmental bridges: Experimental and theoretical research. J. Bridg. Eng. 2019, 24, 04018100. [Google Scholar] [CrossRef]
- Zhou, X.; Mickleborough, N.; Li, Z. Shear strength of joints in precast concrete segmental bridges. ACI Struct. J. 2005, 102, 3–11. [Google Scholar]
- Shamass, R.; Zhou, X.; Alfano, G. Finite-element analysis of shear-off failure of keyed dry joints in precast concrete segmental bridges. J. Bridg. Eng. 2015, 20, 04014084. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, J.; Liu, A.; Liang, W.; Tan, Y.; Liang, H. Effect of specimen thickness and coarse aggregate size on shear strength of single-keyed dry joints in precast concrete segmental bridges. Struct. Concr. 2019, 20, 955–970. [Google Scholar] [CrossRef]
- Jiang, H.; Wei, R.; Ma, Z.J.; Li, Y.; Jing, Y. Shear strength of steel fiber-reinforced concrete dry joints in precast segmental bridges. J. Bridg. Eng. 2016, 21, 04016085. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, L.; Ma, Z.J.; Feng, W. Shear behavior of dry joints with castellated keys in precast concrete segmental bridges. J. Bridg. Eng. 2015, 20, 04014062. [Google Scholar] [CrossRef]
- Jiang, H.B.; Di Wang, S.; Fang, Z.C.; Chen, G.; Li, J.H. Numerical analysis on the shear behavior of single-keyed dry joints in precast high-strength concrete segmental bridges. Math. Biosci. Eng. 2019, 16, 3144–3168. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Chen, M.; Sha, Z.; Xiao, J.; Feng, J. Numeric analysis on shear behavior of high-strength concrete single-keyed dry joints with fixing imperfections in precast concrete segmental bridges. Mater. 2020, 13, 2914. [Google Scholar] [CrossRef] [PubMed]
- Zhenhai, G.; Xudong, S. Principle and Analysis of Reinforced Concrete, 1st ed.; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]
- Wei, L.; Ming, X.; Zhongfan, C. Parameter calibration and verification of ABAQUS concrete damage plasticity model. Ind. Build. 2014, 44, 167–171. [Google Scholar]
- Najar, J. Continuous Damage of Brittle Solids; Springer: Vienna, Austria, 1987; pp. 233–294. [Google Scholar]
- Nan, T.; Jing-jiang, S.; Ke, D. Comparative study on calculation method of damage factor for concrete damage plasticity model. In Proceedings of the 26th National Academic Conference on Structural Engineering, Changsha, Hunan, China, 26–31 July 2007; p. 6. [Google Scholar]
- Ombres, L.; Verre, S. Numerical modeling approaches of FRCMs/SRG confined masonry columns. Front. Built Environ. 2019, 5, 5. [Google Scholar] [CrossRef]






| Test Specimen | FE Results (kN) | Test Results (kN) |
|---|---|---|
| F1.0-d35-A0.714-B100-H100 | 82.27 | 89.70 |
| F2.0-d35-A0.714-B100-H100 | 105.86 | 113.87 |
| F1.0-d25-A1-B100-H100 | 74.86 | 80.79 |
| F1.0-d50-A0.5-B100-H100 | 88.90 | 94.47 |
| Lateral Preload | 1 | 2 | 3 | 4 | 6 | 8 |
|---|---|---|---|---|---|---|
| AASHTO | 83.37 | 102.58 | 121.78 | 140.99 | 179.40 | 217.81 |
| Turmo | 54.01 | 68.41 | 82.81 | 97.21 | 126.01 | 154.81 |
| ATEP | 69.61 | 92.41 | 115.21 | 138.01 | 181.31 | 229.21 |
| Rombach | 71.10 | 84.10 | 97.10 | 110.10 | 136.10 | 162.10 |
| Bakhoum | 110.56 | 137.76 | 164.96 | 192.16 | 246.26 | 300.96 |
| VE | 89.70 | 113.87 | - | - | - | - |
| VF | 82.3 | 105.3 | 124.4 | 140.2 | 159.5 | 175.7 |
| Friction Coefficient | 0.4 | 0.6 | 0.8 | 1.0 | |
|---|---|---|---|---|---|
| Specimen | |||||
| F1.0-d35-A25/35 | 83.12 | 82.27 | 82.81 | 83.43 | |
| F8.0-d35-A25/35 | 161.11 | 161.91 | 161.83 | 162.67 | |
| Group | Specimen Number | σn (MPa) | Ft (MPa) | d (mm) | tanθ | B/H |
|---|---|---|---|---|---|---|
| GF | GF1-1 | 1 | 4.01 | 35 | 0.714 | 1.0 |
| GF1-2 | 2 | |||||
| GF1-3 | 3 | |||||
| GF1-4 | 4 | |||||
| GF1-5 | 5 | |||||
| GF1-6 | 6 | |||||
| GCr | GCr1-1 | 2 | 2.20 | |||
| GCr1-2 | 2.51 | |||||
| GCr1-3 | 2.74 | |||||
| GCr1-4 | 2.93 | |||||
| GCr1-5 | 4.01 | |||||
| Gd | Gd1-1 | 4.01 | 20 | |||
| Gd1-2 | 25 | |||||
| Gd1-3 | 30 | |||||
| Gd1-4 | 35 | |||||
| Gd1-5 | 40 | |||||
| GA | GA1-1 | 35 | 0.429 | |||
| GA1-2 | 0.571 | |||||
| GA1-3 | 0.657 | |||||
| GA1-4 | 0.714 | |||||
| GA1-5 | 0.771 | |||||
| GA1-6 | 1.000 | |||||
| GBH | GBH1-1 | 0.714 | 1.0 | |||
| GBH1-2 | 1.5 | |||||
| GBH1-3 | 2.0 | |||||
| GBH1-4 | 2.5 | |||||
| GBH1-5 | 3.0 | |||||
| GBH1-6 | 4.0 |
| Reference | Specimen Number | Specimen Number | Concrete Strength (MPa) |
|---|---|---|---|
| Jiang [31] | F1.0-d35-A25/35-B100-H100 | J-1 | fcu = 48.5 MPa |
| F2.0-d35-A25/35-B100-H100 | J-2 | fcu = 48.5 MPa | |
| F1.0-d25-A25/25-B100-H100 | J-3 | fcu = 48.5 MPa | |
| F1.0-d50-A25/50-B100-H100 | J-4 | fcu = 48.5 MPa | |
| Zhou [28] | F1.0-D50-A25/50-B250-H100 | Z-1 | fc′ = 38.7 MPa |
| F1.0-D50-A25/50-B250-H100 | Z-2 | fc′ = 50 MPa | |
| F2.0-D50-A25/50-B250-H100 | Z-3 | fc′ = 56.2 MPa | |
| F2.0-D50-A25/50-B250-H100 | Z-4 | fc′ = 59.6 MPa | |
| F3.0-D50-A25/50-B250-H100 | Z-5 | fc′ = 48.8 MPa | |
| F4.0-D50-A25/50-B250-H100 | Z-6 | fc′ = 37.1 MPa | |
| Liu [27] | F10-D50-A25/50-B150-H100 | L-1 | ft = 4.6 MPa |
| Buyukozturk [23] | F0.68-D32-A32/32-B76.2-H100 | B-1 | ft = 4.33 MPa |
| F2.07-D32-A32/32-B76.2-H100 | B-2 | ft = 3.97 MPa | |
| F3.45-D32-A32/32-B76.2-H100 | B-3 | ft = 4.38MPa |
| Specimen | VBuyuk. [23] | VAASHTO [15] | VTurmo [17] | VATEP [26] | VRombach [24] | V Equation (20) | VE |
|---|---|---|---|---|---|---|---|
| J-1 | 110.56 (1.23) | 83.37 (0.93) | 53.95 (0.60) | 69.61 (0.78) | 71.10 (0.79) | 95.44 (1.06) | 89.7 |
| J-2 | 137.76 (1.21) | 102.58 (0.90) | 68.34 (0.60) | 92.41 (0.81) | 84.10 (0.74) | 114.43 (1.01) | 113.9 |
| J-3 | 109.85 (1.36) | 82.71 (1.02) | 53.41 (0.66) | 68.82 (0.85) | 70.12 (0.87) | 91.22 (1.13) | 80.8 |
| J-4 | 109.85 (1.16) | 82.71 (0.88) | 53.41 (0.57) | 68.82 (0.73) | 70.12 (0.74) | 91.22 (0.97) | 94.5 |
| Z1 | 269.25 (1.40) | 201.78 (1.05) | 129.43 (0.67) | 166.13 (0.86) | 167.95 (0.87) | 223.86 (1.16) | 193.0 |
| Z2 | 378.52 (1.13) | 293.51 (0.88) | 202.42 (0.60) | 272.48 (0.81) | 261.70 (0.78) | 316.07 (0.94) | 335.0 |
| Z3 | 296.75 (1.41) | 227.31 (1.08) | 150.74 (0.71) | 198.00 (0.94) | 207.50 (0.98) | 245.74 (1.16) | 211.0 |
| Z4 | 385.75 (1.14) | 301.36 (0.89) | 209.31 (0.62) | 282.07 (0.84) | 273.60 (0.81) | 322.25 (0.96) | 337.0 |
| Z5 | 429.99 (1.19) | 326.35 (0.91) | 225.30 (0.63) | 308.62 (0.86) | 268.30 (0.75) | 349.46 (0.97) | 360.0 |
| Z6 | 469.04 (1.32) | 336.53 (0.95) | 229.66 (0.65) | 332.62 (0.94) | 259.85 (0.73) | 356.51 (1.01) | 354.0 |
| L-1 | 544.15 (1.55) | 410.48 (1.17) | 297.47 (0.85) | 425.25 (1.21) | 298.32 (0.85) | 325.68 (0.93) | 351.9 |
| B-1 | 66.31 (1.01) | 65.34 (0.99) | 43.33 (0.66) | 42.86 (0.65) | 57.10 (0.87) | 62.69 (0.96) | 65.5 |
| B-2 | 84.61 (1.00) | 84.16 (0.99) | 57.94 (0.69) | 56.73 (0.67) | 59.81 (0.71) | 82.01 (0.97) | 84.2 |
| B-3 | 112.6 (1.01) | 116.4 (1.05) | 83.83 (0.76) | 81.88 (0.74) | 80.02 (0.72) | 82.01 (0.74) | 111.0 |
| RAv | 1.222 | 0.978 | 0.662 | 0.835 | 0.800 | 0.998 | |
| R2 | 0.956 | 0.973 | 0.968 | 0.937 | 0.976 | 0.982 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Peng, M.; Jin, B.; Tao, Y.; Guo, W.; Zhou, L. Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading. Appl. Sci. 2020, 10, 6304. https://doi.org/10.3390/app10186304
Hou W, Peng M, Jin B, Tao Y, Guo W, Zhou L. Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading. Applied Sciences. 2020; 10(18):6304. https://doi.org/10.3390/app10186304
Chicago/Turabian StyleHou, Wenqi, Meng Peng, Bo Jin, Yong Tao, Wei Guo, and Lingyu Zhou. 2020. "Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading" Applied Sciences 10, no. 18: 6304. https://doi.org/10.3390/app10186304
APA StyleHou, W., Peng, M., Jin, B., Tao, Y., Guo, W., & Zhou, L. (2020). Influencing Factors and Shear Capacity Formula of Single-Keyed Dry Joints in Segmental Precast Bridges under Direct Shear Loading. Applied Sciences, 10(18), 6304. https://doi.org/10.3390/app10186304






