Quality Assessment of 3D Printed Surfaces Using Combined Metrics Based on Mutual Structural Similarity Approach Correlated with Subjective Aesthetic Evaluation
Abstract
1. Introduction
2. Overview of Similarity-Based Full-Reference Image Quality Assessment Methods
3. The Database of the 3D Printed Surfaces
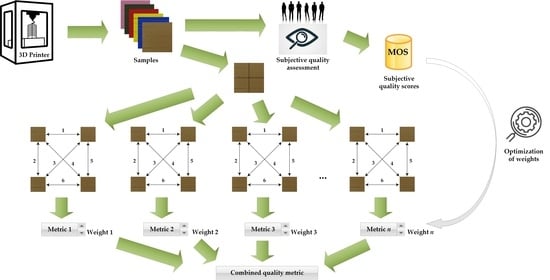
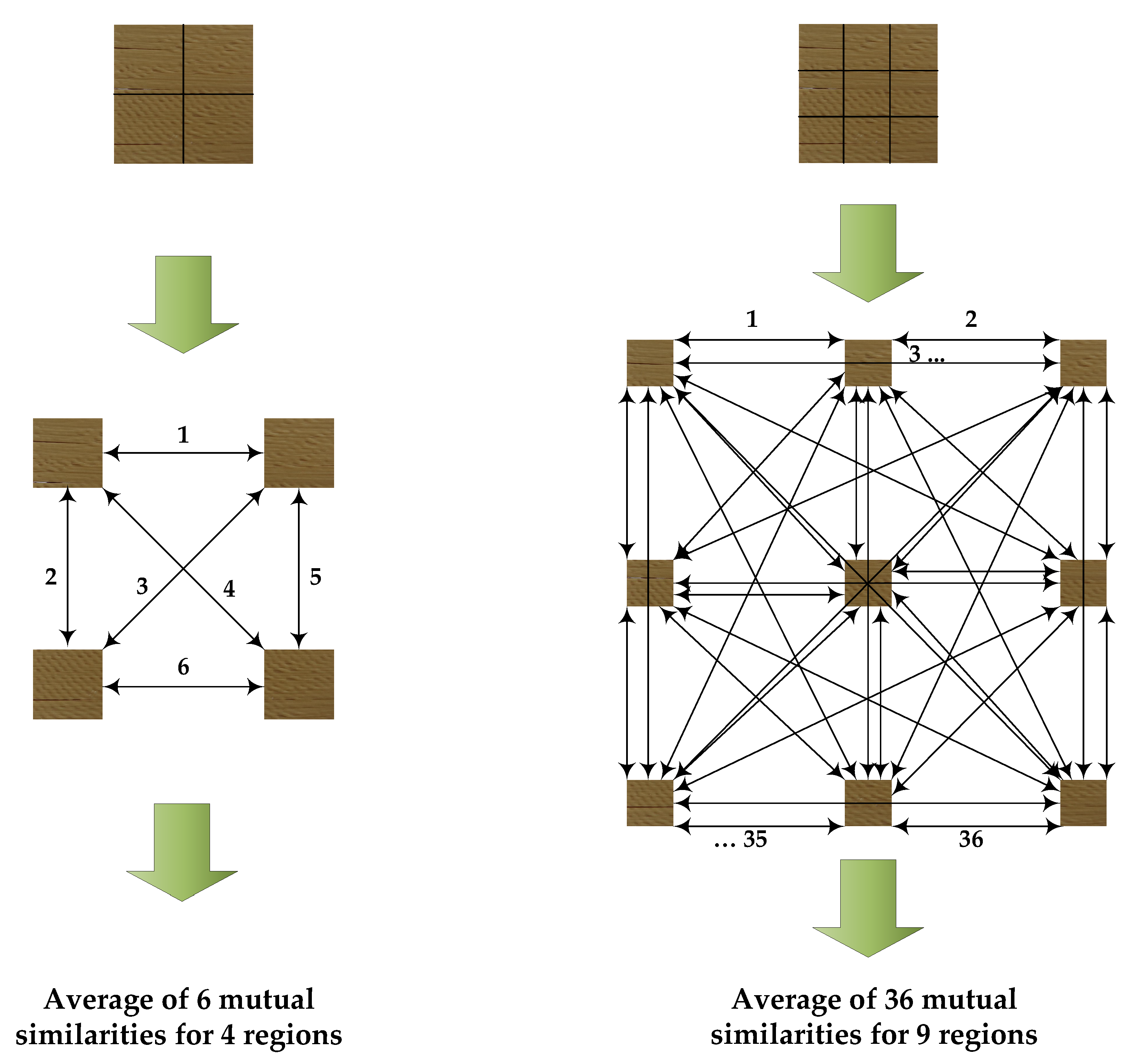
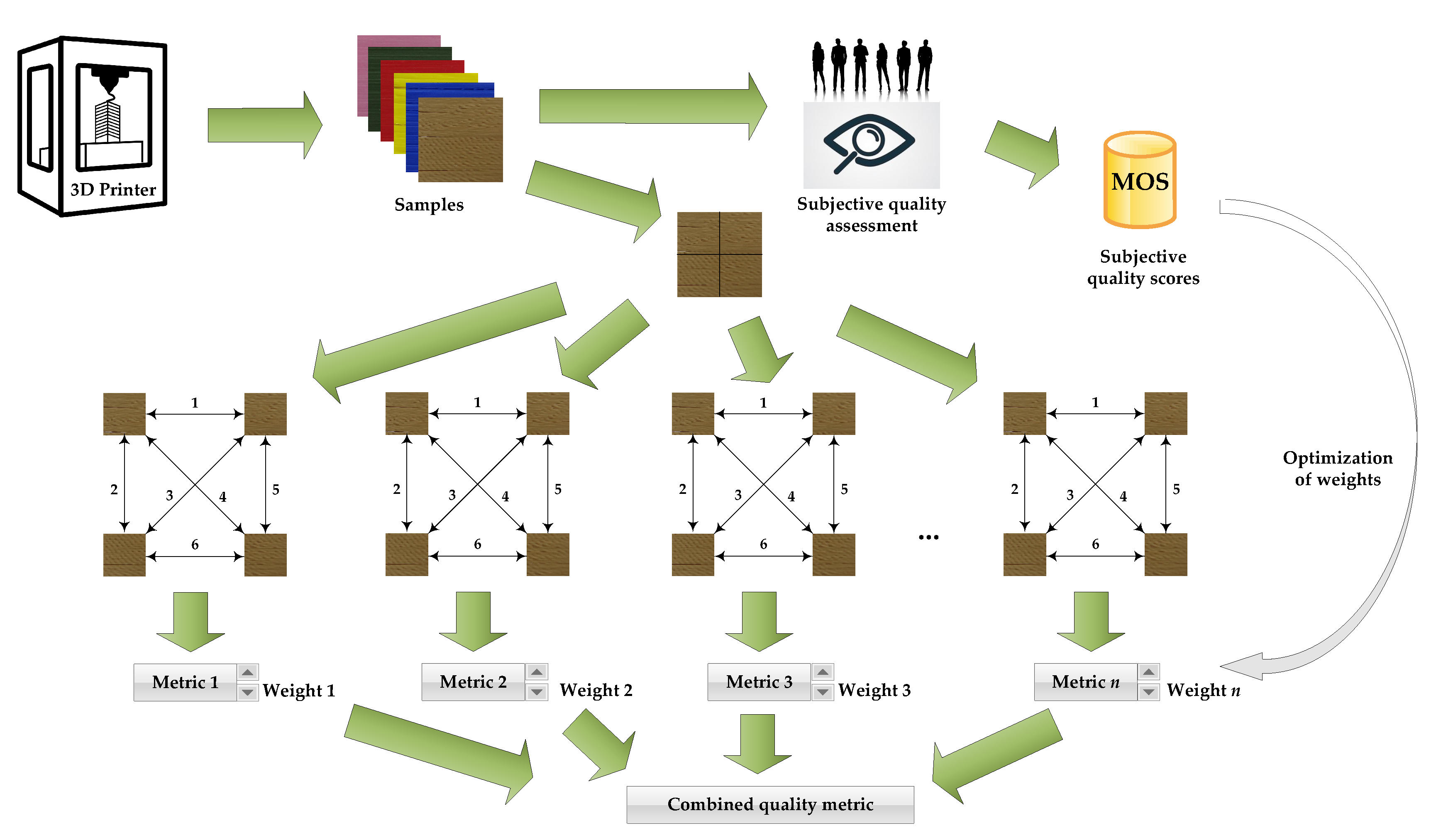
4. Proposed Approach
5. Experimental Results
6. Discussion
7. Conclusions and Further Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABS | Acrylonitrile butadiene styrene |
| ADD-GSIM | Analysis of distortion distribution-based Gradient SIMilarity |
| ADD-SSIM | Analysis of distortion distribution-based Structural SIMilarity |
| CAD | Computer-Aided Design |
| CISI | Combined Image Similarity Index |
| CSF | Contrast Sensitivity Function |
| CSSIM | Color Structural SIMilarity |
| CVSSI | Contrast and Visual Saliency Similarity-Induced Index |
| CW-SSIM | Complex Wavelet Structural SIMilarity |
| DCT | Discrete Cosine Transform |
| CLAHE | Contrast Limited Adaptive Histogram Equalization |
| DSS | DCT subband similarity |
| ESSIM | Edge Strength SIMilarity |
| FDM | Fused deposition modeling |
| FR IQA | Full-reference image quality assessment |
| FSIM | Feature Similarity |
| GM | Gradient magnitude |
| GSM | Gradient Similarity |
| HOG | Histogram of Oriented Gradients |
| HVS | Human Visual System |
| IQA | Image quality assessment |
| ITU | International Telecommunication Union |
| IW-SSIM | Information Content Weighted Structural SIMilarity |
| KROCC | Kendall Rank Order Correlation Coefficient |
| LPBF | Laser powder bed fusion |
| MCSD | Multiscale Contrast Similarity Deviation |
| MOS | Mean Opinion Score |
| MSE | Mean Squared Error |
| MS-SSIM | Multi-Scale Structural SIMilarity |
| NDT | Non-destructive testing |
| NR IQA | No-reference image quality assessment |
| OCT | Optical coherence tomography |
| PLCC | Pearson’s Linear Correlation Coefficient |
| QILV | Quality Index based on Local Variance |
| SROCC | Spearman Rank Order Correlation Coefficient |
| SR-SIM | Spectral residual-based similarity |
| SSIM | Structural SIMilarity |
| PC | Phase congruency |
| PLA | Polyactic acid |
| PSNR | Peak Signal-to-Noise Ratio |
| PVC | Polyvinyl chloride |
| RVSIM | Riesz transform and Visual contrast sensitivity-based feature SIMilarity |
| UIQI | Universal Image Quality Index |
| VQEG | Video Quality Experts Group |
References
- Stephens, B.; Azimi, P.; Orch, Z.E.; Ramos, T. Ultrafine particle emissions from desktop 3D printers. Atmos. Environ. 2013, 79, 334–339. [Google Scholar] [CrossRef]
- Azimi, P.; Zhao, D.; Pouzet, C.; Crain, N.E.; Stephens, B. Emissions of Ultrafine Particles and Volatile Organic Compounds from Commercially Available Desktop Three-Dimensional Printers with Multiple Filaments. Environ. Sci. Technol. 2016, 50, 1260–1268. [Google Scholar] [CrossRef] [PubMed]
- Fastowicz, J.; Grudziński, M.; Tecław, M.; Okarma, K. Objective 3D Printed Surface Quality Assessment Based on Entropy of Depth Maps. Entropy 2019, 21, 97. [Google Scholar] [CrossRef]
- Okarma, K.; Fastowicz, J. Improved quality assessment of colour surfaces for additive manufacturing based on image entropy. Pattern Anal. Appl. 2020, 23, 1035–1047. [Google Scholar] [CrossRef]
- Cheng, Y.; Jafari, M.A. Vision-Based Online Process Control in Manufacturing Applications. IEEE Trans. Autom. Sci. Eng. 2008, 5, 140–153. [Google Scholar] [CrossRef]
- Delli, U.; Chang, S. Automated Process Monitoring in 3D Printing Using Supervised Machine Learning. Procedia Manuf. 2018, 26, 865–870. [Google Scholar] [CrossRef]
- Szkilnyk, G.; Hughes, K.; Surgenor, B. Vision Based Fault Detection of Automated Assembly Equipment. In Proceedings of the ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Parts A and B, Qingdao, China, 15–17 July 2010; ASMEDC: Washington, DC, USA, 2011; Volume 3, pp. 691–697. [Google Scholar] [CrossRef]
- Chauhan, V.; Surgenor, B. A Comparative Study of Machine Vision Based Methods for Fault Detection in an Automated Assembly Machine. Procedia Manuf. 2015, 1, 416–428. [Google Scholar] [CrossRef]
- Chauhan, V.; Surgenor, B. Fault detection and classification in automated assembly machines using machine vision. Int. J. Adv. Manuf. Technol. 2017, 90, 2491–2512. [Google Scholar] [CrossRef]
- Fang, T.; Jafari, M.A.; Bakhadyrov, I.; Safari, A.; Danforth, S.; Langrana, N. Online defect detection in layered manufacturing using process signature. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Diego, CA, USA, 14 October 1998; IEEE: Piscataway, NJ, USA, 1998; Volume 5, pp. 4373–4378. [Google Scholar] [CrossRef]
- Fang, T.; Jafari, M.A.; Danforth, S.C.; Safari, A. Signature analysis and defect detection in layered manufacturing of ceramic sensors and actuators. Mach. Vis. Appl. 2003, 15, 63–75. [Google Scholar] [CrossRef]
- Gardner, M.R.; Lewis, A.; Park, J.; McElroy, A.B.; Estrada, A.D.; Fish, S.; Beaman, J.J.; Milner, T.E. In situ process monitoring in selective laser sintering using optical coherence tomography. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Lane, B.; Moylan, S.; Whitenton, E.P.; Ma, L. Thermographic measurements of the commercial laser powder bed fusion process at NIST. Rapid Prototyp. J. 2016, 22, 778–787. [Google Scholar] [CrossRef] [PubMed]
- Busch, S.F.; Weidenbach, M.; Fey, M.; Schäfer, F.; Probst, T.; Koch, M. Optical Properties of 3D Printable Plastics in the THz Regime and their Application for 3D Printed THz Optics. J. Infrared Millim. Terahertz Waves 2014, 35, 993–997. [Google Scholar] [CrossRef]
- Straub, J. Physical security and cyber security issues and human error prevention for 3D printed objects: Detecting the use of an incorrect printing material. In Dimensional Optical Metrology and Inspection for Practical Applications VI, Proceedings of the SPIE Commercial + Scientific Sensing and Imaging, Anaheim, CA, USA, 9–13 April 2017; Harding, K.G., Zhang, S., Eds.; SPIE: Bellingham, WA, USA, 2017; Volume 10220, pp. 90–105. [Google Scholar] [CrossRef]
- Straub, J. Identifying positioning-based attacks against 3D printed objects and the 3D printing process. In Pattern Recognition and Tracking XXVIII, Proceedings of the SPIE Defense + Security, Anaheim, CA, USA, 16 June 2017; Alam, M.S., Ed.; SPIE: Bellingham, WA, USA, 2017; Volume 10203. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Gupta, N.; Tsoutsos, N.G.; Maniatakos, M.; Rajendran, J.; Karri, R. Manufacturing and Security Challenges in 3D Printing. JOM 2016, 68, 1872–1881. [Google Scholar] [CrossRef]
- Holzmond, O.; Li, X. In situ real time defect detection of 3D printed parts. Addit. Manuf. 2017, 17, 135–142. [Google Scholar] [CrossRef]
- Scime, L.; Beuth, J. Anomaly detection and classification in a laser powder bed additive manufacturing process using a trained computer vision algorithm. Addit. Manuf. 2018, 19, 114–126. [Google Scholar] [CrossRef]
- Tourloukis, G.; Stoyanov, S.; Tilford, T.; Bailey, C. Data driven approach to quality assessment of 3D printed electronic products. In Proceedings of the 38th International Spring Seminar on Electronics Technology (ISSE), Eger, Hungary, 6–10 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 300–305. [Google Scholar] [CrossRef]
- Makagonov, N.G.; Blinova, E.M.; Bezukladnikov, I.I. Development of visual inspection systems for 3D printing. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 1–3 February 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1463–1465. [Google Scholar] [CrossRef]
- Fok, K.; Cheng, C.; Ganganath, N.; Iu, H.H.; Tse, C.K. An ACO-Based Tool-Path Optimizer for 3-D Printing Applications. IEEE Trans. Ind. Inform. 2019, 15, 2277–2287. [Google Scholar] [CrossRef]
- Sitthi-Amorn, P.; Ramos, J.E.; Wangy, Y.; Kwan, J.; Lan, J.; Wang, W.; Matusik, W. MultiFab: A Machine Vision Assisted Platform for Multi-material 3D Printing. ACM Trans. Graph. 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Straub, J. Initial Work on the Characterization of Additive Manufacturing (3D Printing) Using Software Image Analysis. Machines 2015, 3, 55–71. [Google Scholar] [CrossRef]
- Straub, J. An approach to detecting deliberately introduced defects and micro-defects in 3D printed objects. In Pattern Recognition and Tracking XXVIII, Proceedings of the SPIE Defense + Security, Anaheim, CA, USA, 16 June 2017; Alam, M.S., Ed.; SPIE: Bellingham, WA, USA, 2017; Volume 10203. [Google Scholar] [CrossRef]
- Bi, Q.; Wang, M.; Lai, M.; Lin, J.; Zhang, J.; Liu, X. Automatic surface inspection for S-PVC using a composite vision-based method. Appl. Opt. 2020, 59, 1008. [Google Scholar] [CrossRef]
- Zhai, G.; Min, X. Perceptual image quality assessment: A survey. Sci. China Inf. Sci. 2020, 63. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A. A universal image quality index. IEEE Signal Process. Lett. 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Simoncelli, E.; Bovik, A. Multiscale structural similarity for image quality assessment. In Proceedings of the 37th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 9–12 November 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 1398–1402. [Google Scholar] [CrossRef]
- Aja-Fernandez, S.; Estepar, R.S.J.; Alberola-Lopez, C.; Westin, C.F. Image Quality Assessment based on Local Variance. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Sampat, M.; Wang, Z.; Gupta, S.; Bovik, A.; Markey, M. Complex Wavelet Structural Similarity: A New Image Similarity Index. IEEE Trans. Image Process. 2009, 18, 2385–2401. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Q. Information Content Weighting for Perceptual Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 1185–1198. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Lin, W.; Narwaria, M. Image Quality Assessment Based on Gradient Similarity. IEEE Trans. Image Process. 2012, 21, 1500–1512. [Google Scholar] [CrossRef]
- Zhang, L.; Li, H. SR-SIM: A fast and high performance IQA index based on spectral residual. In Proceedings of the 2012 19th IEEE International Conference on Image Processing (ICIP), Orlando, FL, USA, 30 September–3 October 2012; pp. 1473–1476. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Wang, W.; Xue, W. Edge Strength Similarity for Image Quality Assessment. IEEE Signal Process. Lett. 2013, 20, 319–322. [Google Scholar] [CrossRef]
- Balanov, A.; Schwartz, A.; Moshe, Y.; Peleg, N. Image quality assessment based on DCT subband similarity. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, L.; Jia, H.; Li, B.; Shu, H. Multiscale contrast similarity deviation: An effective and efficient index for perceptual image quality assessment. Signal Process. Image Commun. 2016, 45, 1–9. [Google Scholar] [CrossRef]
- Gu, K.; Wang, S.; Zhai, G.; Lin, W.; Yang, X.; Zhang, W. Analysis of Distortion Distribution for Pooling in Image Quality Prediction. IEEE Trans. Broadcast. 2016, 62, 446–456. [Google Scholar] [CrossRef]
- Ponomarenko, M.; Egiazarian, K.; Lukin, V.; Abramova, V. Structural Similarity Index with Predictability of Image Blocks. In Proceedings of the 2018 IEEE 17th International Conference on Mathematical Methods in Electromagnetic Theory (MMET), Kiev, Ukraine, 2–5 July 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, L.; Wang, T. Contrast and Visual Saliency Similarity-Induced Index for Assessing Image Quality. IEEE Access 2018, 6, 65885–65893. [Google Scholar] [CrossRef]
- Yang, G.; Li, D.; Lu, F.; Liao, Y.; Yang, W. RVSIM: A feature similarity method for full-reference image quality assessment. EURASIP J. Image Video Process. 2018, 2018, 6. [Google Scholar] [CrossRef]
- Ieremeiev, O.; Lukin, V.; Okarma, K.; Egiazarian, K. Full-Reference Quality Metric Based on Neural Network to Assess the Visual Quality of Remote Sensing Images. Remote Sens. 2020, 12, 2349. [Google Scholar] [CrossRef]
- Okarma, K. Combined Full-Reference Image Quality Metric Linearly Correlated with Subjective Assessment. In Artificial Intelligence and Soft Computing, Proceedings of the 10th International Conference Proceedings, ICAISC 2010, Zakopane, Poland, 13–17 June 2010; Rutkowski, L., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6113, pp. 539–546. [Google Scholar] [CrossRef]
- Sheikh, H.; Bovik, A. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef] [PubMed]
- Mansouri, A.; Aznaveh, A.M.; Torkamani-Azar, F.; Jahanshahi, J.A. Image quality assessment using the singular value decomposition theorem. Opt. Rev. 2009, 16, 49–53. [Google Scholar] [CrossRef]
- Okarma, K. Combined image similarity index. Opt. Rev. 2012, 19, 349–354. [Google Scholar] [CrossRef]
- Athar, S.; Wang, Z. A Comprehensive Performance Evaluation of Image Quality Assessment Algorithms. IEEE Access 2019, 7, 140030–140070. [Google Scholar] [CrossRef]
- Oszust, M. A Regression-Based Family of Measures for Full-Reference Image Quality Assessment. Meas. Sci. Rev. 2016, 16, 316–325. [Google Scholar] [CrossRef]
- Liu, T.J.; Lin, W.; Kuo, C.C.J. Image Quality Assessment Using Multi-Method Fusion. IEEE Trans. Image Process. 2013, 22, 1793–1807. [Google Scholar] [CrossRef]
- Lukin, V.V.; Ponomarenko, N.N.; Ieremeiev, O.I.; Egiazarian, K.O.; Astola, J. Combining full-reference image visual quality metrics by neural network. In Human Vision and Electronic Imaging XX, Proceedings of the SPIE/IS&T Electronic Imaging, San Francisco, CA, USA, 10–11 February 2015; Rogowitz, B.E., Pappas, T.N., de Ridder, H., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9394. [Google Scholar] [CrossRef]
- Oszust, M. Full-Reference Image Quality Assessment with Linear Combination of Genetically Selected Quality Measures. PLoS ONE 2016, 11, e0158333. [Google Scholar] [CrossRef]
- Okarma, K.; Fastowicz, J.; Tecław, M. Application of Structural Similarity Based Metrics for Quality Assessment of 3D Prints. In Computer Vision and Graphics, Proceedings of the International Conference, ICCVG 2016, Warsaw, Poland, 19–21 September 2016; Chmielewski, L.J., Datta, A., Kozera, R., Wojciechowski, K., Eds.; Springer International Publishing: Cham, Switzerland, 2016; Volume 9972, pp. 244–252. [Google Scholar] [CrossRef]
- Okarma, K.; Fastowicz, J. Adaptation of Full-Reference Image Quality Assessment Methods for Automatic Visual Evaluation of the Surface Quality of 3D Prints. Elektron. Elektrotechnika 2019, 25, 57–62. [Google Scholar] [CrossRef]
- Fastowicz, J.; Okarma, K. Fast quality assessment of 3D printed surfaces based on structural similarity of image regions. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Świnoujście, Poland, 9–12 May 2018. [Google Scholar] [CrossRef]
- International Telecommunication Union. Recommendation ITU-R BT.601-7—Studio Encoding Parameters of Digital Television for Standard 4:3 and Wide-Screen 16:9 Aspect Ratios; International Telecommunication Union: Geneva, Switzerland, 2011. [Google Scholar]
- Fastowicz, J.; Lech, P.; Okarma, K. Combined Metrics for Quality Assessment of 3D Printed Surfaces for Aesthetic Purposes: Towards Higher Accordance with Subjective Evaluations. In Computational Science—ICCS 2020, Proceedings of the 20th International Conference Proceedings, Amsterdam, The Netherlands, 3–5 June 2020; Krzhizhanovskaya, V.V., Závodszky, G., Lees, M.H., Dongarra, J.J., Sloot, P.M.A., Brissos, S., Teixeira, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12143, pp. 326–339. [Google Scholar] [CrossRef]
- Kim, H.; Lin, Y.; Tseng, T.L.B. A review on quality control in additive manufacturing. Rapid Prototyp. J. 2018, 24, 645–669. [Google Scholar] [CrossRef]
- Wu, H.C.; Chen, T.C.T. Quality control issues in 3D-printing manufacturing: A review. Rapid Prototyp. J. 2018, 24, 607–614. [Google Scholar] [CrossRef]

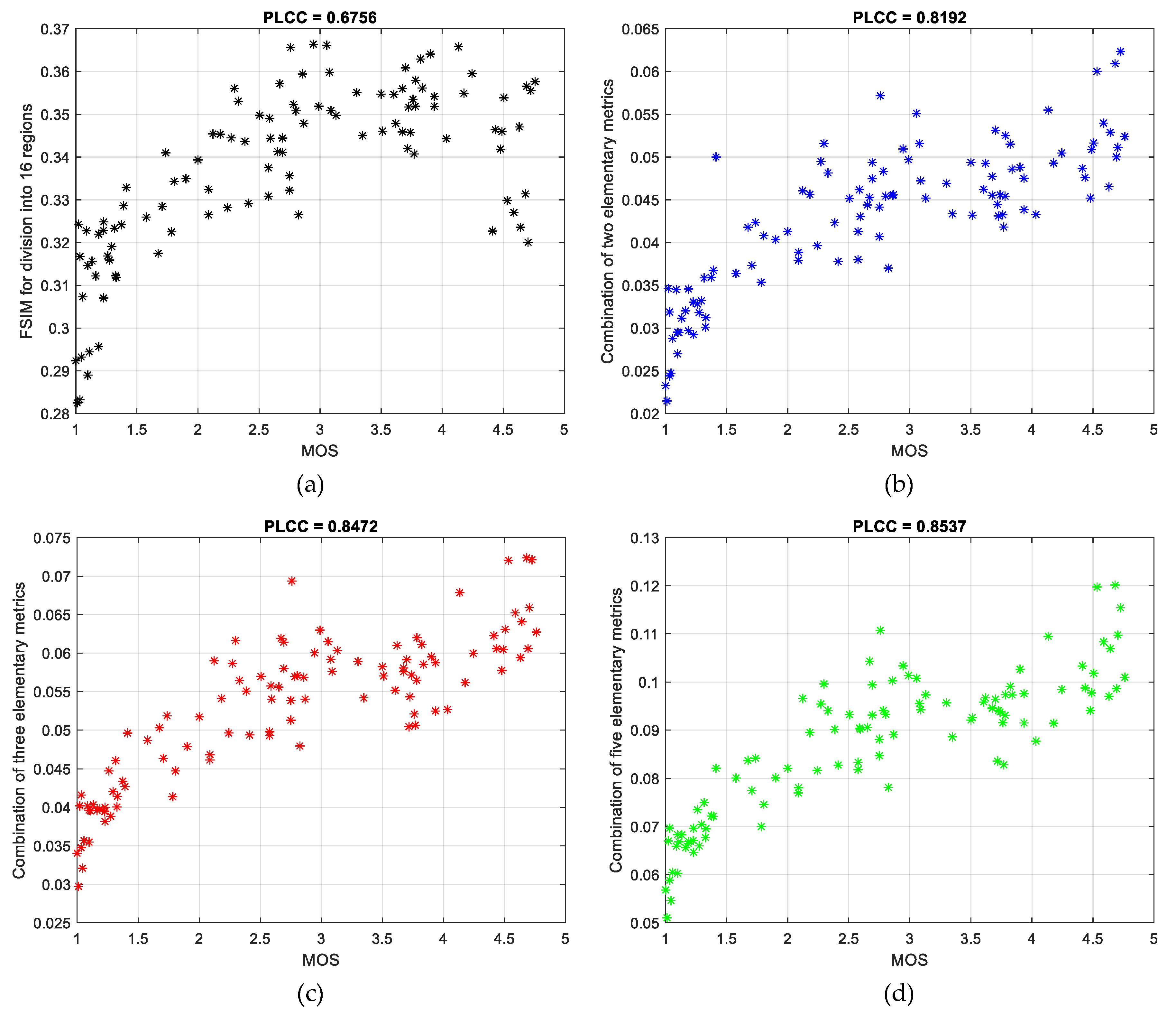
| Metric | Division into 16 Regions | Division into 9 Regions | Division into 4 Regions | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PLCC | SROCC | KROCC | PLCC | SROCC | KROCC | PLCC | SROCC | KROCC | |
| FSIM [34] | 0.6756 | 0.6865 | 0.5195 | 0.6820 | 0.6845 | 0.5185 | 0.6780 | 0.6826 | 0.5114 |
| CW-SSIM [32] | 0.5929 | 0.5823 | 0.4028 | 0.6323 | 0.6098 | 0.4232 | 0.5807 | 0.5633 | 0.3981 |
| AD-GSIM [40] | 0.4081 | 0.3515 | 0.2453 | 0.4020 | 0.3470 | 0.2414 | 0.3873 | 0.3324 | 0.2354 |
| DSS [38] | 0.4066 | 0.3523 | 0.2411 | 0.3842 | 0.3220 | 0.2210 | 0.3921 | 0.3176 | 0.2142 |
| AD-SSIM [40] | 0.4017 | 0.3574 | 0.2562 | 0.3834 | 0.3209 | 0.2270 | 0.3492 | 0.2932 | 0.2065 |
| SSIM [29] | 0.3996 | 0.4012 | 0.2746 | 0.3905 | 0.4039 | 0.2661 | 0.3048 | 0.3017 | 0.1938 |
| CSSIM4 [41] | 0.3596 | 0.3296 | 0.2354 | 0.3329 | 0.2818 | 0.1977 | 0.3233 | 0.2851 | 0.1991 |
| IW-SSIM [33] | 0.3549 | 0.3669 | 0.2619 | 0.3230 | 0.2997 | 0.2044 | 0.3169 | 0.2473 | 0.1627 |
| SR-SIM [36] | 0.3173 | 0.2441 | 0.1588 | 0.3174 | 0.2497 | 0.1652 | 0.3878 | 0.3160 | 0.2150 |
| MCSD [39] | 0.3106 | 0.2958 | 0.2164 | 0.3008 | 0.2889 | 0.2090 | 0.2952 | 0.2825 | 0.2051 |
| QILV [31] | 0.3092 | 0.1330 | 0.0868 | 0.3478 | 0.2662 | 0.1832 | 0.4316 | 0.3555 | 0.2534 |
| CVSSI [42] | 0.2558 | 0.2083 | 0.1370 | 0.2097 | 0.1492 | 0.0935 | 0.1667 | 0.1068 | 0.0593 |
| ESSIM [37] | 0.1865 | 0.2340 | 0.1631 | 0.1754 | 0.2354 | 0.1648 | 0.3160 | 0.2868 | 0.2026 |
| CSSIM [41] | 0.1523 | 0.1078 | 0.0724 | 0.1251 | 0.0755 | 0.0519 | 0.1293 | 0.0862 | 0.0632 |
| SSIM4 [41] | 0.1283 | 0.0852 | 0.0565 | 0.1031 | 0.0447 | 0.0304 | 0.1085 | 0.0673 | 0.0462 |
| GSM [35] | 0.1103 | 0.1689 | 0.1182 | 0.0991 | 0.1631 | 0.1133 | 0.2102 | 0.2253 | 0.1585 |
| RVSIM [43] | 0.0267 | 0.0198 | 0.0219 | 0.0546 | 0.0433 | 0.0395 | 0.0114 | 0.0247 | 0.0304 |
| Metrics | PLCC | Metrics | PLCC | Metrics | PLCC | Metrics | PLCC |
|---|---|---|---|---|---|---|---|
| FSIM + MCSD | 0.8192 | FSIM + SR-SIM | 0.7862 | FSIM + SSIM4 | 0.7581 | FSIM + RVSIM | 0.6875 |
| FSIM + DSS | 0.8029 | FSIM + AS-SSIM | 0.7861 | FSIM + ESSIM | 0.7377 | CSSIM + CSSIM4 | 0.6852 |
| FSIM + CVSSI | 0.8008 | FSIM + CW-SSIM | 0.7766 | FSIM + GSM | 0.7312 | FSIM + SSIM | 0.6809 |
| FSIM + IW-SSIM | 0.7981 | FSIM + CSSIM4 | 0.7719 | SSIM + AD-GSIM | 0.7081 | FSIM + RVSIM | 0.6762 |
| FSIM + AD-GSIM | 0.7921 | FSIM + CSSIM | 0.7593 | FSIM + QILV | 0.6952 | SSIM + CW-SSIM | 0.6731 |
| Metrics | PLCC | Metrics | PLCC | Metrics | PLCC |
|---|---|---|---|---|---|
| FSIM + CW-SSIM + MCSD | 0.8472 | FSIM + MCSD + GSM | 0.8270 | FSIM + MCSD + AD-SSIM | 0.8221 |
| FSIM + CW-SSIM + DSS | 0.8379 | FSIM + ESSIM + MCSD | 0.8256 | FSIM + MCSD + CSSIM | 0.8221 |
| FSIM + CW-SSIM + IW-SSIM | 0.8356 | FSIM + CW-SSIM + CSSIM4 | 0.8250 | FSIM + CVSSI + GSM | 0.8219 |
| FSIM + CW-SSIM + CVSSI | 0.8348 | FSIM + CW-SSIM + SR-SIM | 0.8246 | FSIM + MCSD + RVSIM | 0.8217 |
| FSIM + AD-SSIM + SR-SIM | 0.8341 | FSIM + CW-SSIM + AD-SSIM | 0.8239 | FSIM + DSS + AD-SSIM | 0.8213 |
| FSIM + CW-SSIM + AD-GSIM | 0.8301 | FSIM + MCSD + SR-SIM | 0.8238 | FSIM + ESSIM + AD-GSIM | 0.8213 |
| FSIM + DSS + ESSIM | 0.8284 | FSIM + MCSD + SSIM4 | 0.8225 | FSIM + MCDS + QILV | 0.8201 |
| FSIM + DSS + GSM | 0.8274 | FSIM + MCSD + SSIM | 0.8224 | FSIM + AD-GSIM + GSM | 0.8199 |
| Number of Regions | Metrics | PLCC | SROCC | KROCC |
|---|---|---|---|---|
| 4 | FSIM + CW-SSIM + MCSD + ESSIM | 0.8405 | 0.8431 | 0.6639 |
| FSIM + CW-SSIM + MCSD + GSM | 0.8474 | 0.8485 | 0.6710 | |
| FSIM + CW-SSIM + MCSD + ESSIM + GSM | 0.8565 | 0.8586 | 0.6826 | |
| 9 | FSIM + CW-SSIM + MCSD + ESSIM | 0.8463 | 0.8357 | 0.6558 |
| FSIM + CW-SSIM + MCSD + GSM | 0.8487 | 0.8385 | 0.6565 | |
| FSIM + CW-SSIM + MCSD + ESSIM + GSM | 0.8495 | 0.8397 | 0.6604 | |
| 16 | FSIM + CW-SSIM + MCSD + ESSIM | 0.8502 | 0.8453 | 0.6660 |
| FSIM + CW-SSIM + MCSD + GSM | 0.8514 | 0.8443 | 0.6653 | |
| FSIM + CW-SSIM + MCSD + ESSIM + GSM | 0.8537 | 0.8480 | 0.6748 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okarma, K.; Fastowicz, J.; Lech, P.; Lukin, V. Quality Assessment of 3D Printed Surfaces Using Combined Metrics Based on Mutual Structural Similarity Approach Correlated with Subjective Aesthetic Evaluation. Appl. Sci. 2020, 10, 6248. https://doi.org/10.3390/app10186248
Okarma K, Fastowicz J, Lech P, Lukin V. Quality Assessment of 3D Printed Surfaces Using Combined Metrics Based on Mutual Structural Similarity Approach Correlated with Subjective Aesthetic Evaluation. Applied Sciences. 2020; 10(18):6248. https://doi.org/10.3390/app10186248
Chicago/Turabian StyleOkarma, Krzysztof, Jarosław Fastowicz, Piotr Lech, and Vladimir Lukin. 2020. "Quality Assessment of 3D Printed Surfaces Using Combined Metrics Based on Mutual Structural Similarity Approach Correlated with Subjective Aesthetic Evaluation" Applied Sciences 10, no. 18: 6248. https://doi.org/10.3390/app10186248
APA StyleOkarma, K., Fastowicz, J., Lech, P., & Lukin, V. (2020). Quality Assessment of 3D Printed Surfaces Using Combined Metrics Based on Mutual Structural Similarity Approach Correlated with Subjective Aesthetic Evaluation. Applied Sciences, 10(18), 6248. https://doi.org/10.3390/app10186248