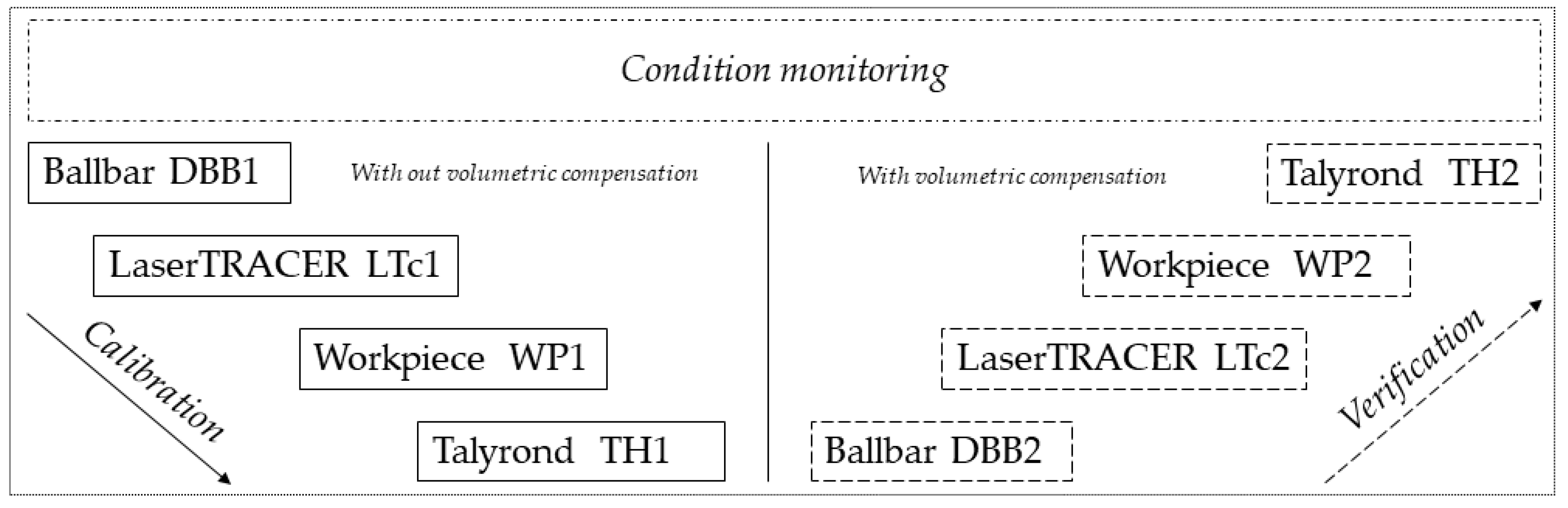
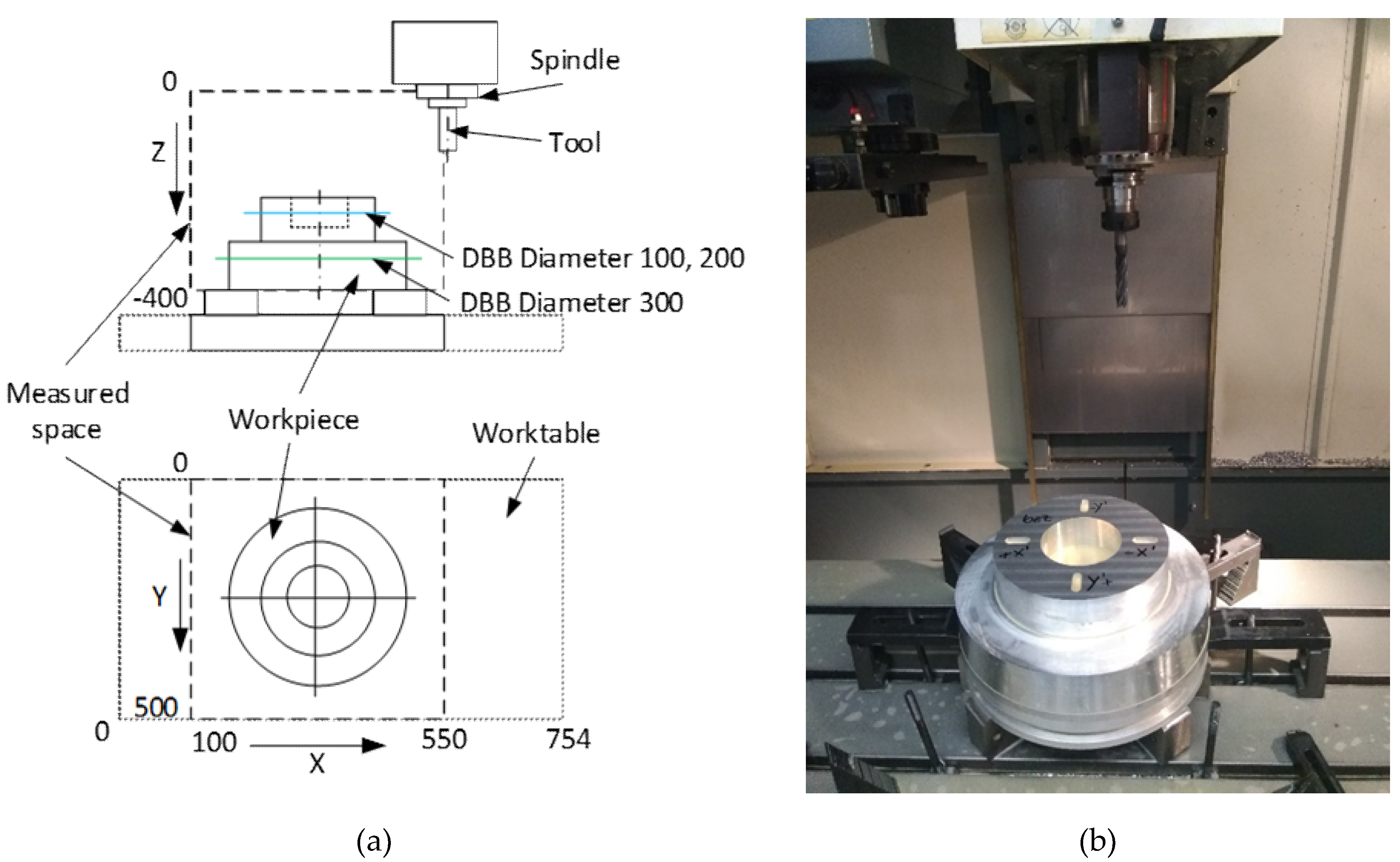
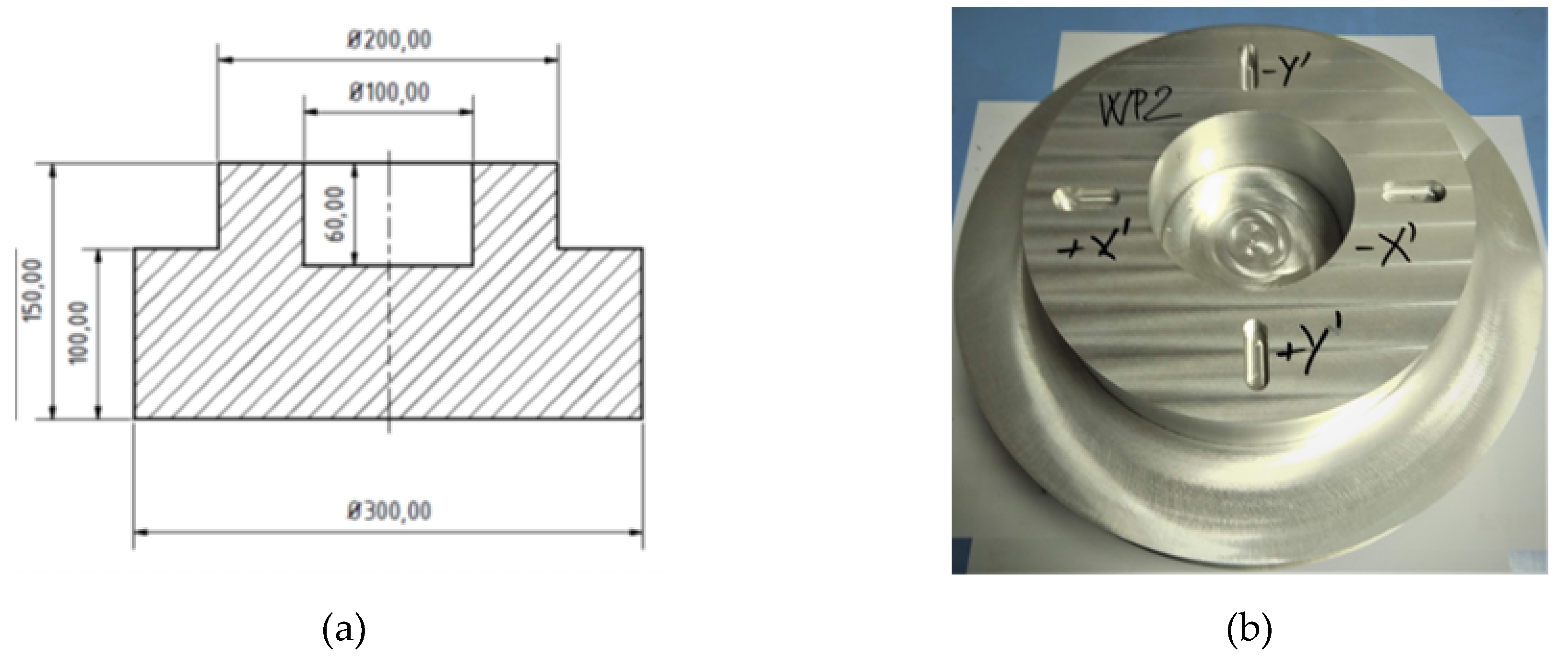
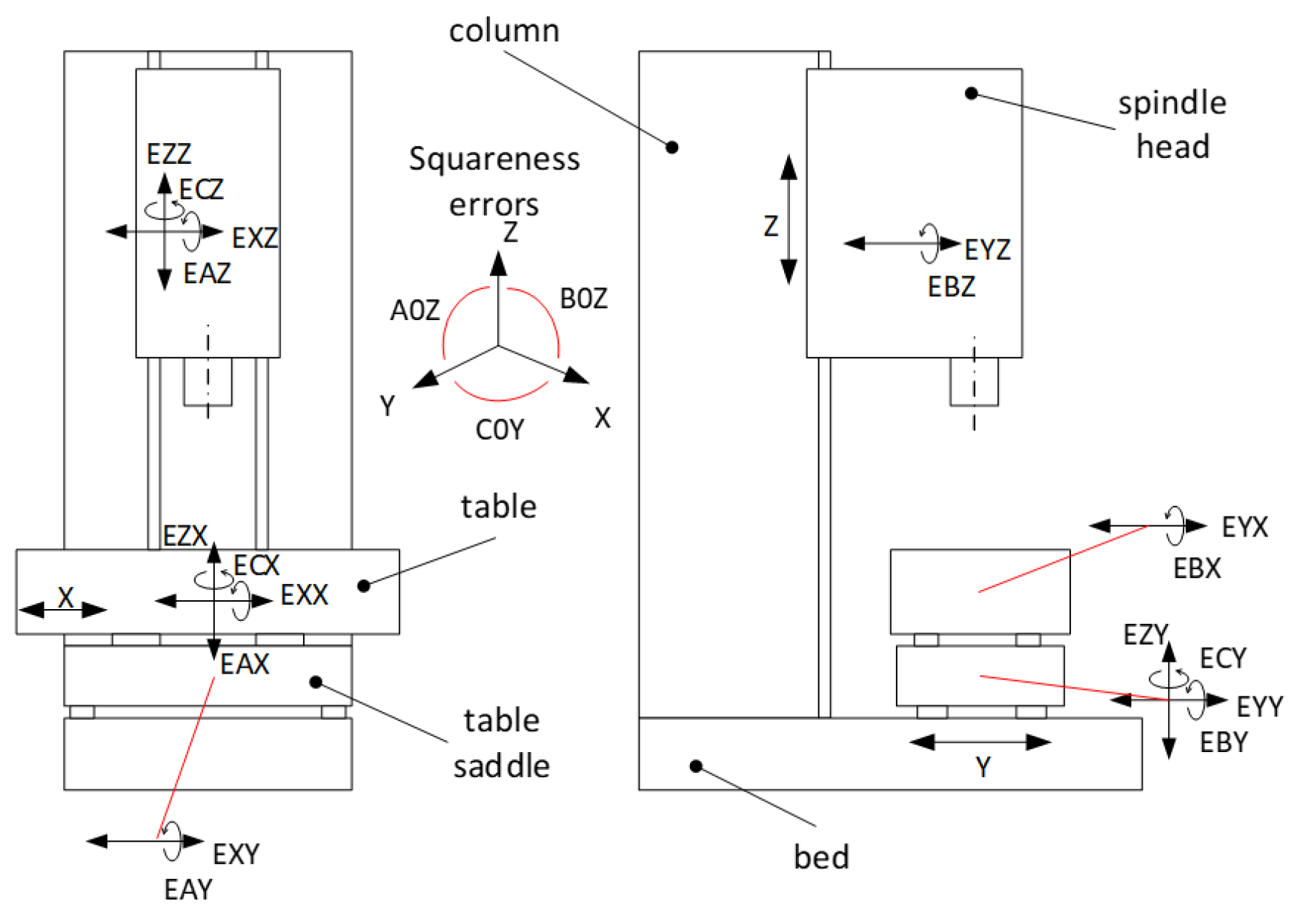
1. Introduction
The increase of the production accuracy of machine tools is a continuous process with the involvement of all manufacturers. Production accuracy is a machine feature that is also an indicator of competitiveness; its continuous improvement is also required by the machine users themselves.
The percentage of quasi-static errors and the resulting accuracy of the three-axis machine tool was described in 2000 by Ramesh [
1]. Here, the percentage was 60–70%. Subsequently, Ibaraki expanded this hypothesis in his 2010 publication [
2] with up to 80% for five-axis machine tools. The increase in the proportion of quasi-static errors is caused by the kinematic pair of rotary axes of five-axis machines.
There are two options to ensure high geometric accuracy. The time-consuming and more expensive option uses a mechanically adjusted machine, i.e., no software compensation. This option is offered by machine manufacturers, especially for their special machines, which are supplied to industries with extremely high requirements for long-term dimensional stability. Another option is the use of software compensation, eliminating the basic sources of machine tool errors. These sources include geometric, thermal, dynamic and tool wear errors. [
3]. Quasi-static errors are defined as errors in the relative position of the tool centre point (TCP) and the workpiece; these change slowly over time. They are directly related to the structure of the machine tool itself and can be divided into geometric, kinematic and thermal errors.
There are several ways of achieving the goal of increasing production accuracy or assessing machine accuracy. These include the use of commercially available software compensations for CNC machine tools, supplemented by new, more effective methodical procedures for measurement and evaluation and the deployment of new measurement technologies. The robustness of a compensation method, with respect to the human factor, is presented in reference [
4]. In reference [
5], the effect of volumetric compensation on the improvement of the geometric accuracy of a small machining centre, by up to 60%, is presented. The increase of the volumetric accuracy of a five-axis machining centre using a reconfigurable artefact is presented in [
6]. The use of tracking interferometers to assess 2D geometric errors influenced by temperature change is described in [
7]. The utilisation of manufacturing accuracy data for rotational error assessment is presented in [
8], linear axis compensation procedures in publications [
9,
10], the use of the Ballbar for machine tool error assessment and compensation in [
11], a comprehensive assessment of measurement methods, overexertion and their effects on large machines in [
12] and the use of on-machine tool measurement in [
13]. When assessing the effects of machine geometric errors on a future workpiece, it is necessary to consider all effects that increase measurement uncertainty and those that minimise these uncertainties.
Another group is the development of new mathematical models that describe the geometry of the machine, which specifies the position of the TCP [
8]. Publication [
14] describes the principle of weighted multilateration and its influence on the positioning of a point in the machine’s working space, including its application to the small machining centre presented in [
15]. The data obtained from the measurement can then be used as compensation values sent for further processing of the CNC program from the CAM. A compensation algorithm for reducing geometric errors by changing the CNC program is published in [
16]. These are mostly designed for basic measuring devices that are commonly available on the market and have already been established in the field of machine inspection and diagnostics.
The same is true of temperature models of machine tools and their compensations [
17], where the thermo-elastic behaviour of machine tool structures and their influence on TCP is described in [
18]. This area also includes temperature measurements of machine tools [
19]. From publication [
20], it is obvious that it is necessary to ensure correct positioning of the temperature sensors in order to obtain valid data for correction of the measured data. Here, this information was used to verify machine stability and to correct the thermal expansion of machine components.
Individual measuring devices can also be categorised according to the size of the machine tools. This classification is divided into small, medium and large CNC machine tools according to the size of the working space and the loading of the machine from the workpiece [
21]. Not all machine tool sizes can be used with all devices and they should be selected according to the accuracy of the measuring equipment.
Geometric accuracy is assessed according to ISO 230. These procedures are usually part of verification when deploying new methods of compensation of machine tools or models to predict machine accuracy [
22]. It is based on the basic methods of compensating for the geometric errors of the tillage machines summarised in publication [
23]. Another standard that can be used to verify the accuracy of a machine is the tests based on ISO 230-4 that mostly use the Ballbar. Publication [
24] presents a methodology for predicting component accuracy based on circular interpolation and the FE model. The use of the Ballbar, a measuring device and the circular interpolation test for the diagnosis of three-axis machine tools is described in [
25] and the use of circular interpolation for measuring the geometric errors of five-axis machines is described in publication [
26]. Roundness error has not been improved.
The working accuracy of a machine can be verified using ISO 10791-7 of the standardised component [
27]. This workpiece is specified to verify the production accuracy of three-axis kinematics with the option of assessing several dimensional and shape deviations. Publications [
22,
28] describe the effect of machine load on the position of the rotary axis, as well as the resulting orientation errors. When assessing the geometric errors of the machine, it is necessary to consider the machining forces and heat dissipation in the machine.
This publication is focused on describing the dependence between the volumetric accuracy of the machine and the resulting working accuracy, assessed on the error of workpiece roundness under finishing conditions of machining. The dependence between volumetric accuracy and roundness error is described in publication [
29], according to ISO 230-4.
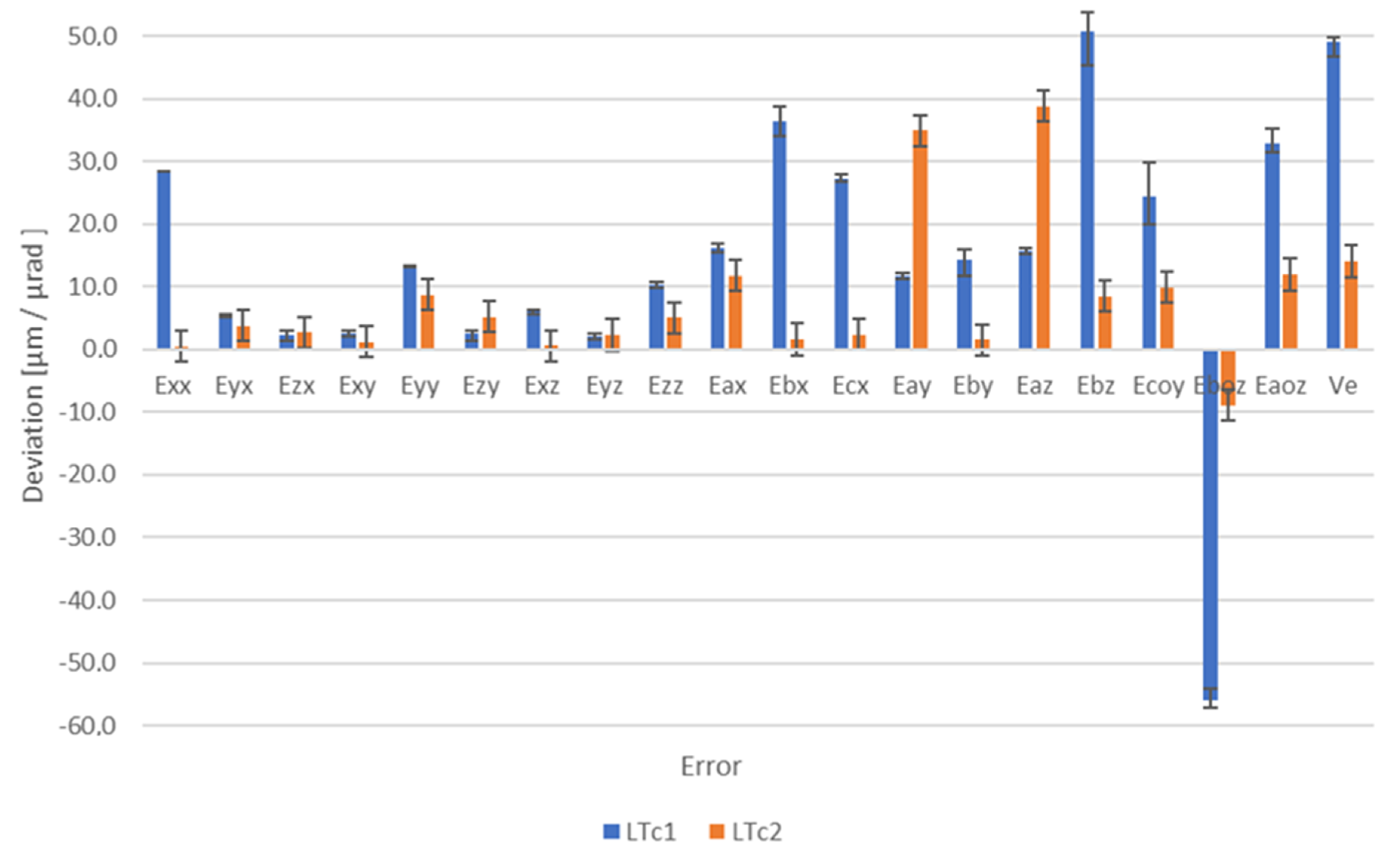
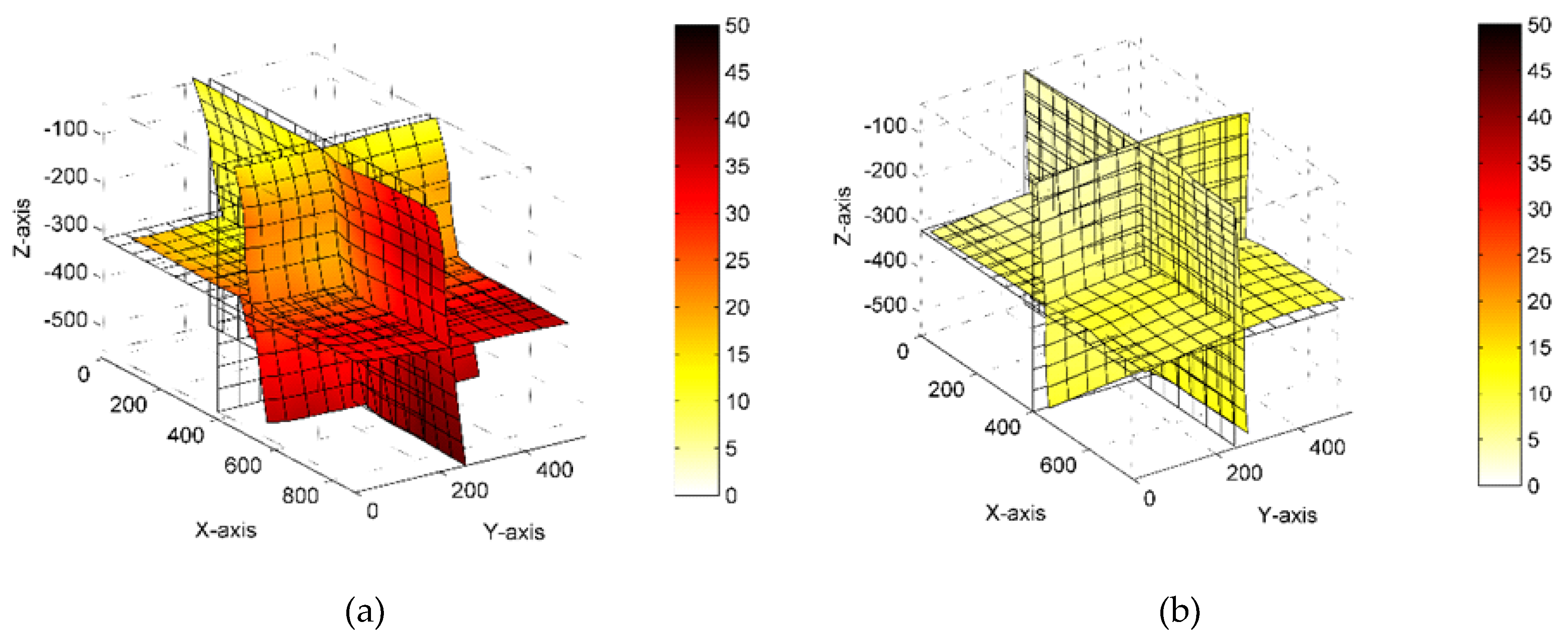
The presented experiment focuses on the verification of the correlation between the volumetric accuracy of machines and production accuracy. In this case, geometric accuracy is represented by volumetric accuracy. The measurements of volumetric accuracy are based on the indirect method, using the self-guiding laser interferometer LaserTRACER. This method is described, for example, in [
3]. In order to assess the influence of volumetric accuracy on the resulting working accuracy, it is important to observe constant ambient conditions due to the repeatability of the production of test workpieces. The negative effect of temperature on the change in volumetric accuracy is described in [
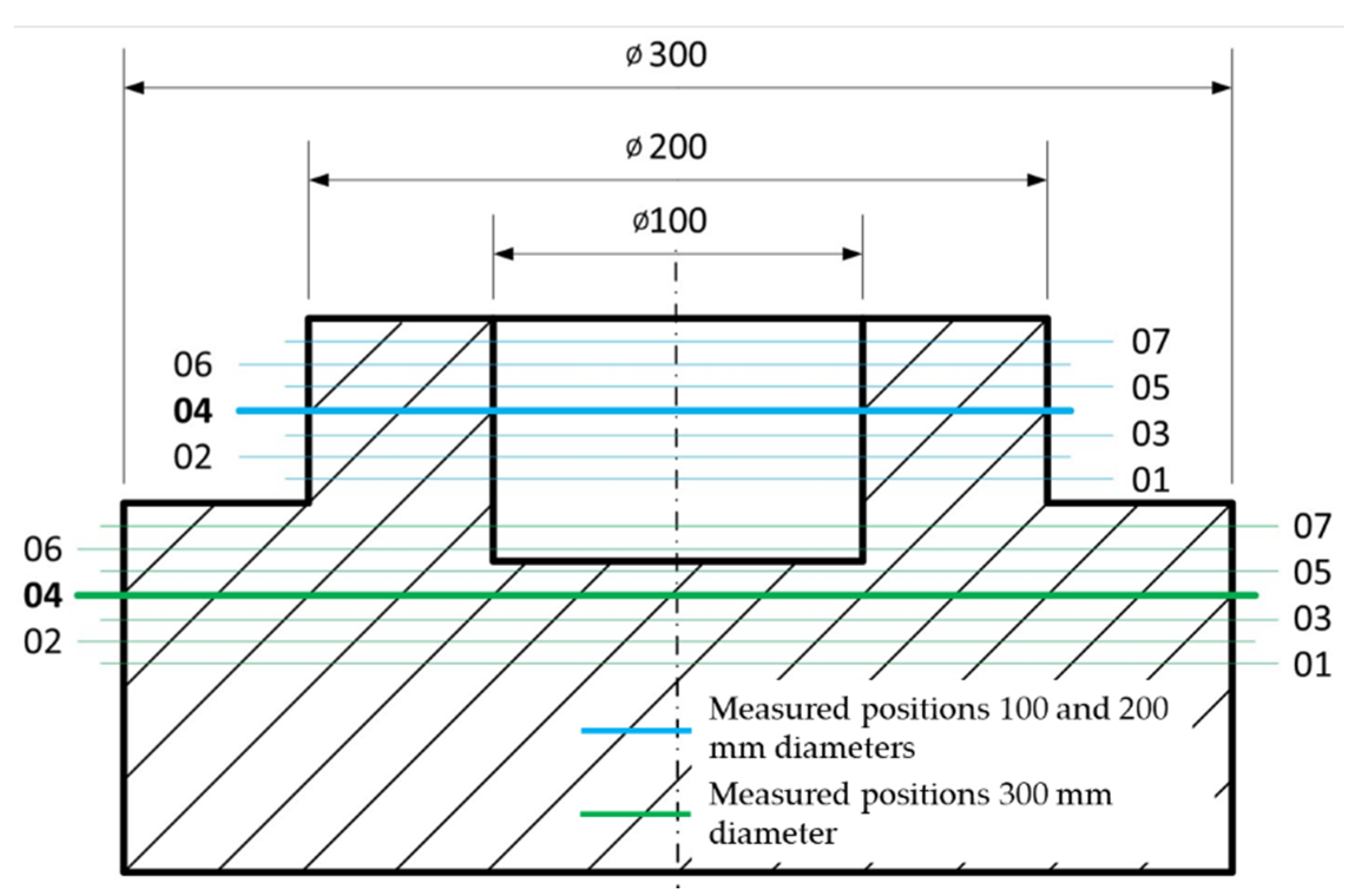
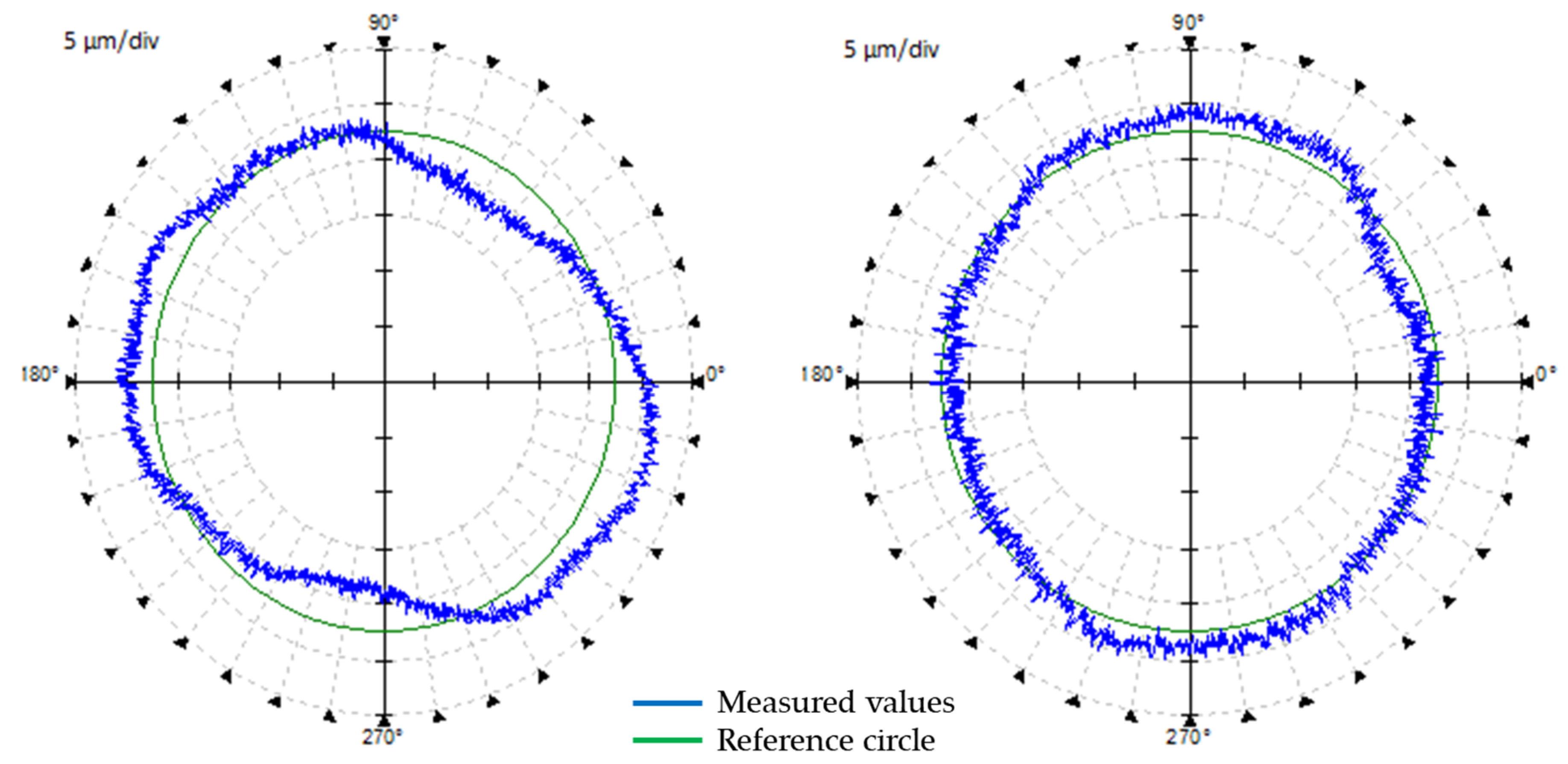
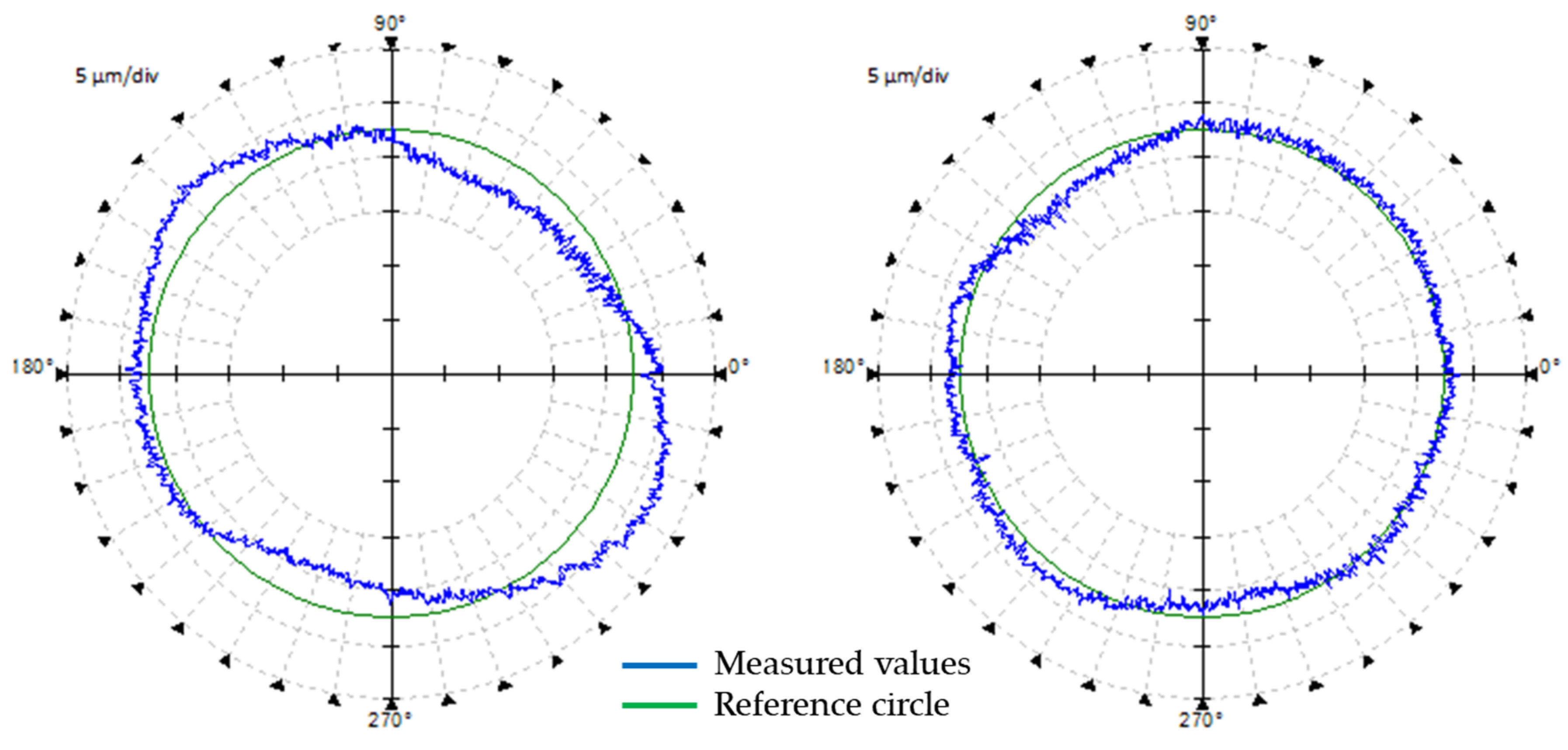
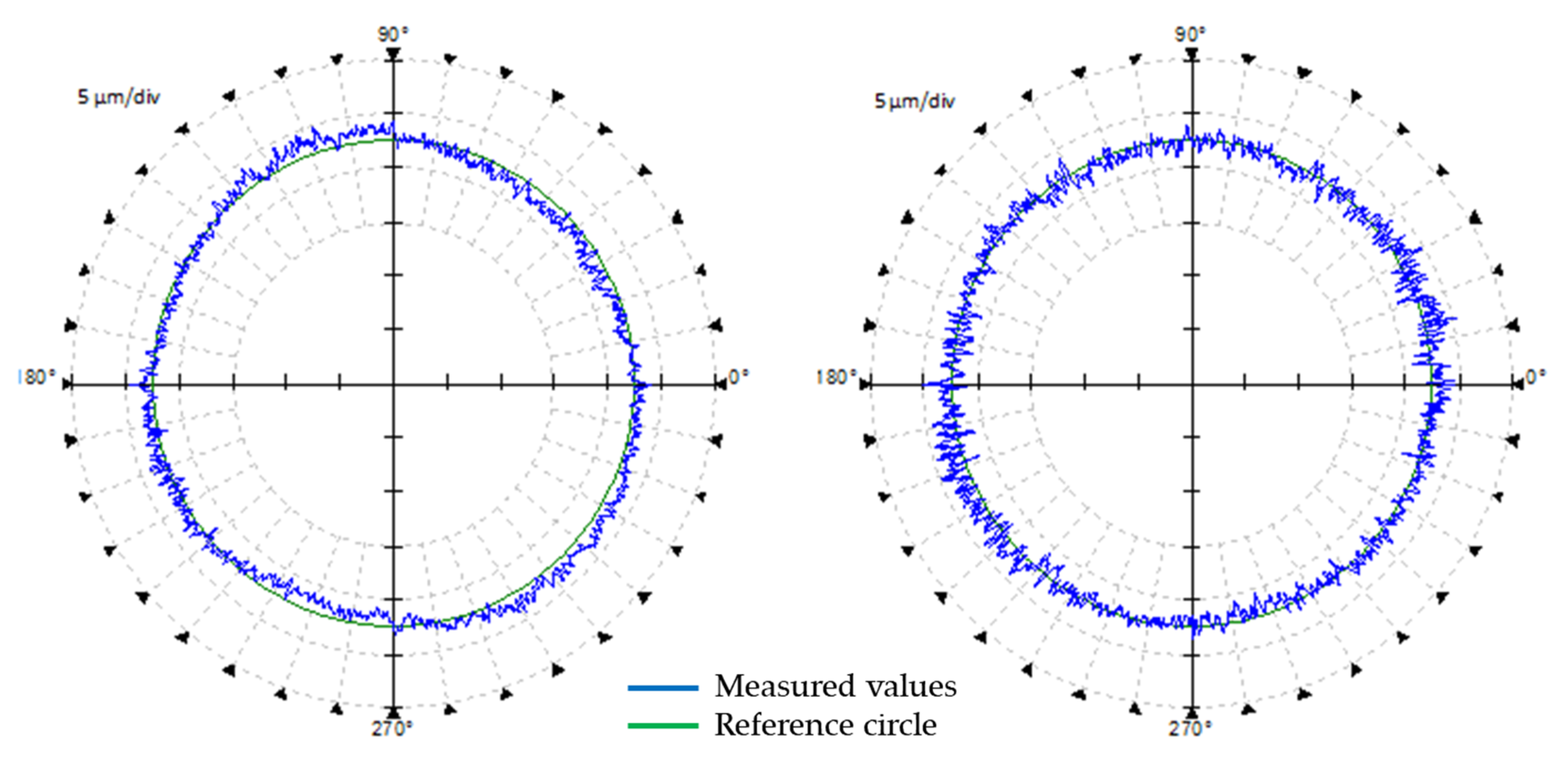
30]. Production accuracy is represented in a test workpiece designed to verify roundness error. This is then verified by the Talyrond 595S measuring device. The roundness results of the workpiece are then compared to those obtained with the circular interpolation test, according to ISO 230-4. The measuring device used is the Ballbar QC20-w.
4. Discussion
In
Figure 18, a dependence can be seen between the roundness error of the workpiece and the machined diameter for machining circular parts (
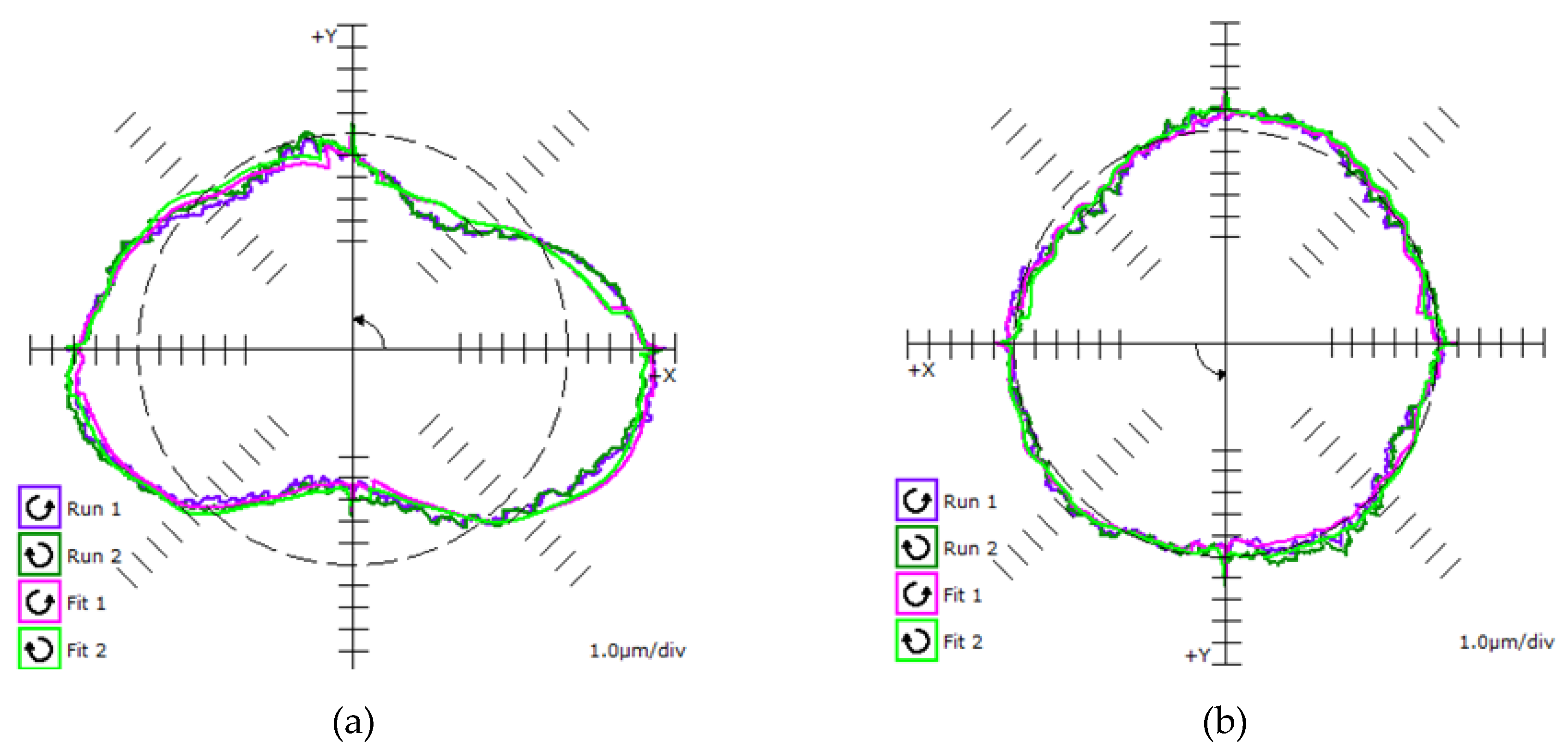
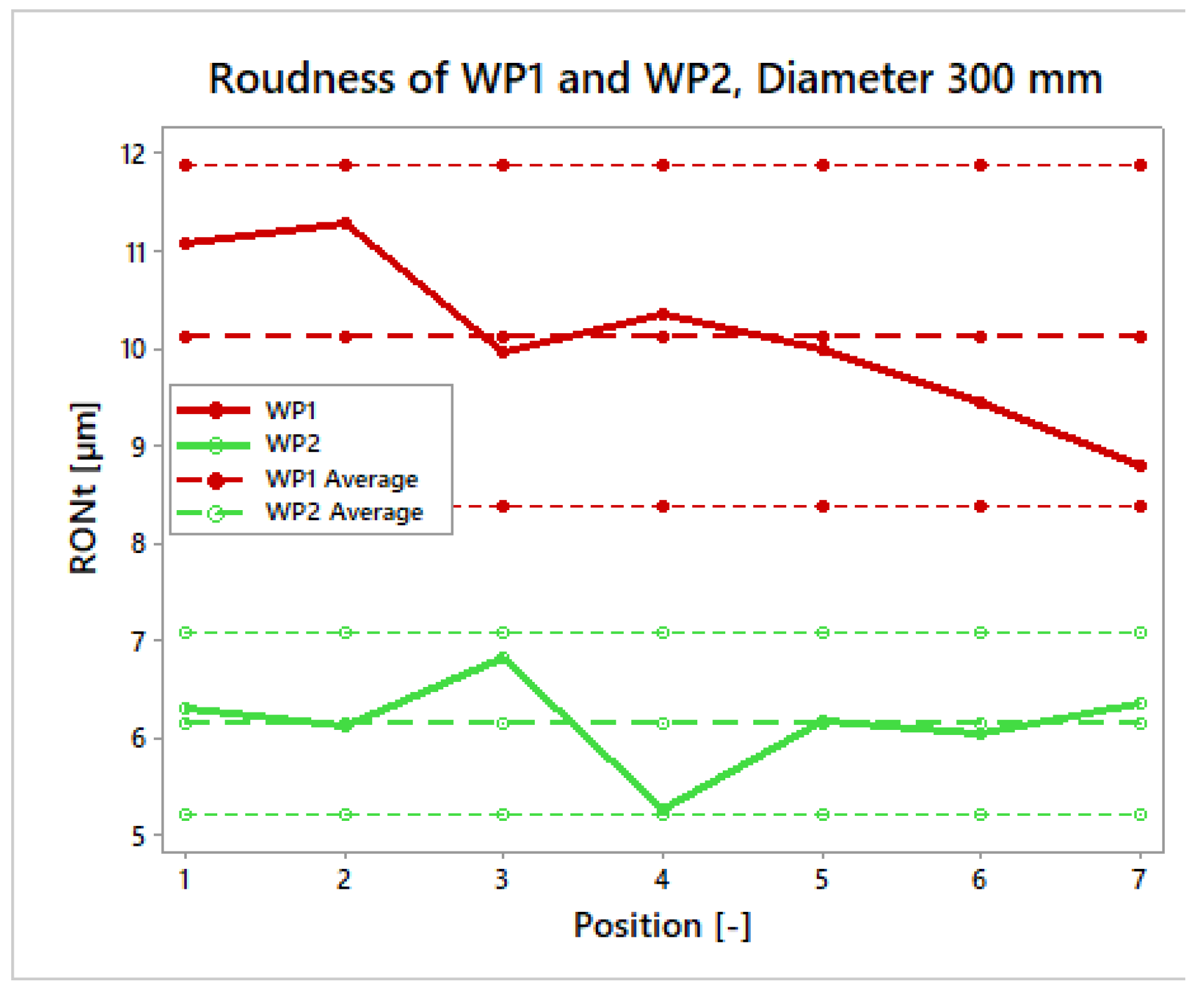
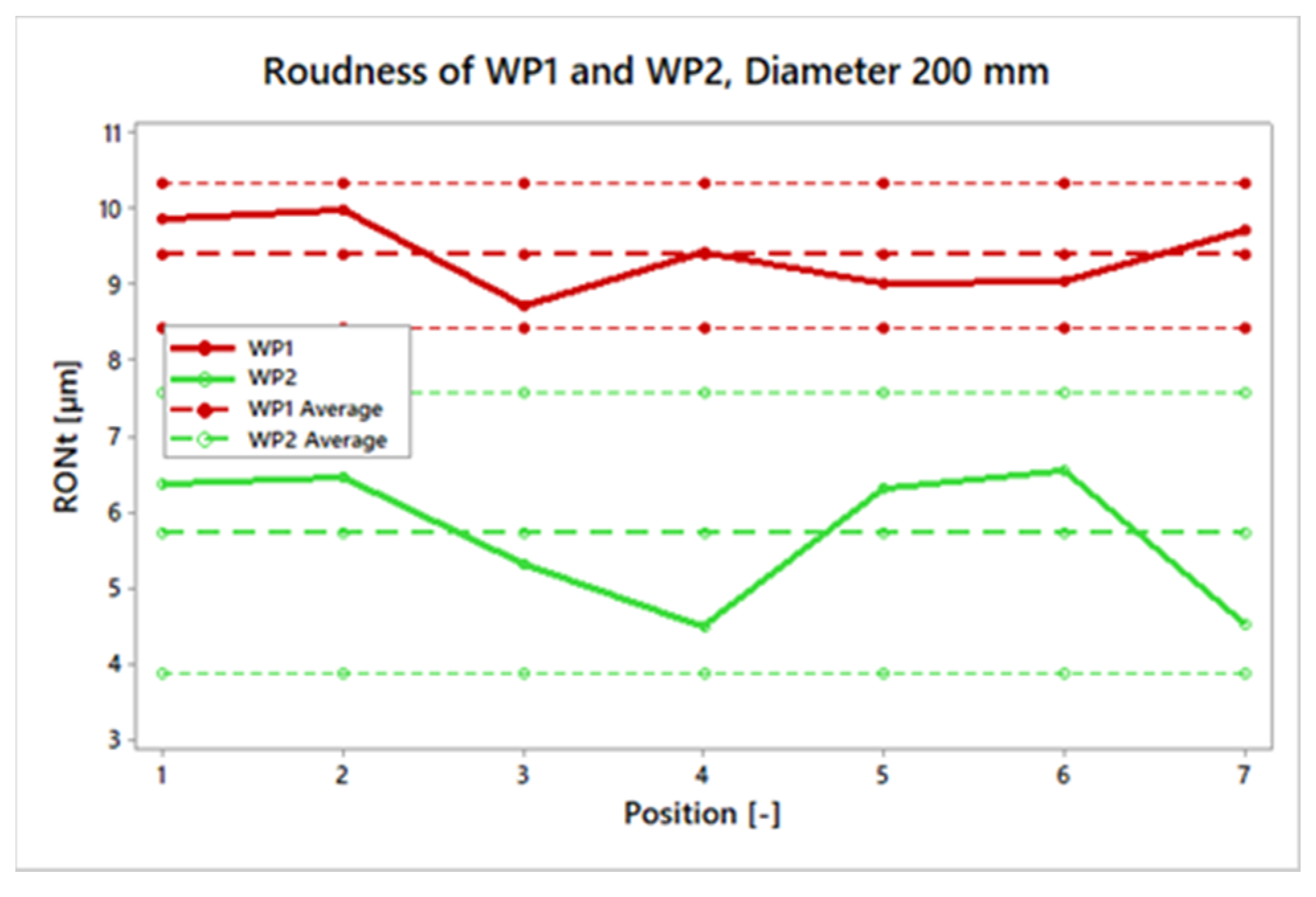
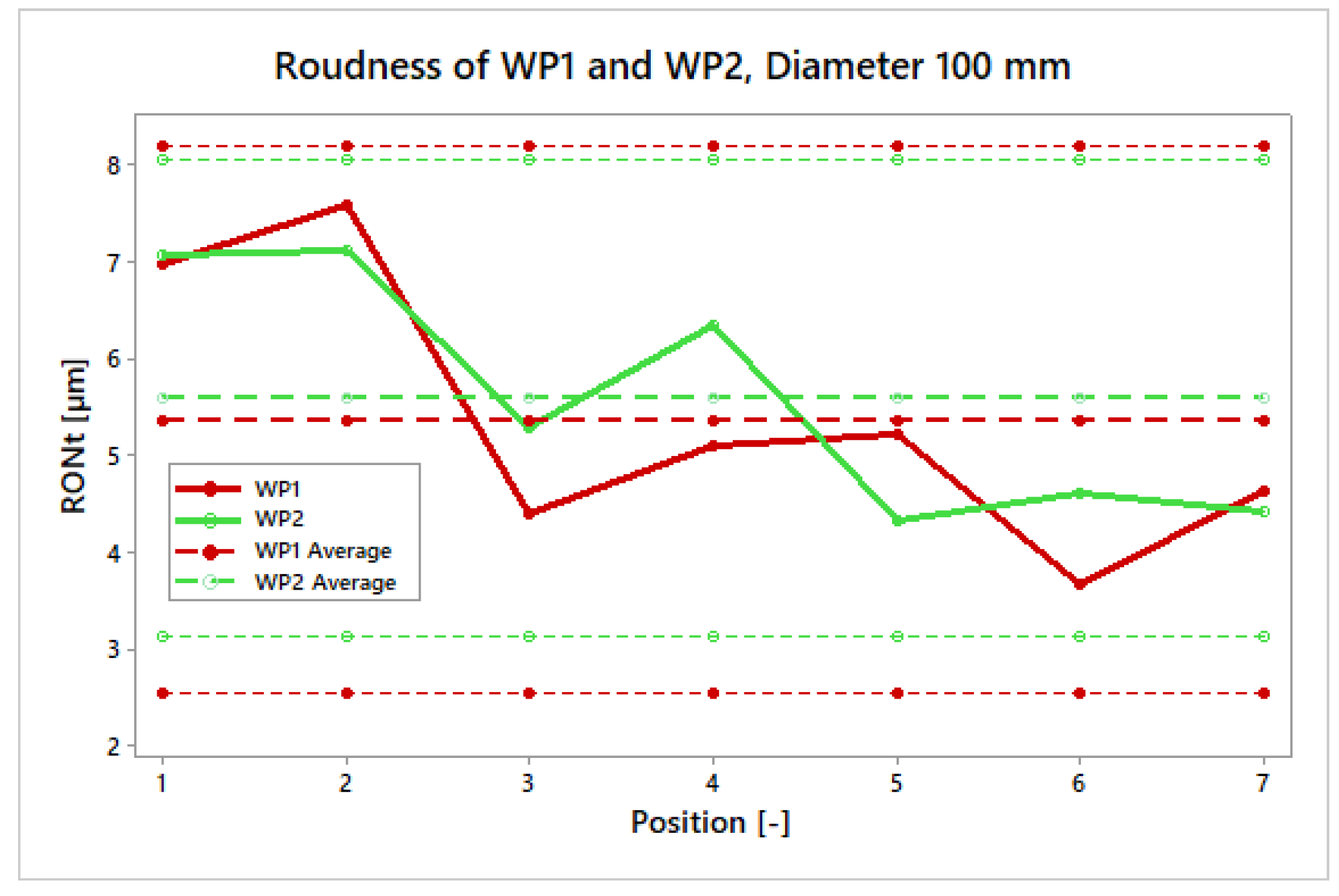
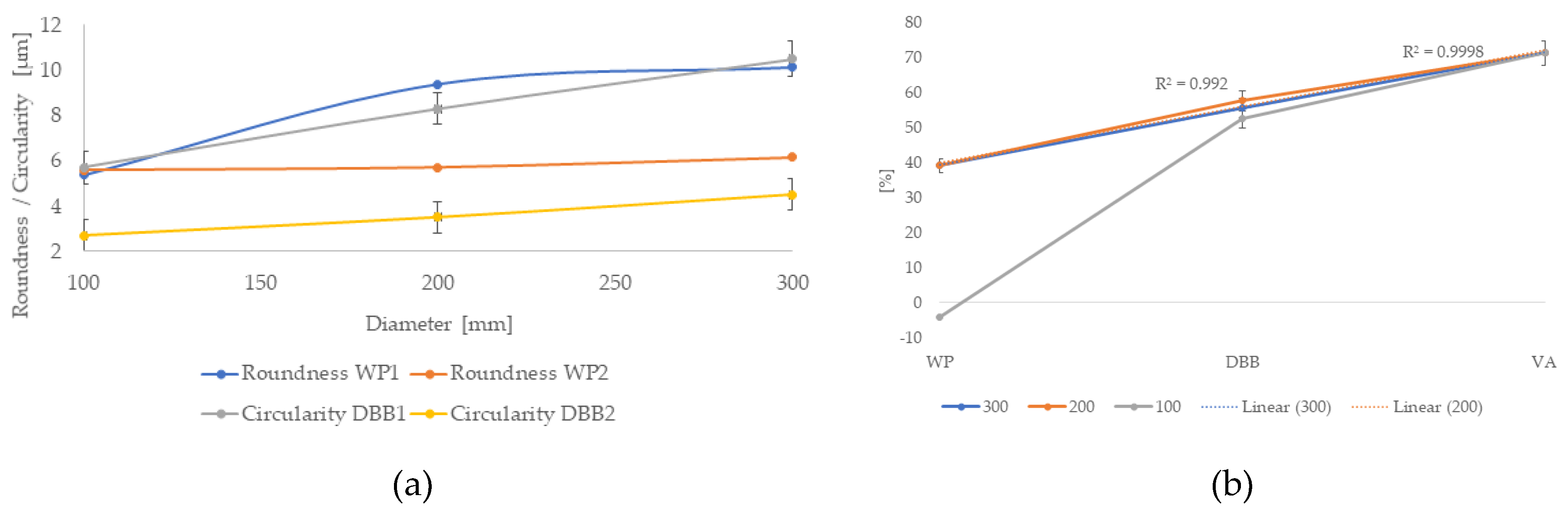
Figure 18a). Furthermore, with WP2, a relatively constant value of roundness can be observed for all inspected diameters. With WP1, an improvement in RONt can be seen with the decrease of machining diameter. Circularity errors DBB1 and DBB2 then show a linear relationship between the size of the error and the machined diameter. The size of the circularity error increases with the increase in machined diameter.
Figure 18b shows a graph of the improvement in percentage versus the volumetric accuracy (VA), circularity (DBB) and roundness (WP) before the volumetric compensation and after the volumetric compensation of the machine. With outside milling technology and diameters of 300 and 200 mm, a strong linear relationship can be seen between WP–DBB–VA with determination indexes I2 equal to 0.9998 (300 mm) and 0.992 (200 mm), respectively. On the 100 mm diameter, even a 4% deterioration of roundness can be seen. This deterioration can be attributed to another type of machining technology and clearance specification due to system stiffness. A description of this behaviour will be the subject of further research.
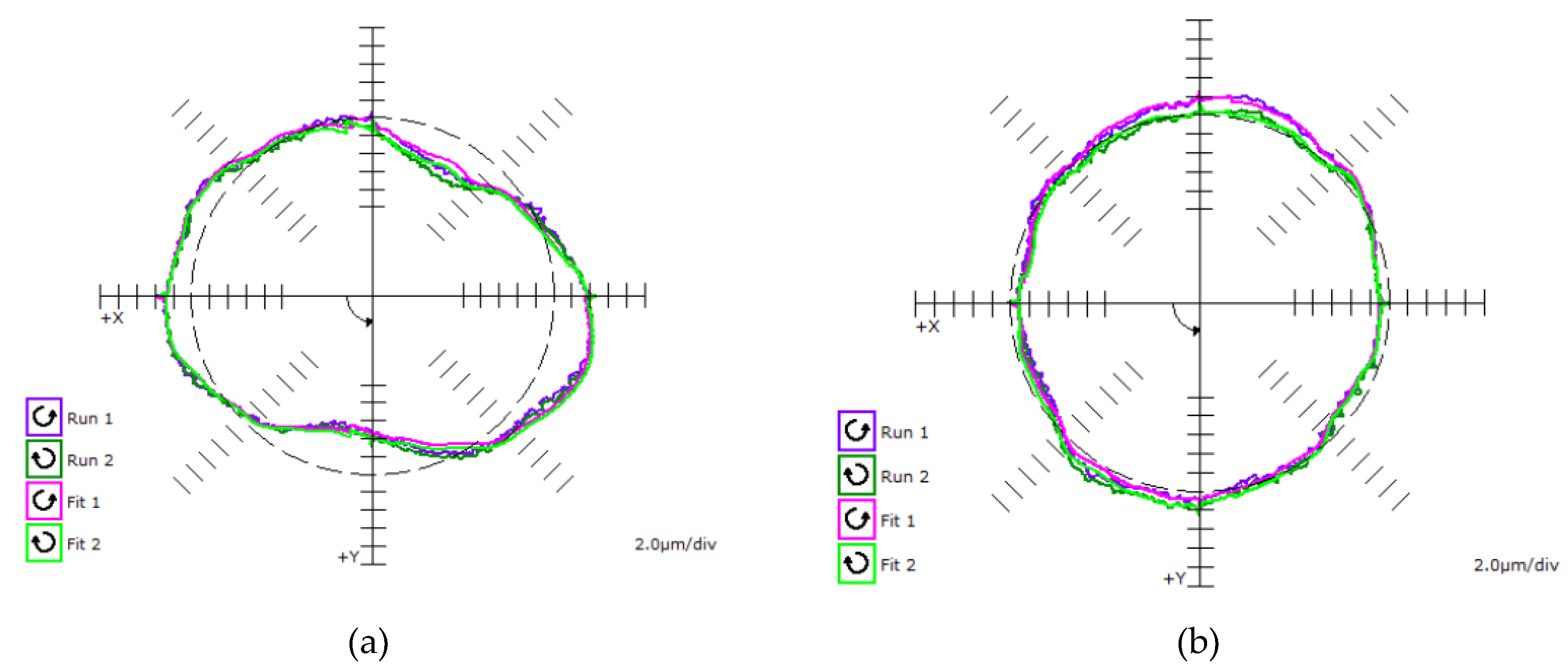
Figure 19 shows the dependence between the squareness measured in the XY machining plane without load from the Ballbar device (DBB1 and DBB2) and the RONt obtained from workpiece measurement (TH1 and TH2). A higher correlation rate can be seen for DBB1and TH1. This can be attributed to a higher squareness error value, which also results in a higher rate on the workpiece. In contrast, the squareness error of DBB2 was reduced by 72% compared to DBB1. Here, squareness error does not have such a dominant effect on the resulting RONt, which is also reflected by the correlation between DBB2 and TH2. The difference between DBB2 and TH2 may be due to the fact that, with less geometric error, the proportion of the error wedged from the cutting forces increases.
The acquired knowledge about the behaviour of machine tools in terms of geometric accuracy can be further used to predict the dimensional and shape errors of workpieces. The results are applicable to finishing technologies where machining forces are negligible and do not burden the machine with deformation from static compliance.
5. Conclusions
This paper describes a new, complex approach for verifying the dependence between the geometric, volumetric and working accuracy of CNC machine tools. The conclusions of this work serve further research in the dimensional and form deviation prediction of workpieces. The experiment proves that the resolution of the method corresponds to the requirements for precise production, where deviations are in the dimension range from 5 to 10 µm.
An improvement in the volumetric accuracy of a small three-axis machine tool by 70% results in an up to 58% improvement in circularity in an unloaded state, measured according to ISO 230-4, and a 40% improvement in the RONt of the workpiece under finishing conditions of machining.
It is also evident from the results of the experiment that circularity error is significantly affected by the squareness error of two relative axes in the machining plane, both in the circular interpolation test of two linear axes according to ISO 230-4 and the impact on the workpiece RONt.
In a small CNC machine tool, including MCV754QUICK, a 40% improvement in RONt can be achieved through the activation of volumetric compensation. Here, the net measurement time was 50 min. The time it took to position the LaserTRACER, implement the compensations and verify using the Ballbar QC20-w was approximately 125 min. This is a highly effective way of increasing production accuracy in terms of machine measurement time, implementation of compensation tables and verification.
Further research in this area will be focused on the verification of dimensional accuracy under various machining conditions.
These results have the potential to further streamline compensations, leading to an increase in production accuracy, and can be used to predict the geometric, volumetric and production accuracy of machine tools, based on the principle described, for example, in [
34,
35].