1. Introduction
Sport-specific performance training is required in all sports to achieve a high international level. In volleyball, an important performance criterion correlating with competition level and a main objective in volleyball conditioning programs is to increase jump height [
1]. This is commonly achieved through various types of strength and power training [
2,
3]. On the other hand, volleyball is known for its severe risk of ankle injuries during jumping [
4] that cannot be prevented by strength training alone [
5]. Therefore, traditional performance training should be accompanied by additional injury prevention programs [
4]. The most frequent injury is ankle sprains [
4], which are associated with chronic ankle instability and an increased chance of recurrence [
5]. Neuromuscular impairment due to traumatized mechanoreceptors of the ligaments and muscles in the ankle is expected to cause the recurrence of sprains [
5]. Unsurprisingly, neuromuscular and proprioceptive training has shown positive effects and is recommended to prevent ankle injuries [
5,
6]. Such training consists of balance exercises on stable and unstable platforms or the combination of, e.g., balance, plyometric, and sport-specific exercises [
6]. The objective is to improve proprioception and neuromuscular responses. Thus, mechanoreceptors and stabilizing muscles around the ankle sense and process the risk of balance loss early and can react in time to prevent falls and injuries.
Recent technical-coordinative jump training [
7] may have targeted both performance and prevention aspects during volleyball spike jumping. The concept was based on differential training [
8,
9], which applies movement variability and allows for adaptations in neuromuscular activation patterns [
10]. Differential training has been shown to provide good transferability of training effects on sport-specific jump performance when compared with traditional concepts [
11]. The program focused on spike jump performance determinants [
12], centering around approach velocity, feet position, and velocity conversion strategy through the dominant leg (i.e., side of the striking arm). The conversion strategy is associated with neuromuscular activation patterns in the lower limbs [
13]. Therefore, the emphasis and implementation of numerous variations in these movement characteristics is expected to constantly create proprioceptive and neuromuscular stimuli for ankle stabilization. The effect of such differential jump training on prevention can be operationalized via balance assessment, since reduced balance performance can be associated with an increased risk of injury [
14]. Both injury prevention and balance performance are affected by the proprioceptive and neuromuscular systems that stabilize and maintain balance [
5,
6,
15,
16]. Therefore, a transfer of effects on balance performance during such differential jump training can be presumed.
For balance assessment, quantitative posturography via force platforms is considered the gold standard and superior to functional balance tests with respect to sensitivity and objectivity [
17]. The most frequently analyzed characteristic is the excursion of the center of pressure (CoP) [
18]. However, there are many variables that can be calculated from the CoP. A systematic review of 32 published articles involving CoP analyses recommended including both distance (e.g., sway area) and time–distance (e.g., mean velocity) based variables [
19]. Its authors advised against the usage of minimal, maximal, and peak-to-peak values as they represent severe data reduction, great variance, and low reliability [
19]. It seems unclear whether to alternatively prioritize analyses on fractal dimensions or on resultant horizontal data [
19]. The drawbacks of posturography via CoP are the numerous variables and uncertainty about the best choice among variables to reflect balance performance [
19]. Moreover, the high costs, complex handling, and space required for the equipment often complicate its usage in clinical settings [
17].
A handy and validated alternative with fair to excellent reliability is found in computerized wobble boards (WBs) [
20]. WBs are unstable platforms frequently used in clinical and therapeutic settings. They can be equipped with, e.g., accelerometers to collect the WB tilt angle that can then be processed by software and displayed on a screen in real time. Besides their practical handling, the strength of WBs is the single output variable of balance performance (i.e., time spent at ~0° tilt). Moreover, classical assessment of the CoP when standing on a force platform can also be applied to standing on a WB [
21]. Poor correlation between WB performance and the outcome of one of the most frequently used validated balance tests, the Y Balance Test [
20], can be explained by the complexity of the underlying mechanisms of postural control [
14] and different test-specific skills of postural control [
20]. Since WBs are a common tool in sprain prevention programs [
5] and are suitable for balance assessment in individuals with chronic ankle instability [
16], their usage is reasonable for the context of the current study (i.e., injury prevention in high-risk individuals).
The objective of this study was to determine the effect of a differential-training-based jump intervention on postural control in high-level female volleyball players. It was hypothesized that a 6-week differential jump training regimen that induces proprioceptive and neuromuscular stimuli for ankle stabilization would improve WB balance performance and CoP characteristics.
3. Results
One ankle sprain occurred during the control phase, with no effect on data collection and presentation. One participant missed the first measurement; removal from analyses was not required thanks to the statistical approach.
The performances at the three measurement sessions, covariance specifications of the final models, and the effects of measurements are presented in
Table 1.
The best model with measurement as the only predictor for WB performance included a fixed and a random intercept, a fixed slope for measurement, and an error. It detected a main effect for measurements (F(2,58.24) = 173.83, p < 0.001), decrease from control to pre-intervention (β = −8.86, SE = 2.36, p < 0.001), and increase from pre- to post-intervention (β = 40.69, SE = 2.29, p < 0.001). The random intercept for participants yielded 65.95% of this model’s overall variance (p < 0.05).
The final model with the best fit consisted of 18 parameters (
X2 = 29.29, ∆
df = 13,
p < 0.01, compared with the initial model). It was expressed by the following equation, where
Yis (WB performance),
Xis (measurement),
Zis (leg), and ε
is (error) vary as functions of individual observations (
i; level 1 variable) and participants (
s; level 2 variable).
b0 and
u0s represent a fixed and a random intercept, respectively;
b1,
b2, and
b3 define the gradients.
Besides the effects of measurements (
Table 1), no effect was found for leg (
F(1,26.10) = 0.33,
p = 0.57), but an effect was found for the interaction of measurement by leg (
F(2,20.19) = 6.98,
p < 0.01). The random intercept for participants yielded 0.41% of this model’s overall variance (
p < 0.05).
Additional fixed and random effects did not produce significantly improved models (best alternative model including player position as a random effect, compared with the final model: X2 = 1.14, ∆df = 1, p = 0.28).
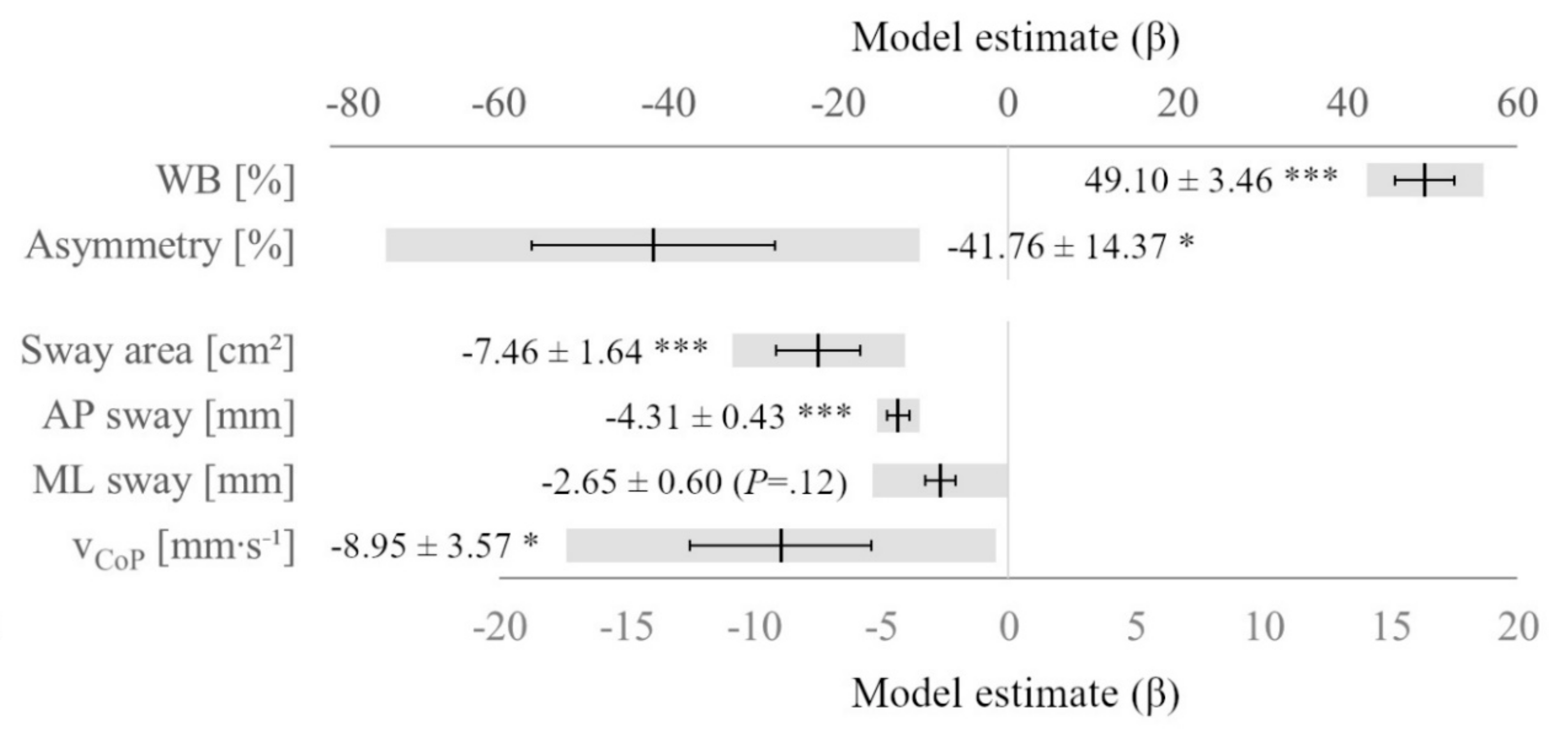
Model-based effects between the control and intervention phases are displayed in
Figure 2.
The final model for WB performance over the phases consisted of three parameters and was expressed by the following equation, where
Yi (WB performance),
Xi (phase), and ε
i (error) vary as functions of individual observations (
i).
b0 represents a fixed intercept and
b1 represents the gradient.
The inclusion of random intercept, phase, leg, player position, and interactions as fixed and/or random effects did not deliver improved models (best models for each additional effect in comparison with the final model: 0 ≤ X2 ≤ 8.06, 1 ≤ ∆df ≤ 20, 0.09 ≤ p ≤ 1). In these alternative models, no effects were found for leg (F(1,46) = 2.87, p = 0.10), leg by phase (F(2,46) = 1.53, p = 0.23), position (F(1,46) = 2.24, p = 0.14), or position by phase (F(2,46) = 1.48, p = 0.24).
For all other criterion variables, the final models included significant random intercepts for participants.
4. Discussion
The objective of this study was to investigate the effects of sport-specific differential jump training on balance performance and associated injury risk in elite female volleyball players. A mixed model analysis was deemed suitable because it is superior to traditional statistical approaches in the current scenario [
29,
30,
31]. The first reason for this was increased power, as mixed models are capable of handling missing data instead of removing a participant from analyses. This applied in the current data since one participant missed the first measurement session. Second, mixed models differentiate between interindividual variance and random error variance. Ignoring occurrent interindividual variability leads to over- or underestimation of statistical significance in repeated measures analysis of variance; in fact, this generates inaccurate results and can affect the overall interpretation [
31]. The significant effects of the random intercept for participants indicated interindividual variance [
29,
31] in the current study and supported the usage of mixed models. In the simple model for WB performance, the random intercept explained two-thirds of the overall variance. This is a great but not exceptional amount (e.g., values of >50% are systematically reported in sleep deprivation) and underlines the relevance of accounting for interindividual variance [
31]. The reduced (yet significant) variance in the more complex model is probably due to the added effects explaining variance that was previously absorbed by the random intercept.
The results showed decreased balance performance during the control phase. This was not surprising as decreased performance during the competitive season is known in volleyball and is explained by increased physiological loads [
7,
22]. Sway area and ML sway increased significantly, which is considered detrimental for postural control. Also, WB performance, AP sway, mean CoP velocity, and inter-limb asymmetry tended (0.08 ≤
p ≤ 0.36) to develop unfavorably. During the intervention, all variables improved significantly (except for AP sway, only indicating (
p = 0.35) a beneficial development).
WB performance is a valid single outcome reflecting postural control [
20], and it was found to be decreased in subjects with chronic ankle instability, which is associated with increased risk of ankle sprains [
16]. Previous data showed that healthy limbs scored 19.6–21.8 s (i.e., 65.33–72.66%) in WB performance [
16]. In the current study, WB performance was comparably low during the control (27.02 ± 13.18%) and pre-intervention (19.60 ± 11.31%) measurements. This indicates and corroborates the assertion that volleyball players are at high risk for ankle sprains [
4], since reduced balance performance is associated with increased ankle instability [
16] and injury incidence [
6]. After the 6-week intervention, WB performance (59.49 ± 16.16%) almost reached the level of the previously reported healthy limbs [
16]. Interestingly, there is some evidence that it takes 8–10 weeks of neuromuscular training to reduce injury risk to a baseline level [
5]. Therefore, it can be presumed that a prolonged intervention of the current type may have closed the gap between the currently achieved WB performance and the baseline level of healthy limbs.
CoP variables were considered insightful in addition to WB performance and were selected in agreement with a review on CoP analyses [
19]. This review recommends the consideration of multiple variables because reports are controversial, no single gold standard is apparent, and various variables may reflect different aspects of postural control [
19]. In the case of conflicting findings, individual assessment of the CoP variables allowed for specific interpretation of single characteristics. However, the developments of all CoP variables were in line with the change in WB performance, showing detrimental trends during the control phase and beneficial changes during the intervention phase. Based on this, we cannot conclude that specific CoP variables were more suitable for WB performance than others. Moreover, the data do not indicate that specific CoP variables reflect different aspects of postural control on WB. Despite mean velocity being the most reliable CoP variable [
19], its values should be interpreted with caution. Mean velocity easily gives the misleading impression of reflecting adaptability (i.e., quick adjustment of CoP to keep the center of mass within the base of stability). However, the mean velocity is calculated as the total path of the CoP normalized by time [
19]. Therefore, it reflects total sway and does not provide additional information about adaptability. No recommendation was found in the literature to properly quantify adaptability in balance performance.
Decreased inter-limb asymmetry is considered desirable. Therefore, a detrimental trend during the control phase and a beneficial change during the intervention phase were observed. The recommended equation to calculate asymmetry includes the smaller of the two values from both legs as the denominator [
28]. Thus, asymmetry values rapidly approach 100% if the smaller value is close to 0, even when only a small absolute discrepancy between both values exists. Such values usually do not occur in the analyses of net peak vertical ground reaction forces where this equation was applied previously [
28]. However, this problem was identified in one case during the current study and should be considered in future investigations. This data point was excluded from further analyses. Removal of this data point did not change the statistical outcome.
The results of the comparison of developments during both phases (
Figure 2) are in line with the analyses across the three measurement sessions (
Table 1). Throughout all variables, beneficial trends were observed during the intervention when compared with the control phase. ML sway was the only variable where this trend did not reach statistical significance (
p = 0.12). However, the full range of the 95% CI was found to be on the negative (i.e., beneficial) side of the scale. Therefore, it can be stated with 95% confidence for this study that the intervention induced a beneficial effect on ML sway compared with the control phase. Considering the large sizes of the model estimates in comparison with the baseline values during the control and pre-intervention measurements, the intervention produced a great, beneficial effect on postural control and inter-limb asymmetry.
The lack of a main effect of leg on performance implies that any leg-specific factors contributing to balance performance (e.g., previous injuries, chronic instability) were distributed equally to both legs. This result indicates that, in general, both legs performed comparably. However, the training program specifically stressed the usage of the dominant leg for approach velocity conversion, and an interaction effect of measurement by leg was observed. Probably, the focus of the jump training on the dominant leg induced different stimuli and resulted in different adaptations in the two legs.
For player position, no main or interaction effects were found. This suggests that, first, position was not a crucial factor in balance performance for volleyball players and, second, training stimuli do not need to be position-specific to achieve improvements.
Neuromuscular prevention training may only be effective in individuals with previous injuries [
5]. Volleyball players are known to be a high-risk group with frequent ankle injuries [
4]. The current data suggest that the participants’ balance performance prior to intervention was poor, even in comparison with individuals with chronic ankle instability [
16]. Therefore, the same effects of training may not be expected in individuals with no history of injuries. However, transferability of the current findings to other high-risk sports and previously injured individuals seems reasonable.
The primary focus of the training program was to improve sports-specific jump performance via coordinative adaptations [
7]. Jump height increased by 11.9%, and promising effects on biomechanical determinants were reported in detail [
7]. Improvements in balance performance and ankle stabilization were expected side-effects thanks to neuromuscular stimuli that accompanied the implemented movement variations in the program. The positive effects of the differential jump training program on both jump and balance performance support its potential for combining two effects that are usually targeted separately. A repeated effect for balance performance may be expected, as a review on ankle sprains [
5] suggested increased risk and training effects after reoccurring injuries. After every ankle sprain, the injury risk can be reduced to baseline risk via neuromuscular training within 8–10 weeks [
5]. However, the repeated effect of the same program was not tested in the current study.
The longitudinal design of this study could be discussed as a limitation. This is a common difficulty; previously published investigations [
7,
22] applied the same study design and, thus, these data serve as a suitable reference. The control and intervention phases were comparable in terms of factors that were deemed potentially influential (except for the intervention program itself). All factors were reported and accounted for during the statistical analyses and interpretations. We are not aware of other factors that contributed to the training effects in a phase-specific fashion. A cross-sectional approach was not feasible for ethical reasons and due to the accessibility of such high-level female athletes.
To achieve the observed improvement in spike jump height, biomechanical understanding of specific performance determinants is required, which could be a challenge for coaches [
7]. This is not the case regarding the effect on balance performance. The current training program did not target certain balance determinants specifically. The applied movement variations were expected to affect the dynamics around the ankle joints and thus induce neuromuscular stimuli for ankle stabilization. Therefore, it can be concluded that these nonspecific stimuli are the essential factor to generate the observed adaptations in postural control. This makes the program practical for a range of coaches, given that neuromuscular stimuli are delivered. It may be presumed that the great coordinative challenge in ballistic balance during the jumping variations has a positive effect on the static balance performance.
A longer intervention period (8–10 weeks) may result in even larger effects [
5]. Preventive effects were not directly measured in this study but can be expected based on the observed effect on postural control and the associated injury risk [
6], especially for interventions conducted immediately after sprains [
5] and in high-risk individuals. Due to its low physiological loads and complementary effects in jump height and postural control, the program is feasible during the competitive season for the whole team. It is also recommended for individuals who cannot fully participate in regular training after an ankle sprain.