Novel Resource Allocation Techniques for Downlink Non-Orthogonal Multiple Access Systems
Abstract
1. Introduction
- An optimal user pairing approach based HNG algorithm is proposed that considers pairing of only two users at each subchannel. This algorithm guarantees an optimal performance of both the sum rate and energy efficiency maximization process in a downlink NOMA system. For comparison, the performance of the proposed algorithm is compared with the center-based user pairing (CEB) method proposed in [16].
- The sum rate maximization problem is formulated by considering SIC for each user in the subchannel in which the constraints are the minimum acceptable data rate and the maximum available transmission power at the BS. To solve this problem and obtain the optimal power for each of the paired users in a subchannel, a power allocation solution is proposed based on Karush–Kuhn–Tucker (KKT) conditions (PKKT). Then, the closed-form optimal power allocation solution for the multiplexed users is obtained. The PKKT solution is applied after pairing users based on HNG to obtain the optimal sum rate in NOMA. Thus, we refer to this technique as NOMA-PKKT-HNG.
- The energy efficiency maximization problem is formulated with power constraint consideration, and SIC is applied to reduce complexity at the receiver. To solve this problem and obtain the optimal power for the multiplexed users, we propose a power allocation solution using PDKL. The formulated objective function is in fractional form. Therefore, the DKL algorithm is used to transform into linear form (subtractive function) and iteratively solve the problem with considerable error tolerance. The PDKL solution is applied after pairing users based on HNG to obtain the optimal energy efficiency in NOMA. Thus, we refer to this technique as NOMA-PDKL-HNG.
2. Related Works
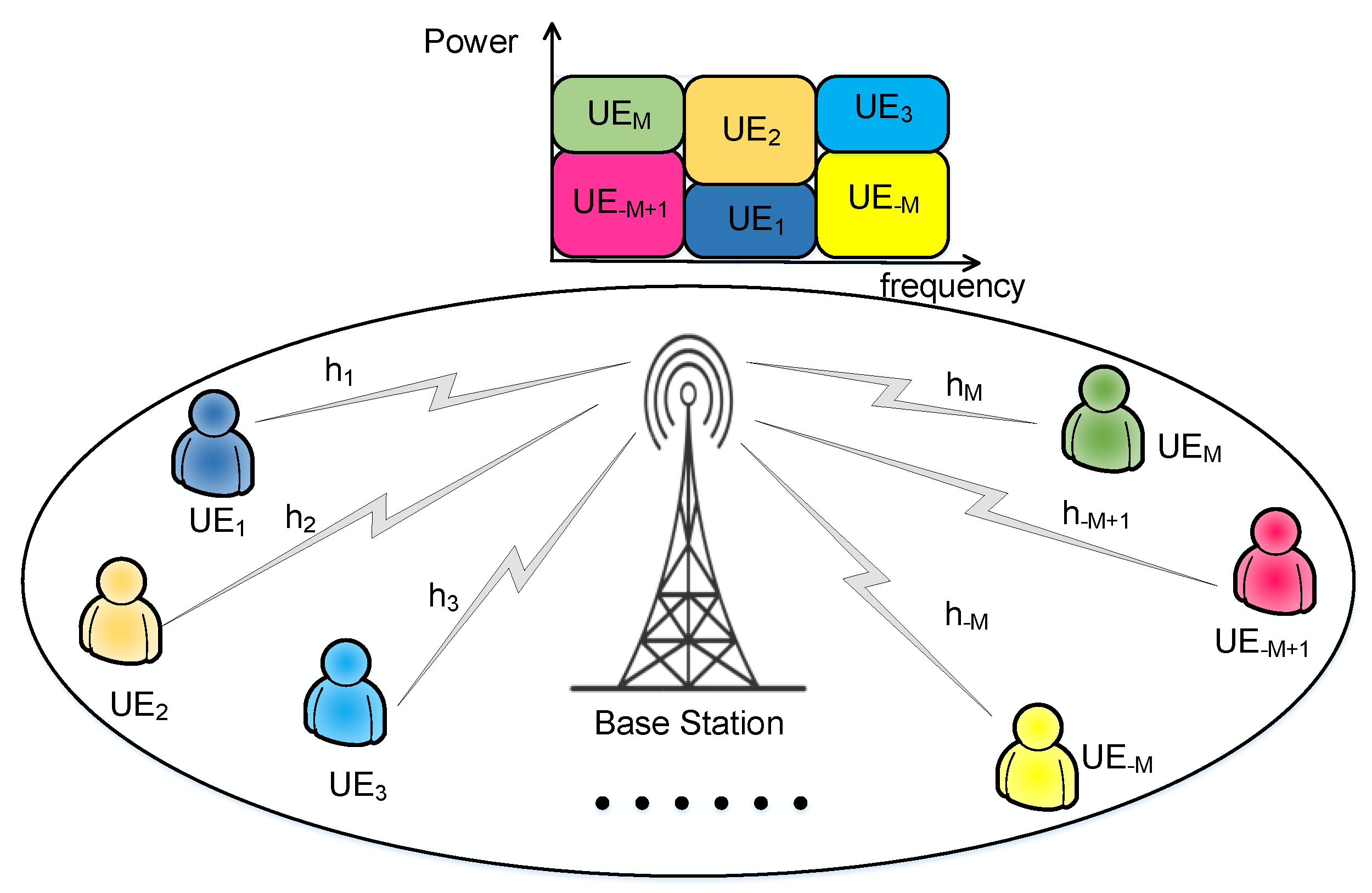
3. System Model and Performance Metrics
3.1. System Model
3.2. Performance Metrics
3.2.1. Throughput
3.2.2. Energy Efficiency
3.2.3. Fairness
4. Proposed Resource Allocation Techniques
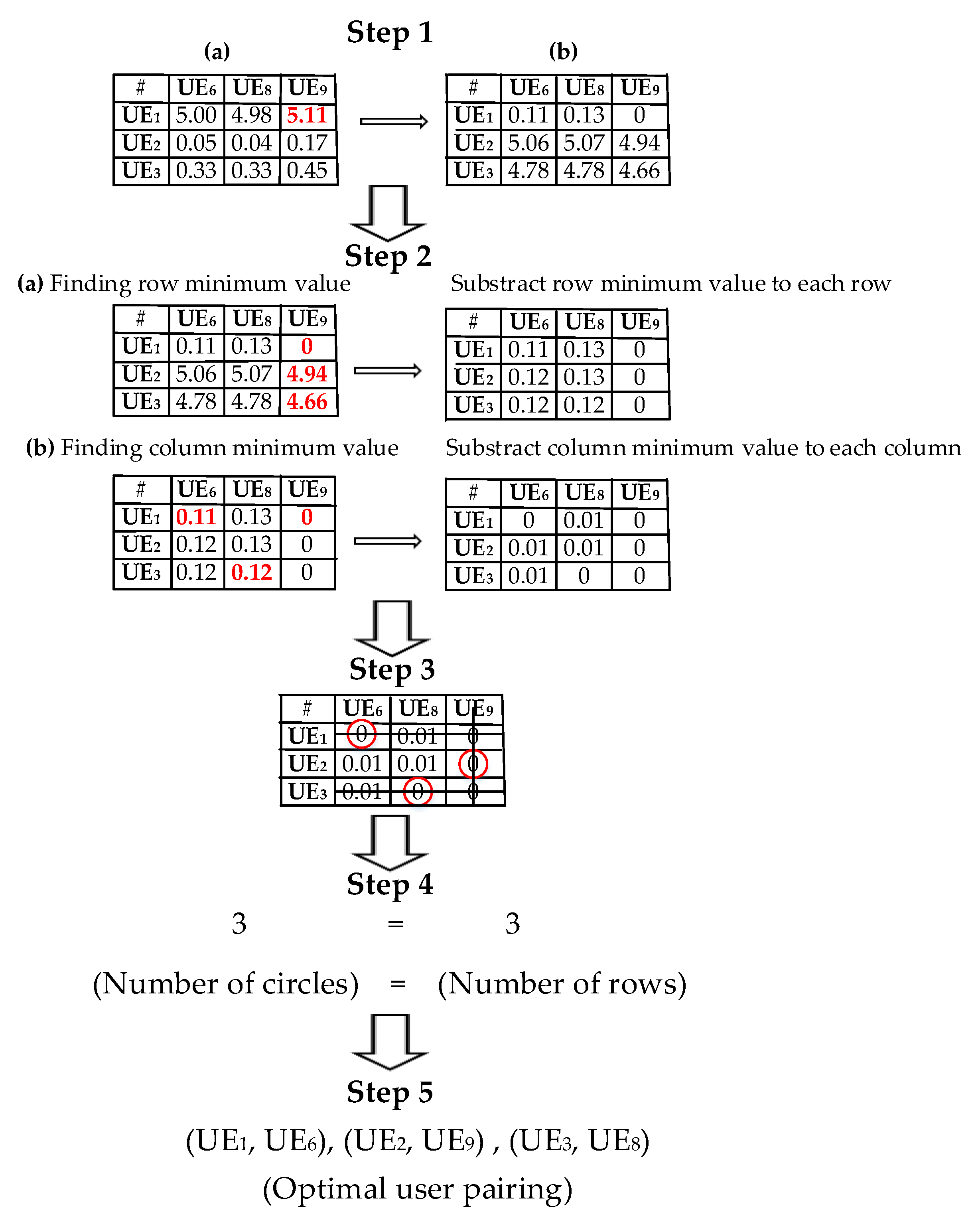
4.1. User Pairing Approach Based on HNG Algorithm
| Algorithm 1. User pairing based on Hungarian algorithm |
| Step 1: Formulation of cost matrix. |
| a) Formulate the cost matrix m. |
| b) Find the largest possible value from the entire cost matrix and subtract it from each cost matrix element. |
| Step 2: Reduction of row and column. |
| a) Find the lowest value from each row and subtract it from every value of the same row. |
| b) Find the lowest value from each column and subtract it from every value of the same column. |
| Step 3: Optimization procedure. |
| a) Checking of row. |
| i If exactly one zero in any row is found, mark the zero with a circle and draw a vertical line across it, but if not, skip that row. |
| ii If all zeros are traversed with lines, then proceed to Step 4. But if not, do column checking. |
| b) Checking of column. |
| i If exactly one zero in any column is found, mark the zero with a circle and draw a horizontal line across it, but if not, skip that column. |
| ii Make confirmation whether all the zeros are traversed with lines. |
| Step 4: If the number of circles is equal to the number of cost matrix rows, then proceed to |
| Step 5, but if not, proceed to Step 3. |
| Step 5: The marked circles are the objective function solutions for all marked users pairs. |
4.2. Power Allocation Solution Using KKT Conditions (PKKT)
4.3. Power Allocation Solution Using DKL Algorithm
| Algorithm 2. Dinkelbach method for energy efficiency maximization |
| Step 1: Initialize , iteration number and |
| Step 2: whiledo |
| Step 3: If |
| break |
| end if |
| end while |
| Step 4: Output |
5. Results and Discussion
5.1. Complexity Analysis
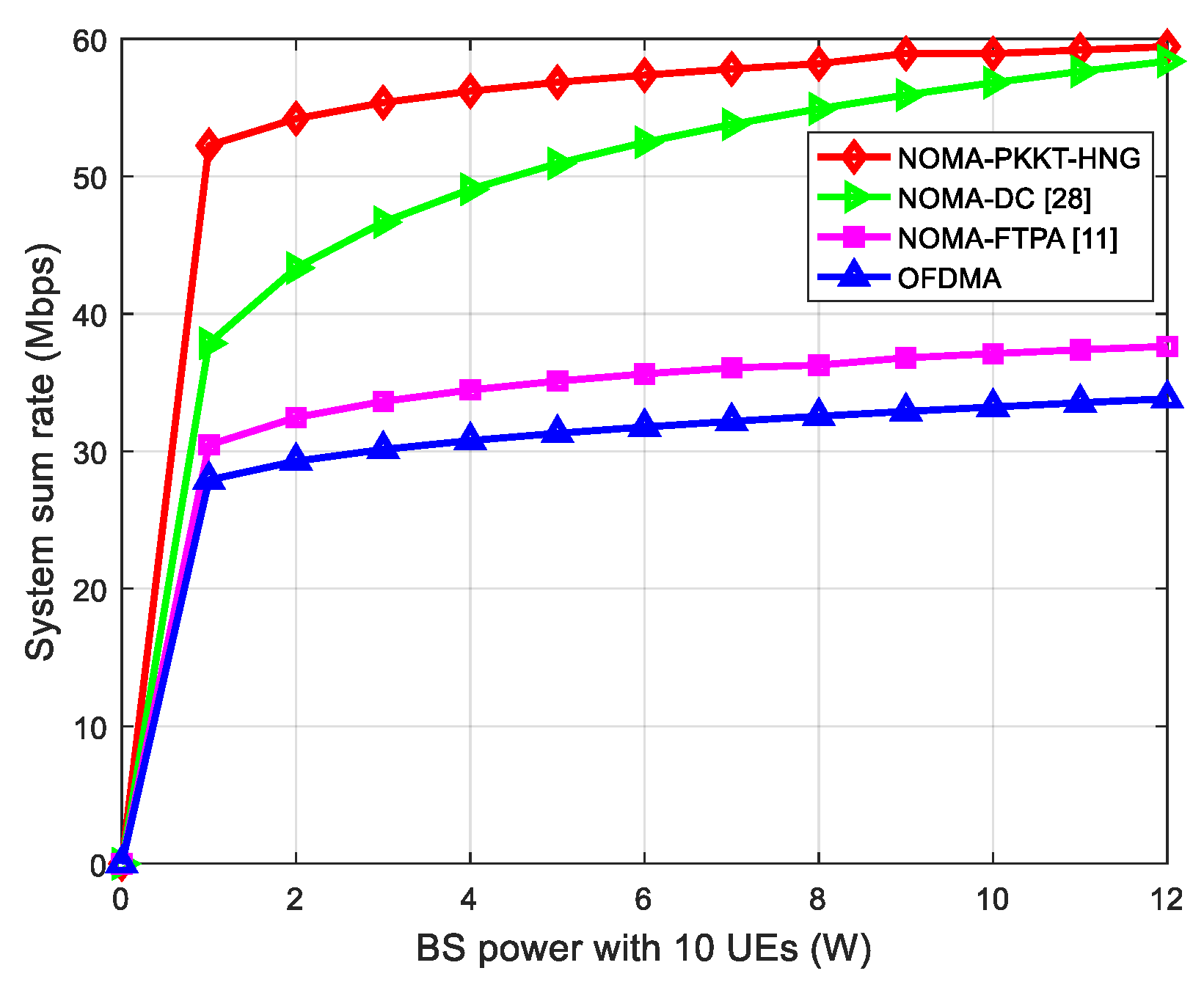
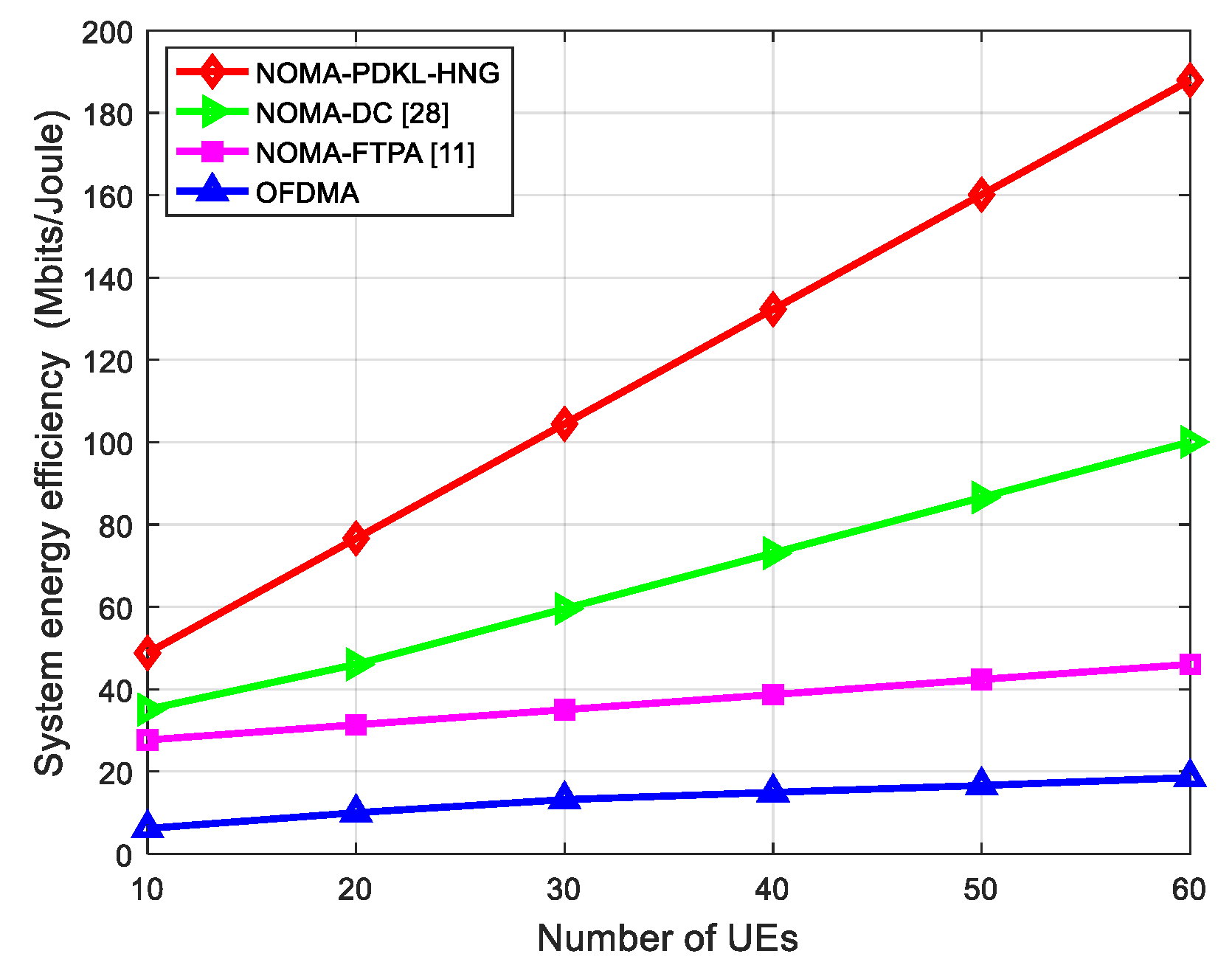
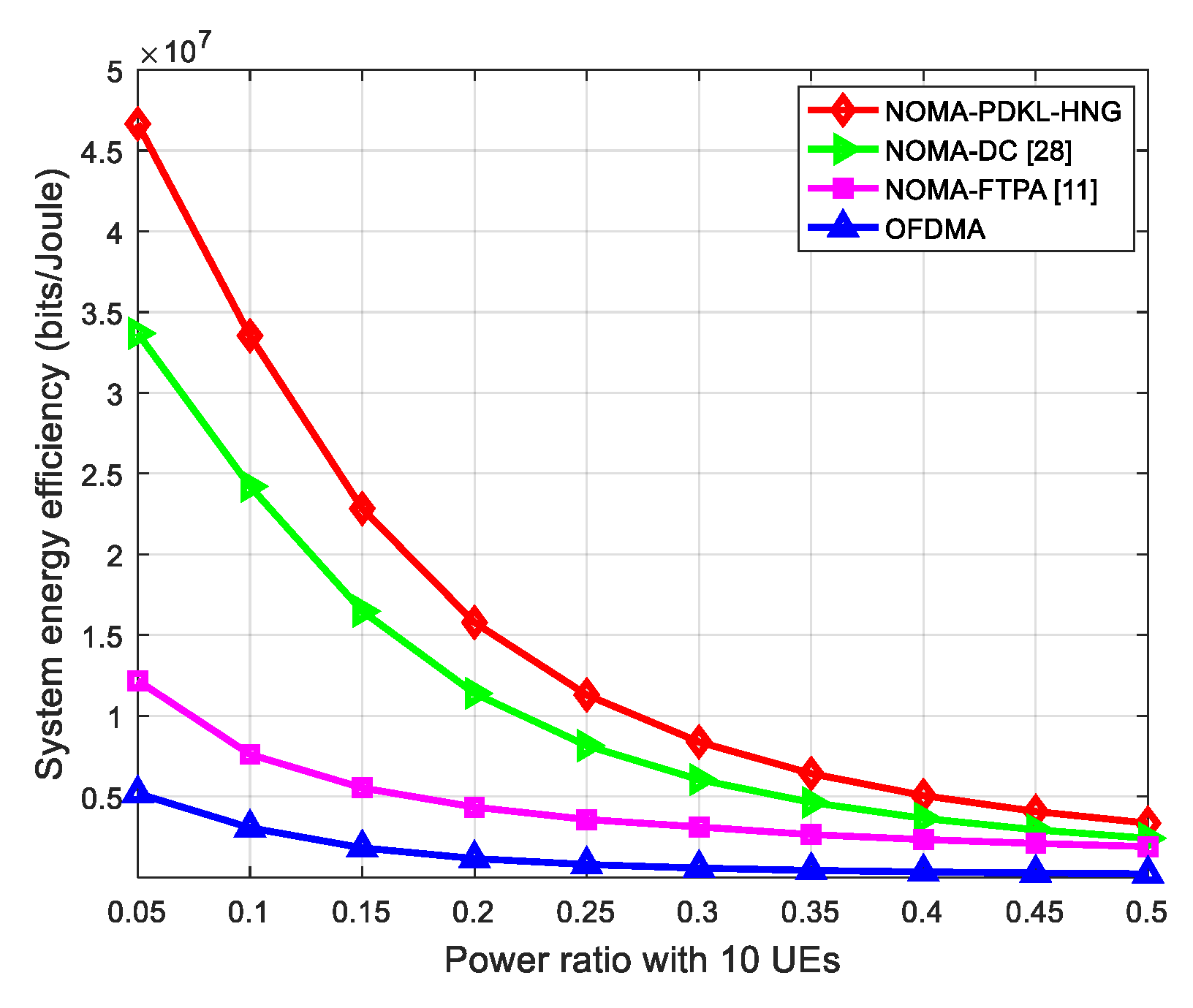
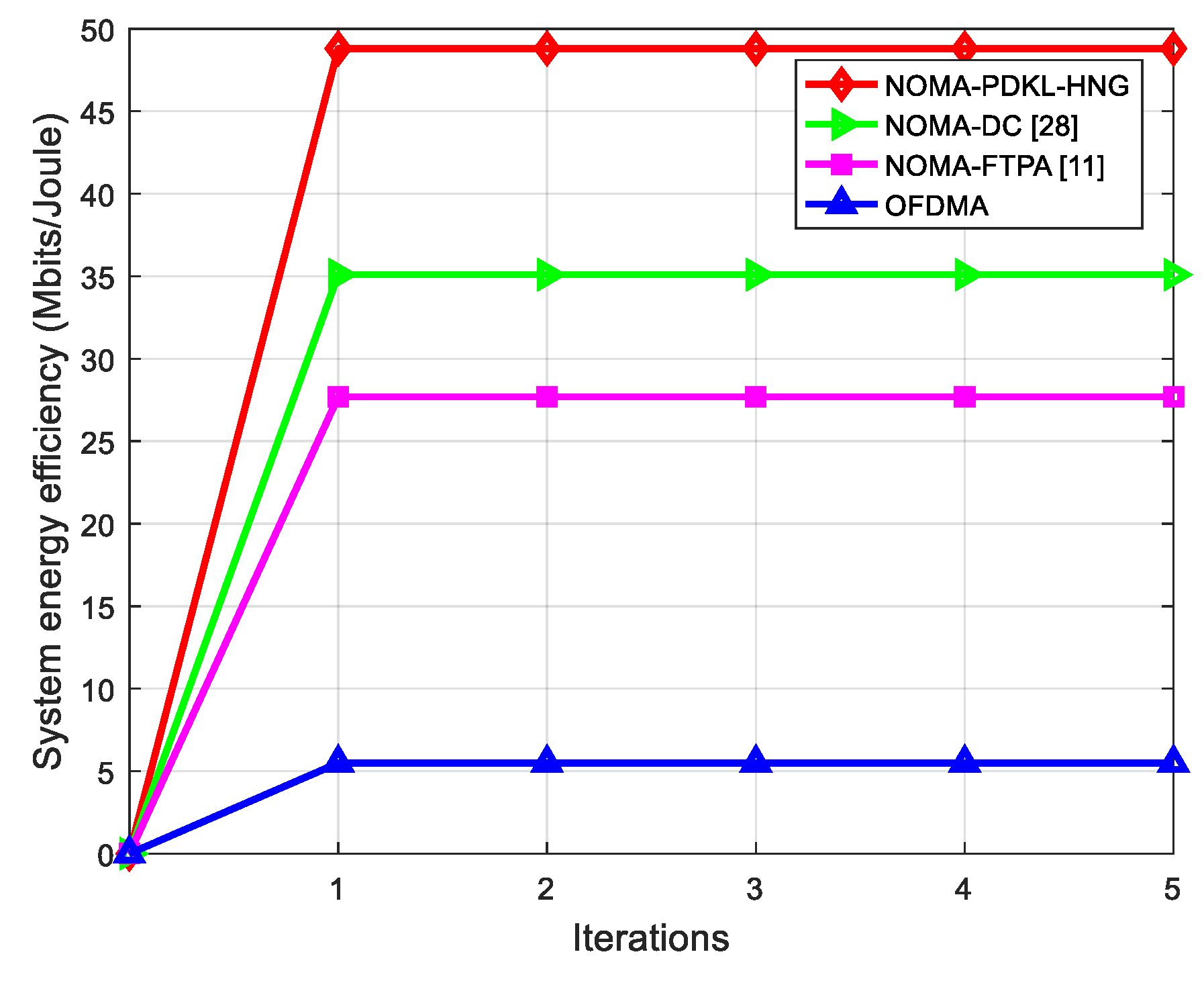
5.2. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Chui, K.T.; Lytras, M.D.; Visvizi, A.J.E. Energy sustainability in smart cities: Artificial intelligence, smart monitoring, and optimization of energy consumption. Energies 2018, 11, 2869. [Google Scholar] [CrossRef]
- Lytras, M.D.; Chui, K.T.; Visvizi, A. Data analytics in smart healthcare: The recent developments and beyond. Appl. Sci. 2019, 9, 2812. [Google Scholar] [CrossRef]
- Visvizi, A.; Lytras, M.D. It’s not a fad: Smart cities and smart villages research in European and global contexts. Sustainability 2018, 10, 2727. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Yuan, Y.; Han, S.; Chih-Lin, I. Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Commun. Mag. 2015, 53, 74–81. [Google Scholar] [CrossRef]
- Al-Falahy, N.; Alani, O.Y. Technologies for 5G networks: Challenges and opportunities. IT Prof. 2017, 19, 12–20. [Google Scholar] [CrossRef]
- Wu, Q.; Li, G.Y.; Chen, W.; Ng, D.W.K.; Schober, R. An overview of sustainable green 5G networks. IEEE Wirel. Commun. 2017, 24, 72–80. [Google Scholar] [CrossRef]
- Andrews, J.G.; Buzzi, S.; Choi, W.; Hanly, S.V.; Lozano, A.; Soong, A.C.K. What will 5G be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, J.; Huang, Y.; He, S.; You, X.; Yang, L. On optimal power allocation for downlink non-orthogonal multiple access systems. IEEE J. Sel. Areas Commun. 2017, 35, 2744–2757. [Google Scholar] [CrossRef]
- Ding, Z.; Liu, Y.; Choi, J.; Sun, Q.; Elkashlan, M.; Chih-Lin, I. Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Commun. Mag. 2017, 55, 185–191. [Google Scholar] [CrossRef]
- Islam, S.; Zeng, M.; Dobre, O.A. NOMA in 5G systems: Exciting possibilities for enhancing spectral efficiency. IEEE 5G Tech. Foc. 2017, 1, 1–6. [Google Scholar]
- Saito, Y.; Kishiyama, Y.; Benjebbour, A.; Nakamura, T.; Li, A.; Higuchi, K. Non-orthogonal multiple access (NOMA) for cellular future radio access. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013. [Google Scholar]
- Al-Abbasi, Z.Q.; So, D.K.C. Resource allocation in non-orthogonal and hybrid multiple access system with proportional rate constraint. IEEE Trans. Wirel. Commun. 2017, 16, 6309–6320. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Zeng, M.; Dobre, O.A.; Kwak, K. Resource allocation for downlink NOMA systems: Key techniques and open issues. IEEE Wirel. Commun. 2018, 25, 40–47. [Google Scholar] [CrossRef]
- Song, L.; Li, Y.; Ding, Z.; Poor, H.V. Resource management in non-orthogonal multiple access networks for 5g and beyond. IEEE Netw. 2017, 31, 8–14. [Google Scholar] [CrossRef]
- Ali, Z.J.; Noordin, N.K.; Sali, A.; Hashim, F.; Balfaqih, M. An efficient method for resource allocation and user pairing in downlink non-orthogonal multiple access system. In Proceedings of the 2019 IEEE 14th Malaysia International Conference on Communication (MICC), Selangor, Malaysia, 2–4 December 2019. [Google Scholar]
- Shahab, M.B.; Irfan, M.; Kader, M.F.; Young Shin, S. User pairing schemes for capacity maximization in non-orthogonal multiple access systems. Wirel. Commun. Mob. Comp. 2016, 16, 2884–2894. [Google Scholar] [CrossRef]
- Sindhu, P.; Deepak, K.S.; Abdul Hammed, K.M. A novel low complexity power allocation algorithm for downlink NOMA networks. In Proceedings of the 2018 IEEE Recent Advances in Intelligent Computational Systems (RAICS), Thiruvananthapuram, India, 6–8 December 2018. [Google Scholar]
- Shi, L.; Li, B.; Chen, H. Pairing and power allocation for downlink nonorthogonal multiple access systems. IEEE Trans. Veh. Techn. 2017, 66, 10084–10091. [Google Scholar] [CrossRef]
- Salaün, L.; Coupechoux, M.; Chen, C.S. Weighted sum-rate maximization in multi-carrier NOMA with cellular power constraint. In Proceedings of the IEEE INFOCOM 2019 IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019. [Google Scholar]
- Sun, Y.; Ng, D.W.K.; Schober, R. Optimal resource allocation for multicarrier MISO-NOMA systems. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar]
- He, J.; Tang, Z. Low-complexity user pairing and power allocation algorithm for 5G cellular network non-orthogonal multiple access. Electr. Lett. 2017, 53, 626–627. [Google Scholar] [CrossRef]
- Fu, Y.; Hong, Y.; Chen, L.; Sung, C.W. Enhanced power allocation for sum rate maximization in OFDM-NOMA VLC systems. IEEE Phot. Techn. Lett. 2018, 30, 1218–1221. [Google Scholar] [CrossRef]
- Manglayev, T.; Kizilirmak, R.C.; Kho, Y.H. Optimum power allocation for non-orthogonal multiple access (NOMA). In Proceedings of the 2016 IEEE 10th International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 12–14 October 2016. [Google Scholar]
- Mahady, I.A.; Bedeer, E.; Ikki, S.; Yanikomeroglu, H. Sum-rate maximization of NOMA systems under imperfect successive interference cancellation. IEEE Commun. Lett. 2019, 23, 474–477. [Google Scholar] [CrossRef]
- Xing, H.; Liu, Y.; Nallanathan, A.; Ding, Z. Sum-rate maximization guaranteeing user fairness for NOMA in fading channels. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018. [Google Scholar]
- Wang, Z.; Wen, C.; Fan, Z.; Wan, X. A novel price-based power allocation algorithm in non-orthogonal multiple access networks. IEEE Wirel. Commun. Lett. 2018, 7, 230–233. [Google Scholar] [CrossRef]
- Liu, G.; Wang, R.; Zhang, H.; Kang, W.; Tsiftsis, T.A.; Leung, V.C.M. Super-modular game-based user scheduling and power allocation for energy-efficient NOMA network. IEEE Trans. Wirel. Commun. 2018, 17, 3877–3888. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Leung, V.C.M. Energy-efficient resource allocation for downlink non-orthogonal multiple access network. IEEE Trans. Commun. 2016, 64, 3722–3732. [Google Scholar] [CrossRef]
- Benjebbour, A.; Li, A.; Saito, Y.; Kishiyama, Y.; Harada, A.; Nakamura, T. System-level performance of downlink NOMA for future LTE enhancements. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013. [Google Scholar]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO networks: Spectral, energy, and hardware efficiency. Found. Tren. Sign. Proc. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems. DEC Research Report TR-301; Digital Equipment Corporation: Maynard, MA, USA, 1984. [Google Scholar]
- Cui, H.; Zhang, J.; Cui, C.; Chen, Q. Solving large-scale assignment problems by Kuhn-Munkres algorithm. In Proceedings of the 2nd International Conference on Advances in Mechanical Engineering and Industrial Informatics (AMEII), Hangzhou, China, 9–10 April 2016. [Google Scholar]
- Wang, H.; Shi, D.; Song, B. A dynamic role assignment formation control algorithm based on Hungarian method. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018. [Google Scholar]
- Zuo, H.; Tao, X. Power allocation optimization for uplink non-orthogonal multiple access systems. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017. [Google Scholar]
- You, F.; Castro, P.M.; Grossmann, I.E. Dinkelbach’s algorithm as an efficient method to solve a class of MINLP models for large-scale cyclic scheduling problems. Comp. Chem. Eng. 2009, 33, 1879–1889. [Google Scholar] [CrossRef]
- Al-Abbasi, Z.Q.; So, D.K.; Tang, J. Energy efficient resource allocation in downlink non-orthogonal multiple access (NOMA) system. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, NSW, Australia, 4–7 June 2017. [Google Scholar]
- Zappone, A.; Jorswieck, E. Energy efficiency in wireless networks via fractional programming theory. Found. Trends. Commun. Inf. Theor. 2015, 11, 185–396. [Google Scholar] [CrossRef]



| # | UE6 | UE7 | UE8 | UE9 | UE10 |
|---|---|---|---|---|---|
| UE1 | 4.9913 | 5.1440 | 4.9890 | 5.1128 | 4.9877 |
| UE2 | 0.0469 | 0.1997 | 0.0446 | 0.1684 | 0.0433 |
| UE3 | 0.3331 | 0.4859 | 0.3307 | 0.4546 | 0.3294 |
| UE4 | 0.0218 | 0.1746 | 0.0195 | 0.1433 | 0.0182 |
| UE5 | 0.2218 | 0.3746 | 0.2194 | 0.3433 | 0.2181 |
| # | UE6 | UE7 | UE8 | UE9 | UE10 |
|---|---|---|---|---|---|
| UE1 | 25.759 | 31.111 | 25.769 | 30.725 | 25.769 |
| UE2 | 0.0057 | 5.3476 | 0.0054 | 4.9617 | 0.0053 |
| UE3 | 6.8344 | 1.2176 | 6.8341 | 11.79 | 6.8339 |
| UE4 | 0.0025 | 5.3444 | 0.0022 | 4.9585 | 0.0021 |
| UE5 | 5.8915 | 11.233 | 5.8912 | 10.847 | 5.891 |
| Algorithm | Complexity |
|---|---|
| Hungarian algorithm | O(N3) |
| Dinkelbach algorithm | O(M1 (M2(Q1+Q2) + O(K))) |
| Exhaustive search | O(2S!/2S) |
| Parameter | Default Value |
|---|---|
| Radius of the cell (R) | 500 m |
| Maximum BS transmit power (Pmax) | 41 dBm |
| Circuit power consumption (Pc) | 1 W |
| System bandwidth (Bw) | 5 MHz |
| Noise power spectral density (N0) | −174 dBm/Hz |
| Decay factor (α) for FTPA | 0.4 |
| Path-loss exponent (β) | 2 [8] |
| Minimum data rate for strong user | 200 Kbps |
| Minimum data rate for weak user | 20 Kbps |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.J.; Noordin, N.K.; Sali, A.; Hashim, F.; Balfaqih, M. Novel Resource Allocation Techniques for Downlink Non-Orthogonal Multiple Access Systems. Appl. Sci. 2020, 10, 5892. https://doi.org/10.3390/app10175892
Ali ZJ, Noordin NK, Sali A, Hashim F, Balfaqih M. Novel Resource Allocation Techniques for Downlink Non-Orthogonal Multiple Access Systems. Applied Sciences. 2020; 10(17):5892. https://doi.org/10.3390/app10175892
Chicago/Turabian StyleAli, Zuhura J., Nor K. Noordin, Aduwati Sali, Fazirulhisyam Hashim, and Mohammed Balfaqih. 2020. "Novel Resource Allocation Techniques for Downlink Non-Orthogonal Multiple Access Systems" Applied Sciences 10, no. 17: 5892. https://doi.org/10.3390/app10175892
APA StyleAli, Z. J., Noordin, N. K., Sali, A., Hashim, F., & Balfaqih, M. (2020). Novel Resource Allocation Techniques for Downlink Non-Orthogonal Multiple Access Systems. Applied Sciences, 10(17), 5892. https://doi.org/10.3390/app10175892





