Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices
Abstract
:1. Introduction
2. The Literature Review of Real Estate Price Predictions
3. Methods
3.1. Least Squares Support Vector Regression
3.2. Classification and Regression Trees
3.3. General Regression Neural Networks
3.4. Backpropagation Neural Networks
4. Data Collection and the Proposed Real Estate Appraising Framework
4.1. Data Collection
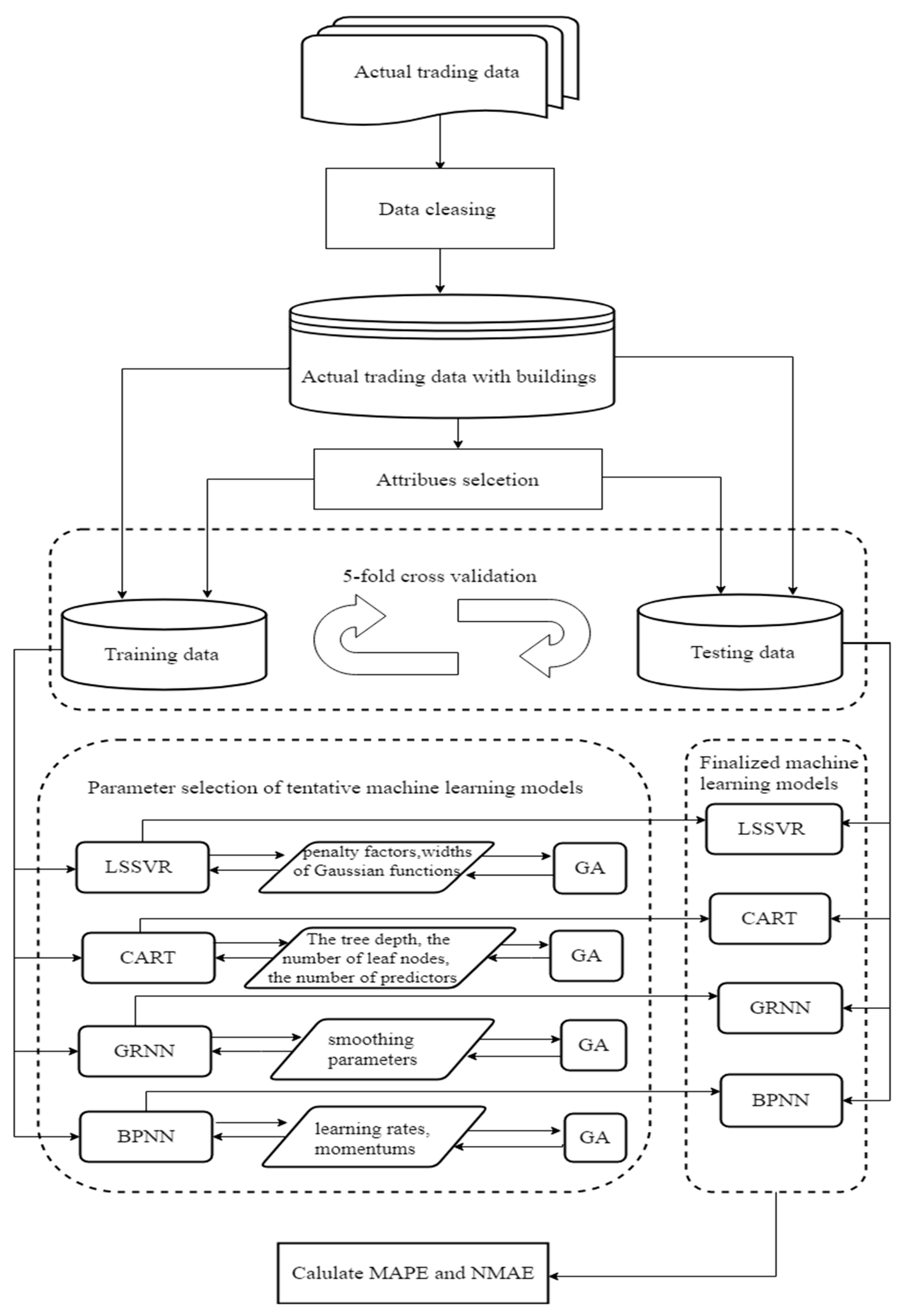
4.2. The Proposed Real Estate Appraising Framework
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahn, J.J.; Byun, H.W.; Oh, K.J.; Kim, T.Y. Using ridge regression with genetic algorithm to enhance real estate appraisal forecasting. Expert Syst. Appl. 2012, 39, 8369–8379. [Google Scholar] [CrossRef]
- Gruma, B.; Govekar, D.K. Influence of Macroeconomic Factors on Prices of Real Estate in Various Cultural Environments: Case of Slovenia, Greece, France, Poland and Norway. Procedia Econ. Financ. 2016, 39, 597–604. [Google Scholar] [CrossRef] [Green Version]
- Leamer, E.E. Housing is the Business Cycle. NBER Working Paper No. 13428. 2007. Available online: http://www.nber.org/papers/w13428 (accessed on 9 August 2020).
- Beimer, W.; Maennig, W. Noise effects and real estate prices: A simultaneous analysis of different noise sources. Transp. Res. Part D 2017, 54, 282–286. [Google Scholar] [CrossRef]
- Ferlan, N.; Bastic, M.; Psunder, I. Influential Factors on the Market Value of Residential Properties. Inz. Ekon. Eng. Econ. 2017, 28, 135–144. [Google Scholar] [CrossRef]
- Singh, A.; Sharma, A.; Dubey, G. Big data analytics predicting real estate prices. Int. J. Syst. Assur. Eng. Manag. 2020. [Google Scholar] [CrossRef]
- Segnon, M.; Gupta, R.; Lesame, K.; Wohar, M.E. High-Frequency Volatility Forecasting of US Housing Markets. J. Real Estate Finance Econ. 2020. [Google Scholar] [CrossRef] [Green Version]
- Kang, H.; Lee, K.; Shin, D.H. Short-Term Forecast Model of Apartment Jeonse Prices Using Search Frequencies of News Article Keywords. Ksce J. Civ. Eng. 2019, 23, 4984–4991. [Google Scholar] [CrossRef]
- Giudice, V.D.; Paola, P.D.; Forte, F. Using Genetic Algorithms for Real Estate Appraisals. Buildings 2017, 7, 31. [Google Scholar] [CrossRef] [Green Version]
- Park, B.; Bae, P.J. Using machine learning algorithms for housing price prediction: The case of Fairfax County, Virginia housing data. Expert Syst. Appl. 2015, 42, 2928–2934. [Google Scholar] [CrossRef]
- Bork, L.; Møller, S.V. Forecasting house prices in the 50 states using Dynamic Model Averaging and Dynamic Model Selection. Int. J. Forecast. 2015, 31, 63–78. [Google Scholar] [CrossRef]
- Plakandaras, V.; Gupta, R.; Gogas, P.; Papadimitriou, T. Forecasting the U.S. real house price index. Econ. Model. 2015, 45, 259–267. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.-H.; Tsai, C.-T.; Yuan, S.-M.; Chou, S.-H.; Chern, J. Big data: Open data and realty website analysis. In Proceedings of the 8th International Conference on Ubi-Media Computing, Colombo, Sri Lanka, 24–26 August 2015; pp. 84–88. [Google Scholar]
- Lee, W.-T.; Chen, J.; Chen, K. Determination of Housing Price in Taipei City Using Fuzzy Adaptive Networks. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 13–15 March 2013. [Google Scholar]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef] [Green Version]
- Kontrimas, V.; Verikas, A. The mass appraisal of the real estate by computational intelligence. Appl. Soft. Comput. 2011, 11, 443–448. [Google Scholar] [CrossRef]
- Gupta, R.; Kabundi, A.; Miller, S.M. Forecasting the US real house price index: Structural and non-structural models with and without fundamentals. Econ. Model. 2011, 28, 2013–2021. [Google Scholar] [CrossRef] [Green Version]
- Kusan, H.; Aytekin, O.; Özdemir, I. The use of fuzzy logic in predicting house selling price. Expert Syst. Appl. 2010, 37, 1808–1813. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. MLear 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Mukherjee, S.; Osuna, E.; Girosi, F. Nonlinear prediction of chaotic time series using support vector machines. In Proceedings of the IEEE Signal Processing Society Workshop, Amelia Island, FL, USA, 24–26 September 1997; pp. 511–520. [Google Scholar]
- Müller, K.-R.; Smola, A.J.; Rätsch, G.; Schölkopf, B.; Kohlmorgen, J.; Vapnik, V. Predicting time series with support vector machines. In Proceedings of the International Conference on Artificial Neural Networks, Munich, Germany, 17–19 September 2019; pp. 999–1004. [Google Scholar]
- Vapnik, V.; Golowich, S.E.; Smola, A.J. Support vector method for function approximation, regression estimation and signal processing. In Proceedings of the Advances Neural Information Processing System, Denver, CO, USA, 2–6 December 1997; pp. 281–287. [Google Scholar]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; Wiley: Hoboken, NJ, USA, 1987; pp. 80–94. [Google Scholar]
- Karush, W. Minima of Functions of Several Variables with Inequalities as Side Conditions. Master’s Thesis, University of Chicago, Chicago, IL, USA, 1939. [Google Scholar]
- Kuhn, H.W.; Tucker, A.W. Nonlinear programming. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probabilities, Berkeley, CA, USA, 31 July–12 August 1951; pp. 481–492. [Google Scholar]
- Mercer, J. Functions of Positive and Negative Type and Their Connection with the Theory of Integral Equations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1909, 209, 415–446. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Chapman and Hall, Wadsworth: New York, NY, USA, 1984. [Google Scholar]
- Liu, Y.Y.; Yang, M.; Ramsay, M.; Li, X.S.; Coid, J.W. A Comparison of Logistic Regression, Classification and Regression Tree, and Neural Networks Models in Predicting Violent Re-Offending. J. Quant. Criminol. 2011, 27, 547–573. [Google Scholar] [CrossRef]
- Parzen, E. On Estimation of a Probability Density Function and Mode. Ann. Math. Statist. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lin, C.T.; Lee, C.G. Neural Fuzzy Systems: A Neuro-Fuzzy Synergism to Intelligent Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975; pp. 439–444. [Google Scholar]
- Lewis, C.D. Industrial and Business Forecasting Methods; Butterworth Scientific: London, UK, 1982. [Google Scholar]
- Zhang, R.; Du, Q.; Geng, J.; Liu, B.; Huang, Y. An improved spatial error model for the mass appraisal of commercial real estate based on spatial analysis: Shenzhen as a case study. Habitat Int. 2015, 46, 196–205. [Google Scholar] [CrossRef]
- Kato, T. Prediction in the lognormal regression model with spatial error dependence. J. Hous. Econ. 2012, 21, 66–76. [Google Scholar] [CrossRef]
- Seya, H.; Yamagata, Y.; Tsutsumi, M. Automatic selection of a spatial weight matrix in spatial econometrics: Application to a spatial hedonic approach. Reg. Sci. Urban. Econ. 2013, 43, 429–444. [Google Scholar] [CrossRef]
| Types of Variables | Codes of Variables | Descriptions Variables | Data Types |
|---|---|---|---|
| Independent Variables | X1 | City or Township | Categorical |
| X2 | With or without parking space | Categorical | |
| X3 | Longitude | Numerical | |
| X4 | Latitude | Numerical | |
| X5 | Transaction area of land | Numerical | |
| X6 | Purpose of land use | Categorical | |
| X7 | Ages of buildings | Numerical | |
| X8 | Transaction amount of property | Numerical | |
| X9 | Transaction floors | Numerical | |
| X10 | Total floors of buildings | Numerical | |
| X11 | Types of buildings | Categorical | |
| X12 | Use of buildings | Categorical | |
| X13 | Materials of buildings | Categorical | |
| X14 | Total transaction areas of buildings | Numerical | |
| X15 | Number of bedrooms | Numerical | |
| X16 | Number of living rooms | Numerical | |
| X17 | Number of bathrooms | Numerical | |
| X18 | With or without compartments | Categorical | |
| X19 | With or without management committee | Categorical | |
| X20 | Prices per square meter | Numerical | |
| X21 | Types of parking space | Categorical | |
| X22 | Area of parking space | Numerical | |
| X23 | Prices of parking space | Numerical | |
| The Dependent Variable | Y | Transaction prices | Numerical |
| Independent Variables (Pearson Correlation Coefficient) | X1(0.01158), X2(0.4097), X3(−0.043), X4(−0.0184), X5(0.3518), X6(−0.0319), X7(−0.2897), X8(0.00465), X9(0.03199), X10(0.09087), X11(−0.0271), X12(0.0884), X13(−0.0382), X14(0.7923), X15(0.4766), X16(0.4391), X17(0.4024), X18(0.05456), X19(−0.0201), X20(0.5299), X21(0.3871), X22(0.3686), X23(0.1932) |
| Models | LSSVR | CART | GRNN | BPNN |
|---|---|---|---|---|
| MAPE (%) | 1.676 | 2.2944 | 22.8936 | 15.0357 |
| NMAE | 4.13 × 10−3 | 6.86 × 10−3 | 1.07 × 106 | 3.82 × 10−2 |
| Models | LSSVR | CART | GRNN | BPNN |
|---|---|---|---|---|
| MAPE (%) | 0.228 | 2.278 | 8.738 | 14.424 |
| NMAE | 8.11 × 10−4 | 6.76 × 10−3 | 4.52 × 105 | 4.13 × 10−2 |
| Forecasting Models | MAPE (%) |
|---|---|
| Kang et al. [8] | 3.84 |
| Giudice et al. [9] | 10.62 |
| Plakandaras et al. [12] | 2.151 |
| Lee et al. [14] | 4.54 |
| Antipov and Pokryshevskaya [15] | 13.95 |
| Kusan et al. [18] | 3.65 |
| *LSSVR 1 | 1.676 |
| **LSSVR 2 | 0.228 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pai, P.-F.; Wang, W.-C. Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices. Appl. Sci. 2020, 10, 5832. https://doi.org/10.3390/app10175832
Pai P-F, Wang W-C. Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices. Applied Sciences. 2020; 10(17):5832. https://doi.org/10.3390/app10175832
Chicago/Turabian StylePai, Ping-Feng, and Wen-Chang Wang. 2020. "Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices" Applied Sciences 10, no. 17: 5832. https://doi.org/10.3390/app10175832
APA StylePai, P.-F., & Wang, W.-C. (2020). Using Machine Learning Models and Actual Transaction Data for Predicting Real Estate Prices. Applied Sciences, 10(17), 5832. https://doi.org/10.3390/app10175832






