Quantifying the Biophysical Impact of Budding Cell Division on the Spatial Organization of Growing Yeast Colonies
Abstract
1. Introduction
2. Results
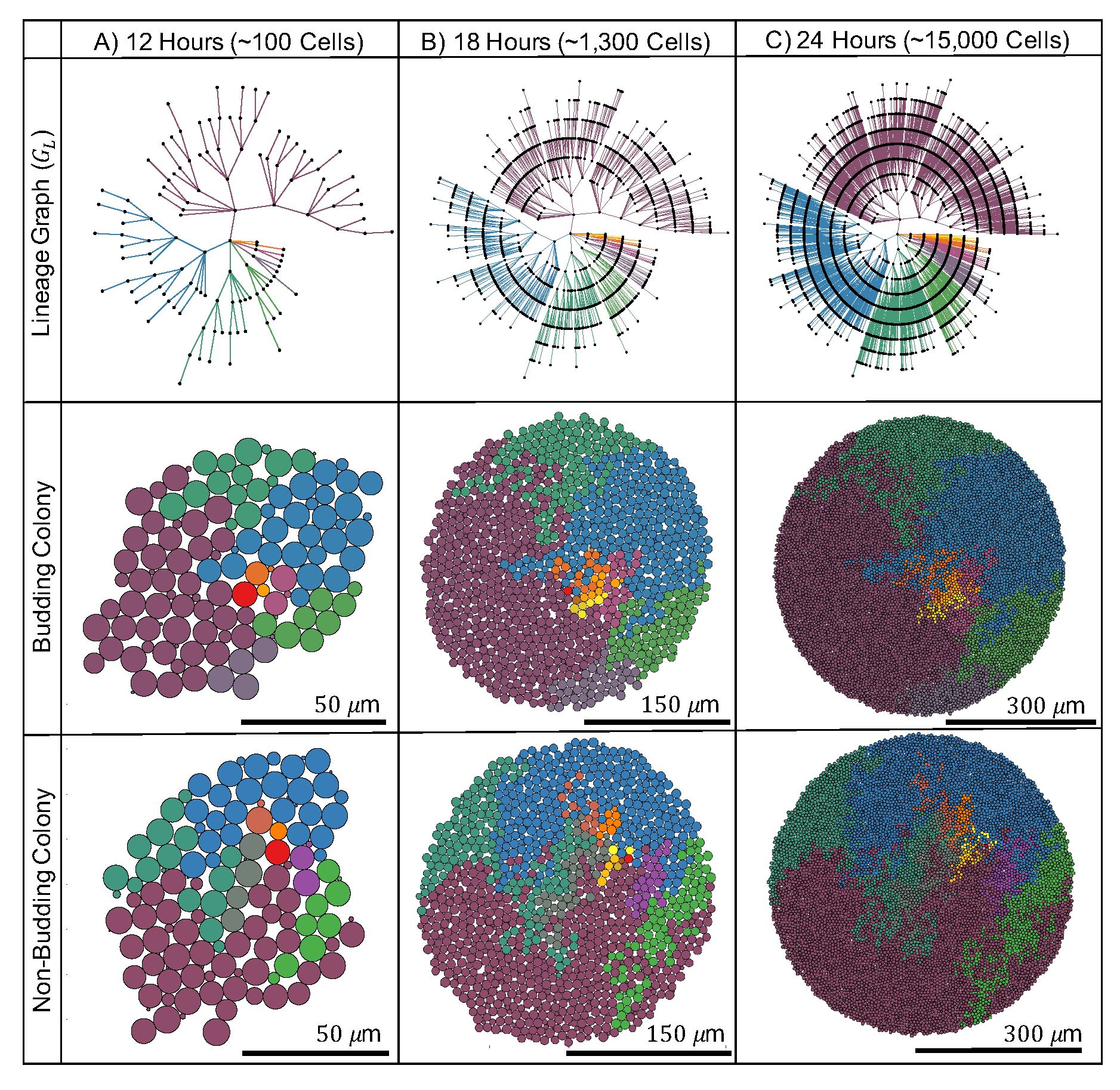
2.1. Nutrient-Rich Growth: Budding Division Impacts Local Colony Organization in Simulated Yeast Colonies
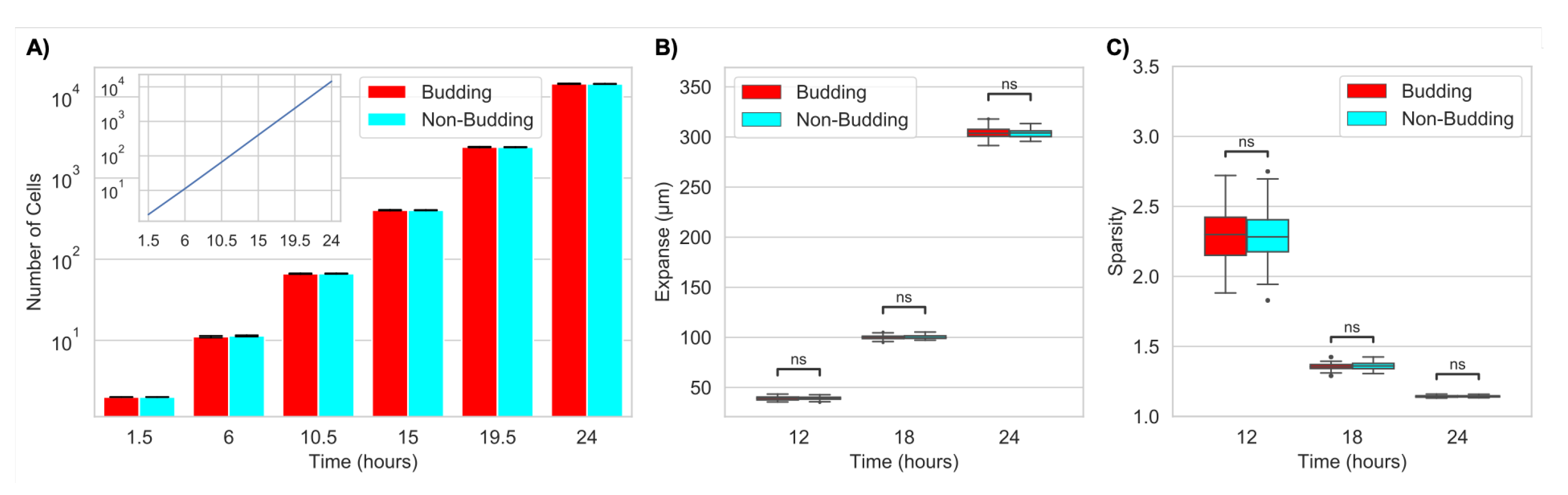
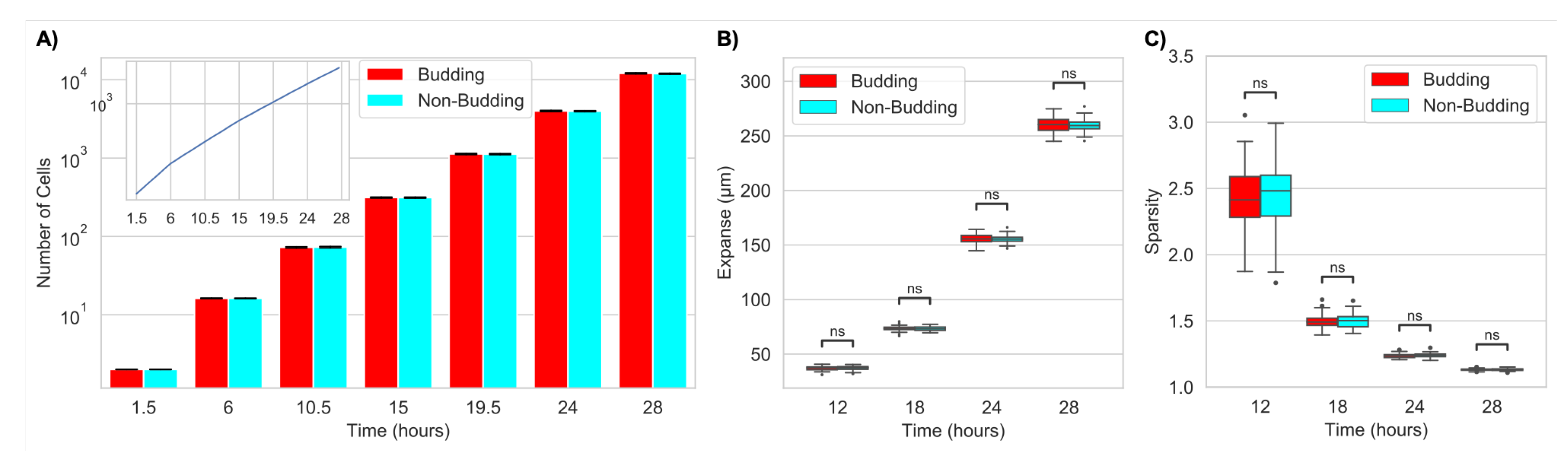
2.1.1. Budding Does Not Impact Large-Scale Colony Growth or Structure (Expanse or Sparsity)
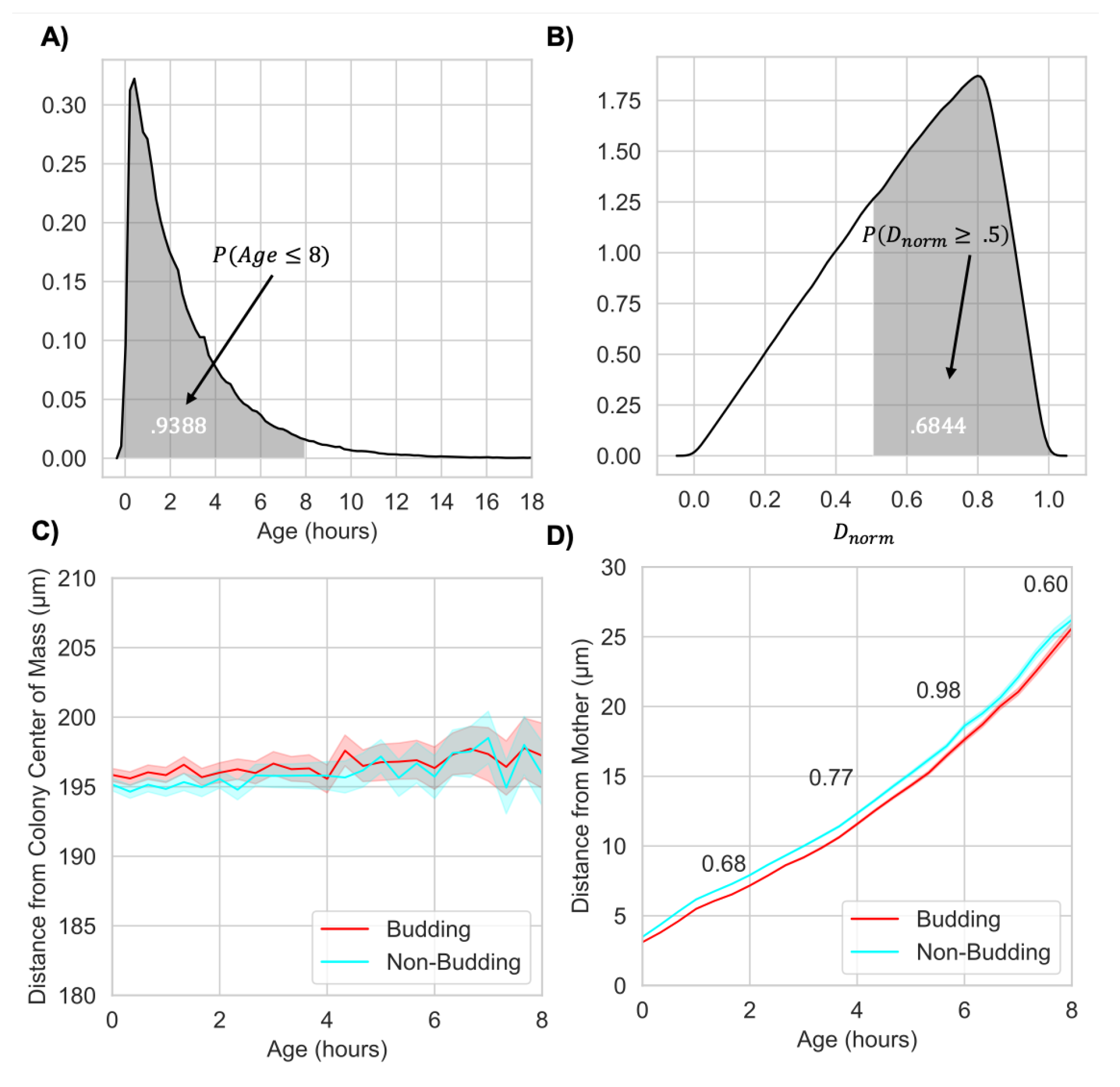
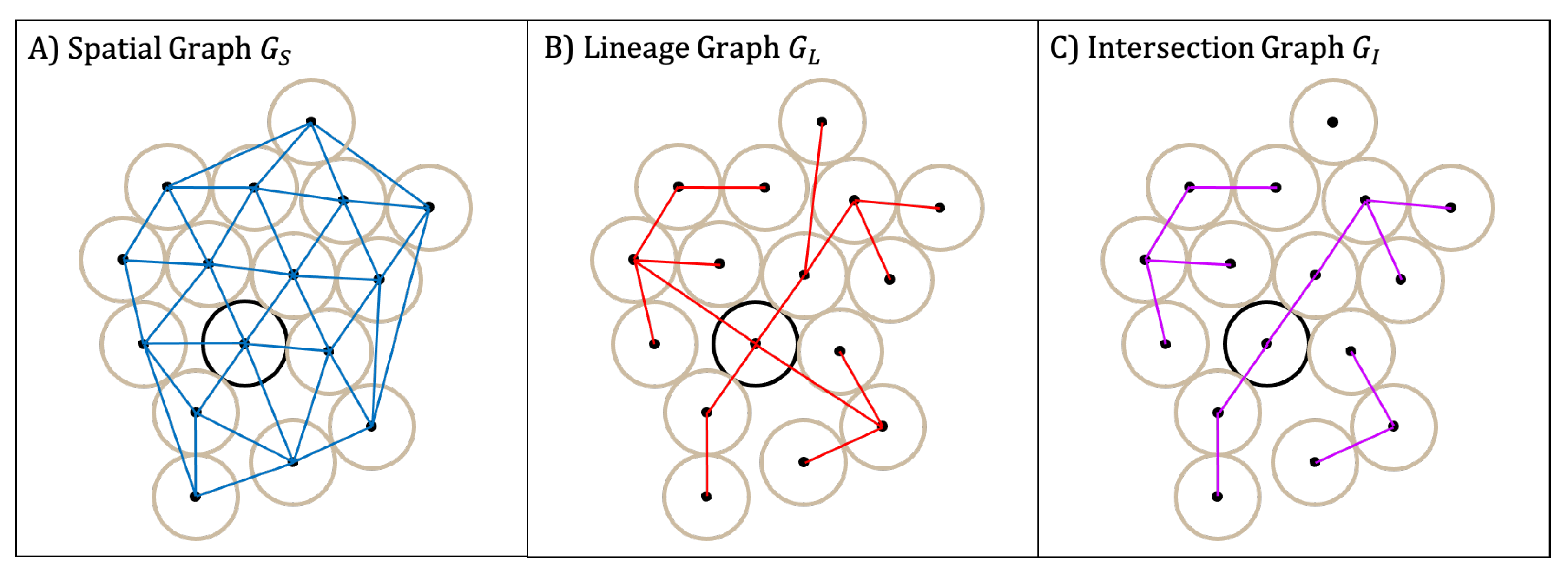
2.1.2. Budding Does Not Change Global Age and Spatial Structure but Impacts Local Connectivity
2.1.3. Budding Division Maintains Closeness between Mothers and Daughters after Physical Separation
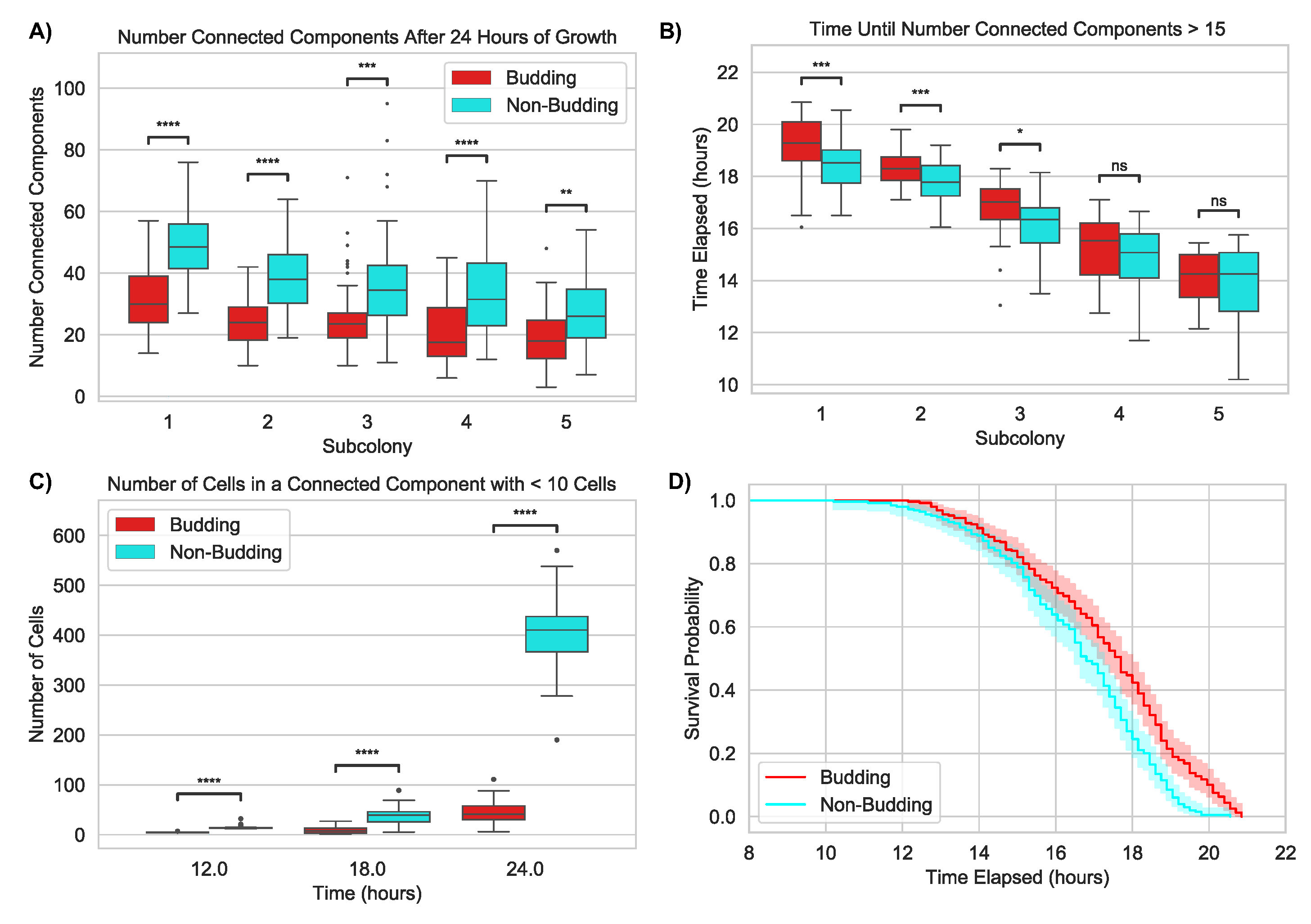
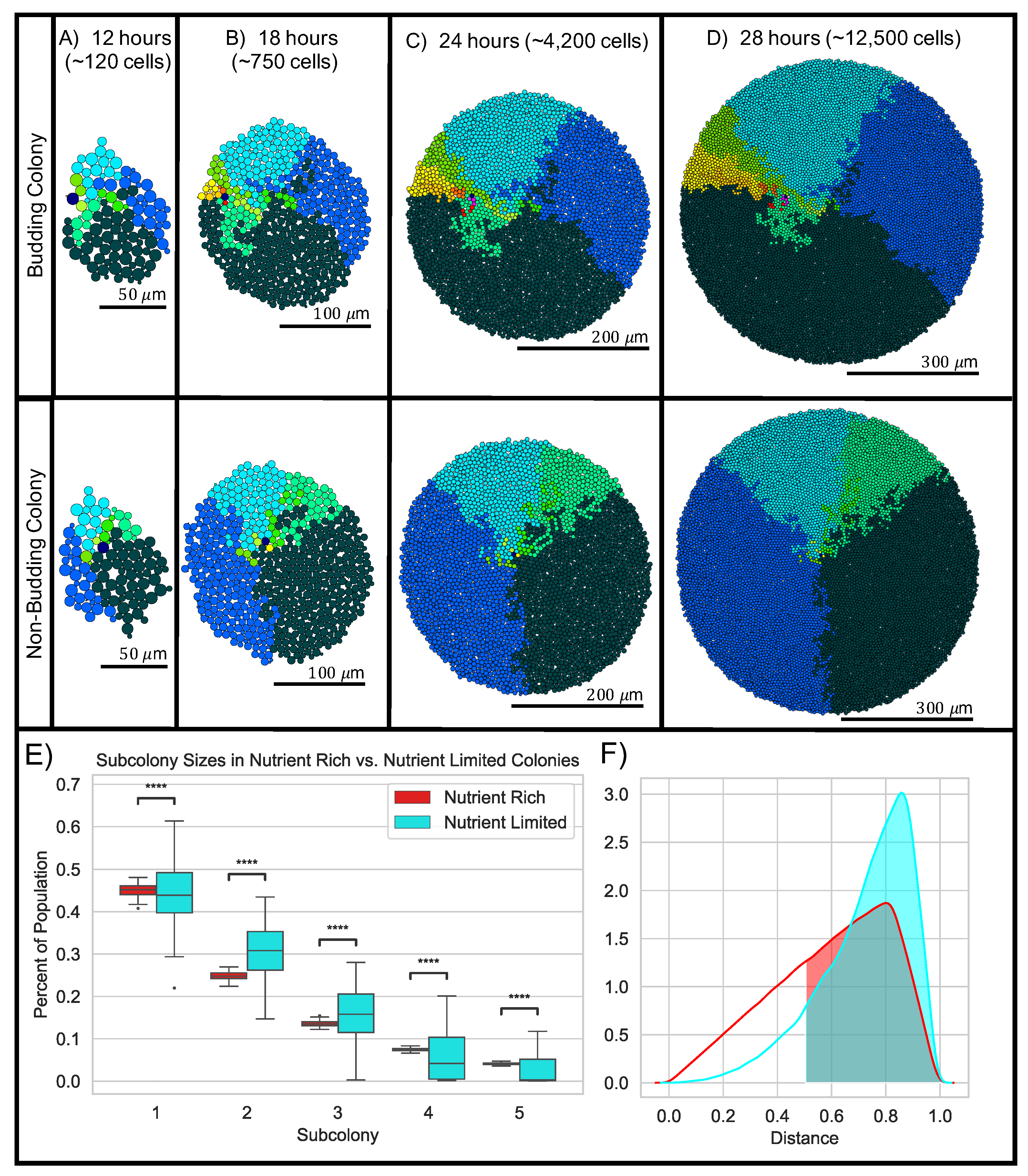
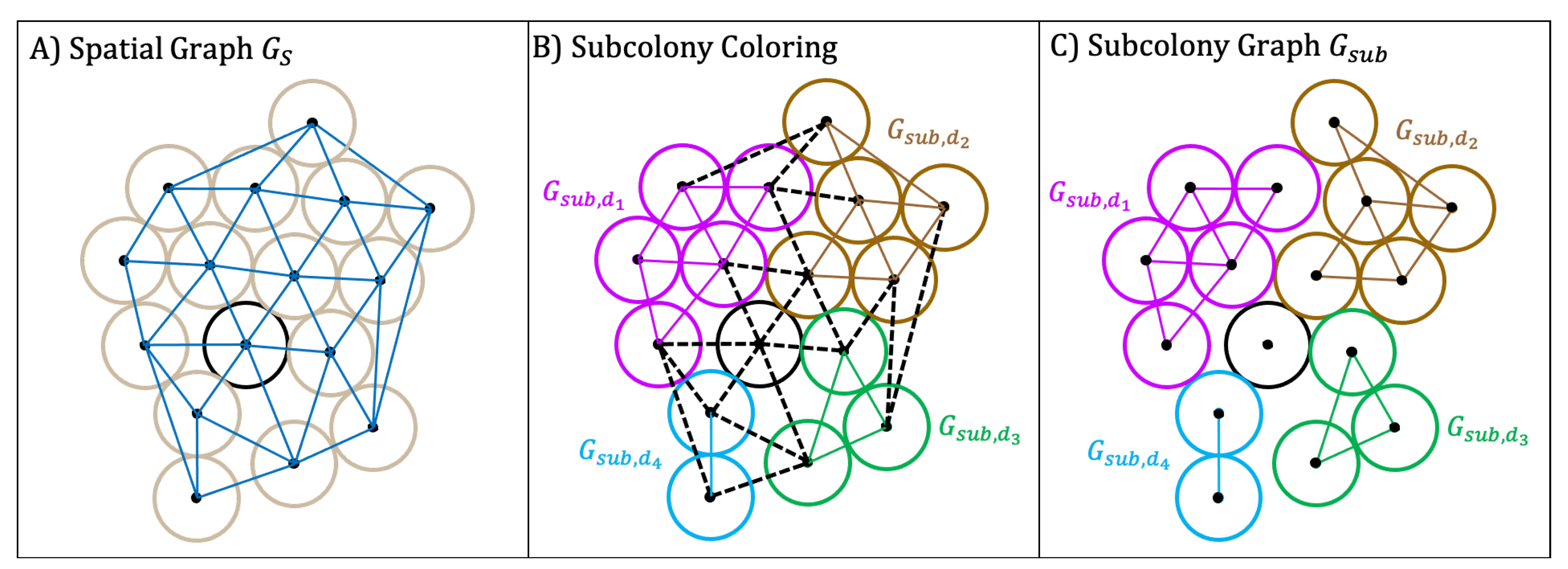
2.1.4. Budding Division Promotes Subcolony Connectivity
2.2. Nutrient-Limited Growth: Differential Growth Rates Impact Global Organization of Yeast Colonies
2.2.1. Nutrient Limitation Slows Colony Growth but Does Not Change Large-Scale Colony Structure
2.2.2. Nutrient Limitation Creates Age-Structured Colonies by Promoting Birth at the Colony Boundary
2.2.3. Nutrient-Limited Growth Promotes Colony Connectivity
2.2.4. Nutrient Limitation Further Promotes Subcolony Connectivity
2.2.5. Nutrient Limitation Changes Global Colony Organization by Driving Variation in Subcolony Sizes
3. Discussion
4. Materials And Methods
4.1. Computational Model
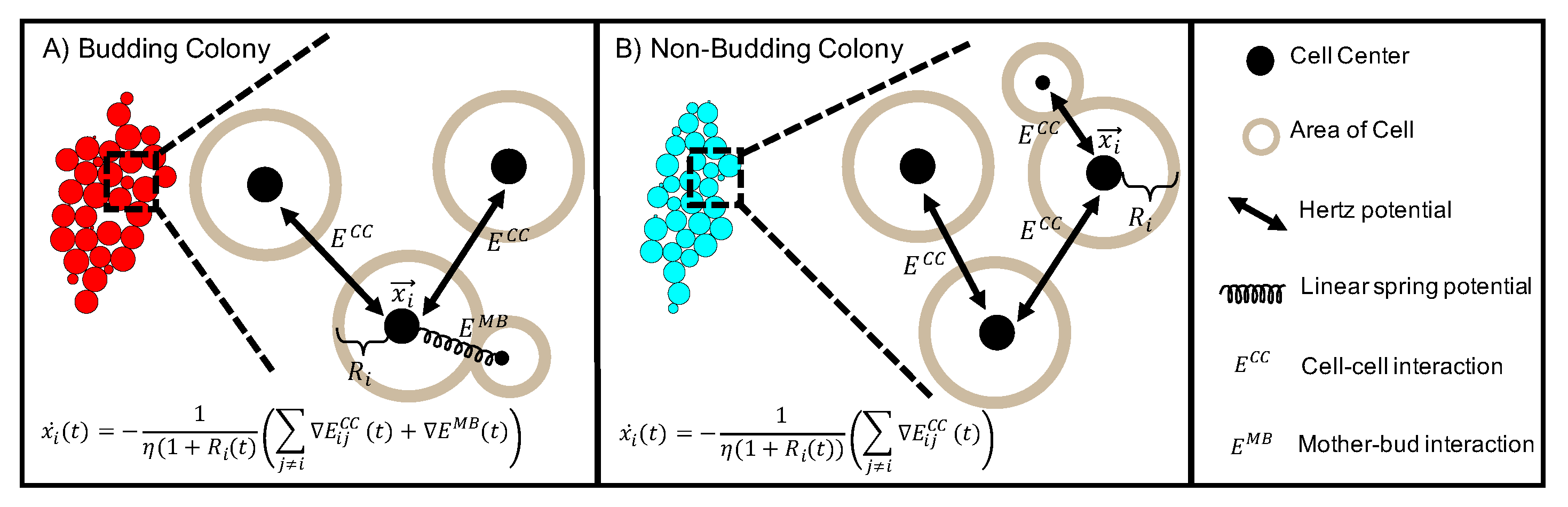
4.1.1. Cell-Cell Interaction and Spatial Arrangement Of Cells
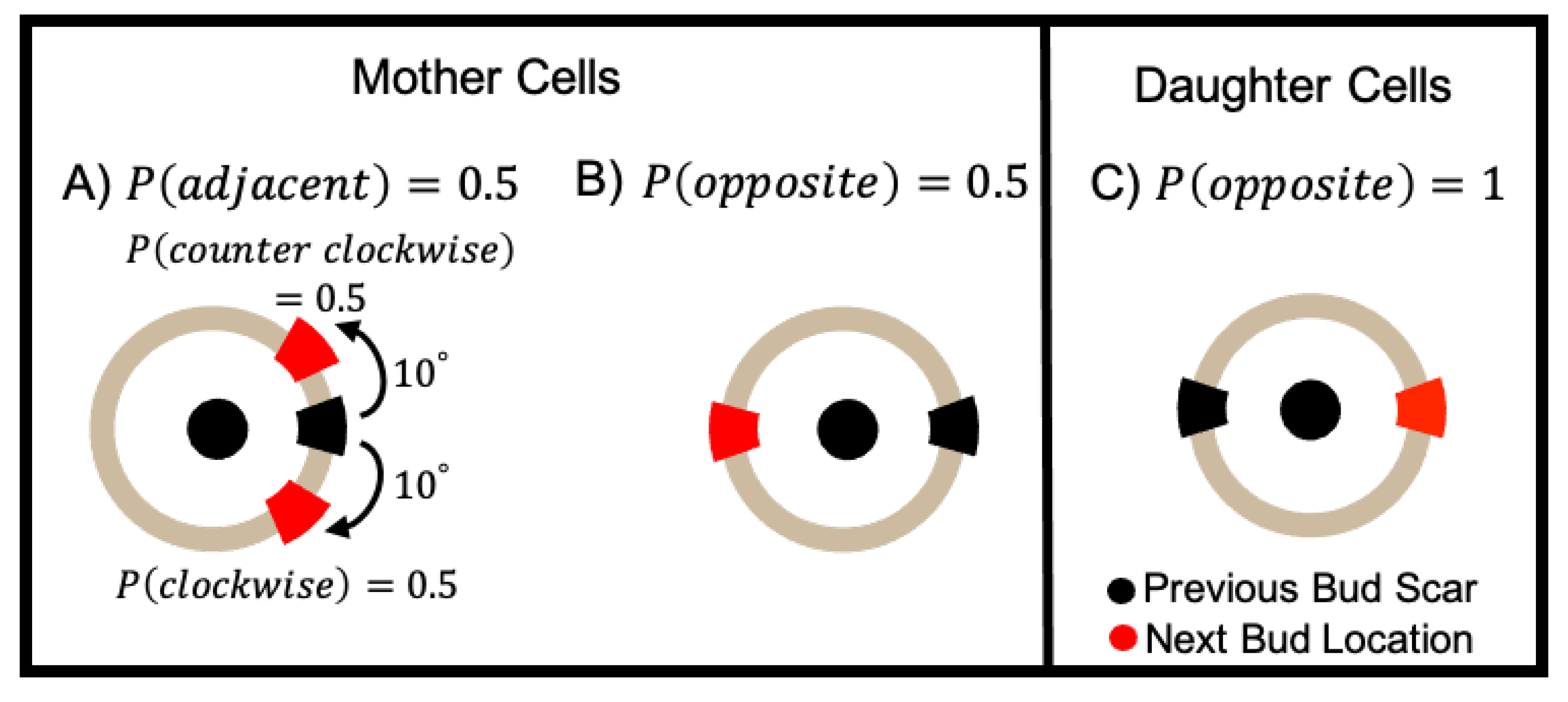
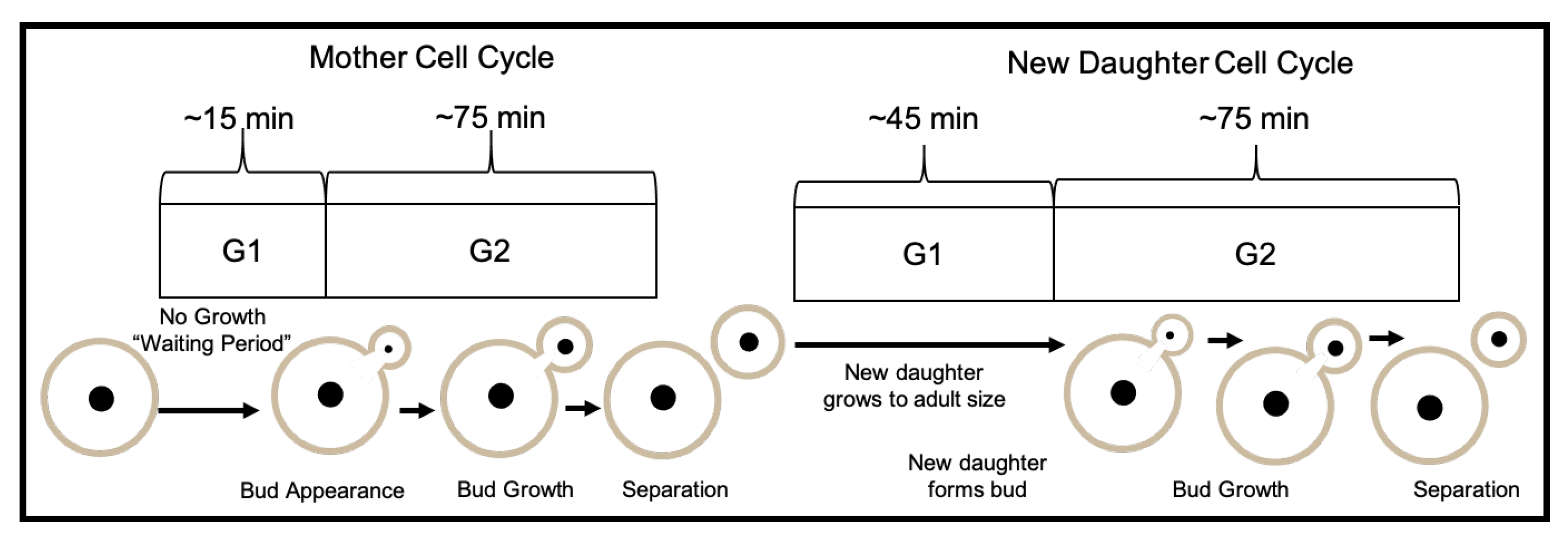
4.1.2. Budding Cell Division
4.1.3. Cell Growth and Cell Cycle Length
4.1.4. Nutrient-Limited Growth
4.1.5. Simulation Run Time
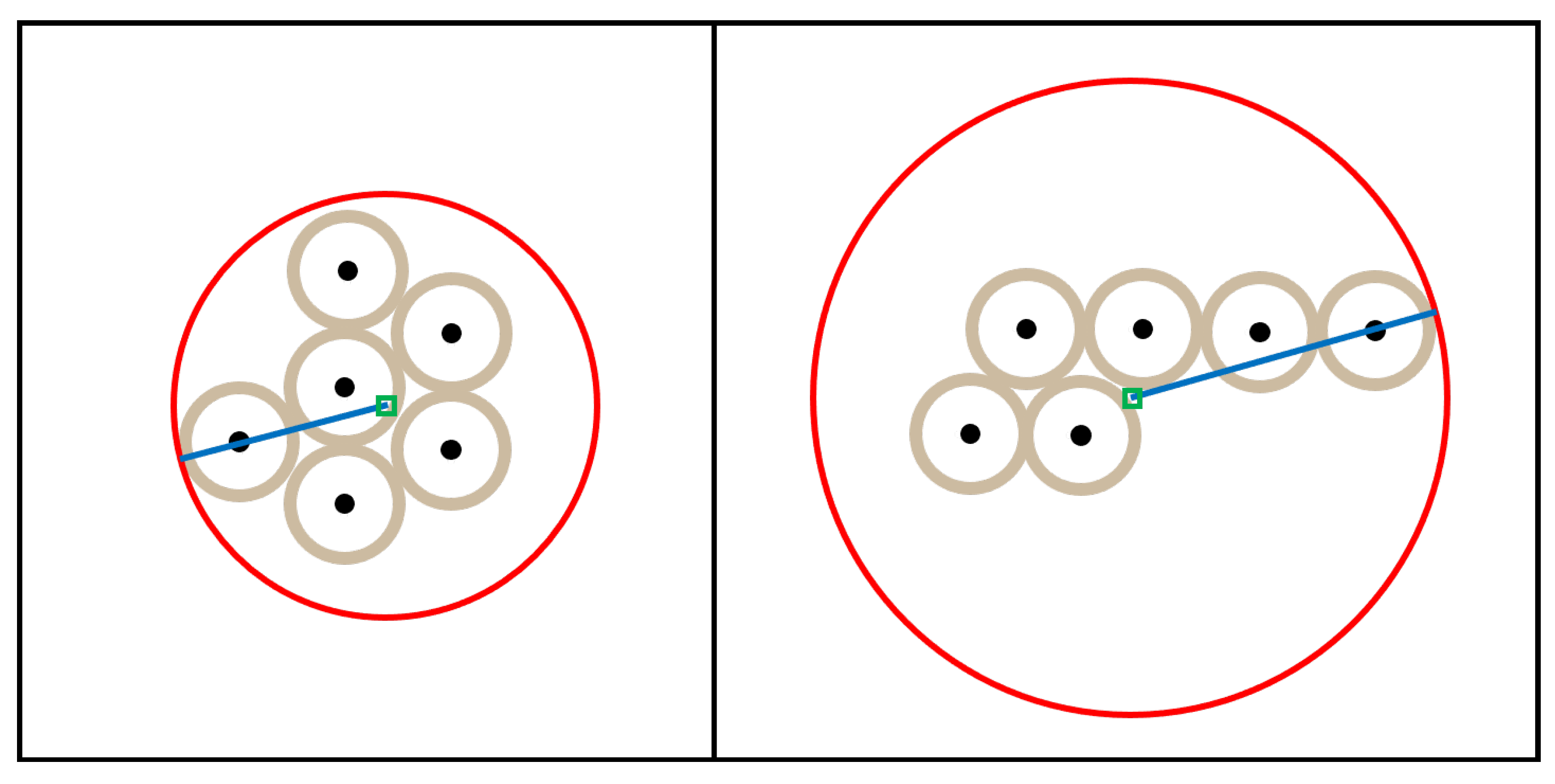
4.2. Colony Metrics
4.2.1. Colony Shape Metrics
4.2.2. Colony Organization Metrics
4.3. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ABM | Agent-Based Model |
References
- DiSalvo, S.; Serio, T.R. Insights into prion biology: Integrating a protein misfolding pathway with its cellular environment. Prion 2011, 5, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Frazer, C.; Hernday, A.D.; Bennett, R.J. Monitoring Phenotypic Switching in Candida albicans and the Use of Next-Gen Fluorescence Reporters. Curr. Protoc. Microbiol. 2019, 53, e76. [Google Scholar] [CrossRef] [PubMed]
- Klaips, C.L.; Hochstrasser, M.L.; Langlois, C.R.; Serio, T.R. Spatial quality control bypasses cell-based limitations on proteostasis to promote prion curing. eLife 2014, 3, e04288. [Google Scholar] [CrossRef] [PubMed]
- Liebman, S.W.; Chernoff, Y.O. Prions in yeast. Genetics 2012, 191, 1041–1072. [Google Scholar] [CrossRef] [PubMed]
- Giometto, A.; Nelson, D.R.; Murray, A.W. Physical interactions reduce the power of natural selection in growing yeast colonies. Proc. Natl. Acad. Sci. USA 2018, 115, 11448–11453. [Google Scholar] [CrossRef]
- Ben-Jacob, E.; Schochet, O.; Tenenbaum, A.; Cohen, I.; Czirok, A.; Vicsek, T. Generic modelling of cooperative growth patterns in bacterial colonies. Nature 1994, 368, 46–49. [Google Scholar] [CrossRef]
- Shapiro, J.A. The significances of bacterial colony patterns. Bioessays 1995, 17, 597–607. [Google Scholar] [CrossRef]
- Mitri, S.; Clarke, E.; Foster, K.R. Resource limitation drives spatial organization in microbial groups. ISME J. 2016, 10, 1471–1482. [Google Scholar] [CrossRef]
- Hallatschek, O.; Hersen, P.; Ramanathan, S.; Nelson, D.R. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. USA 2007, 104, 19926–19930. [Google Scholar] [CrossRef]
- Johnson, C.R.; Boerlijst, M.C. Selection at the level of the community: The importance of spatial structure. Trends Ecol. Evol. 2002, 17, 83–90. [Google Scholar] [CrossRef]
- Hallatschek, O.; Nelson, D.R. Life at the front of an expanding population. Evol. Int. J. Org. Evol. 2010, 64, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Alber, M.S.; Jiang, Y.; Kiskowski, M.A. Lattice gas cellular automation model for rippling and aggregation in myxobacteria. Phys. Nonlinear Phenom. 2004, 191, 343–358. [Google Scholar] [CrossRef]
- Amiri, A.; Harvey, C.; Buchmann, A.; Christley, S.; Shrout, J.D.; Aranson, I.S.; Alber, M. Reversals and collisions optimize protein exchange in bacterial swarms. Phys. Rev. E 2017, 95, 032408. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Fei, C.; Bridges, A.A.; Mashruwala, A.A.; Stone, H.A.; Wingreen, N.S.; Bassler, B.L. Cell position fates and collective fountain flow in bacterial biofilms revealed by light-sheet microscopy. Science 2020, 369, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Noble, S.M.; Gianetti, B.A.; Witchley, J.N. Candida albicans cell-type switching and functional plasticity in the mammalian host. Nat. Rev. Microbiol. 2017, 15, 96. [Google Scholar] [CrossRef]
- Miller, M.G.; Johnson, A.D. White-opaque switching in Candida albicans is controlled by mating-type locus homeodomain proteins and allows efficient mating. Cell 2002, 110, 293–302. [Google Scholar] [CrossRef]
- Lohse, M.B.; Johnson, A.D. White–opaque switching in Candida albicans. Curr. Opin. Microbiol. 2009, 12, 650–654. [Google Scholar] [CrossRef]
- Lee, P.S.; Greenwell, P.W.; Dominska, M.; Gawel, M.; Hamilton, M.; Petes, T.D. A fine-structure map of spontaneous mitotic crossovers in the yeast Saccharomyces cerevisiae. PLoS Genet. 2009, 5, e1000410. [Google Scholar] [CrossRef]
- Krafzig, D.; Klawonn, F.; Gutz, H. Theoretical analysis of the effects of mitotic crossover in large yeast populations. Yeast 1993, 9, 1093–1098. [Google Scholar] [CrossRef]
- Ramírez-Zavala, B.; Reuß, O.; Park, Y.N.; Ohlsen, K.; Morschhäuser, J. Environmental induction of white–opaque switching in Candida albicans. PLoS Pathog. 2008, 4, e1000089. [Google Scholar] [CrossRef]
- Xie, J.; Tao, L.; Nobile, C.J.; Tong, Y.; Guan, G.; Sun, Y.; Cao, C.; Hernday, A.D.; Johnson, A.D.; Zhang, L.; et al. White-opaque switching in natural MTL a/α isolates of Candida albicans: Evolutionary implications for roles in host adaptation, pathogenesis, and sex. PLoS Biol. 2013, 11, e1001525. [Google Scholar] [CrossRef] [PubMed]
- Magno, R.; Grieneisen, V.A.; Marée, A.F. The biophysical nature of cells: Potential cell behaviours revealed by analytical and computational studies of cell surface mechanics. BMC Biophys. 2015, 8, 8. [Google Scholar] [CrossRef] [PubMed]
- Cullen, P.J.; Sprague, G.F. The regulation of filamentous growth in yeast. Genetics 2012, 190, 23–49. [Google Scholar] [CrossRef] [PubMed]
- Kron, S.J.; Styles, C.A.; Fink, G.R. Symmetric cell division in pseudohyphae of the yeast Saccharomyces cerevisiae. Mol. Biol. Cell 1994, 5, 1003–1022. [Google Scholar] [CrossRef] [PubMed]
- Drubin, D.G.; Nelson, W.J. Origins of cell polarity. Cell 1996, 84, 335–344. [Google Scholar] [CrossRef]
- Ni, L.; Snyder, M. A genomic study of the bipolar bud site selection pattern in Saccharomyces cerevisiae. Mol. Biol. Cell 2001, 12, 2147–2170. [Google Scholar] [CrossRef]
- Chant, J.; Mischke, M.; Mitchell, E.; Herskowitz, I.; Pringle, J.R. Role of Bud3p in producing the axial budding pattern of yeast. J. Cell Biol. 1995, 129, 767–778. [Google Scholar] [CrossRef]
- Byers, B. Cytology of the yeast life cycle. In The Molecular Biology of The Yeast Saccharomyces: Life Cycle and Inheritance; Springer: Berlin/Heidelberg, Germany, 1981; pp. 59–96. [Google Scholar]
- Nadell, C.D.; Foster, K.R.; Xavier, J.B. Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS Comput. Biol. 2010, 6, e1000716. [Google Scholar] [CrossRef]
- Tam, A.; Green, J.E.F.; Balasuriya, S.; Tek, E.L.; Gardner, J.M.; Sundstrom, J.F.; Jiranek, V.; Binder, B.J. Nutrient-limited growth with non-linear cell diffusion as a mechanism for floral pattern formation in yeast biofilms. J. Theor. Biol. 2018, 448, 122–141. [Google Scholar] [CrossRef]
- Gontar, A.; Bottema, M.J.; Binder, B.J.; Tronnolone, H. Characterizing the shape patterns of dimorphic yeast pseudohyphae. R. Soc. Open Sci. 2018, 5, 180820. [Google Scholar] [CrossRef]
- Tronnolone, H.; Gardner, J.M.; Sundstrom, J.F.; Jiranek, V.; Oliver, S.G.; Binder, B.J. Quantifying the dominant growth mechanisms of dimorphic yeast using a lattice-based model. J. R. Soc. Interface 2017, 14, 20170314. [Google Scholar] [CrossRef] [PubMed]
- Broach, J.R. Nutritional control of growth and development in yeast. Genetics 2012, 192, 73–105. [Google Scholar] [CrossRef] [PubMed]
- Merchant, S.S.; Helmann, J.D. Elemental economy: Microbial strategies for optimizing growth in the face of nutrient limitation. In Advances in Microbial Physiology; Elsevier: Amsterdam, The Netherlands, 2012; Volume 60, pp. 91–210. [Google Scholar]
- Plocek, V.; Váchová, L.; Št’ovíček, V.; Palková, Z. Cell Distribution within Yeast Colonies and Colony Biofilms: How Structure Develops. Int. J. Mol. Sci. 2020, 21, 3873. [Google Scholar] [CrossRef] [PubMed]
- Kayser, J.; Schreck, C.F.; Yu, Q.; Gralka, M.; Hallatschek, O. Emergence of evolutionary driving forces in pattern-forming microbial populations. Philos. Trans. R. Soc. Biol. Sci. 2018, 373, 20170106. [Google Scholar] [CrossRef]
- Smith, W.P.; Davit, Y.; Osborne, J.M.; Kim, W.; Foster, K.R.; Pitt-Francis, J.M. Cell morphology drives spatial patterning in microbial communities. Proc. Natl. Acad. Sci. USA 2017, 114, E280–E286. [Google Scholar] [CrossRef]
- Van Liedekerke, P.; Palm, M.; Jagiella, N.; Drasdo, D. Simulating tissue mechanics with agent-based models: Concepts, perspectives and some novel results. Comput. Part. Mech. 2015, 2, 401–444. [Google Scholar] [CrossRef]
- Glen, C.M.; Kemp, M.L.; Voit, E.O. Agent-based modeling of morphogenetic systems: Advantages and challenges. PLOS Comput. Biol. 2019, 15, e1006577. [Google Scholar] [CrossRef]
- Gorochowski, T.E. Agent-based modelling in synthetic biology. Essays Biochem. 2016, 60, 325–336. [Google Scholar]
- Jönsson, H.; Levchenko, A. An explicit spatial model of yeast microcolony growth. Multiscale Model. Simul. 2005, 3, 346–361. [Google Scholar] [CrossRef][Green Version]
- Wang, Y.; Lo, W.C.; Chou, C.S. A modeling study of budding yeast colony formation and its relationship to budding pattern and aging. PLoS Comput. Biol. 2017, 13, e1005843. [Google Scholar] [CrossRef]
- Aprianti, D.; Haryanto, F.; Purqon, A.; Khotimah, S.; Viridi, S. Study of budding yeast colony formation and its characterizations by using circular granular cell. J. Phys. Conf. Ser. 2016, 694, 012079. [Google Scholar] [CrossRef]
- Aprianti, D.; Khotimah, S.; Viridi, S. Budding yeast colony growth study based on circular granular cell. J. Phys. Conf. Ser. 2016, 739, 012026. [Google Scholar] [CrossRef]
- Aji, D.P.P.; Aprianti, D.; Viridi, S. Stochastic Simulation of Yeast Cells and Its Colony Growth by Using Circular Granular Model for Cases of Growth and Birth Probabilities Depends on Position. J. Phys. Conf. Ser. 2019, 1245, 012010. [Google Scholar]
- Purnama, F.A.; Meiriska, W.; Aji, D.P.P.; Aprianti, D.; Viridi, S. Network Analysis of Saccharomyces cerevisiae. J. Phys. Conf. Ser. 2019, 1245, 012081. [Google Scholar] [CrossRef]
- Meiriska, W.; Purnama, F.; Aji, D.; Aprianti, D.; Viridi, S. Network Analysis of Saccharomyces Cerevisiae Colony: Relation between Spatial Position and Generation. J. Phys. Conf. Ser. 2019, 1245, 012006. [Google Scholar] [CrossRef]
- Drasdo, D.; Loeffler, M. Individual-based models to growth and folding in one-layered tissues: Intestinal crypts and early development. Nonlinear Anal.-Theory Methods Appl. 2001, 47, 245–256. [Google Scholar] [CrossRef]
- Drasdo, D.; Forgacs, G. Modeling the interplay of generic and genetic mechanisms in cleavage, blastulation, and gastrulation. Dev. Dyn. Off. Publ. Am. Assoc. Anat. 2000, 219, 182–191. [Google Scholar] [CrossRef]
- Drasdo, D.; Höhme, S. A single-cell-based model of tumor growth in vitro: Monolayers and spheroids. Phys. Biol. 2005, 2, 133. [Google Scholar] [CrossRef]
- Drasdo, D.; Hoehme, S.; Block, M. On the role of physics in the growth and pattern formation of multi-cellular systems: What can we learn from individual-cell based models? J. Stat. Phys. 2007, 128, 287. [Google Scholar] [CrossRef]
- Hornung, R.; Grünberger, A.; Westerwalbesloh, C.; Kohlheyer, D.; Gompper, G.; Elgeti, J. Quantitative modelling of nutrient-limited growth of bacterial colonies in microfluidic cultivation. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef]
- Warren, M.R.; Sun, H.; Yan, Y.; Cremer, J.; Li, B.; Hwa, T. Spatiotemporal establishment of dense bacterial colonies growing on hard agar. Elife 2019, 8, e41093. [Google Scholar] [CrossRef] [PubMed]
- De Virgilio, C. The essence of yeast quiescence. FEMS Microbiol. Rev. 2012, 36, 306–339. [Google Scholar] [CrossRef] [PubMed]
- Herskowitz, I. Life cycle of the budding yeast Saccharomyces cerevisiae. Microbiol. Rev. 1988, 52, 536. [Google Scholar] [CrossRef] [PubMed]
- Minois, N.; Frajnt, M.; Wilson, C.; Vaupel, J.W. Advances in measuring lifespan in the yeast Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2005, 102, 402–406. [Google Scholar] [CrossRef]
- Sheu, Y.J.; Barral, Y.; Snyder, M. Polarized growth controls cell shape and bipolar bud site selection in Saccharomyces cerevisiae. Mol. Cell. Biol. 2000, 20, 5235–5247. [Google Scholar] [CrossRef]
- Mable, B. Ploidy evolution in the yeast Saccharomyces cerevisiae: A test of the nutrient limitation hypothesis. J. Evol. Biol. 2001, 14, 157–170. [Google Scholar] [CrossRef]
- Serio, T.R. (The University of Chicago, Chicago, IL, USA). Personal Communication, 2020.
- Binder, B.J.; Sundstrom, J.F.; Gardner, J.M.; Jiranek, V.; Oliver, S.G. Quantifying two-dimensional filamentous and invasive growth spatial patterns in yeast colonies. PLoS Comput. Biol. 2015, 11, e1004070. [Google Scholar] [CrossRef]
- Binder, B.J.; Simpson, M.J. Cell density and cell size dynamics during in vitro tissue growth experiments: Implications for mathematical models of collective cell behaviour. Appl. Math. Model. 2016, 40, 3438–3446. [Google Scholar] [CrossRef]
- Ruiz-Riquelme, A.; Lau, H.H.; Stuart, E.; Goczi, A.N.; Wang, Z.; Schmitt-Ulms, G.; Watts, J.C. Prion-like propagation of β-amyloid aggregates in the absence of APP overexpression. Acta Neuropathol. Commun. 2018, 6, 26. [Google Scholar] [CrossRef]
- Halfmann, R.; Jarosz, D.F.; Jones, S.K.; Chang, A.; Lancaster, A.K.; Lindquist, S. Prions are a common mechanism for phenotypic inheritance in wild yeasts. Nature 2012, 482, 363–368. [Google Scholar] [CrossRef]
- Weinberg, R.P.; Koledova, V.V.; Shin, H.; Park, J.H.; Tan, Y.A.; Sinskey, A.J.; Sambanthamurthi, R.; Rha, C. Oil palm phenolics inhibit the in vitro aggregation of β-amyloid peptide into oligomeric complexes. Int. J. Alzheimer’S Dis. 2018, 2018. [Google Scholar]
- Esler, W.P.; Stimson, E.R.; Jennings, J.M.; Vinters, H.V.; Ghilardi, J.R.; Lee, J.P.; Mantyh, P.W.; Maggio, J.E. Alzheimer’s disease amyloid propagation by a template-dependent dock-lock mechanism. Biochemistry 2000, 39, 6288–6295. [Google Scholar] [CrossRef] [PubMed]
- Brugger, S.D.; Baumberger, C.; Jost, M.; Jenni, W.; Brugger, U.; Mühlemann, K. Automated counting of bacterial colony forming units on agar plates. PLoS ONE 2012, 7, e33695. [Google Scholar] [CrossRef] [PubMed]
- Bewes, J.; Suchowerska, N.; McKenzie, D. Automated cell colony counting and analysis using the circular Hough image transform algorithm (CHiTA). Phys. Med. Biol. 2008, 53, 5991. [Google Scholar] [CrossRef]
- Ferrari, A.; Lombardi, S.; Signoroni, A. Bacterial colony counting with convolutional neural networks in digital microbiology imaging. Pattern Recognit. 2017, 61, 629–640. [Google Scholar] [CrossRef]
- Scherz, R.; Shinder, V.; Engelberg, D. Anatomical analysis of Saccharomyces cerevisiaestalk-like structures reveals spatial organization and cell specialization. J. Bacteriol. 2001, 183, 5402–5413. [Google Scholar] [CrossRef]
- Nguyen, B.; Upadhyaya, A.; van Oudenaarden, A.; Brenner, M.P. Elastic instability in growing yeast colonies. Biophys. J. 2004, 86, 2740–2747. [Google Scholar] [CrossRef]
- Reynolds, T.B.; Fink, G.R. Bakers’ yeast, a model for fungal biofilm formation. Science 2001, 291, 878–881. [Google Scholar] [CrossRef]
- Brückner, S.; Mösch, H.U. Choosing the right lifestyle: Adhesion and development in Saccharomyces cerevisiae. FEMS Microbiol. Rev. 2012, 36, 25–58. [Google Scholar] [CrossRef]
- Dranginis, A.M.; Rauceo, J.M.; Coronado, J.E.; Lipke, P.N. A biochemical guide to yeast adhesins: Glycoproteins for social and antisocial occasions. Microbiol. Mol. Biol. Rev. 2007, 71, 282–294. [Google Scholar] [CrossRef]
- Smith, A.E.; Zhang, Z.; Thomas, C.R.; Moxham, K.E.; Middelberg, A.P. The mechanical properties of Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2000, 97, 9871–9874. [Google Scholar] [CrossRef] [PubMed]
- Stenson, J.D.; Hartley, P.; Wang, C.; Thomas, C.R. Determining the mechanical properties of yeast cell walls. Biotechnol. Prog. 2011, 27, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Hoehme, S.; Drasdo, D. A cell-based simulation software for multi-cellular systems. Bioinformatics 2010, 26, 2641–2642. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.; Drasdo, D. Individual-based and continuum models of growing cell populations: A comparison. J. Math. Biol. 2009, 58, 657. [Google Scholar] [CrossRef]
- Farhadifar, R.; Röper, J.C.; Aigouy, B.; Eaton, S.; Jülicher, F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 2007, 17, 2095–2104. [Google Scholar] [CrossRef]
- Kursawe, J.; Brodskiy, P.A.; Zartman, J.J.; Baker, R.E.; Fletcher, A.G. Capabilities and Limitations of Tissue Size Control through Passive Mechanical Forces. PLoS Comput. Biol. 2015, 11, e1004679. [Google Scholar] [CrossRef]
- Newman, T.J. Modeling multicellular systems using subcellular elements. Math. Biosci. Eng. 2005, 2, 613–624. [Google Scholar] [CrossRef]
- Brewer, B.J.; Chlebowicz-Sledziewska, E.; Fangman, W.L. Cell cycle phases in the unequal mother/daughter cell cycles of Saccharomyces cerevisiae. Mol. Cell. Biol. 1984, 4, 2529–2531. [Google Scholar] [CrossRef][Green Version]
- Di Talia, S.; Skotheim, J.M.; Bean, J.M.; Siggia, E.D.; Cross, F.R. The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 2007, 448, 947–951. [Google Scholar] [CrossRef]
- Váchová, L.; Palková, Z. How structured yeast multicellular communities live, age and die? FEMS Yeast Res. 2018, 18, foy033. [Google Scholar] [CrossRef]
- Milani, M.; Batani, D.; Bortolotto, F.; Botto, C.; Baroni, G.; Cozzi, S.; Masini, A.; Ferraro, L.; Previdi, F.; Ballerini, M.; et al. Differential Two Colour X-ray Radiobiology of Membrane/Cytoplasm Yeast Cells: TMR Large-Scale Facilities Access Programme; NASA: Washington, DC, USA, 1998.
- Finch, A.M.; Wilson, R.C.; Hancock, E.R. Matching delaunay graphs. Pattern Recognit. 1997, 30, 123–140. [Google Scholar] [CrossRef]
- Lee, D.T.; Schachter, B.J. Two algorithms for constructing a Delaunay triangulation. Int. J. Comput. Inf. Sci. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Weatherill, N.P.; Hassan, O. Efficient three-dimensional Delaunay triangulation with automatic point creation and imposed boundary constraints. Int. J. Numer. Methods Eng. 1994, 37, 2005–2039. [Google Scholar] [CrossRef]
- Weier, M.H. Wal-Mart Chooses Neoview Data Warehouse. 2007. Available online: http://www.informationweek.com/news/201202317 (accessed on 2 April 2020).
- Davidson-Pilon, C.; Kalderstam, J.; Jacobson, N.; Kuhn, B.; Zivich, P.; Williamson, M.; Abdeali, J.K.; Datta, D.; Fiore-Gartland, A.; Parij, A.; et al. CamDavidsonPilon/lifelines: v0.24.16; Zenodo: Genève, Switzerland, 2020. [Google Scholar] [CrossRef]
- Efron, B. Logistic regression, survival analysis, and the Kaplan-Meier curve. J. Am. Stat. Assoc. 1988, 83, 414–425. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]





| Parameter | Symbol | Value | Units | Meaning | Reference |
|---|---|---|---|---|---|
| Poisson ratio | 0.3 | Incompressibility of yeast cells | [38,50,74] | ||
| Young’s Modulus | E | 1000 | Mechanical property of yeast cell walls | [38,50,74] | |
| Receptor Surface Density | 10E15 | Density of surface adhesion molecules in the contact area | [38,50] | ||
| Single Bond Binding Energy | 25 | [38,50] | |||
| Linear Spring Constant | 25 | m | Attachment of bud on mother cell | calibrated | |
| Damping Coefficient | 2.5 | Viscosity of the growth media | [38,50] | ||
| Average Length of phase | 75 | min | [82,83] | ||
| Average Length of phase (new daughters) | 120 | min | [82,83] | ||
| Average Length of phase (mothers) | 15 | min | [82,83] | ||
| Average Mature Radius Size | 2.58 | m | [84] | ||
| Carrying Capacity | Maximal possible biomass for each subdomain | calibrated | |||
| Subdomain Size | 25 | Area of each subdomain | calibrated | ||
| Rate of Maximum Cell Cycle Adjustment | r | 0.003 | Controls the amount cell cycle is adjusted at each timestep | calibrated | |
| Timestep | 0.00144 | min | calibrated |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banwarth-Kuhn, M.; Collignon, J.; Sindi, S. Quantifying the Biophysical Impact of Budding Cell Division on the Spatial Organization of Growing Yeast Colonies. Appl. Sci. 2020, 10, 5780. https://doi.org/10.3390/app10175780
Banwarth-Kuhn M, Collignon J, Sindi S. Quantifying the Biophysical Impact of Budding Cell Division on the Spatial Organization of Growing Yeast Colonies. Applied Sciences. 2020; 10(17):5780. https://doi.org/10.3390/app10175780
Chicago/Turabian StyleBanwarth-Kuhn, Mikahl, Jordan Collignon, and Suzanne Sindi. 2020. "Quantifying the Biophysical Impact of Budding Cell Division on the Spatial Organization of Growing Yeast Colonies" Applied Sciences 10, no. 17: 5780. https://doi.org/10.3390/app10175780
APA StyleBanwarth-Kuhn, M., Collignon, J., & Sindi, S. (2020). Quantifying the Biophysical Impact of Budding Cell Division on the Spatial Organization of Growing Yeast Colonies. Applied Sciences, 10(17), 5780. https://doi.org/10.3390/app10175780





