All-t2g Electronic Orbital Reconstruction of Monoclinic MoO2 Battery Material
Abstract
Featured Application
Abstract
1. Introduction
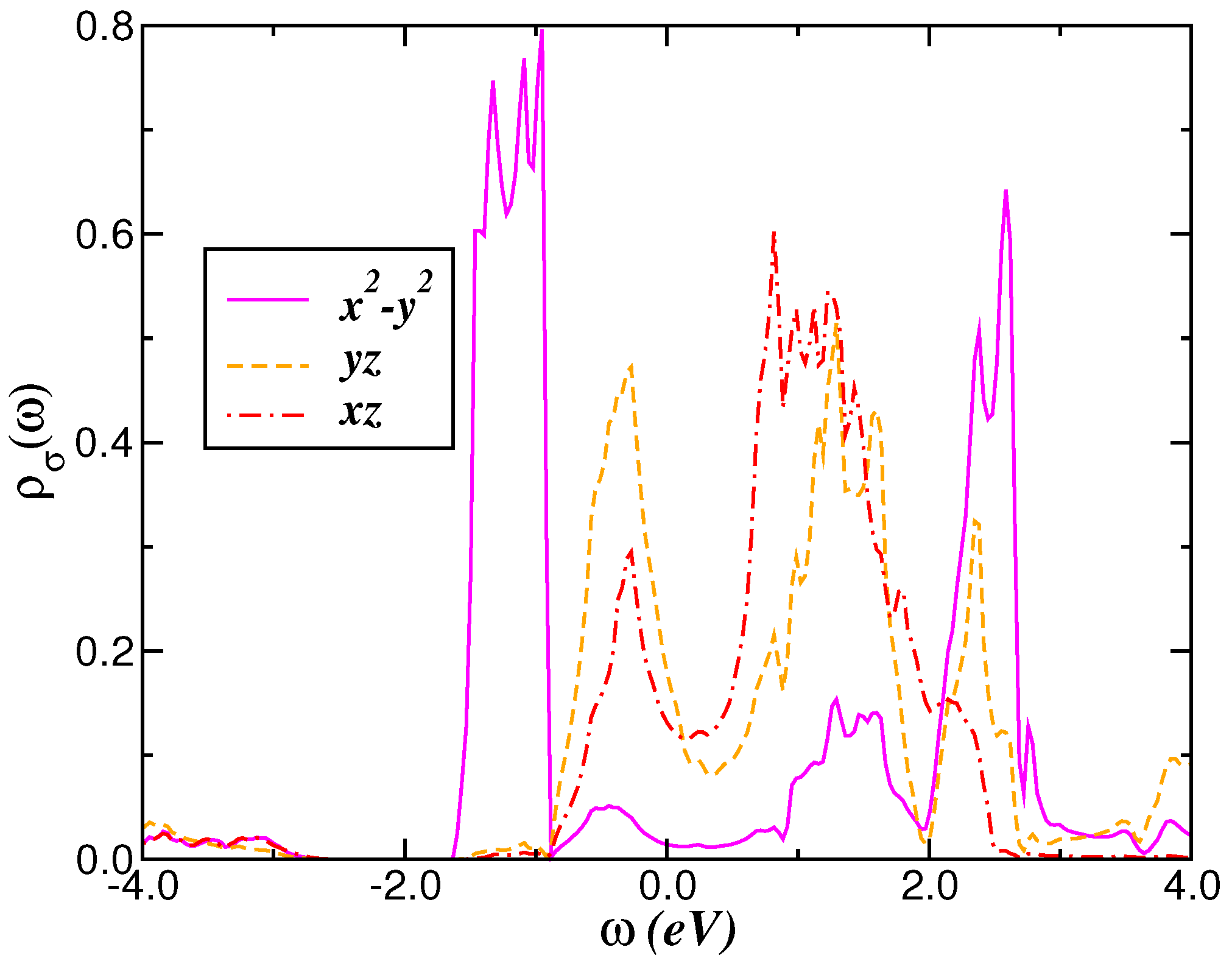
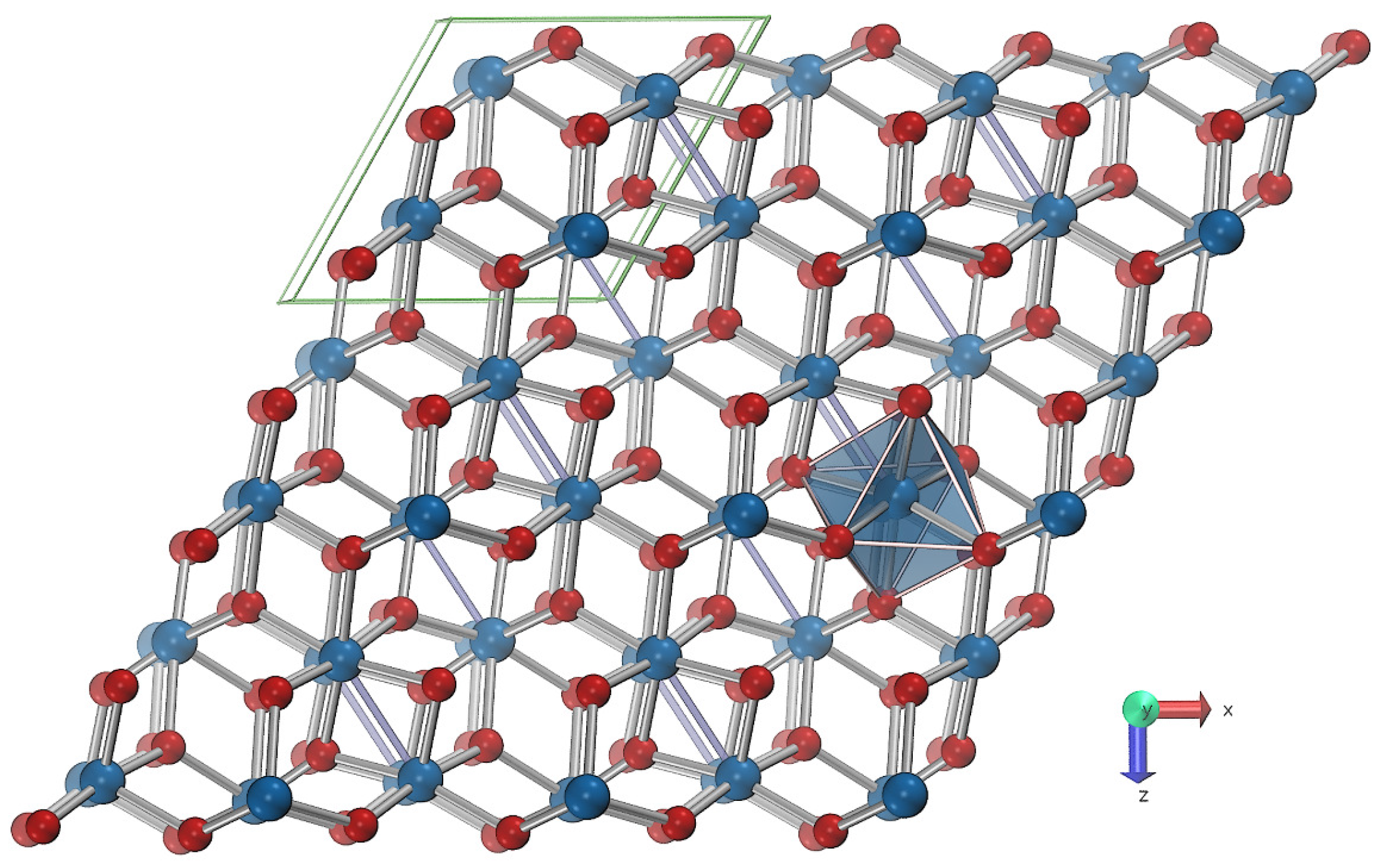
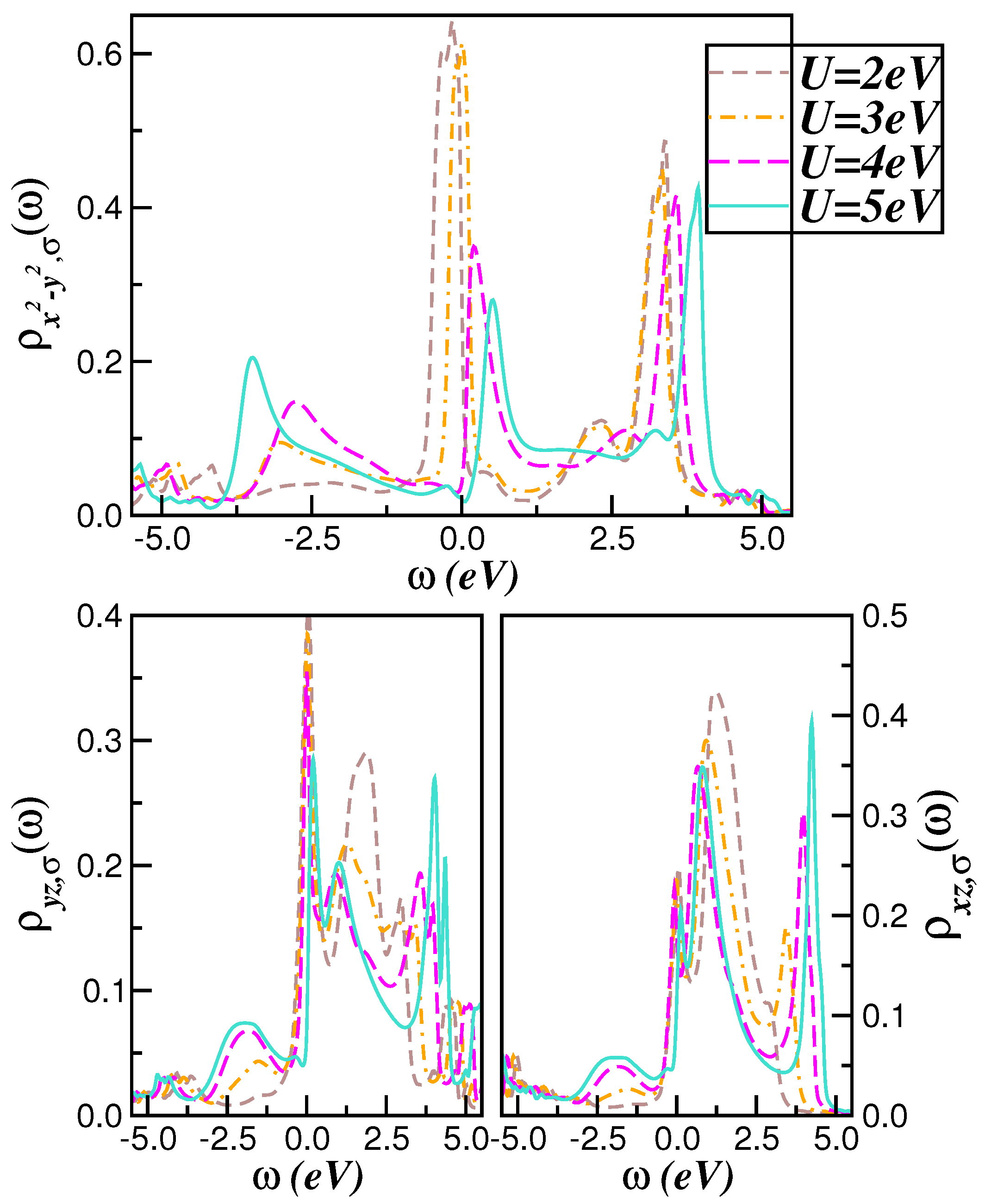
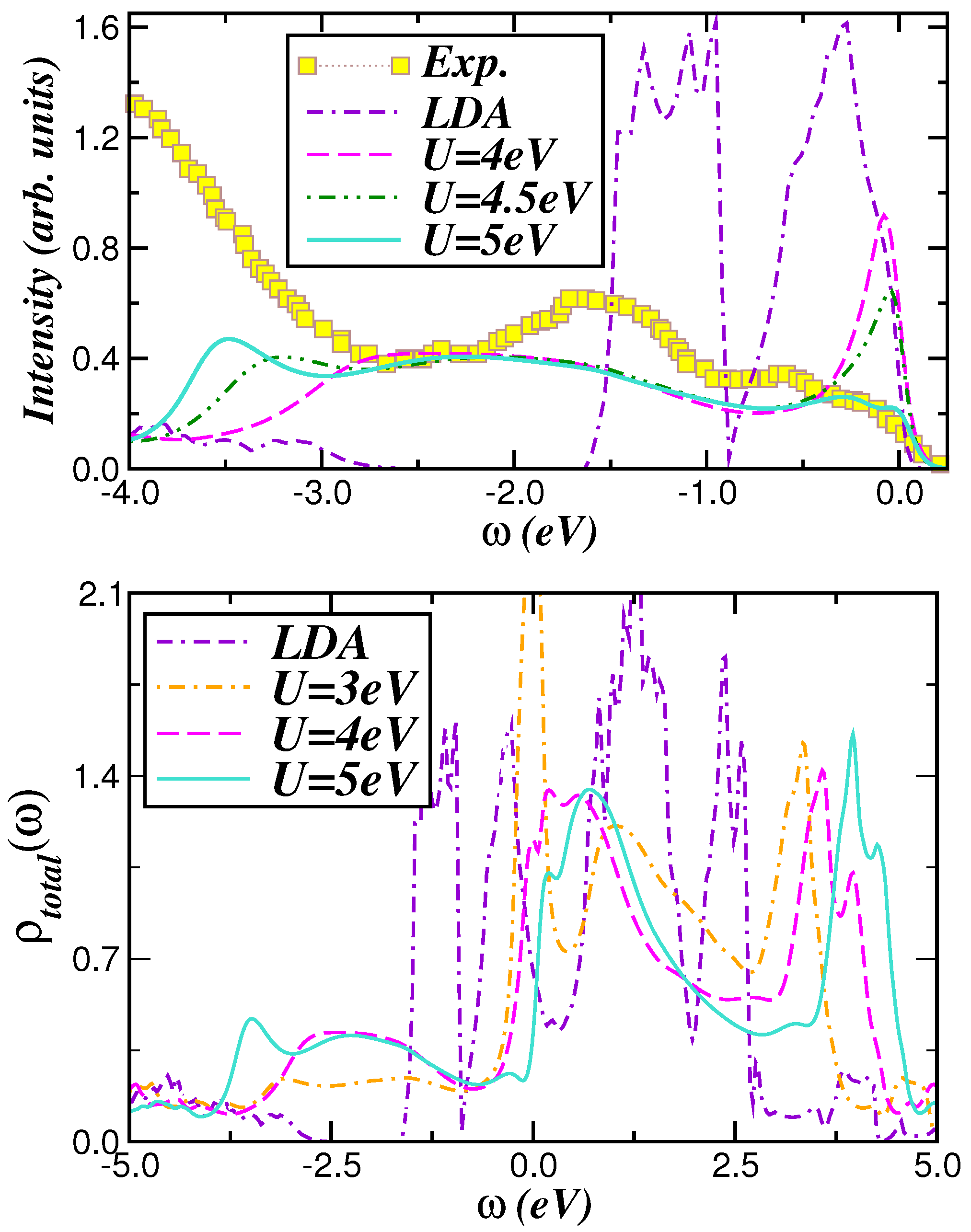
2. Results and Discussion
2.1. Correlated Electronic Structure
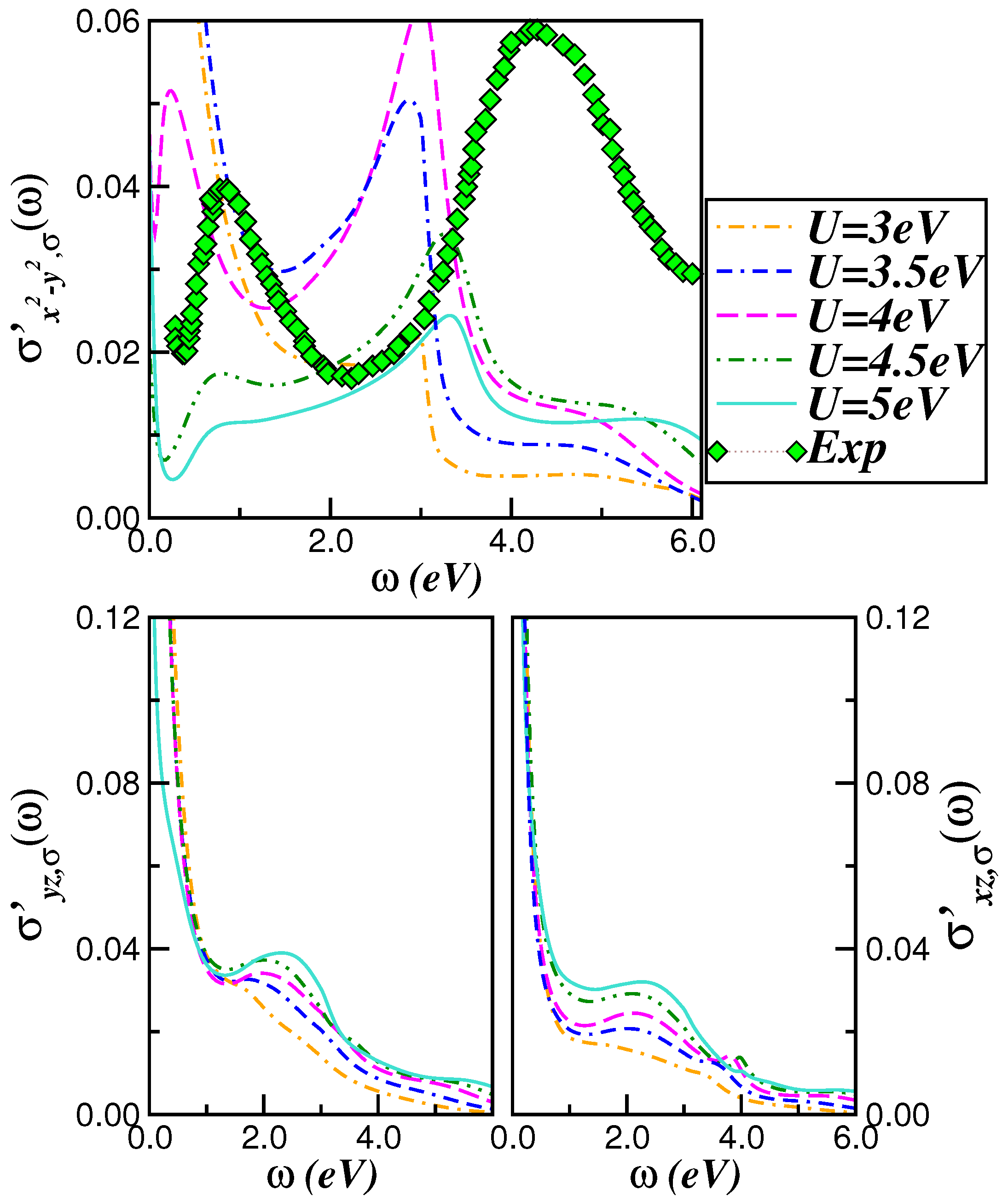
2.2. Optical Conductivity
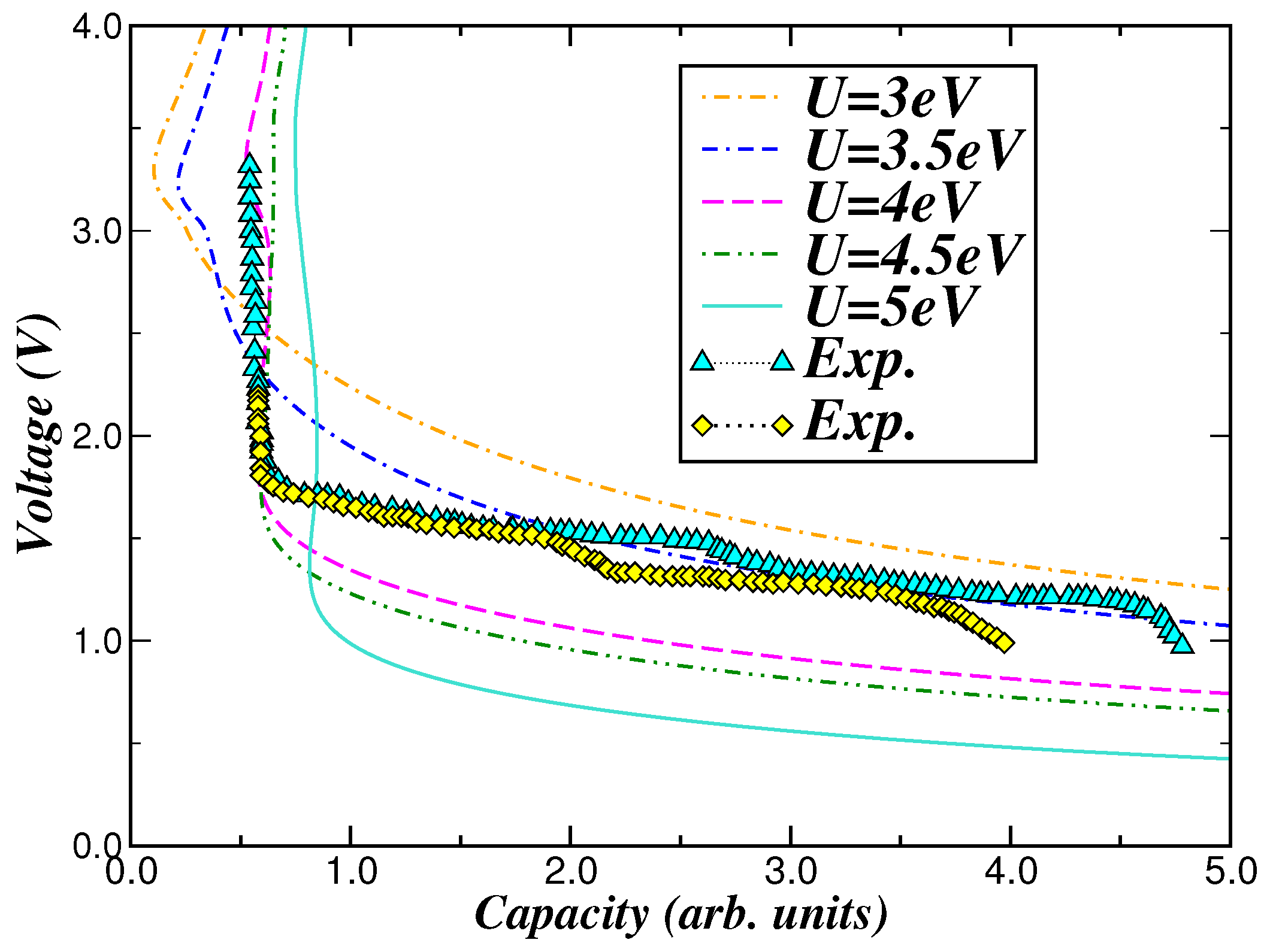
2.3. Voltage-Capacity Using LDA+DMFT
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Imada, M.; Fujimori, A.; Tokura, Y. Metal-insulator transitions. Rev. Mod. Phys. 1998, 70, 1039–1263. [Google Scholar] [CrossRef]
- Juliano, R.C.; de Arruda, A.S.; Craco, L. Coexistence and competition of on-site and intersite Coulomb interactions in Mott-molecular-dimers. Solid State Commun. 2016, 227, 51–55. [Google Scholar] [CrossRef]
- Peierls, R.E. Quantum Theory of Solids; Oxford University Press: Oxford, UK, 1955. [Google Scholar]
- Qazilbash, M.M.; Brehm, M.; Chae, B.-G.; Ho, P.-C.; Andreev, G.O.; Kim, B.-J.; Yun, S.J.; Balatsky, A.V.; Maple, M.B.; Keilmann, F.; et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 2007, 318, 1750–1753. [Google Scholar] [CrossRef] [PubMed]
- Biermann, S.; Poteryaev, A.; Lichtenstein, A.I.; Georges, A. Dynamical singlets and correlation-assisted peierls transition in VO2. Phys. Rev. Lett. 2005, 94, 026404. [Google Scholar] [CrossRef] [PubMed]
- Brito, W.H.; Aguiar, M.G.O.; Haule, K.; Kotliar, G. Metal-insulator transition in VO2: A DFT+DMFT perspective. Phys. Rev. Lett. 2016, 117, 056402. [Google Scholar] [CrossRef]
- Chakhalian, J.; Freeland, J.W.; Habermeier, H.-U.; Cristiani, G.; Khaliullin, G.; van Veenendaal, M.; Keimer, B. Orbital reconstruction and covalent bonding at an oxide interface. Science 2007, 318, 1114–1117. [Google Scholar] [CrossRef]
- Kotliar, G.; Savrasov, S.Y.; Haule, K.; Oudovenko, V.S.; Parcollet, O.; Marianetti, C.A. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 2006, 78, 865–951. [Google Scholar] [CrossRef]
- Ma, C.-H.; Lin, J.-C.; Liu, H.-J.; Do, T.H.; Zhu, Y.-M.; Ha, T.D.; Zhan, Q.; Juang, J.-Y.; He, Q.; Arenholz, E.; et al. Van der Waals epitaxy of functional MoO2 film on mica for flexible electronics. Appl. Phys. Lett. 2016, 108, 253104. [Google Scholar] [CrossRef]
- Kwon, B.W.; Ellefson, C.; Breit, J.; Kim, J.; Norton, M.G.; Ha, S. Molybdenum dioxide-based anode for solid oxide fuel cell applications. J. Power Sources 2013, 243, 203–210. [Google Scholar] [CrossRef]
- Bhosle, V.; Tiwari, A.; Narayan, J. Epitaxial growth and properties of MoOx(2 < x < 2.75) films. J. Appl. Phys. 2005, 97, 083539. [Google Scholar]
- Shon, J.K.; Lee, H.S.; Park, G.O.; Yoon, J.; Park, E.; Park, G.S.; Kong, S.S.; Jin, M.; Choi, J.-M.; Chang, H.; et al. Discovery of abnormal lithium-storage sites in molybdenum dioxide electrodes. Nat. Comm. 2016, 7, 11049. [Google Scholar] [CrossRef]
- Shi, Y.; Guo, B.; Corr, S.A.; Shi, Q.; Hu, Y.-S.; Heier, K.R.; Chen, L.; Seshadri, R.; Stucky, G.D. Ordered mesoporous metallic MoO2 materials with highly reversible lithium storage capacity. Nano Lett. 2009, 9, 4215–4220. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.C.; Gao, Q.S.; Tang, Y.; Wu, Y.P.; Holze, R. MoO2 synthesized by reduction of MoO3 with ethanol vapor as an anode material with good rate capability for the lithium ion battery. J. Power Sources 2008, 179, 357–360. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, X.; Yu, J.C.; Li, Q.; Luo, W.; Yuan, L.; Zhang, W.; Huang, Y. Morphosynthesis of a hierarchical MoO2 nanoarchitecture as a binder-free anode for lithium-ion batteries. Energy Environ. Sci. 2011, 4, 2870–2877. [Google Scholar] [CrossRef]
- Sen, U.K.; Shaligram, A.; Mitra, S. Intercalation anode material for lithium ion battery based on molybdenum dioxide. ACS Appl. Mater. Interfaces 2014, 6, 14311–14319. [Google Scholar] [PubMed]
- Katayama, N.; Takeda, H.; Yamaguchi, T.; Yamada, Y.; Iida, K.; Takigawa, M.; Ohta, Y.; Sawa, H. Robust atomic orbital in the cluster magnet LiMoO2. Phys. Rev. B 2020, 102, 081106. [Google Scholar] [CrossRef]
- Alves, L.M.S.; dos Santos, C.A.M.; Benaion, S.S.; Machado, A.J.S.; de Lima, B.S.; Neumeier, J.J.; Marques, M.D.R.; Aguiar, J.A.; Mossanek, R.J.O.; Abbate, M. Superconductivity and magnetism in the KxMoO22−δ. J. Appl. Phys. 2012, 112, 073923. [Google Scholar] [CrossRef]
- Moosburger-Will, J.; Kündel, J.; Klemm, M.; Horn, S.; Hofmann, P.; Schwingenschlögl, U.; Eyert, V. Fermi surface of MoO2 studied by angle-resolved photoemission spectroscopy, de Haas–van Alphen measurements, and electronic structure calculations. Phys. Rev. B 2009, 79, 115113. [Google Scholar] [CrossRef]
- Eyert, V.; Horny, R.; Höck, K.-H.; Horn, S. Embedded Peierls instability and the electronic structure of MoO2. J. Phys. Condens. Matter 2000, 12, 4923–4946. [Google Scholar] [CrossRef]
- Davenport, M.A.; Krogstad, M.J.; Whitt, L.M.; Hu, C.; Douglas, T.C.; Ni, N.; Rosenkranz, S.; Osborn, R.; Allred, J.M. Fragile 3D Order in V1-xMoxO2. arXiv 2019, arXiv:1909.12704. [Google Scholar]
- Chase, L.L. Optical properties of CrO2 and MoO2 from 0.1 to 6 eV. Phys. Rev. B 1974, 10, 2226–2231. [Google Scholar] [CrossRef]
- Prakash, R.; Phase, D.M.; Choudhary, R.J.; Kumar, R. Structural, electrical, and magnetic properties of Mo1-xFexO2 (x = 0–0.05) thin films grown by pulsed laser ablation. J. Appl. Phys. 2008, 103, 043712. [Google Scholar] [CrossRef]
- Scanlon, D.O.; Watson, G.W.; Payne, D.J.; Atkinson, G.R.; Egdell, R.G.; Law, D.S.L. Theoretical and experimental study of the electronic structures of MoO3 and MoO2. J. Phys. Chem. C 2010, 114, 4636–4645. [Google Scholar] [CrossRef]
- Ataca, C.; Şahin, H.; Ciraci, S. Stable, Single-layer MX2 transition-metal oxides and dichalcogenides in a honeycomb-like structure. J. Phys. Chem. C 2012, 116, 8983–8999. [Google Scholar] [CrossRef]
- Wadati, H.; Yoshimatsu, K.; Kumigashira, H.; Oshima, M.; Sugiyama, T.; Ikenaga, E.; Fujimori, A.; Mravlje, J.; Georges, A.; Radetinac, A.; et al. Photoemission and DMFT study of electronic correlations in SrMoO3: Effects of Hund’s rule coupling and possible plasmonic sideband. Phys. Rev. B 2014, 90, 205131. [Google Scholar] [CrossRef]
- Kim, A.; Park, E.; Lee, H.; Kim, H. Highly reversible insertion of lithium into MoO2 as an anode material for lithium ion battery. J. Alloys Compd. 2016, 681, 301–306. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Mott and pseudogap localization in pressurized NbO2. Phys. Rev. B 2020, in press. [Google Scholar] [CrossRef]
- Brito, W.H.; Aguiar, M.C.O.; Haule, K.; Kotliar, G. Dynamic electronic correlation effects in NbO2 as compared to VO2. Phys. Rev. B 2017, 96, 195102. [Google Scholar] [CrossRef]
- Chadov, S.; Qi, X.; Kübler, J.; Fecher, G.H.; Felser, C.; Zhang, S.C. tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 2010, 9, 541–545. [Google Scholar] [CrossRef]
- Craco, L. Quantum orbital entanglement: A view from the extended periodic Anderson model. Phys. Rev. B 2008, 77, 125122. [Google Scholar] [CrossRef]
- Laad, M.S.; Craco, L.; Müller-Hartmann, E. Orbital-selective insulator-metal transition in V2O3 under external pressure. Phys. Rev. B 2006, 73, 045109. [Google Scholar] [CrossRef]
- Grenzebach, C.; Anders, F.B.; Czycholl, G.; Pruschke, T. Transport properties of heavy-fermion systems. Phys. Rev. B 2006, 74, 195119. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Biermann, S. Optical properties of correlated materials: Generalized Peierls approach and its application to VO2. Phys. Rev. B 2009, 80, 085117. [Google Scholar] [CrossRef]
- Laad, M.S.; Craco, L.; Leoni, S.; Rosner, H. Electrodynamic response of incoherent metals: Normal phase of iron pnictides. Phys. Rev. B 2009, 79, 024515. [Google Scholar] [CrossRef]
- Brandt, B.G.; Skapski, A.C. Refinement of the crystal structure of molybdenum dioxide. Acta Chem. Scand. 1967, 21, 661–672. [Google Scholar] [CrossRef]
- Alves, L.M.S.; Damasceno, V.I.; dos Santos, C.A.M.; Bortolozo, A.D.; Suzuki, P.A.; Izario Filho, H.J.; Machado, A.J.S.; Fisk, Z. Unconventional metallic behavior and superconductivity in the K-Mo-O system. Phys. Rev. B 2010, 81, 174532. [Google Scholar] [CrossRef]
- Lechermann, F.; Biermann, S.; Georges, A. Competing itinerant and localized states in strongly correlated BaVS3. Phys. Rev. B 2007, 76, 085101. [Google Scholar] [CrossRef]
- Bobrov, V.B.; Trigger, S.A.; van Heijst, G.J.F.; Schram, P.P.J.M. Kramers-Kronig relations for the dielectric function and the static conductivity of Coulomb systems. Europhys. Lett. 2010, 90, 10003. [Google Scholar] [CrossRef]
- Basov, D.N.; Averitt, R.D.; van der Marel, D.; Dressel, M.; Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 2011, 83, 471–541. [Google Scholar] [CrossRef]
- Craco, L.; Leoni, S. Electrodynamics and quantum capacity of LixFePO4 battery material. Appl. Phys. Lett. 2011, 99, 192103. [Google Scholar] [CrossRef]
- Urasaki, K.; Saso, T. correlation effects on optical conductivity of FeSi. J. Phys. Soc. Jpn. 1999, 68, 3477–3480. [Google Scholar] [CrossRef]
- Baldassarre, L.; Perucchi, A.; Nicoletti, D.; Toschi, A.; Sangiovanni, G.; Held, K.; Capone, M.; Ortolani, M.; Malavasi, L.; Marsi, M.; et al. Quasiparticle evolution and pseudogap formation in V2O3: An infrared spectroscopy study. Phys. Rev. B 2008, 77, 113107. [Google Scholar] [CrossRef]
- Pavarini, E.; Yamasaki, A.; Nuss, J.; Andersen, O.K. How chemistry controls electron localization in 3d1 perovskites: A Wannier-function study. New J. Phys. 2005, 7, 188. [Google Scholar] [CrossRef]
- Ferry, D.; Goodnick, S.M. Transport in Nanostructures; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Liu, X.; Yang, J.; Hou, W.; Wang, J.; Nuli, Y. Highly reversible lithium-ions storage of molybdenum dioxide nanoplates for high power lithium-ion batteries. Chem. Sustain. Chem. 2015, 8, 2621–2624. [Google Scholar] [CrossRef]
- Guo, B.; Fang, X.; Li, B.; Shi, Y.; Ouyang, C.; Hu, Y.-S.; Wang, Z.; Stucky, G.D.; Cheng, L. Synthesis and lithium storage mechanism of ultrafine MoO2 nanorods. Chem. Mater. 2012, 24, 457–463. [Google Scholar] [CrossRef]
- Baldoni, M.; Craco, L.; Seifert, G.; Leoni, S. A two-electron mechanism of lithium insertion into layered α-MoO3: A DFT and DFT+U study. J. Mat. Chem. A 2013, 1, 1778–1784. [Google Scholar] [CrossRef]
- Wang, W.; Qin, J.; Yin, Z.; Cao, M. Achieving fully reversible conversion in MoO3 for lithium ion batteries by rational introduction of CoMoO4. ACS Nano 2016, 10, 10106–10116. [Google Scholar] [CrossRef]
- Gao, S.; Tang, Y.; Gao, Y.; Liu, L.; Zhao, H.; Li, X.; Wang, X. Highly Crystalized Co2Mo3O8 hexagonal nanoplates interconnectedby coal-derived carbon via the molten-salt-assisted method forcompetitive li-ion battery anodes. ACS Appl. Mater. Interfaces 2019, 11, 7006–7013. [Google Scholar] [CrossRef]
- Cabana, J.; Monconduit, L.; Larcher, S.; Palacín, M.R. Beyond Intercalation-Based Li-ion Batteries: The State of the Art and Challenges of Electrode Materials Reacting Through Conversion Reactions. Adv. Energy Mater. 2010, 22, E170–E192. [Google Scholar] [CrossRef]
- Zhou, Y.-N.; Ma, J.; Hu, E.; Yu, X.; Gu, L.; Nam, K.-W.; Chen, L.; Wang, Z.; Yang, X.-Q. Tuning charge-discharge induced unit cell breathing in layer-structured cathode materials for lithium-ion batteries. Nat. Comm. 2014, 5, 538. [Google Scholar] [CrossRef]
- Meng, T.; Hao, Y.-N.; Qin, J.; Cao, M. Interface-engineering-induced electric field effect and atomic disorder in cobalt selenide for high-rate and large-capacity lithium storage. ACS Sustain. Chem. Eng. 2019, 7, 4657–4665. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Craco, L.; Leoni, S. All-t2g Electronic Orbital Reconstruction of Monoclinic MoO2 Battery Material. Appl. Sci. 2020, 10, 5730. https://doi.org/10.3390/app10175730
Craco L, Leoni S. All-t2g Electronic Orbital Reconstruction of Monoclinic MoO2 Battery Material. Applied Sciences. 2020; 10(17):5730. https://doi.org/10.3390/app10175730
Chicago/Turabian StyleCraco, Luis, and Stefano Leoni. 2020. "All-t2g Electronic Orbital Reconstruction of Monoclinic MoO2 Battery Material" Applied Sciences 10, no. 17: 5730. https://doi.org/10.3390/app10175730
APA StyleCraco, L., & Leoni, S. (2020). All-t2g Electronic Orbital Reconstruction of Monoclinic MoO2 Battery Material. Applied Sciences, 10(17), 5730. https://doi.org/10.3390/app10175730





