High-Efficiency All-Dielectric Metasurfaces for the Generation and Detection of Focused Optical Vortex for the Ultraviolet Domain
Abstract
Featured Application
Abstract
1. Introduction
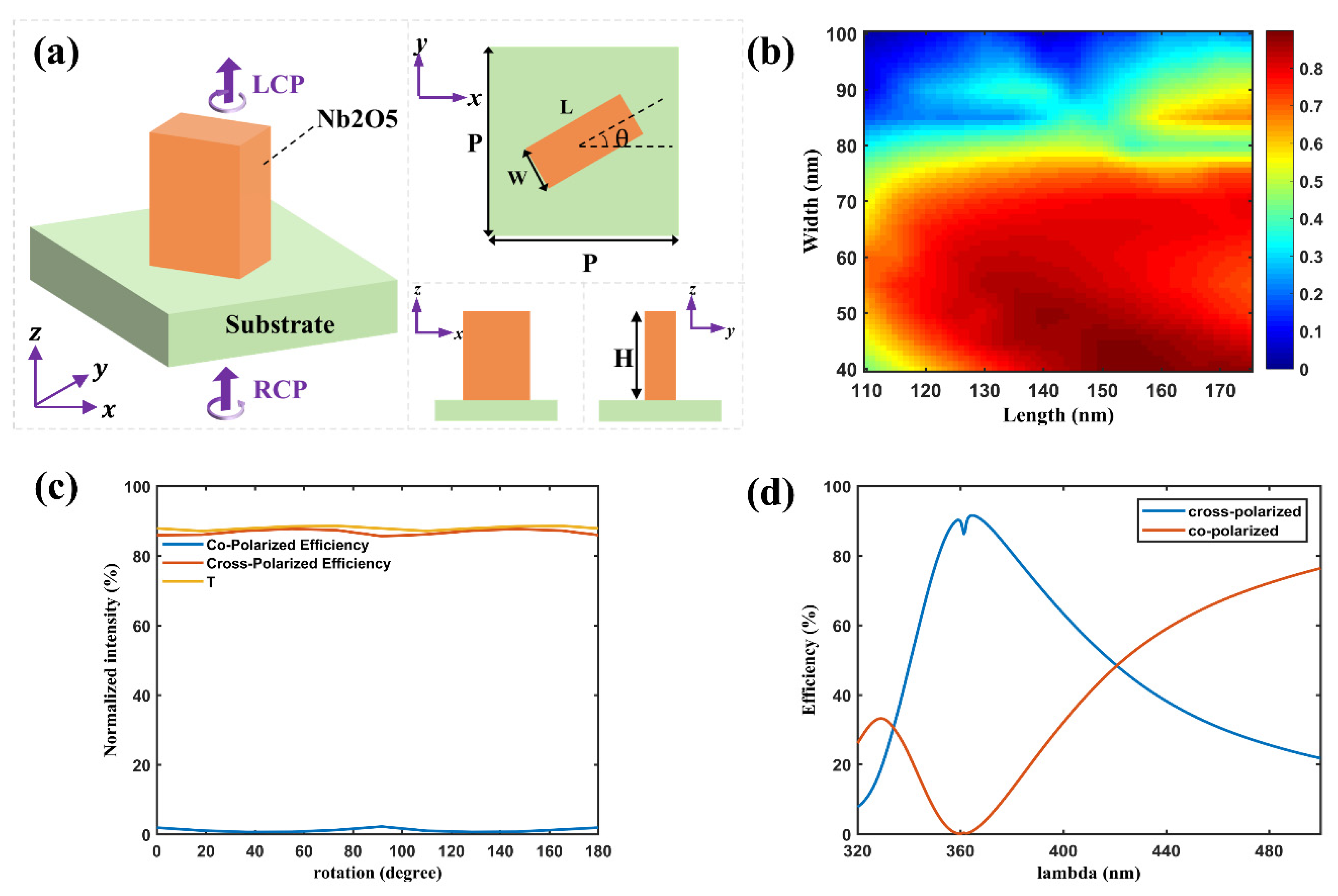
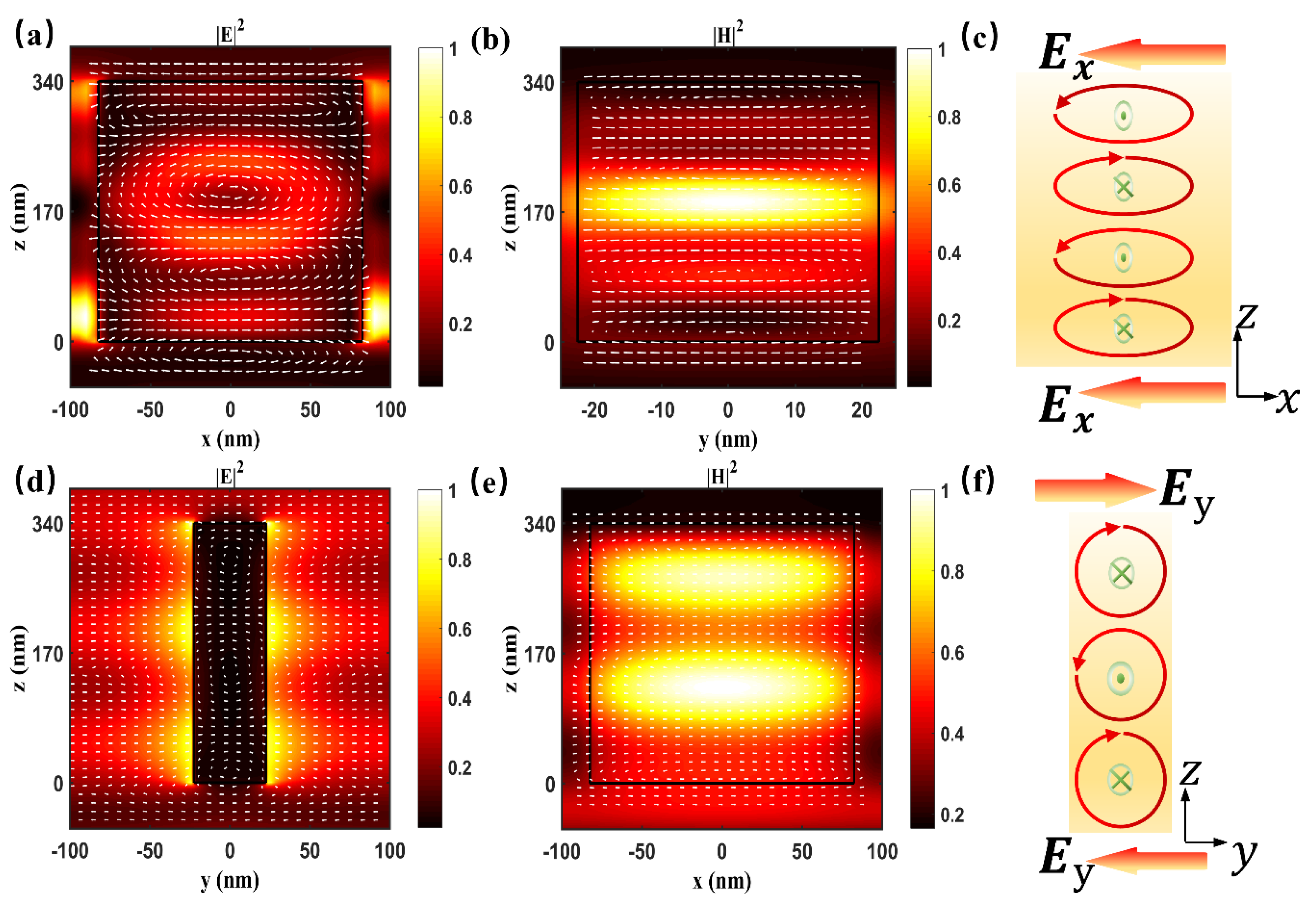
2. Theory and Meta-Atom Design
3. Results and Discussion
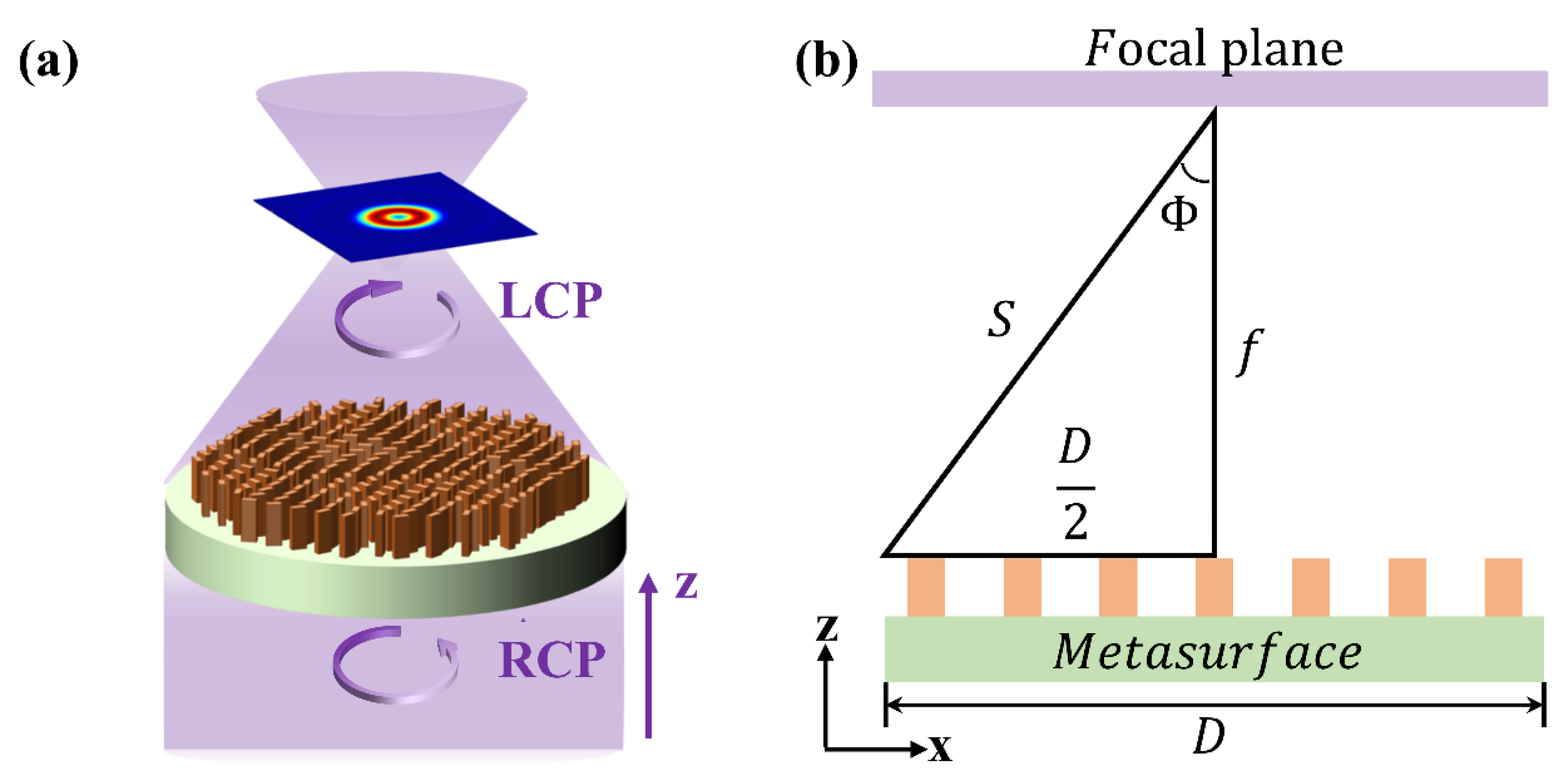
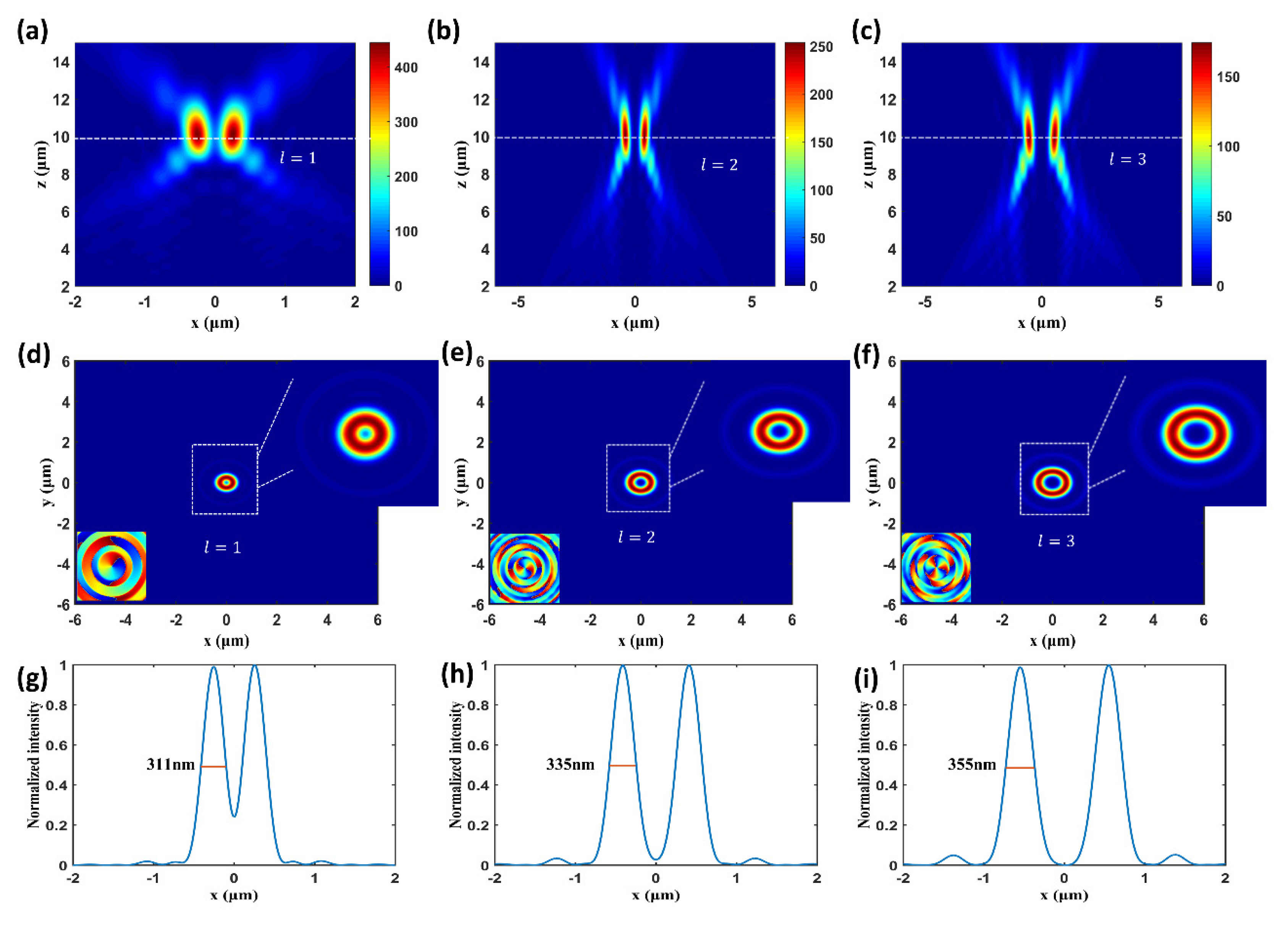
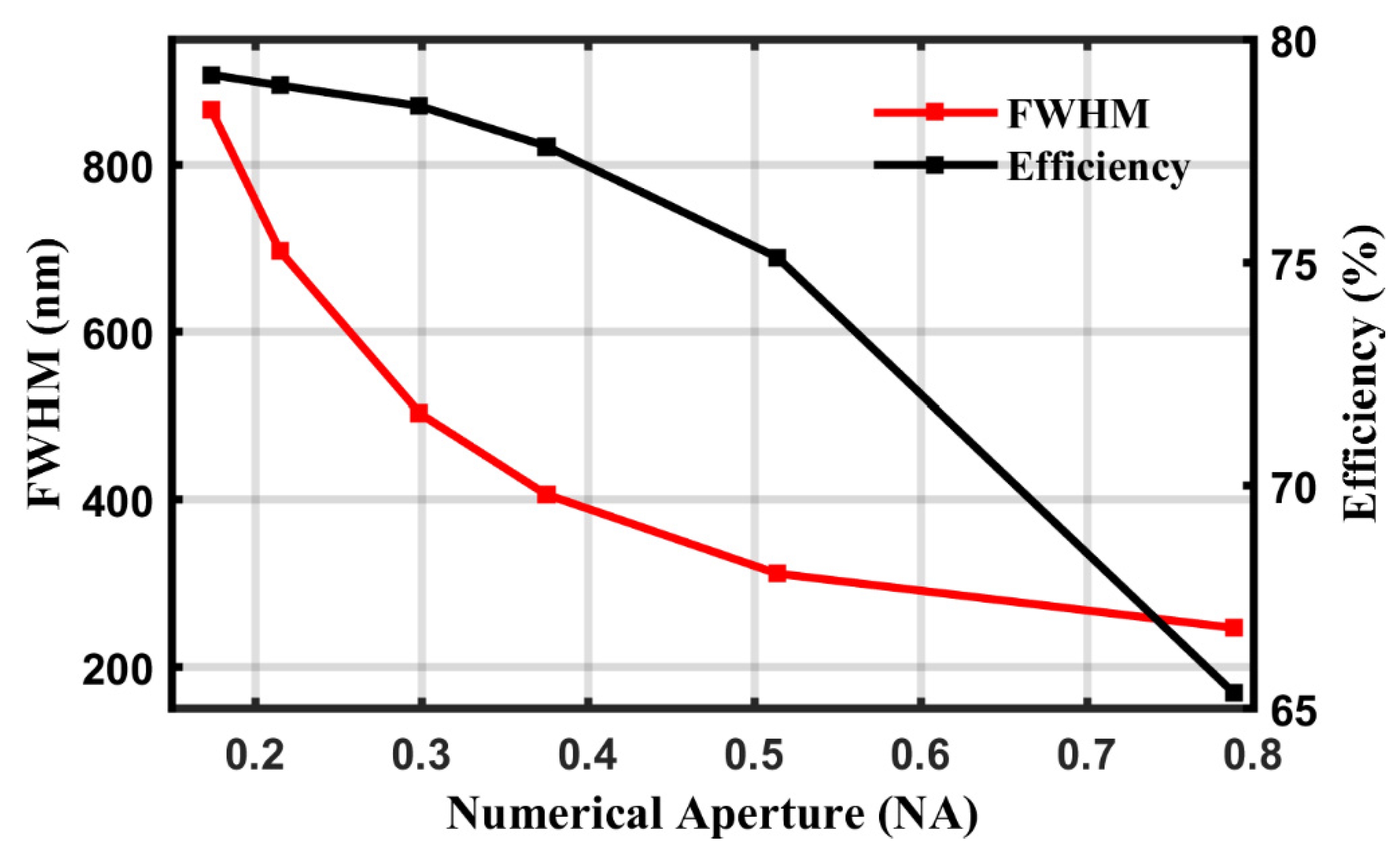
3.1. Focused Optical Vortex Generation
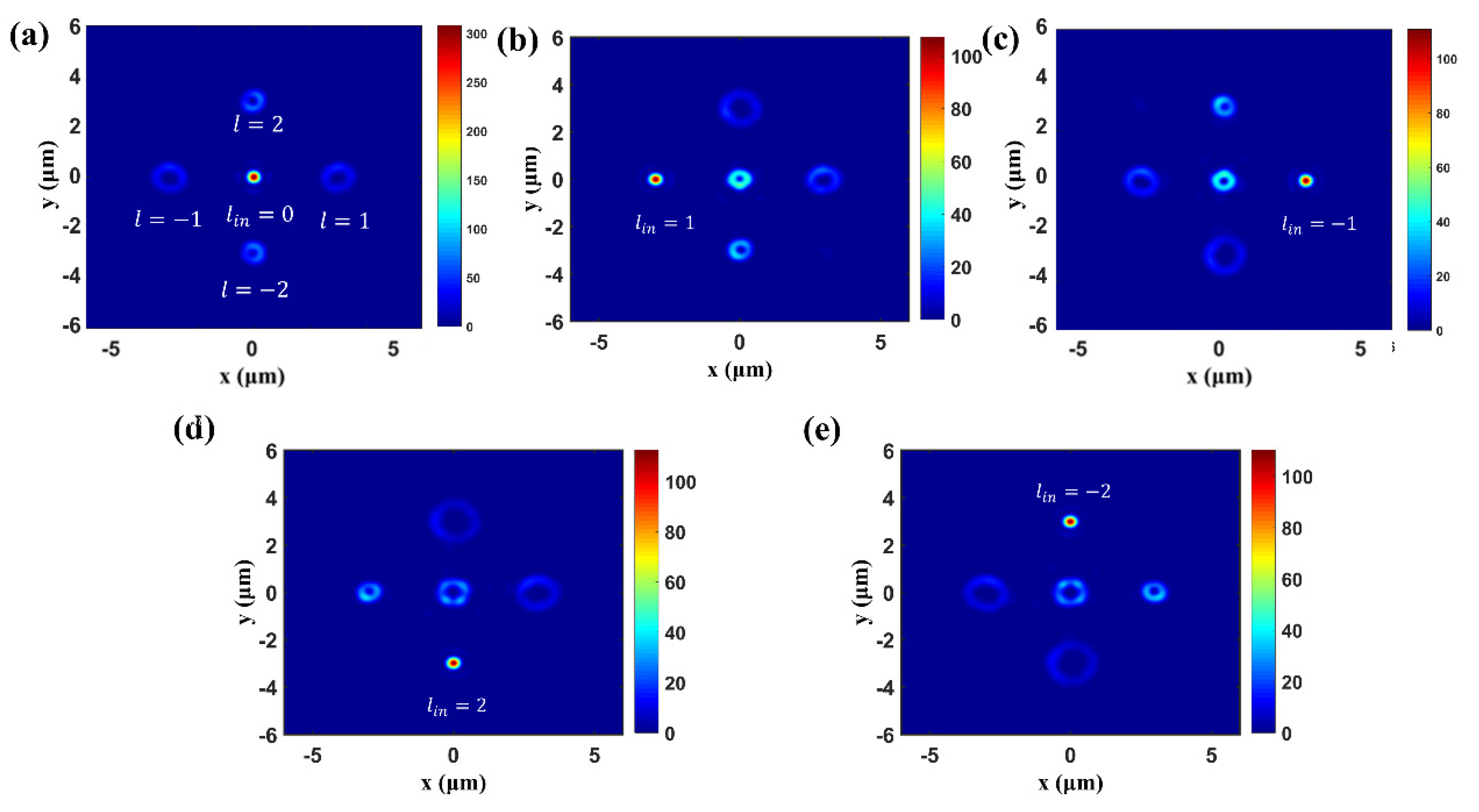
3.2. Multichannel FOV Generation and Detection
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, W.; Shen, Z.; Man, Z.; Min, C.; Shen, J.; Zhu, S.; Urbach, H.P.; Yuan, X. A Plasmonic Spanner for Metal Particle Manipulation. Sci. Rep. 2015, 5, 15446. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, J.; Min, C.; Jin, Y.; Jiang, Y.; Liu, J.; Zhu, S.; Sheng, Y.; Zayats, A.V.; Yuan, X. Nonlinearity-Induced Multiplexed Optical Trapping and Manipulation with Femtosecond Vector Beams. Nano Lett. 2018, 18, 5538–5543. [Google Scholar] [CrossRef]
- Toninelli, E.; Ndagano, B.; Vallés, A.; Sephton, B.; Nape, I.; Ambrosio, A.; Capasso, F.; Padgett, M.J.; Forbes, A. Concepts in quantum state tomography and classical implementation with intense light: A tutorial. Adv. Opt. Photonics 2019, 11. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, J.; Jiao, Z.Q.; Sun, K.; Shen, W.G.; Qiao, L.F.; Tang, H.; Lin, X.F.; Jin, X.M. Mapping Twisted Light into and out of a Photonic Chip. Phys. Rev. Lett. 2018, 121, 233602. [Google Scholar] [CrossRef]
- Jeffries, G.D.M.; Edgar, J.S.; Zhao, Y.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using Polarization-Shaped Optical Vortex Traps for Single-Cell Nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef] [PubMed]
- Karabchevsky, A. On-chip optical vortex-based nanophotonic detectors. Light Sci. Appl. 2020, 9, 115. [Google Scholar] [CrossRef] [PubMed]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for high intensity laser pulses. Opt. Express 2004, 12, 3548–3553. [Google Scholar] [CrossRef] [PubMed]
- Padgett, M.; Allen, L. Orbital angular momentum exchange in cylindrical-lens mode converters. J. Opt. B Quantum Semiclass Opt. 2002, 4, S17. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; van der Veen, H.E.L.O.; Woerdman, J.P. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Aieta, F.; Genevet, P.; Kats, M.A.; Gaburro, Z.; Capasso, F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 2012, 12, 6328–6333. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Hu, Y.; Li, X.; Jiang, Y.; Wang, Y.; Dai, P.; Liu, Q.; Shu, Z.; Duan, H.J.A.O.M. Integrated Metasurfaces with Microprints and Helicity-Multiplexed Holograms for Real-Time Optical Encryption. Adv. Opt. Mater. 2020, 8, 1902020. [Google Scholar] [CrossRef]
- Zheng, G.; Muhlenbernd, H.; Kenney, M.; Li, G.; Zentgraf, T.; Zhang, S. Metasurface holograms reaching 80% efficiency. Nat. Nanotechnol. 2015, 10, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Avrahamy, R.; Zohar, M.; Auslender, M.; Milgrom, B.; Hava, S.; Shikler, R. In-depth investigation and applications of novel silicon photonics microstructures supporting optical vorticity and waveguiding for ultra-narrowband near-infrared perfect absorption. Photonics Res. 2020, 8, 381–394. [Google Scholar] [CrossRef]
- Chen, D.C.; Zhu, X.F.; Wu, D.J.; Liu, X.J. Broadband Airy-like beams by coded acoustic metasurfaces. Appl. Phys. Lett. 2019, 114. [Google Scholar] [CrossRef]
- Jin, R.; Tang, L.; Li, J.; Wang, J.; Wang, Q.; Liu, Y.; Dong, Z.G. Experimental Demonstration of Multidimensional and Multifunctional Metalenses Based on Photonic Spin Hall Effect. ACS Photonics 2020, 7, 512–518. [Google Scholar] [CrossRef]
- Avayu, O.; Almeida, E.; Prior, Y.; Ellenbogen, T. Composite functional metasurfaces for multispectral achromatic optics. Nat. Commun. 2017, 8, 14992. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, J.; Zheng, H.; An, S.; Lin, H.; Zheng, B.; Du, Q.; Yin, G.; Michon, J.; Zhang, Y.; et al. Ultra-thin high-efficiency mid-infrared transmissive Huygens meta-optics. Nat. Commun. 2018, 9, 1481. [Google Scholar] [CrossRef]
- Zhang, S.; Soibel, A.; Keo, S.A.; Wilson, D.; Rafol, S.B.; Ting, D.Z.; She, A.; Gunapala, S.D.; Capasso, F. Solid-immersion metalenses for infrared focal plane arrays. Appl. Phys. Lett. 2018, 113. [Google Scholar] [CrossRef]
- Vo, S.; Fattal, D.; Sorin, W.V.; Peng, Z.; Tran, T.; Fiorentino, M.; Beausoleil, R.G. Sub-Wavelength Grating Lenses With a Twist. IEEE Photonics Technol. Lett. 2014, 26, 1375–1378. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Zhu, A.Y.; Roques-Carmes, C.; Chen, W.T.; Oh, J.; Mishra, I.; Devlin, R.C.; Capasso, F. Polarization-Insensitive Metalenses at Visible Wavelengths. Nano Lett. 2016, 16, 7229–7234. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wu, P.C.; Su, V.C.; Lai, Y.C.; Chen, M.K.; Kuo, H.Y.; Chen, B.H.; Chen, Y.H.; Huang, T.T.; Wang, J.H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.B.; Shao, Z.K.; Xie, M.Y.; Pang, X.N.; Ruan, W.S.; Zhao, F.L.; Chen, Y.J.; Yu, S.Y.; Dong, J.W. Silicon Nitride Metalenses for Close-to-One Numerical Aperture and Wide-Angle Visible Imaging. Phys. Rev. Appl. 2018, 10, 014005. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, X.; Gong, Z.; Dong, K.; Lou, S.; Pegard, N.; Tom, K.B.; Yang, F.; You, Z.; Waller, L.; et al. All-Silicon Broadband Ultraviolet Metasurfaces. Adv. Mater. 2018, 30, e1802632. [Google Scholar] [CrossRef]
- Zhang, C.; Divitt, S.; Fan, Q.; Zhu, W.; Agrawal, A.; Lu, Y.; Xu, T.; Lezec, H.J. Low-loss metasurface optics down to the deep ultraviolet region. Light Sci. Appl. 2020, 9, 55. [Google Scholar] [CrossRef]
- Gao, X.; Wan, R.; Yan, J.; Wang, L.; Yi, X.; Wang, J.; Zhu, W.; Li, J. Design of AlN ultraviolet metasurface for single-/multi-plane holography. Appl. Opt. 2020, 59, 4398–4403. [Google Scholar] [CrossRef]
- Rani, R.A.; Zoolfakar, A.S.; O’Mullane, A.P.; Austin, M.W.; Kalantar-Zadeh, K. Thin films and nanostructures of niobium pentoxide: Fundamental properties, synthesis methods and applications. J. Mater. Chem. A 2014, 2, 15683–15703. [Google Scholar] [CrossRef]
- Hota, M.K.; Bera, M.K.; Maiti, C.K. Flexible metal–insulator–metal capacitors on polyethylene terephthalate plastic substrates. Semicond. Sci. Technol. 2012, 27. [Google Scholar] [CrossRef]
- Menzel, C.; Rockstuhl, C.; Lederer, F. Advanced Jones calculus for the classification of periodic metamaterials. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
- Kang, M.; Feng, T.; Wang, H.T.; Li, J. Wave front engineering from an array of thin aperture antennas. Opt. Express 2012, 20, 15882–15890. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Lemarchand, F.; Lequime, M.J.O.e. Exploitation of multiple incidences spectrometric measurements for thin film reverse engineering. Opt. Express 2012, 20, 15734–15751. [Google Scholar] [CrossRef] [PubMed]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
- Luo, W.; Sun, S.; Xu, H.X.; He, Q.; Zhou, L. Transmissive Ultrathin Pancharatnam-Berry Metasurfaces with nearly 100% Efficiency. Phys. Rev. Appl. 2017, 7. [Google Scholar] [CrossRef]
- Huang, K.; Deng, J.; Leong, H.S.; Yap, S.L.K.; Yang, R.B.; Teng, J.; Liu, H. Ultraviolet Metasurfaces of ≈80% Efficiency with Antiferromagnetic Resonances for Optical Vectorial Anti-Counterfeiting. Laser Photonics Rev. 2019, 13. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Ball, A.J.; Bagheri, M.; Faraon, A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nat. Commun. 2015, 6, 7069. [Google Scholar] [CrossRef]
- Ahmed, H.; Rahim, A.A.; Maab, H.; Ali, M.M.; Mahmood, N.; Naureen, S. Phase engineering with all-dielectric metasurfaces for focused-optical-vortex (FOV) beams with high cross-polarization efficiency. Opt. Mater. Express 2020, 10. [Google Scholar] [CrossRef]
- Mahmood, N.; Kim, I.; Mehmood, M.Q.; Jeong, H.; Akbar, A.; Lee, D.; Saleem, M.; Zubair, M.; Anwar, M.S.; Tahir, F.A.; et al. Polarisation insensitive multifunctional metasurfaces based on all-dielectric nanowaveguides. Nanoscale 2018, 10, 18323–18330. [Google Scholar] [CrossRef]
- Jin, J.; Pu, M.; Wang, Y.; Li, X.; Ma, X.; Luo, J.; Zhao, Z.; Gao, P.; Luo, X. Multi-Channel Vortex Beam Generation by Simultaneous Amplitude and Phase Modulation with Two-Dimensional Metamaterial. Adv. Mater. Technol. 2017, 2. [Google Scholar] [CrossRef]
- Kanwal, S.; Wen, J.; Yu, B.; Kumar, D.; Chen, X.; Kang, Y.; Bai, C.; Zhang, D. High-Efficiency, Broadband, Near Diffraction-Limited, Dielectric Metalens in Ultraviolet Spectrum. Nanomaterials 2020, 10, 490. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, T.; Jiao, X.; Song, G.; Xu, Y. High-Efficiency All-Dielectric Metasurfaces for the Generation and Detection of Focused Optical Vortex for the Ultraviolet Domain. Appl. Sci. 2020, 10, 5716. https://doi.org/10.3390/app10165716
Zhang Z, Li T, Jiao X, Song G, Xu Y. High-Efficiency All-Dielectric Metasurfaces for the Generation and Detection of Focused Optical Vortex for the Ultraviolet Domain. Applied Sciences. 2020; 10(16):5716. https://doi.org/10.3390/app10165716
Chicago/Turabian StyleZhang, Ziheng, Tong Li, Xiaofei Jiao, Guofeng Song, and Yun Xu. 2020. "High-Efficiency All-Dielectric Metasurfaces for the Generation and Detection of Focused Optical Vortex for the Ultraviolet Domain" Applied Sciences 10, no. 16: 5716. https://doi.org/10.3390/app10165716
APA StyleZhang, Z., Li, T., Jiao, X., Song, G., & Xu, Y. (2020). High-Efficiency All-Dielectric Metasurfaces for the Generation and Detection of Focused Optical Vortex for the Ultraviolet Domain. Applied Sciences, 10(16), 5716. https://doi.org/10.3390/app10165716



