Analyzing Zone-Based Registration Using a Three Zone System: A Semi-Markov Process Approach
Abstract
1. Introduction
2. Zone-Based Registration
3. New Mathematical Model
3.1. Notations and Assumptions
- ▪
- Cp: Signaling cost for paging per cell on radio channels
- ▪
- Cu: Signaling cost for one location registration on radio channels
- ▪
- θ: Probability of returning to the registered zone
- ▪
- n: Number of cells per zone
- ▪
- Ti: Interval between two incoming calls (r.v. (random variable), Ti ~Exp(1/λi), E(Ti) = 1/λi)
- ▪
- To: Interval between two outgoing calls (r.v., To ~Exp(1/λo), E(To) = 1/λo)
- ▪
- Tc: Interval between two calls (r.v., Tc ~Exp(1/λ), E(Tc) = 1/λ)
- ▪
- Tm: Sojourn time in a zone (r.v., E(Tm) = 1/μ)
- ▪
- Rm: Interval between the arrival of the call, and the time when the UE moves out of the zone (r.v.)
- ▪
- ρ: Incoming calls to mobility ratio (CMR = λi/μ = ρ)
- ▪
- : Laplace–Stieltjes transform for Tm (=
- ▪
- The interval between two calls, Tc, follows an exponential distribution with mean 1/λ.
- ▪
- The UE’s sojourn time in a zone, Tm, follows a general distribution with mean 1/μ.
- ▪
- The probability that UE returns to the last zone is θ.
- ▪
- The probability that UE moves to one of the three zones except the last zone is the same (in other words, (1 − θ)/3).
- ▪
- Call holding time is so short that it can be ignored.
3.2. Semi-Markov Process Model for 3Z
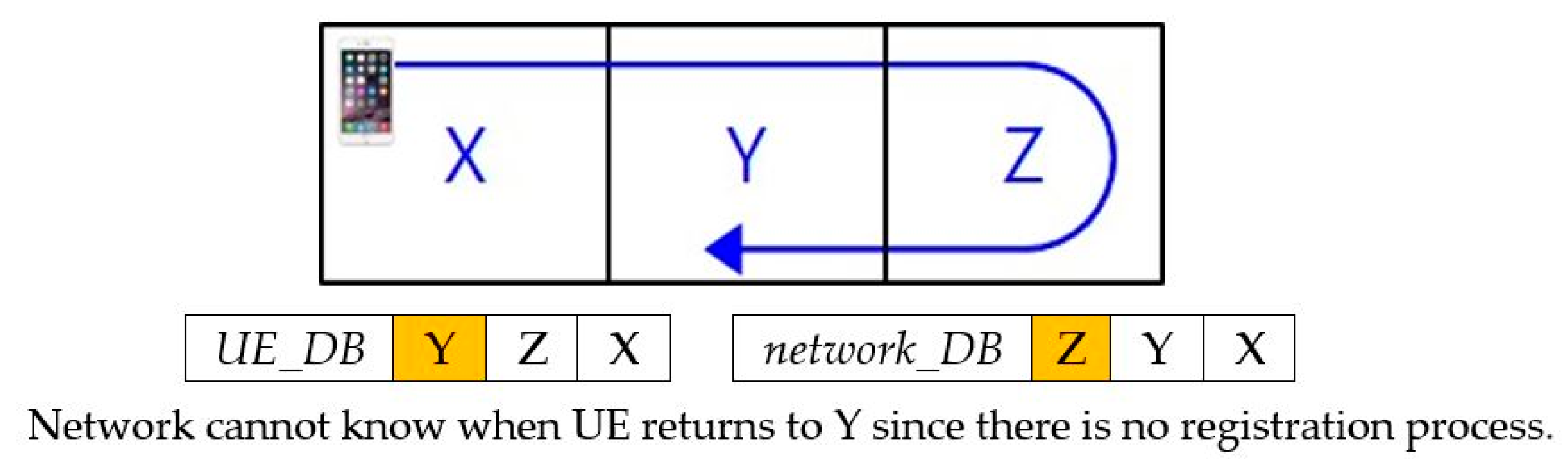
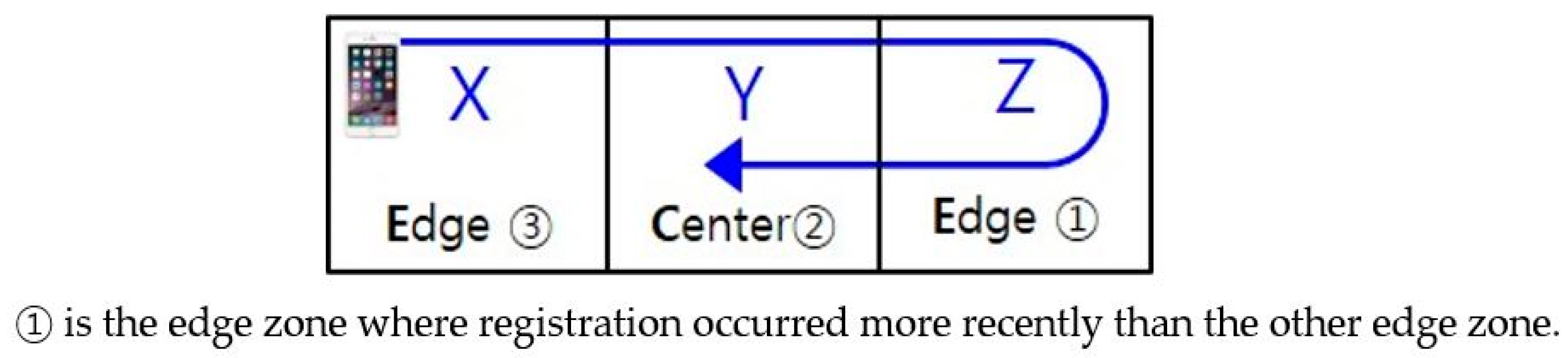
3.2.1. Definition of State by the Position of Each Zone in a 3Z System
3.2.2. Definition of States by the Call Occurrence of Each Zone in a 3Z System
3.2.3. Paging Procedure
3.2.4. States for Semi-Markov Process and Transition Diagram
3.2.5. Calculation of State Transition Probabilities
3.2.6. Calculation of Sojourn Time in Each State
3.2.7. Calculation of Steady-State Probabilities
3.3. Registration Cost
3.4. Paging Cost
3.5. Total Cost
4. Numerical Results
- ▪
- The number of cells in a zone, n, is 4.
- ▪
- The probability of returning to the last zone, θ, is 0.4.
- ▪
- Registration cost of one registration, U, is 4 and paging cost for one cell, V, is 1 (U = 4, V = 1).
- ▪
- Incoming and outgoing call rates are both 1 call per hour (λi = λo = 1).
- ▪
- UE’s sojourn time in a zone, Tm, follows an exponential distribution with mean 1/4 (μ = 4).
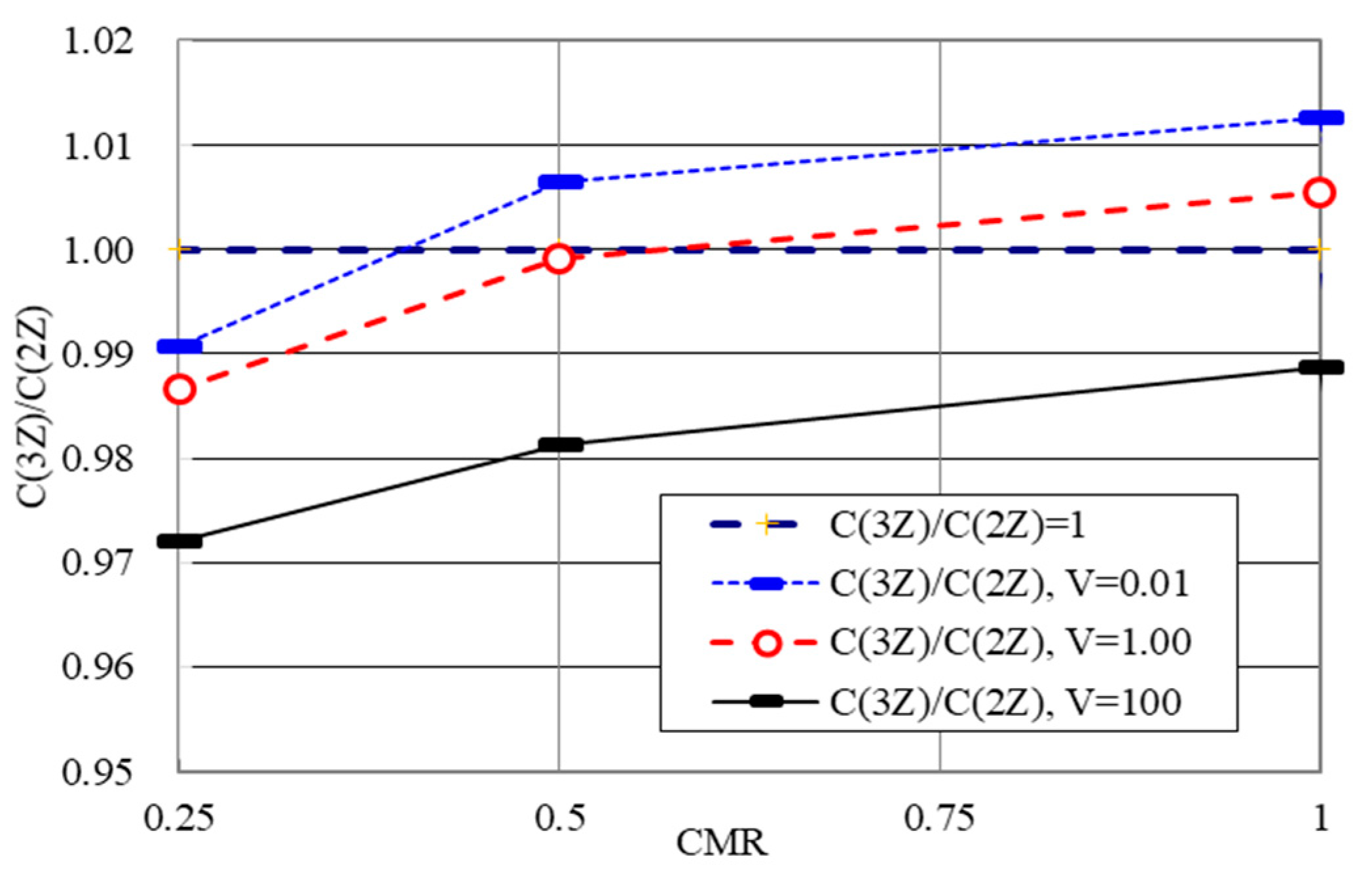
4.1. Total Cost for Various CMRs
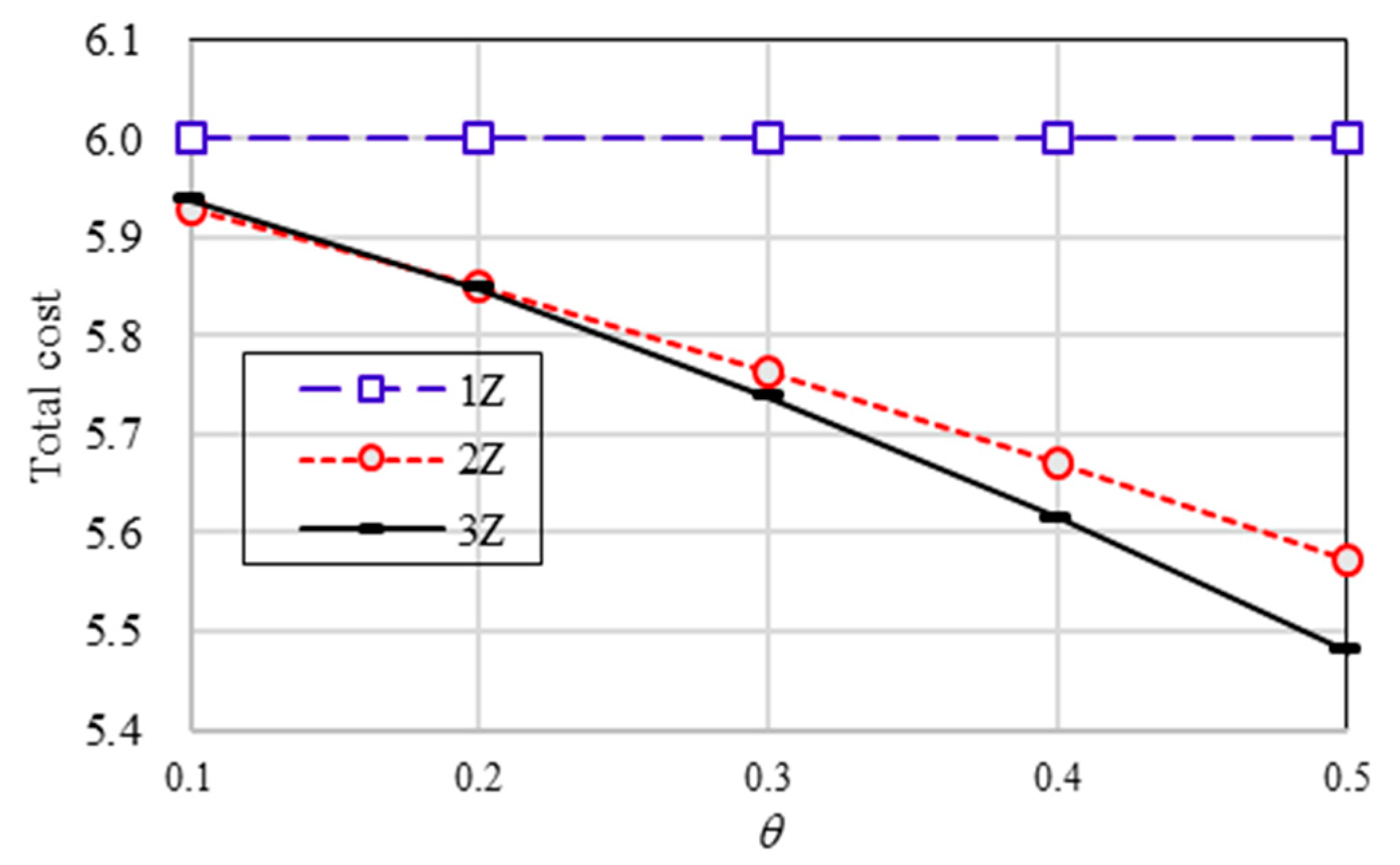
4.2. Total Cost for Various Probabilities of Moving Back to the Last Zone
4.3. Total Cost for Various Gamma Distributions
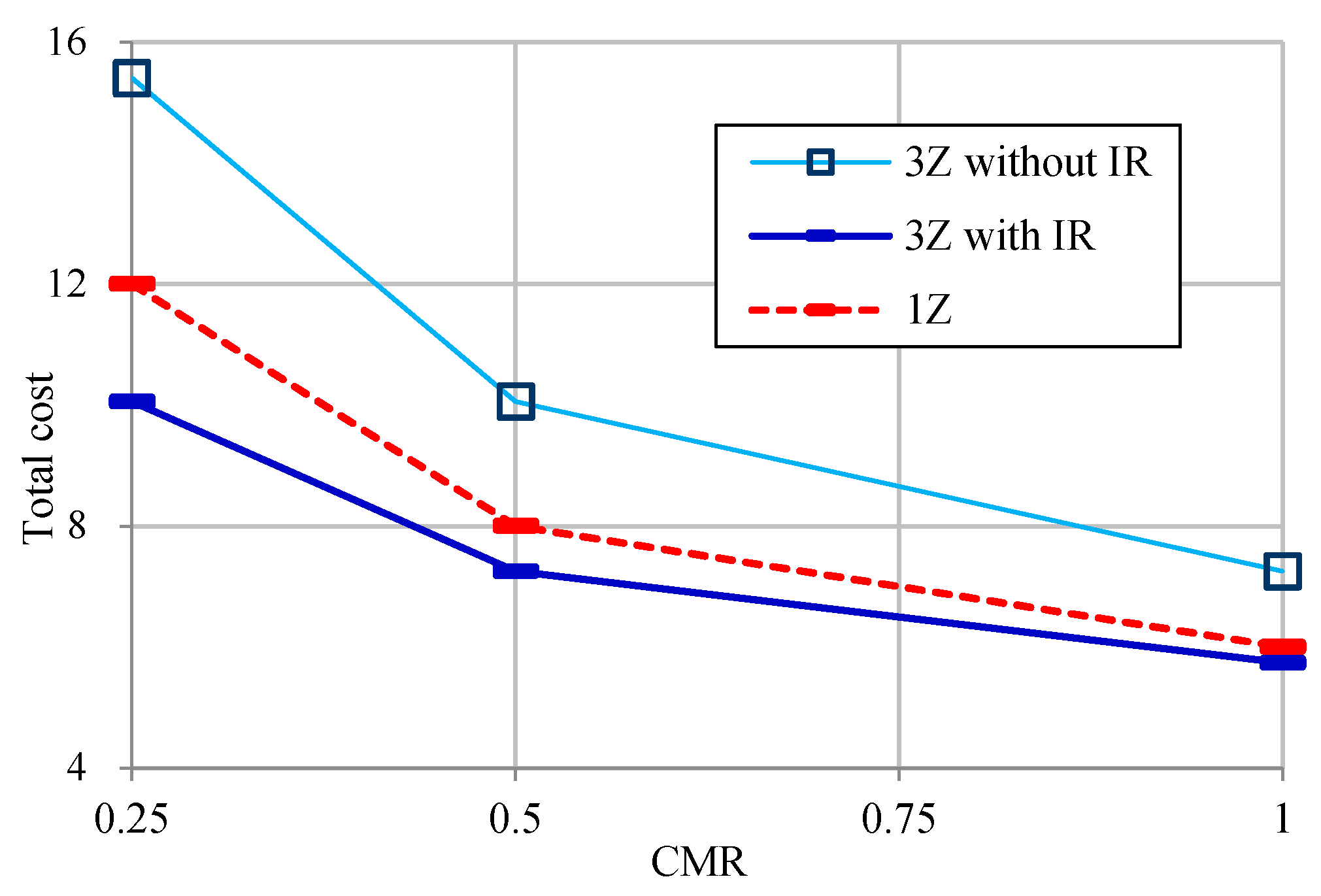
4.4. Effect of Implicit Registration by Outgoing Calls
4.5. Effects of the Number of Cells in a Zone and the Registration Cost of One Registration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, Y.B. Reducing location update cost in a PCS network. IEEE/ACM Trans. Netw. 1997, 5, 25–33. [Google Scholar]
- 3GPP2 C.S0005-E Version 3.0, Upper Layer (Layer 3) Signaling Standard for cdma2000 Spread Spectrum Systems. June 2011. Available online: http://www.3gpp2.org/Public_html/Specs/C.S0005-E_v3.0_cdma2000_1x_Layer-3_20110620.pdf (accessed on 17 August 2020).
- Li, J.; Kameda, H.; Li, K. Optimal dynamic mobility management for PCS networks. IEEE/ACM Trans. Netw. 2000, 8, 319–327. [Google Scholar]
- Wang, X.; Lei, X.; Fan, P.; Hu, R.; Horng, S. Cost analysis of movement-based location management in PCS networks: An embedded Markov chain approach. IEEE Trans. Veh. Technol. 2014, 63, 1886–1902. [Google Scholar] [CrossRef]
- Mao, Z.; Douligeris, C. A location-based mobility tracking scheme for PCS networks. Comput. Commun. 2000, 23, 1729–1739. [Google Scholar] [CrossRef]
- Baek, J.H.; Lee, T.H.; Kim, J.S. Performance analysis of 2-location distance-based registration in mobile communication networks. IEICE Trans. Commun. 2013, E96-B, 914–917. [Google Scholar] [CrossRef]
- Seo, K.H.; Baek, J.H.; Eom, C.S.; Lee, W. Optimal management of distance-based location registration using embedded Markov chain. Int. J. Distrib. Sens. Netw. 2020, 16. [Google Scholar] [CrossRef]
- Baek, J.H.; Ryu, B.H.; Lim, S.K.; Kim, K.S. Mobility model and performance analysis for zone-based registration in CDMA mobile communication system. Telecommun. Syst. 2000, 14, 13–30. [Google Scholar] [CrossRef]
- Jang, H.S.; Hwang, H.; Jun, K.P. Modeling and analysis of two-location algorithm with implicit registration in CDMA personal communication network. Comput. Ind. Eng. 2001, 41, 95–108. [Google Scholar] [CrossRef]
- Baek, W.M.; Yoon, J.H.; Kim, C.S. Modeling and analysis of mobility management in mobile communication networks. Sci. World J. 2014, 2014, 250981. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.H. Analyzing zone-based registration in mobile cellular networks. IEICE Trans. Commun. 2017, E100-B, 2070–2078. [Google Scholar] [CrossRef]
- Jung, J.; Baek, J.H. Modeling and cost analysis of zone-based registration in mobile cellular networks. ETRI J. 2018, 40, 736–744. [Google Scholar] [CrossRef]
- Liou, R.H.; Lin, Y.B. Mobility management with the central-based location area policy. Comput. Netw. 2013, 57, 847–857. [Google Scholar] [CrossRef][Green Version]
- Lin, Y.B.; Liou, R.H.; Chang, C.T. A dynamic paging scheme for long-term evolution mobility management. Wirel. Commun. Mob. Comput. 2015, 15, 629–638. [Google Scholar] [CrossRef]
- Deng, T.; Wang, X.; Fan, P.; Li, K. Modeling and performance analysis of a tracking-area-list-based location management scheme in LTE networks. IEEE Trans. Veh. Technol. 2016, 65, 6417–6431. [Google Scholar] [CrossRef]
- Jung, J.; Baek, J.H. Reducing paging cost of tracking area list-based mobility management in LTE network. J. Supercomput. 2018. [Google Scholar] [CrossRef]
- Alsaeedy, A.A.R.; Chong, E.K.P. Tracking area update and paging in 5G networks: A survey of problems and solutions. Mob. Netw. Appl. 2019, 24, 578–595. [Google Scholar] [CrossRef]
- Chen, L.; Liu, H.L.; Fan, Z.; Xie, S.; Goodman, E.D. Modeling the tracking area planning problem using an evolutionary multi-objective algorithm. IEEE Comput. Intell. Mag. 2017, 12, 29–41. [Google Scholar] [CrossRef]
- Alsaeedy, A.A.R.; Chong, E.K.P. Mobility management for 5G IoT devices: Improving power consumption with lightweight signaling overhead. IEEE Internet Things J. 2019, 6, 8237–8247. [Google Scholar] [CrossRef]
- Ross, S. Introduction to Probability Models, 11th ed.; Elsevier: Cambridge, MA, USA, 2014. [Google Scholar]

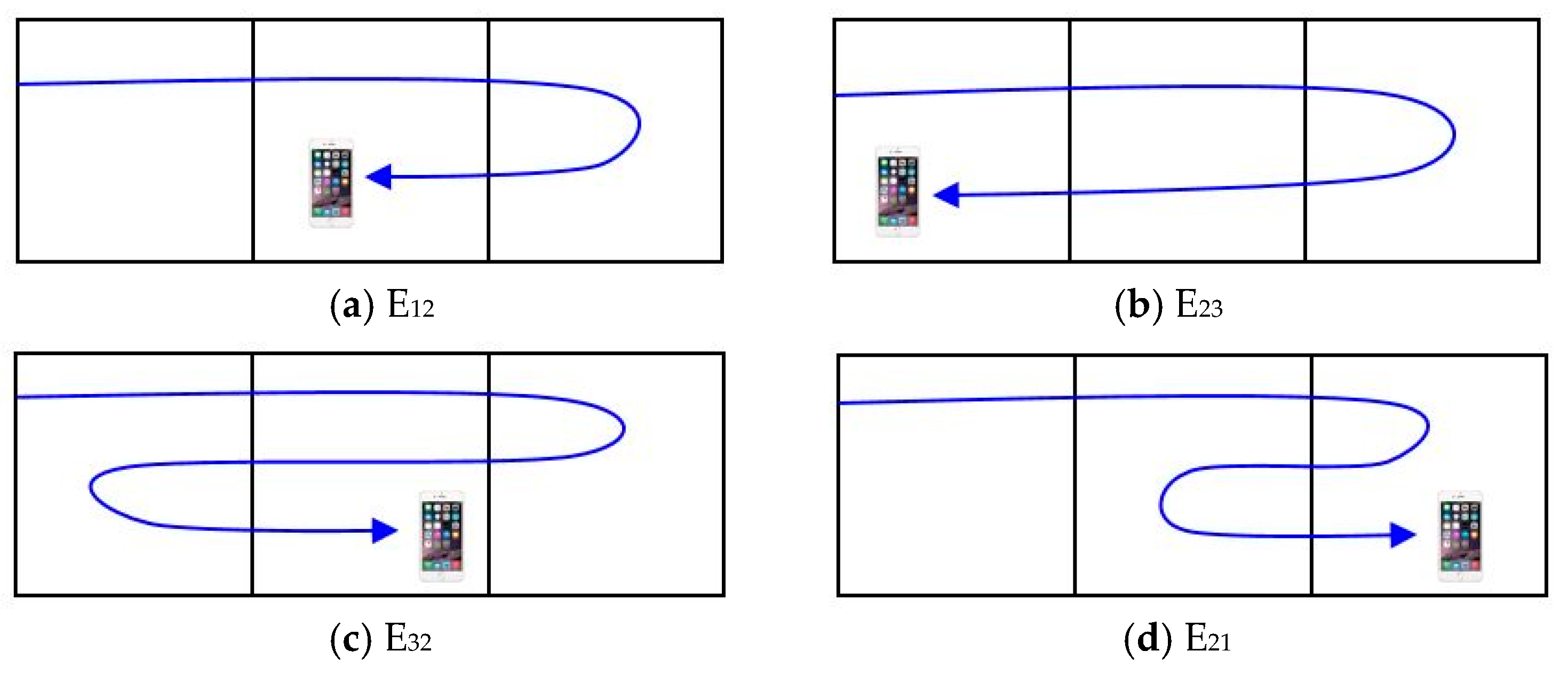
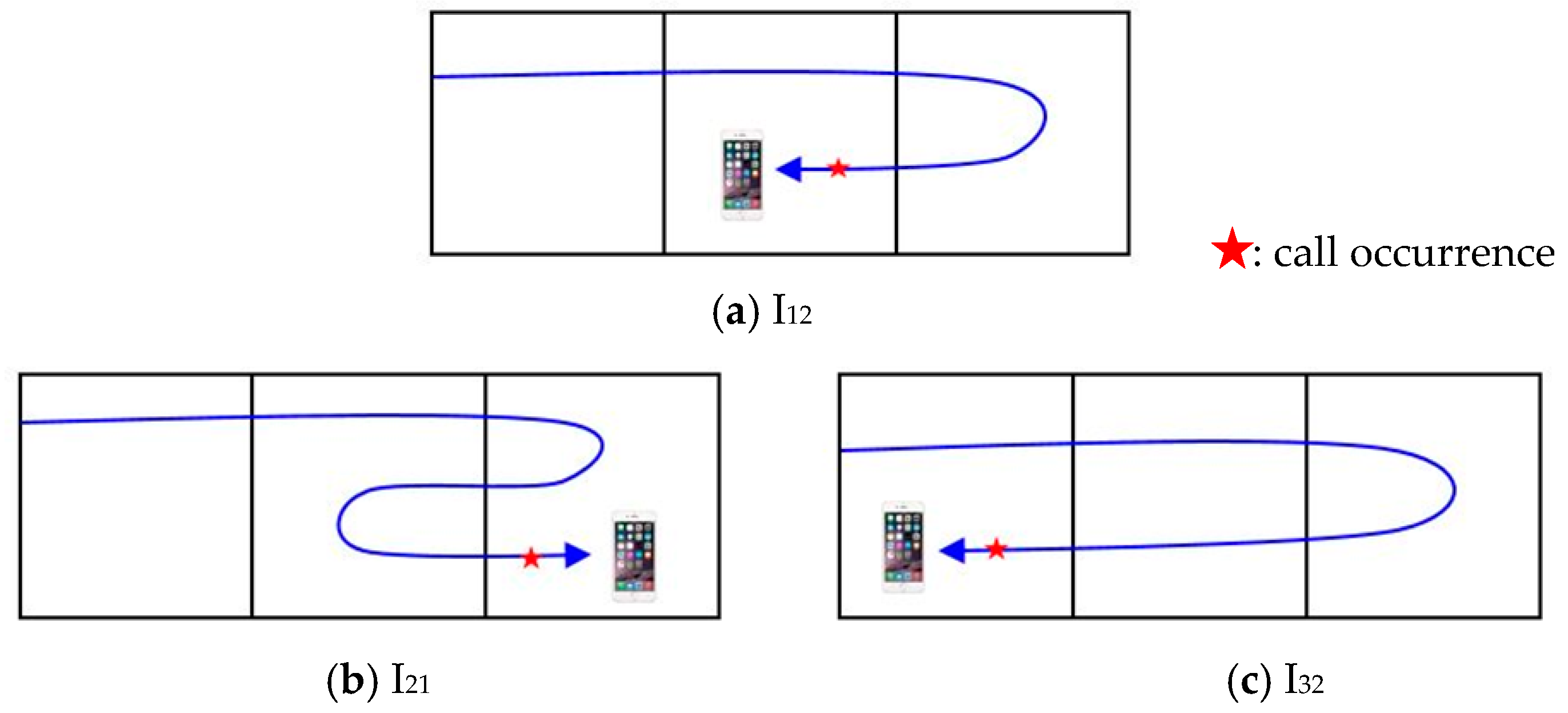
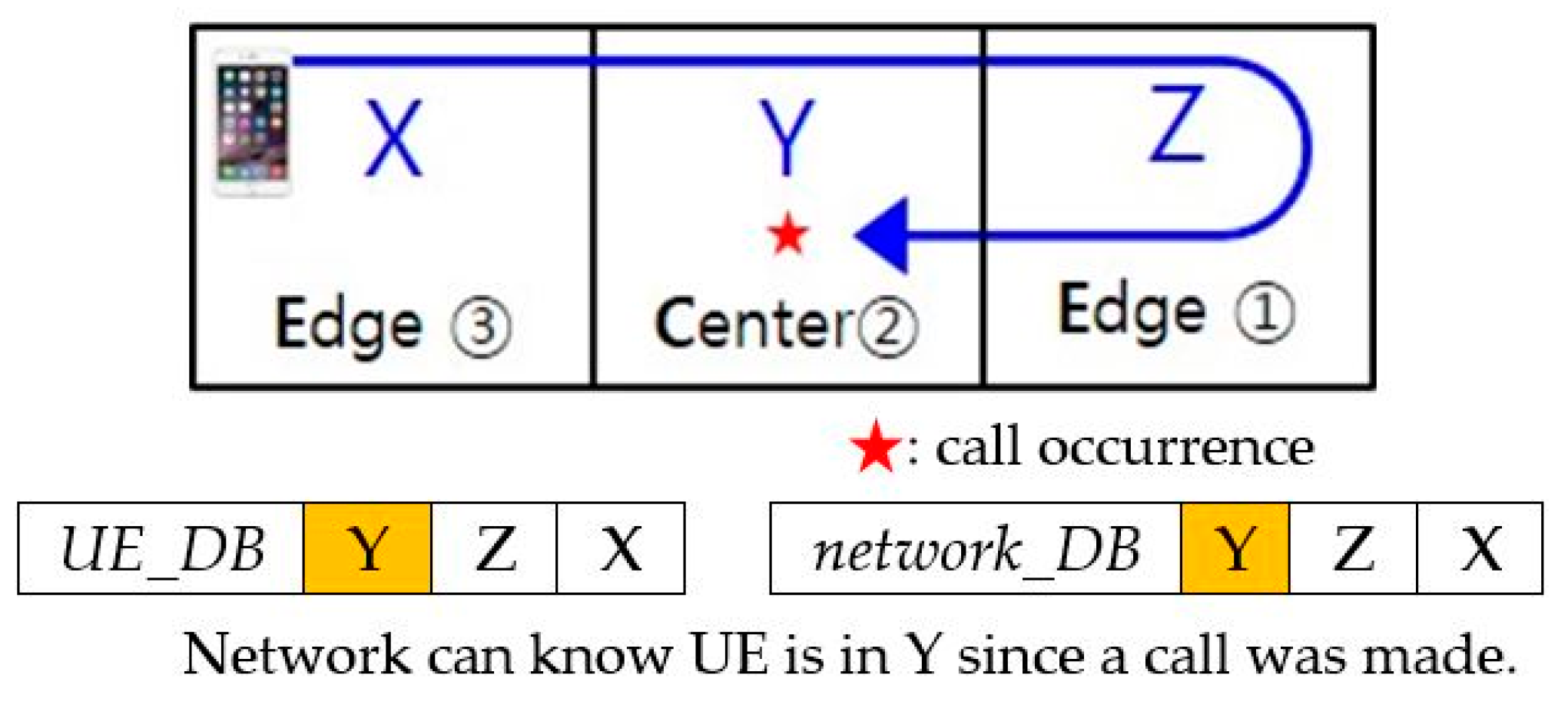
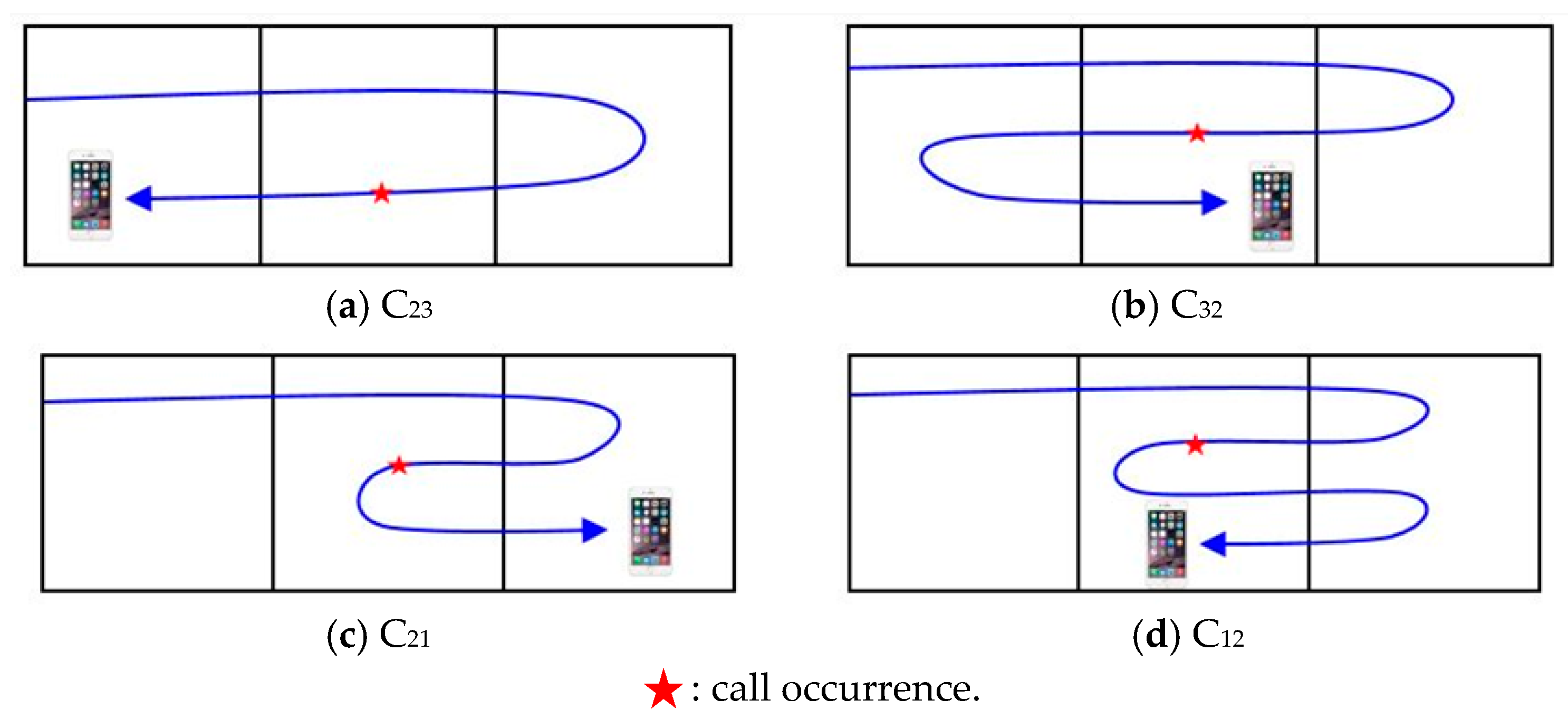
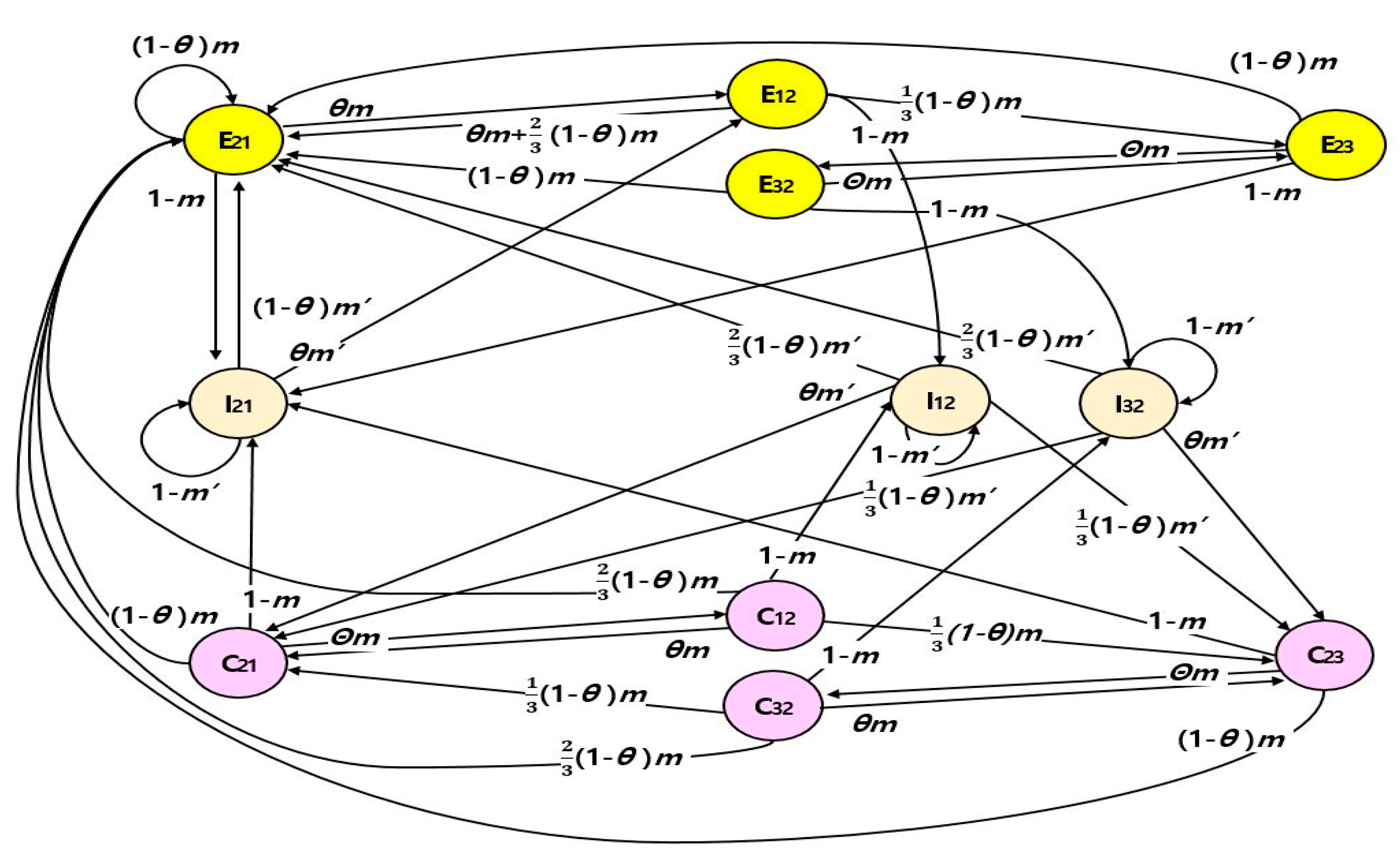
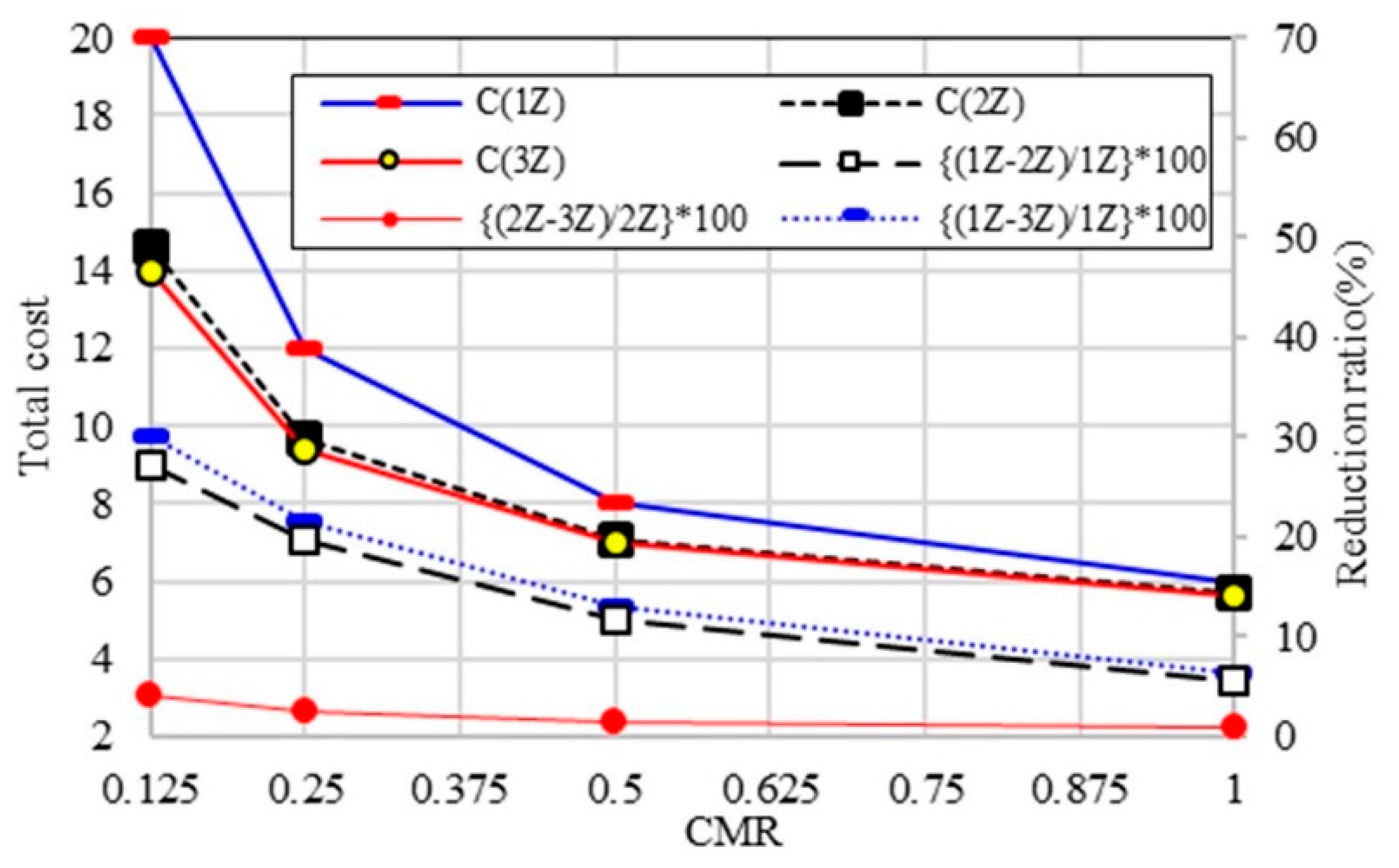
| State | The Last Zone | Current Zone | Most Recently Registered Zone | No. of Paging |
|---|---|---|---|---|
| E21 | 2 | 1 | edge (1) | 1 |
| E32 | 3 | 2 | edge (1) | 2 |
| E12 | 1 | 2 | edge (1) | 2 |
| E23 | 2 | 3 | edge (1) | 3 |
| C21 | 2 | 1 | center (2) | 2 |
| C12 | 1 | 2 | center (2) | 1 |
| C32 | 3 | 2 | center (2) | 1 |
| C23 | 2 | 3 | center (2) | 3 |
| I21 | 2 | 1 | edge (1) | 1 |
| I12 | 1 | 2 | center (2) | 1 |
| I32 | 3 | 2 | center (2) | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Baek, J.H. Analyzing Zone-Based Registration Using a Three Zone System: A Semi-Markov Process Approach. Appl. Sci. 2020, 10, 5705. https://doi.org/10.3390/app10165705
Jung J, Baek JH. Analyzing Zone-Based Registration Using a Three Zone System: A Semi-Markov Process Approach. Applied Sciences. 2020; 10(16):5705. https://doi.org/10.3390/app10165705
Chicago/Turabian StyleJung, Jihee, and Jang Hyun Baek. 2020. "Analyzing Zone-Based Registration Using a Three Zone System: A Semi-Markov Process Approach" Applied Sciences 10, no. 16: 5705. https://doi.org/10.3390/app10165705
APA StyleJung, J., & Baek, J. H. (2020). Analyzing Zone-Based Registration Using a Three Zone System: A Semi-Markov Process Approach. Applied Sciences, 10(16), 5705. https://doi.org/10.3390/app10165705





