Microscopic Characteristic Analysis on Sandstone under Coupling Effect of Freeze–Thaw and Acidic Treatment: From Nuclear Magnetic Resonance Perspective
Abstract
1. Introduction
2. Material and Methodology
2.1. Rock Samples
2.2. Acid Solution
2.3. Freeze–Thaw Test
2.4. Nuclear Magnetic Resonance (NMR) Test
2.5. Permeability and Fractal Dimensions by NMR
2.5.1. Permeability by NMR
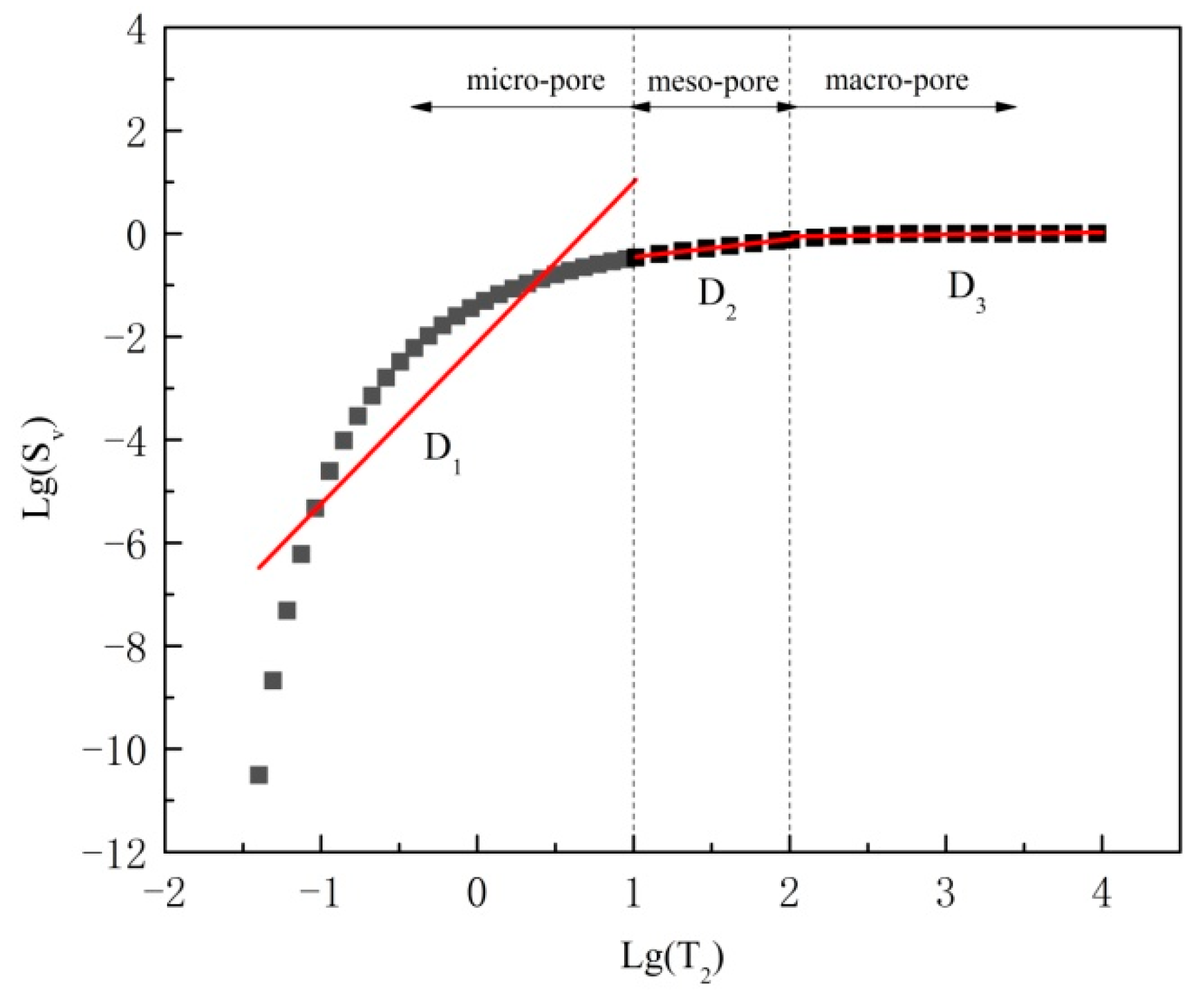
2.5.2. Fractal Dimensions by NMR
3. Result and Discussion
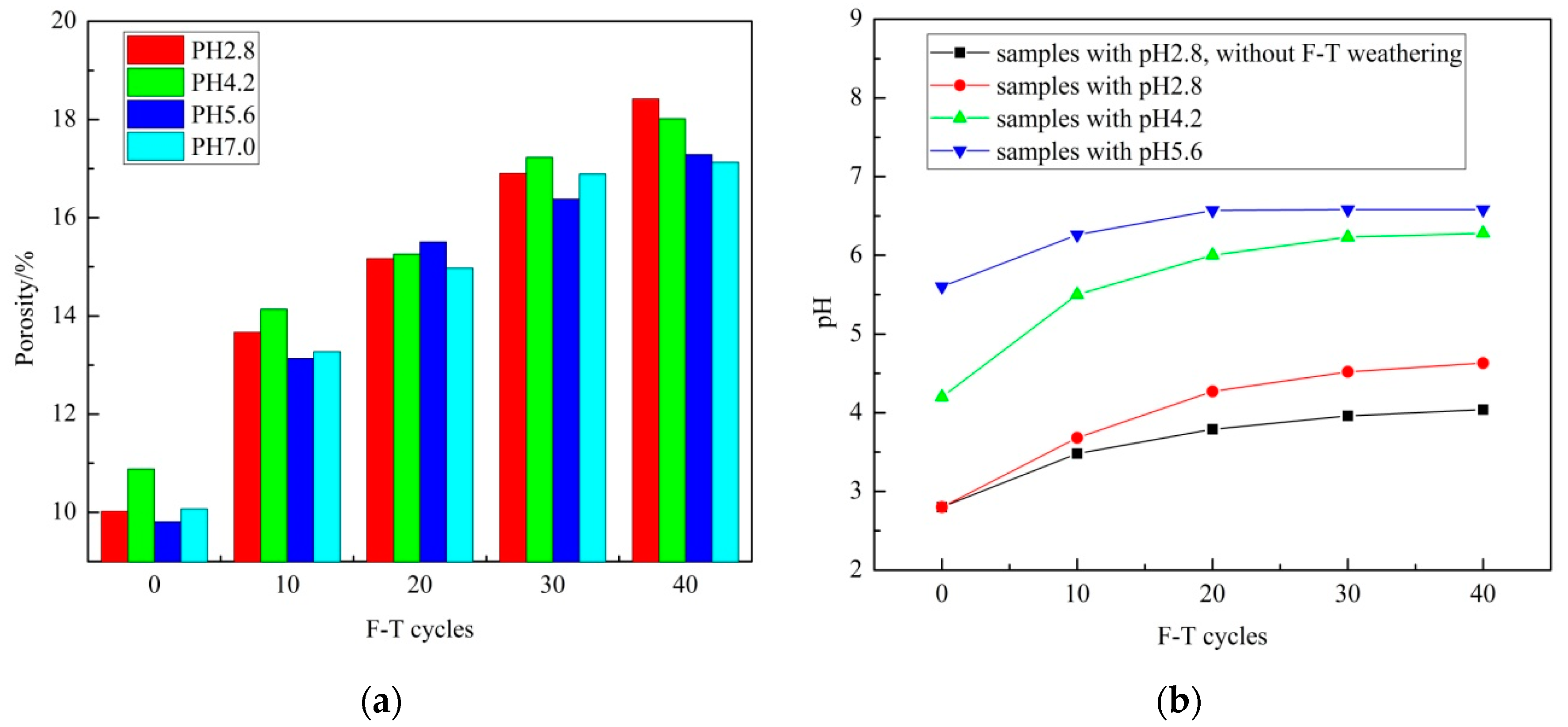
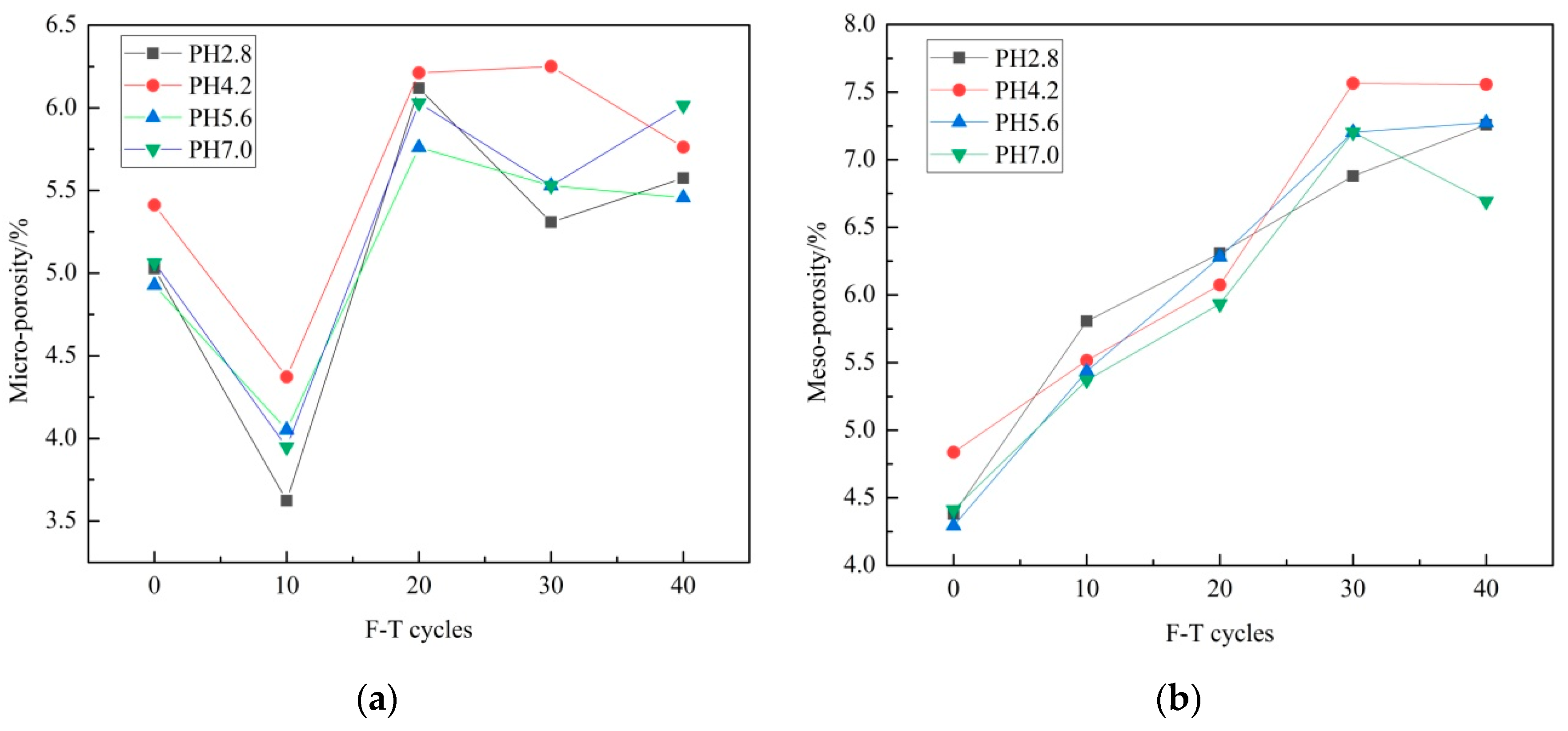
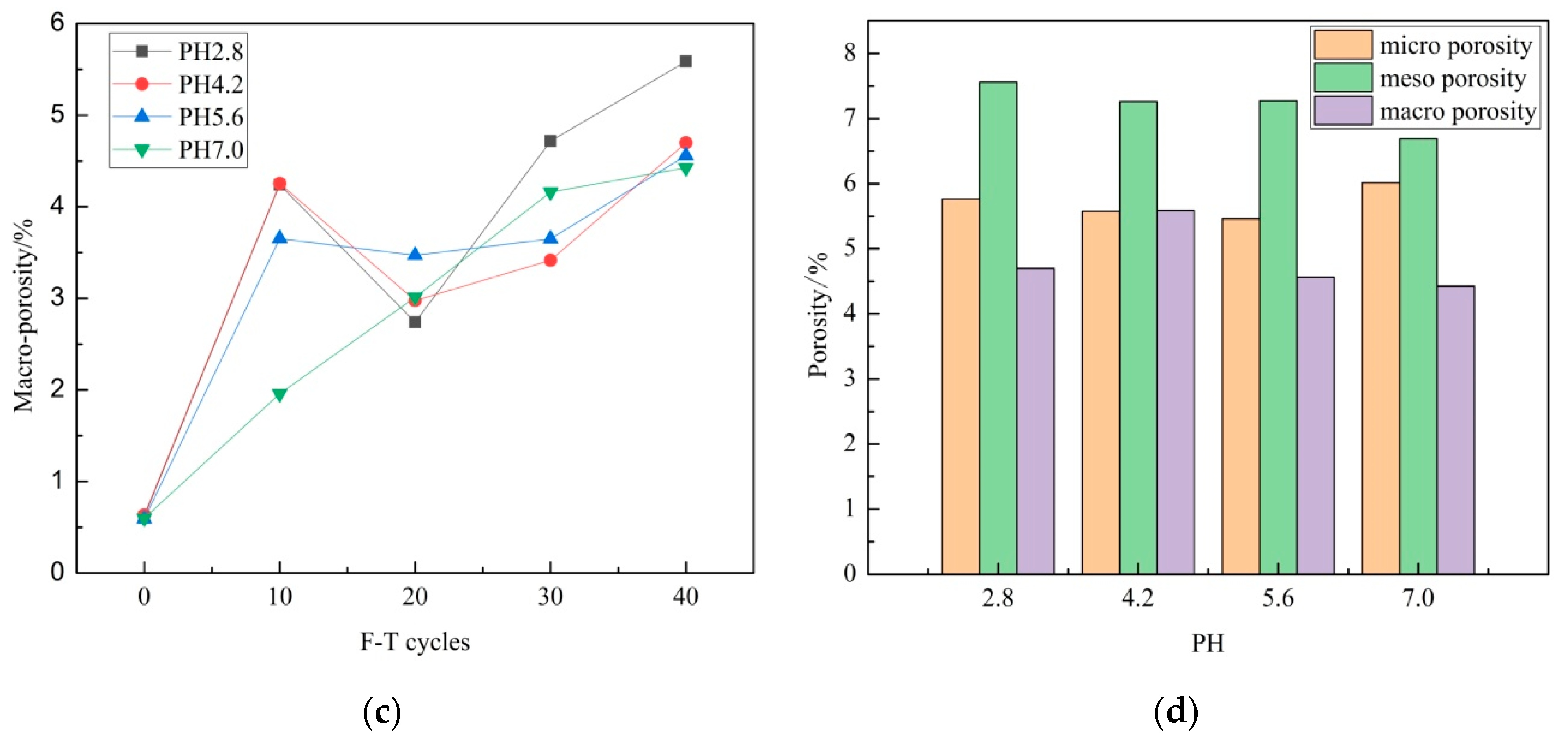
3.1. Porosity
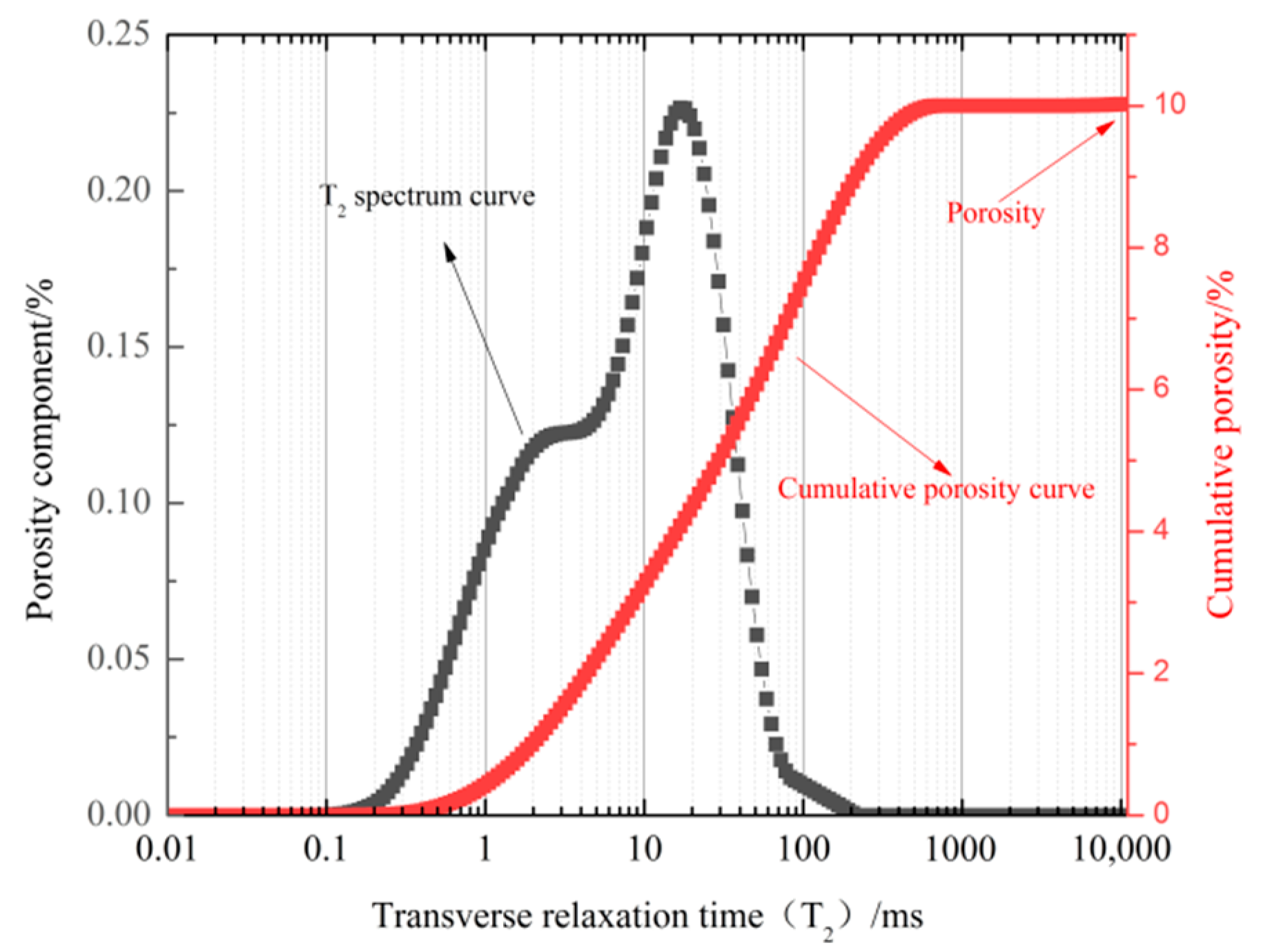
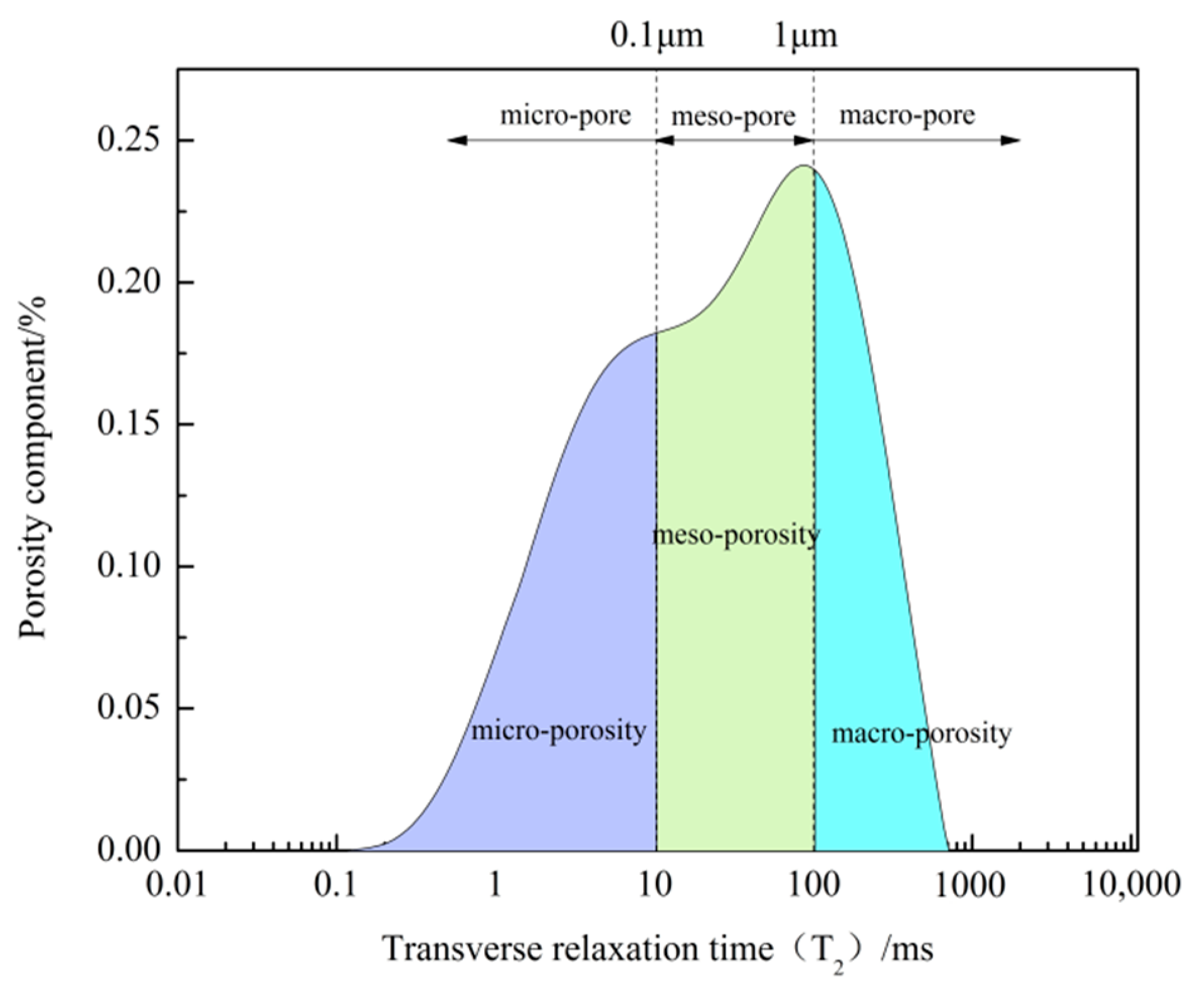
3.2. Pore Size Distribution
3.3. Permeability
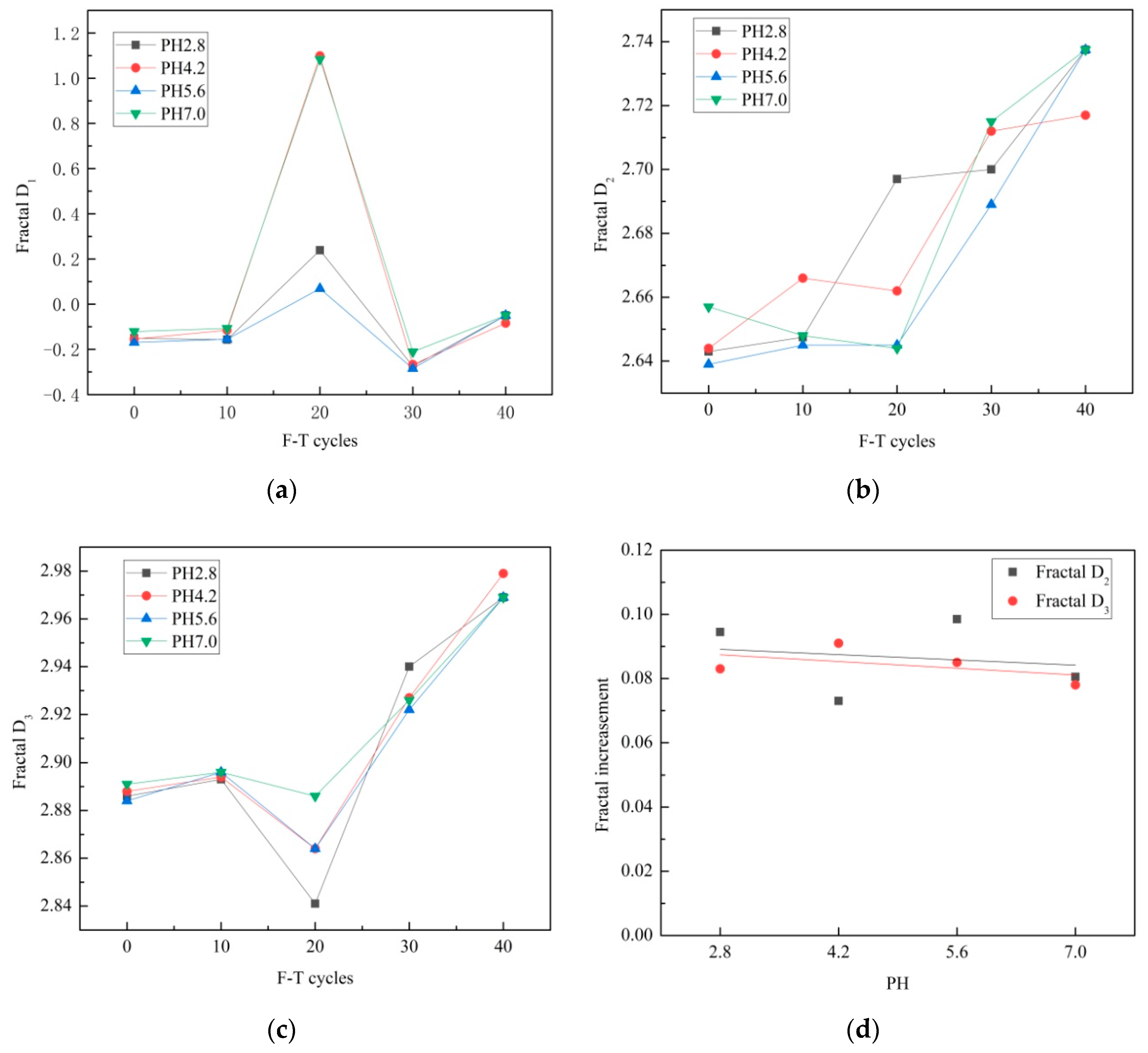
3.4. Fractal Dimensions
3.5. Relation between Parameters
3.5.1. Relation between Porosity and Permeability
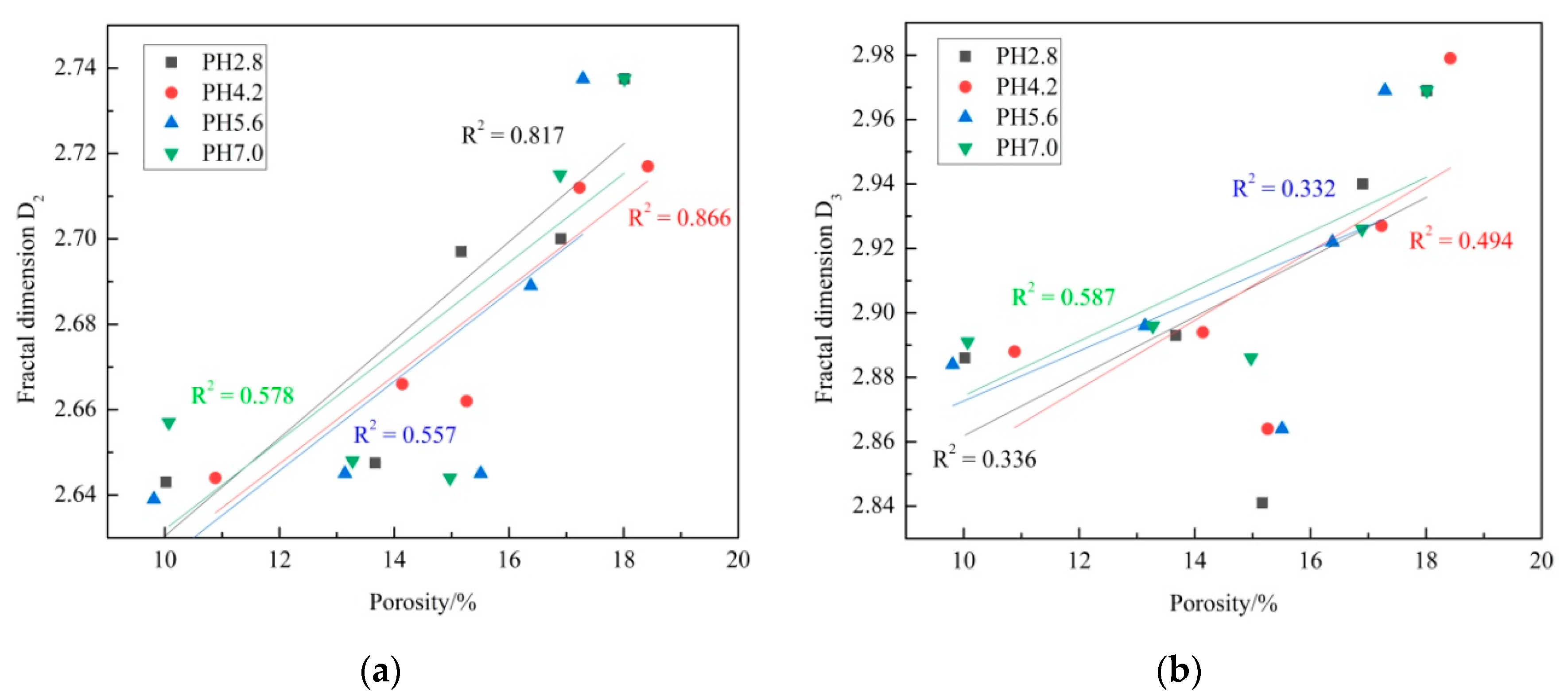
3.5.2. Relation between Porosity and Fractal Dimensions
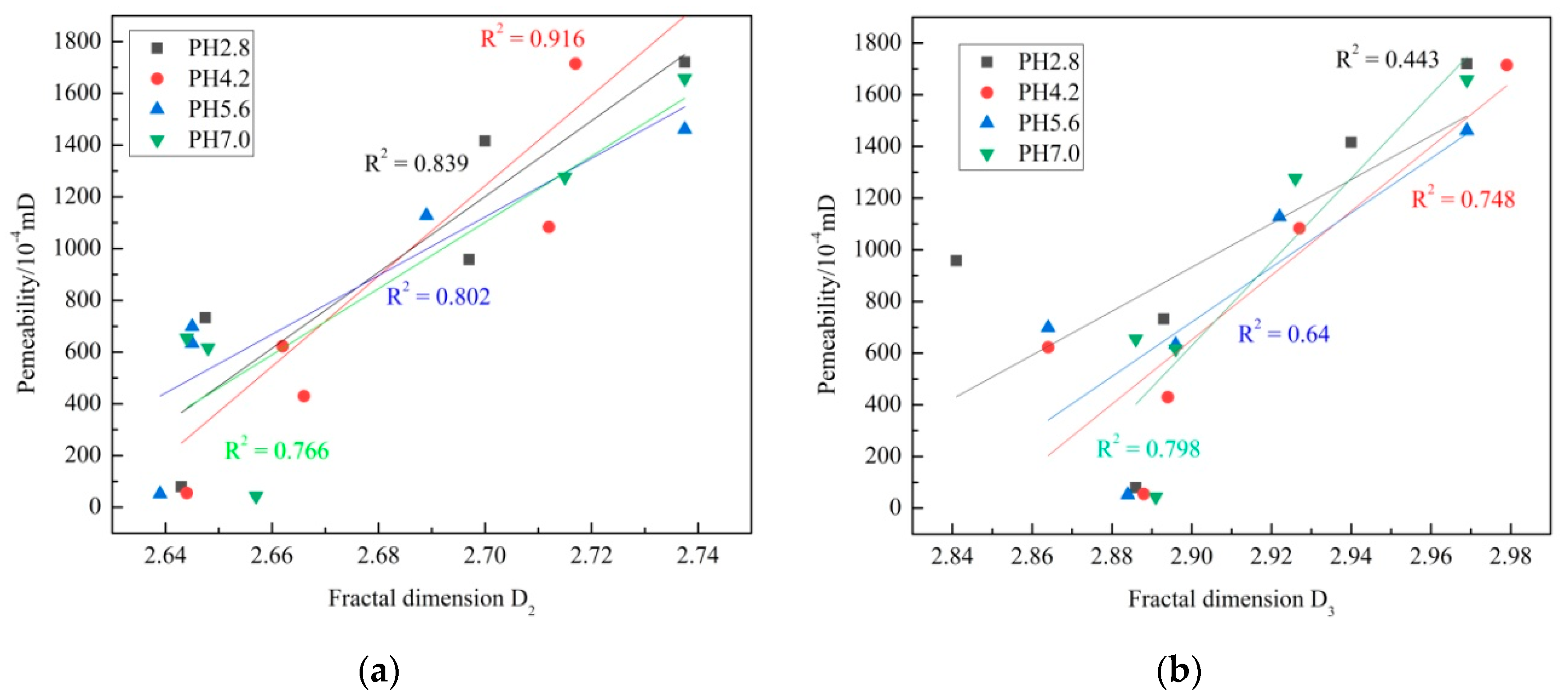
3.5.3. Relation between Permeability and Fractal Dimensions
3.6. Discussion
4. Conclusions
- (1)
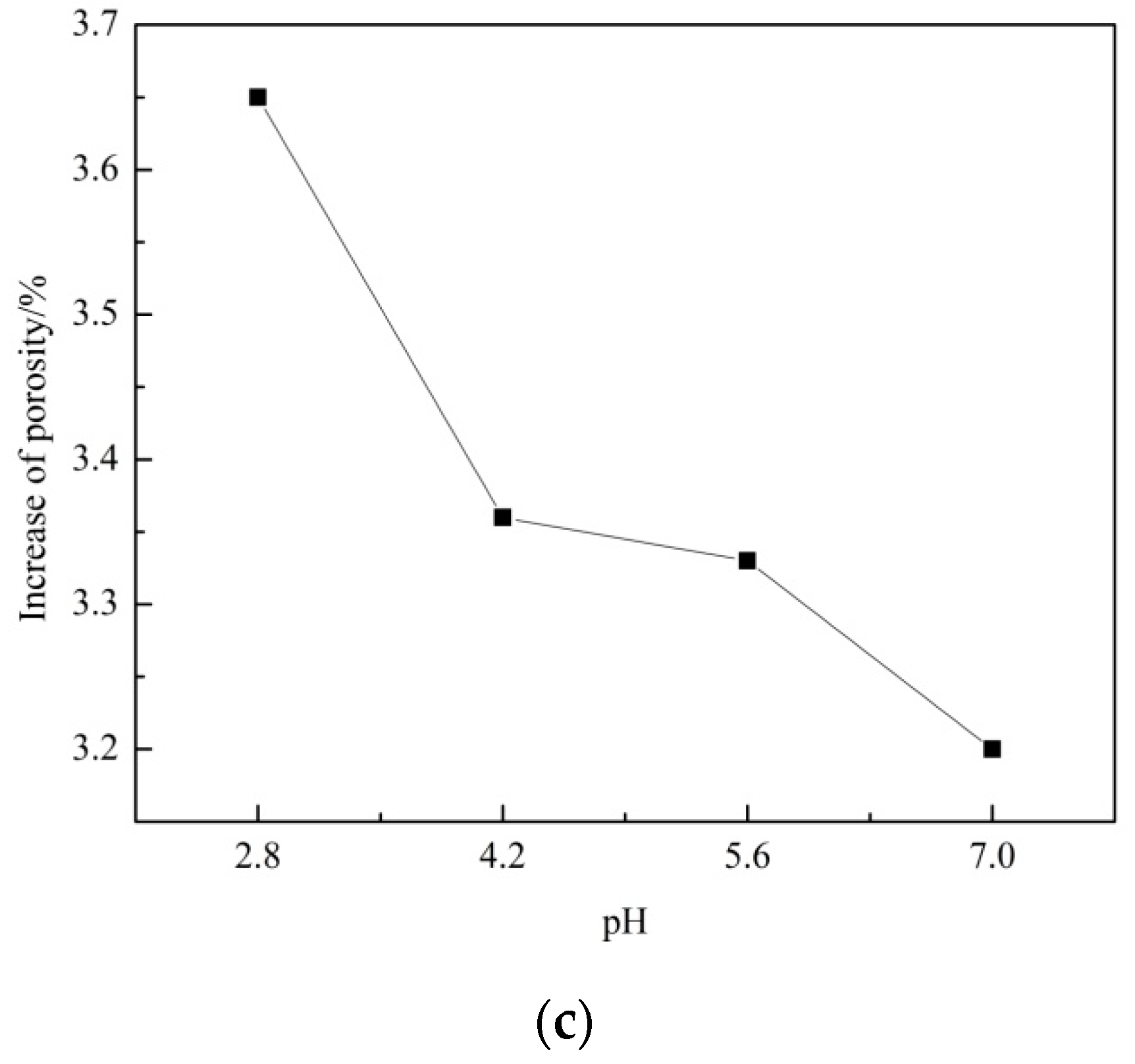
- The porosity of sandstone increases with F–T cycle increase, while the porosity increase grows with pH decrease during 10 F–T cycles. F–T weathering contributes more to porosity growth than acid erosion in this experiment.
- (2)
- In the experiment, macro porosity, meso porosity and micro porosity account for the largest, second and least ratio of porosity growth. Meso porosity, micro porosity and macro porosity account for the largest, second and least ratio of total porosity after 40 F–T cycles. Acid erosion plays a major role in micro pores’ development. F–T weathering plays major role in meso pores’ and macro pores’ development.
- (3)
- Permeability obviously increases with F–T cycle increase, while acid erosion exerts little influence on permeability increase overall. The permeability of sandstone immersed in acid solution with pH equal to 2.8 reached 1720.76 × 10−4 mD from the original 79.46 × 10−4 mD after 40 F–T cycles.
- (4)
- The fractal dimensions of meso pores (D2) range from 2.639 to 2.738, and the fractal dimensions of macro pores (D3) range from 2.841 to 2.979. D2 and D3 increase with F–T cycle increase overall, and they increase with pH decrease overall.
- (5)
- Porosity has an exponentially strong correlation with permeability. D2 and D3 have good linear correlation with permeability, while the correlations between porosity and fractal dimensions are not that obvious.
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, J.; Miao, L.; Yang, Z. Research on rock degradation and deterioration mechanisms and mechanical characteristics under cyclic freezing-thawing. Chin. J. Rock Mech. Eng. 2008, 27, 1688–1694. [Google Scholar]
- Chatterji, S. Aspects of the freezing process in a porous material–water system. Cem. Concr. Res. 1999, 29, 627–630. [Google Scholar] [CrossRef]
- Taber, S. The Mechanics of Frost Heaving. J. Geol. 1930, 38, 303–317. [Google Scholar] [CrossRef]
- Taber, S. Frost Heaving. J. Geol. 1929, 37, 428–461. [Google Scholar] [CrossRef]
- Yamabe, T.; Neaupane, K. Determination of some thermo-mechanical properties of Sirahama sandstone under subzero temperature condition. Int. J. Rock Mech. Min. Sci. 2001, 38, 1029–1034. [Google Scholar] [CrossRef]
- Zhang, H.; Yang, G. Freeze-thaw cycling and mechanical experiment and damage propagation characteristics of rock. J. China Univ. Min. Technol. 2011, 40, 140–146. [Google Scholar]
- Jia, H.; Xiang, W.; Tan, L.; Zhang, W.; Zeng, W.; Cao, S.; Cheng, C. Theoretical analysis of the mechanism of frost damage of sandstone and further experimental verification. Chin. J. Rock Mech. Eng. 2016, 35, 1–17. [Google Scholar]
- Inada, Y.; Yokota, K. Some studies of low temperature rock strength. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1984, 21, 145–153. [Google Scholar] [CrossRef]
- Feng, B.I.N. Study on Dynamic Mechanical Properties and Micro-Structure Mechanism of Rock under Freeze-Thaw Cycles; Central South University: Changsha, China, 2014. [Google Scholar]
- Ke, B.; Zhou, K.; Xu, C.; Deng, H.; Li, J.; Bin, F. Dynamic Mechanical Property Deterioration Model of Sandstone Caused by Freeze–Thaw Weathering. Rock Mech. Rock Eng. 2018, 51, 2791–2804. [Google Scholar] [CrossRef]
- Liu, C.; Deng, J.; Yu, S.; Li, P.; Lin, Y. Effect of Freezing and Thawing on Microstructure Damage and Dynamic Flexural Tension of Granite. Rock Mech. Rock Eng. 2020, 1–6. [Google Scholar] [CrossRef]
- Vlahou, I.; Worster, M.G. Ice growth in a spherical cavity of a porous medium. J. Glaciol. 2010, 56, 271–277. [Google Scholar] [CrossRef]
- Kranz, R.L. Crack-crack and crack-pore interactions instresses granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 37–47. [Google Scholar] [CrossRef]
- Monteiro, P.J.M.; Rashed, A.I.; Bastacky, S.J.; Hayes, T.L. Ice in cementpaste as analyzed in the low-temperature scanning electron microscope. Cem. Concr. Res. 1989, 19, 306–314. [Google Scholar] [CrossRef]
- Li, J.; Kaunda, R.B.; Zhu, L.; Zhou, K.; Gao, F. Experimental Study of the Pore Structure Deterioration of Sandstones under Freeze-Thaw Cycles and Chemical Erosion. Adv. Civ. Eng. 2019, 2019, 9687843. [Google Scholar] [CrossRef]
- Ke, B.; Zhou, K.; Deng, H.; Bin, F. NMR Pore Structure and Dynamic Characteristics of Sandstone Caused by Ambient Freeze-Thaw Action. Shock. Vib. 2017, 2017, 9728630. [Google Scholar] [CrossRef]
- Ding, W.; Xu, T.; Wang, H.; Chen, J.P. Experimental study of mechanical property of limestone under coupled chemical solution and freeze-thaw process. Chin. J. Rock Mech. Eng. 2015, 34, 979–985. [Google Scholar]
- Tian, W. Experiment Study on Freezing-Thawing Damage Mechanism of Rock under the Condition of Coupling of Multiple Factors; Central South University: Changsha, China, 2014. [Google Scholar]
- Lin, Y.; Zhou, K.; Gao, R.; Li, J.; Zhang, J. Influence of Chemical Corrosion on Pore Structure and Mechanical Properties of Sandstone. Geofluids 2019, 2019, 9728630. [Google Scholar] [CrossRef]
- Yang, G.S.; Zhang, Q.S.; Ren, J.X. Study on the effect of freezing rate on the damage CT values of Tongchuan sandstone. Chin. J. Rock Mech. Eng. 2004, 23, 4099–4104. [Google Scholar]
- Yang, G.; Zhang, Q.; Pu, Y. Preliminary study on meso-damage propagation characteristics of rock under condition of freezing temperature. Chin. J. Rock Soil Mech. 2004, 25, 1409–1412. [Google Scholar]
- Lai, J.; Wang, G.; Wang, Z.; Chen, J.; Pang, X.; Wang, S.; Zhou, Z.; He, Z.; Qin, Z.; Fan, X. A review on pore structure characterization in tight sandstones. Earth-Science Rev. 2018, 177, 436–457. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Taheri, A.; Ke, B.; Liu, C.-J.; Yang, X. Degradation of physical and mechanical properties of sandstone subjected to freeze-thaw cycles and chemical erosion. Cold Reg. Sci. Technol. 2018, 155, 37–46. [Google Scholar] [CrossRef]
- Liu, C.-J.; Deng, H.; Zhao, H.; Zhang, J. Effects of freeze-thaw treatment on the dynamic tensile strength of granite using the Brazilian test. Cold Reg. Sci. Technol. 2018, 155, 327–332. [Google Scholar] [CrossRef]
- Li, J.; Zhou, K.-P.; Liu, W.-J.; Deng, H.-W. NMR research on deterioration characteristics of microscopic structure of sandstones in freeze–thaw cycles. Trans. Nonferrous Met. Soc. China 2016, 26, 2997–3003. [Google Scholar] [CrossRef]
- Deng, H.; Yu, S.; Deng, J. Damage Characteristics of Sandstone Subjected to Coupled Effect of Freezing-Thawing Cycles and Acid Environment. Adv. Civ. Eng. 2018, 2018, 3560780. [Google Scholar] [CrossRef]
- Gao, R.; Zhou, K.; Li, J. Research of the mechanisms of backfill formation and damage. Mater. Tehnol. 2018, 52, 163–169. [Google Scholar] [CrossRef]
- Skjetne, T.; Southon, T.; Hafskjold, B.; Selle, O.; Svorstøl, I.; Buller, A.; Rueslåtten, H.; Brayshaw, A.; Kalam, M. Nuclear magnetic resonance studies of reservoir core plugs: A preliminary investigation of the influence of mineralogy on T1. Magn. Reson. Imaging 1991, 9, 673–679. [Google Scholar] [CrossRef]
- Mao, Z.-Q.; Xiao, L.; Wang, Z.-N.; Jin, Y.; Liu, X.-G.; Xie, B. Estimation of Permeability by Integrating Nuclear Magnetic Resonance (NMR) Logs with Mercury Injection Capillary Pressure (MICP) Data in Tight Gas Sands. Appl. Magn. Reson. 2012, 44, 449–468. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Zhang, Z.; Weller, A. Fractal dimension of pore-space geometry of an Eocene sandstone formation. Geophysics 2014, 79, D377–D387. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, D.; Cai, Y.; Yao, Y. Fractal characterization of pore–fracture in low-rank coals using a low-field NMR relaxation method. Fuel 2016, 181, 218–226. [Google Scholar] [CrossRef]
- Kenyon, W.E. Nuclear magnetic resonance as petro physical measurement. Int. J. Radiat. Appl. Instrum. Part E Nucl. Geophys. 1992, 6, 153–171. [Google Scholar]
- Li, J.; Kaunda, R.B.; Zhou, K. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, H.; Deng, J.; Gao, R. Fractal Analysis of Pore Structure Development of Sandstone: A Nuclear Magnetic Resonance Investigation. IEEE Access 2019, 7, 47282–47293. [Google Scholar] [CrossRef]
- Xiao, L.Z. NMR Imaging Logging Principles and Applications; Science Press: Beijing, China, 1998. [Google Scholar]
- Yan, J.P.; Wen, D.N.; Li, Z.Z.; Geng, B.; Jin-Gong, C.; Qiang, L.; Yu, Y. The quantitative evaluation method of low permeable sandstone pore structure based on nuclear magnetic resonance (NMR) logging. Chin. J. Geophys. 2016, 59, 1543–1552. [Google Scholar]
- Giri, A.; Tarafdar, S.; Gouze, P.; Dutta, T. Fractal pore structure of sedimentary rocks: Simulation in 2-d using a relaxed bidisperse ballistic deposition model. J. Appl. Geophys. 2012, 87, 40–45. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Mei, M. Fractal analysis of invasion depth of extraneous fluids in porous media. Chem. Eng. Sci. 2010, 65, 5178–5186. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, M.; Shi, Y.; Liu, L.; Xiong, F.; Qin, Z. Fractal Analysis of Dong he tang Sandstones Using NMR Measurements. Energy Fuels 2018, 32, 2973–2982. [Google Scholar] [CrossRef]


| Permeability/10−4 mD | PH of Acid Solution | ||||
|---|---|---|---|---|---|
| 2.8 | 4.2 | 5.6 | 7.0 | ||
| F–T cycles | 0 | 79.46 | 54.92 | 51.78 | 43.17 |
| 10 | 732.59 | 429.78 | 633.42 | 616.06 | |
| 20 | 957.74 | 622.90 | 698.76 | 654.34 | |
| 30 | 1415.71 | 1083.41 | 1127.65 | 1275.99 | |
| 40 | 1720.76 | 1714.75 | 1461.22 | 1657.65 | |
| PH | F–T Cycles | D1 | R2 | D2 | R2 | D3 | R2 |
|---|---|---|---|---|---|---|---|
| 2.8 | 0 | −0.151 | 0.788 | 2.643 | 0.998 | 2.886 | 0.870 |
| 10 | −0.157 | 0.791 | 2.648 | 0.997 | 2.893 | 0.861 | |
| 20 | 0.239 | 0.831 | 2.697 | 0.998 | 2.841 | 0.823 | |
| 30 | −0.275 | 0.786 | 2.700 | 0.995 | 2.940 | 0.735 | |
| 40 | −0.050 | 0.772 | 2.738 | 0.882 | 2.969 | 0.877 | |
| 4.2 | 0 | −0.154 | 0.789 | 2.644 | 0.997 | 2.888 | 0.870 |
| 10 | −0.115 | 0.788 | 2.666 | 0.998 | 2.894 | 0.856 | |
| 20 | 1.099 | 0.857 | 2.662 | 0.999 | 2.864 | 0.828 | |
| 30 | −0.267 | 0.784 | 2.712 | 0.999 | 2.927 | 0.826 | |
| 40 | −0.084 | 0.778 | 2.717 | 0.969 | 2.979 | 0.987 | |
| 5.6 | 0 | −0.169 | 0.793 | 2.639 | 0.996 | 2.884 | 0.894 |
| 10 | −0.155 | 0.789 | 2.645 | 0.997 | 2.896 | 0.861 | |
| 20 | 0.069 | 0.86 | 2.645 | 0.998 | 2.864 | 0.833 | |
| 30 | −0.285 | 0.788 | 2.689 | 0.999 | 2.922 | 0.807 | |
| 40 | −0.050 | 0.772 | 2.738 | 0.882 | 2.969 | 0.877 | |
| 7.0 | 0 | −0.121 | 0.789 | 2.657 | 0.997 | 2.891 | 0.876 |
| 10 | −0.107 | 0.787 | 2.648 | 0.997 | 2.896 | 0.861 | |
| 20 | 1.084 | 0.864 | 2.644 | 0.999 | 2.886 | 0.842 | |
| 30 | −0.211 | 0.78 | 2.715 | 0.999 | 2.926 | 0.800 | |
| 40 | −0.050 | 0.772 | 2.738 | 0.882 | 2.969 | 0.877 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Deng, H.; Tian, G.; Deng, J. Microscopic Characteristic Analysis on Sandstone under Coupling Effect of Freeze–Thaw and Acidic Treatment: From Nuclear Magnetic Resonance Perspective. Appl. Sci. 2020, 10, 5699. https://doi.org/10.3390/app10165699
Yu S, Deng H, Tian G, Deng J. Microscopic Characteristic Analysis on Sandstone under Coupling Effect of Freeze–Thaw and Acidic Treatment: From Nuclear Magnetic Resonance Perspective. Applied Sciences. 2020; 10(16):5699. https://doi.org/10.3390/app10165699
Chicago/Turabian StyleYu, Songtao, Hongwei Deng, Guanglin Tian, and Junren Deng. 2020. "Microscopic Characteristic Analysis on Sandstone under Coupling Effect of Freeze–Thaw and Acidic Treatment: From Nuclear Magnetic Resonance Perspective" Applied Sciences 10, no. 16: 5699. https://doi.org/10.3390/app10165699
APA StyleYu, S., Deng, H., Tian, G., & Deng, J. (2020). Microscopic Characteristic Analysis on Sandstone under Coupling Effect of Freeze–Thaw and Acidic Treatment: From Nuclear Magnetic Resonance Perspective. Applied Sciences, 10(16), 5699. https://doi.org/10.3390/app10165699





