Enhancement of the Purcell Effect by the Wire Metamaterials Formed by the Hexagonal Unit Cells
Abstract
1. Introduction
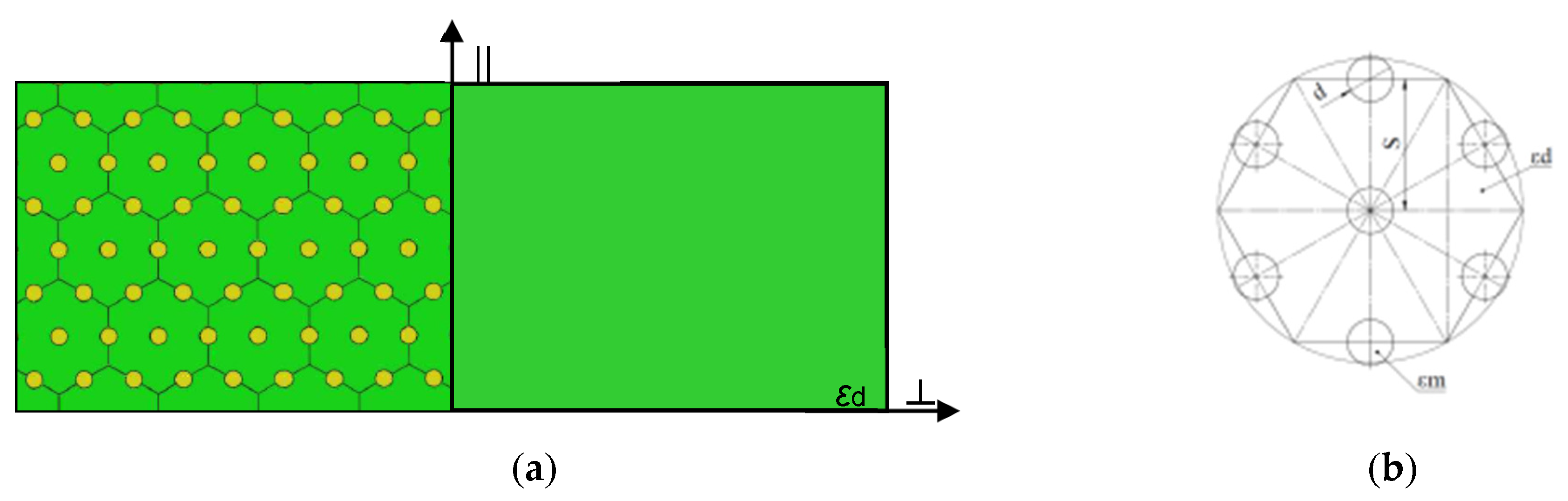
2. Methods
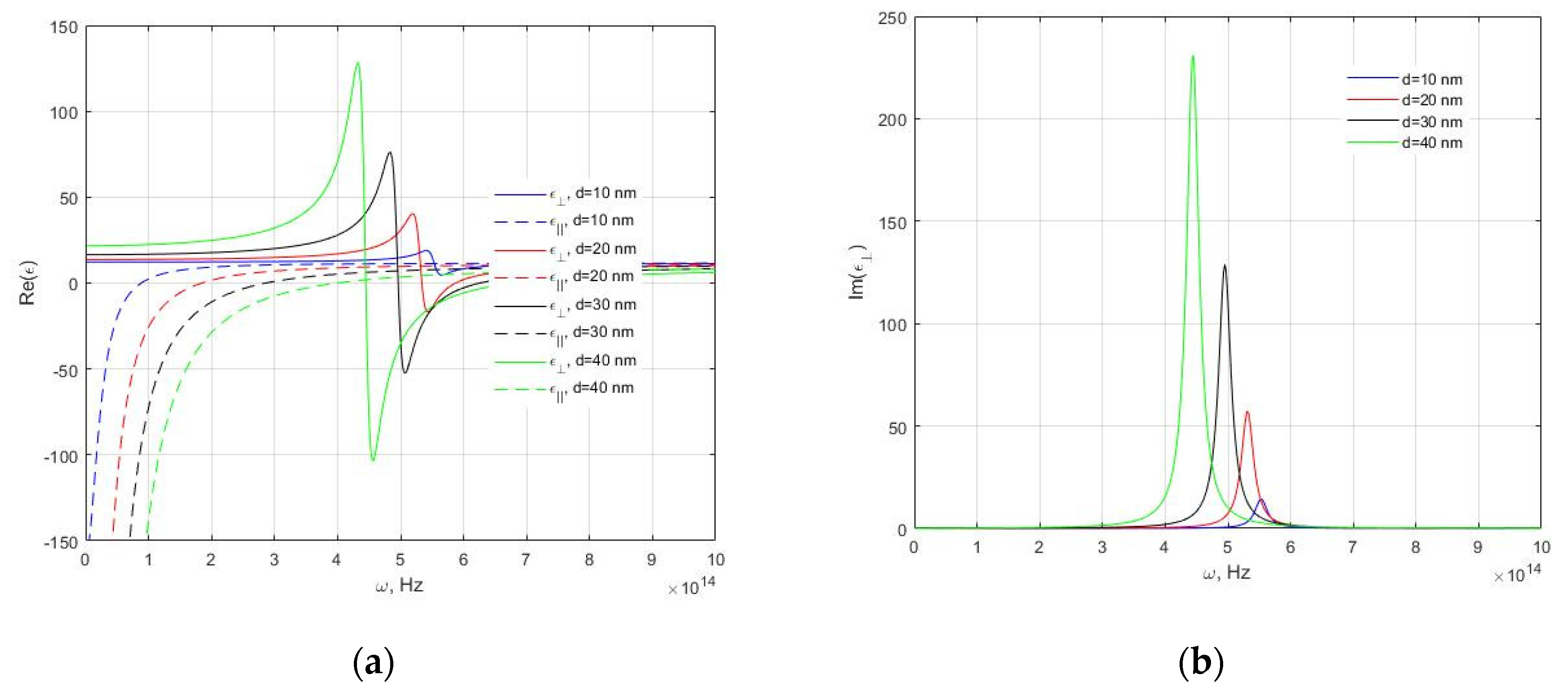
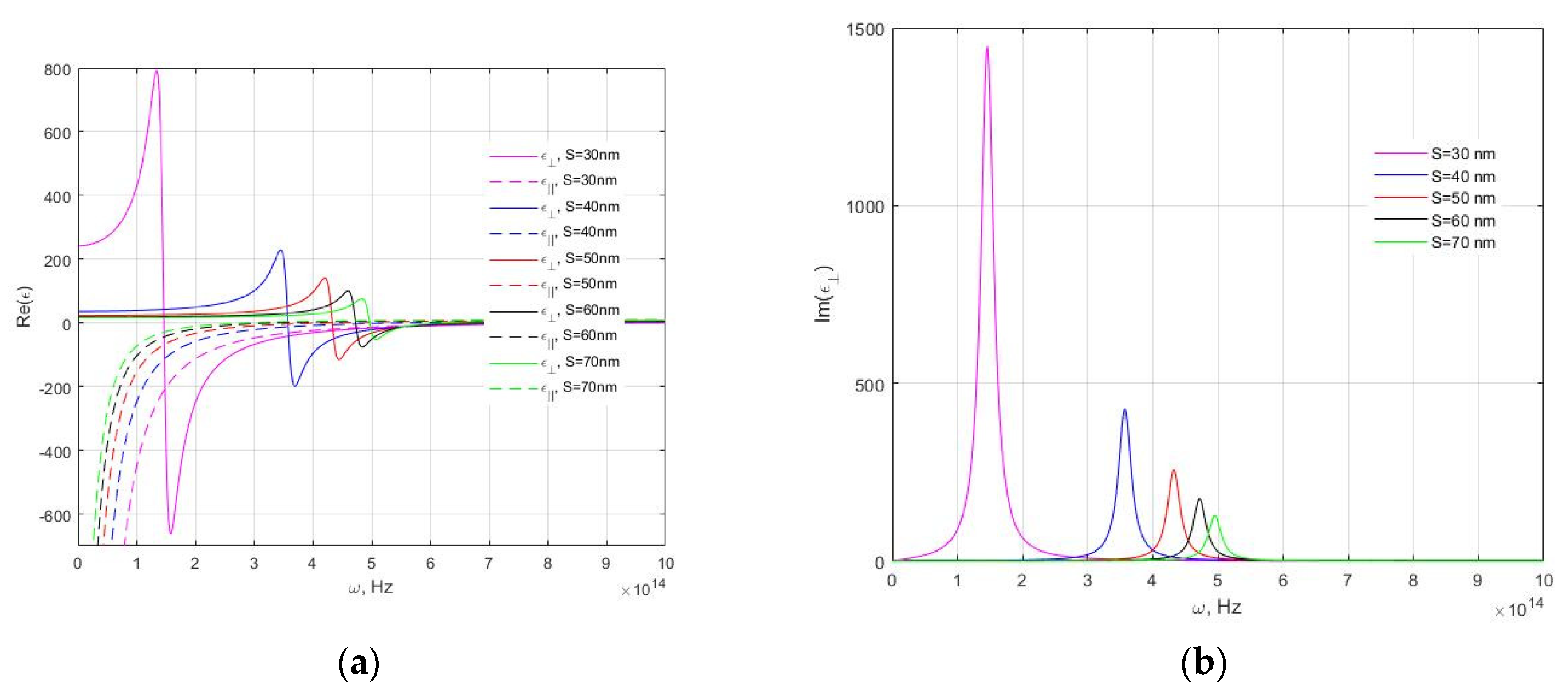
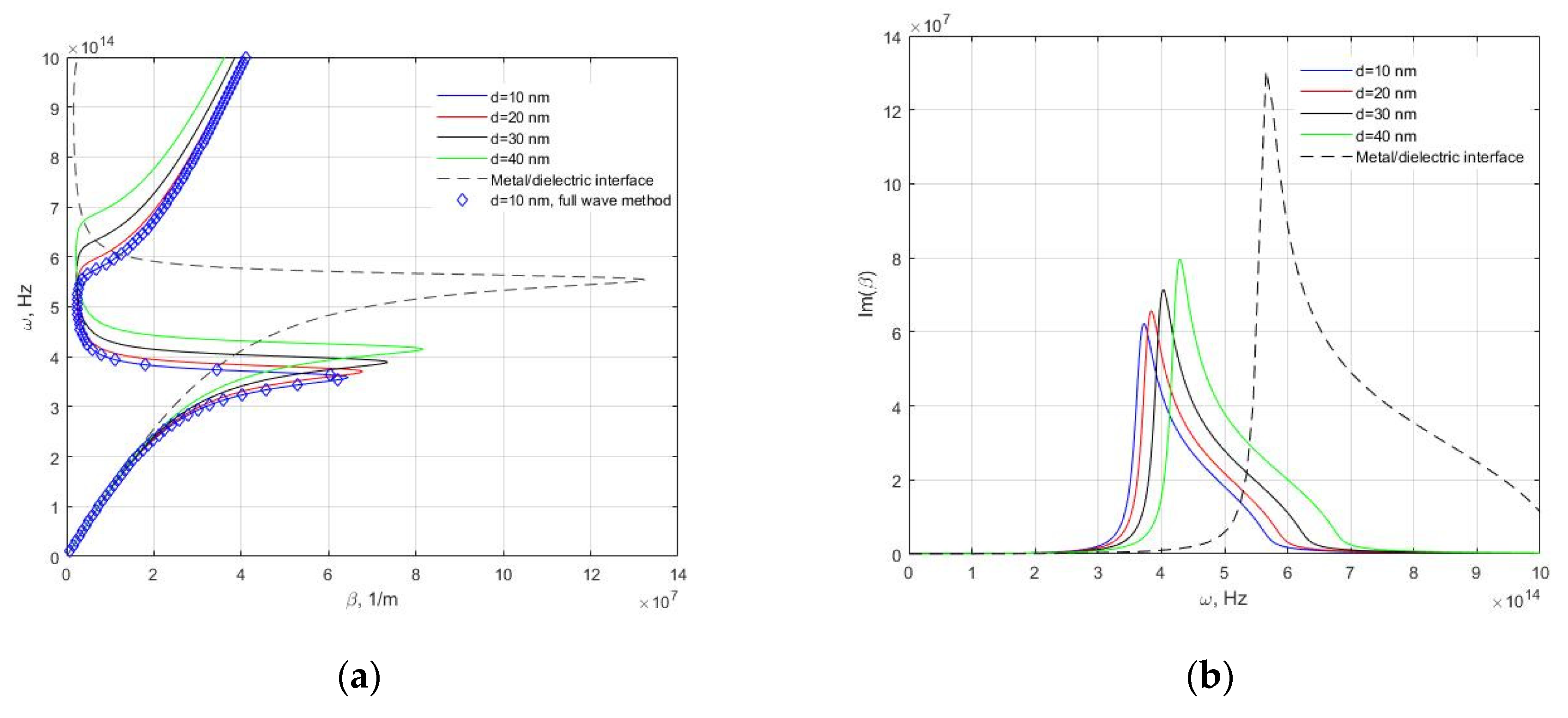
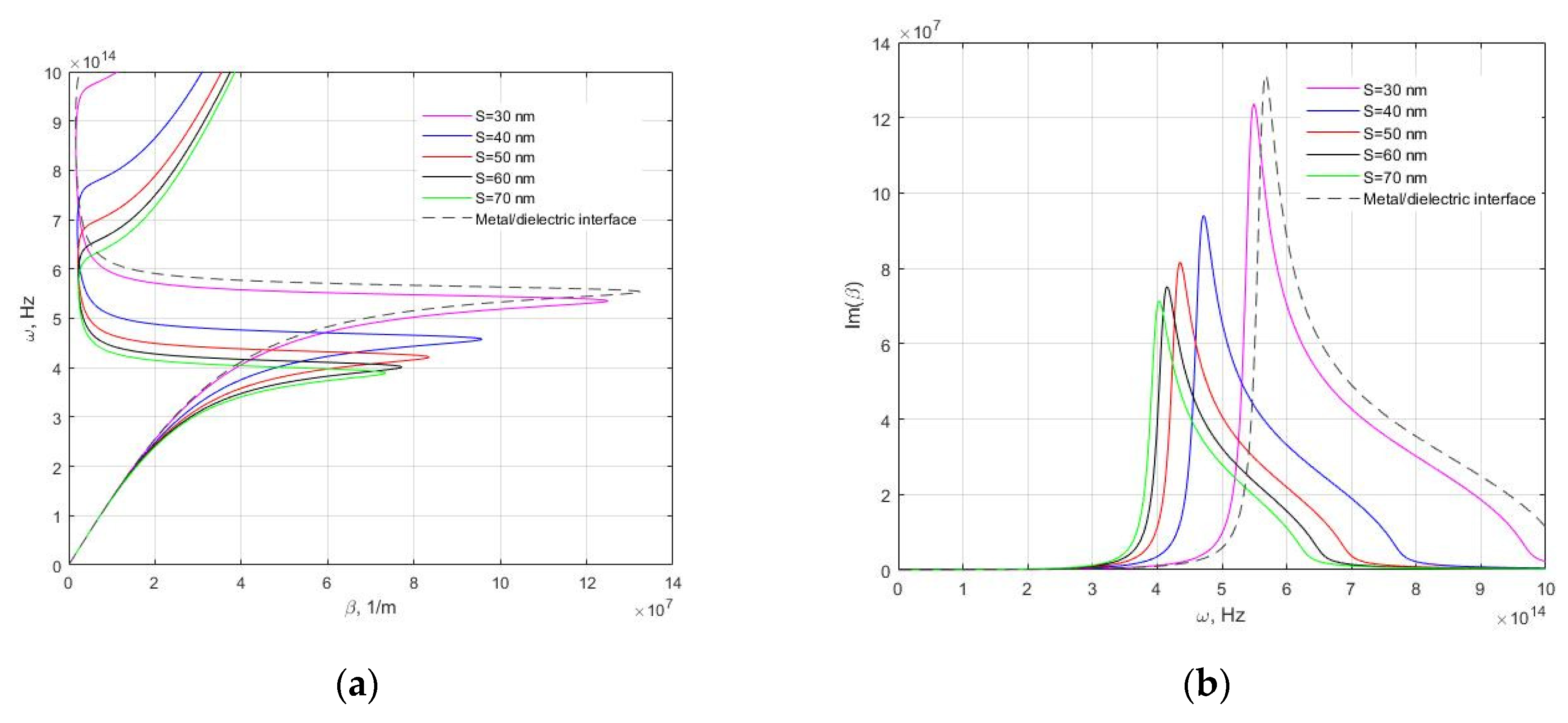
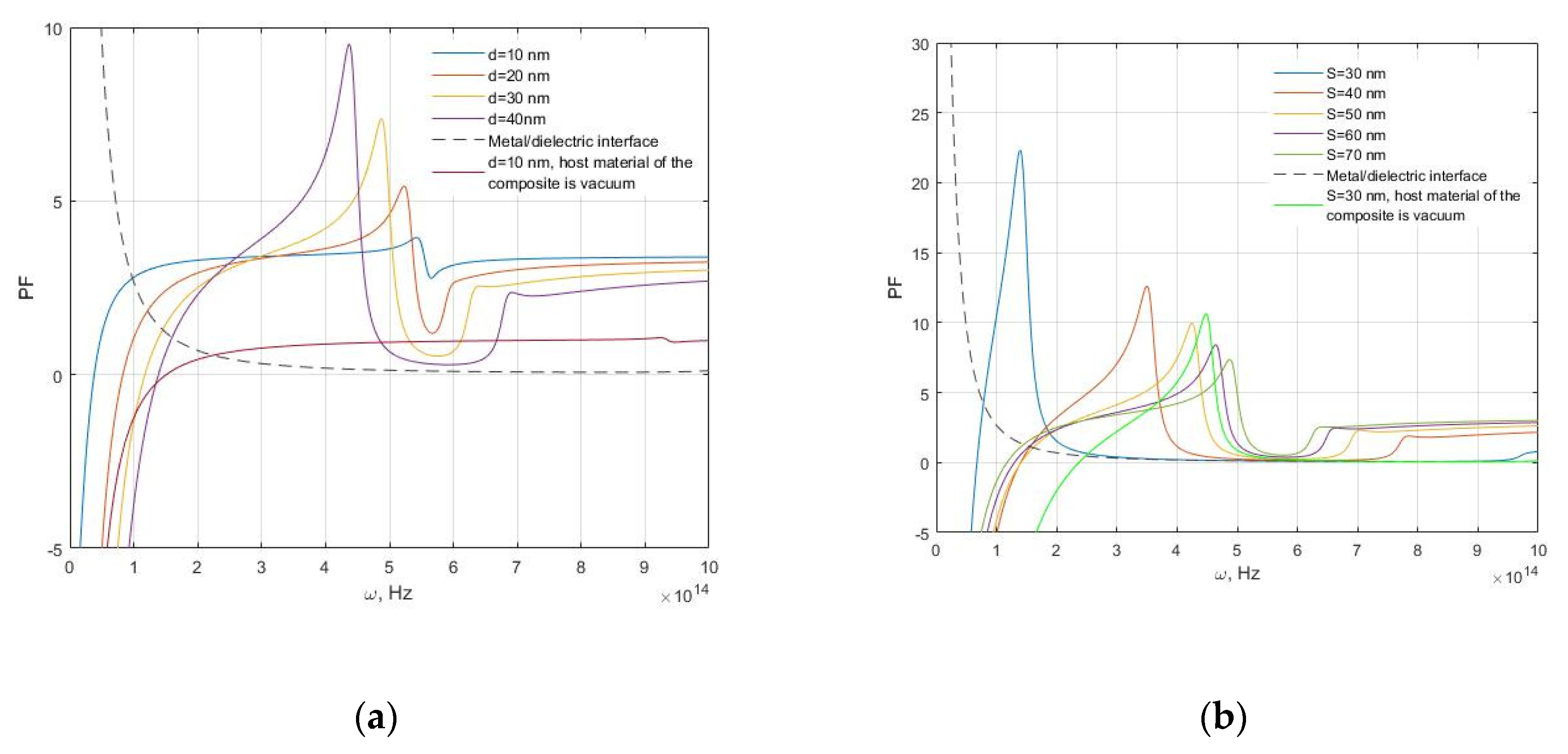
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef] [PubMed]
- Noginov, M.A.; Barnakov, Y.A.; Zhu, G.; Tumkur, T.; Li, H.; Narimanov, E.E. Bulk photonic metamaterial with hyperbolic dispersion. Appl. Phys. Lett. 2009, 94, 151105. [Google Scholar] [CrossRef]
- Jacob, Z.; Smolyaninov, I.I.; Narimanov, E.E. Broadband Purcell effect: Radiative decay engineering with metamaterials. Appl. Phys. Lett. 2012, 100, 181105. [Google Scholar] [CrossRef]
- Gric, T. Surface-plasmon-polaritons at the interface of nanostructured metamaterials. Prog. Electromagn. Res. M 2016, 46, 165–172. [Google Scholar] [CrossRef]
- Liu, Y.M. Plasmonic Metamaterials. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2009. [Google Scholar]
- Jacob, Z.; Shalaev, V.M. Physics. Plasmonics goes quantum. Science 2011, 334, 463. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, H.N.S.; Jacob, Z.; Narimanov, E.; Kretzschmar, I.; Menon, V.M. Topological transitions in metamaterials. Science 2012, 336, 205. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948. [Google Scholar] [CrossRef]
- Silveirinha, M.G.; Maslovski, S.I. Radiation from elementary sources in a uniaxial wire medium. Phys. Rev. B 2012, 85, 155125. [Google Scholar] [CrossRef]
- Lemoult, F.; Fink, M.; Lerosey, G. Revisiting the wire medium: An ideal resonant metalens. Waves Random Complex Media 2011, 21, 591. [Google Scholar] [CrossRef]
- Noginov, M.A.; Li, H.; Barnakov, Y.A.; Dryden, D.; Nataraj, G.; Zhu, G.; Bonner, C.E.; Mayy, M.; Jacob, Z.; Narimanov, E.E. Controlling spontaneous emission with metamaterials. Opt. Lett. 2010, 35, 1863. [Google Scholar] [CrossRef]
- Poddubny, A.N.; Belov, P.A.; Kivshar, Y.S. Purcell effect in wire metamaterials. Phys. Rev. B 2013, 87, 035136. [Google Scholar] [CrossRef]
- Fernandes, D.E.; Maslovski, S.I.; Silveirinha, M.G. Cherenkov emission in a nanowire material. Phys. Rev. B 2012, 85, 155107. [Google Scholar] [CrossRef]
- Vorobev, V.V.; Tyukhtin, A.V. Nondivergent Cherenkov radiation in a wire metamaterial. Phys. Rev. Lett. 2012, 108, 184801. [Google Scholar] [CrossRef] [PubMed]
- Biehs, S.-A.; Tschikin, M.; Ben-Abdallah, P. Hyperbolic metamaterials as an analog of a backbody in the near field. Phys. Rev. Lett. 2012, 109, 104301. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, D.E.; Maslovski, S.I.; Hanson, G.W.; Silveirinha, M.G. Fano resonances in nested wire media. Phys. Rev. B 2013, 88, 045130. [Google Scholar] [CrossRef]
- Julin, S.; Korpi, A.; Nonappa, N.; Shen, B.; Liljeström, V.; Ikkala, O.; Keller, A.; Linko, V.; Kostiainen, M.A. DNA origami directed 3D nanoparticle superlattice via electrostatic assembly. Nanoscale 2019, 11, 4546. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Oubre, C.; Nordlander, P. Finite-difference time-domain studies of the optical properties of nanoshell dimers. J. Phys. Chem. B 2005, 109, 10042–10051. [Google Scholar] [CrossRef]
- Starko-Bowes, R.; Atkinson, J.; Newman, W.; Hu, H.; Kallos, T.; Palikaras, G.; Fedosejevs, R.; Pramanik, S.; Jacob, Z. Optical characterization of Epsilon Near Zero, Epsilon Near Pole and hyperbolic response in nanowire metamaterials. J. Opt. Soc. Am. B 2015, 32, 2074–2080. [Google Scholar] [CrossRef]
- Iorsh, I.; Orlov, A.; Belov, P.; Kivshar, Y. Interface modes in nanostructured metal-dielectric metamaterials. Appl. Phys. Lett. 2011, 99, 151914. [Google Scholar] [CrossRef]
- Chebykin, A.V.; Orlov, A.A.; Shalin, A.S.; Poddubny, A.N.; Belov, P.A. Strong Purcell effect in anisotropic epsilonnear-zero metamaterials. Phys. Rev. B 2015, 91, 205126. [Google Scholar] [CrossRef]
- Mirmoosa, M.S.; Kosulnikov, S.Y.; Simovski, C.R. Double resonant wideband Purcell effect in wire metamaterials. J. Opt. 2016, 18, 095101. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gric, T.; Rafailov, E. Enhancement of the Purcell Effect by the Wire Metamaterials Formed by the Hexagonal Unit Cells. Appl. Sci. 2020, 10, 5687. https://doi.org/10.3390/app10165687
Gric T, Rafailov E. Enhancement of the Purcell Effect by the Wire Metamaterials Formed by the Hexagonal Unit Cells. Applied Sciences. 2020; 10(16):5687. https://doi.org/10.3390/app10165687
Chicago/Turabian StyleGric, Tatjana, and Edik Rafailov. 2020. "Enhancement of the Purcell Effect by the Wire Metamaterials Formed by the Hexagonal Unit Cells" Applied Sciences 10, no. 16: 5687. https://doi.org/10.3390/app10165687
APA StyleGric, T., & Rafailov, E. (2020). Enhancement of the Purcell Effect by the Wire Metamaterials Formed by the Hexagonal Unit Cells. Applied Sciences, 10(16), 5687. https://doi.org/10.3390/app10165687





