Quantum Turing Machines: Computations and Measurements

Abstract

Contrary to the classical case, the relation between quantum programming languages and quantum Turing Machines (QTM) has not been fully investigated. In particular, there are features of QTMs that have not been exploited, a notable example being the intrinsic infinite nature of any quantum computation. In this paper, we propose a definition of QTM, which extends and unifies the notions of Deutsch and Bernstein & Vazirani. In particular, we allow both arbitrary quantum input, and meaningful superpositions of computations, where some of them are “terminated” with an “output”, while others are not. For some infinite computations an “output” is obtained as a limit of finite portions of the computation. We propose a natural and robust observation protocol for our QTMs, which does not modify the probability of the possible outcomes of the machines. Finally, we use QTMs to define a class of quantum computable functions—any such function is a mapping from a general quantum state to a probability distribution of natural numbers. We expect that our class of functions, when restricted to classical input-output, will not be different from the set of the recursive functions.

1. Introduction

It is an early recognition of computer science that programming (and programming languages) could benefit from solid semantical foundations. At the end of the 50s of the last century, both for clarity purposes and for the need of an entrance ticket into the “science club”, some prominent scientists started using mathematical techniques for the description of programming languages (e.g., Chomsky’s generative grammars, in the form of Backus-Naur Form [1]). Even more important is the proposal of general semantical models for the meaning of programs, represented at its best by McCarthy’s “mathematical theory of computation” [2], where a definition of the class of computable functions is presented as a general model for the semantics of (Algol) programs. The model is clearly idealised, in which it assumes that execution happens without physical limitations of space and time, in what will be, from that moment onwards, the standard model for programming languages, where one may assume Turing-completeness, despite each implementation being a finite state machine. The standard model builds on a long process during which Turing machines are viewed as idealised models of actual computers, and thus provide a basis for some theoretical investigation, among which the first studies on computational complexity.

Quantum computations and quantum programming languages have followed a different path. A solid and ever growing body of research is present on semantics and mathematical methods (e.g., see [3,4,5,6,7,8,9]), but the relations of these languages with the basic notion of (quantum) Turing machines (as introduced by Deutsch in his seminal paper on quantum computation [10]; also see [11] for a quantum-mechanical model of Turing machines) has received much less study than in the classical case. The exception is, of course, the definition of quantum Turing machines (QTMs) by Bernstein & Vazirani [12] (B&V, from now on) and its use in the establishment of a sound quantum computational complexity. However, their machines, have several strong constraints, reasonable for the purpose of a theory of computational complexity, but that do not permit to exploit all the features of the idealised model of computation that QTMs provide. In particular, meaningful computations are defined only for classical inputs (a single natural number with amplitude 1), and B&V’s “well-behaved” QTMs “terminate” synchronously—either all paths in superpositions enter a final state at the same time, or all of them diverge. As a consequence, there is no chance to study—and give meaning—to infinite computations, since for B&V’s “well-behaved” QTMs “non termination” corresponds to classical divergence.

Our aim is to provide a definition of QTMs with both quantum data and quantum control, hence broader than B&V’s one, and to base on this notion an explicit definition of a class of functions “computed by QTMs”. First of all, we allow a QTM to “start” its computation on an arbitrary quantum input—that is, a denumerable superposition of configurations, each representing a natural number. Second, because any computation of a QTM is always an infinite one, we want to give meaning also to some of these infinite computations. For such infinite behaviours, an “output” is obtained as a limit of finite portions of the computation. In order to accommodate these two aims with the unitary condition of the evolution, we have first to carefully define the very notion of QTM, in such a way that, when a computation of the machine enters into a “final state”, its evolution continues to remain in that final state, without changing the output written on the tape. This kind of evolution is obtained by enriching the machines by means of a suitable counter, which plays no role during the standard evolution of the machine, but starts to be increased when a path of the computation enters into a final state (a dual treatment, by reversibility, is done for the initial state). Differently from B&V, any computation path (that is, any element of the superposition) evolves independently from the others: any path may terminate at its own time, or may diverge. Like B&V, we give local conditions ensuring that the resulting evolution respects the unitary condition.

We propose a suitable protocol for termination and observation of the result, which is robust with respect to the choice of the time instants in which the measurements for observing the results are made. This is in contrast to both B&V, where one has to know the exact termination time, and to Deutsch, where a partial measurement is made at every single step of the computation. The termination criteria for B&V and Deutsch is also one of the main obstacles for their use to define meaningful infinite computations. In all the paper, with the exception of Section 6.2 when discussing papers of other authors, we use “termination” and not “halting”. Because there is no real halting for QTMs, we use a term different from the standard one used for classical TMs, to remark the difference.

Once we have a robust notion of QTMs and their observation protocol, we define the notion of “function computable by a QTM”, as a mapping between superpositions of initial classical configurations to probability distributions of natural numbers, which is obtained (in general) as a limit of an infinite QTM computation. Because not all infinite computations are meaningful to the limit, the resulting class of quantum computable functions also contains non-total functions, as is usual in computability theory.

We stress that we are not proposing a kind of “super Turing computability”. We expect that our class of functions, when restricted to classical input-output and computable amplitudes, will not be different from the set of the recursive functions (see the end of Section 3.5).

We believe it is interesting to have a class of machines and functions that could be seen as a simple, and standard, model of quantum programs, thus opening the door to a quantum computability theory that could be of use for the semantics of quantum programming languages.

Organization of the Paper

Section 2 introduces the central notion of Quantum Turing Machines; the technical definitions are preceded by a lengthy discussion on the motivations of the most delicate issues. We conclude the section with a theorem giving local conditions for unitarity, as in [12]. Section 3 uses QTMs to define a class of partial quantum computable functions. Section 4 deals with the problem of observables with respect to QTM computations. The protocols of Deutsch [10,12] are discussed, and a new observational protocol is proposed, proving that it agrees with the notion of computable functions of the previous section. In particular, we discuss, in detail, Deutsch’s protocol, in which sense our proposal is different, and how it is related to Ozawa’s termination protocol [13]. In Section 5, we propose a detailed comparison with the approach of B&V. Section 6 is a detailed discussion of related work and other approaches. Finally, we discuss in the Appendix A some additional technical issues.

2. Quantum Turing Machines

In this section, we define quantum Turing machines. Before the formal statements (Definitions 1, 3 and 4, etc.), we will discuss, in detail, some of the notions that will be introduced, to motivate and explain our technical choices. We assume the reader be familiar with classical Turing machines (otherwise, see [14]), which we assume defined with a tape infinite in both directions.

Like a classical Turing Machine (TM), a Quantum Turing Machine (QTM) has a tape (a sequence of cells) containing symbols (one in each cell) from a finite tape alphabet $\mathsf{\Sigma }$, which includes at least the symbols 1 and □: 1 is used to code natural numbers in unary notation, while □ is the blank symbol. We shall consider computations starting from tapes containing a sequence of $n+1$ symbols 1 (the encoding of the natural number n); thus, in the following, for any $n\in \mathbb{N}$, we shall use $\underline{n}$ to denote the string $1^{n+1}$. By the Greek letters $\alpha ,\beta$, possibly indexed, we shall instead denote strings in ${\mathsf{\Sigma }}^{*}$, and by $\alpha \beta$, we shall denote the concatenation of $\alpha$ and $\beta$. Finally, we shall use $\lambda$ to denote the empty string.

2.1. Plain Configurations

The basic elements to describe the configuration of a QTM are the finite sequences of symbols on the tape (as usual, we assume that only a finite portion of the tape contains non-blank symbols), the current internal state of the machine, and the current position of the head reading a symbol in a cell of the tape. We assume that each cell of the tape has a fixed address (an integer number), corresponding to its position on the tape. That is, we assume the tape to be a function $T:\mathbb{Z}\to \mathsf{\Sigma }$, such that, at any moment of the execution, only a finite, contiguous part of the tape is not empty, i.e., at any step of the execution, there are two constants $h\le k$ s.t., $T\left(i\right)=\square$ for $i<h$ and $i\ge k$ (thus, when $h=k$ the tape is empty).

A canonical plain configuration of a given QTM M is a quadruple $\langle \alpha ,q,\beta ,i\rangle \in {\mathsf{\Sigma }}^{*}\times Q\times {\mathsf{\Sigma }}^{*}\times \mathbb{Z}$, s.t.:

1.

$q\in Q$ is the current state, where Q is the finite set of the internal states of M.

2.

$\beta \in {\mathsf{\Sigma }}^{*}$ is the right content of the tape (w.r.t. the head position), where $\mathsf{\Sigma }$ is the tape alphabet of the machine M. If $\beta =u{\beta }^{\prime }\ne \lambda$, the symbol $u\in \mathsf{\Sigma }$ is the current symbol, which is the content of the current cell, while ${\beta }^{\prime }\in {\mathsf{\Sigma }}^{*}$ is the longest string on the tape ending with a symbol different from □ and whose first symbol (if any) is written in the cell immediately to the right of the current cell. When $\beta =\lambda$ instead, the right content of the tape, including the current cell, is empty, and the current symbol is □.

3.

$\alpha$ is the left content of the tape (w.r.t. the head position). That is, it is either the empty string $\lambda$, or it is the longest string on the tape starting with a symbol different from □, and whose last symbol is written in the cell immediately to the left of the current cell.

4.

i is the address of the current cell.

Given $\alpha ,\beta \in {\mathsf{\Sigma }}^{*}$, let $\alpha =a_0{a}_1\dots a_{u-1}$ and $\beta =b_0{b}_1\dots b_{v-1}$, with $u,v\ge 0$. The plain configuration $\langle \alpha ,q,\beta ,i\rangle$ corresponds to the tape

$$T\left(j\right)=\left\{\begin{array}{cc}{a}_{j-i+u}\hfill & \mathrm{for}i-u\le j<i\hfill \\ b_{j-i}\hfill & \mathrm{for}i\le j<i+v\hfill \\ \square \hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

where $T\left(j\right)\ne \square$, implies that $i-u\le j<i+v$.

In a canonical plain configuration $\langle \alpha ,q,\beta ,i\rangle$ the string $\alpha$ does not start with a □, and $\beta$ does not end with a □. This ensures that each tape corresponds to a unique canonical plain configuration, and vice versa. However, because it will be useful to manipulate configurations that are extended with blank cells to the right (of the right content) or to the left (of the left content), we shall also consider plain configurations $\langle \alpha ,q,\beta ,i\rangle$ in which there is no restriction on $\alpha$ and $\beta$ and we equate them up to the three equivalence relations that are induced by the following equations

$$\begin{array}{c}\alpha {\simeq }_l\square \alpha \beta {\simeq }_r\beta \square \\ \langle \alpha ,q,\beta ,i\rangle \simeq \langle {\alpha }^{\prime },q,{\beta }^{\prime },i\rangle \mathrm{when}\alpha {\simeq }_l{\alpha }^{\prime }\mathrm{and}\beta {\simeq }_r{\beta }^{\prime }\end{array}$$

It is readily seen that any plain configuration is equivalent to a unique canonical plain configuration, and that two configurations are equivalent if and only if they are in the same state, the address of the head is the same, and they correspond to the same tape.

2.2. Hilbert Space of Configurations

We will see in the following that a quantum configuration of a QTM cannot simply be a plain configuration, but it must be a weighted superposition of configurations: a vector of the Hilbert space ${\ell }^2\left(\mathcal{C}\right)$, where $\mathcal{C}$ is a set of configurations, like the plain ones defined above.

We recall that, for any denumerable set $\mathcal{B}$, ${\ell }^2\left(\mathcal{B}\right)$ is the Hilbert space of square summable $\mathcal{B}$-indexed sequences of complex numbers

$$\left\{\varphi :\mathcal{B}\to \mathbb{C}\mid \sum _{C\in \mathcal{B}}{\left|\varphi \left(C\right)\right|}^2<\infty \right\}$$

equipped with an inner product $\langle .\mid .\rangle$ and the euclidean norm $\parallel \varphi \parallel =\sqrt{\langle \varphi \mid \varphi \rangle }$, and that ${\ell }_1^2\left(\mathcal{B}\right)$ denotes the set of vectors $\{\varphi \mid \varphi \in {\ell }^2\left(\mathcal{B}\right)\&\parallel \varphi \parallel =1\}$.

By using Dirac notation, we shall write $|\varphi \rangle$ to denote the vector of ${\ell }^2\left(B\right)$ corresponding to the function $\varphi :\mathcal{B}\to \mathbb{C}$. Moreover, for every $C\in \mathcal{B}$, we shall write $|C\rangle$ to denote the vector corresponding to C, which is, the function equal to 1 on C, and equal to 0 on the other elements of $\mathcal{B}$. Finally, we remark that any vector $|\varphi \rangle$ of ${\ell }^2\left(\mathcal{B}\right)$ can be written as ${\sum }_{i\in I}{d}_i|C_i\rangle$, for some denumerable set of indexes I s.t. $\{C_i\mid i\in I\}\subseteq \mathcal{B}$ and $d_i\in \mathbb{C}$, for every $i\in I$. For more details on the basic notions of Hilbert spaces, see Appendix A.

2.3. Transitions of a QTM

Given a quantum configuration $\varphi$ of a QTM M (see Section 2.7 for the formal definition), the main idea that is introduced by Deutsch [10] is that the machine evolves into another quantum configuration $|\psi \rangle =U|\varphi \rangle$, where U is a unitary operator on the Hilbert space of the configurations of M. By linearity and continuity, this also means that, if $\mathcal{C}$ is the set of configurations on which we define the Hilbert space of quantum configuration ${\ell }^2\left(\mathcal{C}\right)$ of M, the operator U, and then the behaviour of M, is completely determined by the value of U on the elements of $\mathcal{C}$. B&V [12] refines this point by assuming that, as in a classical TM, for every $C\in \mathcal{C}$, the transition from $|C\rangle$ to a new configuration $U|C\rangle$ only depends on the current state of M and on the current symbol of C, and that $U|C\rangle$ is formed of configurations obtained by replacing the current symbol u of C with a new one, and by moving the tape head to the left or the right. Therefore, if we denote by $\mathbb{D}=\{L,R\}$ the set of the possible movements on the tape (where L stands for left and R for right), and q is the current state of M, we have

$$U\left(\right|C\rangle )=\sum _{p,v,d}\delta (q,u)(p,v,d)|C_{p,v,d}\rangle ,$$

where p ranges over the states of M, v ranges over its tape alphabet, $\delta (q,u)(p,v,d)\in \mathbb{C}$, and $C_{p,v,d}$ is the new configuration obtained from C by changing the current state from q to p, by replacing the current symbol u with v, and by moving the tape head in the direction d.

2.4. Initial and Final Configurations

In B&V, the transition rule described above applies to every state of the machine. However, as already remarked in the introduction, this implies a severe restriction on the machines that one can actually consider as valid ones—the reversibility of unitary operators, and the problem of how to read the output, force to ask that, in a “well-behaved” QTM, if a configuration in superposition enters the final state, then all other configurations of the superposition must also enter into the final state.

The key point is that a QTM cannot stop into some final configuration $C_f$, since the unitarity of U requires that $U\left(\right|C_f\rangle )$ be defined. On the other hand, we cannot assume that, after reaching some final configuration $C_f$, the computation loops on it neither. As this would imply that $C_f$ could not be reached from any other configuration $D\in \mathcal{C}$: if $U\left(\right|C_f\rangle )=|C_f\rangle$, then $|C_f\rangle =U^{-1}\left(\right|C_f\rangle )$, and $U\left(\right|D\rangle )\left(C_f\right)=\langle U\left(\right|D\rangle )\mid C_f\rangle =\langle D\mid U^{-1}\left(\right|C_f\rangle )\rangle =\langle D\mid C_f\rangle =0$, for $D\ne C_f$. When a final configuration $C_f$ is reached, the machine must evolve into a different configuration that preserves the output written on the tape, without breaking the unitarity of the evolution operator U. Let us assume to have a denumerable set of indexed configurations $\langle C_f,n\rangle$ obtained by adding a counter $n\in \mathbb{N}$ to $C_f$, for every final configuration $C_f$. The configuration $\langle C_f,0\rangle$ plays the usual role of the plain configuration $C_f$ and it is the only one that can be reached from a non final configuration; for every $n\in \mathbb{N}$, the configuration $\langle C_f,n+1\rangle$ is instead the only successor of $\langle C_f,n\rangle$, which is, $U\left(\right|C_f,n\rangle )=|C_f,n+1\rangle$, where $|C_f,n\rangle$ is the base vector corresponding to $\langle C_f,n\rangle$. In other words, the counter n is initialised to 0 and plays no role while the state is not final; when a branch of the computation enters a final state, the counter is still at 0, but it is increased by 1 at each following step.

Final configurations are not the only configurations on which it would be useful to loop. In some cases, in order to assure that the operator U is unitary, we need to introduce additional target configurations that behave as sinks, from which the machine cannot get out (see Remark 1, and the example in Section 5.3, whose graph representation is given in Figure 4). We have then to consider a whole set ${\mathcal{Q}}_t$ of target states, containing the final state $q_f$, s.t. for every plain configuration $C_t=\langle \alpha ,q_t,\beta ,i\rangle$, with $q_t\in {\mathcal{Q}}_t$, we have a set of indexed configurations $\langle C_t,n\rangle$, for $n\in \mathbb{N}$, s.t. $U\left(\right|C_t,n\rangle )=|C_t,n+1\rangle$.

Moreover, when U is unitary, its inverse $U^{-1}$ is unitary too, and it can be applied to any initial configuration. Therefore, even if we assume that a computation always starts from some initial plain configuration $C_j=\langle \alpha ,q_j,\beta ,i\rangle$, such a $C_j$ must have a predecessor $|C_{j,1}\rangle =U^{-1}\left(\right|C_j\rangle )$, and more generally a n-predecessor $|C_{j,n}\rangle =U^{-n}\left(\right|C_j\rangle )$. As already done for final configurations, we associate to every $C_j$ a set of indexed configurations $\langle C_j,n\rangle$, with $n\in \mathbb{N}$, s.t. $U^{-1}\left(\right|C_j,n\rangle )=|C_j,n+1\rangle$, for $n\in \mathbb{N}$. For $n>0$, we get then $U\left(\right|C_j,n\rangle )=|C_j,n-1\rangle$; while $U\left(\right|C_j,0\rangle )$ has the usual behaviour expected from the machine on the plain initial configuration $C_j$. As for final state and final configurations, it is useful to generalise the above behaviour to a set of source configurations corresponding to a set ${\mathcal{Q}}_s$ of source states that contains the initial state $q_j$.

2.5. Pre Quantum Turing Machines

In order to formally define QTMs, we first define a notion of pre Quantum Turing Machine, or pQTM. As we shall see later (Definition 7), a QTM is a pQTM whose evolution operator is unitary. Because the behaviour on target states and on source states whose counter is greater than 0 is fixed, in order to completely describe a pQTM, it suffices to give a transition function ${\delta }_0:((\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma })\to {\ell }_1^2((\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D})$, which, for every configuration C with current state q and current symbol u, gives the weight ${\delta }_0(q,u)(p,v,d)$ of $|C_{p,v,d}\rangle$ in the superposed configuration reached from $|C\rangle$, where $C_{p,v,d}$ is obtained by replacing v for u, by moving the tape in the d direction, and by changing the current state to p.

Definition 1

(Pre Quantum Turing Machine). Given a finite set of states $\mathcal{Q}$ and an alphabet Σ, a pre Quantum Turing Machine (pQTM) is a tuple

$$M=\langle \mathsf{\Sigma },\mathcal{Q},{\mathcal{Q}}_s,{\mathcal{Q}}_t,{\delta }_0,q_i,q_f\rangle$$

where

• ${\mathcal{Q}}_s\subseteq \mathcal{Q}$ is the set of source states of M, and $q_i\in {\mathcal{Q}}_s$ is a distinguished source state named the initial state of M;
• ${\mathcal{Q}}_t\subseteq \mathcal{Q}$ is the set of target states of M, and $q_f\in {\mathcal{Q}}_t$ is a distinguished target state named the final state of M;
• ${\mathcal{Q}}_s$ and ${\mathcal{Q}}_t$ have the same cardinality and ${\mathcal{Q}}_s\cap {\mathcal{Q}}_t=\varnothing$;
• ${\delta }_0:((\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma })\to {\ell }_1^2((\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D})$ is the quantum transition function of M, where $\mathbb{D}=\{L,R\}$.

Remark 1

(Source and target states). Source and target states must be introduced to complete a QTM when the transitions implementing its expected behaviour fail to assure the local conditions of Theorem 1, required to get a unitary time evolution operator. In particular, the first condition states that the norm of the vector $\delta (q,u)$ corresponding to the transition from a configuration C with current state q and current symbol u, to a superposed configuration $\sum \delta (q,u)(p,v,d)|C_{p,v,d}\rangle$ must be equal to 1. Anyhow, in some case, the norm of the vector of the weights implementing the expected behavior of the machine might give a value smaller than 1, while, in no case, it cannot exceed the value of 1. To achieve the required local condition, we can add some new transitions to some special target state acting as a sink (i.e., from which the machine cannot get out), with a procedure reminding the one used to complete a non-deterministic automata by connecting all of the omitted transitions to a sink state. The main difference is that in the QTM case more than one target state may be necessary to achieve the goal. Moreover, because of the reversibility of QTMs, a similar condition must hold for the transitions entering into a given state. Accordingly, we must also take into account the case in which we need to complete the implementation of the expected behaviour by adding new transitions from some source states. Finally, we remark that the requirement that the sets of source and target states have the same cardinality is used to prove the unitarity of the evolution operator associated to our QTMs via a reduction to the B&V QTMs (see Theorem 1). We do have another, independent, and direct proof of this result (that we omit in this paper), and that also exploits the equinumerosity of source and target states. We conjecture then that this is indeed a necessary condition.

Remark 2

(On gödelization of QTMs). For a definition of gödelizable QTMs, we must restrict the definition of the transition function to computable complex numbers (see also [12].)

Definition 2 (computable numbers).

A real number x is computable if there exists a deterministic Turing machine that on input $1^n$ computes a binary representation of an integer $m\in \mathbb{Z}$, such that $|\frac{m}{2^n}-x|\le \frac{1}{2^n}$. The set $\tilde{\mathbb{C}}$ of the computable complex numbers is the set of the complex numbers whose real and imaginary parts are both computable.

Now, let ${\tilde{\ell }}_1^2\left(\mathcal{B}\right)$ be the subset of ${\ell }_1^2\left(\mathcal{B}\right)$ s.t. the coefficients of the vectors are bound to be in $\tilde{\mathbb{C}}$. We can say that a transition function ${\tilde{\delta }}_0$ is computable when

$${\tilde{\delta }}_0:((\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma })\to \widetilde{{\ell }_1^2}((\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D}).$$

The gödelization of a QTM whose transition function is computable proceeds in the usual way. First of all, just observe that ${\ell }_1^2((\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D})$ is a finite dimensional space, then each complex number $x+iy\in \tilde{\mathbb{C}}$ involved in the gödelization of ${\tilde{\delta }}_0$ can be replaced by a pair $(n_x,n_y)$, where $n_x$ and $n_y$ are the Gödel numbers of the Turing machines computing x and y, respectively.

2.6. Configurations

We have already seen that, in order to properly deal with source and target states, we have to associate a counter to those states. For the sake of uniformity, we shall add a counter to every plain configuration. The counter will always be 0 for every non-source or non-target configuration.

Remark 3

(The counter). The counter can be seen as an additional device (for instance, as an additional tape or as a counting register) or directly implemented by a suitable extension of the basic Turing machine (for instance, by extending the tape alphabet). None of these implementations is canonical or it has a direct influence in what will be presented in the following. Appendix B provides a more detailed discussion of the implementation of the counter.

Definition 3

(configurations). Let $M=(\mathsf{\Sigma },\mathcal{Q},{\mathcal{Q}}_s,{\mathcal{Q}}_t,{\delta }_0,q_0,q_f)$ be a pQTM. A configuration of M is a quintuple $\langle \alpha ,q,\beta ,i,n\rangle \in {\mathsf{\Sigma }}^{*}\times \mathcal{Q}\times {\mathsf{\Sigma }}^{*}\times \mathbb{Z}\times \mathbb{N}$, where $\langle \alpha ,q,\beta ,i\rangle$ is a plain configuration, and n is a counter associated to the configuration s.t. $n=0$, when $q\notin {\mathcal{Q}}_s\cup {\mathcal{Q}}_t$. A configuration of M is a source/target configuration when the corresponding state is a source/target state, and it is a final/initial configuration when the current state is final/initial. We have the following notations:

• ${\mathfrak{C}}_M$ is the set of the configurations of M.
• ${\mathfrak{C}}_M^s$ and ${\mathfrak{C}}_M^t$ are the sets of the source and of the target configurations of M, respectively.
• ${\mathfrak{C}}_M^{init}$ and ${\mathfrak{C}}_M^{fin}$ are the sets of the initial and final configurations of M, respectively.
• ${\mathfrak{C}}_M^0$ is the set of the configurations $\langle \alpha ,q,\beta ,i,0\rangle$ of M.

In the following, the subscript M in ${\mathfrak{C}}_M$ and in the other names indexed by the machine may be dropped when clear from the context.

2.7. Quantum Configurations

The evolution of a pQTM is described by superpositions of configurations in ${\mathfrak{C}}_M$. If $\mathcal{B}\subseteq {\mathfrak{C}}_M$ is a set of configurations, a superposition of configurations in $\mathcal{B}$ is a vector of the Hilbert space ${\ell }^2\left(\mathcal{B}\right)$ (see, e.g., [15,16]). Quantum configurations of a pQTM M are the elements of ${\ell }_1^2\left({\mathfrak{C}}_M\right)$ (namely, the unit vectors of ${\ell }^2\left({\mathfrak{C}}_M\right)$). Because there is no bound on the size of the tape in a configuration, the set ${\mathfrak{C}}_M$ is infinite and the Hilbert space of the configurations ${\ell }^2\left({\mathfrak{C}}_M\right)$ is infinite dimensional.

Definition 4

(quantum configurations). Let M be a pQTM. The elements of ${\ell }_1^2\left({\mathfrak{C}}_M\right)$ are the quantum configurations (or more succinctly, q-configurations) of M.

We shall use Dirac notation (see Appendix A) for the elements $\varphi ,\psi$ of ${\ell }^2\left({\mathfrak{C}}_M\right)$, writing them $|\varphi \rangle ,|\psi \rangle$.

Definition 5

(computational basis). For any set of configurations $\mathcal{B}\subseteq {\mathfrak{C}}_M$ and any $C\in \mathcal{B}$, let $|C\rangle :\mathcal{B}\to \mathbb{C}$ be the function

$$|C\rangle \left(D\right)=\left\{\begin{array}{cc}1\hfill & ifC=D\hfill \\ 0\hfill & ifC\ne D.\hfill \end{array}\right.$$

The set $\mathsf{CB}\left(\mathcal{B}\right)$ of all such functions is a Hilbert basis for ${\ell }^2\left(\mathcal{B}\right)$ (see, e.g., [17]). In particular, following the literature on quantum computing, $\mathsf{CB}\left({\mathfrak{C}}_M\right)$ is called the computational basis of ${\ell }^2\left({\mathfrak{C}}_M\right)$. Each element of the computational basis is called base q-configuration.

With a little abuse of language, we shall write $|C\rangle \in |\varphi \rangle$ when $\varphi \left(C\right)\ne 0$. The span of $\mathsf{CB}\left(\mathcal{B}\right)$, denoted by $\mathsf{span}\left(\mathsf{CB}\right(\mathcal{B}\left)\right)$, is the set of the finite linear combinations with complex coefficients of elements of $\mathsf{CB}\left(\mathcal{B}\right)$; $\mathsf{span}\left(\mathcal{B}\right)$ is a vector space, but not a Hilbert space. In order to get a Hilbert space from $\mathsf{span}\left(\mathsf{CB}\right(\mathcal{B}\left)\right)$, we have to complete it, and ${\ell }^2\left(\mathcal{B}\right)$ is indeed the unique (up to isomorphism) completion of $\mathsf{span}\left(\mathsf{CB}\right(\mathcal{B}\left)\right)$ (see [12]). As a consequence, any bounded linear operator U on $\mathsf{span}\left(\mathsf{CB}\right(\mathcal{B}\left)\right)$ has a unique extension on ${\ell }^2\left(\mathcal{B}\right)$, and, when U is unitary, its extension is unitary too.

For some basic definitions, properties, and notations on Hilbert spaces with denumerable basis, see Appendix A. In particular, Appendix A.1 presents a synoptic table of the so-called Dirac notation that we shall use in the paper.

2.8. Time Evolution Operator and QTM

In order to define the evolution operator of a pQTM M, it suffices to give its behaviour on the computational basis $\mathsf{CB}\left({\mathfrak{C}}_M\right)$. In particular, we have to distinguish three cases:

1.

$C\in {\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^t$.

Let $C_{p,v,d}\in {\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^s$ be the configuration obtained by leaving the counter to 0, by replacing the symbol u in the current cell with the symbol v, by moving the head on the d direction, and by setting the machine into the new state p. In detail, if $C\simeq \langle \alpha w,q,u\beta ,i,0\rangle$ we have

$$C_{p,v,d}\simeq \left\{\begin{array}{cc}\langle \alpha wv,p,\beta ,i+1,0\rangle \hfill & \mathrm{when}d=R\hfill \\ \langle \alpha ,p,wv\beta ,i-1,0\rangle \hfill & \mathrm{when}=L.\hfill \end{array}\right.$$

and we define

$$W_{0,M}\left(\right|C\rangle )=\sum _{(p,v,d)\in (\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D}}{\delta }_0(q,u)(p,v,d)|C_{p,v,d}\rangle$$

where ${\delta }_0$ is the quantum transition function of M, and, as already introduced at the end of Section 2.3, $C_{p,v,d}$ is the new configuration obtained from C by changing the current state from q to p, by replacing the current symbol u with v, and by moving the tape head in the direction d.

2.

$C\in {\mathfrak{C}}_M^s\setminus {\mathfrak{C}}_M^0$.

Let $C_{-1}\in {\mathfrak{C}}_M^s$ be the source configuration obtained by decreasing by 1 the counter of C, we define

$$W_{s,M}\left(\right|C\rangle )=|C_{-1}\rangle$$

3.

$C\in {\mathfrak{C}}_M^t$.

Let $C_{+1}\in {\mathfrak{C}}_M^t\setminus {\mathfrak{C}}_M^0$ be the target configuration obtained by increasing by 1 the counter of C, we define

$$W_{t,M}\left(\right|C\rangle )=|C_{+1}\rangle$$

We have then three linear operators

$$\begin{array}{cc}\hfill W_{0,M}& :\mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^t)\right)\to \mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^s)\right)\hfill \\ \hfill W_{s,M}& :\mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^s\setminus {\mathfrak{C}}_M^0)\right)\to \mathsf{span}\left(\mathsf{CB}\left({\mathfrak{C}}_M^s\right)\right)\hfill \\ \hfill W_{t,M}& :\mathsf{span}\left(\mathsf{CB}\left({\mathfrak{C}}_M^t\right)\right)\to \mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^t\setminus {\mathfrak{C}}_M^0)\right)\hfill \end{array}$$

defined on three disjoint subspaces. Moreover, because even the images of these three operators are disjoint, their sum

$$W_M=W_{0,M}+W_{s,M}+W_{t,M}$$

defines an automorphism on the linear space of q-configurations

$$W_M:\mathsf{span}\left(\mathsf{CB}\left(\mathfrak{C}\right)\right)\to \mathsf{span}\left(\mathsf{CB}\left(\mathfrak{C}\right)\right).$$

Indeed, since $W_M$ is bounded, it extends in a unique way to a continuous operator on the Hilbert space of q-configurations.

Definition 6

(time evolution operator). The time evolution operator of M is the unique continuous extension

$$U_M:{\ell }^2\left({\mathfrak{C}}_M\right)\to {\ell }^2\left({\mathfrak{C}}_M\right)$$

of the bounded linear operator $W_M:\mathsf{span}\left(\mathsf{CB}\left(\mathfrak{C}\right)\right)\to \mathsf{span}\left(\mathsf{CB}\left(\mathfrak{C}\right)\right)$.

As it is the case for the operator $W_M$, also the time evolution operator $U_M$ can be decomposed into three operators

$$\begin{array}{cc}\hfill U_{0,M}& :{\ell }^2({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^t)\to {\ell }^2({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^s)\hfill \\ \hfill U_{s,M}& :{\ell }^2({\mathfrak{C}}_M^s\setminus {\mathfrak{C}}_M^0)\to {\ell }^2\left({\mathfrak{C}}_M^s\right)\hfill \\ \hfill U_{t,M}& :{\ell }^2\left({\mathfrak{C}}_M^t\right)\to {\ell }^2({\mathfrak{C}}_M^t\setminus {\mathfrak{C}}_M^0)\hfill \end{array}$$

s.t.

$$U_M=U_{0,M}+U_{s,M}+U_{t,M}.$$

Definition 7

(QTM). A pQTM is a Quantum Turing Machine (QTM) when its time evolution operator $U_M$ is unitary.

As usual, $U_M^i$ (the i-th iterate of $U_M$) is defined as $U_M^0=id$, and $U_M^{i+1}=U_M\circ U_M^i$.

2.9. Computations

A computation of a QTM is an iteration of its evolution operator on some q-configuration. Because the time evolution operator of a QTM is unitary, it preserves the norm of its argument and maps q-configurations into q-configurations. By the way, this also holds for the inverse $U_M^{-1}$ of the time evolution operator.

Property 1.

Let M be a QTM. If $|\varphi \rangle \in {\ell }_1^2\left({\mathfrak{C}}_M\right)$, then $U_M^i|\varphi \rangle \in {\ell }_1^2\left({\mathfrak{C}}_M\right)$, for every $i\in \mathbb{Z}$.

Definition 8

(initial and final configurations). A q-configuration $|\varphi \rangle$ is initial when $|\varphi \rangle \in {\ell }_1^2\left({\mathfrak{C}}_M^{init}\right)$ and is final when $|\varphi \rangle \in {\ell }_1^2\left({\mathfrak{C}}_M^{fin}\right)$. By $|\underline{n}\rangle$, we denote the initial configuration $\langle \lambda ,q_0,\underline{n},0,0\rangle \in {\mathfrak{C}}_M^{init}$.

Definition 9

(computations). Let M be a QTM and let $U_M$ be its time evolution operator. For an initial q-configuration $|\varphi \rangle \in {\ell }_1^2\left({\mathfrak{C}}^{init}\right)$, the computation of M on $|\varphi \rangle$ is the denumerable sequence $\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ s.t.

1. 

$|{\varphi }_0\rangle =|\varphi \rangle$;

2. 

$|{\varphi }_i\rangle =U_M^i|\varphi \rangle$.

Clearly, any computation of a QTM M is uniquely determined by its initial q-configuration. The computation of M on the initial q-configuration $|\varphi \rangle$ will be denoted by $K_{|\varphi \rangle }^M$.

Remark 4.

The definition of the time evolution operator ensures that the final configurations reached along a computation are stable and do not interfere with other branches of the computation in superposition, which may enter into a final configuration later. Indeed, given a configuration $|\varphi \rangle =|{\varphi }_f\rangle +|{\varphi }_{nf}\rangle$, where $|{\varphi }_f\rangle \in {\ell }^2\left({\mathfrak{C}}^{fin}\right)$ and $|{\varphi }_{nf}\rangle$ does not contain any final configuration, let $|\psi \rangle =U^i|\varphi \rangle =U^i|{\varphi }_f\rangle +U^i|{\varphi }_{nf}\rangle$. Any final configuration in $U^i|{\varphi }_{nf}\rangle$ has a value of the counter less than i, while any final configuration $|C,k\rangle \in |\varphi \rangle$ formed of a plain configuration C and a counter k is mapped into a configuration $|C,i+k\rangle \in \psi$. Moreover, $|C,k\rangle$ and $|C,i+k\rangle$ have the same coefficient in $|\varphi \rangle$ and $|\psi \rangle$, respectively, since $\langle \psi \mid C,i+k\rangle =\langle U^i|\varphi \rangle ,U^i|C,k\rangle \rangle =\langle \varphi \mid C,k\rangle$.

2.10. Local Conditions for Unitary Evolution

In analogy to the main approaches in the literature [12,18], it is possible to state a set of local condition for the quantum transition function ${\delta }_0$ of pQTMs in order to ensure that the time evolution operator is unitary.

Theorem 1.

Let M be a pQTM with quantum transition function ${\delta }_0$. The time evolution operator $U_M:$${\ell }^2\left({\mathfrak{C}}_M\right)\to {\ell }^2\left({\mathfrak{C}}_M\right)$ of M is unitary if and only if ${\delta }_0$ satisfies the local conditions:

1. 

for any $(q,a)\in (\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma }$

$$\sum _{(p,b,d)\in (\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D}}{\left|{\delta }_0(q,a)(p,b,d)\right|}^2=1$$

2. 

for any $(q,a),(q^{\prime },a^{\prime })\in (\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma }$ with $(q,a)\ne (q^{\prime },a^{\prime })$

$$\sum _{(p,b,d)\in (\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D}}{\delta }_0(q^{\prime },a^{\prime }){(p,b,d)}^{*}{\delta }_0(q,a)(p,b,d)=0$$

3. 

for any $(q,a,b),(q^{\prime },a^{\prime },b^{\prime })\in (\mathcal{Q}\setminus {\mathcal{Q}}_t)\times {\mathsf{\Sigma }}^2$

$$\sum _{p\in (\mathcal{Q}\setminus {\mathcal{Q}}_s)}{\delta }_0(q^{\prime },a^{\prime }){(p,b^{\prime },L)}^{*}{\delta }_0(q,a)(p,b,R)=0$$

where ${\left(\right)}^{*}$ denote the complex conjugate operator.

Proof. 

We show that, to any QTM M (as defined above), we can associate a B&V QTM N, which differs on the behaviour on source and target states only. The unitarity of M follows then from the unitarity of N.

Let $M=\langle \mathsf{\Sigma },\mathcal{Q},{\mathcal{Q}}_s,{\mathcal{Q}}_t,{\delta }_0,q_i,q_f\rangle$. We take the B&V QTM N with the same states $\mathcal{Q}$ and the same alphabet $\mathsf{\Sigma }$, and whose transition function $\rho$ satisfies the following conditions:

1.

$\rho$ is the same of the transition function ${\delta }_0$ of M for any non-terminal state;

2.

for any terminal state $q_t$ and every current symbol u, $\rho$ has a unique non-null transition, with weight 1, that leaves the current symbol on the tape unchanged, moves the head to the right, and goes into an initial state $q_s$; and,

3.

the non-null out transitions from two distinct terminal states lead to two distinct source states, defining in this way a bijection between the set of the target and source states.

In other words, $\rho$ is defined by:

$$\begin{array}{cccc}\hfill \rho (q,u)(p,v,d)& ={\delta }_0(q,u)(p,v,d)\hfill & \hfill & \mathrm{for}q\in \mathcal{Q}\setminus {\mathcal{Q}}_t,p\in \mathcal{Q}\setminus {\mathcal{Q}}_s,u,v\in \mathsf{\Sigma },d\in \mathbb{D}\hfill \\ \hfill \rho (q,u)(s,v,d)& =0\hfill & \hfill & \mathrm{for}q\in \mathcal{Q}\setminus {\mathcal{Q}}_t,s\in {\mathcal{Q}}_s,u,v\in \mathsf{\Sigma },d\in \mathbb{D}\hfill \end{array}$$

and, assuming ${\mathcal{Q}}_s={\left\{s_i\right\}}_{0\le i\le k}$ and ${\mathcal{Q}}_t={\left\{t_i\right\}}_{0\le i\le k}$

$$\begin{array}{cccc}\hfill \rho (t_i,u)(s_i,u,R)& =1\hfill & \hfill & \mathrm{for}u\in \mathsf{\Sigma }\hfill \end{array}$$

$$\begin{array}{cccc}\hfill \rho (t_i,u)(s_i,v,L)& =0\hfill & \hfill & \mathrm{for}u,v\in \mathsf{\Sigma }\hfill \end{array}$$

$$\begin{array}{cccc}\hfill \rho (t_i,u)(q,v,d)& =0\hfill & \hfill & \mathrm{for}q\in \mathcal{Q}\setminus {\mathcal{Q}}_t,q\ne s_i,u,v\in \mathsf{\Sigma },d\in \mathbb{D}\hfill \end{array}$$

The above definition ensures that N is a B&V QTM whose configurations are the plain configurations of M, and s.t. its transition function $\rho$ verifies B&V local conditions. By B&V, the evolution operator $U_N$ of N is then a unitary operator on the Hilbert space of the plain configurations of N and, as a consequence, its adjoint $U_N^{*}$ is its inverse. We can take three linear operators

$$\begin{array}{cc}\hfill V_{0,M}& :\mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^s)\right)\to \mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^t)\right)\hfill \\ \hfill V_{s,M}& :\mathsf{span}\left(\mathsf{CB}\left({\mathfrak{C}}_M^s\right)\right)\to \mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^s\setminus {\mathfrak{C}}_M^0)\right)\hfill \\ \hfill V_{t,M}& :\mathsf{span}\left(\mathsf{CB}({\mathfrak{C}}_M^t\setminus {\mathfrak{C}}_M^0)\right)\to \mathsf{span}\left(\mathsf{CB}\left({\mathfrak{C}}_M^t\right)\right)\hfill \end{array}$$

defined by

$$\begin{array}{cccc}\hfill V_{0,M}|C\rangle & =|D\rangle \hfill & \hfill & \mathrm{with}|D\rangle =U_N^{*}|C\rangle \mathrm{when}|C\rangle \in {\mathfrak{C}}_M^0\setminus {\mathfrak{C}}_M^s\hfill \\ \hfill V_{s,M}|C\rangle & =|C_{+1}\rangle \hfill & \hfill & \mathrm{when}|C\rangle \in {\mathfrak{C}}_M^s\hfill \\ \hfill V_{t,M}|C\rangle & =|C_{-1}\rangle \hfill & \hfill & \mathrm{when}|C\rangle \in {\mathfrak{C}}_M^t\setminus {\mathfrak{C}}_M^0\hfill \end{array}$$

Which are the inverses of the three corresponding linear operators $W_{0,M}$, $W_{s,M}$, and $W_{tM}$, respectively (see Section 2.8). Thus, the bounded linear operator $V_M=V_{0,M}+V_{s,M}+V_{tM}$ is the inverse of $W_M=W_{0,M}+W_{s,M}+W_{tM}$, and its continuous extension (obtained by completion) is the inverse of $U_M$. Moreover, such an operator is also the adjoint $U_M^{*}$ of $U_M$. Summing up, the adjoint $U_M^{*}$ of $U_M$ is its inverse and, as a consequence, $U_M$ is unitary.  □

Remark 5.

The reader may wonder why we need to have cell indexes in configurations, when they are not used in many definitions of classical TMs. In fact, cell indexes are only needed in a very special case, which is of a completely empty tape. Let us suppose, indeed, to eliminate indexes, and to feed a completely blank tape to a QTM with only two states $\{q,r\}$, with no source and final states and no tape symbols, except □; let the transition function ${\delta }_0$ be s.t.

• ${\delta }_0(q,\square )(q,\square ,L)=1/2$
• ${\delta }_0(q,\square )(q,\square ,R)=1/2$
• ${\delta }_0(q,\square )(r,\square ,L)=1/2$
• ${\delta }_0(q,\square )(r,\square ,R)=-1/2$
• ${\delta }_0(r,\square )(q,\square ,L)=1/2$
• ${\delta }_0(r,\square )(q,\square ,R)=-1/2$
• ${\delta }_0(r,\square )(r,\square ,L)=1/2$
• ${\delta }_0(r,\square )(r,\square ,R)=1/2$

It is easy to check that the conditions of Theorem 1 are satisfied, but trivially the induced time evolution operator U is not an isometry, since, given the empty string λ we have $U(\lambda ,q,\lambda )=U(\lambda ,r,\lambda )=(\lambda ,q,\lambda )$ (we omit here the counter, which always remains set to zero). The indexing we use is consistent with the one adopted by Bernstein & Vazirani, [12]—Definition 3.2, pag. 1419. Here, we just want to point out that Bernstein & Vazirani only provides a fairly light informal definition of configuration. We have preferred a more pedantic formulation, which, in our opinion, is necessary to eliminate all of the reader’s doubts about the correctness of the proposed theorems.

2.11. A Comparison with Bernstein and Vazirani’s QTMs: Part 1

We refer to B&V [12] for the precise definitions of the QTMs used in that paper. For the sake of readability, we informally recall the notion of what they call well formed, stationary, normal form QTMs (B&V-QTMs in the following).

A B&V-QTM $M=\langle \mathsf{\Sigma },\mathcal{Q},\delta ,q_0,q_f\rangle$ is defined as our QTM (with one source state and one target state only) with the following differences:

1.

the set of configurations coincides with all possible classical configurations, namely all the set ${\mathsf{\Sigma }}^{*}\times \mathcal{Q}\times {\mathsf{\Sigma }}^{*}\times \mathbb{Z}$;

2.

no superposition is allowed in the initial q-configuration (it must be a classical configuration $\langle \alpha ,q,\beta ,i\rangle$ with amplitude 1);

3.

given an initial configuration $|C\rangle$, the q-configuration ${\varphi }_k=U_M^k|C\rangle$ is the final q-configuration for the computation starting in $|C\rangle$, when: (i) all of the configurations in ${\varphi }_k$ are final; (ii) for all $i<k$, the q-configuration ${\varphi }_i={U_M}^i|C\rangle$ does not contain any final configuration. When this is the case, we also say that the QTM halts in k steps in ${\varphi }_k$;

4.

if a QTM halts, then the tape head is on the start cell of the initial configuration; and,

5.

there is no counter and for every symbol a there is loop from the only final state $q_f$ into the only initial state $q_0$, which is, $\delta (q_f,a)(q_0,a,R)=1$ for every $a\in \mathsf{\Sigma }$. Therefore, because of the local unitary conditions (that must hold in the final state too), these are the only outgoing transitions from $q_f$, and the only incoming ones into $q_0$. Accordingly, $\delta (q_f,a)(q^{\prime },a^{\prime },d)=0$ if $(q^{\prime },a^{\prime },d)\ne (q_0,a,R)$ and $\delta (q^{\prime },a^{\prime })(q_0,a,d)=0$ if $(q^{\prime },a^{\prime },d)\ne (q_f,a,R)$.

Theorem 2.

For any B&V-QTM M there is a QTM $M^{\prime }$ s.t. for each initial configuration $|C\rangle$, if M with input $|C\rangle$ halts in k steps in a final configuration $|\varphi \rangle =U_M^k|C\rangle$, then $U_{M^{\prime }}^k|C\rangle =|\varphi \rangle$.

Proof. 

The QTM $M^{\prime }$ has the same states of M, the initial state $q_0$ is its only source state, and the final state $q_f$ is its only target state. Therefore, if $M=\langle \mathsf{\Sigma },\mathcal{Q},\delta ,q_0,q_f\rangle$, we take $M^{\prime }=\langle \mathsf{\Sigma },\mathcal{Q},\left\{q_0\right\},\left\{q_f\right\},{\delta }_0,q_0,q_f\rangle$, where ${\delta }_0$ is the restriction of $\delta$ to $((\mathcal{Q}\setminus {\mathcal{Q}}_t)\times \mathsf{\Sigma })\to {\ell }^2((\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D})$, which is, for each $q\ne q_f$ and $a\in \mathsf{\Sigma }$, we have ${\delta }_0(q,a)(p,b,d)=\delta (q,a)(p,b,d)$, for every $(p,b,d)\in (\mathcal{Q}\setminus {\mathcal{Q}}_s)\times \mathsf{\Sigma }\times \mathbb{D}$. Because the local unitary conditions hold for $\delta$ and, in a B&V-QTM, $\delta (q,a)(q_0,b,d)=0$, when $q\ne q_f$, the unitary local conditions hold for ${\delta }_0$ too.

By construction, if $U_M^i|C\rangle$ is not final for $0\le i<k$, then $|{\varphi }_k\rangle =U_M^k|C\rangle =U_{M^{\prime }}^k|C\rangle$. In particular, this holds when $|{\varphi }_k\rangle$ is the final configuration of the B&V-QTM M.  □

We remark that the inverse cannot hold true: A B&V-QTM for a given input cannot exhibit both a non terminated computation and a terminated one (see Section 5.3 for a machine that cannot be simulated by a B&V-QTM).

3. Quantum Computable Functions

In this section, we address the problem of defining the concept of quantum computable function in an “ideal” way, without taking into account any measurement protocol. The problem of the observation protocol will be addressed in Section 4. Here, we show how each QTM naturally defines a computable function from the sphere of radius 1 in ${\ell }^2\left({\mathfrak{C}}_M\right)$ to the set of (partial) probability distributions on the set of natural numbers.

3.1. Probability Distributions

Definition 10

(Probability distributions).

1. 

A partial probability distribution (PPD) of natural numbers is a function ${\mathbf{P}}_{}:\mathbb{N}\to {\mathbb{R}}_{[0,1]}$ such that ${\sum }_{n\in \mathbb{N}}{\mathbf{P}}_{}\left(n\right)\le 1$.

2. 

If ${\sum }_{n\in \mathbb{N}}{\mathbf{P}}_{}\left(n\right)=1$, ${\mathbf{P}}_{}$ is a probability distribution (PD).

3. 

$\mathbb{P}$ and ${\mathbb{P}}_1$ denote the sets of all the PPDs and PDs, respectively.

4. 

If the set $\{n:{\mathbf{P}}_{}\left(n\right)\ne 0\}$ is finite, ${\mathbf{P}}_{}$ is finite.

5. 

Let ${\mathbf{P}}_{}^{\prime },{\mathbf{P}}_{}^{″}$ be two PPDs, we say that ${\mathbf{P}}_{}^{\prime }\le {\mathbf{P}}_{}^{″}$ (${\mathbf{P}}_{}^{\prime }<{\mathbf{P}}_{}^{″}$) if and only if for each $n\in \mathbb{N}$, ${\mathbf{P}}_{}^{\prime }\left(n\right)\le {\mathbf{P}}_{}^{″}\left(n\right)$ (${\mathbf{P}}_{}^{\prime }\left(n\right)<{\mathbf{P}}_{}^{″}\left(n\right)$).

6. 

Let $\mathcal{P}={\left\{{\mathbf{P}}_i\right\}}_{i\in \mathbb{N}}$ be a denumerable sequence of PPDs; $\mathcal{P}$ is monotone if and only if ${\mathbf{P}}_i\le {\mathbf{P}}_j$, for each $i<j$.

Remark 6.

In the following, we shall also use the notation ${\mathbf{P}}_{}\left(\perp \right)=1-{\sum }_{n\in \mathbb{N}}{\mathbf{P}}_{}\left(n\right)$. By definition, $0\le {\mathbf{P}}_{}\left(\perp \right)\le 1$, and a PPD is a PD if and only if ${\mathbf{P}}_{}\left(\perp \right)=0$. We also stress that ≤ is a partial order of PPDs and that any PD ${\mathbf{P}}_{}$ is maximal w.r.t. to ≤.

Definition 11

(limit of a sequence of PPDs). Let $\mathcal{P}={\left\{{\mathbf{P}}_i\right\}}_{i\in \mathbb{N}}$ be a sequence of PPDs. If, for each $n\in \mathbb{N}$, there exists $l_n={lim}_{i\to \infty }{\mathbf{P}}_i\left(n\right)$, we say that ${lim}_{i\to \infty }{\mathbf{P}}_i={\mathbf{P}}_{}:\mathbb{N}\to {\mathbb{R}}_{[0,1]}$, with ${\mathbf{P}}_{}\left(n\right)=l_n$.

3.2. Monotone Sequences of Probability Distributions

Proposition 1.

Let $\mathcal{P}={\left\{{\mathbf{P}}_i\right\}}_{i\in \mathbb{N}}\subseteq \mathbb{P}$ be a monotone sequence of PPDs.

1. 

${lim}_{i\to \infty }{\mathbf{P}}_i$ exists and it is the supremum $⨆\mathcal{P}$ of $\mathcal{P}$;

2. 

${\sum }_{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)=⨆{\left\{{\sum }_{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}$;

3. 

$⨆\mathcal{P}\in \mathbb{P}$.

Proof. 

Because ${\mathbf{P}}_i\left(n\right)\le 1$, every non-decreasing sequence ${\left\{{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}$ has a supremum $sup{\left\{{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}={lim}_{i\to \infty }{\mathbf{P}}_i\left(n\right)$. Thus, ${lim}_{i\to \infty }{\mathbf{P}}_i$ is defined and ${\mathbf{P}}_i\le {lim}_{i\to \infty }{\mathbf{P}}_i$, for every $i\in \mathbb{N}$. On the other hand, for any ${\mathbf{P}}_{}^{\prime }$ s.t. ${\mathbf{P}}_i\le {\mathbf{P}}_{}^{\prime }$ for $i\in \mathbb{N}$, we have ${lim}_{i\to \infty }{\mathbf{P}}_i\left(n\right)=sup{\left\{{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\le {\mathbf{P}}_{}^{\prime }\left(n\right)$, for every $n\in \mathbb{N}$; namely, ${lim}_{i\to \infty }{\mathbf{P}}_i\le {\mathbf{P}}_{}^{\prime }$. We can then conclude (item 1 of Proposition 1) that $⨆\mathcal{P}={lim}_{i\to \infty }{\mathbf{P}}_i$.

Let us now prove item 2 of Proposition 1. First of all, since $0\le {\mathbf{P}}_i\left(n\right)\le (⨆\mathcal{P})\left(n\right)$ for $i,n\in \mathbb{N}$, we have ${\sum }_{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)\ge sup{\left\{{\sum }_{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}$ and

$$\begin{array}{c}sup{\left\{\sum _{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\ge sup{\left\{\sum _{n\le k}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\hfill \\ \hfill =\sum _{n\le k}sup{\left\{{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}=\sum _{n\le k}(⨆\mathcal{P})\left(n\right)\end{array}$$

for any $k\in \mathbb{N}$. Thus,

$$\begin{array}{c}sup{\left\{\sum _{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\ge sup{\left\{\sum _{n\le k}(⨆\mathcal{P})\left(n\right)\right\}}_{k\in \mathbb{N}}\hfill \\ \hfill =\underset{k\to \infty }{lim}\sum _{n\le k}(⨆\mathcal{P})\left(n\right)=\sum _{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)\end{array}$$

Summing up, we can conclude, as

$$\sum _{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)\ge sup{\left\{\sum _{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\ge \sum _{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)$$

Finally, by hypothesis, ${\sum }_{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\le 1$, for any $i\in \mathbb{N}$. Therefore, ${\sum }_{n\in \mathbb{N}}(⨆\mathcal{P})\left(n\right)=sup{\left\{{\sum }_{n\in \mathbb{N}}{\mathbf{P}}_i\left(n\right)\right\}}_{i\in \mathbb{N}}\le 1$. Which proves (item 3 of Proposition 1) that $⨆\mathcal{P}\in \mathbb{P}$.  □

3.3. PPD Sequence of a Computation

The computed output of a QTM will be defined (Definition 14) as the limit of the sequence of PPDs obtained along its computations.

Definition 12

(probability and q-configurations). Given a configuration $C=\langle \alpha ,q,\beta ,i,n\rangle$, let $\mathbf{val}\left[C\right]$ be the number of 1s in $\alpha \beta$. For any $|\varphi \rangle \in {\ell }^2\left(\mathfrak{C}\right)$, let us define ${\mathbf{P}}_{|\varphi \rangle }:\mathbb{N}\to {\mathbb{R}}_{\ge 0}$ s.t.

$${\mathbf{P}}_{|\varphi \rangle }\left(n\right)=\sum _{C\in {\mathfrak{C}}^{fin},\mathbf{val}\left[C\right]=n}{\left|e_C\right|}^2$$

when $|\varphi \rangle ={\sum }_{C\in \mathfrak{C}}{e}_C|C\rangle$.

Proposition 2.

If $|\varphi \rangle$ is a q-configuration, ${\mathbf{P}}_{|\varphi \rangle }$ is a PPD. Moreover, it is a PD if and only if $|\varphi \rangle$ is final.

Proof. 

Let $|\varphi \rangle =|{\varphi }_0\rangle +|{\varphi }_f\rangle$ with $|{\varphi }_0\rangle \in {\ell }^2({\mathfrak{C}}_M\setminus {\mathfrak{C}}_M^{fin})$, and $|{\varphi }_f\rangle \in {\ell }^2\left({\mathfrak{C}}_M^{fin}\right)$. By the definition of ${\mathbf{P}}_{|\varphi \rangle }$, it is readily seen that ${\mathbf{P}}_{|\varphi \rangle }={\mathbf{P}}_{|{\varphi }_f\rangle }$ and that ${\sum }_{n\in \mathbb{N}}{\mathbf{P}}_{|\varphi \rangle }\left(n\right)={\sum }_{n\in \mathbb{N}}{\mathbf{P}}_{|{\varphi }_f\rangle }\left(n\right)=\parallel |{\varphi }_f\rangle \parallel \le 1$. Therefore, ${\mathbf{P}}_{|\varphi \rangle }$ is a PPD. Moreover, since $\parallel |{\varphi }_f\rangle \parallel =1$ if and only if $\parallel |{\varphi }_0\rangle \parallel =0$. We see that ${\mathbf{P}}_{|\varphi \rangle }$ is a PD if and only if $|{\varphi }_0\rangle =0$, that is, if and only if $|\varphi \rangle =|{\varphi }_f\rangle$.  □

Definition 13.

For any q-configuration $|\varphi \rangle$, we shall say that ${\mathbf{P}}_{|\varphi \rangle }$ is the PPD associated to $|\varphi \rangle$, and we shall denote by ${\mathbf{P}}_{K_{|\varphi \rangle }^M}$ the sequence of PPDs ${\left\{{\mathbf{P}}_{|{\varphi }_i\rangle }\right\}}_{i\in \mathbb{N}}$ associated to the computation $K_{|\varphi \rangle }^M=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$.

The PPD sequence of any QTM computation is monotone. In the simple proof of this key property (Theorem 3) we see at work all of the constraints on the time evolution of a QTM M.

1.

That when in a final (target) configuration, the machine can only increment the counter; as a consequence, the $\mathbf{val}$ of final (target) configurations does not change.

2.

That when entering for the first time into a final (target) state, the value of the counter is initialised to 0.

3.

That when in a final (target) configuration $|\varphi ,n\rangle$, the counter gives the number of steps n since M is looping into the plain configuration $\varphi$.

We stress that the last two properties defuse quantum interference between final configurations reached in a different number of steps.

Theorem 3

(monotonicity of computations). For any computation $K_{|\varphi \rangle }^M$ of a QTM M, the sequence of PPDs ${\mathbf{P}}_{K_{|\varphi \rangle }^M}$ is monotone.

Proof. 

Let us prove that ${\mathbf{P}}_{|\varphi \rangle }\le {\mathbf{P}}_{U|\varphi \rangle }$, for every $|\varphi \rangle \in {\ell }^2\left({\mathfrak{C}}_M\right)$. Let $|\varphi \rangle =|{\varphi }_0\rangle +{\sum }_{k\in \mathbb{N}}|{\varphi }_{f,k}\rangle$, with $|{\varphi }_0\rangle \in {\ell }^2({\mathfrak{C}}_M\setminus {\mathfrak{C}}_M^{fin})$, and $|{\varphi }_{f,k}\rangle \in {\ell }^2({\mathfrak{C}}_M^{fin}\cap {\mathfrak{C}}_M^k)$, where ${\mathfrak{C}}_M^k$ is the set of the configurations of M whose counter is equal to $k\in \mathbb{N}$. For every $n\in \mathbb{N}$, we see that ${\mathbf{P}}_{|\varphi \rangle }\left(n\right)={\sum }_{k\in \mathbb{N}}{\mathbf{P}}_{|{\varphi }_{f,k}\rangle }\left(n\right)$. Let $|\psi \rangle =|{\psi }_0\rangle +{\sum }_{k\in \mathbb{N}}|{\psi }_{f,k}\rangle =U|\varphi \rangle$. By the definition of U, we see that $U|{\varphi }_0\rangle =|{\psi }_0\rangle +|{\psi }_{f,0}\rangle$ and $U|{\varphi }_{f,k}\rangle =|{\psi }_{f,k+1}\rangle$. Therefore, ${\mathbf{P}}_{|\psi \rangle }\left(n\right)={\sum }_{k\in \mathbb{N}}{\mathbf{P}}_{|{\psi }_{f,k}\rangle }\left(n\right)={\mathbf{P}}_{|{\psi }_{f,0}\rangle }\left(n\right)+{\sum }_{k\in \mathbb{N}}{\mathbf{P}}_{|{\varphi }_{f,k}\rangle }\left(n\right)={\mathbf{P}}_{|{\psi }_{f,0}\rangle }\left(n\right)+{\mathbf{P}}_{|\varphi \rangle }\left(n\right)\ge {\mathbf{P}}_{|\varphi \rangle }\left(n\right)$.  □

3.4. Computed Output

We can now come back to the definition of the computed output of a QTM computation. The easy case is when a computation reaches a final q-configuration $|\psi \rangle \in {\mathfrak{C}}^{fin}$ (meaning that all of the classical computations in superposition are “terminated”)—in this case the computed output is the PD ${\mathbf{P}}_{|\psi \rangle }$. The QTM keeps computing and transforming $|\psi \rangle$ into other configurations, but all of these configurations have the same PD. However, we want to give meaning also to infinite” computations, which never reach a final q-configuration, yet producing some final configurations in the superpositions. For this purpose, we define the computed output as the limit of the PPDs yielded by the computation.

Definition 14

(computed output of a QTM). Let $K_{|\varphi \rangle }^M=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ be the computation of the QTM M on the initial q-configuration $|\varphi \rangle$. The computed output of M on the initial q-configuration $|\varphi \rangle$ is the PPD ${\mathbf{P}}_{}={lim}_{i\to \infty }{\mathbf{P}}_{|{\varphi }_i\rangle }$, which we shall also denote by $lim{K}_{|\varphi \rangle }^M$, or by the notation $M_{|\varphi \rangle }\to {\mathbf{P}}_{}$.

Let us remark that, by Proposition 1 and Theorem 3, the limit in the above definition is well-defined for any computation. Therefore, a QTM has a computed output for any initial q-configuration $|\varphi \rangle$.

Definition 15

(finitary computations). Given a QTM M, a q-configuration $|\varphi \rangle$ is finite if it is an element of $\mathsf{span}\left(\mathsf{CB}\left({\mathfrak{C}}_{\mathsf{M}}\right)\right)$. A computation $K_{|\varphi \rangle }^M=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ is finitary with computed output ${\mathbf{P}}_{}$ if there exists a k s.t. $|{\varphi }_k\rangle$ is final and ${\mathbf{P}}_{|{\varphi }_k\rangle }={\mathbf{P}}_{}$.

Proposition 3.

Let $K_{|\varphi \rangle }^M=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ be a finitary computation with computed output ${\mathbf{P}}_{}$, which is, $M_{|\varphi \rangle }\to {\mathbf{P}}_{}$.

1. 

There exists a k, such that, for each $j\ge k$, $|{\varphi }_j\rangle$ is final and ${\mathbf{P}}_{|{\varphi }_j\rangle }={\mathbf{P}}_{}$.

2. 

${\mathbf{P}}_{}$ is a PD.

Proof. 

By definition, there is a k s.t. $|{\varphi }_k\rangle$ is final. Let ${\mathbf{P}}_{|{\varphi }_k\rangle }={\mathbf{P}}_{}$. By Proposition 2, ${\mathbf{P}}_{}$ is a PD. By monotonicity, ${\mathbf{P}}_{}\le {\mathbf{P}}_{|{\varphi }_j\rangle }$, for every $j\ge k$. Thus, because any PD is maximal for ≤ (see Remark 6), ${\mathbf{P}}_{}={\mathbf{P}}_{|{\varphi }_j\rangle }$, for every $j\ge k$.  □

Given a computation $K_{|\varphi \rangle }^M$, we can then distinguish the following cases:

1.

$K_{|\varphi \rangle }^M$ is finitary. In this case, $M_{|\varphi \rangle }\to {\mathbf{P}}_{}\in {\mathbb{P}}_1$; the output of the computation is then a PD and is determined after a finite number of steps;

2.

$K_{|\varphi \rangle }^M$ is not finitary, but $M_{|\varphi \rangle }\to {\mathbf{P}}_{}\in {\mathbb{P}}_1$. The output is a PD and is determined as a limit; and,

3.

$K_{|\varphi \rangle }^M$ is not finitary, and $M_{|\varphi \rangle }\to {\mathbf{P}}_{}\in \mathbb{P}\setminus {\mathbb{P}}_1$ (the sum of the probabilities of observing natural numbers is $p<1$). Not only the result is determined as a limit, but we cannot extract a PD from the output.

The first two cases above give rise to what Definition 16 calls a q-total function. However, observe that, for an external observer, cases (2) and (3) are in general indistinguishable, since, at any finite stage of the computation, we may only observe a finite part of the computed output.

For some examples of QTMs and their computed output, see Section 5.

3.5. Quantum Partial Computable Functions

We want our quantum computable functions to be defined over a natural extension of the natural numbers. When using a QTM for computing a function, we stipulate that initial q-configurations are superpositions of initial classical (plain) configurations $|C_n\rangle$, where the tape of the configuration $C_n$ encodes the number n. A natural choice for this encoding corresponds to take $C_n=|\underline{n}\rangle =|\langle \lambda ,q_0,\underline{n},0,0\rangle \rangle$, where $\underline{n}$ denotes the string $1^{n+1}$. Such q-configurations are naturally isomorphic to the space ${\ell }_1^2\left(\mathbb{N}\right)=\left\{\varphi :\mathbb{N}\to \mathbb{C}\mid {\sum }_{n\in \mathbb{N}}{\left|\varphi \left(n\right)\right|}^2=1\right\}$ of square summable, denumerable sequences with unitary norm, under the bijective mapping $\nu (\sum d_k{n}_k)=\sum d_k|\underline{n_k}\rangle$. Observe that, for output, we simply count the number of (non contiguous) 1s on the tape, according to Definition 12.

Definition 16

(partial quantum computable functions).

1. 

A function $f:{\ell }_1^2\to \mathbb{P}$ is partial quantum computable (q-computable) if there exists a QTM M s.t. $f\left(\mathbf{x}\right)={\mathbf{P}}_{}$ if and only if $M_{\nu \left(\mathbf{x}\right)}\to {\mathbf{P}}_{}$.

2. 

A q-partial computable function f is quantum total (q-total) if for each $\mathbf{x}$, $f\left(\mathbf{x}\right)\in {\mathbb{P}}_1$.

It is out of the scope of the paper to investigate in details how this class exactly relates to other classes of computable functions when the input of QTMs is restricted to classical inputs. However, observe, that when the output is also required to be classical, and all amplitudes are computable, we expect to obtain the classical (partial) recursive functions. Indeed, any classical deterministic TM may be simulated by a reversible TM [19]; moreover, B&V show that reversible TMs are a special case of QTMs (Section 4 of [12]; see also our Section 5.2). On the other direction, when we have classical inputs and computable amplitudes, it is easy to simulate a QTM via a classical TM.

4. Observables

While the evolution of a closed quantum system (e.g., a QTM) is reversible and deterministic once its evolution operator is known, a (global) measurement of a q-configuration is an irreversible process, which causes the collapse of the quantum state to a new state. Technically, a measurement corresponds to a projection on a subspace of the Hilbert space of quantum states. For the sake of simplicity, in the case of QTMs, let us restrict to measurements observing if a configuration belongs to the subspace described by some set of base configurations $\mathcal{B}$. The effect of such a measurement is summarised by the following:

Measurement

Given a set of configurations $\mathcal{B}\subseteq \mathfrak{C}$, a measurement observing if a quantum configuration $|\varphi \rangle ={\sum }_{C\in \mathfrak{C}}{e}_C|C\rangle$ belongs to the subspace generated by $\mathsf{CB}\left(\mathcal{B}\right)$ gives a positive answer with a probability $p={\sum }_{C\in \mathcal{B}}{\left|e_C\right|}^2$, equal to the square of the norm of the projection of $|\varphi \rangle$ onto ${\ell }^2\left(\mathcal{B}\right)$, causing at the same time a collapse of the configuration into the normalised projection ${\sum }_{C\in \mathcal{B}}{p}^{-\frac{1}{2}}{e}_C|C\rangle$; dually, with probability $1-p={\sum }_{C\notin \mathcal{B}}{\left|e_C\right|}^2$, it gives a negative answer and a collapse onto the subspace ${\ell }^2(\mathfrak{C}\setminus \mathcal{B})$ orthonormal to ${\ell }^2\left(\mathcal{B}\right)$, which is, into the normalised configuration ${\sum }_{C\notin \mathcal{B}}{(1-p)}^{-\frac{1}{2}}{e}_C|C\rangle$,

This kind of measurement is a special case of the so called projective measurement that is a consequence of the postulates of quantum mechanics. For a detailed discussion, see e.g., [8,20].

Because of the irreversible modification produced by any measurement on the current configuration and, therefore, on the rest of the computation, we must deal with the problem of how to read the result of a computation. In other words, we need to establish some protocol to observe when a QTM has eventually reached a final configuration, and to read the corresponding result.

4.1. The Approach of Bernstein and Vazirani

We already discussed how B&V’s “sensible” QTMs are machines where all of the computations in superposition are in some sense terminating, and reach the final state at the same time (are “stationary”, in their terminology). More precisely, Definition 3.11 of B&V reads: “A final configuration of a QTM is any configuration in [final] state. If, when QTM M is run with input x, at time T the superposition contains only final configurations, and at any time less than T the superposition contains no final configuration, then M halts with running time T on input x.”

This is a good definition for a theory of computational complexity (where the problems are classical, and the inputs of QTMs are always classical) but it is of limited use in the semantics of quantum programming languages. Indeed, inputs of a B&V-QTM must be classical—we cannot extend by linearity a B&V-QTM on inputs in ${\ell }_1^2$, since there is no guarantee whatsoever that on different inputs the same QTM halts with the same running time.

4.2. The Approach of Deutsch

Deutsch [10] assumes that QTMs are enriched with a termination bit T. At the beginning of a computation, T is set to 0, then, the machine sets this termination bit to 1 when it enters into a final configuration. If we write $|T=i\rangle$ for the function that returns 1 when the termination bit is set to i, and 0 otherwise, a generic q-configuration of a Deutsch’s QTM can be written as

$$|\varphi \rangle =|T=0\rangle \otimes \sum _{C\notin {\mathfrak{C}}^{fin}}{e}_C|C\rangle +|T=1\rangle \otimes \sum _{D\in {\mathfrak{C}}^{fin}}{d}_D|D\rangle$$

The observer periodically measures T in a non destructive way (that is, without modifying the rest of the state of the machine).

1.

If the result of the measurement of T gives the value 0, $|\varphi \rangle$ collapses (with a probability equal to ${\sum }_{C\notin {\mathfrak{C}}^{fin}}{\left|e_C\right|}^2$) to the q-configuration

$$|{\psi }^{\prime }\rangle =\frac{|T=0\rangle \otimes {\sum }_{C\notin {\mathfrak{C}}^{fin}}{e}_C|C\rangle }{\sqrt{{\sum }_{C\notin {\mathfrak{C}}^{fin}}{\left|e_C\right|}^2}}$$

and the computation continues with $|{\psi }^{\prime }\rangle$.

2.

If the result of the measurement of T gives the value 1, $|\varphi \rangle$ collapses (with probability ${\sum }_{D\in {\mathfrak{C}}^{fin}}{\left|d_D\right|}^2$) to

$$|{\psi }^{″}\rangle =\frac{|T=1\rangle \otimes {\sum }_{D\in {\mathfrak{C}}^{fin}}{d}_D|D\rangle }{\sqrt{{\sum }_{D\phantom{\neg }\in {\mathfrak{C}}^{fin}}{\left|d_D\right|}^2}}$$

and, immediately after the collapse, the observer makes a further measurement of the component ${\displaystyle \frac{{\sum }_{D\in {\mathfrak{C}}^{fin}}{d}_D|D\rangle }{\sqrt{{\sum }_{D\in {\mathfrak{C}}^{fin}}{\left|d_D\right|}^2}}}$ in order to read-back a final configuration.

Note that Deutsch’s protocol (in an irreversible way) spoils at each step the superposition of configurations. The main point of Deutsch’s approach is that a measurement must be performed immediately after some computation enters into a final state. In fact, since, at the following step, the evolution might lead the machine to exit the final state modifying the content of the tape, we would not be able to measure this output at all. In other words, either the termination bit acts as a trigger that forces a measurement each time it is set, or we perform a measurement after each step of the computation.

4.3. Problems with Deutsch Measurement

Because a QTM must be physically feasible, at least “in principle”, let us analyse, in detail, whether the termination protocol proposed by Deutsch [10] is realizable.

As any quantum system, a QTM evolves with respect to a continuos time. This means that the time evolution operator U of a machine M is the solution of the Schrödinger equation with a given Hamiltonian H and depends on the time [21]. In particular, when H is constant, the solution of the equation is

$$U_t=e^{-(i/h)Ht}\mathrm{for}t\in {\mathbb{R}}^{+}$$

Now, let $\Delta$ be the duration of a single step of a Deutsch QTM. This means that after n steps of the QTM, we are at time $t=n\Delta$, and that for the corresponding configurations $|{\psi }_n\rangle$ of the QTM, it holds the following property

$$\begin{array}{cc}\hfill |{\psi }_{n+1}\rangle & =U_{(n+1)\Delta }|{\psi }_0\rangle \hfill \\ \hfill & =e^{-(i/h)H(n+1)\Delta }|{\psi }_0\rangle =e^{-(i/h)H\Delta }{e}^{-(i/h)Hn\Delta }|{\psi }_0\rangle =U_{\Delta }{U}_{n\Delta }|{\psi }_0\rangle \hfill \\ \hfill & =U_{\Delta }|{\psi }_n\rangle \hfill \end{array}$$

In other words, at each step n, the next configuration $|{\psi }_{n+1}\rangle$ is obtained by applying the evolution operator $U_{\Delta }$ to the current configuration $|{\psi }_n\rangle$.

Now, let us suppose that, as a consequence of the measurement of the halt qubit T, after n steps, and, therefore, at time $t_n=n\Delta$, the system collapses to the quantum configuration

$$|{\psi }_n\rangle =\frac{|T=1\rangle \otimes {\sum }_{D\in {\mathfrak{C}}^{fin}}{d}_D|D\rangle }{\sqrt{{\sum }_{D\phantom{\neg }\in {\mathfrak{C}}^{fin}}{\left|d_D\right|}^2}}$$

According to Deutsch’s approach, one has to perform a second measurement to read the actual value of the output on the tape. However, since we are in a continuous time setting, what is the time of this second measurement? Since it can be done only after the measure of the halt qubit T, this must take place at a time $t_{n+ϵ}=(n+ϵ)\Delta$, with $ϵ>0$. We can distinguish two cases (analogous reasonings apply for $ϵ>1$):

1.

$0<ϵ<1$. In this case, the tape is measured at an intermediate time between $t_n$ and $t_{n+1}$, and the machine is in an intermediate configuration $|{\psi }_{n+ϵ}\rangle$ between $|{\psi }_n\rangle$ and $|{\psi }_{n+1}\rangle$. Because the QTM is defined in terms of the unitary operator $U_{\Delta }$, its configurations are well-defined only at time $t_n$, for $n\in \mathbb{N}$. The quantum configuration $|{\psi }_{n+ϵ}\rangle$ is therefore unknown and depends on how the unitary operator $U_{\Delta }$ is physically realised. In any case, in general it differs from $|{\psi }_n\rangle$.

2.

$ϵ=1$. In this case the second measurement takes place at time $t_{n+1}$, on the configuration $|{\psi }_{n+1}\rangle =U_{\Delta }|{\psi }_n\rangle$. That implies $|{\psi }_n\rangle \ne |{\psi }_{n+1}\rangle$, since $|{\psi }_n\rangle =|{\psi }_{n+1}\rangle$ may hold only in the trivial case the unitary operator $U_{\Delta }$ is the identity and the $|{\psi }_n\rangle =|{\psi }_0\rangle$, for every n.

As a consequence, without additional restrictions on its evolution operator, Deutsch’s approach does not allow for extracting the result of the computation of a QTM.

4.4. Fixing the Measurement Protocol

Ozawa was the first to notice the above problem. In [13], he gave a revised formulation of the measurement protocol:

Once the halt qubit is set to the state $|T=1\rangle$, the quantum Turing machine no longer changes the halt qubit or the tape string.

However, since such a constraint would be too strong (as already remarked, if $|{\psi }_{n+\Delta }\rangle =|{\psi }_n\rangle$, then $U_{\Delta }$ must be the identity), Ozawa adds the footnote 11:

If the relevant outcome of the computation is designed to be written by the program in a restricted part of the tape, this condition can be weakened so that the quantum Turing machine may change the part of the tape string except that part of the tape.

In other words, instead of requiring that all tape stays unchanged after reaching a final configuration, only the interesting part of the output must become stable after the halt qubit is set to 1.

Unfortunately, Linden and Popescu maybe skipped that note, and in their unpublished paper [22] claimed that even Ozawa’s was unsatisfactory. Accordingly, a few years later, Ozawa replied harshly in [23]:

Recently, Linden and Popescu [22] claimed that the halt scheme given in [13] is not consistent with unitarity of the evolution operator. However, their argument applies only to the special case in which the whole tape is required not to change after the halt. As suggested in footnote 11 of [13], the conclusion in [13] can be obtained from the weaker condition for the general case where the tape is allowed to change except for the data slot. Linden and Popescu [22] disregarded this case and hence their conclusion is not generally true.

Although Ozawa was right, he did not explain how to stabilise what he called the data slot. The approach that we shall present in the following is then a sort of implementation of Ozawa’s protocol, for which we also prove in details the irrelevance of the number of executed measurements and of the measurement time.

4.5. Our Approach

The measurement of the output computed by our QTMs can be performed by following a variant of Deutsch’s approach. Because of the particular structure of the transition function of our QTMs, we shall see that we do not need any additional termination bit, that a measurement can be performed at any moment of the computation, and that, indeed, we can perform several measurements at distinct points of the computation without altering the result (in terms of the probabilistic distribution of the observed output).

Given a q-configuration $|\varphi \rangle =|{\varphi }_f\rangle +|{\varphi }_{nf}\rangle$, where $|{\varphi }_f\rangle \in {\ell }^2\left({\mathfrak{C}}^{fin}\right)$ and $|{\varphi }_{nf}\rangle \in {\ell }^2(\mathfrak{C}\setminus {\mathfrak{C}}^{fin})$, our output measurement tries to get an output value from $|\varphi \rangle$ by the following procedure:

1.

first of all, we observe the final states of $|\varphi \rangle$, forcing the q-configuration to collapse either into the final q-configuration $|{\varphi }_f\rangle /\parallel |{\varphi }_f\rangle \parallel$, or into the q-configuration $|{\varphi }_{nf}\rangle /\parallel |{\varphi }_{nf}\rangle \parallel$, which does not contain any final configuration;

2.

then, if the q-configuration collapses into $|{\varphi }_f\rangle /\parallel |{\varphi }_f\rangle \parallel$, we observe one of these configurations, say $|C\rangle$, which gives us the observed output $\mathbf{val}\left[C\right]=n$, forcing the q-configuration to collapse into the final base q-configuration $(e_c/|e_c\left|\right)|C\rangle$;

3.

otherwise, we leave unchanged the q-configuration $|{\varphi }_{nf}\rangle /\parallel |{\varphi }_{nf}\rangle \parallel$ obtained after the first observation, and we say that we have observed the special value ⊥.

Summing up, an output measurement of $|\varphi \rangle$ may lead to observe an output value $n\in \mathbb{N}$ associated to a collapse into a base final configuration $|C\rangle \in |\varphi \rangle$ s.t. $\mathbf{val}\left[\varphi \right]=n$ or to observe the special value ⊥ associated to a collapse into a q-configuration, which does not contain any final configuration.

Definition 17

(output observation). An output observation with collapsed q-configuration $|\psi \rangle$ and observed output $x\in \mathbb{N}\cup \left\{\perp \right\}$ is the result of an output measurement of the q-configuration $|\varphi \rangle ={\sum }_{C\in \mathfrak{C}}{e}_C|C\rangle$. Therefore, it is a triple ${|\varphi \rangle \downarrow }_x|\psi \rangle$ s.t.

1. 

either $x=n\in \mathbb{N}$, and

$$|\psi \rangle =\frac{e_C}{|e_C|}|C\rangle withC\in {\mathfrak{C}}^{fin}and\mathbf{val}\left[C\right]=n and e_c\ne 0$$

2. 

or $x=\perp$, and

$$|\psi \rangle =\frac{|{\varphi }_{nf}\rangle }{\parallel |{\varphi }_{nf}\rangle \parallel }where|{\varphi }_{nf}\rangle =\sum _{C\notin {\mathfrak{C}}^{fin}}{e}_C|C\rangle and |{\varphi }_{nf}\rangle \ne 0$$

The probability of an output observation is defined by

$${\mathsf{Pr}\left\{\right|\varphi \rangle \downarrow }_x|\psi \rangle \}=\left\{\begin{array}{cc}|e_C{|}^2\hfill & ifx=n\in \mathbb{N}\hfill \\ \parallel |{\varphi }_{nf}{\rangle \parallel }^2\hfill & ifx=\perp \hfill \end{array}\right.$$

Remark 7.

For $e\in \mathbb{C}$, ${e|C\rangle \downarrow }_x|\varphi \rangle$, with $C\in {\mathfrak{C}}^{fin}$ and $\mathbf{val}\left[C\right]=n$. Since $e|C\rangle$ is a q-configuration, $\left|e\right|=1$. By the definition of output observation, $x=n$ and $|\varphi \rangle =(e/\left|e\right|\left)U\right|C\rangle =e|D\rangle$, with $|D\rangle =U|C\rangle \in \mathsf{CB}\left({\mathfrak{C}}^{fin}\right)$ and $\mathbf{val}\left[D\right]=n$. Moreover, ${\mathsf{Pr}\left\{e\right|C\rangle \downarrow }_x|\varphi \rangle \}={\left|e\right|}^2=1$.

Remark 8.

For every pair ${|\varphi \rangle \downarrow }_{x_1}|{\psi }_1\rangle$ and ${|\varphi \rangle \downarrow }_{x_2}|{\psi }_2\rangle$ of distinct output observations, ${\psi }_1$ and ${\psi }_2$ are in the orthonormal subspaces generated by the two disjoint sets ${\mathcal{B}}_1,{\mathcal{B}}_2\subseteq \mathfrak{C}$, where ${\mathcal{B}}_i=\{C\in \mathfrak{C}\mid |C\rangle \in |{\psi }_i\rangle \}$.

Definition 18

(observed run). Let M be a QTM and $U_M$ be its time evolution operator. For any monotone increasing function $\tau :\mathbb{N}\to \mathbb{N}$ (that is, $\tau \left(i\right)<\tau \left(j\right)$ for $i<j$):

1. 

a$\tau$-observed runof M on the initial q-configuration $|\varphi \rangle$ is a sequence $\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ s.t.:

(a) 

$|{\varphi }_0\rangle =|\varphi \rangle$;

(b) 

$U_M|{\varphi }_h{\rangle \downarrow }_{x_i}|{\varphi }_{h+1}\rangle$, when $h=\tau \left(i\right)$ for some $i\in \mathbb{N}$;

(c) 

$|{\varphi }_{h+1}\rangle =U_M|{\varphi }_h\rangle$ otherwise.

2. 

Afinite $\tau$-observed runof length k is any finite prefix of length $k+1$ of some τ-observed run. Notation: if $R=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$, then $R\left[k\right]=\left\{\right|{\varphi }_i\rangle {\}}_{i\le k}$.

In particular, let $id$ be the identity function on $\mathbb{N}$. In the corresponding $id$-observed run, a measurement of the tape is performed after each step of the machine.

Remark 9.

We stress that, given a τ-observed run $R=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}:$

1. 

either it never obtains a value $n\in \mathbb{N}$ as the result of an output observation, and then it never reaches a final configuration; and,

2. 

or it eventually obtains such a value collapsing the q-configuration into a base final configuration $e|C\rangle$ s.t. $\left|e\right|=1$ and $\mathbf{val}\left[C\right]=n$, and from that point onward all the configurations of the run are base final configurations $e|C_j\rangle =e{U}^j|C\rangle$ s.t. $\mathbf{val}\left[C_j\right]=n$, and all the following observed outputs are equal to n (see Remark 7).

Definition 19.

Let $R=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ be a τ-observed run.

1. 

The sequence ${\left\{x_i\right\}}_{i\in \mathbb{N}}$ s.t. $|{\varphi }_h{\rangle \downarrow }_{x_i}|{\varphi }_{h+1}\rangle$, with $h=\tau \left(i\right)$, is the output sequence of the τ-observed run R.

2. 

The observed output of R is the value $x\in \mathbb{N}\cup \left\{\perp \right\}$ (notation: ${R\downarrow }_x$) defined by:

(a) 

$x=n\in \mathbb{N}$, if $x_i=n$ for some $i\in \mathbb{N}$;

(b) 

$x=\perp$ otherwise.

3. 

For any k, the output sequence of the finite τ-observed run $R\left[\tau \right(k)+1]$ is the finite sequence ${\left\{x_i\right\}}_{i\le k}$ and $x_k$ is its observed output.

Definition 20

(probability of a run). Let $R=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ be a τ-observed run.

1. 

For $k\in \mathbb{N}$, the probability of the finite τ-observed run $R\left[k\right]$ is inductively defined by

(a) 

$\mathsf{Pr}\left\{R\right[0\left]\right\}=1$;

(b) 

$\mathsf{Pr}\left\{R[k+1]\right\}=\left\{\begin{array}{cc}\mathsf{Pr}\left\{R\left[k\right]\right\}\mathsf{Pr}\left\{\right|{\varphi }_k\rangle {\downarrow }_{x_i}|{\varphi }_{k+1}\rangle \}\hfill & when k=\tau \left(i\right) for some i\in \mathbb{N}\hfill \\ \mathsf{Pr}\left\{R\right[k\left]\right\}\hfill & otherwise\hfill \end{array}\right.$

2. 

$\mathsf{Pr}\left\{R\right\}={lim}_{k\to \infty }\mathsf{Pr}\left\{R\left[k\right]\right\}$.

We remark that $\mathsf{Pr}\left\{R\right\}$ is well-defined, since $1\ge \mathsf{Pr}\left\{R\right[i\left]\right\}\ge \mathsf{Pr}\left\{R\right[j\left]\right\}>0$, for every $i\le j$. Therefore,

$$1\ge \mathsf{Pr}\left\{R\right\}=\underset{k\to \infty }{lim}\mathsf{Pr}\left\{R\left[k\right]\right\}=inf{\left\{\mathsf{Pr}\left\{R\left[k\right]\right\}\right\}}_{k\in \mathbb{N}}\ge 0.$$

Remark 10.

Let $R=\left\{\right|{\varphi }_i\rangle {\}}_{i\in \mathbb{N}}$ be a τ-observed run s.t. ${R\downarrow }_n$, for some $n\in \mathbb{N}$. As observed in Remark 9, for some k, we have ${R\left[\tau \left(k\right)\right]\downarrow }_n$ and ${R\left[\tau \left(j\right)\right]\downarrow }_{\perp }$, for $j<k$; moreover, for $i>\tau \left(k\right)$, $|{\varphi }_i\rangle =e|C_i\rangle$ with $\left|e\right|=1$, $C_i\in {\mathfrak{C}}^{fin}$, and $\mathbf{val}\left[C_i\right]=n$. As a consequence, $\mathsf{Pr}\left\{R\right[\tau \left(k\right)+1\left]\right\}=\mathsf{Pr}\left\{R\right[i\left]\right\}$, for any $i>\tau \left(k\right)$ (since, by Remark 7, $\mathsf{Pr}\left\{\right|{\varphi }_{\tau \left(i\right)}\rangle {\downarrow }_n|{\varphi }_{\tau \left(i\right)+1}\rangle \}=1$) and $\mathsf{Pr}\left\{R\right\}={lim}_{i\to \infty }R\left[i\right]=\mathsf{Pr}\left\{R[\tau \left(k\right)+1]\right\}$.

Definition 21

(observed computation). The$\tau$-observed computationof a QTM M on the initial q-configuration $|\varphi \rangle$, is the set ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$ of the τ-observed runs of M on $|\varphi \rangle$ with the measure $\mathsf{Pr}:\mathcal{P}\left({\mathcal{K}}_{|\varphi \rangle ,\tau }^M\right)\to \mathbb{C}$ (where $\mathcal{P}\left({\mathcal{K}}_{|\varphi \rangle ,\tau }^M\right)$ is the set of the subsets of ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$) defined by

$$Pr\mathcal{B}=\sum _{R\in \mathcal{B}}\mathsf{Pr}\left\{R\right\}$$

for every $\mathcal{B}\subseteq {\mathcal{K}}_{|\varphi \rangle ,\tau }^M$.

By $\mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M$ we shall denote the set of the finite $\tau$-observed runs of length k of M on $|\varphi \rangle$, with the measure $\mathsf{Pr}$ on its subsets (see Definition 21).

It is immediate to observe that the set ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$ naturally defines an infinite tree labelled with q-configurations, where each infinite path starting from the root $|\varphi \rangle$ corresponds to a $\tau$-observed run in ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$.

Lemma 1.

Given $R_1,R_2\in {\mathcal{K}}_{|\varphi \rangle ,\tau }^M$ with $R_1={\left\{{\varphi }_{1,i}\right\}}_{i\in \mathbb{N}}\ne {\left\{{\varphi }_{2,i}\right\}}_{i\in \mathbb{N}}=R_2$, there is $k\ge 0$ s.t.

1. 

${\varphi }_{1,i}={\varphi }_{2,i}$ for $i\le \tau \left(k\right)$, that is, $R_1\left[\tau \left(k\right)\right]=R_2\left[\tau \left(k\right)\right]$;

2. 

for $i>\tau \left(k\right)$, the q-configurations ${\varphi }_{1,i}\ne {\varphi }_{2,i}$ are in two orthonormal subspaces generated by two distinct subsets of $\mathfrak{C}$.

Proof. 

Let $R_1\left[h\right]=R_2\left[h\right]$ be the longest common prefix of $R_1$ and $R_2$. Because they both starts with $|\varphi \rangle$, such a prefix is not empty; moreover, by the definition of $\tau$-observed run, it is readily seen that $h=\tau \left(k\right)$, for some k.

Let us now prove item 2 of Lemma 1. If we take ${\mathcal{B}}_{a,j}=\{C\in \mathfrak{C}\mid |C\rangle \in |{\psi }_{a,h+1+j}\rangle \}$, for $a=1,2$ and $j\in \mathbb{N}$, we need to prove that ${\mathcal{B}}_{1,j}\cap {\mathcal{B}}_{2,j}=\varnothing$, for every j. By construction, ${\varphi }_{1,h+1}\ne {\varphi }_{2,h+1}$ and, for $a=1,2$, ${\varphi }_h{\downarrow }_{x_a}{\varphi }_{a,h+1}$, for some $x_a$, with ${\varphi }_h={\varphi }_{a,h}$. Moreover, ${\mathcal{B}}_{1,0}\cap {\mathcal{B}}_{2,0}=\varnothing$ (see Remark 8), at least one of the two observed values $x_1,x_2$ is not ⊥, and one of the two q-configurations $|{\varphi }_{1,h+1}\rangle ,|{\varphi }_{2,h+1}\rangle$ is a final base q-configuration. W.l.o.g., let us assume that $x_1\in \mathbb{N}$ and let $|{\varphi }_{1,h+1}\rangle =e|C,n\rangle$, for some final plain configuration C and some $n\in \mathbb{N}$. Subsequently, $|{\varphi }_{1,h+1+j}\rangle =e{U}^j|C,n\rangle =e|C,n+j\rangle$ (see Remark 9) and ${\mathcal{B}}_{1,j}=\left\{\right|C,n+j\rangle \}$, for $j\in \mathbb{N}$. Thus, to prove the assertion, it suffices to show that $|C,n+j\rangle \notin {\mathcal{B}}_{2,j}$, for $j\in \mathbb{N}$. Let us distinguish two cases:

1.

$x_2\in \mathbb{N}$ and $|{\psi }_{2,h+1}\rangle =e^{\prime }|D,m\rangle$, where D is a final plain configuration and $m\in \mathbb{N}$. As already seen for $|{\psi }_{1,h+1+j}\rangle$, for $j\in \mathbb{N}$, we have $|{\psi }_{2,h+1+j}\rangle =e^{\prime }{U}^j|D,m\rangle =e^{\prime }|D,m+j\rangle$ and ${\mathcal{B}}_{2,j}=\left\{\right|D,m+j\rangle \}$. Therefore, $|C,n+j\rangle \notin {\mathcal{B}}_{2,j}$, since $|C,n+j\rangle \ne |D,m+j\rangle$, for $|C,n\rangle \ne |D,m\rangle$ by construction.

2.

$|{\psi }_{2,h+1}\rangle \in {\ell }^2(\mathfrak{C}\setminus {\mathfrak{C}}^{fin})$. Let $|D,m\rangle \in {\mathcal{B}}_{2,j}\cap {\mathfrak{C}}^{fin}$, where D is a plain configuration and $m\in \mathbb{N}$. By induction on j, it is readily seen that $m<j\le n+j$. Thus, $|D,m\rangle \ne |C,n+j\rangle$.

 □

Lemma 2.

Let $K_{|\varphi \rangle }^M={\left\{{\varphi }_i\right\}}_{i\in \mathbb{N}}$ be the computation of the QTM M on the initial q-configuration $|\varphi \rangle$ and ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$ be the τ-observed computation on the same initial configuration. For every $k\in \mathbb{N}$, we have that

$$|{\varphi }_k\rangle =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R\right\}}|{\psi }_R\rangle$$

where $|{\psi }_R\rangle$ is the last q-configuration of the finite run R of length k.

Proof. 

By definition, $\varphi ={\varphi }_0$ and $R=\left\{\varphi \right\}$ with $\mathsf{Pr}\left\{R\right\}=1$, and ${\psi }_R=\varphi$ is the only run of length 0 in ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$. Therefore, the assertion trivially holds for $k=0$.

Let us then prove the assertion by induction on k. By definition and the induction hypothesis

$$|{\varphi }_{k+1}\rangle =U_M|{\varphi }_k\rangle =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R\right\}}{U}_M|{\psi }_R\rangle$$

We have two possibilities:

1.

$k\ne \tau \left(i\right)$, for any i. In this case, there is a bijection between the runs of length k and those of length $k+1$, since each run $R^{\prime }\in \mathcal{K}{[k+1]}_{|\varphi \rangle ,\tau }^M$ is obtained from a run $R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M$ with last q-configuration $|{\psi }_R\rangle$, by appending to R the q-configuration $|{\psi }_{R^{\prime }}\rangle =U_M|{\psi }_R\rangle$. Moreover, because, by definition, $\mathsf{Pr}\left\{R^{\prime }\right\}=\mathsf{Pr}\left\{R\right\}$, we can conclude that

$$|{\varphi }_{k+1}\rangle =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R\right\}}{U}_M|{\psi }_R\rangle =\sum _{R^{\prime }\in \mathcal{K}{[k+1]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R^{\prime }\right\}}|{\psi }_{R^{\prime }}\rangle$$

2.

$k=\tau \left(i\right)$, for some i. In this case, every $R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M$ with last q-configuration $|{\psi }_R\rangle$ generates a run $R^{\prime }$ of length $k+1$ for every output observation $|{\psi }_R{\rangle \downarrow }_x|{\psi }_{R^{\prime }}\rangle$, where $R^{\prime }$ is obtained by appending $|{\psi }_{R^{\prime }}\rangle$ to R. Therefore, let $R=\left\{\right|{\psi }_i\rangle {\}}_{i\le k}\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M$ and

$${\mathcal{B}}_R=\{{\left\{{\psi }_i\right\}}_{i\le k+1}\mid |{\psi }_k\rangle {\downarrow }_x|{\psi }_{k+1}\rangle \}$$

By applying Definition 17, we easily check that

$$U_M|{\psi }_R\rangle =\sum _{R^{\prime }\in {\mathcal{B}}_R}\sqrt{\mathsf{Pr}\left\{\right|{\psi }_R\rangle {\downarrow }_x|{\psi }_{R^{\prime }}\rangle \}}|{\psi }_{R^{\prime }}\rangle$$

Thus, by substitution, and $\mathsf{Pr}\left\{R\right\}\mathsf{Pr}\left\{\right|{\psi }_R\rangle {\downarrow }_x|{\psi }_{R^{\prime }}\rangle \}=\mathsf{Pr}\left\{R^{\prime }\right\}$

$$\begin{array}{cc}\hfill |{\varphi }_{k+1}\rangle & =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R\right\}}{U}_M|{\psi }_R\rangle \hfill \\ \hfill & =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sum _{R^{\prime }\in {\mathcal{B}}_R}\sqrt{\mathsf{Pr}\left\{R\right\}}\sqrt{\mathsf{Pr}\left\{\right|{\psi }_R\rangle {\downarrow }_x|{\psi }_{R^{\prime }}\rangle \}}|{\psi }_{R^{\prime }}\rangle \hfill \\ \hfill & =\sum _{R^{\prime }\in {\bigcup }_{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}{\mathcal{B}}_R}\sqrt{\mathsf{Pr}\left\{R^{\prime }\right\}}|{\psi }_{R^{\prime }}\rangle \hfill \\ \hfill & =\sum _{R^{\prime }\in \mathcal{K}{[k+1]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R^{\prime }\right\}}|{\psi }_{R^{\prime }}\rangle \hfill \end{array}$$

since ${\bigcup }_{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}{\mathcal{B}}_R=\mathcal{K}{[k+1]}_{|\varphi \rangle ,\tau }^M$.  □

We are finally in the position to prove that our observation protocol is compatible with the probability distributions that we defined as computed output of a QTM computation.

Theorem 4.

Let $K_{|\varphi \rangle }^M={\left\{{\varphi }_i\right\}}_{i\in \mathbb{N}}$ be the computation of the QTM M on the initial q-configuration $|\varphi \rangle$ and ${\mathcal{K}}_{|\varphi \rangle ,\tau }^M$ be the τ-observed computation on the same initial configuration. For every $n\in \mathbb{N}$:

1. 

${\mathbf{P}}_{|{\varphi }_k\rangle }\left(n\right)=\mathsf{Pr}\{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}$, for $k=\tau \left(i\right)+1$ and $i\in \mathbb{N}$; and,

2. 

${\mathbf{P}}_{K_{|\varphi \rangle }^M}\left(n\right)=\mathsf{Pr}\{R\in {\mathcal{K}}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}$.

Proof. 

Let us start with the first item. By Lemma 2, we know that

$$|{\varphi }_k\rangle =\sum _{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M}\sqrt{\mathsf{Pr}\left\{R\right\}}|{\psi }_R\rangle ,$$

where $|{\psi }_R\rangle$ is the last q-configuration of R. Because $k=\tau \left(i\right)+1$, for some i, we also know that either ${\psi }_R\in \mathfrak{C}\setminus {\mathfrak{C}}^{fin}$ or $|{\psi }_R\rangle =u_R|C_R\rangle$ with $C_R\in {\mathfrak{C}}^{fin}$ and $|u_R|=1$. Therefore,

$${\mathbf{P}}_{|{\varphi }_k\rangle }\left(n\right)=\parallel \sum _{R\in \mathcal{B}[k,n]}\sqrt{\mathsf{Pr}\left\{R\right\}}{u}_R|C_R{\rangle \parallel }^2$$

where

$$\begin{array}{cc}\hfill \mathcal{B}[k,n]& =\{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}\hfill \\ \hfill & =\{R\in \mathcal{K}{\left[k\right]}_{|\varphi \rangle ,\tau }^M\mid |{\psi }_R\rangle =u_R|C_R\rangle \mathrm{with}\mathbf{val}\left[C_R\right]=n\}\hfill \end{array}$$

By Lemma 1, we know that for every $R_1,R_2\in \mathcal{B}[k,n]$, we have $|C_{R_1}\rangle \ne |C_{R_2}\rangle$. Therefore

$${\mathbf{P}}_{|{\varphi }_k\rangle }\left(n\right)=\sum _{R\in \mathcal{B}[k,n]}\mathsf{Pr}\left\{R\right\}{\left|u_R\right|}^2=\sum _{R\in \mathcal{B}[k,n]}\mathsf{Pr}\left\{R\right\}=\mathsf{Pr}\mathcal{B}[k,n]$$

since $|u_R|=1$. Which concludes the proof of the first item of the assertion.

In order to prove the second item, let $\mathcal{B}[\omega ,n]=\{R\in {\mathcal{K}}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}$. We have that

$$\begin{array}{cc}\hfill \mathsf{Pr}\{R\in {\mathcal{K}}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}& =\sum _{R\in \mathcal{B}[\omega ,n]}\mathsf{Pr}\left\{R\right\}=\underset{i\to \infty }{lim}\sum _{\genfrac{}{}{0.0pt}{}{R\in \mathcal{B}[\omega ,n]}{{R[\tau \left(i\right)+1]\downarrow }_n}}\mathsf{Pr}\left\{R\right\}\hfill \\ \hfill {}^{(*)}& =\underset{i\to \infty }{lim}\sum _{\genfrac{}{}{0.0pt}{}{R\in \mathcal{B}[\omega ,n]}{{R[\tau \left(i\right)+1]\downarrow }_n}}\mathsf{Pr}\left\{R[\tau \left(i\right)+1]\right\}\hfill \\ \hfill {}^{(**)}& =\underset{i\to \infty }{lim}\sum _{R^{\prime }\in \mathcal{B}[\tau \left(i\right)+1,n]}\mathsf{Pr}\left\{R^{\prime }\right\}=\underset{i\to \infty }{lim}\mathsf{Pr}\mathcal{B}[\tau \left(i\right)+1,n]\hfill \end{array}$$

since: $(*)$$\mathsf{Pr}\left\{R\right\}=\mathsf{Pr}\left\{R\right[\tau \left(i\right)+1\left]\right\}$, when ${R[\tau \left(i\right)+1]\downarrow }_n$ (see Remark 10); $(**)$, there is a bijection between $\mathcal{B}\left[\tau \right(i)+1,n]$ and $\{R\in \mathcal{B}[\omega ,n]\mid R[\tau \left(i\right)+1]{\downarrow }_n\}$ (see Remark 9) mapping every $R^{\prime }\in \mathcal{B}[\tau \left(i\right)+1,n]$ with last q-configuration $u|C\rangle$ into $R={\left\{{\psi }_j\right\}}_{j\in \mathbb{N}}\in \{R\in \mathcal{B}[\omega ,n]\mid R[\tau \left(i\right)+1]{\downarrow }_n\}$ s.t $R^{\prime }=R[\tau \left(i\right)+1]$ and $|{\psi }_j\rangle =u{U}_M^{j-\tau \left(i\right)-1}|C\rangle$ for $j>\tau \left(i\right)$.

Therefore, by the (already proved) first item of the assertion

$$\mathsf{Pr}\{R\in {\mathcal{K}}_{|\varphi \rangle ,\tau }^M\mid R{\downarrow }_n\}=\underset{i\to \infty }{lim}\mathsf{Pr}\mathcal{B}[\tau \left(i\right)+1,n]=\underset{i\to \infty }{lim}{\mathbf{P}}_{|{\varphi }_{\tau \left(i\right)+1}\rangle }\left(n\right)={\mathbf{P}}_{K_{|\varphi \rangle }^M}\left(n\right)$$

 □

The above theorem shows that our protocol is not only realistic (unlike those of B&V and Deutsch), but also compatible with the theoretical probabilities defined for configurations in superposition. In particular, the theorem shows how it is possible to make measurements in a totally free way, without destroying the expressive power of quantum parallelism, i.e., without destroying the ability of a QTM to use quantum interference.

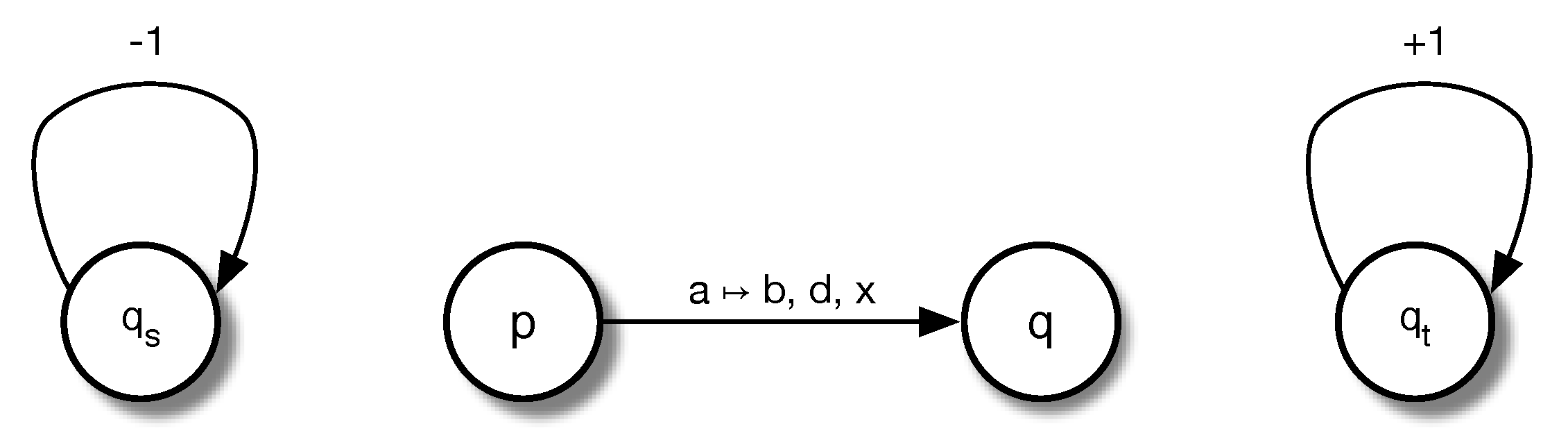
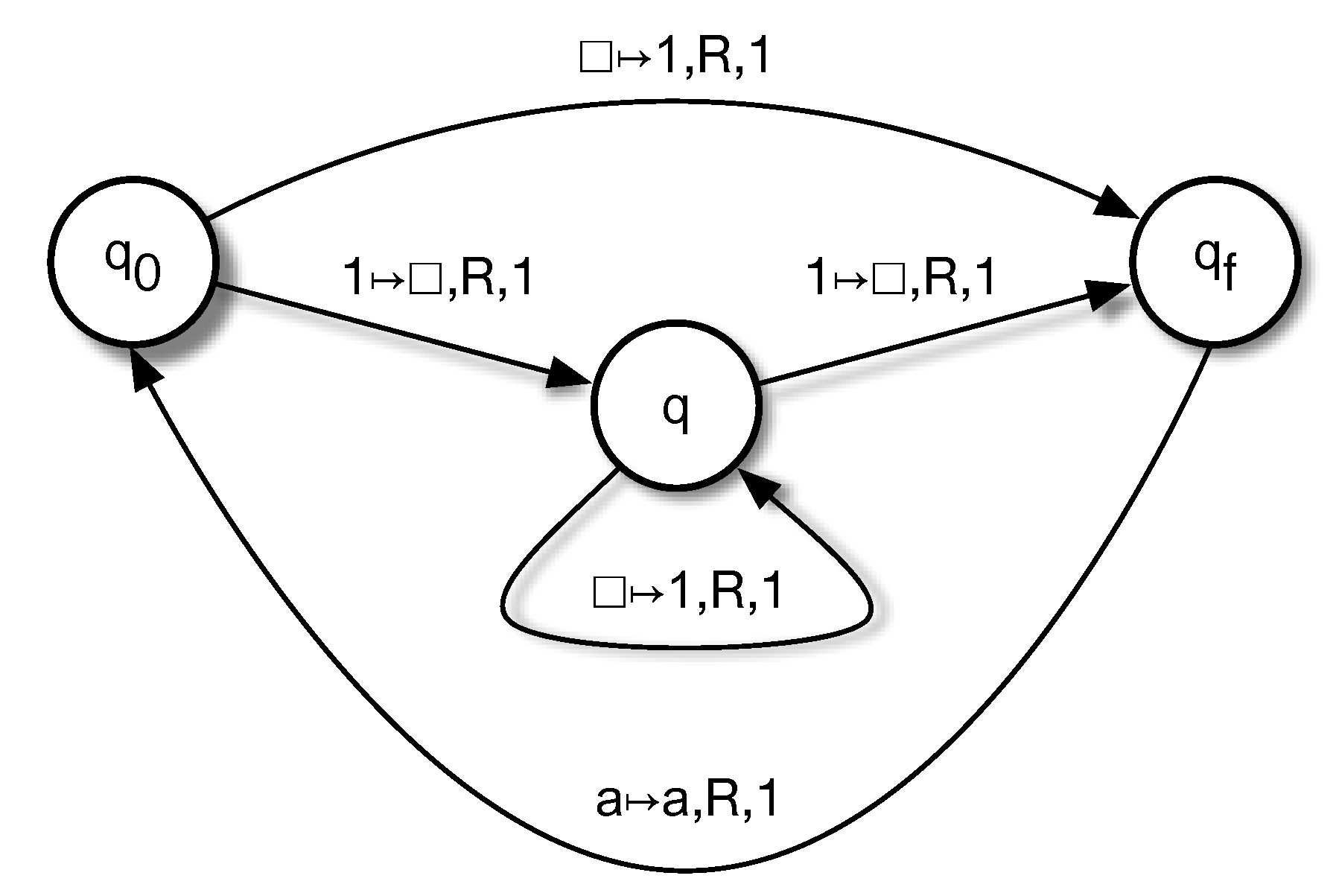
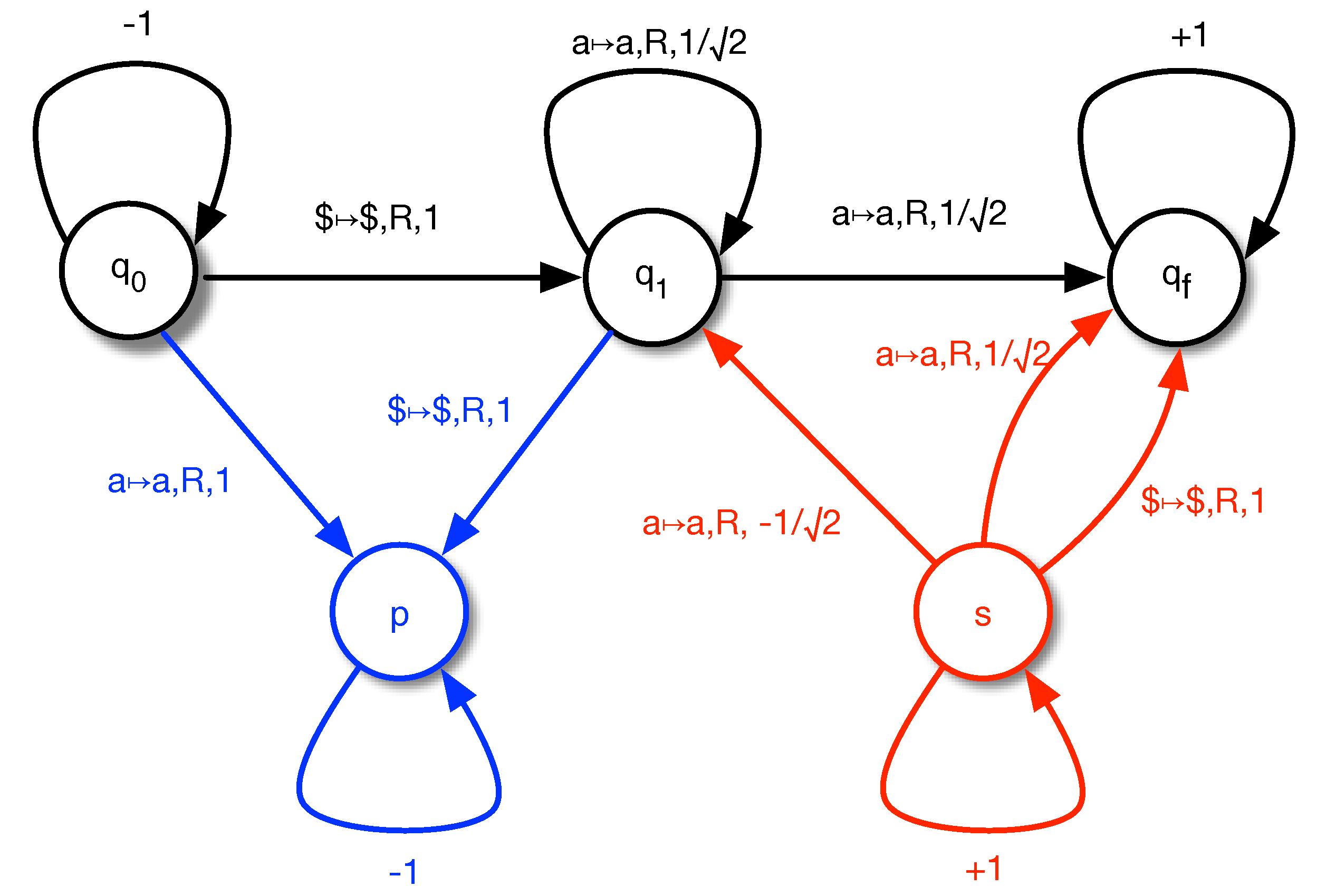
5. A Comparison With Bernstein and Vazirani’s QTMs: Part 2

Theorem 2 has shown that our QTMs generalise B&V-QTMs, since the computation of any B&V-QTM can be simulated by a corresponding QTM with the same transition function (up to transitions entering/leaving the initial/final state). The general framework, however, is substantially modified, and the “same” machine behaves in different ways in the two approaches. In this section, we give two simple examples of this.

5.1. QTM Transition Graphs

Let us represent a QTM M by means of a transition graph (a directed graph) whose nodes are the states of M, and whose arrows give its transition function (see Figure 1). Namely, if ${\delta }_0(p,a)(q,b,d)=x\ne 0$, the graph of M contains an arrow from the node of p to the node of q, labelled by the tuple $(a\mapsto b,d,x)$. Every non-target node has at least one outgoing edge labelled by such a tuple, for any symbol a of the tape alphabet.

In addition to the arrows of ${\delta }_0$, to represent the looping transitions of target nodes, the graph contains a self-loop labelled by $+1$ on any target node $q_t$: to denote the fact that the only transition of any target configuration is the one that increases the counter by 1, without modifying the rest of the configuration. Dually, every source node $q_s$ has a self-loop labelled by $-1$. The self-loop of $q_s$ is not its only outgoing arrow, since the corresponding counter decreasing transition applies to source configurations with a counter greater than 0 only; indeed, when the counter of a source configuration reaches the 0, the ${\delta }_0$ transition function applies. On the other hand, the self-loop is the only incoming arrow of any source state $q_s$, because no transition from another state can enter into it. The situation is dual for target states, for which the self-loop is the only outgoing arrow.

See Figure 4 for an example of source and target nodes of a transition graph: the state s and $q_0$ (which is also initial) are source states; the states p and $q_f$ (which is also final) are target states.

5.2. A Classical Reversible TM With Quantum Behaviour

In Figure 2, we give the transition graph of a B&V-QTM corresponding to a reversible TM: any reversible TM M can be transformed into a B&V-QTM by assuming that the weight of any transition of M is 1, and by adding a back-transition from the final state to the initial state.

In the example presented in Figure 2, $q_0$ is the initial state and $q_f$ is the final one, and they are connected by an arrow $(a\mapsto a,R,1)$ from $q_f$ to $q_0$, where $a\in \{\square ,1\}$. When started on an initial tape containing $\underline{n+1}$ (that is, $n+2$ symbols 1, see Section 2), the machine M erases two 1s from the tape. When the initial tape contains instead $\underline{0}$, M loops indefinitely on the middle state q, after erasing the unique symbol 1 on the tape. Summing up (remembering that for the computed output we just count the number of 1s on the tape, see Definition 12), M computes the predecessor $n-1$ (with probability 1), when fed with a representation of $n>0$, while it diverges (with probability 1) for $n=0$. However, if we feed M with a non classical input as $|\psi \rangle =\frac{1}{\sqrt{2}}|\underline{0}\rangle +\frac{1}{\sqrt{2}}|\underline{2}\rangle$, then M fails to give an answer according to B&V’s framework, since it reaches a q-configuration in which final and non-final base configurations superpose.

To transform M into a QTM according to our formalism (see Theorem 2), it suffices to replace the arrow from $q_f$ to $q_0$ by two self-loops: one (labelled $-1$) on the initial state $q_0$, and one (labelled $+1$) on the final state $q_f$. We obtain then the QTM in Figure 3. By the definition of computed output, we can see that $M_{\frac{1}{\sqrt{2}}|\underline{0}\rangle +\frac{1}{\sqrt{2}}|\underline{2}\rangle }\to \{1\mapsto 1/2;n\mapsto 0,ifn\ne 1\}$; namely, with probability $1/2$ the QTM halts with computed output 1; while with probability $1/2$ it diverges.

5.3. A PD Obtained as a Limit

The example presented in Figure 4 shows a QTM that produces a PD only as an infinite limit. The tape alphabet of the machine M is $\mathsf{\Sigma }=\{\$,1,\square \}$, the set of its source states is $Q_s=\{q_0,s\}$, the set of its target states is $Q_t=\{q_f,p\}$, the state $q_0$ is initial, the state $q_f$ is final. In the figure, the symbol a stands for any symbol of the alphabet but $, which is, $a\in \{1,\square \}$.

The machine M applies properly on initial configurations $\langle \lambda ,q_0,\$\underline{n},0,0\rangle$, whose corresponding base vector will be denoted by $|\$\underline{n}\rangle$ (to simplify the definition of the machine, we use a slight variant of the enconding given in Section 3.5 in which the sequence $\underline{n}$ coding the number n is preceded by a $, which is indeed the only $ on the tape). On such inputs, after moving from the initial state $q_0$ to $q_1$, M either ends up in the final state $q_f$ with probability $1/2$, or it loops on $q_1$ with probability $1/2$. We remark the source state s and the target state p: such states do not play any role when the machine computes on $\$\underline{n}$, since none of them can be reached. Nevertheless, they must be added to deal with error situations, and to satisfy the local unitary conditions, in order to obtain a proper unitary time evolution for M (see Remark 1).

A simple calculation shows that $M_{|\$\underline{n}\rangle }\to {\mathbf{P}}_{}$, with ${\mathbf{P}}_{}=\{n+1\mapsto 1;m\mapsto 0,ifm\ne n+1\}$; namely, on the input $\$\underline{n}$, M computes with probability 1 the successor $n+1$ (the machine is indeed the identity w.r.t. the tape, since no transition of the machine changes any symbol on the tape; however, since $\underline{n}$ is a sequence of $n+1$ symbols 1, the computation leaves all these symbols 1 on the tape, leading then to a computed output of $n+1$). We stress that the PD ${\mathbf{P}}_{}$ is obtained as a limit, since for every $j\in \mathbb{N}$, ${\mathbf{P}}_{U^j|\$\underline{n}\rangle }$ is a PPD s.t. ${\mathbf{P}}_{U^j|\$\underline{n}\rangle }(n+1)<1$ and ${\mathbf{P}}_{U^j|\$\underline{n}\rangle }\left(m\right)=0$, for $m\ne n+1$. Of course, this does not mean that we have to wait an infinite time to readback the result! A correct way to interpret this fact is that, for each $n\in \mathbb{N}$, and each $ϵ\in (0,1/2]$, there exists $k\in \mathbb{N}$ s.t, for every $j>k$, $1-ϵ<{\mathbf{P}}_{U^j|\$\underline{n}\rangle }(n+1)\le 1$.

6. Related Works

After having analysed at the length the notions of B&V and Deutsch, we discuss in this section some other papers related to our work.

6.1. On Quantum Extensions of Turing Machines, And of Related Complete Formalisms

• Strictly following the B&V approach, Nishimura and Ozawa [17,24] study the relationship between QTMs and quantum circuits (extending previous results by Yao [25]). They show that there exists a perfect computational correspondence between QTMs and uniform, finitely generated families of quantum circuits. Such a correspondence preserves the quantum complexity classes EQP, BQP, and ZQP.
• Perdrix and Jorrand [26] proposes a new way to deal with quantum extensions of Turing Machines. The basic idea is reminiscent of the quantum-data/classical-control paradigm coined by Selinger [27,28]. In fact, in Perdrix QTM’s, the only quantum component is the tape whereas the control is completely classical.
• Dal Lago, Masini, and Zorzi [3,29,30] extend the quantum-data/classical-control paradigm to a type free quantum $\lambda$-calculus that is proven to be in perfect correspondence with the QTMs of B&V. Following the ideas of the so-called Implicit Computational Complexity, the authors propose an alternative way to deal with the quantum classes EQP, BQP, and ZQP.

6.2. On the Readout Problem

The following papers address the problem of how to readout the result of a quantum computation. Because this is a key question in the definition of any quantum computing formalism, they deserve some deeper attention.

We recall, however, that our main interest is in QTMs as devices computing distributions of probability, and not functions over natural numbers.

• Myers [31] tries to show that it is not possible to define a truly quantum general computer. The article highlights how the B&V approach fails on truly quantum data. In fact, in such a case, it is impossible to guarantee the synchronous termination of all the computations in superposition. Consequently, the use of a termination bit spoils the quantum superposition of the computation. This defect was well known, and it is for this reason that B&V did not define a general notion of quantum computability, but rather a notion sufficient to solve—in a quantum way—only classical decision problems. Myers’s criticism does not apply to our approach. Our QTMs are fully quantum, and they have an observational protocol of the result that does not depend on the synchronous termination of the computations in superposition.
• In an unpublished note, Kieu and Danos [32] claim that: “For halting, it is desirable of the dynamics to be able to store the output, which is finite in terms of qubit resources, invariantly (that is, unchanged under the unitary evolution) after some finite time when the desirable output has been computed”. Unfortunately, it is not possible to enter into a truly invariant final quantum configuration—only a machine starting in a final configuration and computing the identity can accomplish this constraint. We overcome the problem by introducing a feasible (i.e., correct from a quantum point of view) notion of invariant, w.r.t. the readout, of final configurations. In this way, even if the final configuration changes, the output we read from that configuration does not change.
• In another unpublished note, Linden and Popescu [22] address the problem of how to readout the result of a general quantum computer. The authors write: “We explicitly demonstrate the difficulties that arise in a quantum computer when different branches of the computation halt at different, unknown, times”, implicitly referring to the problems in extending the approach of B&V to general quantum inputs (see again [31], discussed above). In the first part of the work, the authors show that the problem cannot be solved by means of the so-called “ancilla”. The ancilla is an additional information added to the main information encoded by a configuration of the quantum machine. The idea is that, once a final state is reached, the machine keeps modifying the ancilla only. The authors show that the ancilla approach destroys the quantum capabilities of quantum machines, since only classical computations can survive to this treatment of ancilla. Even if reminiscent of the ancilla, our approach is technically different—the problems addressed by Linden and Popescu do not apply—since we carefully tailor the space of the possible configurations of the machines, allowing for the ancilla to play a role only during its final and initial evolution.
  In the second part of the work, the authors launch a strong attack against the use of termination bit, the solution originally proposed by Deutsch and successively refined by Ozawa [13]. The authors try to argue that the approach that was proposed by Deutsch/Ozawa cannot work. In fact, they show that, even if it is true that once the termination bit is set to 1, it remains firmly with such a value forever, any terminal configuration cannot be frozen, and keeps evolving according to the Hamiltonian of the system. Once again, our proposal does not have the defect depicted in the paper, because, far away to force a final configuration to remain stable, only the readout of a final configuration is stable in our approach.
• Hines [33] shows how to ensure simultaneous coherent halting, provided that termination is guaranteed for a restricted class of quantum algorithms. This kind of approach that is based on coherent halting is intentionally not followed in our paper. Indeed, as previously remarked, we are interested in treating systems which includes, as a particular case, all classical computable functions—we cannot restrict to terminating computations.
• Miyadera and Ohya [34] discuss the notion of probabilistic halting. In particular, “[…] the notion of halting is still probabilistic. That is, a QTM with an input sometimes halts and sometimes does not halt. If one can not get rid of the possibility of such a probabilistic halting, one can not tell anything certain for one experiment since one can not say whether an event of halting or non-halting occurred with probability one or just by accident, say with probability ${10}^{-40}$”. Therefore, they wonder about the existence of any algorithm to decide whether or not a QTM probabilistic halts. With no surprise, they conclude that such an algorithm cannot exist. In fact, because the non-probabilistic halting of a QTM corresponds to the simultaneous halting of all the superposing branchings of its computation, an algorithm deciding the probabilistic halting would decide the simultaneous termination of two classical reversible machines (by combining them into a unique QTM), which is clearly an undecidable problem. In a sense, the question of probabilistic or non-probabilistic halting is irrelevant for our approach. In our QTMs, the result of a computation is defined as a limit, and any computation converges to some result. Accordingly, the only possible readouts that we can get are approximations of such a result. At the same time, because we show that a repeated-measures protocol can retrieve the distribution associated to the output of a computation, we can accept to say that our approach is probabilistic.

7. Conclusions and Further Work

We find surprising that, in the thirty years since [10], a theory of quantum computable functions did not develop, and that the main interest remained in QTMs as computing devices for classical problems/functions. This is in sharp contrast with the original (Feynman’s and Deutsch’s) aim to have a better computing simulation of the physical world.

As always in these foundational studies, we had to go back to the basics, and look for a notion of QTM general enough to encompass previous approaches. We started with pre Quantum TMs (Definition 1), and defined then QTMs as those pre QTMs whose time evolution operator is unitary (Definition 7). Following analogous results in the literature, we showed that unitarity of the evolution operator for a QTM M is equivalent to a set of constraints formulated on the transition function of M (Theorem 1). Our QTMs are able to simulate B&V-QTMs (Theorem 2), but, contrary to B&V-QTMs, they may be used to give meaning to some “infinite” computations. Indeed, in Section 3 we showed that each QTM M naturally defines a computable function from the sphere of radius 1 in ${\ell }^2\left({\mathfrak{C}}_M\right)$ (i.e., the superpositions of the configurations of M) to the set of (partial) probability distributions on the set of natural numbers. Such a definition is one of the main reasons for our definition of QTM, for it involves computations where some path “terminates”, while others do not. We remark that the definition implies monotonicity of quantum computations (Theorem 3), which is a consequence of the particular way final states are treated in order to defuse quantum interference, once such states are entered.

Particularly tricky is the way in which one reads a result from a quantum computation, which is the subject of Section 4, and, in particular, Section 4.5, which shows that our protocol is compatible with the theoretical probabilities defined for configurations in superposition (Theorem 4).

While several details of the proposed approach may well change during further study, we are confident the general picture may allow a fresh look to the problem of a quantum universal machine, to the termination of QTMs (for instance, characterising termination into the arithmetical hierarchy), and to the various degrees of partiality of quantum computable functions.