Estimating Algorithmic Information Using Quantum Computing for Genomics Applications
Abstract
1. Introduction
2. Background
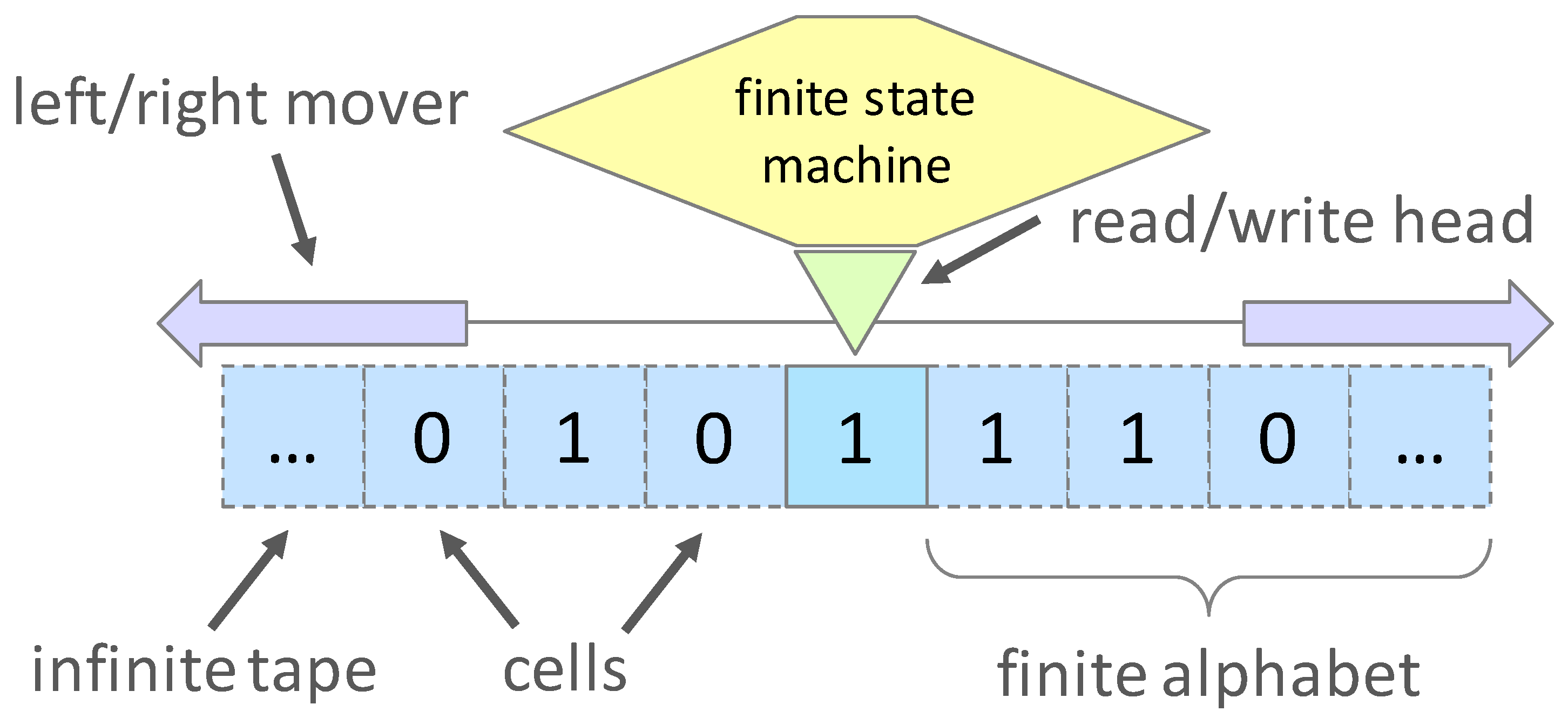
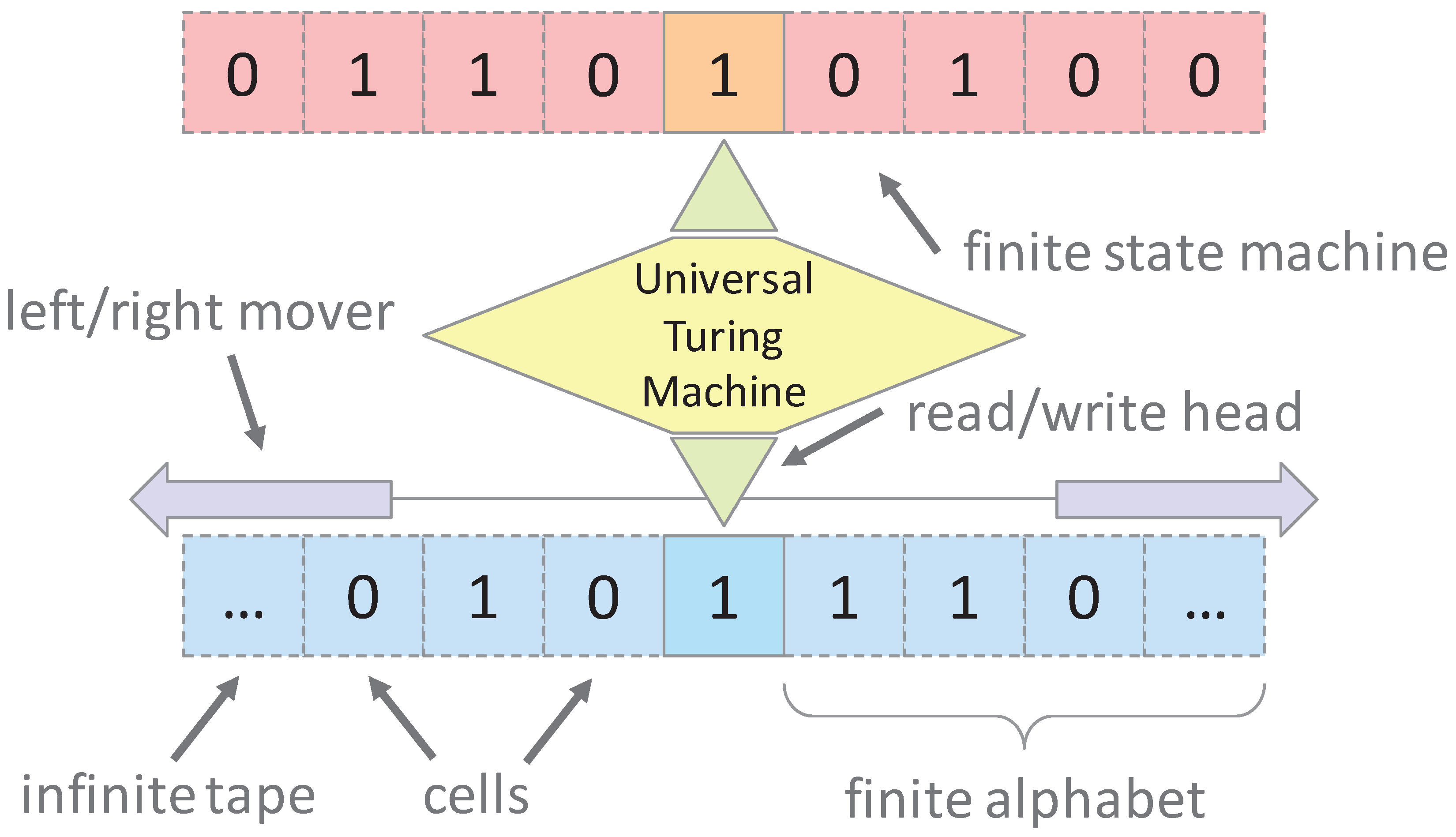
2.1. Automata Models
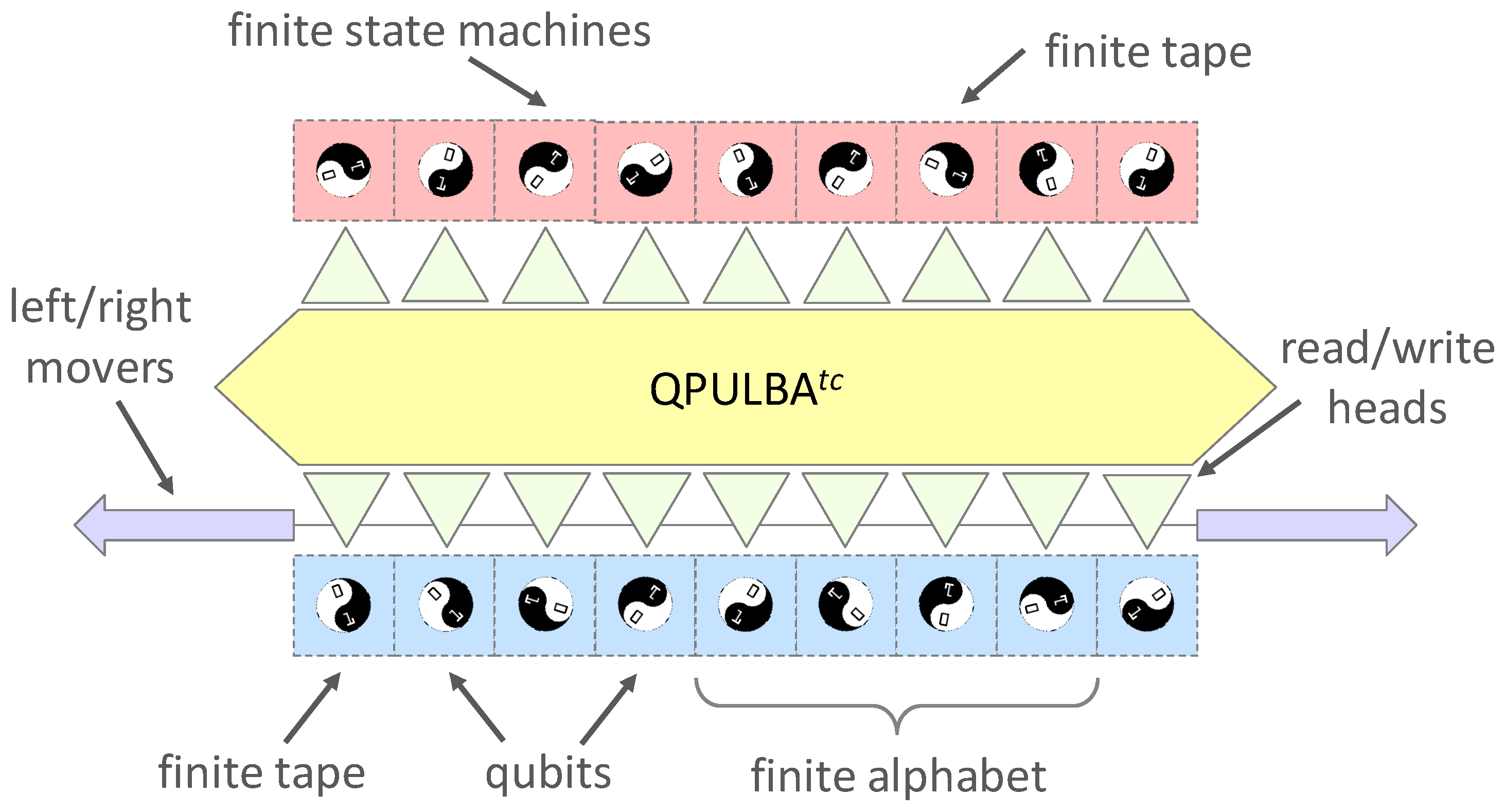
2.2. Restricted Parallel Universal Linear Bounded Automata
2.3. Algorithmic Information
- Algorithmic complexity: Algorithmic complexity (AC), also called Kolmogorov complexity, is the length of the shortest program that produces a particular output and halts on a specific TM. Formally, it is defined as:where T is a TM, p is a program, is the length of the program, s is a string, and denotes the fact that p executed on T outputs s and halts.AC is not a computable quantity in the general case due to fundamental limits of computations that arise from the halting problem (i.e., it is impossible to determine whether any given program will ever halt without actually running this program, possibly for infinite time). However, it has bounded lower-approximate property, i.e., if we can find a program in a language L (e.g., Java, Assembly), .Since AC depends on the particular model of computation (i.e., the TM and the language), it is always possible to design a language where a particular string s will have a short encoding no matter how random. However, the invariance theorem guarantees that, there exists a constant additive factor independent of s, such thatThis constant is the compiler length for translating any arbitrary program for to for .
- Algorithmic probability: Algorithmic probability (AP), also called Solomonoff’s probability, is the chance that a randomly selected program will output s when executed on T. The probability of choosing such a program is inversely proportional to the length of the program.Thus, the largest contribution to the term comes from the shortest program that satisfies the condition. It is uncomputable for the same reasons as AC. AP is related to AC via the following law:i.e., if there are many programs that generate a dataset, then there has to be also a shorter one. The arbitrary constant is dependent on the choice of a programming language.AP can be approximated by enumerating programs on a TM of a given type and counting how many of them produce a given output and then divide by the total number of machines that halt. When exploring machines with n symbols and m states algorithmic probability of a string s can be approximated as follows:The coding theorem method (CTM) [11] approximates the AC as:Calculating CTM, although theoretically computable, is extremely expensive in terms of computation time. The space of possible Turing machines may span thousands of billions of instances.Block decomposition method (BDM) approximates the CTM value for an arbitrarily large object by decomposing into smaller slices of appropriate sizes for which CTM values are known and aggregated back to a global estimate. The algorithmic complexity of these small slices are precomputed and make into a look-up table using CTM. The BDM aggregates this as:where is the approximate algorithmic complexity of the string and i.e., the together forms the string s. Small variations on the method of dividing the string into blocks becomes negligible in the limit, e.g., to take a sliding window or blocks.
- Universal distribution: The universal a priori probability distribution (UD) is the distribution of the algorithmic probability of all strings of a specific size. It can be calculated for all computable sequences. This mathematically formalizes the notion of Occam’s razor and Epicurus’ principle of multiple explanations using modern computing theory for the Bayesian prediction framework. It explains observations of the world by the smallest computer program that outputs those observations, thus, all computable theories which describe previous observations are used to calculate the probability of the next observation, with more weight put on the shorter computable theories. This is known as Solomonoff’s theory of inductive inference.
- Speed prior: The universal distribution does not take into account the computing resource (tape and time) required when assigning the probability of certain data. This does not match our intuitive notion of simplicity (Occam’s razor). Jürgen Schmidhuber proposed [12] the measure speed prior (SP), derived from the fastest way of computing data.where program p generates an output with prefix s after instructions. Thus, it is even more difficult to estimate it as all possible runtimes for all possible programs need to be taken into account.
- Omega number: The Omega number, also called Chaitin constant or halting probability of a prefix-free TM T is a real number that represents the probability that a randomly constructed program will halt.
3. Computation Model
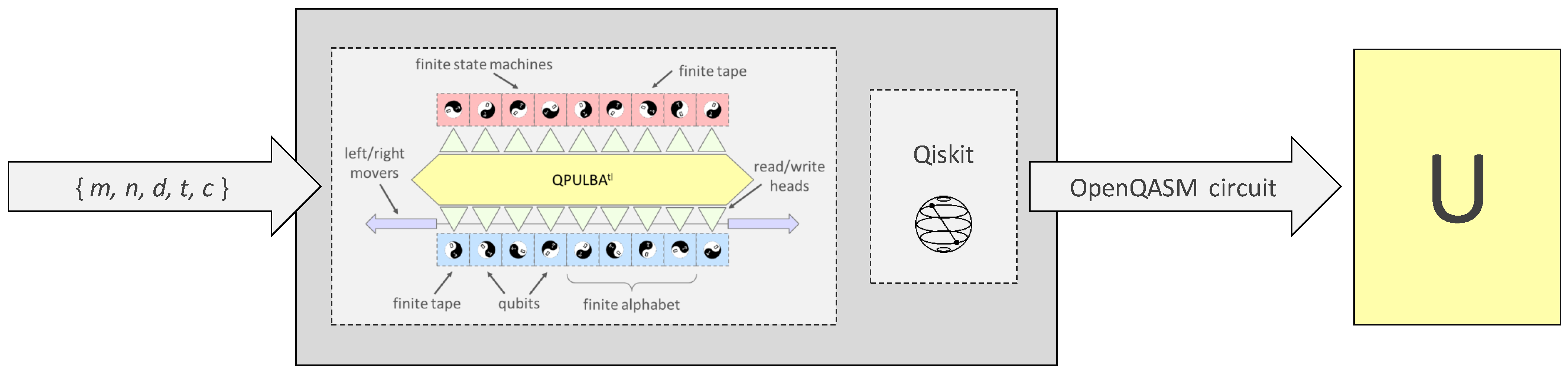
3.1. Quantum Implementation
- presenting a mechanistic perspective where the quantum circuit has the corresponding functions of a classical universal Turing machine,
- this allows the user to readily translate a superposition of classical programs for a Turing machine (e.g., FSMs from assembly language code) as input states, in contrast to the cellular automata-based construction in [15],
- Turing machine’s mechanistic model does not preserve locality and homogeneity, thus reducing both the number of qubits and gate operations required to execute the automata compared to [15]
- the core value of our construction stems from the feature that, in our model, the program can also be in a superposition along with the input data, thus allowing a superposition of classical functions to be evolved in parallel (this feature is denoted by the ‘P’ in QPULBA) and is generally not true for a description of a QTM.
- In [3] We provide a complete and scalable circuit description of the full construction in two popular quantum programming languages and provide simulation results taking into account realistic resource assumptions on the runtime and qubits
- thus, besides being a theoretical computation model, our implementation has practical applicability in the field of experimental algorithmic information theory, where the space of program-output behaviors needs to be explored exhaustively in a classical supercomputer. Thus, it forms the framework the application presented in this article.
3.2. An Enumerated Example
3.3. Quantum Advantage
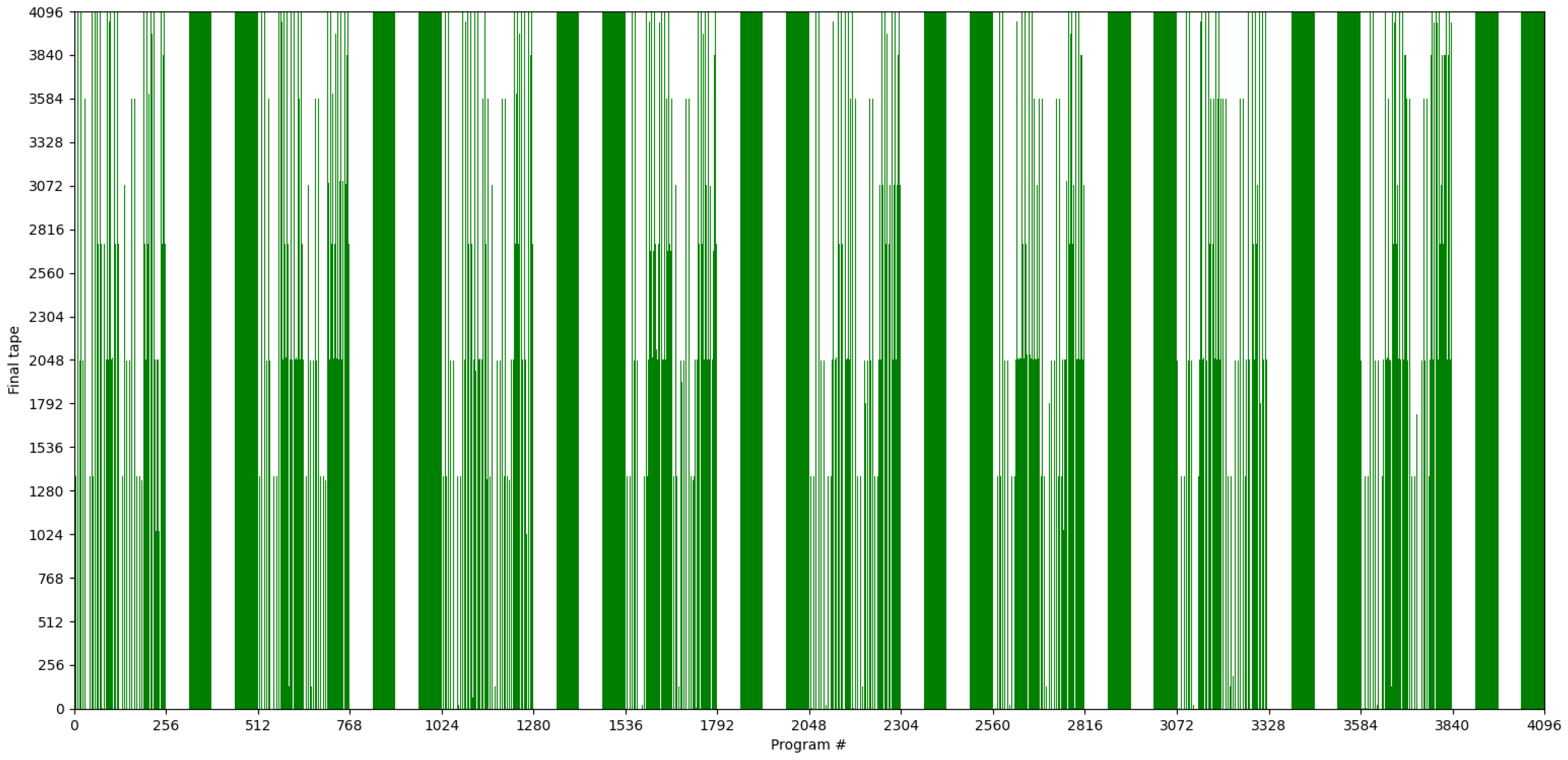
3.3.1. Reconstructing the Universal Distribution
3.3.2. Finding Output with Highest Algorithmic Probability
3.3.3. Finding Specific Program-Output Characteristics
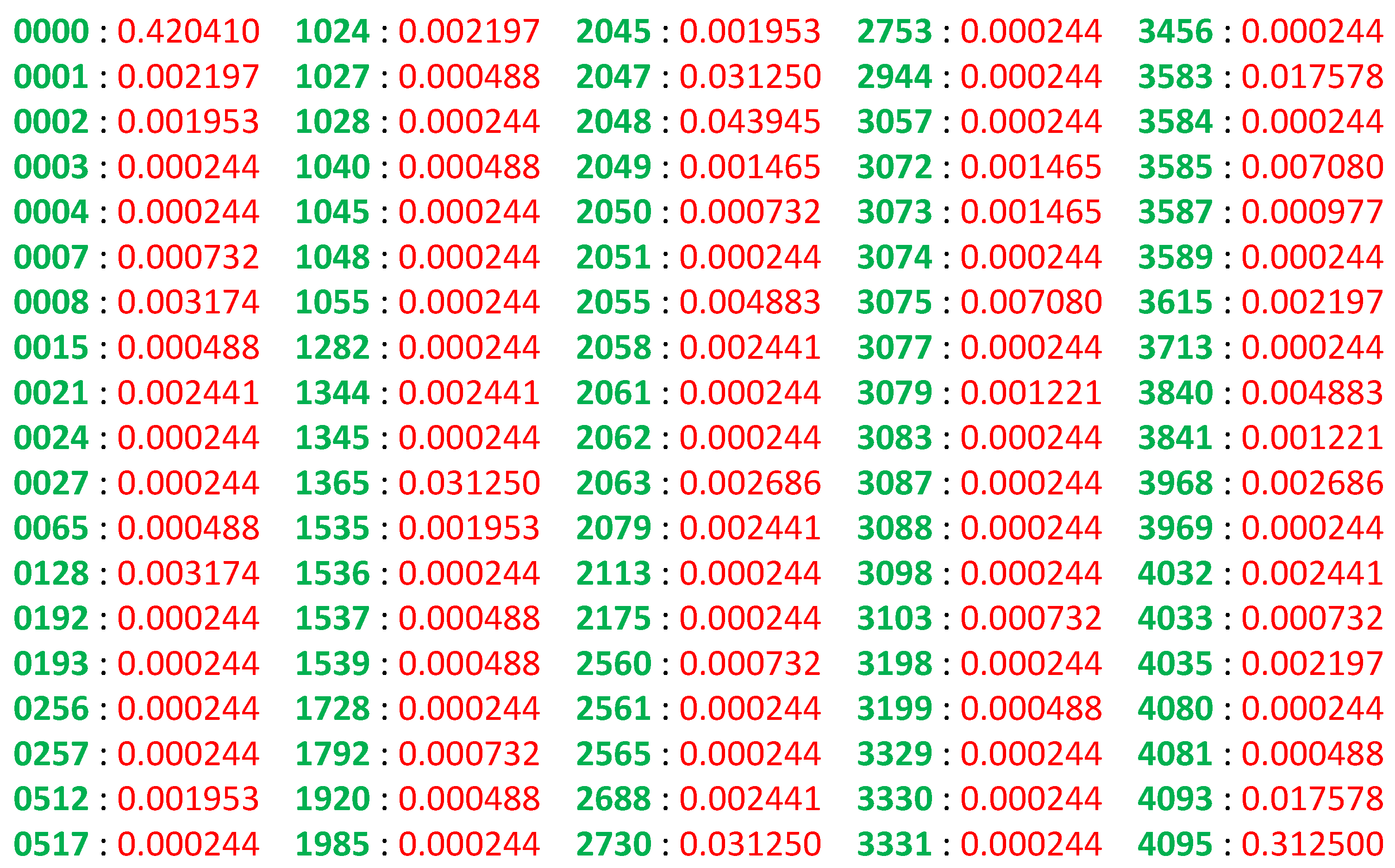
3.3.4. Finding Algorithmic Probability of a Specific Output
3.3.5. Finding Programs with Specific End State
4. Experimental Use Cases
4.1. Distribution of Quines
- a program or description of itself
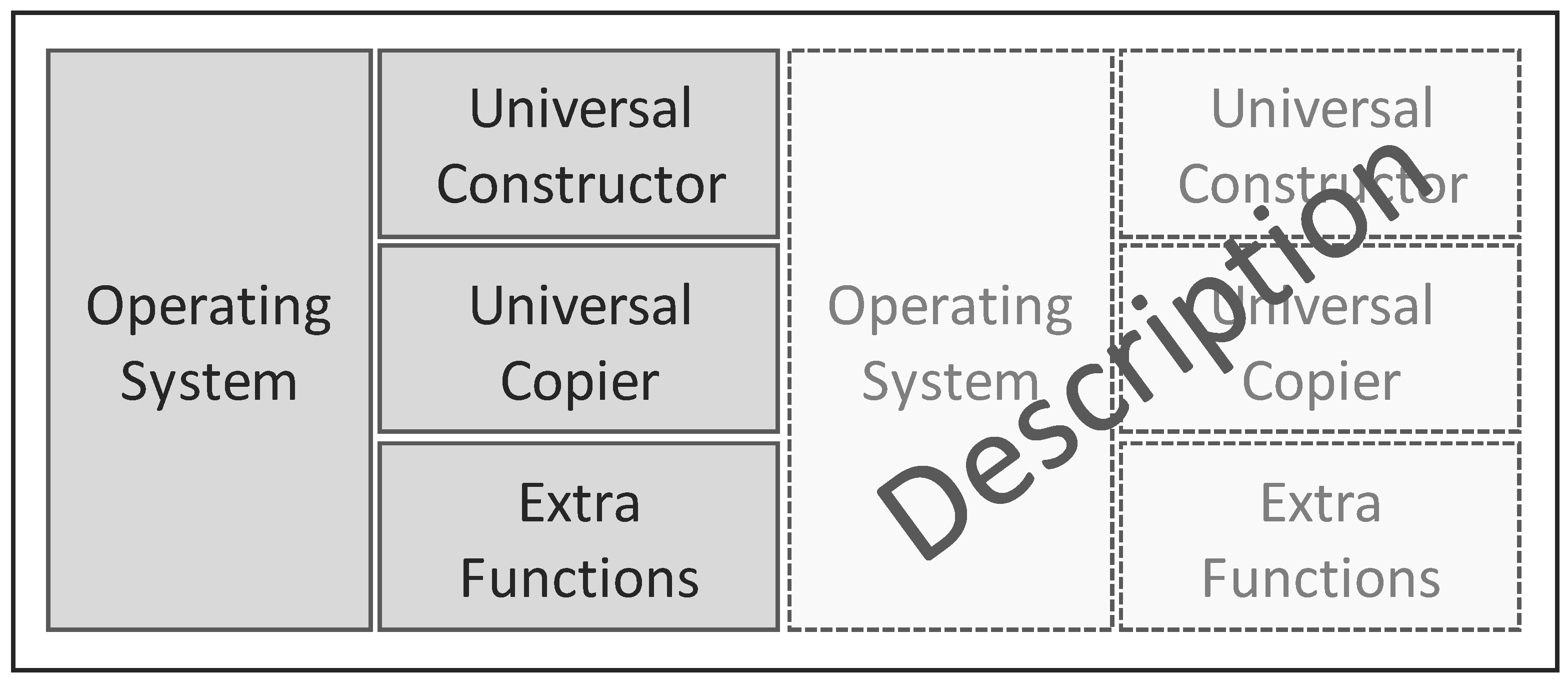
- a universal constructor mechanism that can read any description and construct the machine or description encoded in that description
- a universal copier machine that can make copies of any description (if this allows mutating the description it is possible to evolve to a higher complexity)
Implementation Using the QEAIT Framework
4.2. Estimation of Algorithmic Complexity
Analysis Using the QEAIT Framework
| Algorithm 1: Quantum counting CTM algorithm |
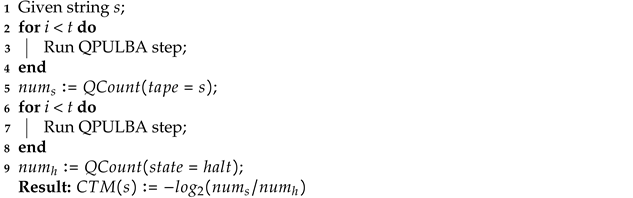 |
5. Application Framework
5.1. Meta-Biology and Artificial Life
5.2. Phylogenetic Tree Analysis Using EAIT
5.3. Protein-Protein Interaction Analysis Using EAIT
5.4. In-Quanto Synthetic Biology
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
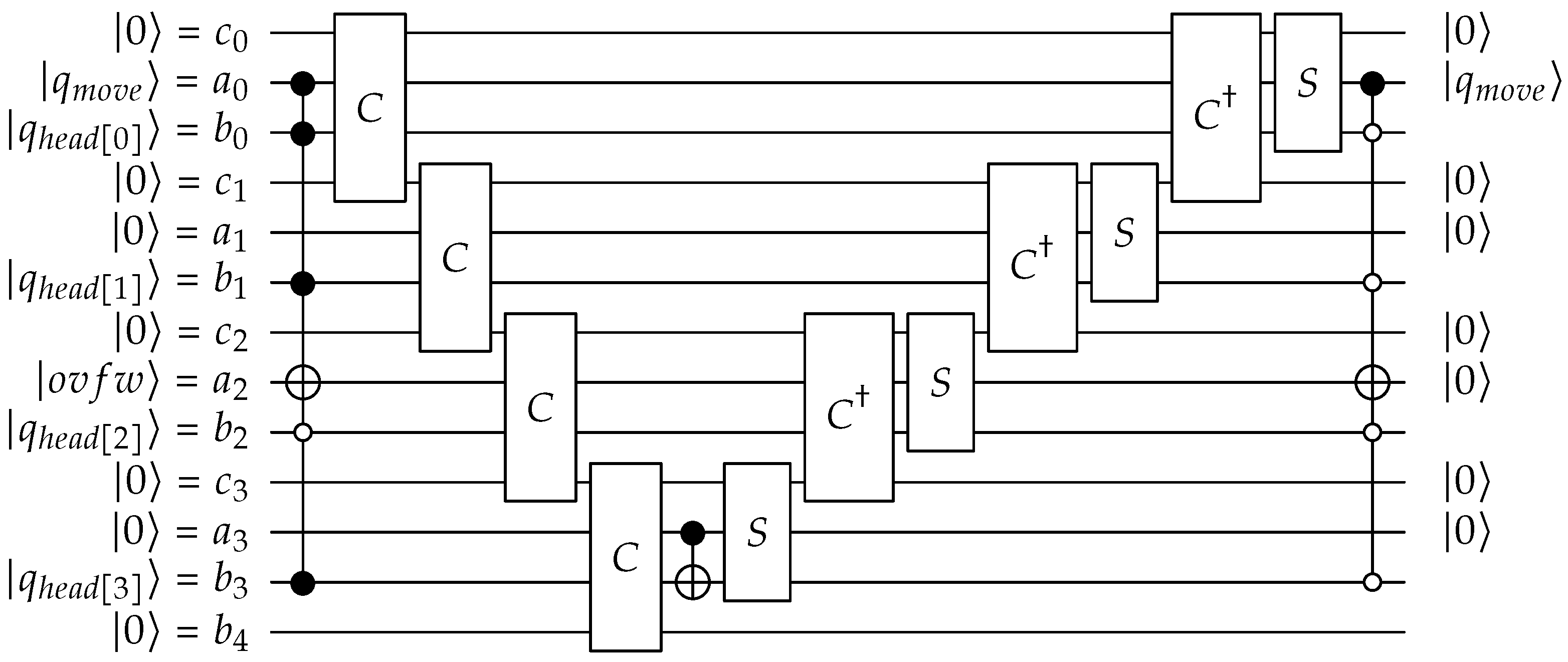
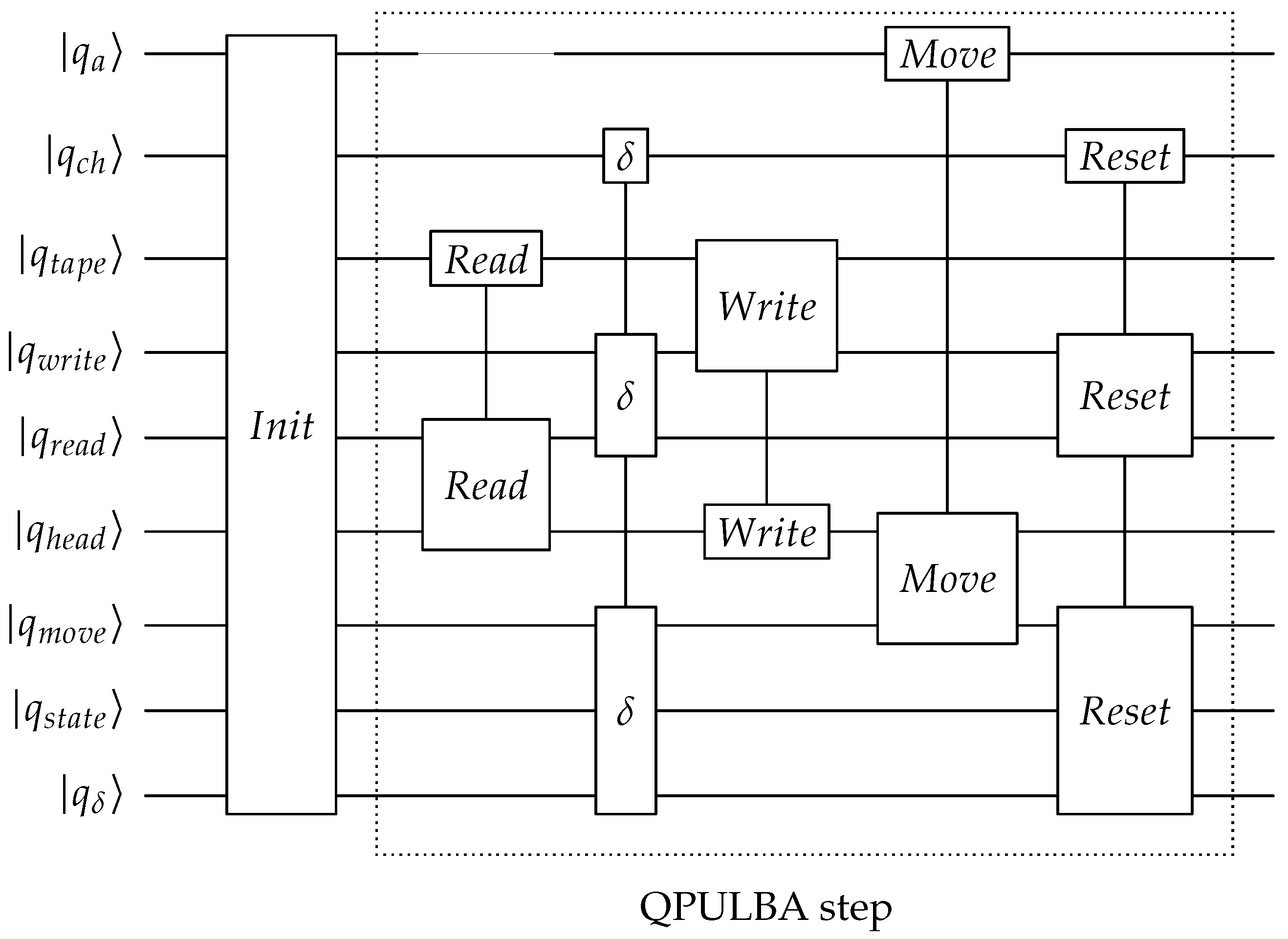
Appendix A. QPULBA Quantum Circuit
- Read:
- Transition evaluation:
- Write:
- Move:
- Reset
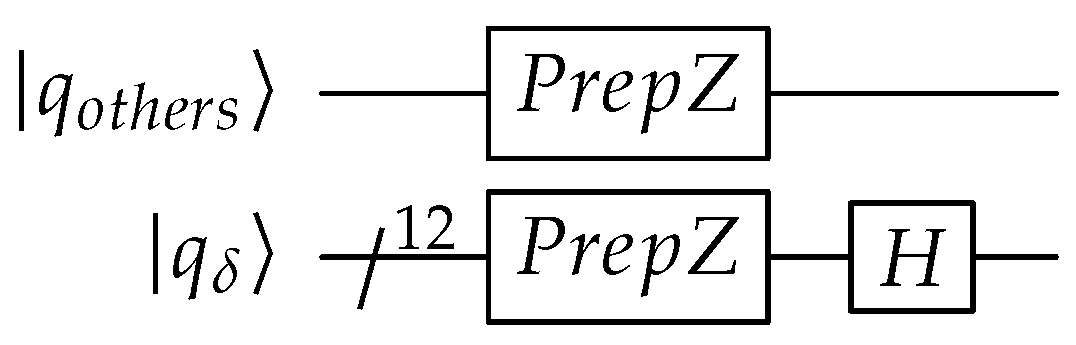


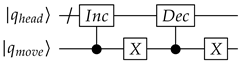 |
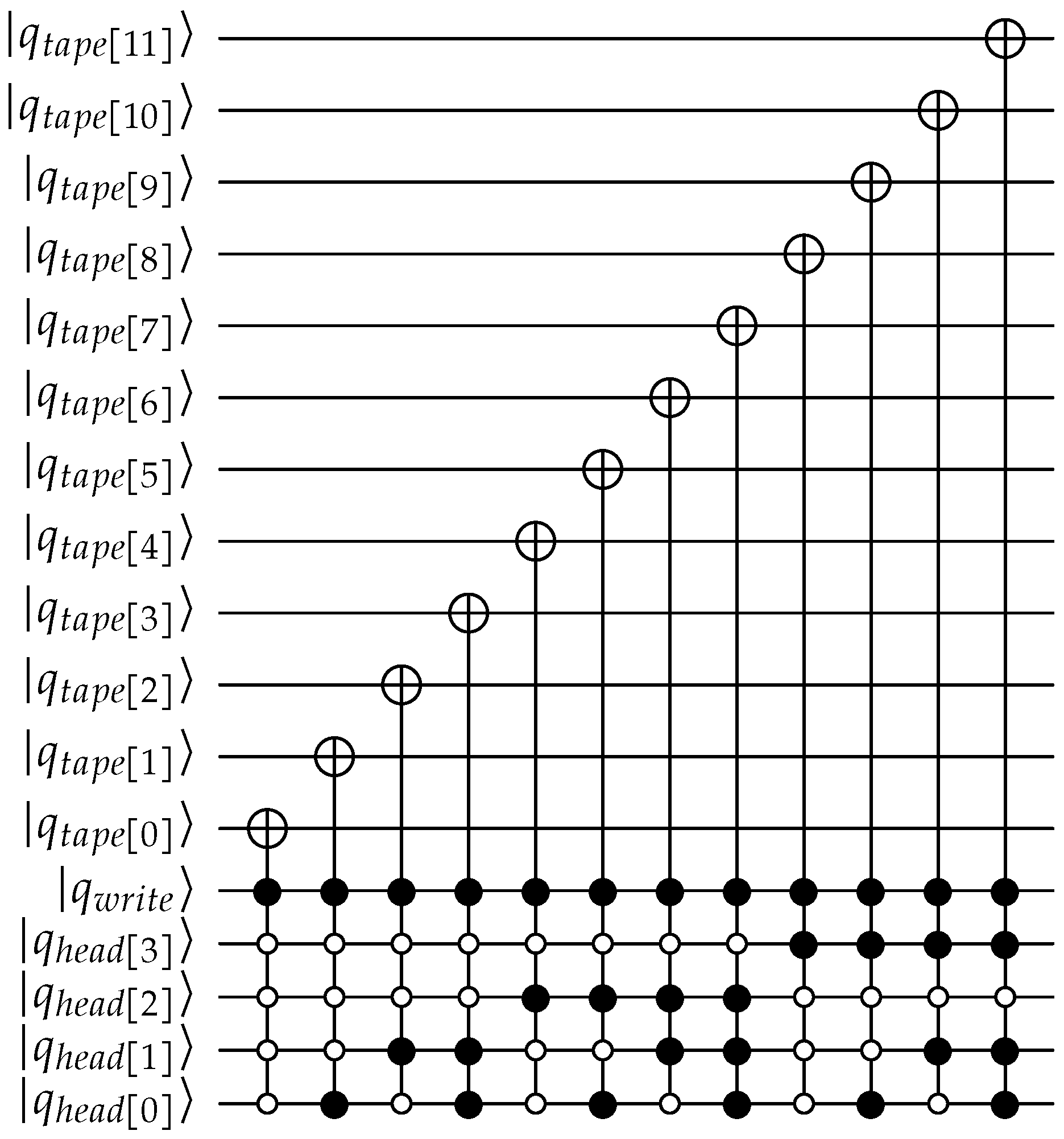
| .sum | .carry | .reverse_carry | ||
| cnot A0,S0 | toffoli A0,B0,C1 | toffoli C0,B0,C1 | ||
| cnot B0,S0 | cnot A0,B0 | cnot A0,B0 | ||
| toffoli C0,B0,C1 | toffoli A0,B0,C1 |

References
- Chaitin, G. Proving Darwin: Making Biology Mathematical; Vintage Books: Nwe York, NY, USA, 2012. [Google Scholar]
- Brenner, S. Life’s code script. Nature 2012, 482, 461. [Google Scholar] [CrossRef]
- Sarkar, A.; Al-Ars, Z.; Bertels, K. Quantum Accelerated Estimation of Algorithmic Information. arXiv 2020, arXiv:2006.00987. [Google Scholar]
- Neary, T.; Woods, D. Small weakly universal Turing machines. In International Symposium on Fundamentals of Computation Theory; Springer: Berlin/Heidelberg, Germany, 2009; pp. 262–273. [Google Scholar]
- Zenil, H.; Badillo, L.; Hernández-Orozco, S.; Hernández-Quiroz, F. Coding-theorem like behaviour and emergence of the universal distribution from resource-bounded algorithmic probability. Int. J. Parallel Emergent Distrib. Syst. 2019, 34, 161–180. [Google Scholar] [CrossRef]
- Hutter, M. Algorithmic information theory: A brief non-technical guide to the field. arXiv 2007, arXiv:cs/0703024. [Google Scholar]
- Solomonoff, R.J. A formal theory of inductive inference. Part I. Inf. Control 1964, 7, 1–22. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Int. J. Comput. Math. 1968, 2, 157–168. [Google Scholar] [CrossRef]
- Chaitin, G.J. On the length of programs for computing finite binary sequences. JACM 1966, 13, 547–569. [Google Scholar] [CrossRef]
- Li, M.; Vitányi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Cham, Switzerland, 2008; Volume 3. [Google Scholar]
- Levin, L.A. Laws of information conservation (nongrowth) and aspects of the foundation of probability theory. Probl. Peredachi Inf. 1974, 10, 30–35. [Google Scholar]
- Schmidhuber, J. The Speed Prior: A new simplicity measure yielding near-optimal computable predictions. In International Conference on Computational Learning Theory; Springer: Berlin/Heidelberg, Germany, 2002; pp. 216–228. [Google Scholar]
- Soler-Toscano, F.; Zenil, H.; Delahaye, J.P.; Gauvrit, N. Calculating Kolmogorov complexity from the output frequency distributions of small Turing machines. PLoS ONE 2014, 9, e96223. [Google Scholar] [CrossRef] [PubMed]
- Catt, E.; Hutter, M. A Gentle Introduction to Quantum Computing Algorithms with Applications to Universal Prediction. arXiv 2020, arXiv:2005.03137. [Google Scholar]
- Molina, A.; Watrous, J. Revisiting the simulation of quantum Turing machines by quantum circuits. Proc. R. Soc. A 2019, 475, 20180767. [Google Scholar] [CrossRef]
- Gorard, J. Some Quantum Mechanical Properties of the Wolfram Model; Complex Systems: Champaign, IL, USA, 2020; pp. 537–598. [Google Scholar]
- Hollenberg, L.C. Fast quantum search algorithms in protein sequence comparisons: Quantum bioinformatics. Phys. Rev. E 2000, 62, 7532. [Google Scholar] [CrossRef]
- Hutter, M. Universal Artificial Intelligence: Sequential Decisions Based on Algorithmic Probability; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Stanley, K.O.; Clune, J.; Lehman, J.; Miikkulainen, R. Designing neural networks through neuroevolution. Nat. Mach. Intell. 2019, 1, 24–35. [Google Scholar] [CrossRef]
- Chaitin, G.J. Meta math! the quest for omega. arXiv 2004, arXiv:math/0404335. [Google Scholar]
- Marletto, C. Constructor theory of life. J. R. Soc. Interface 2015, 12, 20141226. [Google Scholar] [CrossRef] [PubMed]
- Endoh, Y. Mame/Doublehelix. 2020. Available online: https://github.com/mame/doublehelix (accessed on 3 February 2021).
- Sarkar, A.; Al-Ars, Z.; Bertels, K. Quines are the Fittest Programs-Nesting Algorithmic Probability Converges to Constructors. Preprints 2020. [Google Scholar] [CrossRef]
- Noireaux, V.; Maeda, Y.T.; Libchaber, A. Development of an artificial cell, from self-organization to computation and self-reproduction. Proc. Natl. Acad. Sci. USA 2011, 108, 3473–3480. [Google Scholar] [CrossRef]
- Sipper, M.; Reggia, J.A. Go forth and replicate. Sci. Am. 2001, 285, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Condon, A.; Kirchner, H.; Larivière, D.; Marshall, W.; Noireaux, V.; Tlusty, T.; Fourmentin, E. Will biologists become computer scientists? EMBO Rep. 2018, 19, e46628. [Google Scholar] [CrossRef]
- Zenil, H.; Minary, P. Training-free measures based on algorithmic probability identify high nucleosome occupancy in DNA sequences. Nucleic Acids Res. 2019, 47, e129. [Google Scholar] [CrossRef] [PubMed]
- Gauvrit, N.; Zenil, H.; Delahaye, J.P.; Soler-Toscano, F. Algorithmic complexity for short binary strings applied to psychology: A primer. Behav. Res. Methods 2014, 46, 732–744. [Google Scholar] [CrossRef] [PubMed]
- Zenil, H. Compression-based investigation of the dynamical properties of cellular automata and other systems. arXiv 2009, arXiv:0910.4042. [Google Scholar] [CrossRef]
- Zenil, H.; Villarreal-Zapata, E. Asymptotic behavior and ratios of complexity in cellular automata. Int. J. Bifurc. Chaos 2013, 23, 1350159. [Google Scholar] [CrossRef]
- Brandouy, O.; Delahaye, J.P.; Ma, L.; Zenil, H. Algorithmic complexity of financial motions. Res. Int. Bus. Financ. 2014, 30, 336–347. [Google Scholar] [CrossRef]
- Zenil, H.; Delahaye, J.P. An algorithmic information theoretic approach to the behaviour of financial markets. J. Econ. Surv. 2011, 25, 431–463. [Google Scholar] [CrossRef]
- Delahaye, J.P.; Zenil, H. On the Kolmogorov-Chaitin Complexity for short sequences. arXiv 2007, arXiv:abs/0704.1043. [Google Scholar]
- Gauvrit, N.; Singmann, H.; Soler Toscano, F.; Zenil, H. Algorithmic Complexity for Short Strings [R Package Acss Version 0.2-5]. Available online: https://cran.r-project.org/web/packages/acss/index.html (accessed on 3 February 2021).
- Calude, C.S.; Stay, M.A. Most Programs Stop Quickly or Never Halt. arXiv 2006, arXiv:cs/0610153. [Google Scholar] [CrossRef]
- Valiant, L.G. The complexity of computing the permanent. Theor. Comput. Sci. 1979, 8, 189–201. [Google Scholar] [CrossRef]
- Complexity Zoo. Available online: https://complexityzoo.net/Complexity_Zoo (accessed on 3 February 2021).
- Aaronson, S. Quantum computing, postselection, and probabilistic polynomial-time. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 3473–3482. [Google Scholar] [CrossRef]
- Aaronson, S.; Arkhipov, A. The computational complexity of linear optics. In Proceedings of the 43rd Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011; pp. 333–342. [Google Scholar]
- Abrams, D.S.; Lloyd, S. Simulation of many-body Fermi systems on a universal quantum computer. Phys. Rev. Lett. 1997, 79, 2586. [Google Scholar] [CrossRef]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [PubMed]
- Brassard, G.; Høyer, P.; Tapp, A. Quantum counting. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 1998; pp. 820–831. [Google Scholar]
- Wie, C.R. Simpler quantum counting. arXiv 2019, arXiv:1907.08119. [Google Scholar]
- Suzuki, Y.; Uno, S.; Raymond, R.; Tanaka, T.; Onodera, T.; Yamamoto, N. Amplitude estimation without phase estimation. Quantum Inf. Process. 2020, 19, 75. [Google Scholar] [CrossRef]
- Aaronson, S.; Rall, P. Quantum approximate counting, simplified. In Proceedings of the Symposium on Simplicity in Algorithms, Salt Lake City, UT, USA, 6–7 January 2020; pp. 24–32. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum approximate optimization algorithm. arXiv 2014, arXiv:1411.4028. [Google Scholar]
- Jiang, Z.; Rieffel, E.G.; Wang, Z. Near-optimal quantum circuit for Grover’s unstructured search using a transverse field. Phys. Rev. A 2017, 95, 062317. [Google Scholar] [CrossRef]
- Morales, M.E.; Tlyachev, T.; Biamonte, J. Variational learning of Grover’s quantum search algorithm. Phys. Rev. A 2018, 98, 062333. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; Volume 5. [Google Scholar]
- Adams, A.; Zenil, H.; Davies, P.C.; Walker, S.I. Formal definitions of unbounded evolution and innovation reveal universal mechanisms for open-ended evolution in dynamical systems. Sci. Rep. 2017, 7, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Atlan, H.; Koppel, M. The cellular computer DNA: Program or data. Bull. Math. Biol. 1990, 52, 335–348. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Searls, D.B. Gene structure prediction by linguistic methods. Genomics 1994, 23, 540–551. [Google Scholar] [CrossRef] [PubMed]
- Coste, F. Learning the language of biological sequences. In Topics in Grammatical Inference; Springer: Berlin/Heidelberg, Germany, 2016; pp. 215–247. [Google Scholar]
- Vallejo, E.E.; Ramos, F. Evolving Turing machines for biosequence recognition and analysis. In European Conference on Genetic Programming; Springer: Berlin/Heidelberg, Germany, 2001; pp. 192–203. [Google Scholar]
- Antão, R.; Mota, A.; Machado, J.T. Kolmogorov complexity as a data similarity metric: Application in mitochondrial DNA. Nonlinear Dyn. 2018, 93, 1059–1071. [Google Scholar] [CrossRef]
- Bertels, K.; Ashraf, I.; Nane, R.; Fu, X.; Riesebos, L.; Varsamopoulos, S.; Mouedenne, A.; Van Someren, H.; Sarkar, A.; Khammassi, N. Quantum computer architecture: Towards full-stack quantum accelerators. arXiv 2019, arXiv:1903.09575. [Google Scholar]
- Sarkar, A.; Al-Ars, Z.; Almudever, C.G.; Bertels, K. An algorithm for DNA read alignment on quantum accelerators. arXiv 2019, arXiv:1909.05563. [Google Scholar]
- Sarkar, A.; Al-Ars, Z.; Bertels, K. QuASeR–Quantum Accelerated De Novo DNA Sequence Reconstruction. arXiv 2020, arXiv:2004.05078. [Google Scholar]
- Machado, J.T.; Rocha-Neves, J.M.; Andrade, J.P. Computational analysis of the SARS-CoV-2 and other viruses based on the Kolmogorov’s complexity and Shannon’s information theories. Nonlinear Dyn. 2020, 101, 1731–1750. [Google Scholar] [CrossRef] [PubMed]
- Gordon, D.E.; Jang, G.M.; Bouhaddou, M.; Xu, J.; Obernier, K.; White, K.M.; O’Meara, M.J.; Rezelj, V.V.; Guo, J.Z.; Swaney, D.L.; et al. A SARS-CoV-2 protein interaction map reveals targets for drug repurposing. Nature 2020, 583, 459–468. [Google Scholar] [CrossRef] [PubMed]
- Adams, A. The Role of Emergence in Open-ended Systems. AUTOMATA 2020, unpublished. [Google Scholar]
- Angermueller, C.; Belanger, D.; Gane, A.; Mariet, Z.; Dohan, D.; Murphy, K.; Colwell, L.; Sculley, D. Population-Based Black-Box Optimization for Biological Sequence Design. arXiv 2020, arXiv:2006.03227. [Google Scholar]
- Vedral, V.; Barenco, A.; Ekert, A. Quantum networks for elementary arithmetic operations. Phys. Rev. A 1996, 54, 147. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkar, A.; Al-Ars, Z.; Bertels, K. Estimating Algorithmic Information Using Quantum Computing for Genomics Applications. Appl. Sci. 2021, 11, 2696. https://doi.org/10.3390/app11062696
Sarkar A, Al-Ars Z, Bertels K. Estimating Algorithmic Information Using Quantum Computing for Genomics Applications. Applied Sciences. 2021; 11(6):2696. https://doi.org/10.3390/app11062696
Chicago/Turabian StyleSarkar, Aritra, Zaid Al-Ars, and Koen Bertels. 2021. "Estimating Algorithmic Information Using Quantum Computing for Genomics Applications" Applied Sciences 11, no. 6: 2696. https://doi.org/10.3390/app11062696
APA StyleSarkar, A., Al-Ars, Z., & Bertels, K. (2021). Estimating Algorithmic Information Using Quantum Computing for Genomics Applications. Applied Sciences, 11(6), 2696. https://doi.org/10.3390/app11062696






