Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment
Abstract
1. Introduction
2. Theories and Methods
2.1. Soil–Water Characteristic Curve
2.2. Bayesian Model Updating
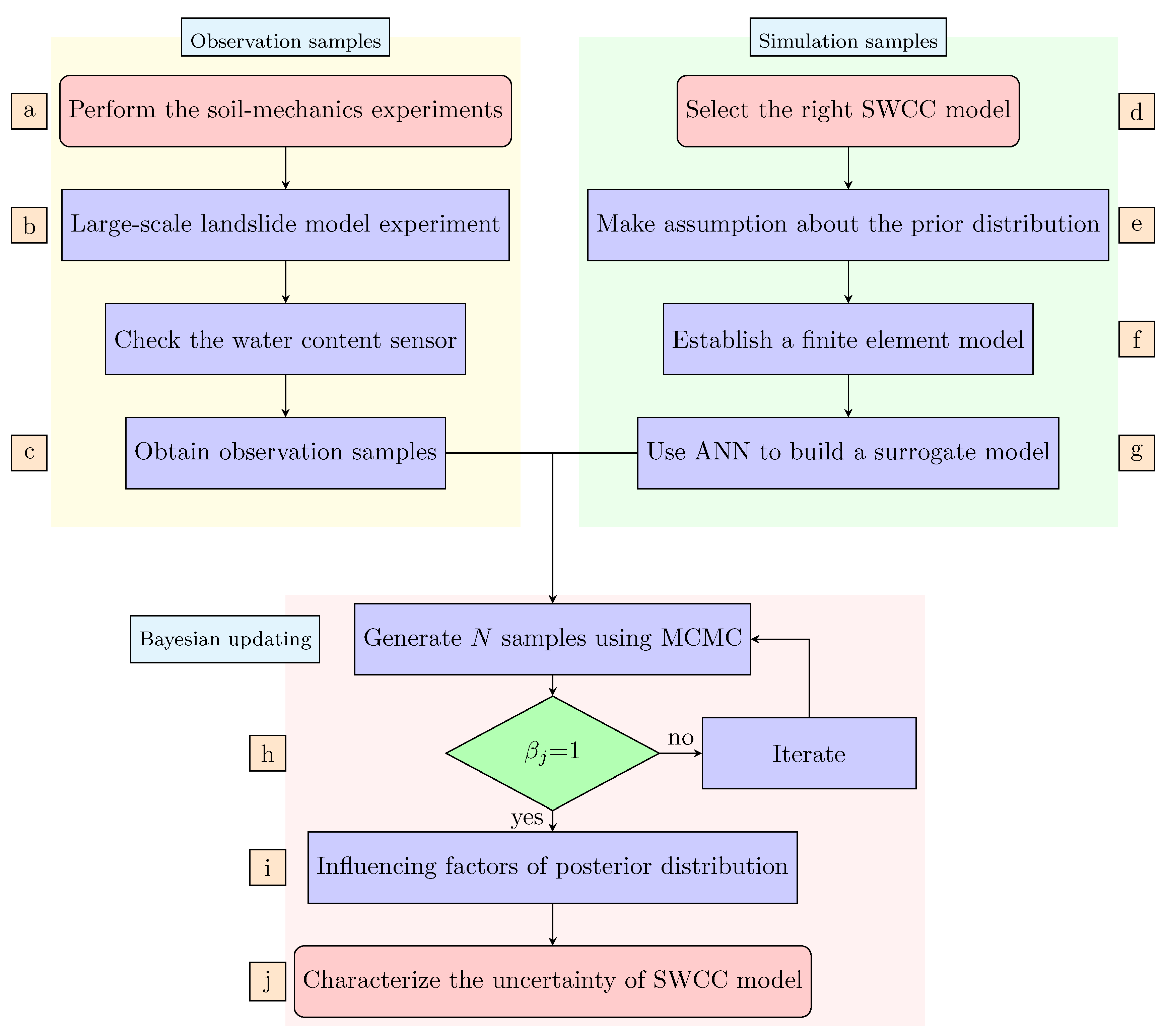
3. The Bayesian Updating Procedure of Monitor Data in the Large-Scale Landslide Model Experiment
- Regarding the left branch, the main goal was to obtain Bayesian updating evidence (water content observation samples ) through the water content detection of large-scale landslide models:
- (a)
- Infiltration experiments and a triaxial experiment were carried out, and the material ratio of landslide body was determined to be 7:3 for soil:stone through these experiments.
- (b)
- Large-scale landslide models were built according to the layer-by-layer compaction method. The place where the sensor was buried was carefully compacted to avoid damage to the sensor.
- (c)
- After the landslide model and sensor were ready, the moisture content sensor was tested to determine the reliability of its data.
- In the right branch, the main work was to obtain the Bayesian updating simulation samples () through the finite element model:
- (d)
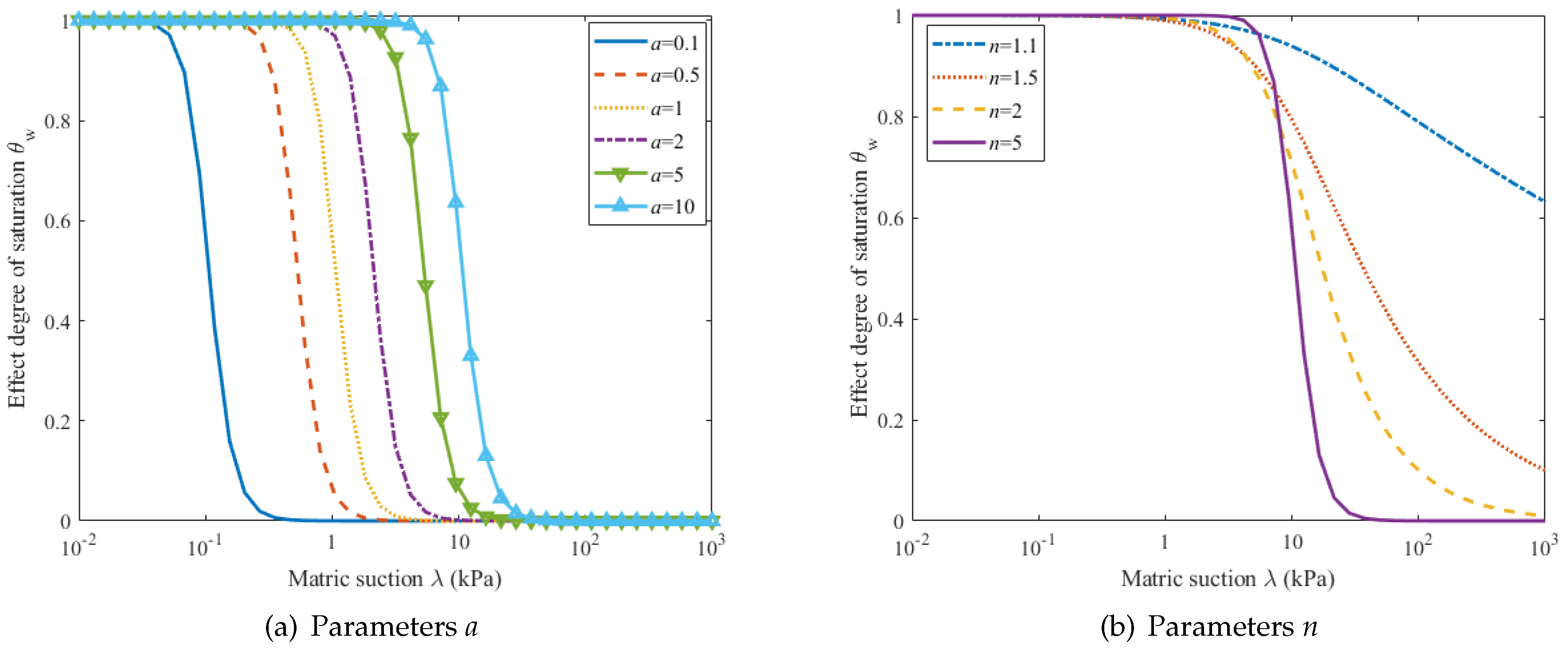
- The SWCC model was selected (VG model), and we analyzed the two model parameters within its range to observe their influences on the curve shape.
- (e)
- We assumed the prior distribution as normal or lognormal according to existing research. Then we determined the prior distribution of SWCC for the model parameters a and n, based on experimental data and research results.
- (f)
- A finite element (FE) numerical model was developed according to the large-scale landslide test; we evaluated the seepage flow under the conditions of the reservoir water level.
- (g)
- In the Bayesian updating process, it is necessary to call the FE model, taking a long time to obtain the large number of output values. Therefore, this paper used an artificial neural network (ANN) as a surrogate model to speed up the analysis.
- In the lower part of the flowchart, the main work was to perform Bayesian updating by combining the water content observation samples () of the large landslide model of the left branch and the simulation samples () of the right branch:
- (h)
- The MCMC algorithm was used to generate N random samples that followed the posterior distribution of SWCC parameters and iteratively continued until = 1. We got the posterior distribution of SWCC model parameters (posterior most likely value, posterior mean, posterior standard deviation, etc.).
- (i)
- We analyzed the factors influencing the posterior distribution results, such as the number of observation datums, the prior distribution, and the observation data that changed over time.
- (j)
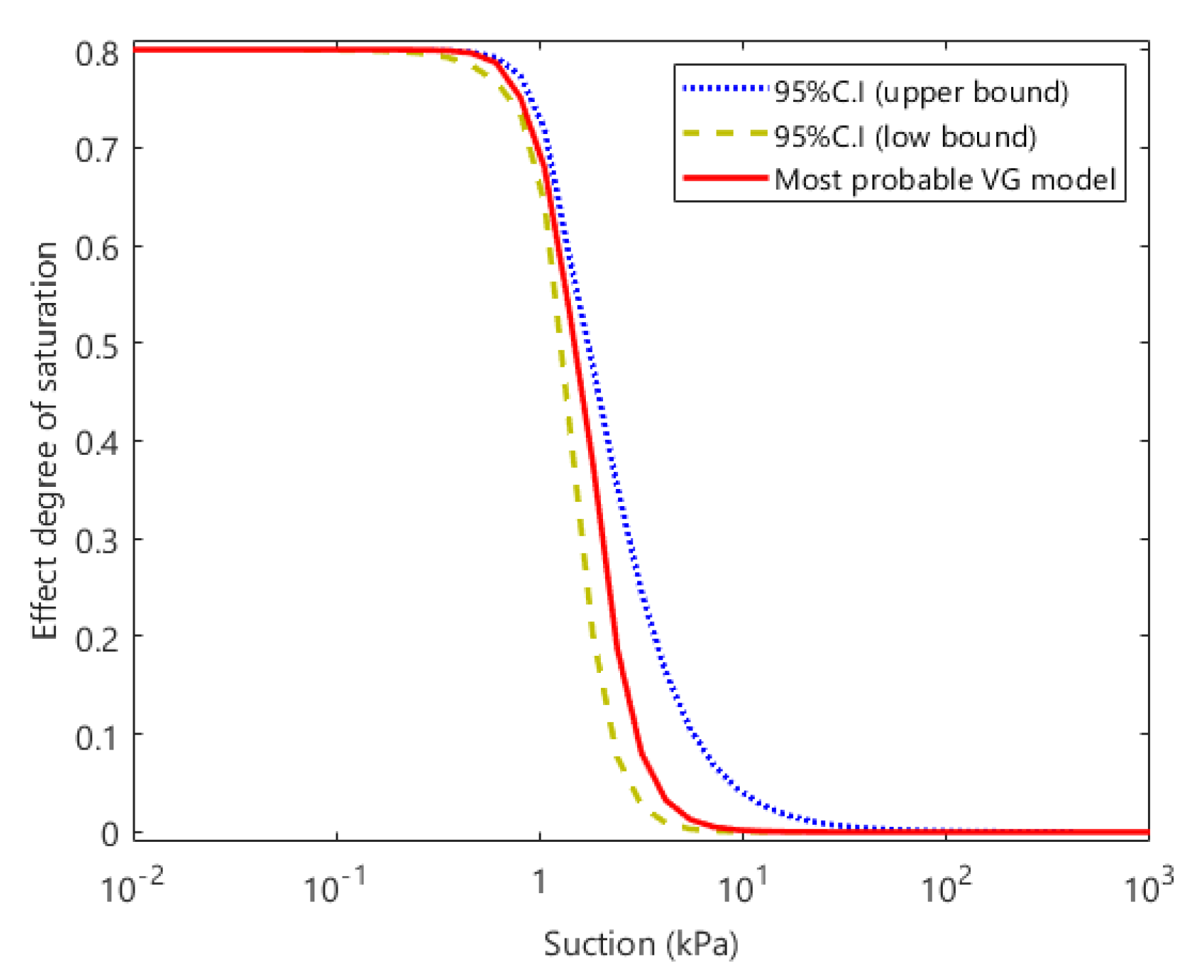
- We characterized the uncertainty of the SWCC model. For the parameters of the SWCC, the N samples generated from the MCMC algorithm were ranked, and a 95% confidence interval was obtained.
4. The Large-Scale Landslide Model Experiment and Bayesian Updating
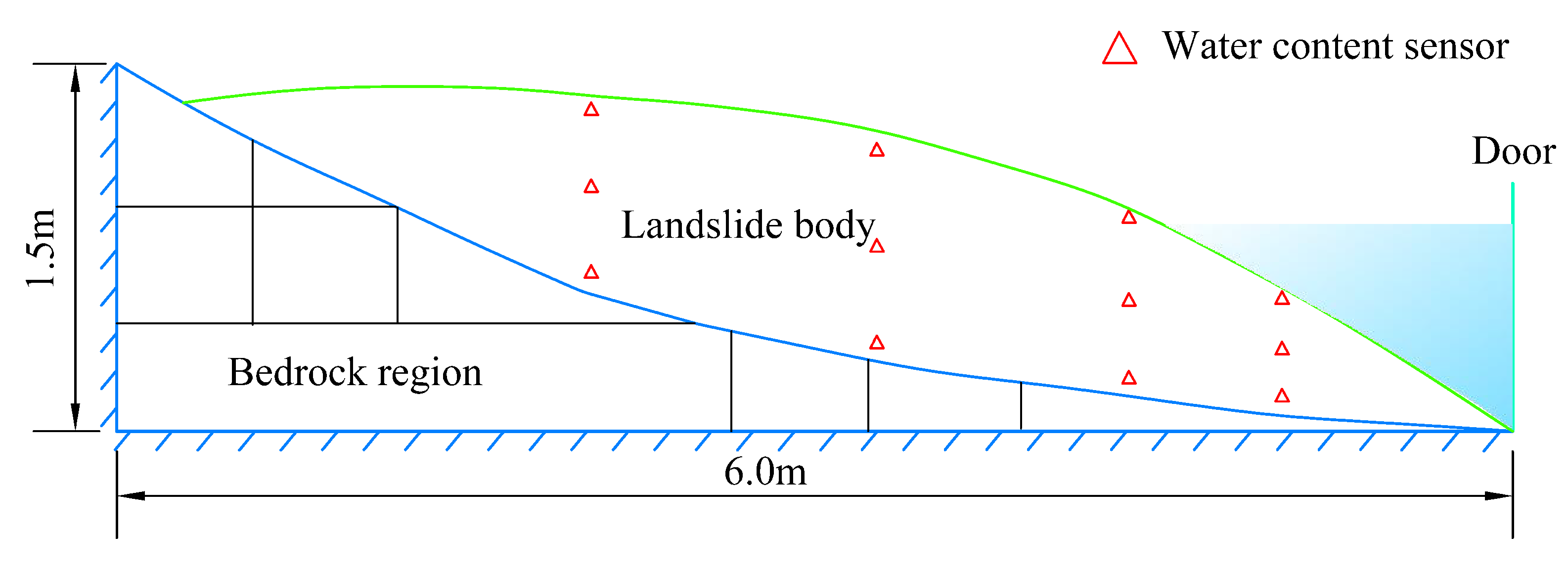
4.1. Experiment Setup
4.2. FEM Simulation
4.3. Surrogate Model
5. Results
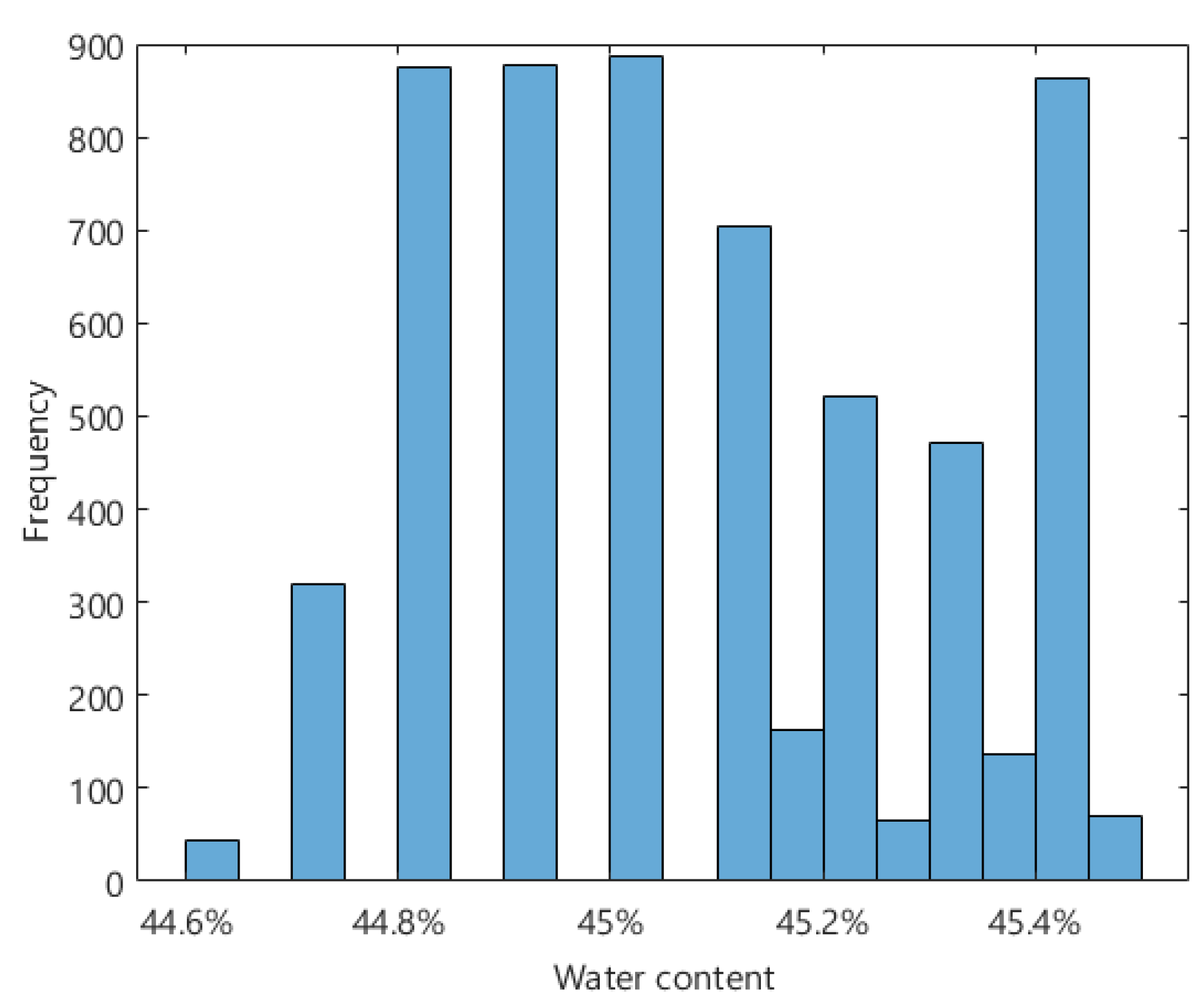
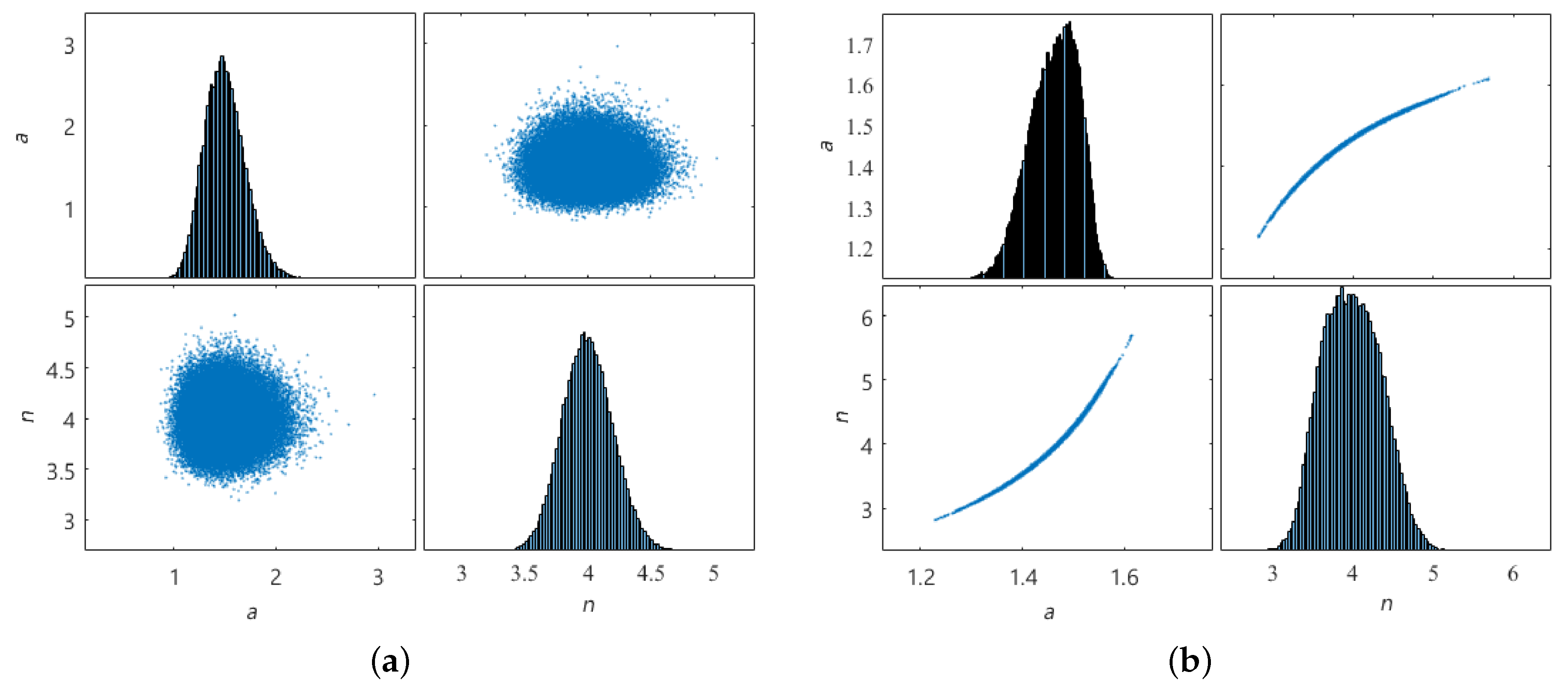
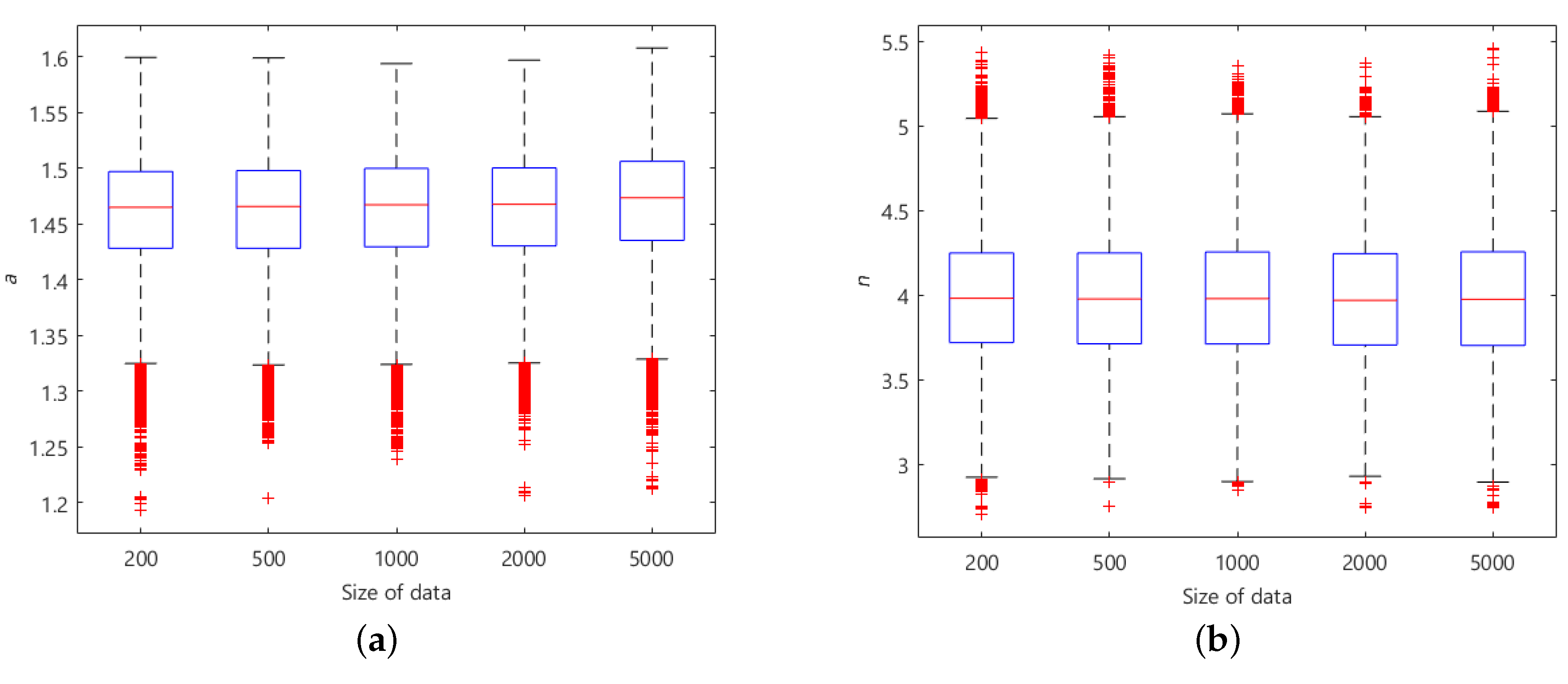
5.1. Effect of Dataset Size on the Outcome of Bayesian Updating
5.2. The Effect of Prior Distribution on the Outcome of Bayesian Updating
5.3. The Effects of Six Stages on the Outcome of Bayesian Updating
5.4. Characterization of Uncertainty
6. Discussion
7. Conclusions
- This paper proposes a Bayesian-based analysis method that can take the parameters’ uncertainty into account, and is different from conventional deterministic analysis methods. The feasibility of the Bayesian updating method in the monitoring data of a large landslide model was demonstrated. Through the Bayesian updating, the posterior value ranges of the SWCC parameters will be narrowed compared to the prior ones.
- The Bayesian updating method has good application prospects in landslide monitoring. When the prior distribution is lognormal, the coefficient of variation of the posterior distribution is smaller than that of the normal distribution. The SWCC parameter a tends to increase when the posterior distribution changes with time.
- In the process of Bayesian updating, a numerical simulation based in a FE model was used. Alternatively, a ANN surrogate model was also trained based on the FE model. This method can greatly improve the efficiency of Bayesian model updating—its accuracy being acceptable.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, X.; Wang, X.; Khoshnevisan, S.; Hou, X.; Zha, F. Seepage analysis of earth dams considering spatial variability of hydraulic parameters. Eng. Geol. 2017, 228, 260–269. [Google Scholar] [CrossRef]
- Zheng, D.; Huang, J.; Li, D.Q.; Kelly, R.; Sloan, S.W. Embankment prediction using testing data and monitored behaviour: A Bayesian updating approach. Comput. Geotech. 2018, 93, 150–162. [Google Scholar] [CrossRef]
- Wang, B.; Li, J.; Jiang, Q.; Yang, Y.; Feng, X.T. An improved FE-Meshfree method for solving steady seepage problems. Comput. Geotech. 2020, 119, 103223. [Google Scholar] [CrossRef]
- Guan, X.; Jha, R.; Liu, Y. Model selection, updating, and averaging for probabilistic fatigue damage prognosis. Struct. Saf. 2011, 33, 242–249. [Google Scholar] [CrossRef]
- Mia, M.; Dhar, N.R. Response surface and neural network based predictive models of cutting temperature in hard turning. J. Adv. Res. 2016, 7, 1035–1044. [Google Scholar] [CrossRef]
- Strauss, A.; Frangopol, D.M.; Kim, S. Use of monitoring extreme data for the performance prediction of structures: Bayesian updating. Eng. Struct. 2008, 30, 3654–3666. [Google Scholar] [CrossRef]
- Hsein Juang, C.; Luo, Z.; Atamturktur, S.; Huang, H. Bayesian updating of soil parameters for braced excavations using field observations. J. Geotech. Geoenviron. Eng. 2013, 139, 395–406. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Uncertainty of the soil–water characteristic curve and its effects on slope seepage and stability analysis under conditions of rainfall using the Markov Chain Monte Carlo Method. Water 2017, 9, 758. [Google Scholar] [CrossRef]
- Lam, H.F.; Yang, J.; Au, S.K. Bayesian model updating of a coupled-slab system using field test data utilizing an enhanced Markov chain Monte Carlo simulation algorithm. Eng. Struct. 2015, 102, 144–155. [Google Scholar] [CrossRef]
- Rocchetta, R.; Broggi, M.; Huchet, Q.; Patelli, E. On-line Bayesian model updating for structural health monitoring. Mech. Syst. Signal Process. 2018, 103, 174–195. [Google Scholar] [CrossRef]
- Bi, S.; Broggi, M.; Beer, M. The role of the Bhattacharyya distance in stochastic model updating. Mech. Syst. Signal Process. 2019, 117, 437–452. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Neuman, S.P.; Witherspoon, P.A. Finite element method of analyzing steady seepage with a free surface. Water Resour. Res. 1970, 6, 889–897. [Google Scholar] [CrossRef]
- Leong, E.C.; Rahardjo, H. Review of soil-water characteristic curve equations. J. Geotech. Geoenviron. Eng. 1997, 123, 1106–1117. [Google Scholar] [CrossRef]
- Thu, T.M.; Rahardjo, H.; Leong, E.C. Elastoplastic model for unsaturated soil with incorporation of the soil-water characteristic curve. Can. Geotech. J. 2007, 44, 67–77. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Gardner, W. Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 1958, 85, 228–232. [Google Scholar] [CrossRef]
- Li, D.Q.; Qi, X.H.; Phoon, K.K.; Zhang, L.M.; Zhou, C.B. Effect of spatially variable shear strength parameters with linearly increasing mean trend on reliability of infinite slopes. Struct. Saf. 2014, 49, 45–55. [Google Scholar] [CrossRef]
- Li, D.Q.; Wang, L.; Cao, Z.J.; Qi, X.H. Reliability analysis of unsaturated slope stability considering SWCC model selection and parameter uncertainties. Eng. Geol. 2019, 260, 105207. [Google Scholar] [CrossRef]
- Johari, A.; Talebi, A. Stochastic Analysis of Rainfall-Induced Slope Instability and Steady-State Seepage Flow Using Random Finite-Element Method. Int. J. Geomech. 2019, 19, 04019085. [Google Scholar] [CrossRef]
- Han, Z.; Vanapalli, S.K. Model for predicting resilient modulus of unsaturated subgrade soil using soil-water characteristic curve. Can. Geotech. J. 2015, 52, 1605–1619. [Google Scholar] [CrossRef]
- Brutsaert, W. Probability laws for pore-size distributions. Soil Sci. 1966, 101, 85–92. [Google Scholar] [CrossRef]
- Chiu, C.; Yan, W.; Yuen, K.V. Reliability analysis of soil–water characteristics curve and its application to slope stability analysis. Eng. Geol. 2012, 135, 83–91. [Google Scholar] [CrossRef]
- Ching, J.; Chen, Y.C. Transitional Markov chain Monte Carlo method for Bayesian model updating, model class selection, and model averaging. J. Eng. Mech. 2007, 133, 816–832. [Google Scholar] [CrossRef]
- Patelli, E.; Govers, Y.; Broggi, M.; Gomes, H.M.; Link, M.; Mottershead, J.E. Sensitivity or Bayesian model updating: A comparison of techniques using the DLR AIRMOD test data. Arch. Appl. Mech. 2017, 87, 905–925. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Z.J.; Li, D.Q.; Phoon, K.K.; Au, S.K. Determination of site-specific soil-water characteristic curve from a limited number of test data—A Bayesian perspective. Geosci. Front. 2018, 9, 1665–1677. [Google Scholar] [CrossRef]
- Kelly, R.; Huang, J. Bayesian updating for one-dimensional consolidation measurements. Can. Geotech. J. 2015, 52, 1318–1330. [Google Scholar] [CrossRef]
- Papaioannou, I.; Straub, D. Reliability updating in geotechnical engineering including spatial variability of soil. Comput. Geotech. 2012, 42, 44–51. [Google Scholar] [CrossRef]
- He, L.; Liu, Y.; Bi, S.; Wang, L.; Broggi, M.; Beer, M. Estimation of failure probability in braced excavation using Bayesian networks with integrated model updating. Undergr. Space 2019. [Google Scholar] [CrossRef]
- Tian, M.; Li, D.Q.; Cao, Z.J.; Phoon, K.K.; Wang, Y. Bayesian identification of random field model using indirect test data. Eng. Geol. 2016, 210, 197–211. [Google Scholar] [CrossRef]
- Phoon, K.K.; Tang, C. Characterisation of geotechnical model uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 101–130. [Google Scholar] [CrossRef]
- Beck, J.L.; Katafygiotis, L.S. Updating models and their uncertainties. I: Bayesian statistical framework. J. Eng. Mech. 1998, 124, 455–461. [Google Scholar] [CrossRef]
- Katafygiotis, L.S.; Beck, J.L. Updating models and their uncertainties. II: Model identifiability. J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E. Understanding the metropolis-hastings algorithm. Am. Stat. 1995, 49, 327–335. [Google Scholar]
- Arshad, I.; Baber, M. Finite element analysis of seepage through an earthen dam by using geo-slope (SEEP/W) software. Int. J. Res 2014, 1, 612–619. [Google Scholar]
- Wang, L.; Tang, L.; Wang, Z.; Liu, H.; Zhang, W. Probabilistic characterization of the soil-water retention curve and hydraulic conductivity and its application to slope reliability analysis. Comput. Geotech. 2020, 121, 103460. [Google Scholar] [CrossRef]




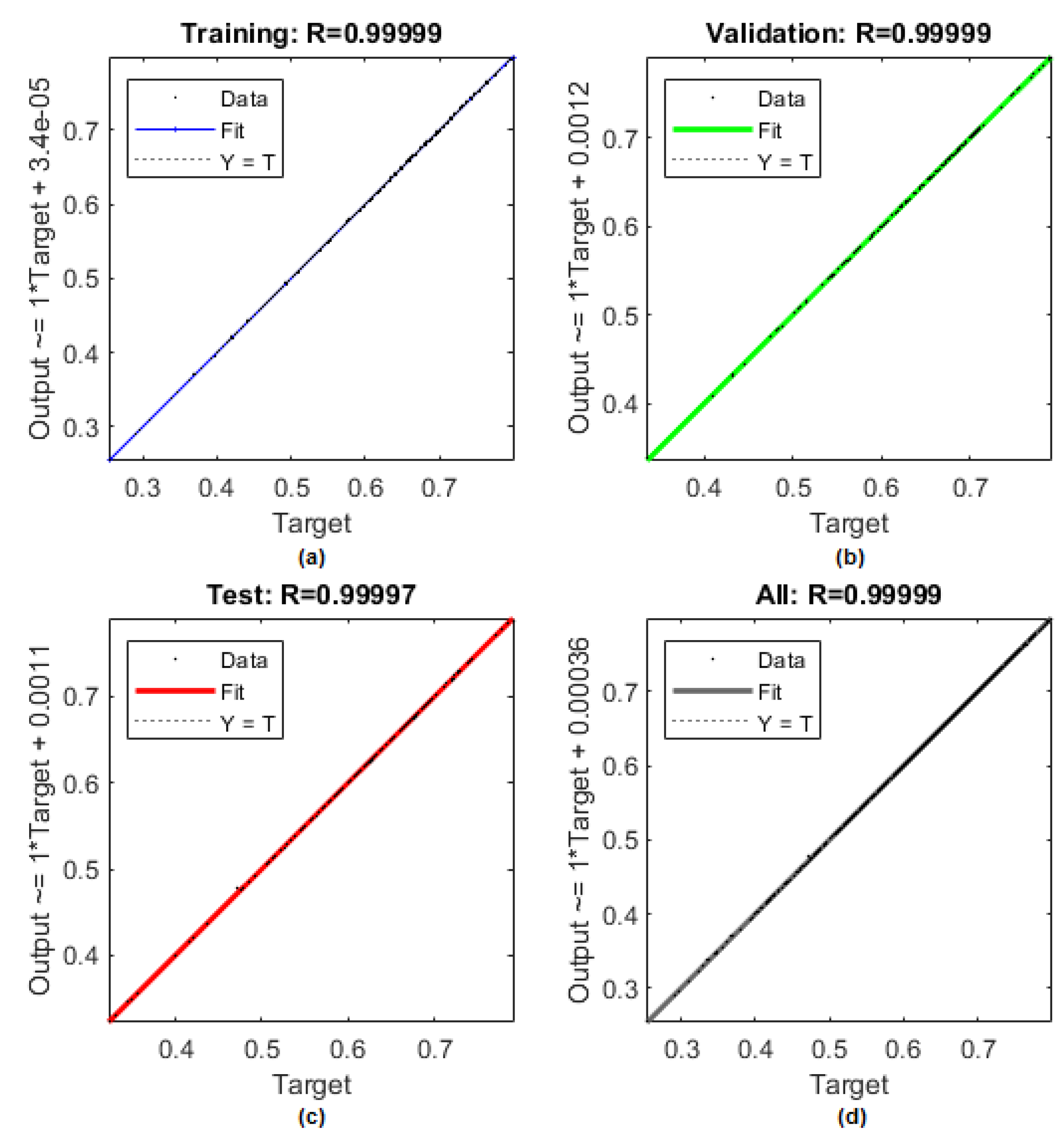


| Samples | MSE | R | |
|---|---|---|---|
| Training | 700 | 1.43430 × 10 | 9.99991 × 10 |
| Validations | 150 | 1.67754 × 10 | 9.99989 × 10 |
| Testing | 150 | 5.56267 × 10 | 9.99968 × 10 |
| Most Probable VG Model Parameters | Posterior Mean | Posterior Standard Deviation | ||||
|---|---|---|---|---|---|---|
| Dataset Size | ||||||
| 200 | 1.47 | 3.94 | 1.459 | 3.981 | 0.048 | 0.363 |
| 500 | 1.48 | 3.92 | 1.460 | 3.980 | 0.048 | 0.359 |
| 1000 | 1.49 | 3.85 | 1.462 | 3.985 | 0.048 | 0.364 |
| 2000 | 1.49 | 3.85 | 1.464 | 3.988 | 0.048 | 0.367 |
| 5000 | 1.50 | 3.84 | 1.468 | 3.978 | 0.048 | 0.364 |
| Most Probable VG Model Parameters | Posterior Mean | Posterior Standard Deviation | ||||
|---|---|---|---|---|---|---|
| Type | ||||||
| normal distribution | 1.48 | 4.06 | 1.462 | 3.987 | 0.048 | 0.367 |
| lognormal distribution | 1.49 | 3.85 | 1.462 | 3.985 | 0.048 | 0.364 |
| Most Probable VG Model Parameters | Posterior Mean | Posterior Standard Deviation | ||||
|---|---|---|---|---|---|---|
| Stage | ||||||
| 1 | 1.49 | 3.85 | 1.462 | 3.985 | 0.048 | 0.364 |
| 2 | 1.483 | 4.03 | 1.465 | 3.978 | 0.048 | 0.362 |
| 3 | 1.486 | 4.01 | 1.469 | 3.984 | 0.047 | 0.360 |
| 4 | 1.498 | 3.98 | 1.472 | 3.983 | 0.048 | 0.369 |
| 5 | 1.508 | 3.80 | 1.476 | 3.985 | 0.047 | 0.364 |
| 6 | 1.513 | 3.82 | 1.480 | 3.983 | 0.047 | 0.365 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Tian, B.; Lu, X.; Beer, M.; Broggi, M.; Bi, S.; Xiong, B.; He, T. Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment. Appl. Sci. 2020, 10, 5526. https://doi.org/10.3390/app10165526
Feng C, Tian B, Lu X, Beer M, Broggi M, Bi S, Xiong B, He T. Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment. Applied Sciences. 2020; 10(16):5526. https://doi.org/10.3390/app10165526
Chicago/Turabian StyleFeng, Chengxin, Bin Tian, Xiaochun Lu, Michael Beer, Matteo Broggi, Sifeng Bi, Bobo Xiong, and Teng He. 2020. "Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment" Applied Sciences 10, no. 16: 5526. https://doi.org/10.3390/app10165526
APA StyleFeng, C., Tian, B., Lu, X., Beer, M., Broggi, M., Bi, S., Xiong, B., & He, T. (2020). Bayesian Updating of Soil–Water Character Curve Parameters Based on the Monitor Data of a Large-Scale Landslide Model Experiment. Applied Sciences, 10(16), 5526. https://doi.org/10.3390/app10165526





