Pole Assignment for Active Vibration Control of Linear Vibrating Systems through Linear Matrix Inequalities
Abstract
1. Introduction
1.1. State of the Art
1.2. Motivations and Contributions of This Paper
2. Definitions
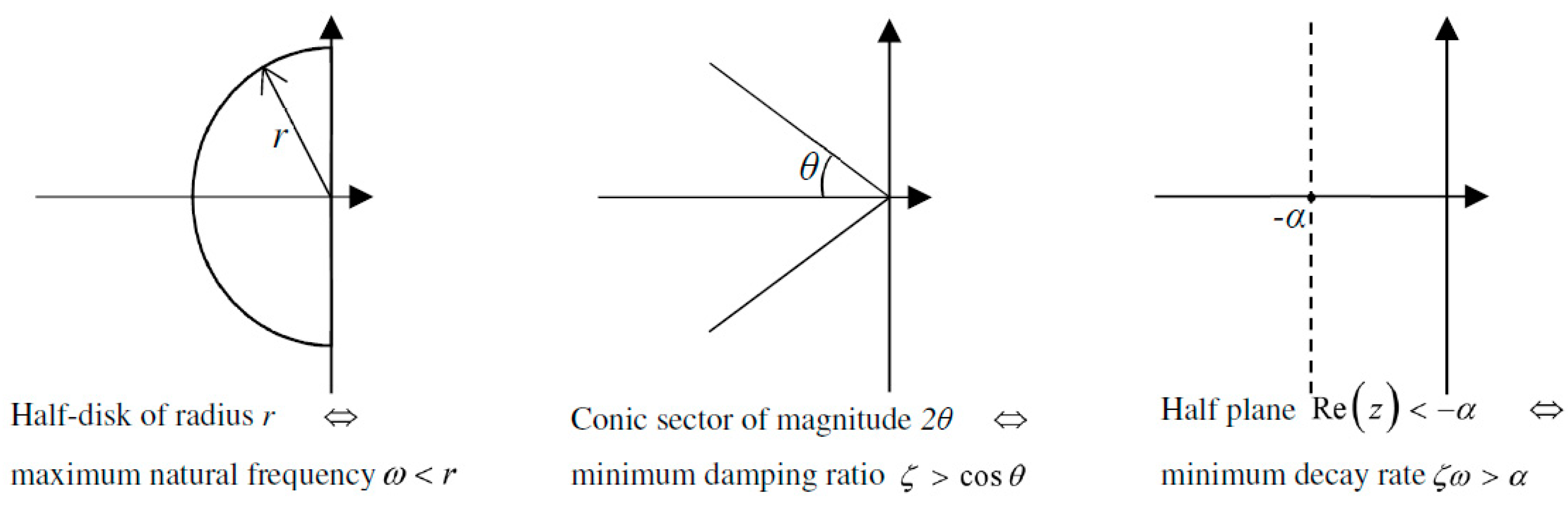
Control Specifications
- the controlled system has exactly the p desired poles in ,
- the remaining poles must belong to some prescribed regions of the complex plane.
3. First Step: Exact Placement of the Dominant Poles
3.1. Formulation for Symmetric Systems
3.2. Extension to Asymmetric Systems
4. Second Step: Regional Pole Placement
4.1. Overview
4.2. Linear Matrix Inequalities
4.3. Control Gain Synthesis
4.4. Insights on the Reduced Model and on the Inclusion Principle
5. Results
5.1. Test-Case 1: Three-Mass System
5.2. Test-Case 2: Slider-Belt System
5.3. Test-Case 3: Aircraft Wing System
5.4. Test-Case 4: Four-Bar Flexible-Link Multibody System
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ram, Y.M.; Mottershead, J.E. Receptance method in active vibration control. AIAA J. 2007. [Google Scholar] [CrossRef]
- Ouyang, H. Pole assignment of friction-induced vibration for stabilisation through state-feedback control. J. Sound Vib. 2010. [Google Scholar] [CrossRef]
- Ghandchi Tehrani, M.; Mottershead, J.E.; Shenton, A.T.; Ram, Y.M. Robust pole placement in structures by the method of receptances. Mech. Syst. Signal Process. 2011. [Google Scholar] [CrossRef]
- Ouyang, H.; Richiedei, D.; Trevisani, A. Pole assignment for control of flexible link mechanisms. J. Sound Vib. 2013. [Google Scholar] [CrossRef]
- Olanipekun, K.A.; Rustighi, E.; Ferguson, N.S. Active vibration control of planetary gears by pole placement. J. Phys. Conf. Ser. 2019, 1264, 012004. [Google Scholar] [CrossRef]
- Tehrani, M.G.; Ouyang, H. Receptance-Based Partial Pole Assignment for Asymmetric Systems Using State-Feedback. Shock Vib. 2012. [Google Scholar] [CrossRef]
- Ghandchi Tehrani, M.; Elliott, R.N.R.; Mottershead, J.E. Partial pole placement in structures by the method of receptances: Theory and experiments. J. Sound Vib. 2010. [Google Scholar] [CrossRef]
- Liang, Y.; Ouyang, H.J.; Yamaura, H. Active partial eigenvalue assignment for friction-induced vibration using receptance method. J. Phys. Conf. Ser. 2016, 744, 012008. [Google Scholar] [CrossRef]
- Araujo, J.M.; Dorea, C.E.; Goncalves, L.M.; Carvalho, J.B.; Datta, B.N. Robustness of the quadratic partial eigenvalue assignment using spectrum sensitivities for state and derivative feedback designs. J. Low Freq. Noise Vib. Act. Control 2018, 37, 253–268. [Google Scholar] [CrossRef]
- Bai, Z.J.; Wan, Q.Y. Partial quadratic eigenvalue assignment in vibrating structures using receptances and system matrices. Mech. Syst. Signal Process 2017, 88, 290–301. [Google Scholar] [CrossRef]
- Ou, L.; Han, S.; Wang, Y.; Dong, S.; Liu, L. Partial pole placement in LMI region. J. Control Sci. Eng. 2014. [Google Scholar] [CrossRef]
- Haddad, W.M.; Bernstein, D.S. Controller Design with Regional Pole Constraints. IEEE Trans. Automat. Contr. 1992. [Google Scholar] [CrossRef]
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Automat. Contr. 1996. [Google Scholar] [CrossRef]
- Datta, S.; Chakraborty, D.; Chaudhuri, B. Partial pole placement with controller optimization. IEEE Trans. Automat. Contr. 2012. [Google Scholar] [CrossRef][Green Version]
- de Almeida, M.O.; Araújo, J.M. Partial Eigenvalue Assignment for LTI Systems with D-Stability and LMI. J. Control Autom. Electr. Syst. 2019. [Google Scholar] [CrossRef]
- Belotti, R.; Richiedei, D. Pole assignment in vibrating systems with time delay: An approach embedding an a-priori stability condition based on Linear Matrix Inequality. Mech. Syst. Signal Process. 2020. [Google Scholar] [CrossRef]
- Caracciolo, R.; Richiedei, D.; Trevisani, A. Robust piecewise-linear state observers for flexible link mechanisms. J. Dyn. Syst. Meas. Control. Trans. ASME 2008. [Google Scholar] [CrossRef]
- Xiang, J.; Zhen, C.; Li, D. Partial pole assignment with time delay by the receptance method using multi-input control from measurement output feedback. Mech. Syst. Signal Process. 2016. [Google Scholar] [CrossRef]
- Ouyang, H. A hybrid control approach for pole assignment to second-order asymmetric systems. Mech. Syst. Signal Process. 2011. [Google Scholar] [CrossRef]
- Chen, M.; Ouyang, H.; Li, W.; Wang, D.; Liu, S. Partial Frequency Assignment for Torsional Vibration Control of Complex Marine Propulsion Shafting Systems. Appl. Sci. 2020, 10, 147. [Google Scholar] [CrossRef]
- Richiedei, D.; Tamellin, I.; Trevisani, A. Simultaneous assignment of resonances and antiresonances in vibrating systems through inverse dynamic structural modification. J. Sound Vib. 2020, 485, 115552. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA USA, 1994. [Google Scholar]
- Ikeda, M.; Siljak, D.D.; White, D.E. An Inclusion Principle for Dynamic Systems. IEEE Trans. Automat. Contr. 1984. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the Proceedings of the IEEE International Symposium on Computer-Aided Control System Design, New Orleans, LA, USA, 2–4 September 2004. [Google Scholar]
- Pappalardo, C.M.; Guida, D. Development of a new inertial-based vibration absorber for the active vibration control of flexible structures. Eng. Lett. 2018, 3, 372–385. [Google Scholar]
- Liang, Y.; Yamaura, H.; Ouyang, H. Active assignment of eigenvalues and eigen-sensitivities for robust stabilization of friction-induced vibration. Mech. Syst. Signal Process. 2017. [Google Scholar] [CrossRef]
- Soong, T.T. Active Structural Control: Theory and Practice, 1st ed.; Longman Scientific & Technical: Harlow, UK, 1990. [Google Scholar]
- Henrion, D.; Šebek, M.; Kučera, V. Robust pole placement for second-order systems: An LMI approach. Kybernetika 2005, 41, 1–14. [Google Scholar] [CrossRef]
- Abdelaziz, T.H.S. Robust pole assignment using velocity-acceleration feedback for second-order dynamical systems with singular mass matrix. ISA Trans. 2015. [Google Scholar] [CrossRef]
- Belotti, R.; Caracciolo, R.; Palomba, I.; Richiedei, D.; Trevisani, A. An Updating Method for Finite Element Models of Flexible-Link Mechanisms Based on an Equivalent Rigid-Link System. Shock Vib. 2018. [Google Scholar] [CrossRef]
- Boscariol, P.; Gasparetto, A.; Zanotto, V. Simultaneous position and vibration control system for flexible link mechanisms. Meccanica 2011. [Google Scholar] [CrossRef]
- Boscariol, P.; Gasparetto, A.; Zanotto, V. Active position and vibration control of a flexible links mechanism using model-based predictive control. J. Dyn. Syst. Meas. Control. Trans. ASME 2010. [Google Scholar] [CrossRef]





| Test-Case Section | 5.1 | 5.2 | 5.3 | 5.4 |
|---|---|---|---|---|
| System matrices | M, C, K Symmetric | M, C Symmetric K Asymmetric | M Symmetric C, K Asymmetric | M Symmetric C, K Asymmetric |
| Number of DOFs | 3 | 4 | 3 | 16 |
| Modeling approach | Lumped parameters | Lumped parameters | Lumped parameters | ERLS with FEM |
| Number of Assigned poles | 2 complex conjugate pole pair | 2 complex conjugate pole pairs | 1 complex conjugate pole pairs | 2 real poles and 3 complex conjugate pole pairs |
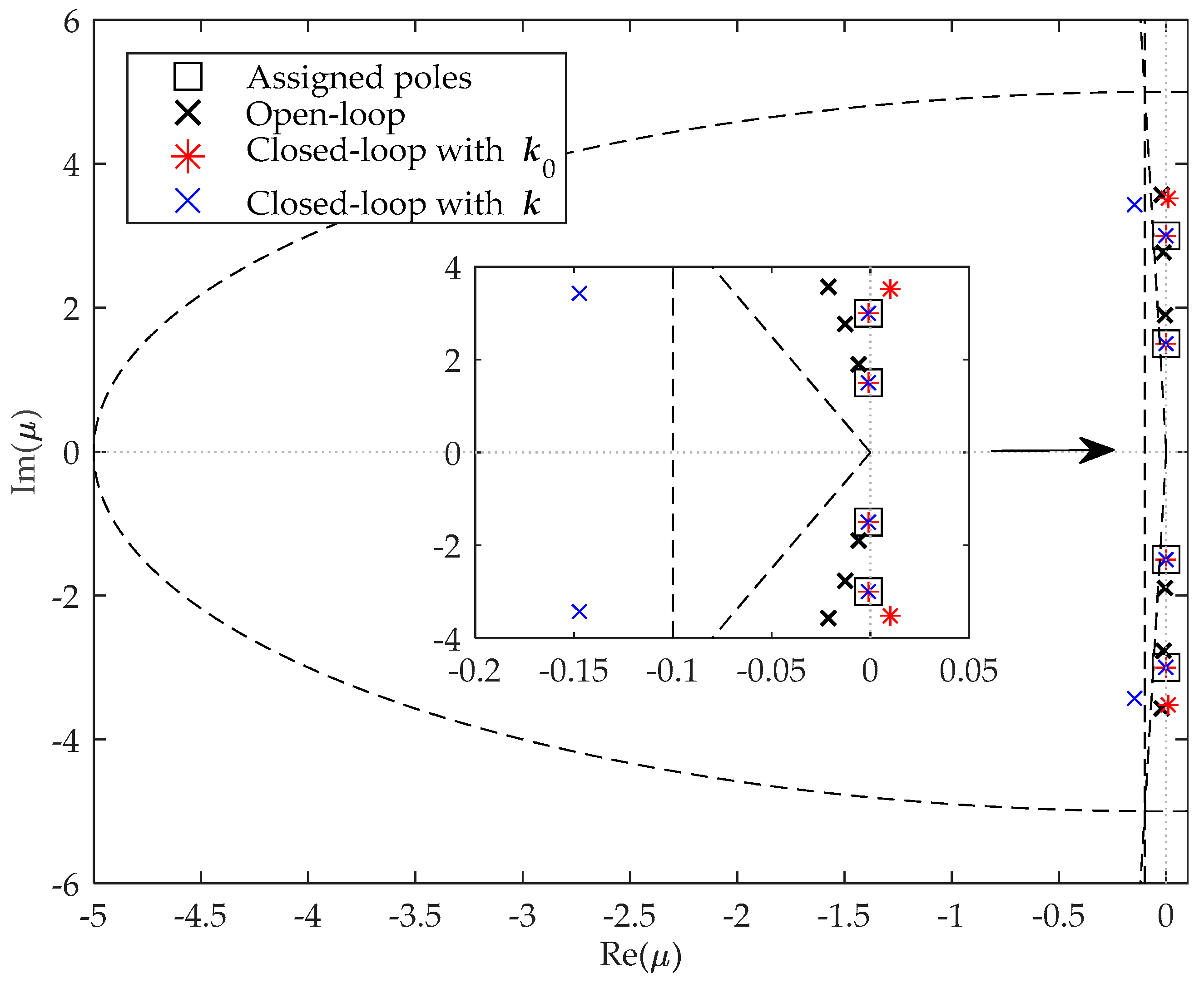
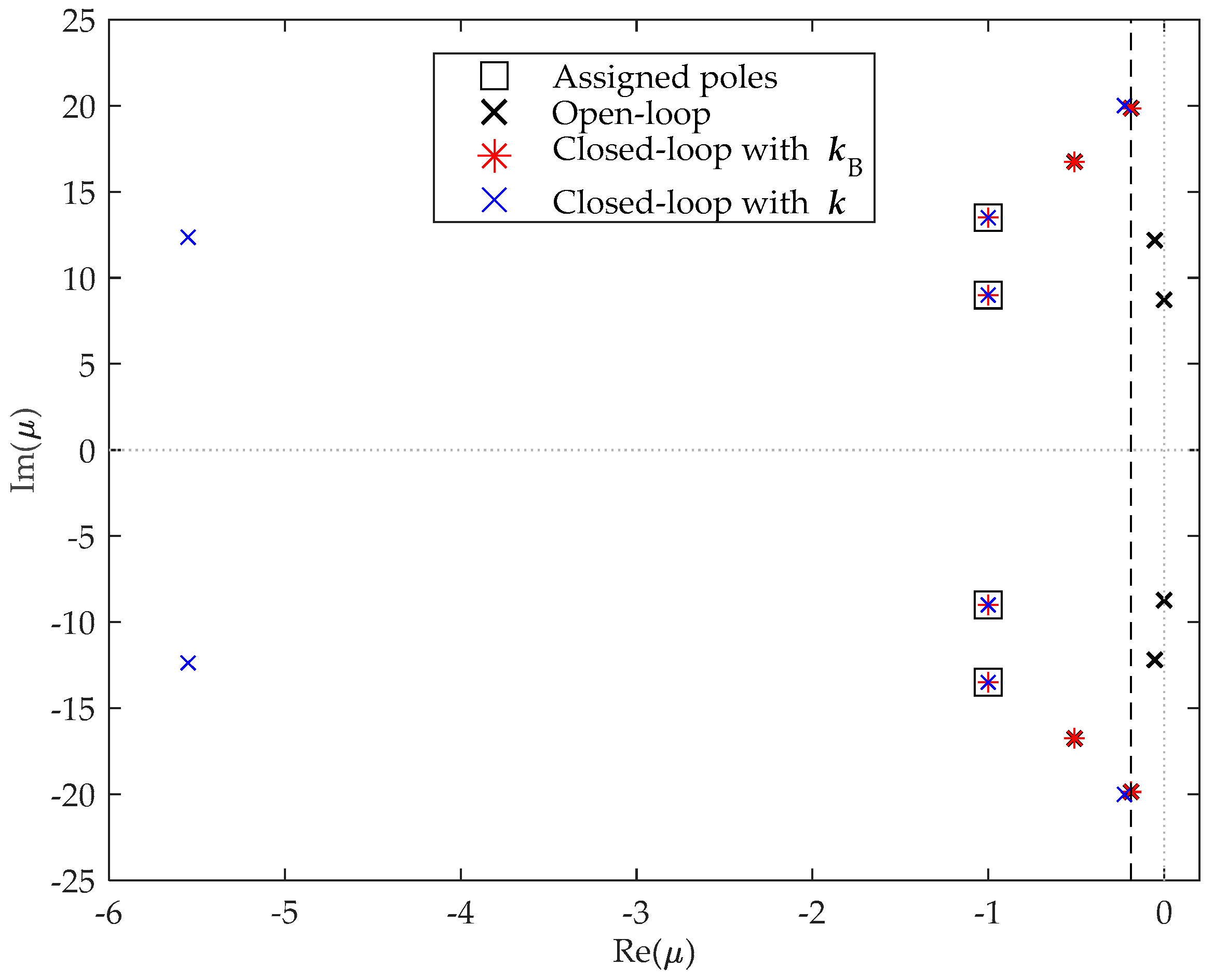
| LMI constraint | Real part, minimum damping and maximum natural frequency | Real part | Shifted disk | Minimum damping |
| Open-loop poles | Desired Closed-Loop Poles | ||
|---|---|---|---|
| −0.006 ± 1.896i | −0.001 ± 1.500i | −0.001 ± 1.500i | −0.001 ± 1.500i |
| −0.013 ± 2.769i | −0.001 ± 3.000i | −0.001 ± 3.000i | −0.001 ± 3.000i |
| −0.021 ± 3.569i | - | 0.010 ± 3.520i | −0.146 ± 3.430i |
| −0.0962 | −0.3545 | 0.2185 | −0.9705 |
| 0.1581 | −1.6452 | −0.5433 | −0.2314 |
| −0.0349 | −3.3434 | 0.2670 | −4.0191 |
| Open-Loop Poles | Desired Closed-Loop Poles | Closed-Loop Poles | Desired Closed-Loop Poles | Closed-Loop Poles | |
|---|---|---|---|---|---|
| 0.00 ± 8.73i | −1 ± 9i | −1 ± 9i | −1 ± 9i | −1 ± 9i | −1 ± 9i |
| −0.05 ± 12.19i | −1 ± 13.5i | −1 ± 13.5i | −1 ± 13.5i | −1 ± 13.5i | −1 ± 13.5i |
| −0.51 ± 16.75i | −0.51 ± 16.75i | −0.51 ± 16.75i | - | −5.55 ± 12.4i | −5.55 ± 12.4i |
| −0.19 ± 19.86i | −0.19 ± 19.86i | −0.19 ± 19.86i | - | −0.15 ± 19.98i | −0.23 ± 20.0 |
| 3.8949 | 43.7930 | 13.9035 | −12.3773 | 14.0522 | −8.9368 |
| −4.2244 | −150.4119 | −13.0355 | −6.5512 | −13.0777 | −33.0146 |
| 4.3004 | 26.3084 | −1.8911 | −5.1848 | −1.9718 | −16.8434 |
| −2.3322 | −79.6829 | −10.6007 | −3.5384 | −10.6159 | 51.3344 |
| 1.0479 | −0.0053 | 7.0008 | 25.6070 |
| 1.1222 | 3.8335 | 1.709 | 1.9598 |
| 2.8765 | 1.3771 | 4.5693 | 1.8524 |
| Open-Loop Poles | Desired Closed-Loop Poles | ||
|---|---|---|---|
| −0.918 ±1.7606i | −1.500 ± 3.000i | −1.500 ± 3.000i | −1.500 ± 3.000i |
| 0.0947 ± 2.5229i | - | 0.1306 ± 2.7016i | −2.6323 ± 0.2707i |
| −0.8848 ± 8.4415i | - | −4.6282 ± 5.5858i | −3.134 ± 0.3095i |
| Link Parameters [unit] | Value |
|---|---|
| Young modulus [Pa] | 210 · 109 |
| Second area moment [m4] | 11.1 · 10−10 |
| Width [m] | 6 · 10−3 |
| Thickness [m] | 6 · 10−3 |
| Linear mass density [kg m−1] | 272 · 10−3 |
| Link 0 length [m] | 0.360 |
| Link 1 length [m] | 0.390 |
| Link 2 length [m] | 0.535 |
| Link 3 length [m] | 0.632 |
| Rayleigh coefficients [s−1], [s] | αR = 8.5·10−2, βR = 2·10−5 |
| Nodal lumped masses [kg]: | |
| Joint B | 70 · 10−3 |
| Joint C | 70 · 10−3 |
| Joint inertia [kg m2] | |
| Joint A | 5 · 10−4 |
| Joint D | 12 · 10−6 |
| Open-Loop Poles | Desired Closed-Loop Poles | ||||
|---|---|---|---|---|---|
| 3.17 | −15 | −15 | 1 | −15 | 1 |
| -3.17 | −20 | −20 | 1 | −20 | 1 |
| −1.20 ± 226.2i | −10 ± 220i | −10 ± 220i | 0.045 | −10 ± 220i | 0.045 |
| −2.40 ± 322.3i | - | 28.6 ± 244.7i | −0.116 | −74.0 ± 215.7i | 0.324 |
| −5.33 ± 483.1i | −15 ± 320i | −15 ± 320i | 0.047 | −15 ± 320i | 0.047 |
| −20.86 ± 958.4i | −50 ± 500i | −50 ± 500i | 0.100 | −50 ± 500i | 0.100 |
| −46.24 ± 1427.4i | −22.19 ± 966.96i | 0.023 | −66.59 ± 923.49i | 0.072 | |
| −58.49 ± 1605.3i | - | −46.41 ± 1429.3i | 0.033 | −85.13 ± 1426.8i | 0.060 |
| −121.1 ± 2308.9i | - | −121.1 ± 2308.5i | 0.052 | −121.1 ± 2308.5i | 0.052 |
| −287.6 ± 3551.7i | - | −287.6 ± 3551.7i | 0.080 | −287.6 ± 3551.7i | 0.081 |
| −390.8 ± 4134.8i | - | −390.7 ± 4134.9i | 0.094 | −390.7 ± 4134.9i | 0.094 |
| −947.0 ± 6396.2i | - | −947.0 ± 6396i | 0.147 | −947.0 ± 6396.2i | 0.147 |
| −1820 ± 8777.4i | - | −1820.0 ± 8777i | 0.203 | −1819.8 ± 8777.3i | 0.203 |
| −3440.7 ± 11835i | - | −3440.1 ± 11834i | 0.279 | −3439.9 ± 11834i | 0.279 |
| −6348.2 ± 15491i | - | −6348.2 ± 15490i | 0.379 | −6348.3 ± 15490i | 0.379 |
| −23417 ± 22033i | - | −23417 ± 22033i | 0.728 | −23417 ± 22033i | 0.728 |
| −40747 ± 11774i | - | −40747 ± 11773i | 0.961 | −40747 ± 11774i | 0.961 |
| −0.00359 | −639.62 | 0.0738 | −639.26 |
| 0.00000 | -0.01 | −9.8664 | −4850.30 |
| 0.00000 | 0.13 | −5.5614 | −3456.7 |
| 0.00163 | −951.75 | 0.1526 | −950.73 |
| −0.02214 | 15.34 | 0.5697 | 302.04 |
| 0.00277 | −0.34 | −1.8326 | −618.71 |
| 0.00245 | −0.23 | 2.1344 | 719.62 |
| −0.000001 | −10.26 | −1.1898 | −587.82 |
| 0.00000 | 0.02 | 8.7912 | 5210.00 |
| 0.02216 | 8.43 | 0.6184 | 313.22 |
| 0.00011 | 29.19 | 0.2044 | −68.49 |
| 0.00000 | −2.00 | 0.3313 | 53.01 |
| 0.00000 | 1.39 | −0.0977 | 95.78 |
| −0.00008 | −27.40 | −0.4665 | 158.70 |
| 0.00006 | 34.45 | 0.2638 | −62.60 |
| 0.04228 | 0.36 | 0.0343 | 0.30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belotti, R.; Richiedei, D.; Tamellin, I.; Trevisani, A. Pole Assignment for Active Vibration Control of Linear Vibrating Systems through Linear Matrix Inequalities. Appl. Sci. 2020, 10, 5494. https://doi.org/10.3390/app10165494
Belotti R, Richiedei D, Tamellin I, Trevisani A. Pole Assignment for Active Vibration Control of Linear Vibrating Systems through Linear Matrix Inequalities. Applied Sciences. 2020; 10(16):5494. https://doi.org/10.3390/app10165494
Chicago/Turabian StyleBelotti, Roberto, Dario Richiedei, Iacopo Tamellin, and Alberto Trevisani. 2020. "Pole Assignment for Active Vibration Control of Linear Vibrating Systems through Linear Matrix Inequalities" Applied Sciences 10, no. 16: 5494. https://doi.org/10.3390/app10165494
APA StyleBelotti, R., Richiedei, D., Tamellin, I., & Trevisani, A. (2020). Pole Assignment for Active Vibration Control of Linear Vibrating Systems through Linear Matrix Inequalities. Applied Sciences, 10(16), 5494. https://doi.org/10.3390/app10165494







