A Novel Adaptive Mode Decomposition Method Based on Reassignment Vector and Its Application to Fault Diagnosis of Rolling Bearing
Abstract
1. Introduction
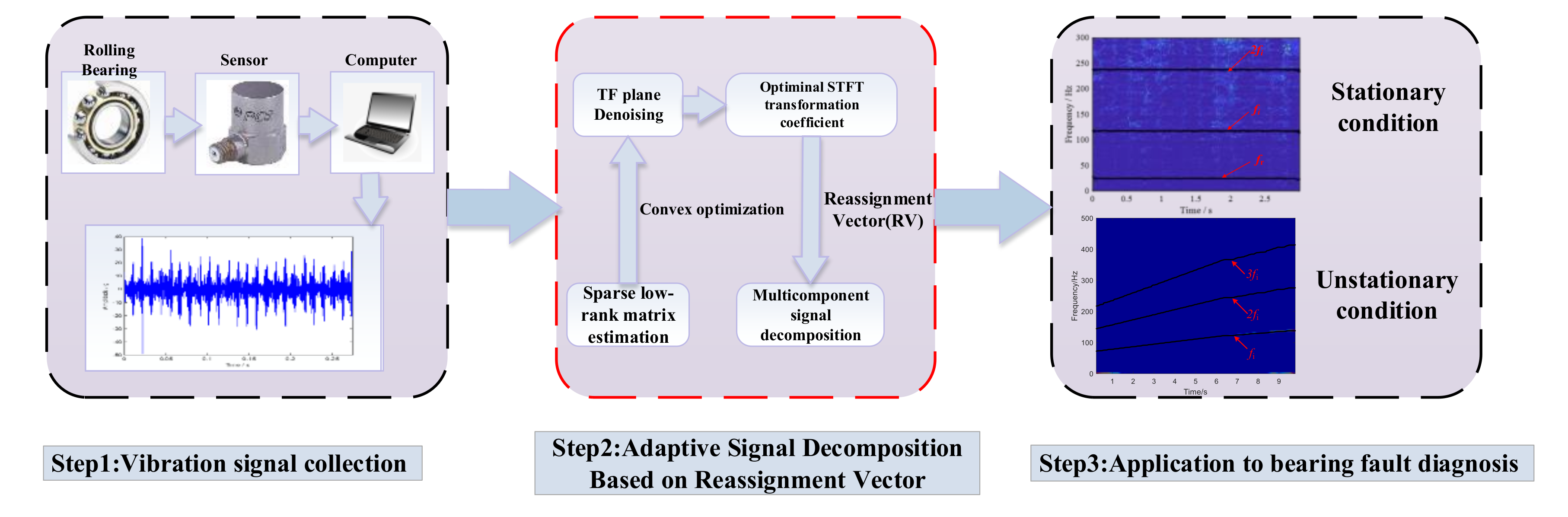
2. Theory Description
2.1. TF Plane Denoising Using Sparse Low-rank Matrix Estimation
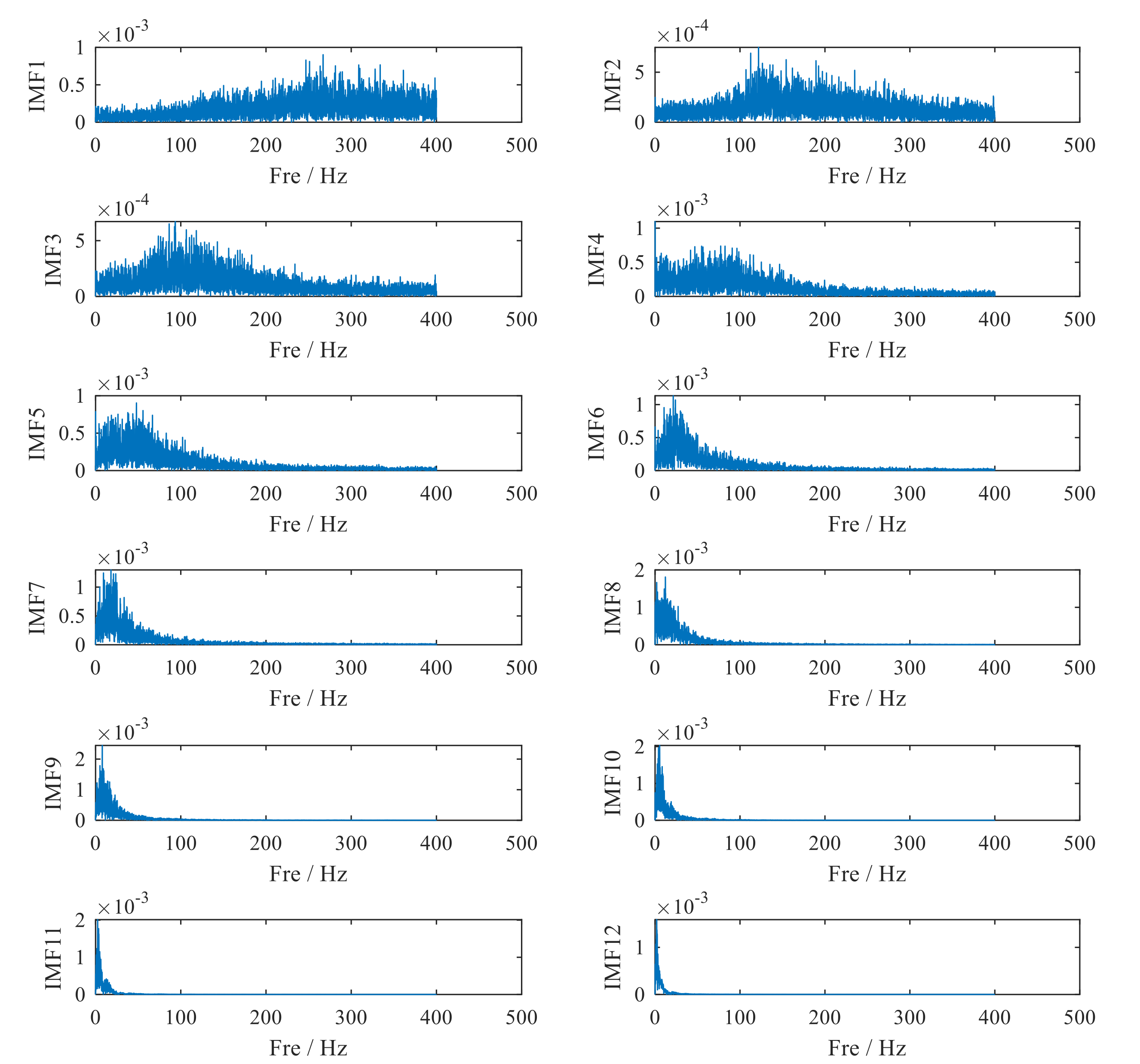
2.2. Adaptive Signal Decomposition Based on Reassignment Vector
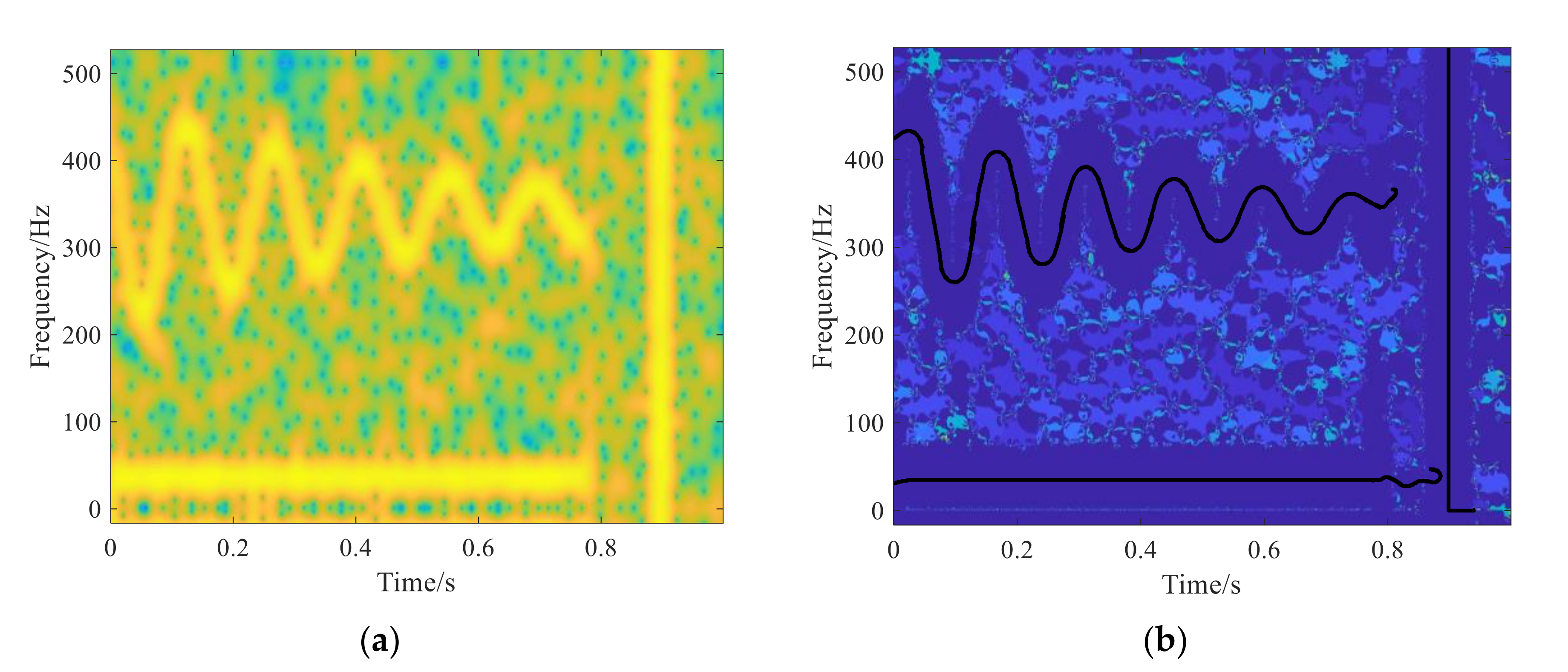
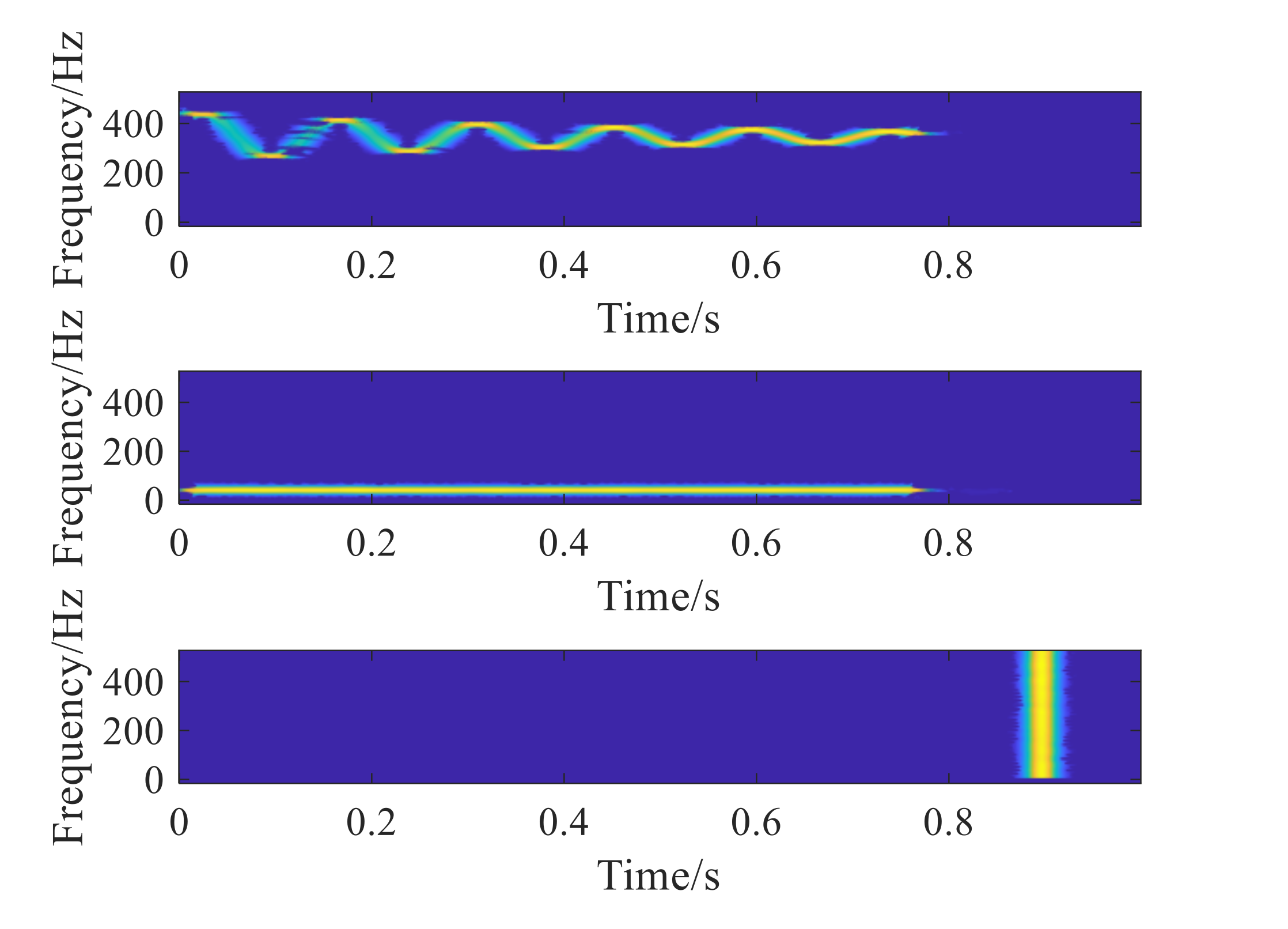
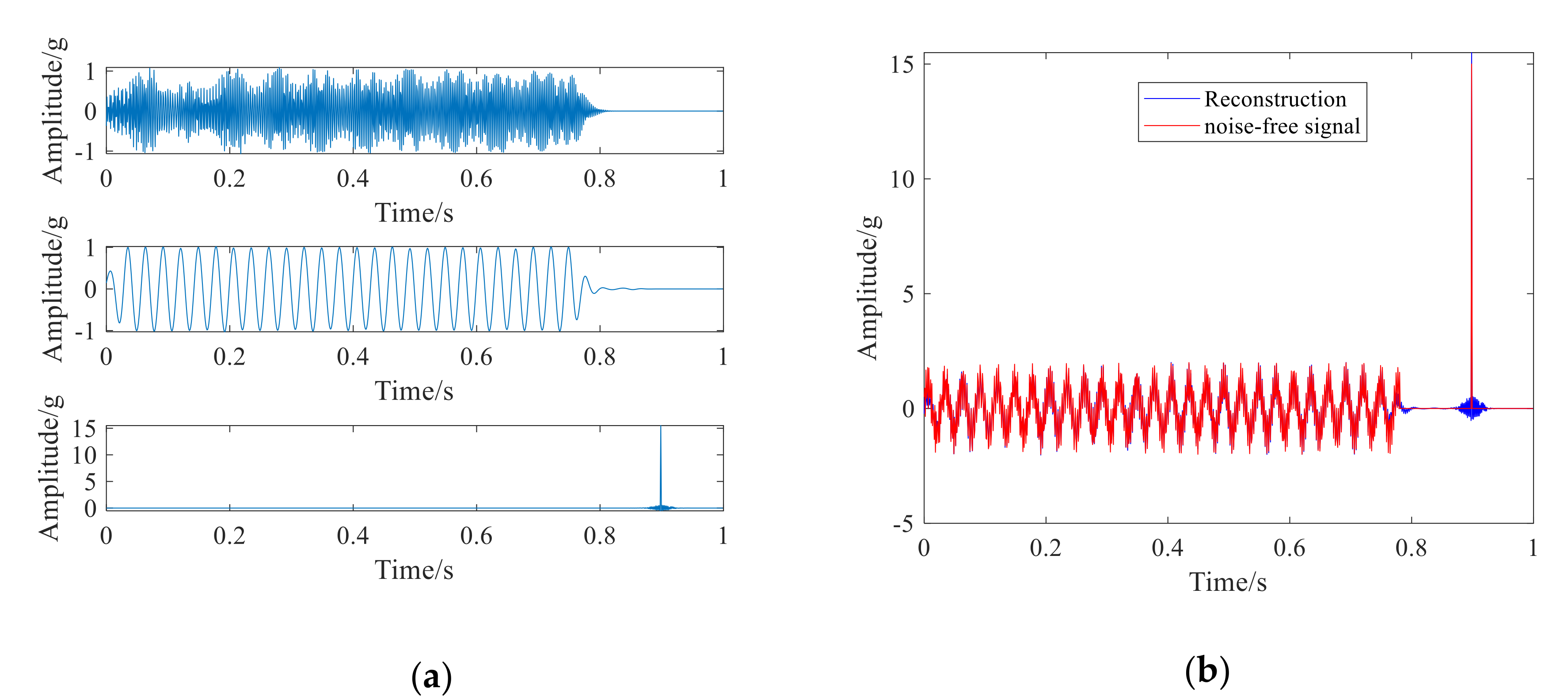
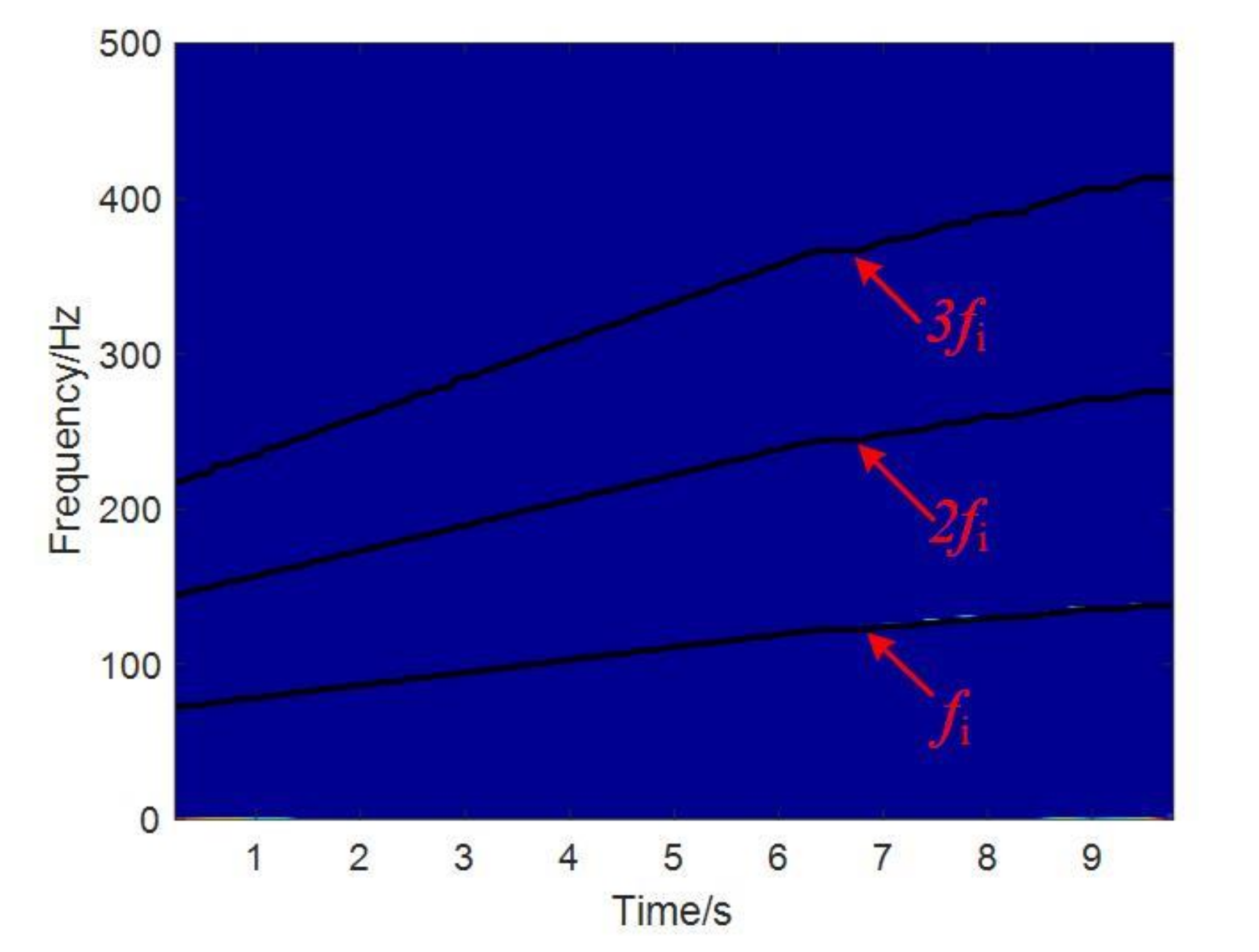
3. Numerical Simulation Signal Analysis
4. Experimental Data Analysis
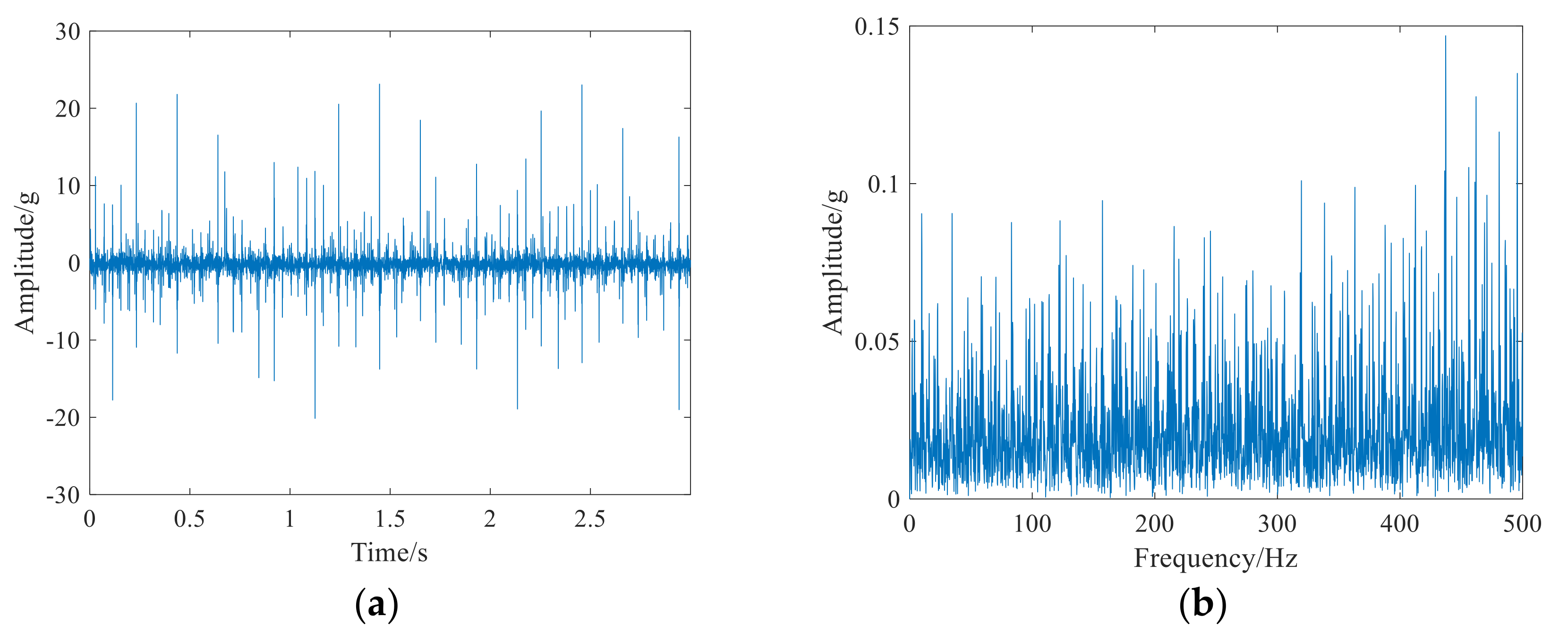
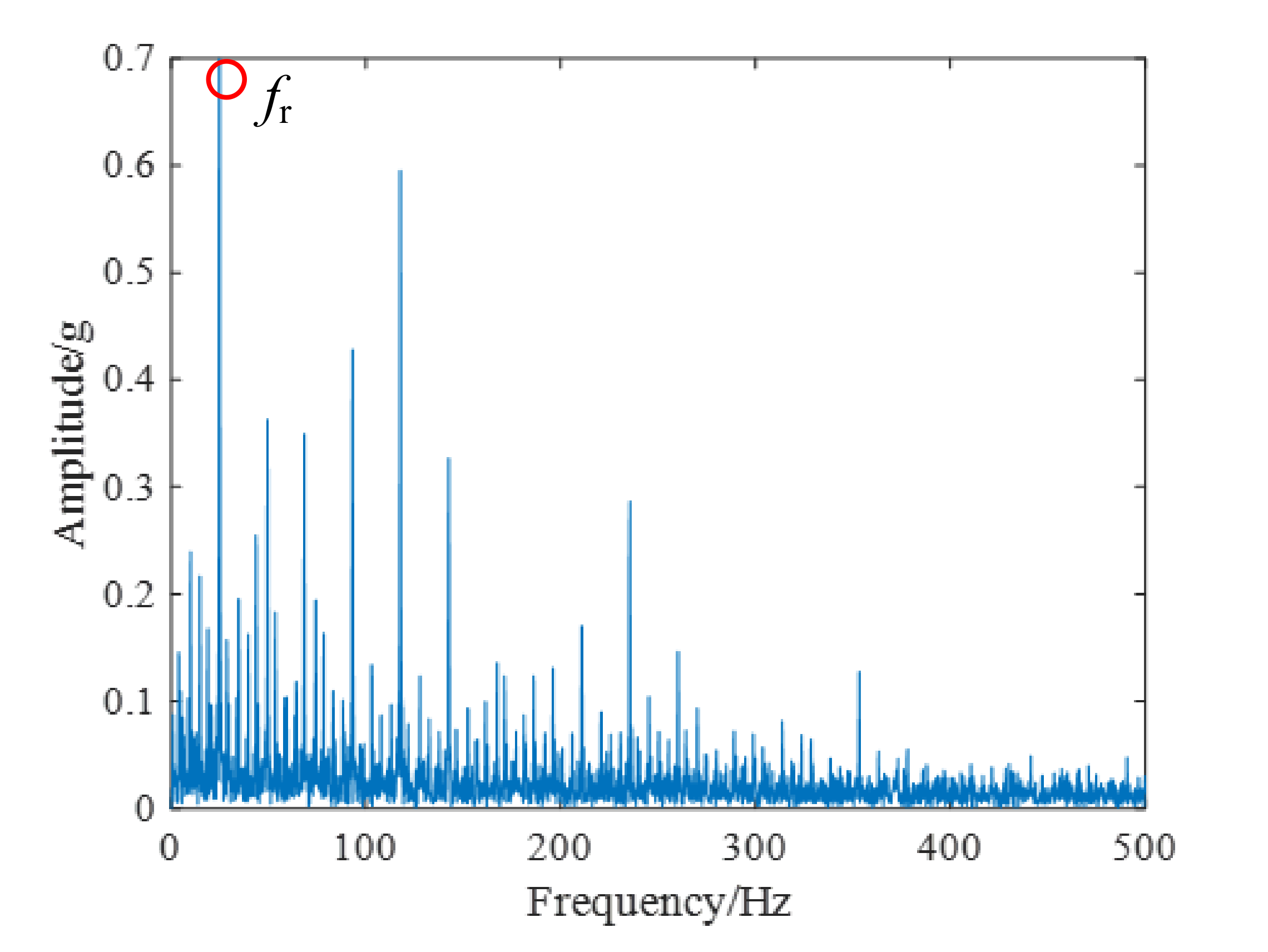
4.1. Case.1 Application to Stationary Feature Extraction of Bearing
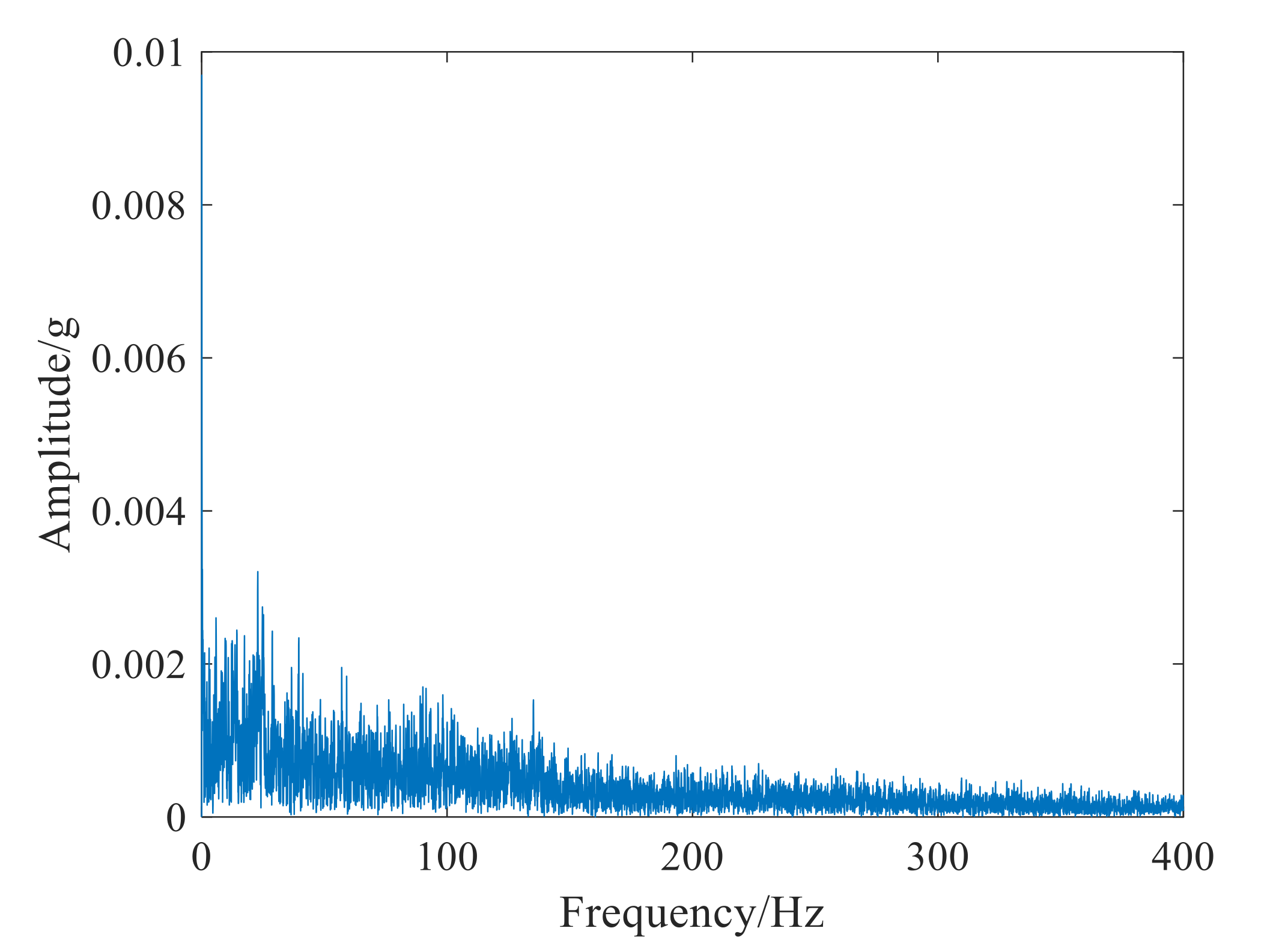
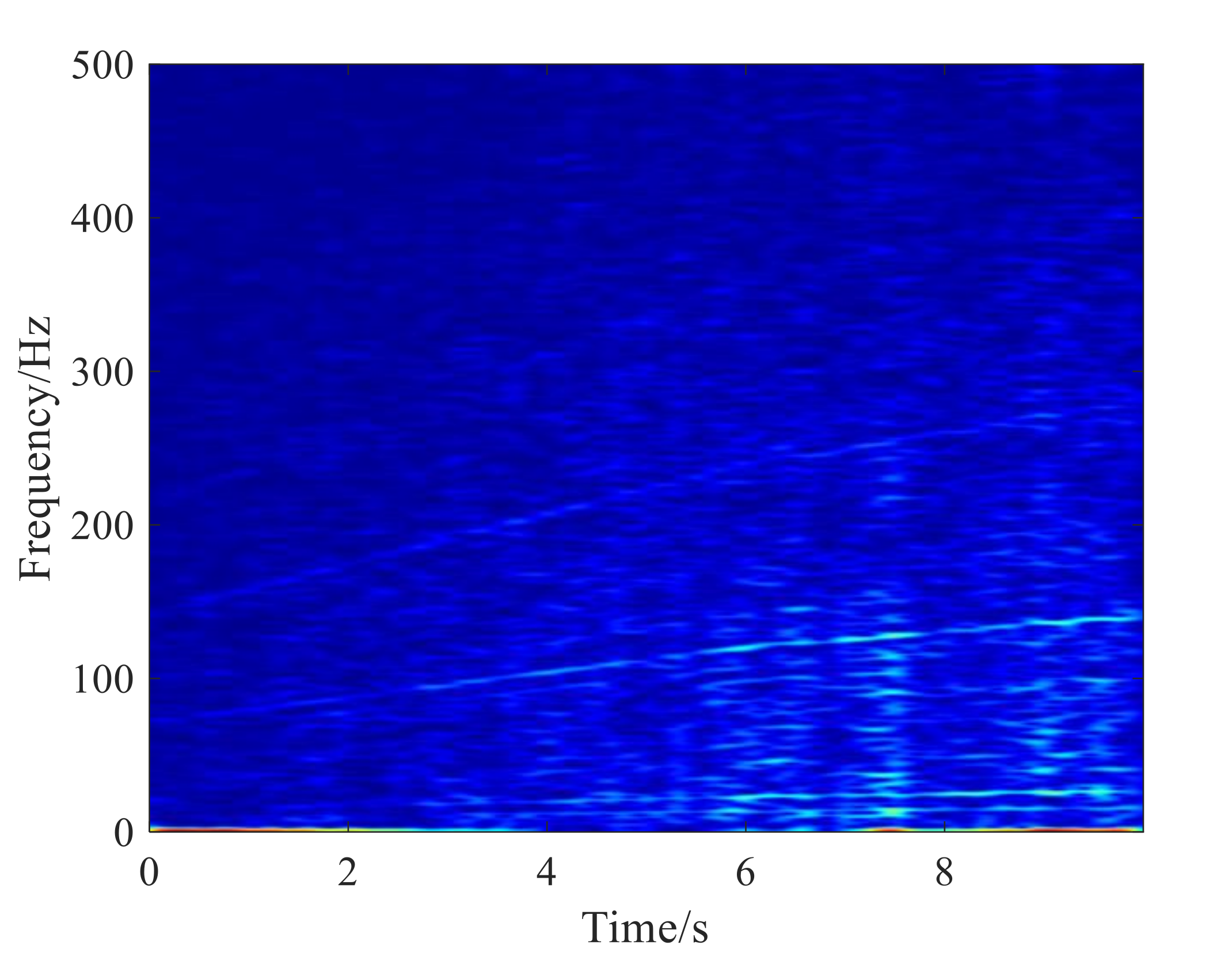
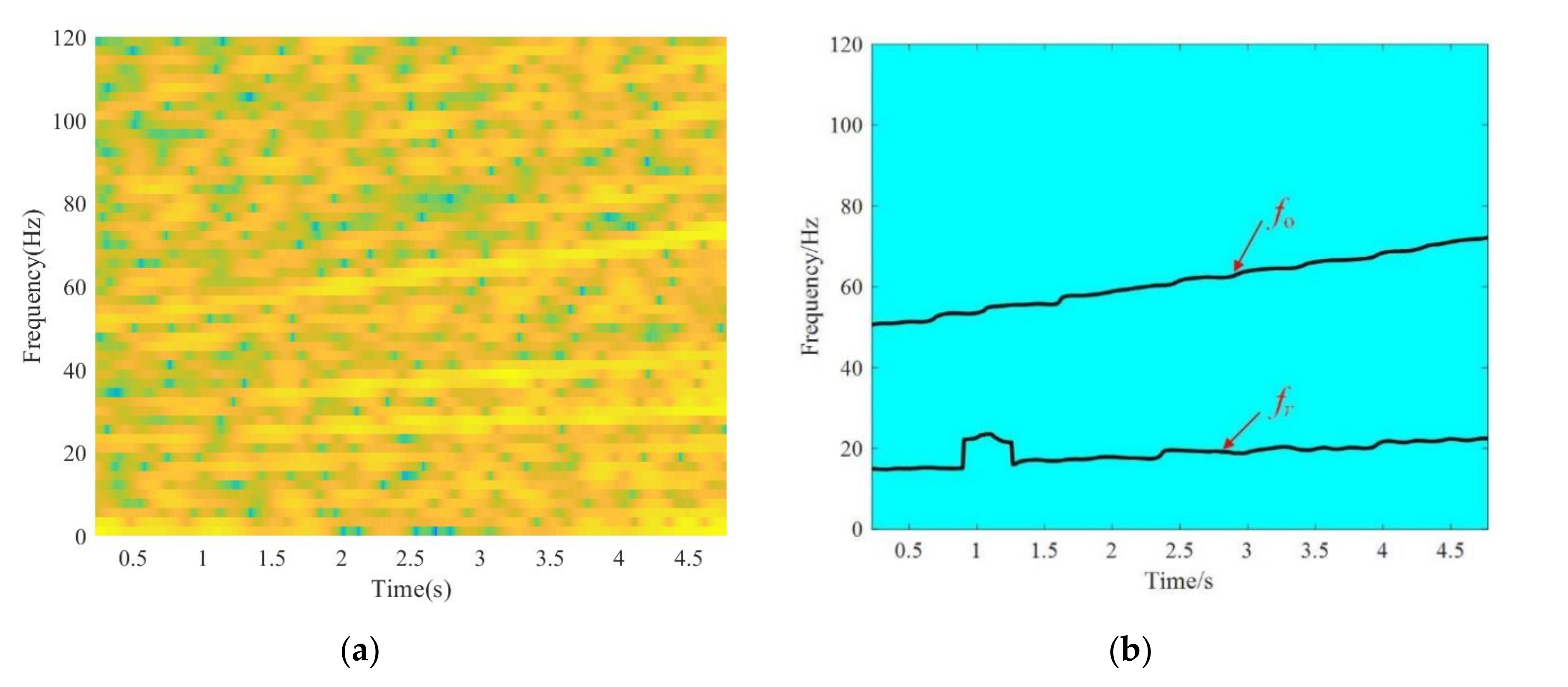
4.2. Case.2 Application to Time-varying Feature Extraction of Bearing
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jerome, A.; Julien, G.; Hugo, A. Feedback on the surveillance 8 challenge: Vibration-based diagnosis of a safran aircraft engine. Mech. Syst. Signal Process. 2017, 97, 112–114. [Google Scholar]
- Milos, B.; Vesna, P.B. Post-processing of time-frequency representations in instantaneous frequency estimation based on ant colony optimization. Signal Process. 2017, 138, 195–210. [Google Scholar]
- Feng, Z.; Chen, X.; Wang, T. Time-varying demodulation analysis for rolling bearing fault diagnosis under variable speed conditions. J. Sound Vib. 2017, 400, 71–85. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P.; Lin, Y.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the readability of time-frequency and time-scale representations by the reassignment method. IEEE Signal Process. Mag. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Ghoreishi, S.F.; Imani, M. Offline fault detection in gene regulatory networks using next-generation sequencing data. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 1344–1348. [Google Scholar]
- Mahdi, I.; Edward, D. Boolean Kalman Filter and Smoother Under Model Uncertainty. Automatica 2020, 111, 108609. [Google Scholar]
- He, D.; Cao, H.; Wang, S.; Chen, X. Time-reassigned synchrosqueezing transform: The algorithm and its applications in mechanical signal processing. Mech. Syst. Signal Process. 2019, 117, 255–279. [Google Scholar] [CrossRef]
- Roehri, N.; Lina, J.; Mosher, J.C.; Bartolomei, F.; Benar, C. Time-Frequency Strategies for Increasing High-Frequency Oscillation Detectability in Intracerebral EEG. IEEE Trans Bio. Med. Eng 2016, 63, 2595–2606. [Google Scholar] [CrossRef]
- Kiran, G.; Parimalasundar, E.; Elangovan, D.; Sanjeevikumar, P.; Lannuzzo, F.; Holm-Nielsen, J.B. Fault Investigation in Cascaded H-Bridge Multilevel Inverter through Fast Fourier Transform and Artificial Neural Network Approach. Energies 2020, 13, 1299. [Google Scholar] [CrossRef]
- Shalu, C.; Sachin, T.; Varun, B. A flexible analytic wavelet transform based approach for motor-imagery tasks classification in BCI applications. Comput. Methods Programs Biomed. 2020, 187, 105–325. [Google Scholar]
- Yi, C.; Lv, Y.; Dang, Z. Quaternion singular spectrum analysis using convex optimization and its application to fault diagnosis of rolling bearing. Measurement 2017, 103, 321–332. [Google Scholar] [CrossRef]
- Meignen, S.; Pham, D. Retrieval of the Modes of Multicomponent Signals From Downsampled Short-Time Fourier Transform. IEEE Signal. Process. 2018, 66, 6204–6215. [Google Scholar] [CrossRef]
- Wang, Y.; Rao, Y.; Xu, D. Multichannel maximum-entropy method for the Wigner-Ville distribution. Geophysics 2020, 85, 25–31. [Google Scholar] [CrossRef]
- Li, L.; Cai, H.; Han, H.; Jiang, Q.; Ji, H. Adaptive short-time Fourier transform and synchrosqueezing transform for non-stationary signal separation. IEEE Signal. Process. 2020, 166, 107231. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; Huang, T.; You, G. Multisensor signal denoising based on matching synchrosqueezing wavelet transform for mechanical fault condition assessment. Meas. Sci. Technol. 2018, 29, 45104. [Google Scholar] [CrossRef]
- Zhou, P.; Dong, X.; Chen, S. Parameterized Model Based Short-time Chirp Component Decomposition. Signal Process. 2018, 145, 146–154. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. A 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-Order Synchrosqueezing Transform or Invertible Reassignment? Towards Ideal Time-Frequency Representations. IEEE Signal Process. 2015, 63, 1335–1344. [Google Scholar] [CrossRef]
- Moghadasian, S.S.; Gazor, S. Sparsely Localized Time-Frequency Energy Distributions for Multi-Component LFM Signals. IEEE Signal Process. 2020, 27, 6–10. [Google Scholar] [CrossRef]
- Yu, G. A geometry study on reassignment method and synchrosqueezing transform. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xian, China, 30 November–2 December 2018; IEEE: Picataway, NJ, USA, 2019. [Google Scholar]
- Bruni, V.; Tartaglione, M.; Vitulano, D. A Fast and Robust Spectrogram Reassignment Method. Mathematics 2019, 7, 358. [Google Scholar] [CrossRef]
- Pham, D.; Meignen, S. An Adaptive Computation of Contour Representations for Mode Decomposition. IEEE Signal Process. 2017, 24, 1596–1600. [Google Scholar] [CrossRef]
- Meignen, S.; Oberlin, T.; Depalle, P.; Flandrin, P.; McLaughlin, S. Adaptive multimode signal reconstruction from time–frequency representations. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 201–205. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Xiao, H.; You, G.; Dang, Z. Research on the Blind Source Separation Method Based on Regenerated Phase-Shifted Sinusoid-Assisted EMD and Its Application in Diagnosing Rolling-Bearing Faults. Appl. Sci. 2017, 7, 414. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Y.; Cui, Z.; Shen, J. Vibration fault diagnosis of wind turbines based on variational mode decomposition and energy entropy. Energy 2019, 174, 1100–1109. [Google Scholar] [CrossRef]
- Ding, Y.; He, W.; Chen, B.; Zi, Y.; Selesnick, I.W. Detection of faults in rotating machinery using periodic time-frequency sparsity. J. Sound Vib. 2016, 382, 357–378. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Enhanced Low-Rank Matrix Approximation. IEEE Signal Process. 2016, 23, 493–497. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Improved sparse low-rank matrix estimation. IEEE Signal Process. 2017, 139, 62–69. [Google Scholar] [CrossRef]
- Giselsson, P.; Boyd, S. Linear Convergence and Metric Selection in Douglas-Rachford Splitting and ADMM. IEEE Trans. Autom. Control 2016, 62, 532–544. [Google Scholar] [CrossRef]
- Bechhoefer, E. A Quick Introduction to Bearing Envelope Analysis, MFPT Data. Available online: http://www.mfpt.org/FaultData/FaultData.htm.Set (accessed on 10 March 2020).
- Huang, H.; Baddour, N.; Liang, M. Multiple time-frequency curve extraction Matlab code and its application to automatic bearing fault diagnosis under time-varying speed conditions. Methods X 2019, 6, 1415–1432. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Baddour, N. Bearing vibration data collected under time-varying rotational speed conditions. Data Brief 2018, 21, 1745–1749. [Google Scholar] [CrossRef] [PubMed]
- Antoni, J.; Randall, B.R. A Stochastic Model for Simulation and Diagnostics of Rolling Element Bearings with Localized Faults. J. Vib. Acoust. 2003, 125, 282–289. [Google Scholar] [CrossRef]









| Roller Diameter | Pitch Diameter | Number of Elements | Contact Angle | Load/lbs |
|---|---|---|---|---|
| 0.235 | 1.245 | 8 | 0 | 300 |
| Bearing Type | Pitch Diameter | Ball Diameter | Number of Balls | FCCI | FCCO |
|---|---|---|---|---|---|
| ER16K | 38.52 mm | 7.94 mm | 9 | 5.43 | 3.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, C.; Wang, X.; Zhu, Y.; Ke, W. A Novel Adaptive Mode Decomposition Method Based on Reassignment Vector and Its Application to Fault Diagnosis of Rolling Bearing. Appl. Sci. 2020, 10, 5479. https://doi.org/10.3390/app10165479
Yi C, Wang X, Zhu Y, Ke W. A Novel Adaptive Mode Decomposition Method Based on Reassignment Vector and Its Application to Fault Diagnosis of Rolling Bearing. Applied Sciences. 2020; 10(16):5479. https://doi.org/10.3390/app10165479
Chicago/Turabian StyleYi, Cancan, Xing Wang, Yajun Zhu, and Wei Ke. 2020. "A Novel Adaptive Mode Decomposition Method Based on Reassignment Vector and Its Application to Fault Diagnosis of Rolling Bearing" Applied Sciences 10, no. 16: 5479. https://doi.org/10.3390/app10165479
APA StyleYi, C., Wang, X., Zhu, Y., & Ke, W. (2020). A Novel Adaptive Mode Decomposition Method Based on Reassignment Vector and Its Application to Fault Diagnosis of Rolling Bearing. Applied Sciences, 10(16), 5479. https://doi.org/10.3390/app10165479




