3D Dilatometer Time-Series Analysis for a Better Understanding of the Dynamics of a Giant Slow-Moving Landslide
Abstract
Featured Application
Abstract
1. Introduction
2. Study Area
3. Monitoring Data Collection and Preparation
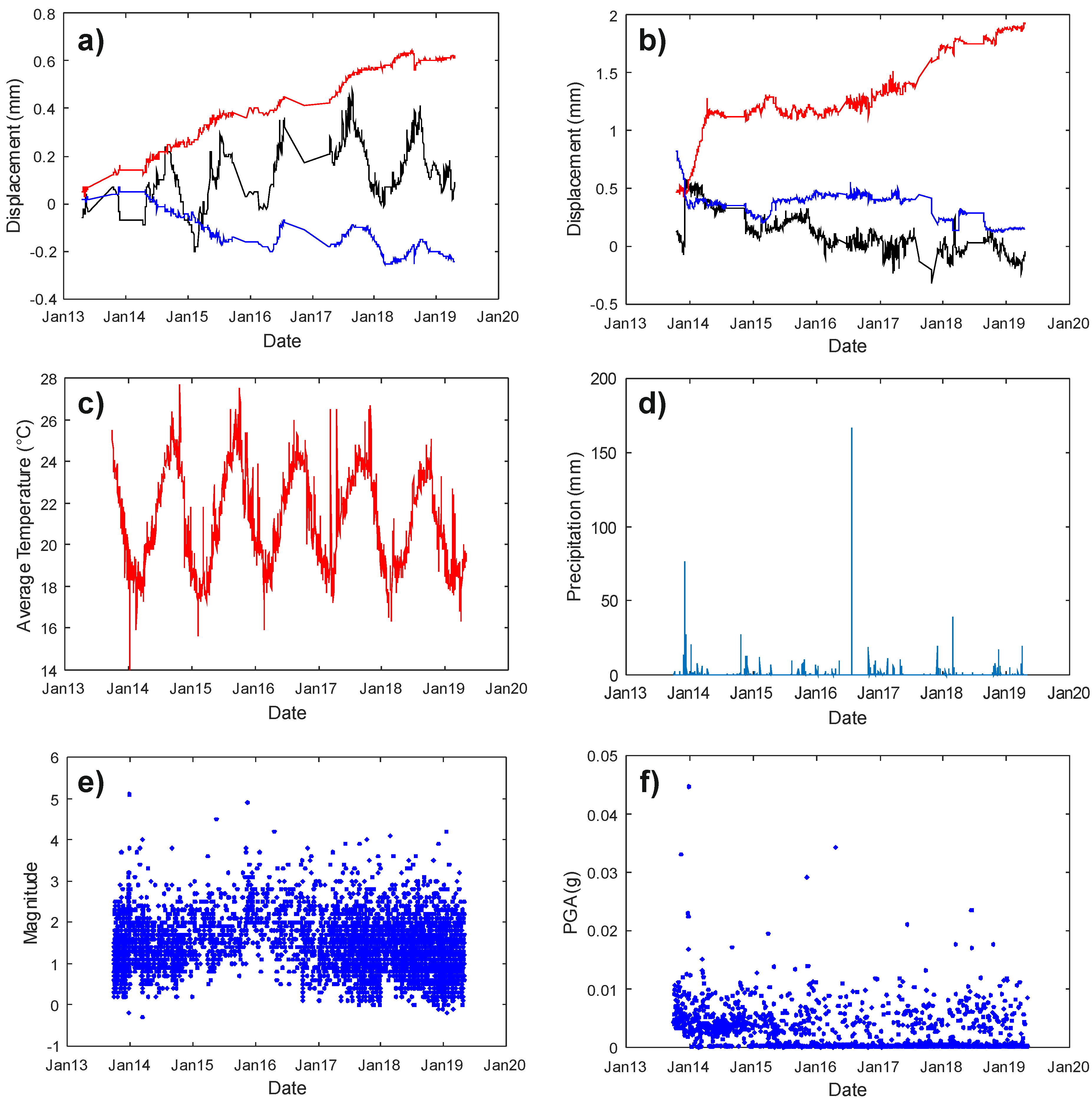
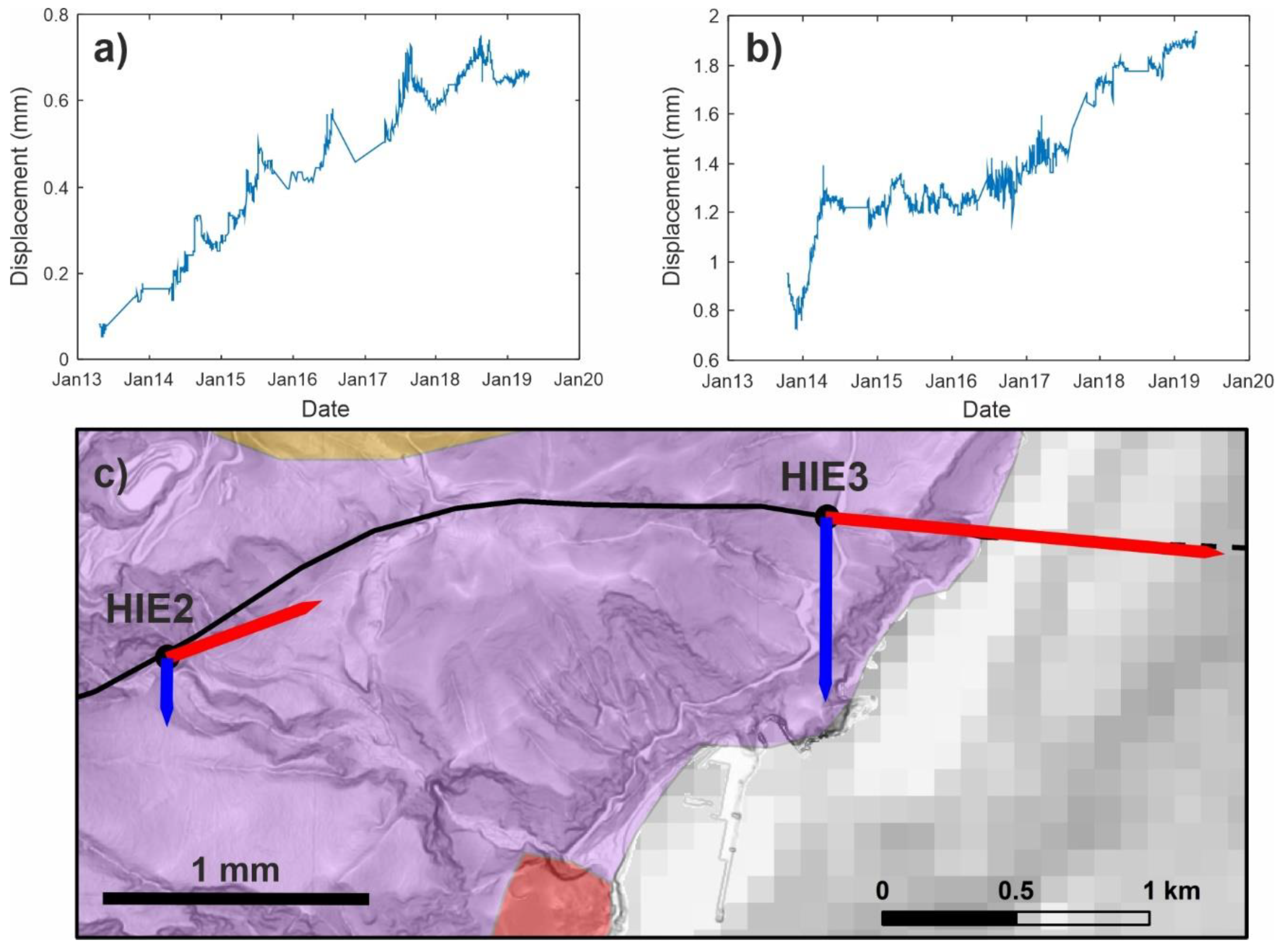
3.1. 3D Dilatometer Data
3.2. Climatic Variables
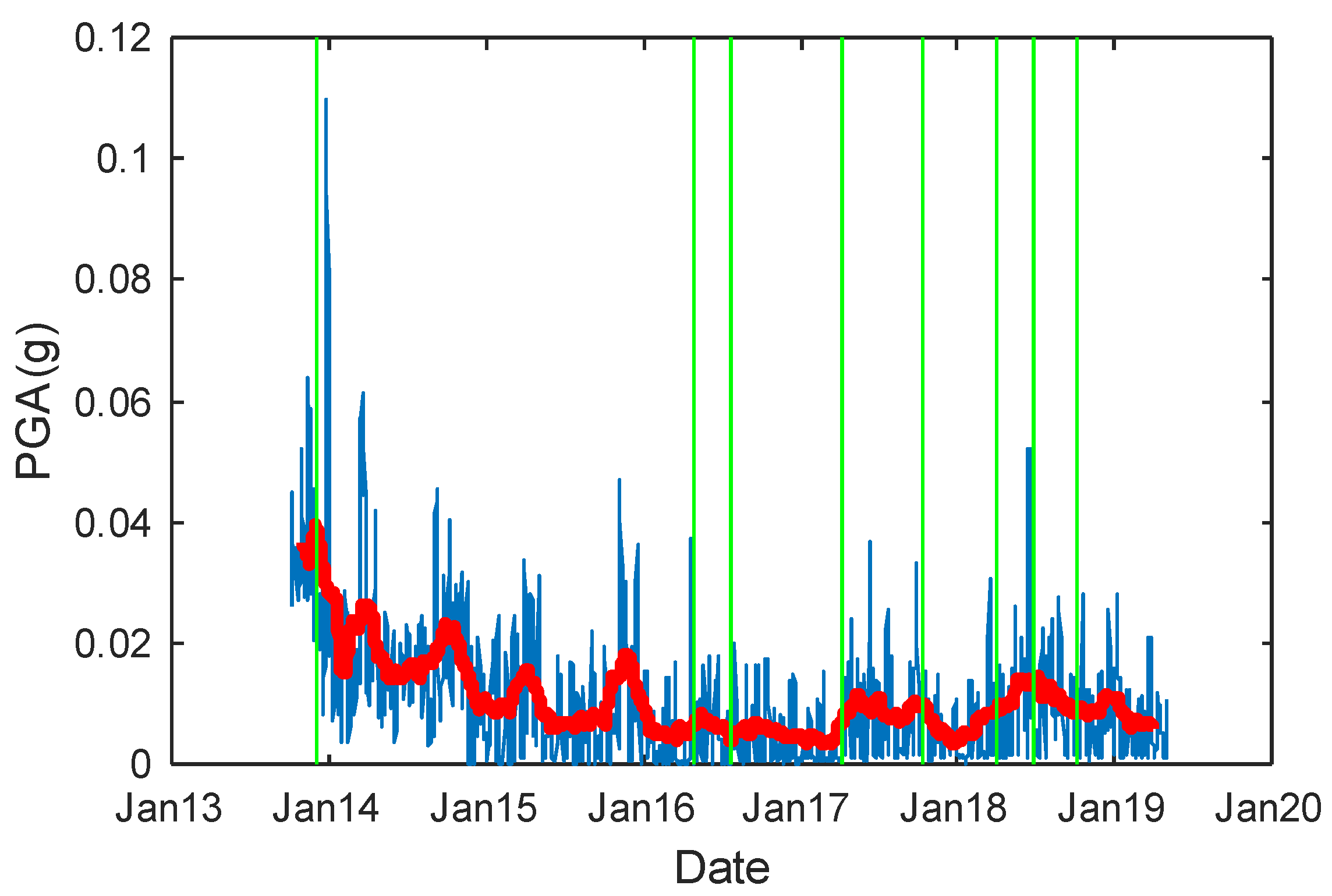
3.3. Seismic Data
4. Methodological Approach
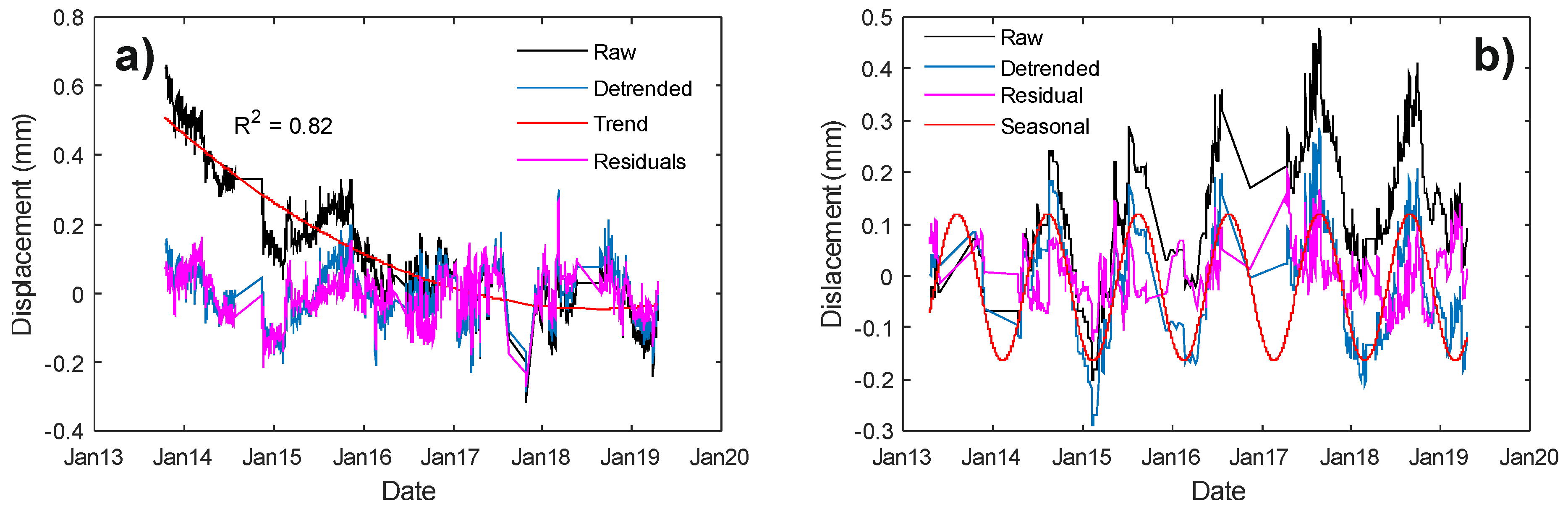
4.1. Input Data Pre-Processing
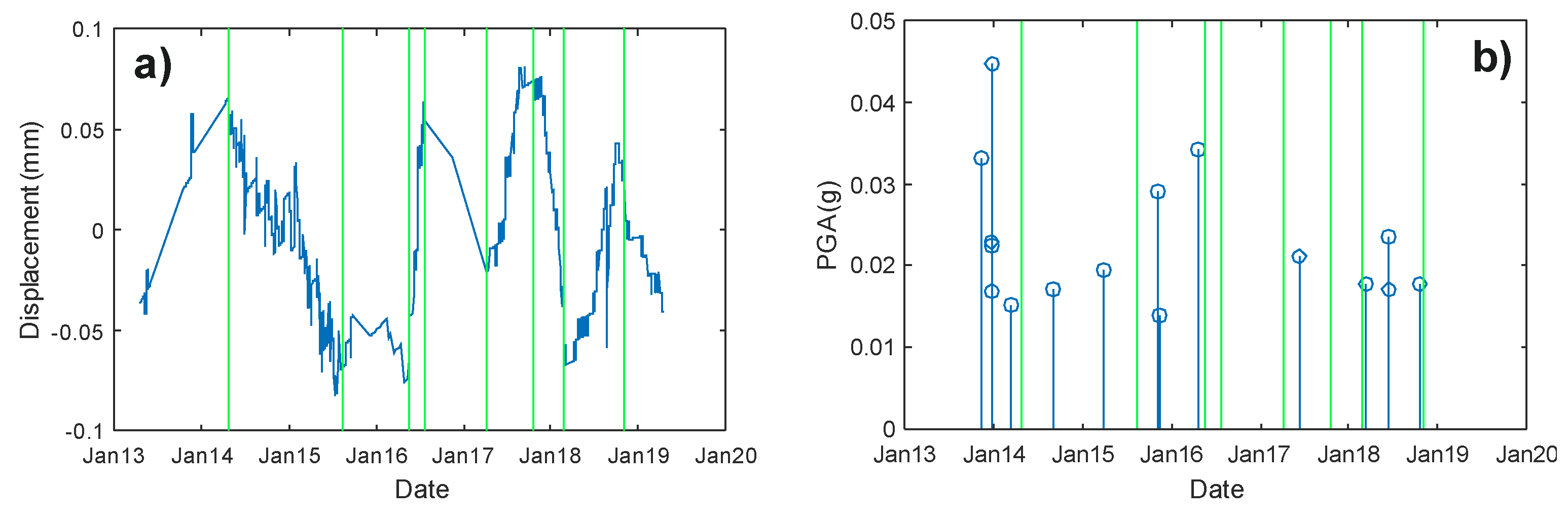
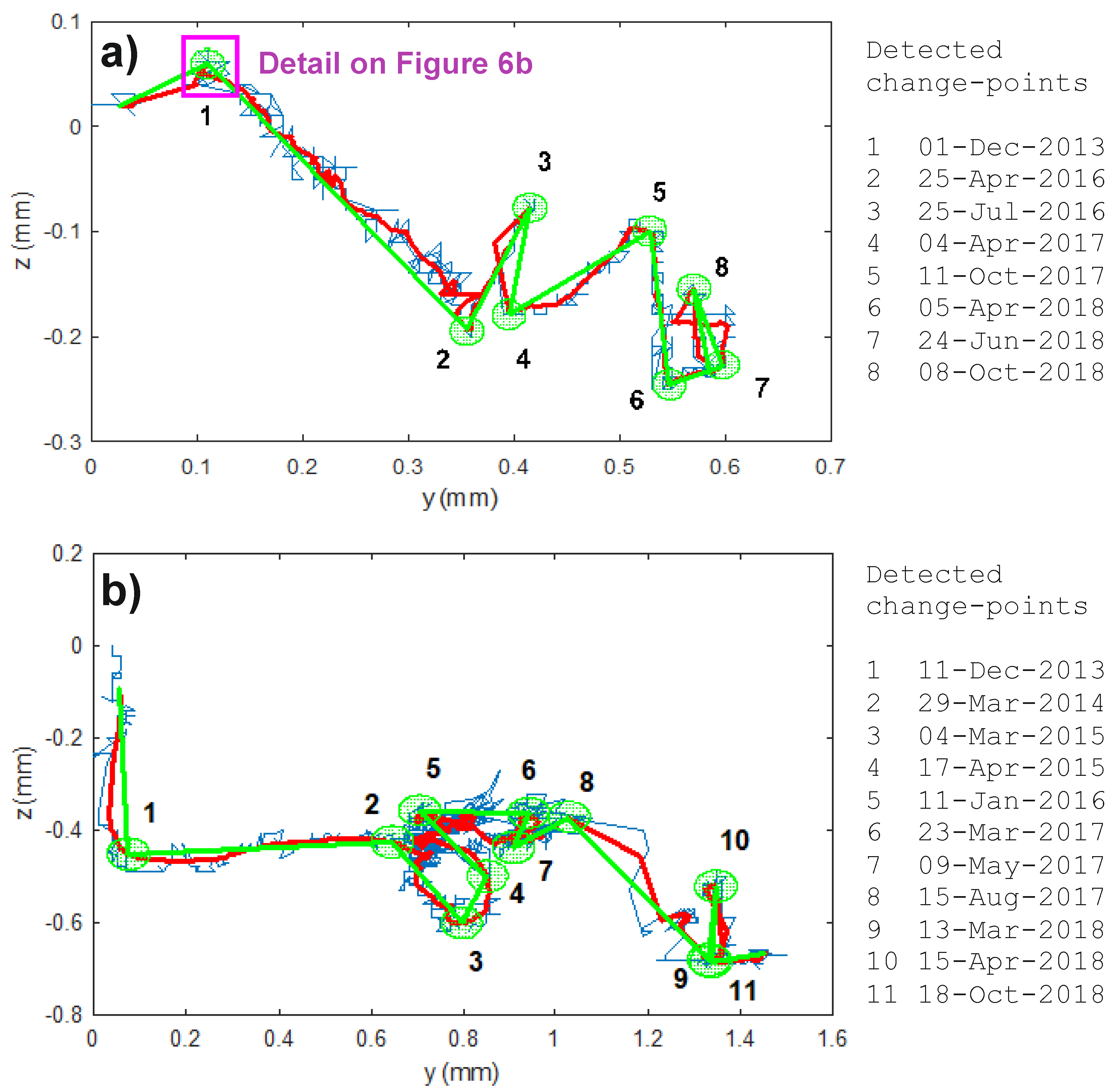
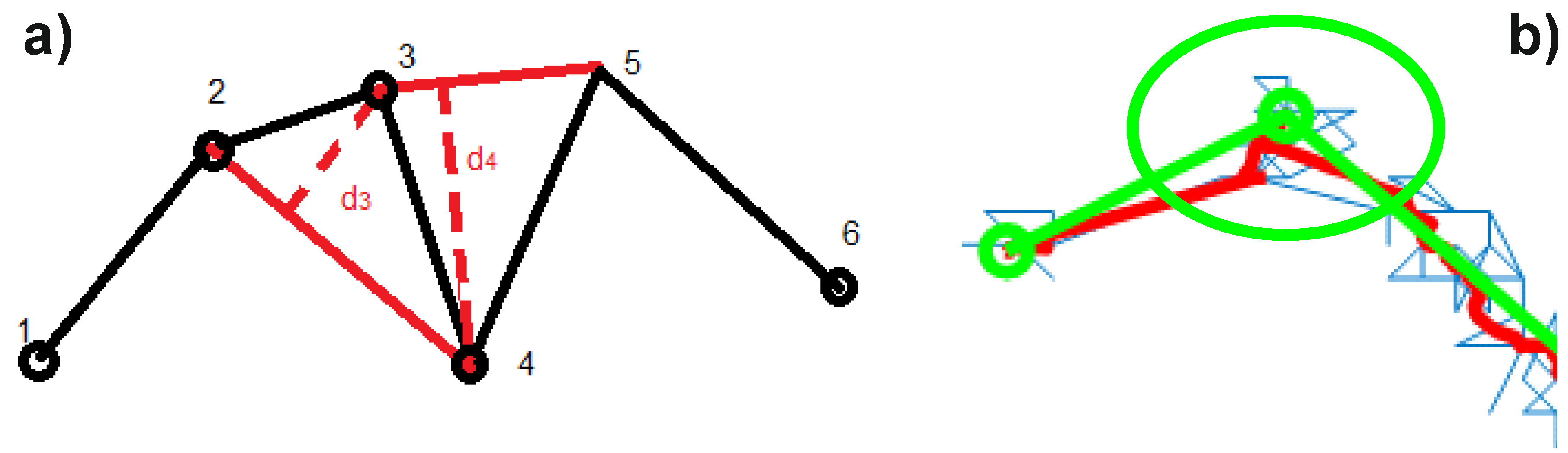
4.2. Detection of Change-Points in Time Series of Individual Components
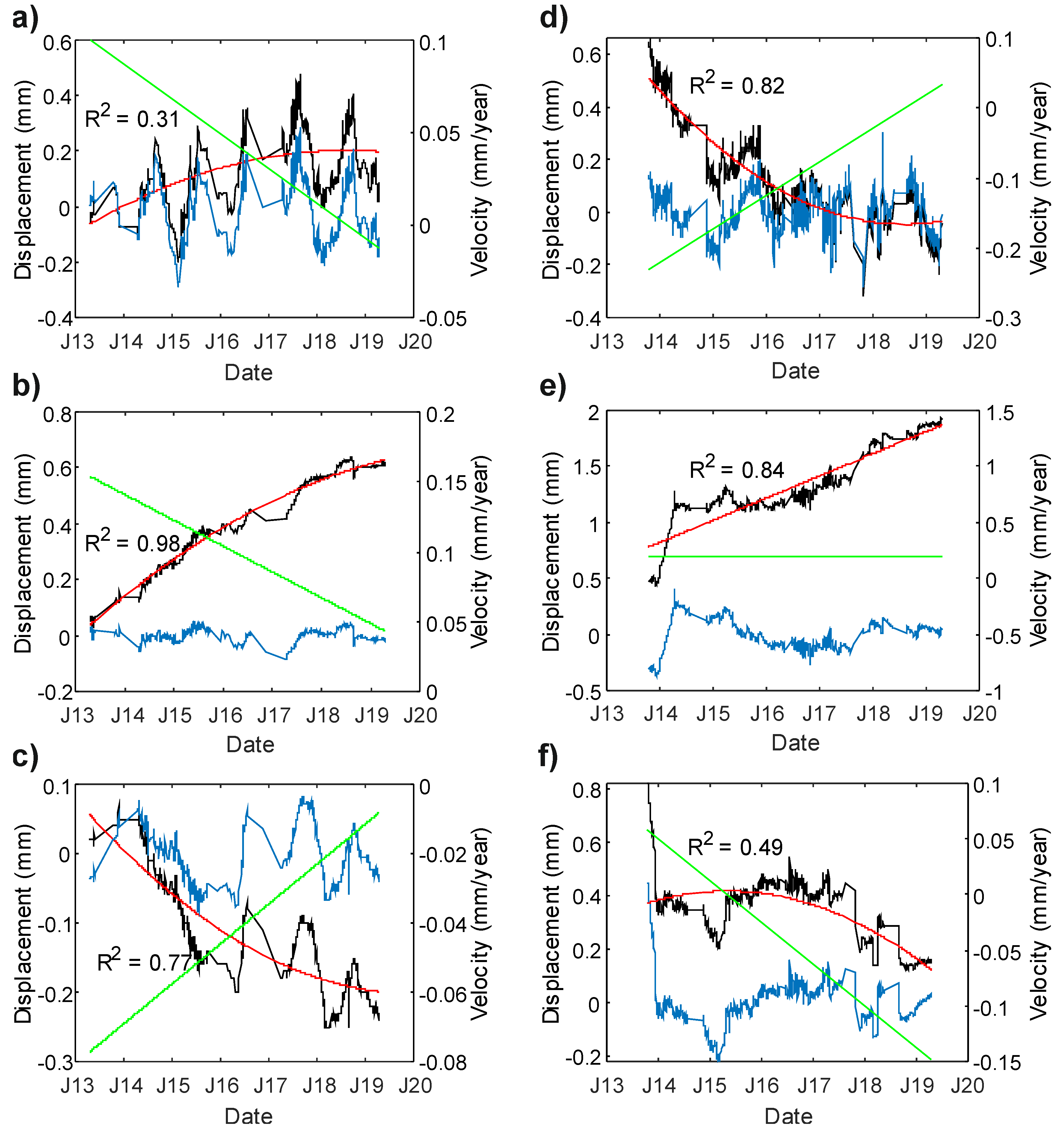
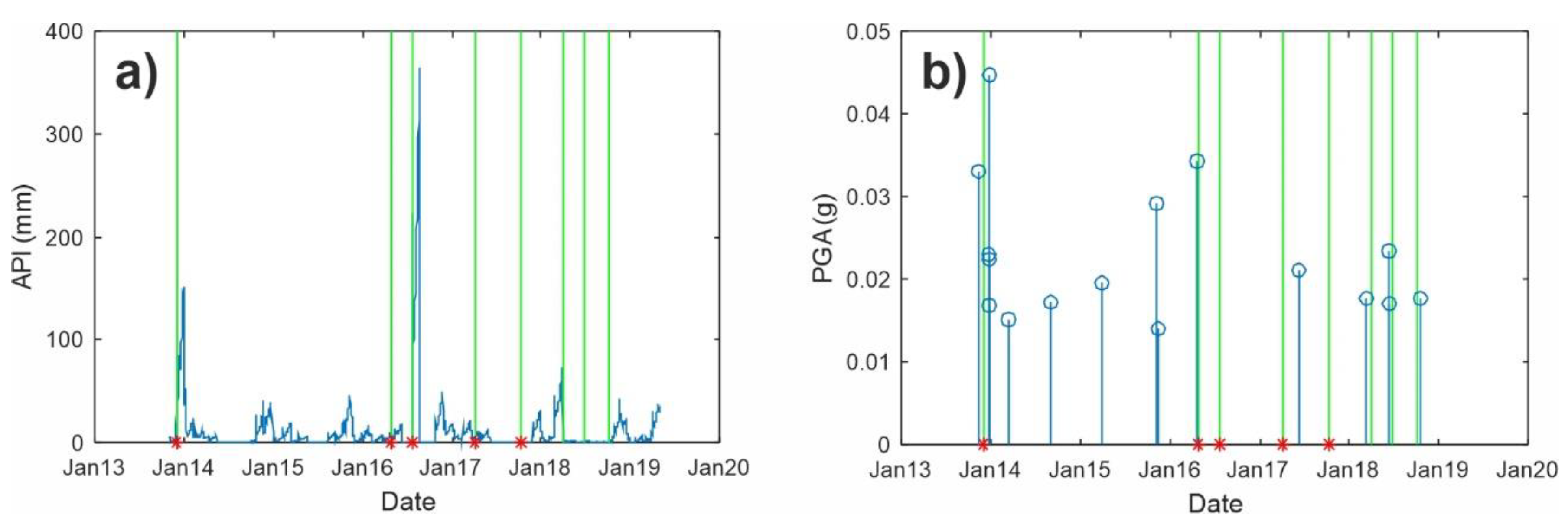
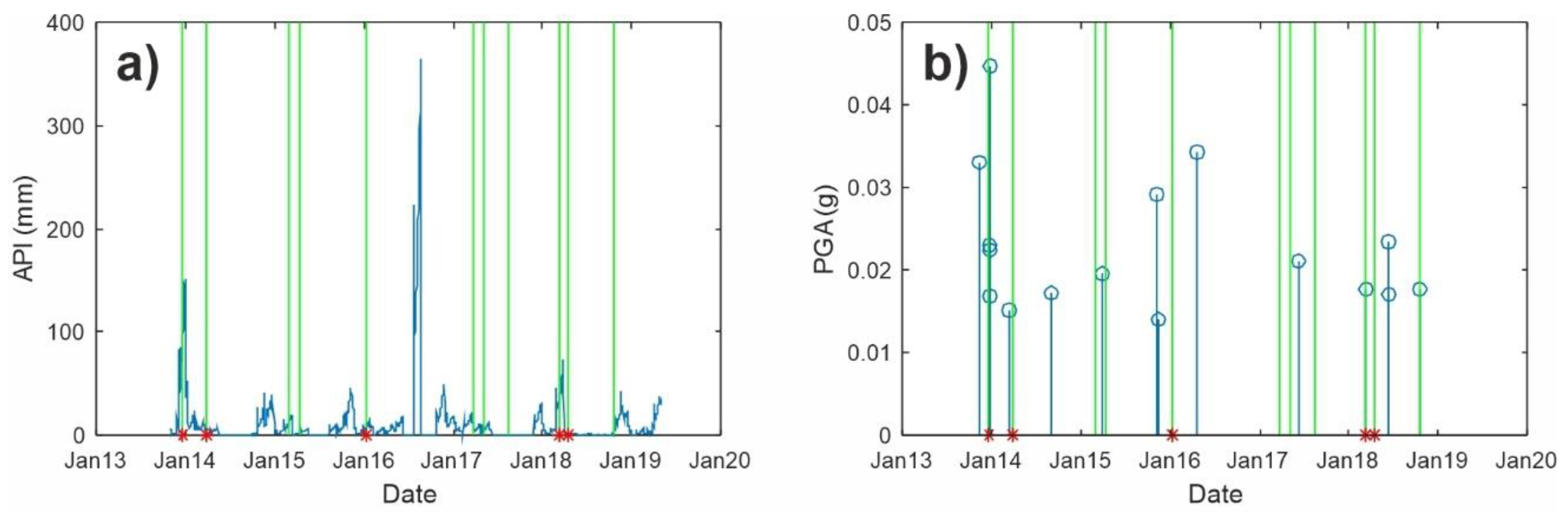
5. Results and Discussion
6. Conclusions
- (i)
- decreasing the subjectivity of interpretation and
- (ii)
- allowing fully quantitative analysis of the monitored data of a slow-moving landslide.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corominas, J.; Moya, J.; Ledesma, A.; Lloret, A.; Gill, J.A. Prediction of ground displacements and velocities from groundwater level changes at the Vallcebre Landslide (Eastern Pyrenees, Spain). Landslides 2005, 2, 83–96. [Google Scholar] [CrossRef]
- Van Asch, T.W.J.; Van Beek, L.P.H.; Bogaard, T.A. Problems in predicting the mobility of slow-moving landslides. Eng. Geol. 2007, 91, 46–55. [Google Scholar] [CrossRef]
- Klimeš, J.; Rowberry, M.; Blahůt, J.; Briestenský, M.; Hartvich, F.; Košťák, B.; Rybář, J.; Stemberk, J.; Štěpančíková, P. The monitoring of slow-moving landslides and assessment of stabilisation measures using an optical–mechanical crack gauge. Landslides 2012, 9, 407–415. [Google Scholar] [CrossRef]
- Carey, J.M.; Massey, C.I.; Lyndsell, B.; Petley, D.N. Displacement mechanisms of slow-moving landslides in response to changes in porewater pressure and dynamic stress. Earth Surf. Dynam. 2019, 7, 707–722. [Google Scholar] [CrossRef]
- Singh, L.P.; Van Westen, C.J.; Champati Ray, P.K.; Pasquali, P. Accuracy assessment of InSAR derived input maps for landslide susceptibility analysis: A case study from the Swiss Alps. Landslides 2005, 2, 221–228. [Google Scholar] [CrossRef]
- Schmidt, K.; Reimann, J.; Tous Ramon, N.; Schwerdt, M. Geometric accuracy of Sentinel-1A and 1B derived from SAR raw data with GPS surveyed corner reflector positions. Remote Sens. 2018, 10, 523. [Google Scholar] [CrossRef]
- Sinharay, S. An Overview of Statistics in Education. In International Encyclopedia of Education, 3rd ed.; Peterson, P., Baker, E., McGaw, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–11. [Google Scholar] [CrossRef]
- Brillinger, D.R. Time Series: General. In International Encyclopedia of the Social & Behavioral Sciences, 1st ed.; Smelser, N.J., Baltes, P.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 15724–15731. [Google Scholar] [CrossRef]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Heidelberg, Germany, 2005; p. 764. [Google Scholar]
- Neusser, K. Time Series Econometrics; Springer: Heidelberg, Germany, 2016; p. 409. [Google Scholar] [CrossRef]
- Montillet, J.-P.; Bos, M.S. Geodetic Time Series Analysis in Earth Sciences; Springer: Heidelberg, Germany, 2020; p. 422. [Google Scholar] [CrossRef]
- Mudelsee, M. Climate Time Series Analysis; Springer: Heidelberg, Germany, 2014; p. 454. [Google Scholar] [CrossRef]
- Sun, L.; Muller, J.-P.; Chen, J. Time series analysis of very slow landslides in the Three Gorges Region through small baseline SAR offset tracking. Remote Sens. 2017, 9, 1314. [Google Scholar] [CrossRef]
- Pfeiffer, J.; Zieher, T.; Rutzinger, M.; Bremer, M.; Wichmann, V. Comparison and time series analysis of landslide displacement mapped by airborne, terrestrial and unmanned aerial vehicle based platforms. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-2/W5, 421–428. [Google Scholar] [CrossRef]
- Huang Lin, C.; Liu, D.; Liu, G. Landslide detection in La Paz City (Bolivia) based on time series analysis of InSAR data. Int. J. Remote Sens. 2019, 40, 6775–6795. [Google Scholar] [CrossRef]
- Zvelebil, J.; Stemberk, J. Slope monitoring applied to rock fall management in NW Bohemia. In Landslide Research, Theory and Practice: Proceedings of the 8th International Symposium on Landslides held in Cardiff on 26–30 June 2000; Broomhead, E., Ed.; Thomas-Telford: London, UK, 2000; Volume 3, pp. 1659–1664. [Google Scholar]
- Košťák, B. Deformation effects in rock massifs and their long-term monitoring. Q. J. Eng. Geol. Hydrogeol. 2006, 39, 249–258. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.; Kavoura, K.; Depountis, N.; Kyriou, A.; Argyropoulos, N.; Koukouvelas, I.; Sabatakakis, N. Preliminary results from active landslide monitoring using multidisciplinary surveys. Eur. J. Remote Sens. 2017, 50, 280–299. [Google Scholar] [CrossRef]
- Guignard, F.; Laib, M.; Amato, F.; Kanevski, M. Advanced analysis of temporal data using Fisher-Shannon Information: Theoretical development and application in Geosciences. Fron. Earth Sci. 2020, 8, 255. [Google Scholar] [CrossRef]
- Toutounji, H.; Durstewitz, D. Detecting multiple change points using adaptive regression splines with application to neural recordings. Front. Neuroinform. 2018, 12, 67. [Google Scholar] [CrossRef] [PubMed]
- Alippi, C.; Camplani, R.; Galperti, C.; Marullo, A.; Roveri, M. An hybrid wireless-wired monitoring system for real-time rock collapse forecasting. In Proceedings of the 7th International Conference on Mobile Ad hoc and Sensor System (MASS), San Francisco, CA, USA, 8–12 November 2010; pp. 224–231. [Google Scholar]
- Barile, G.; Leoni, A.; Pantoli, L.; Stornelli, V. Real-Time Autonomous System for Structural and Environmental Monitoring of Dynamic Events. Electronics 2018, 7, 420. [Google Scholar] [CrossRef]
- Tordesillas, A.; Zhou, Z.; Batterham, R. A data-driven complex systems approach to early prediction of landslides. Mech. Res. Commun. 2018, 92, 137–141. [Google Scholar] [CrossRef]
- Bontemps, N.; Lacroix, P.; Larose, E.; Jara, J.; Taipe, E. Rain and small earthquakes maintain a slow-moving landslide in a persistent critical state. Nat. Commun. 2020, 11, 780. [Google Scholar] [CrossRef]
- Guillou, H.; Carracedo, J.-C.; Pérez Torrado, F.; Rodríguez Badiola, E. K-Ar ages and magnetic stratigraphy of a hotspot-induced, fast grown oceanic island: El Hierro, Canary Islands. J. Volcanol. Geotherm. Res. 1996, 73, 141–155. [Google Scholar] [CrossRef]
- Becerril, L.; Ubide, T.; Sudo, M.; Martí, J.; Galindo, I.; Galé, C.; Morales, J.; Yepes, J.; Lago, M. Geochronological constraints on the evolution of El Hierro (Canary Islands). J. Afr. Earth Sci. 2016, 113, 88–94. [Google Scholar] [CrossRef]
- Carracedo, J.-C.; Rodríguez Badiola, E.; Guillou, H.; de la Nuez, H.; Pérez Torrado, F. Geology and volcanology of the western Canaries: La Palma and El Hierro. Estudios Geológicos 2001, 57, 171–295. [Google Scholar] [CrossRef]
- López, C.; Blanco, M.J.; Abella, R.; Brenes, B.; Cabrera Rodríguez, V.; Casas, B.; Domínguez Cerdeña, I.; Felpeto, A.; Fernández de Villalta, M.; del Fresno, C.; et al. Monitoring the volcanic unrest of El Hierro (Canary Islands) before the onset of the 2011–2012 submarine eruption. Geophys. Res. Lett. 2012, 39, L13303. [Google Scholar] [CrossRef]
- Benito-Saz, M.; Parks, M.; Sigmundsson, F.; Hooper, A.; García-Cañada, L. Repeated magmatic intrusions at El Hierro Island following the 2011–2012 submarine eruption. J. Volcanol. Geotherm. Res. 2017, 344, 79–91. [Google Scholar] [CrossRef]
- Meletlidis, S.; Di Roberto, A.; Domínguez Cerdeña, I.; Pompilio, M.; García-Cañada, L.; Bertagnini, A.; Benito-Saz, M.; Del Carlo, P.; Sainz-Maza Aparicio, S. New insight into the 2011–2012 unrest and eruption of El Hierro Island (Canary Islands) based on integrated geophysical, geodetical, and petrological data. Ann. Geophys. 2015, 58, S0546. [Google Scholar] [CrossRef]
- Carracedo, J.-C.; Troll, V. The Geology of Canary Islands, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2016; p. 622. [Google Scholar]
- Blahůt, J.; Baroň, I.; Sokol, Ľ.; Meletlidis, S.; Klimeš, J.; Rowberry, M.; Melichar, R.; García-Cañada, L.; Martí, X. Large landslide stress states calculated during extreme climatic and tectonic events on El Hierro, Canary Islands. Landslides 2018, 15, 1801–1814. [Google Scholar] [CrossRef]
- Masson, D. Catastrophic collapse of the volcanic island of Hierro 15 ka ago and the history of landslides in the Canary Islands. Geology 1996, 24, 231–234. [Google Scholar] [CrossRef]
- Urgeles, R.; Canals, M.; Baraza, J.; Alonso, B. The submarine El Golfo debris avalanche and the Canary debris flow, west Hierro Island: The last major slides in the Canary Archipelago. Geogaceta 1996, 20, 390–393. [Google Scholar]
- Urgeles, R.; Canals, M.; Baraza, J.; Alonso, B.; Masson, D. The most recent megalandslides on the Canary Islands: The El Golfo debris avalanche and the Canary debris flow, west El Hierro Island. J. Geophys. Res. Solid Earth 1997, 102, 20305–20323. [Google Scholar] [CrossRef]
- Carracedo, J.-C.; Day, S.; Guillou, H.; Pérez Torrado, F. Giant quaternary landslides in the evolution of La Palma and El Hierro, Canary Islands. J. Volcanol. Geotherm. Res. 1999, 94, 169–190. [Google Scholar] [CrossRef]
- Masson, D.; Watts, A.B.; Gee, M.J.; Urgeles, R.; Mitchell, N.; Le Bas, T.; Canals, M. Slope failures on the flanks of the western Canary Islands. Earth Sci. Rev. 2002, 57, 1–35. [Google Scholar] [CrossRef]
- Longpré, M.; Chadwick, J.; Wijbrans, J.; Iping, R. Age of the El Golfo debris avalanche, El Hierro (Canary Islands): New constraints from laser and furnace 40Ar/39Ar dating. J. Volcanol. Geotherm. Res. 2011, 203, 76–80. [Google Scholar] [CrossRef]
- Becerril, L.; Galve, J.; Morales, J.; Romero, C.; Sánchez, N.; Martí, J.; Galindo, I. Volcanostructure of El Hierro (Canary Islands). J. Maps 2016, 12, 43–52. [Google Scholar] [CrossRef]
- León, R.; Somoza, L.; Urgeles, R.; Medialdea, T.; Ferrer, M.; Biain, A.; García-Crespo, J.; Mediato, J.; Galindo, I.; Yepes, J.; et al. Multi-event oceanic island landslides: New onshore-offshore insights from El Hierro Island, Canary archipelago. Mar. Geol. 2017, 393, 156–175. [Google Scholar] [CrossRef]
- Blahůt, J.; Klimeš, J.; Rowberry, M.; Kusák, M. Database of giant landslides on volcanic islands—First results from the Atlantic Ocean. Landslides 2018, 15, 823–827. [Google Scholar] [CrossRef]
- Blahůt, J.; Balek, J.; Klimeš, J.; Rowberry, M.; Kusák, M.; Kalina, J. A comprehensive global database of giant landslides on volcanic islands. Landslides 2019, 16, 2045–2052. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.; Zanchi, A. Structural constraints on deep seated slope deformation kinematics. Eng. Geol. 2001, 59, 83–102. [Google Scholar] [CrossRef]
- Moscardelli, L.; Wood, L. New classification system for mass transport complexes in offshore Trinidad. Basin Res. 2008, 20, 73–98. [Google Scholar] [CrossRef]
- Day, S.; Carracedo, J.-C.; Guillou, H. Age and geometry of an aborted rift flank collapse: The San Andres fault system, El Hierro, Canary Islands. Geol. Mag. 1997, 134, 523–537. [Google Scholar] [CrossRef]
- Blahůt, J.; Mitrovic-Woodell, I.; Baroň, I.; René, M.; Rowberry, M.; Blard, P.-H.; Hartvich, F.; Balek, J.; Meletlidis, S. Volcanic edifice slip events recorded on the fault plane of the San Andrés Landslide, El Hierro, Canary Islands. Tectonophysics 2020, 776, 228317. [Google Scholar] [CrossRef]
- Klimeš, J.; Yepes, J.; Becerril, L.; Kusák, M.; Galindo, I.; Blahůt, J. Development and recent activity of the San Andrés Landslide on El Hierro, Canary Islands, Spain. Geomorphology 2016, 261, 119–131. [Google Scholar] [CrossRef]
- Blahůt, J.; Rowberry, M.; Balek, J.; Klimeš, J.; Baroň, I.; Meletlidis, S.; Martí, X. Monitoring giant landslide detachment planes in the era of big data analytics. In Advancing Culture of Living with Landslides; Mikoš, M., Arbanas, Ž., Yin, Y., Sassa, K., Eds.; Springer: Cham, Switzerland, 2017; Volume 3, pp. 333–340. [Google Scholar] [CrossRef]
- Blahůt, J.; Olejár, F.; Rott, J.; Petružálek, M. Current stability modelling of an incipient San Andrés giant landslide on El Hierro Island, Canaries, Spain—First attempt using limited input data. Acta Geodyn. Geomater. 2020, 17, 89–99. [Google Scholar] [CrossRef]
- Martí, X.; Rowberry, M.D.; Blahůt, J. A MATLAB® code for counting the moiré fringe patterns recorded on the optical-mechanical crack gauge TM-71. Comput. Geosci. 2013, 52, 164–167. [Google Scholar] [CrossRef]
- Stemberk, J.; Briestenský, M.; Cacoń, S. The recognition of transient compressional fault slow-slip along the northern shore of Hornsund Fjord, SW Spitsbergen, Svalbard. Pol. Polar Res. 2015, 36, 109–123. [Google Scholar] [CrossRef]
- Weather Information Service. Available online: http://www.ogimet.com/index.phtml.en (accessed on 6 June 2019).
- Kohler, M.A.; Linsley, R.K., Jr. Predicting Runoff from Storm Rainfall, Research Paper 34; US Weather Bureau: Washington, DC, USA, 1951.
- Mishra, S.K.; Singh, V.P. Soil Conservation Service Number (SCS-CN) Methodology; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2003; p. 516. [Google Scholar]
- Smolíková, J.; Blahůt, J.; Vilímek, V. Analysis of rainfall preceding debris flows on the Smědavská hora Mt., Jizerské hory Mts., Czech Republic. Landslides 2016, 13, 683–696. [Google Scholar] [CrossRef]
- Viessman, W.; Lewis, G.L. Introduction to Hydrology, 4th ed.; Harper Collins: New York, NY, USA, 1996; p. 760. [Google Scholar]
- Racek, O.; Blahůt, J.; Hartvich, F. Monitoring of thermoelastic wave within a rock mass coupling information from IR camera and crack meters: A 24-hour experiment on “Branická skála” Rock in Prague, Czechia. In WLF5 Book—Volume 3 “Monitoring and Early Warning”; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Instituto Geográfico Nacional. Available online: https://www.ign.es/web/ign/portal/sis-catalogo-terremotos (accessed on 6 June 2019).
- Munson, C.G.; Thurber, C.H. Analysis of the attenuation of strong ground motion on the Island of Hawaii. Bull. Seismol. Soc. Am. 1997, 87, 945–960. [Google Scholar]
- Gonzáles de Vallejo, L.I.; García-Mayordomo, J.; Insua, J.M. Probabilistic seismic-hazard assessment of the Canary Islands. Bull. Seismol. Soc. Am. 2006, 96, 2040–2049. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Balek, J.; Urban, R.; Štroner, M. Laboratory testing of the precision and accuracy of the TM-71 dilatometer. Pap. SGEM 2018, 18, 433–439. [Google Scholar] [CrossRef]
- Visvalingam, M.; Whyatt, J.D. The Douglas-Peucker algorithm for line simplification: Re-evaluation through visualization. Comput. Graph. Forum 1990, 9, 213–228. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Brasca Merlin, A.; Lanfri, M.; Carignano, C.; Pascual, I.; Schlögel, R.; Cuozzo, G. Sensado Remoto de procesos de remoción en masa: Pautas para el monitoreo operativo. In Proceedings of the 2018 IEEE Biennial Congress of Argentina (ARGENCON), San Miguel de Tucumán, Argentina, 6 June 2018; p. 8. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blahůt, J.; Balek, J.; Eliaš, M.; Meletlidis, S. 3D Dilatometer Time-Series Analysis for a Better Understanding of the Dynamics of a Giant Slow-Moving Landslide. Appl. Sci. 2020, 10, 5469. https://doi.org/10.3390/app10165469
Blahůt J, Balek J, Eliaš M, Meletlidis S. 3D Dilatometer Time-Series Analysis for a Better Understanding of the Dynamics of a Giant Slow-Moving Landslide. Applied Sciences. 2020; 10(16):5469. https://doi.org/10.3390/app10165469
Chicago/Turabian StyleBlahůt, Jan, Jan Balek, Michal Eliaš, and Stavros Meletlidis. 2020. "3D Dilatometer Time-Series Analysis for a Better Understanding of the Dynamics of a Giant Slow-Moving Landslide" Applied Sciences 10, no. 16: 5469. https://doi.org/10.3390/app10165469
APA StyleBlahůt, J., Balek, J., Eliaš, M., & Meletlidis, S. (2020). 3D Dilatometer Time-Series Analysis for a Better Understanding of the Dynamics of a Giant Slow-Moving Landslide. Applied Sciences, 10(16), 5469. https://doi.org/10.3390/app10165469





