Internal Force Analysis of Buried-boring Piles in the Yuanzishan Landslide
Abstract
1. Introduction
2. Methodology and Validation
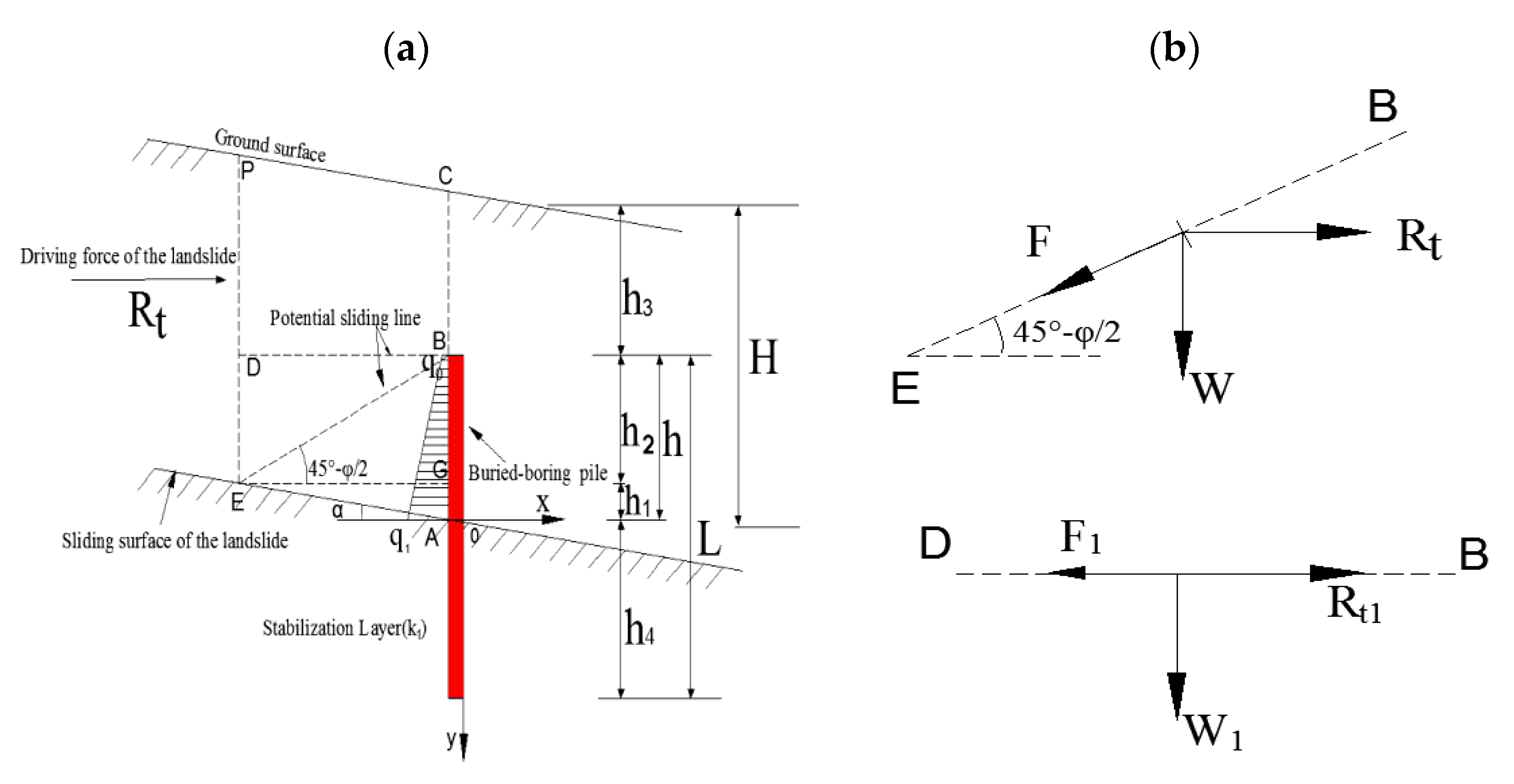
2.1. Simplified Calculations of Buried-Boring Piles during a Landslide
2.1.1. Basic Assumptions
- (1)
- it was assumed that the driving force of the landslide was transmitted to the foundation of the bored pile, with the friction force at the top of the pile and the reaction force at the pile bottom assumed to be negligible;
- (2)
- the bored pile was assumed to be in a fragile state, such that the displacement of the soil in front of the pile was equal to the pile displacement above the slip surface. The pile was simplified as a cantilever beam; thus, the resistance force of the soil in front of the pile is negligible;
- (3)
- the potential fracture surface in the slope body was assumed to be the Coulomb fracture surface [25], such that the shear strength of the soil above the slip surface was constant at φ and the slope, a, of the slip surface at the pile location was parallel to the ground slope. By making these assumptions, the thrust distribution was simplified to a trapezoidal load.
2.1.2. Determination of the Pile Length above the Slip Surface
2.1.3. Internal Force the of Bored Pile above the Slip Surface
2.1.4. Internal Force of the Bored Pile below the Slip Surface
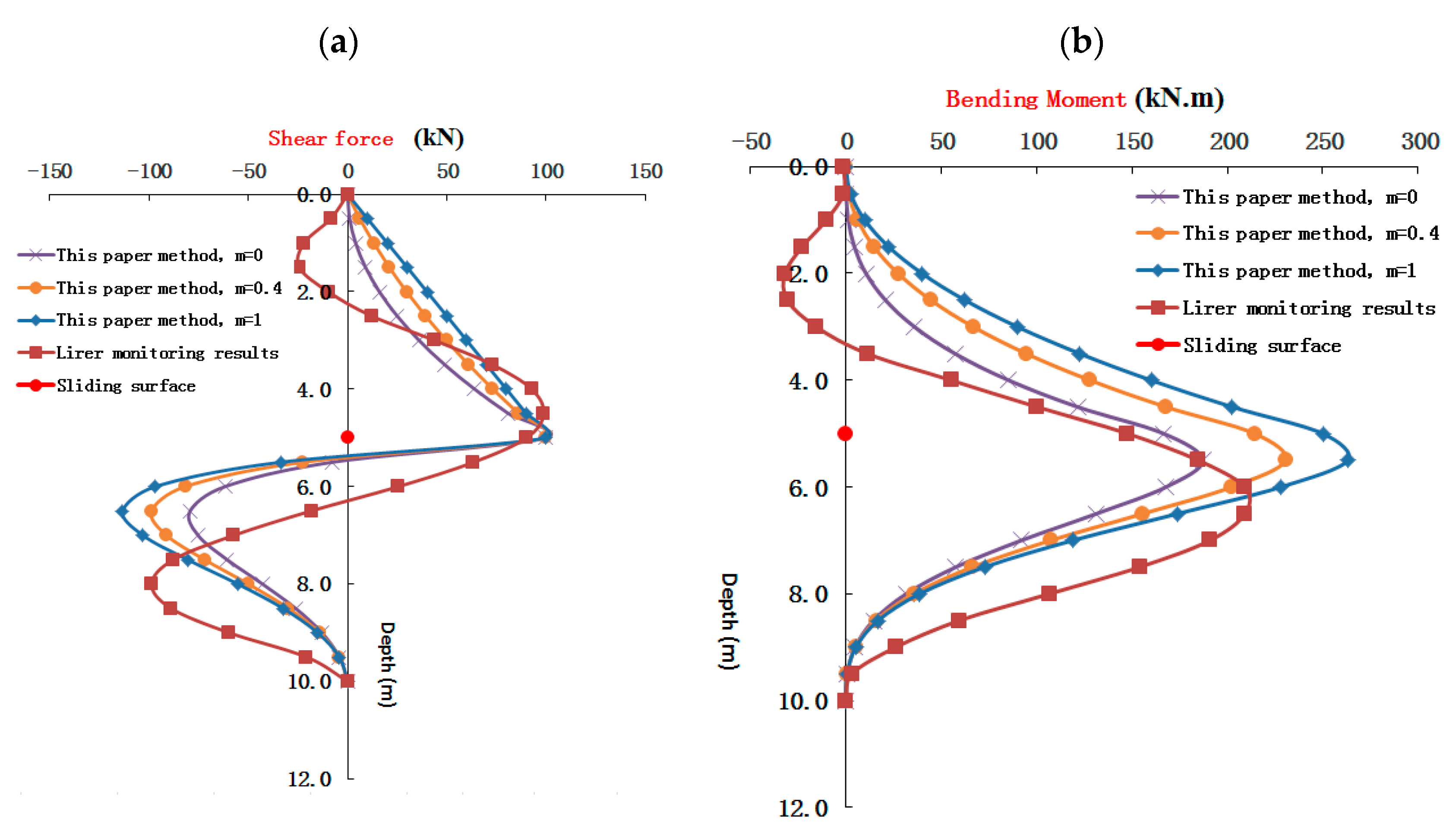
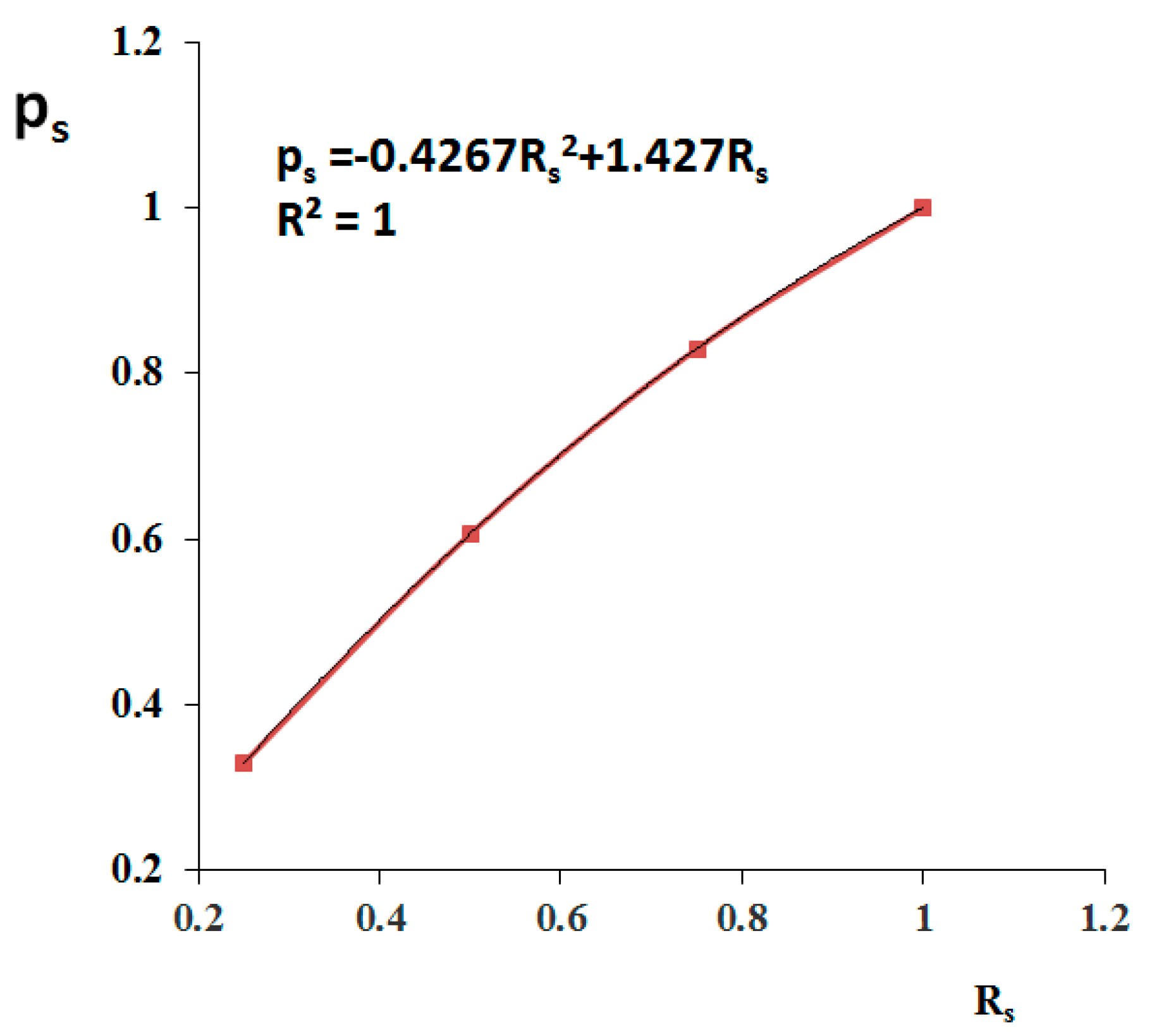
2.2. Validation of the Calculation Method and Determination of the Driving Force Distribution Coefficient
3. Application of Buried-Boring Piles in the Yanzishan Landslide
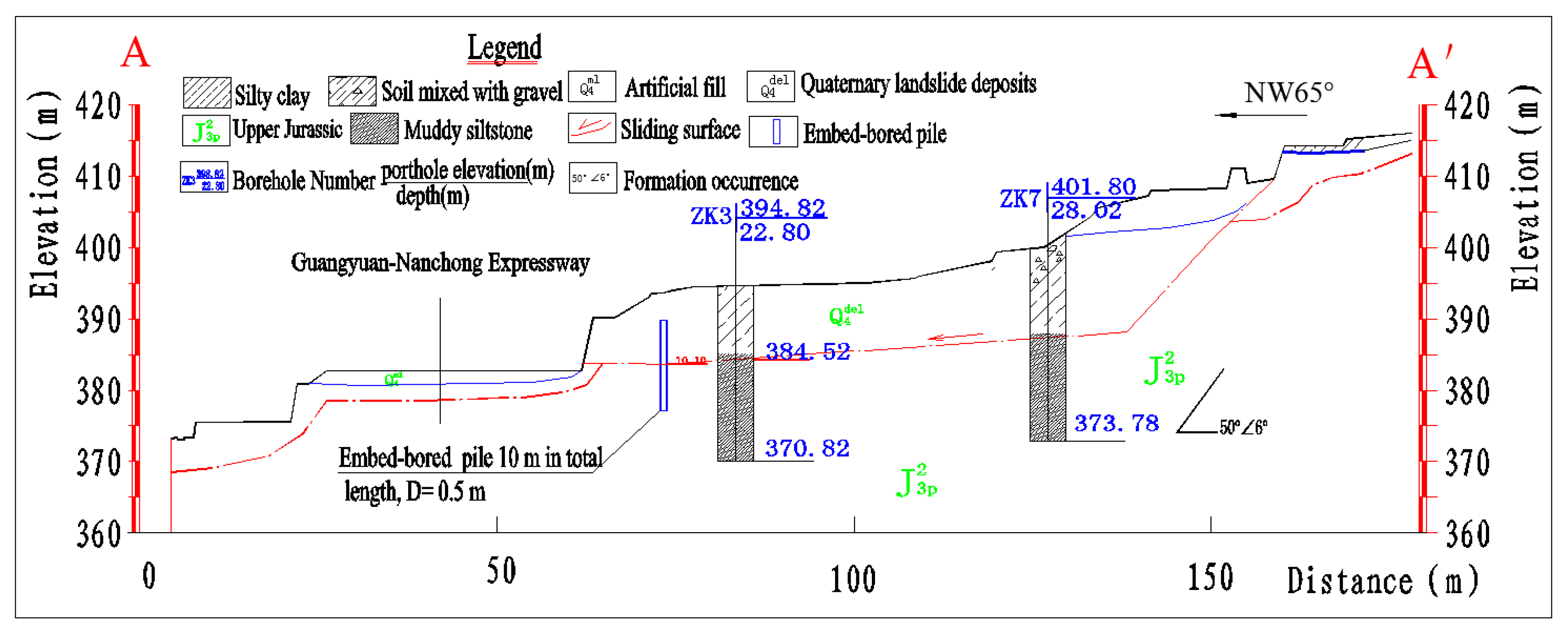
3.1. Geological Background of the Yanzishan Landslide
3.2. Application of Buried-Boring Piles to the Yanzishan Landslide
4. Influence of Parameter Changes on the Internal Force of the Buried-Boring Pile
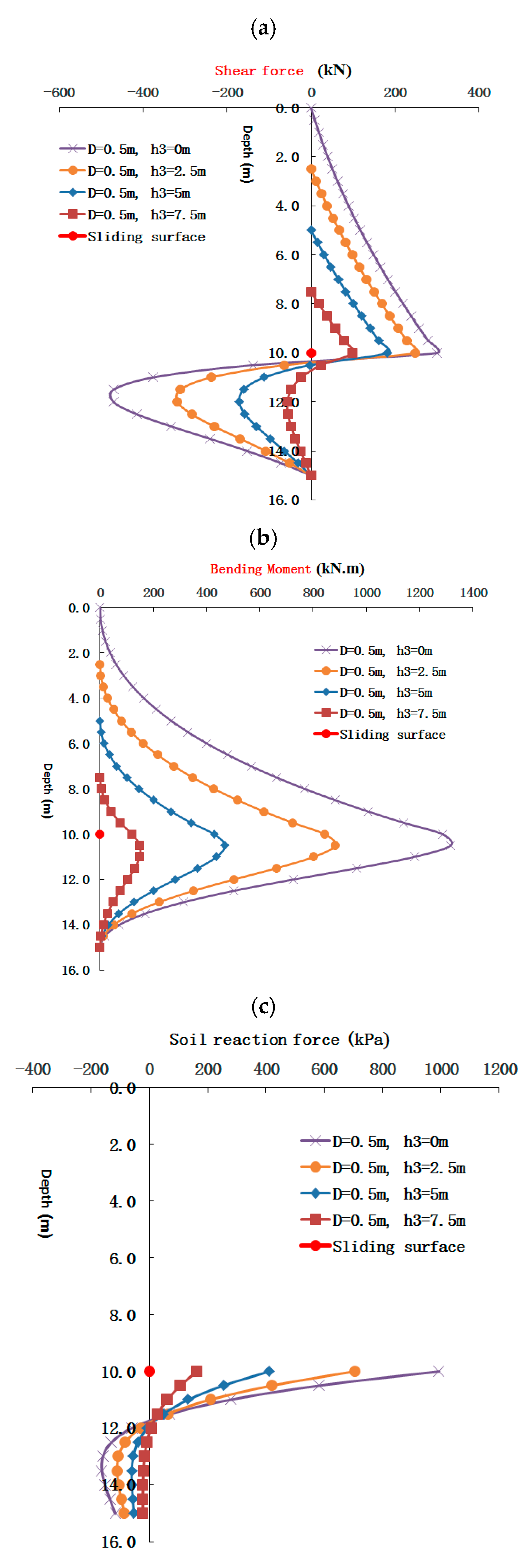
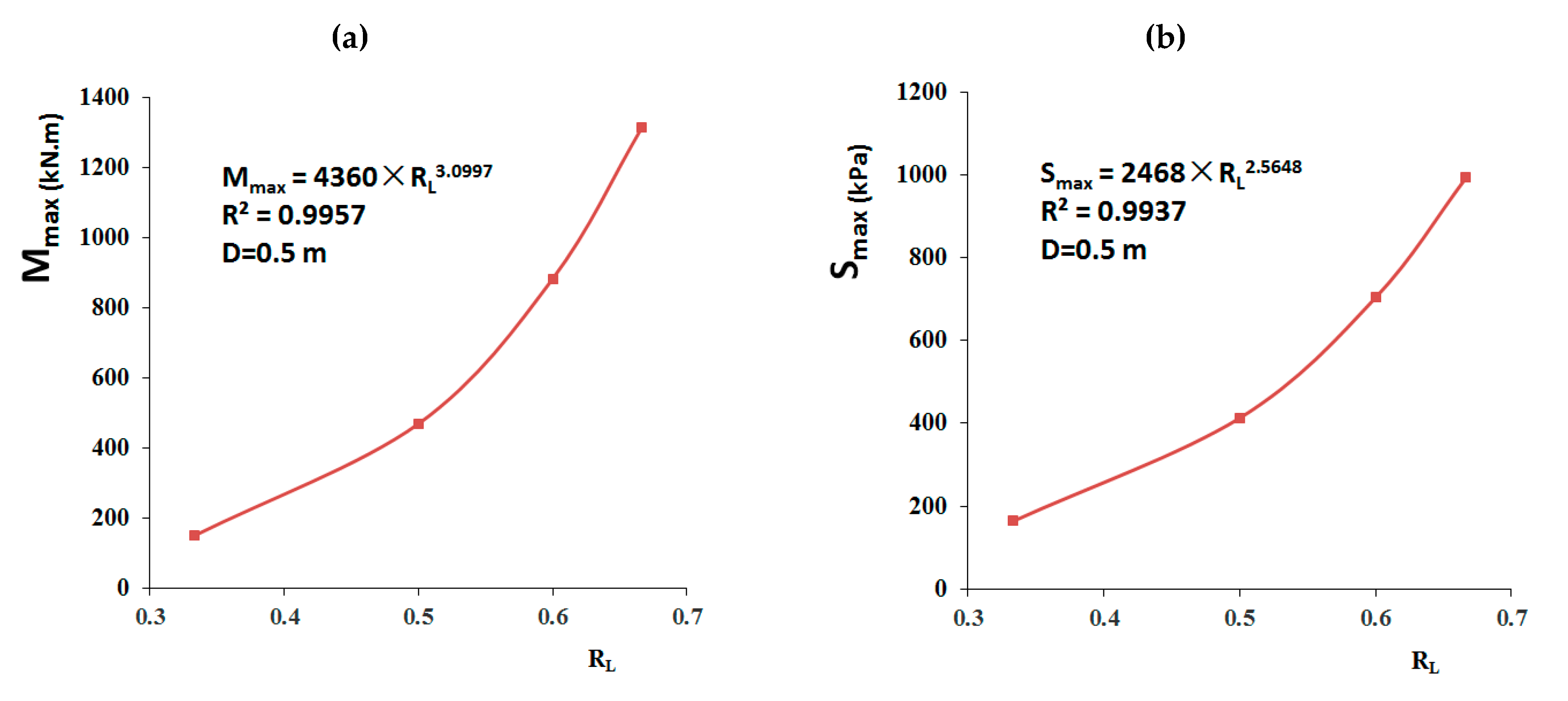
4.1. Influence of Depth of Buried Length above Slip Surface on the Internal Force of the Pile
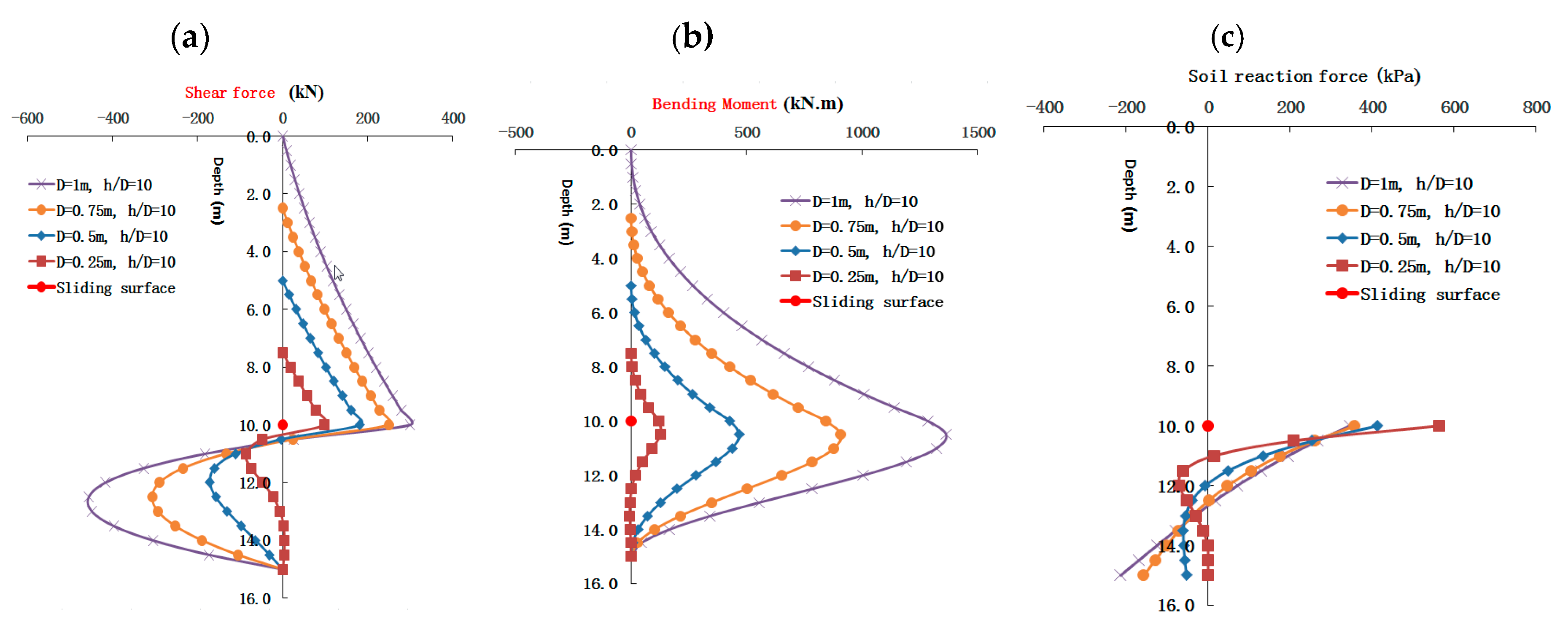
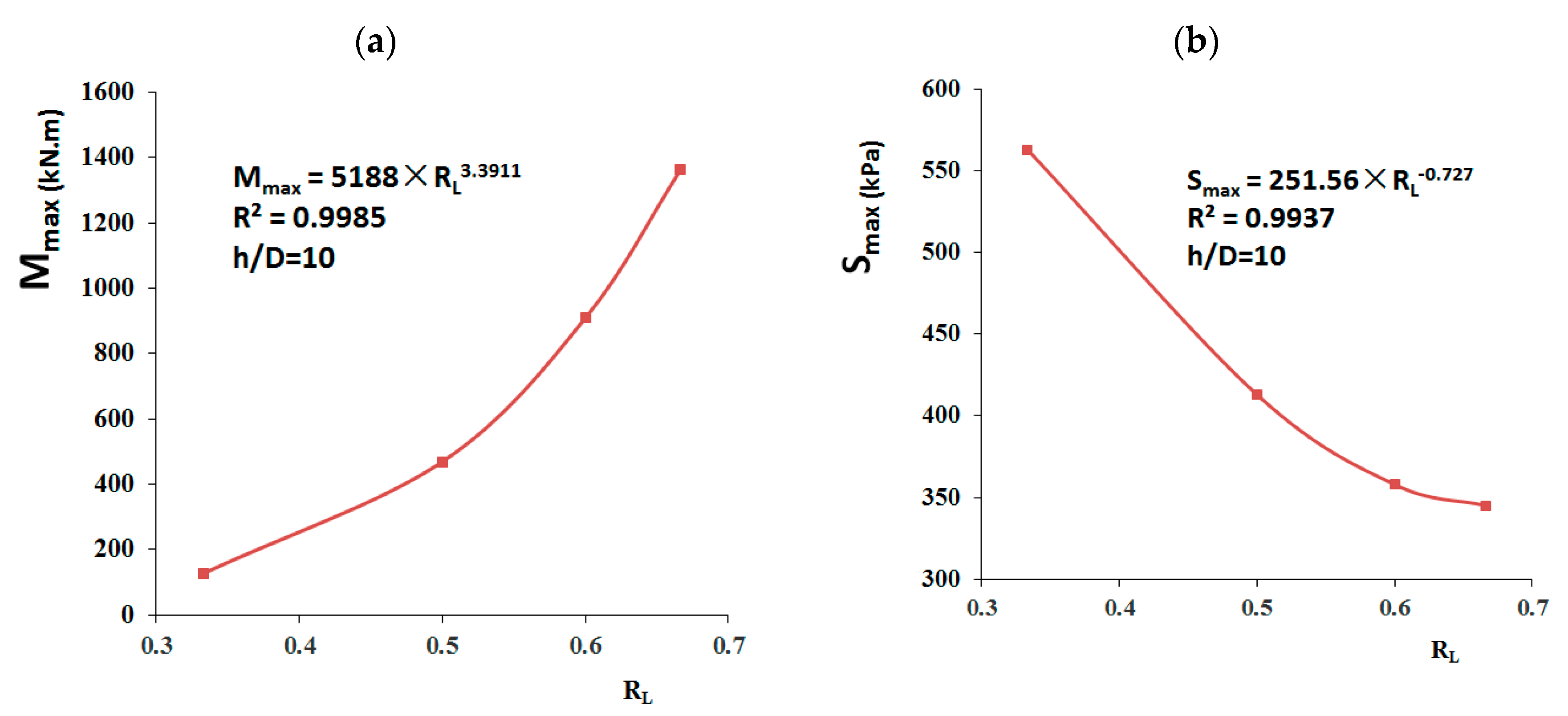
4.2. Influence of Pile Diameter Change on the Internal Force of the Buried-Boring Pile
5. Discussion
5.1. Effect of the Pile Depth above the Slip Surface on the Internal Forces of the Buried-Boring Pile
5.2. Effect of the Pile Diameter on the Lateral Reaction of the Soil below the Slip Surface
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ding, Y.; Wang, Q.C. Remediation and analysis of kinematic behaviour of a roadway landslide in the upper Minjiang River, Southwest China. Environ. Geol. 2009, 58, 1521–1532. [Google Scholar] [CrossRef]
- Motta, E. Lateral deflection of horizontally loaded rigid piles in elastoplastic medium. J. Geotech. Geoenviron. Eng. 2013, 139, 1–6. [Google Scholar] [CrossRef]
- Broms, B.B. Lateral resistance of piles in cohesionless soils. J. Soil Mech. Found. Div. 1964, 90, 123–159. [Google Scholar]
- Broms, B.B. Lateral resistance of piles in cohesive soils. J. Soil Mech. Found. Div. 1964, 90, 27–63. [Google Scholar]
- Hsiung, Y.M.; Chen, S.S.; Chou, Y.C. Analytical solution for piles supporting combined lateral loads. J. Geotech. Geoenviron. Eng. 2006, 132, 1315–1324. [Google Scholar] [CrossRef]
- Basu, D.; Salgado, R.; Prezzi, M. Analysis of laterally loaded piles in multilayered soil deposits. In Technical Report of Joint Transportation Research Program; Purdue University: West Lafayette, IN, USA, 2008. [Google Scholar]
- Xu, L.Y.; Cai, F.; Wang, G.X.; Ugai, K. Nonlinear analysis of laterally loaded single piles in sand using modified strain wedge model. Comput. Geotech. 2013, 51, 60–71. [Google Scholar] [CrossRef]
- Xu, L.Y.; Pan, J.M.; Xue, Y.Y.; Cai, F.F. A Numerical Investigation of Influence of Low-Plasticity Fines in Sand on Lateral Response of Piles. Mar. Geores. Geotech. 2019, 132, 1–10. [Google Scholar] [CrossRef]
- Khalili-Tehrani, P.; Ahlberg, E.R.; Rha, C.; Lemnitzer, A.; Stewart, J.P.; Taciroglu, E.; Wallace, J.W. Nonlinearload-deflection behavior of reinforced concrete drilled piles in stiff clay. J. Geotech. Geoenviron. Eng. 2013, 140. [Google Scholar] [CrossRef]
- Stacul, S.; Squeglia, N.; Morelli, F. Laterally Loaded Single Pile Response Considering the Influence of Suction and Non-Linear Behaviour of Reinforced Concrete Sections. Appl. Sci. 2017, 7, 1310. [Google Scholar] [CrossRef]
- Mardfekri, M.; Gardoni, P.; Roesset, J.M. Modeling laterally loaded single piles accounting for nonlinear soil-pile interactions. J. Eng. 2013, 243, 179. [Google Scholar] [CrossRef]
- Mohammad, M.Y.; Mousa, F.A.; Zahid, K. Lateral Response of Drilled Shafts in A Moving Cohesive Soil. Inter. J. Civ. Eng. 2020, 18, 735–742. [Google Scholar] [CrossRef]
- Li, F.; Han, J.; Lin, C. Effect of Scour on the Behavior of Laterally Loaded Single Piles in Marine Clay. Mar. Geores. Geotech. 2013, 31, 271–289. [Google Scholar] [CrossRef]
- Yang, Z.; Jeremić, B. Numerical analysis of pile behaviour under lateral loads in layered elastic–plastic soils. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 1385–1406. [Google Scholar] [CrossRef]
- Wu, G.; Finn, W.L.; Dowling, J. Quasi-3D analysis: Validation by full 3D analysis and field tests on single piles and pile groups. Soil Dyn. Earthq. Eng. 2015, 78, 61–70. [Google Scholar] [CrossRef]
- Mokwa, R.L.; Duncan, J.M. Experimental evaluation of lateral-load resistance of pile caps. J. Geotech.Geoenviron. Eng. 2001, 127, 185–192. [Google Scholar] [CrossRef]
- Qin, H.; Guo, W. Response of piles subjected to progressive soil movement. Geotech. Test. J. 2016, 39, 106–125. [Google Scholar] [CrossRef]
- Khari, M.; Kassim, K.A.; Adnan, A. Development of Curves of Laterally Loaded Piles in Cohesionless Soil. Sci. World J. 2014, 2014, 917174. [Google Scholar] [CrossRef]
- Fatahi, B.; Basack, S.; Ryan, P.; Zhou, W.H.; Khabbaz, H. Performance of laterally loaded piles considering soil and interface parameters. Geomech. Eng. 2014, 7, 495–524. [Google Scholar] [CrossRef]
- Ashour, M.; Pilling, P.; Norris, G. Lateral Behavior of Pile Groups in Layered Soils. J. Geotech. Geoenviron. Eng. 2004, 130, 580–592. [Google Scholar] [CrossRef]
- Brown, D.; Reese, L.; O’Neill, M. Cyclic lateral loading of a large-scale pile group. J. Geotech. Eng. 1987, 113, 1326–1343. [Google Scholar] [CrossRef]
- Rollins, K.M.; Olsen, K.G.; Jensen, D.H.; Garrett, B.H.; Olsen, R.J.; Egbert, J.J. Pile spacing effects on lateral pile group behavior: Analysis. J. Geotech. Geoenviron. Eng. 2006, 132, 1272–1283. [Google Scholar] [CrossRef]
- Standardization Administration of China. GB/T 38509-2020: Code for Design of Landslide Stabilization; Standardization Administration of China: Beijing, China, 2020. (In Chinese) [Google Scholar]
- Wang, G.X. Landslide Science and Landslide Prevention Technology; China Railway Publishing: Beijing, China, 2004; pp. 355–458. [Google Scholar]
- Zeng, S.R. Design of subsidence anti-slide pile. Chongqing Archit. 2003, 1, 22–24. (In Chinese) [Google Scholar]
- Hui, H. Application of Embedded Piles in Landslide Control of Songjiayao; Chang’an University: Xi’an, China, 2018. (In Chinese) [Google Scholar]
- Zhao, S.Y.; Zheng, Y.R.; Wang, Y.F.; Tang, X.S. The Application of Combined Full-length and Embedded Anti-slide Piles in Landslide Treatment of Waduan Village. J. Logist. Eng. Univer. 2014, 30, 1–7. (In Chinese) [Google Scholar]
- Xiong, Z.W. Force distribution rule of deeply buried anti-slide pile. China Railw. Sci. 2000, 21, 48–51. (In Chinese) [Google Scholar]
- Second Surveying and Design Institute of the National Department of Chinese Railways. Design and Computation of Anti-Slide Piles; Chinese Railway Publishing House: Beijing, China, 1983. (In Chinese) [Google Scholar]
- Wang, H.; Lv, Z.Y.; Qin, H.Y. Deformation Control Method of the Antislide Pile under Trapezoidal Load in the Zhangjiawan Landslide. Adv. Civ. Eng. 2020. [Google Scholar] [CrossRef]
- Zhou, C.M.; Shao, W.; Yin, K.L.; Yang, Z.J. Estimating the properties of weathered bedrock and pilerock interaction from the geological strength index. J. Mt. Sci. 2018, 15, 1757–1776. [Google Scholar] [CrossRef]
- Standardization Administration of China. JGJ 94-2008: Technical Code for Building Pile Foundations; Standardization Administration of China: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Wang, H.; Wang, P.; Qin, H.Y. Method to Control the Deformation of Anti-Slide Piles in Zhenzilin Landslide. Appl. Sci. 2020, 10, 2832. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Tang, H.; Lei, G.; Yan, J.; Zhang, Y. A preliminary study on the location of the stabilizing piles for colluvial landslides with interbedding hard and soft bedrocks. Eng. Geol. 2017, 224, 15–28. [Google Scholar] [CrossRef]
- Lirer, S. Landslide stabilizing piles: Experimental evidences and numerical interpretation. Eng. Geol. 2012, 149, 70–77. [Google Scholar] [CrossRef]
- Tang, H.; Hu, X.; Xu, C.; Li, C.; Yong, R.; Wang, L. A novel approach for determining landslide pushing force based on landslide-pile interactions. Eng. Geol. 2014, 182, 15–24. [Google Scholar] [CrossRef]
- Carranza-Torres, C. Dimensionless Graphical Representation of the Exact Elastoplastic Solution of a Circular Tunnel in a Mohr-Coulomb Material Subject to Uniform Far-field Stresses. Rock. Mech. Rock Eng. 2003, 36, 237–253. [Google Scholar] [CrossRef]
- Guo, W.; Qin, H. Thrust and bending moment of rigid piles subjected to moving soil. Can. Geotech. J. 2010, 47, 180–196. [Google Scholar] [CrossRef]
- Poulos, H. Design of reinforcing piles to increase slope stability. Can. Geotech. J. 1995, 32, 808–818. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Tang, H.; Hu, X.; Liu, X.; Wang, C.; Liu, T.; Zhang, Y. Model testing of the response of stabilizing piles in landslides with upper hard and lower weak bedrock. Eng. Geol. 2016, 204, 65–76. [Google Scholar] [CrossRef]
- Kahyaoğlu, M.R.; Imançlı, G.; Özden, G.; Kayalar, A.S.; Imançli, G. Numerical simulations of landslide-stabilizing piles: A remediation project in Söke, Turkey. Environ. Earth Sci. 2017, 76, 656. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Response of flexible piles under laterally linear movement of the sliding layer in landslides. Can. Geotech. J. 2003, 40, 46–53. [Google Scholar] [CrossRef]


| Geotechnical Classification | Moisture Content (%) | Density ρ (g/cm3) | Undrained Strength of Soil Su (kPa) | OCR | |
|---|---|---|---|---|---|
| Soil | 19 | 2.05 | 50 | 27.23 | 2 |
| Varicolored clay | 15 | 2.22 | 100 | - | 10 |
| Geotechnical Classification | Density (g/cm3) | Internal Friction Angle(°) | Cohesion c (kPa) | Moisture Content (%) |
| Soil | 2.00 | 30 | 13.8 | 28.9 |
| Muddy siltstone | 2.45 | - | - | - |
| Geotechnical Classification | Poisson’s Ratio | Saturated Compressive Strength (MPa) | Natural Compressive Strength (MPa) | Young’s Modulus E (× 104 MPa) |
| Soil | - | - | - | 0.000048 |
| Muddy siltstone | 0.25 | 3 | 5 | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Lv, Z.; Zhang, J.; Yue, J.; Qin, H.; Hung, C. Internal Force Analysis of Buried-boring Piles in the Yuanzishan Landslide. Appl. Sci. 2020, 10, 5416. https://doi.org/10.3390/app10165416
Wang H, Lv Z, Zhang J, Yue J, Qin H, Hung C. Internal Force Analysis of Buried-boring Piles in the Yuanzishan Landslide. Applied Sciences. 2020; 10(16):5416. https://doi.org/10.3390/app10165416
Chicago/Turabian StyleWang, Hao, Zhiying Lv, Jianwei Zhang, Jianwei Yue, Hongyu Qin, and Chaoying Hung. 2020. "Internal Force Analysis of Buried-boring Piles in the Yuanzishan Landslide" Applied Sciences 10, no. 16: 5416. https://doi.org/10.3390/app10165416
APA StyleWang, H., Lv, Z., Zhang, J., Yue, J., Qin, H., & Hung, C. (2020). Internal Force Analysis of Buried-boring Piles in the Yuanzishan Landslide. Applied Sciences, 10(16), 5416. https://doi.org/10.3390/app10165416





