Abstract
In Indonesia, the solar photovoltaic (PV) market is rapidly growing. However, studies on the outdoor performance of PV systems in this tropical rainforest country is lacking. In this work, we compare the performance of PV systems in Indonesia with PV systems in Australia (arid, desert, hot) and Italy (temperate, dry summer, hot summer). Monitoring data from 2008 to 2019, ranging from two to nine years, from fifteen PV systems of six technologies were analyzed. The performance of the PV systems was presented using their performance ratio (PR) and performance loss rate (PLR). PR was calculated using IEC standard 61724, and PLR was calculated using seasonal and trend decomposition, applying locally weighted scatterplot smoothing (STL decomposition) and the year-on-year approach from NREL/RdTools. The results showed that the CIGS (copper indium gallium selenide) system had the highest average PR value of 0.88 ± 0.04. The lowest average PR was found in the a-Si (amorphous silicon) PV systems (0.78 ± 0.05). The p-Si (polycrystalline silicon) systems in the Cfb (temperate, no dry season, warm summer) climate of Italy had a higher average PR of 0.84 than those operated in climates BWh (arid, desert, hot) of Australia and Af (tropical, rainforest) of Indonesia, with the same value of 0.81. The p-Si systems showed the lowest PLR, with a value of −0.6%/year. The fastest degradation was experienced by a-Si modules at −1.58%/year. The methodological differences in the calculation of PLR using both tested approaches resulted in a significant difference in the degradation value, which demands standardization of the term and calculation methodology.
1. Introduction
Photovoltaic (PV) energy generation will dominate the future energy mix [1]. Thus, quantitative information about the long term performance of photovoltaic (PV) systems is important for many stakeholders, including researchers, companies, integrators, regulators, and investors. The performance of PV systems is influenced by many factors, such as local climatological circumstances, system components, installation, cost, and other miscellaneous factors [2]. In this work, we present the performance evolution of fifteen photovoltaic (PV) systems of six different PV module technologies in three different climates. Changes in performance are presented using the performance ratio (PR) and the performance loss rate (PLR). PV technologies applied in these PV plants are amorphous silicon (a-Si) solar cells (one system), heterojunction with intrinsic thin layer (HIT) hybrid silicon (one system), copper indium gallium selenide (CIGS, one system), monocrystalline silicon (mono-Si, three systems), cadmium telluride (CdTe, three systems), and polycrystalline silicon (p-Si, six systems). The PV systems are located in three different climates, namely, Alice Springs, Australia (arid, desert, hot), Cirata and Pekanbaru, Indonesia (tropical, rainforest), and Bolzano, Italy (temperate, dry summer, hot summer). Data from all PV systems were obtained directly from their monitoring systems. Table 1 shows the systems’ features, including their PV technologies and locations.

Table 1.
General information about the photovoltaic (PV) systems studied.
The performance of PV systems can change during their operation. As such, the assessment of the time-series of their monitoring data can be useful to get an insight into their long-term energy yield, reliability, and hence, financial feasibility. Performance ratio has been widely used as a performance indicator of PV systems for more than 25 years. Using PR, one can quantify and compare the quality of different PV systems or module technologies operating at various climate conditions [3].
Performance ratio, PR, is the ratio of the actual and theoretically possible energy outputs. PR measures how effectively the plant converts the sunlight collected by the PV panels into AC energy delivered to the off-taker, relative to what would be expected from the panel nameplate rating. The calculation of PR, therefore, quantifies the overall effect of losses due to inverter inefficiency, wiring, cell mismatch, elevated PV module temperature, reflection from the module front surface, soiling, system downtime, shading, and component failures. Several PV systems installed in different climates can be relatively compared using their PR values because PR is independent of location, the orientation of a PV array, and the incident solar irradiance. The result of the PR calculation is a percentage or decimal value. The present range of typical PR values of different PV technologies is 80–90% [4].
However, rather than being constant, the power of PV systems usually follows a negative trend over time due to a decline in module and system performance. To capture this trend, the performance loss rate (PLR) is calculated. Understanding system performance losses over time is crucial to minimize investment risk because a higher PLR translates directly into a lower amount of energy generation and, therefore, reduces future cash flows [5]. Despite the differences in the assessment methods, the rate of performance loss is influenced by location, design, and operation [6]. The accuracy of the estimations of these indicators depends on data availability, accuracy, and resolution, as well as the methods used in the calculation.
The PLR, sometimes also erroneously called degradation rate, is a measure used in the PV industry to quantify a rate of change, with a negative rate representing a decrease in performance [7]. The term PLR is more accurate as it combines actual degradation mechanisms with reversible and irreversible performance loss factors both on module and system level. Module degradation refers to appearing degradation modes such as cell cracks, delamination, or hot spots. System degradation instead affects larger parts of the plant and can be triggered through shading, soiling, etc. Therefore, an analysis of PLR can be useful to understand the long-term financial performance of a PV system with respect to anticipating energy production over the project lifetime. Different types of PV modules degrade at a different rate. A meta-analysis of 11,000 PV systems concluded that the median PLR was −0.5% to −0.6% per year and the mean average PLR was −0.8% to −0.9% per year [8]. Although the PLR was found to be lower, it still exceeded 1%/year in the first year of operation and then was stable between the second and the third year [5].
Another study found that the average and median values of PLR for mono-Si installed before 2000 were, respectively, −0.7% per year and −0.5% per year, whereas the values for thin-film technologies installed after 2000 were higher at −1.5% per year and −1% per year, respectively [6]. Although the PLR is often used to quantify the performance change at the module level based on laboratory or outdoor test conditions [9], the indicator can also be applied on the PV system level [10,11,12].
PLR is calculated using the following general steps:
- -
- Reading in available input data;
- -
- Data filtering;
- -
- Selection of performance metric;
- -
- Possible correction and data aggregation;
- -
- Application of the statistical method to calculate the final PLR.
In this work, two different raw data irradiance sources, namely measured irradiance and clear sky modeled irradiance [7], are tested and two different methodologies were used to calculate PLR.
A study in Cyprus [9] found that the annual PLR of mc-Si was −0.64%/year, with −0.62%/year for mc-Si, and −1.78%/year for thin-film systems. Although the study uses quite a small sample size, it could indicate that the PLR value of thin-film is nearly three-fold of the PLR value of c-Si PV systems in warm climates.
Unlike the calculation of PR, which is basically straightforward, the calculation of PLR does not follow a pre-determined procedure. To estimate the PLR of a PV system, a performance metric must be selected and calculated first. After possible correction and aggregation steps, a statistical method is applied to extract the performance trend. Many methods decompose the metric time-series into their components. Using additive decomposition, the sum of the components at each point of time is the same as the value of the data at that specific time as represented by Equation (1) [13].
where yt is the data, St is the seasonal component, Tt is the trend-cycle component, and εt is the remainder, all at period t. The “seasonality” component is a repeated pattern observed between regular intervals due to seasonal factors such as the time of the day or the month of the year. Seasonality in weather data related to PV systems shows the regular variation in the environmental conditions such as the irradiance, the spectral content, the angle of incidence (θ), the ambient temperature (), and wind speed (ν) [14]. Seasonality affects both c-Si and thin-film technologies, although c-Si technologies are more dependent on temperature changes and spectral effects [15]. The “trend” component shows the overall increasing or decreasing slope of the metric over time. The “remainder” component is the activity that is not explained by the trend or the seasonal value. The remainder is also expressed as the “error”, “residual”, or “irregular” component.
The time-series are sequence of observations recorded at regular time intervals. They contain information about the inherent nature of the measured phenomenon, such as the physical world, which displays interesting movements over longer periods. Understanding time-series can also be used as a basis for forecasting the future characteristics of the measured phenomenon. Time-series can contain features such as autocorrelation and periodic movements, stationarity and nonstationarity, volatility, seasonality, trends, and other common features [16]. In this work, we will focus on seasonality and trend features of the time-series.
Various statistical models are used to extract the components of time-series. The most commonly used methods are moving averages (either moving average smoothing or weighted moving averages), X11 method, SEATS decomposition, or Seasonal and Trend decomposition using Locally weighted scatterplot smoothing (STL decomposition) [13]. Other methods include Simple Linear Regression (SLR), Classical Seasonal Decomposition (CSD), Holt-Winters exponential smoothing (HW) [17], as well as X12 ARIMA [15]. All of the extraction methods give better or worse estimates of the ‘trend’ between them. However, SLR was found to be the least accurate method for c-Si and thin-film because it is sensitive to seasonality and outliers in the time-series, especially when long term data are not available [17].
In this work, we use STL decomposition as a statistical method for computing PLR. STL uses locally weighted regression and thereby provides robust estimates of the trend and seasonal components that are not distorted by outliers and missing values compared to other methods [18,19]. STL handles any type of seasonality, not only monthly or quarterly data. The seasonal component is allowed to change over time. The user can control the rate of change and the smoothness of the trend-cycle. However, STL does not handle trading day or calendar variation automatically, and it only provides facilities for additive decompositions. A complete description of STL procedure is given in [18].
In this work, we also evaluate the calculation of PLR using the year-on-year (YoY) approach which follows a different concept. The idea behind the YoY approach is explained in Section 3.4.
The performance of PV systems has been extensively evaluated worldwide [20,21] mainly in Europe [5] and the US. In particular, among the comprehensive study of the performance of PV systems in China, Japan, the US, Europe, and Australia have been reported in respectively [22,23,24,25]. In South-East Asia, PR of PV system operations has been reported such as in [26,27,28].
Recent studies about the PLR are available among others in [1,5,6,7,8,9,10,14,15,26,27,29,30,31,32,33,34,35,36]. However, only two studies were based on PV systems in South-East Asia, and no study was found in Indonesia. Therefore, in this work, we include PV systems in Indonesia to fill the gap of PLR study of PV systems located in the tropical rainforest climate in South-East Asia. We present the performance of fifteen grid-connected PV systems using six different module types operating under the real outdoor conditions in three climates in Europe, Australia, and Indonesia. The quality of the PV systems will be evaluated using the performance indicators previously discussed: PR and PLR. The available time-series gathered by outdoor PV system monitoring and meteorological data used in this work ranged from two to nine years depending on the PV systems.
2. Experimental Set-up
Figure 1 shows the geographical distribution of fifteen PV systems used in this work. For each system, we provide the location, coordinates, climate, and annual global horizontal irradiation in kWh/m2 per year. The PV systems are located in Bolzano, Italy (EURAC), Pekanbaru, Indonesia (OTH Amberg-Weiden, maintained by UIN Suska Riau University), Cirata, Indonesia (PJB), and Alice Springs, Australia (Desert Knowledge Australia Solar Center (DKASC), maintained by Ekistica). The PV systems are located at the Southern hemisphere, with the highest irradiation of around 2245 kWh/m2/year, near the equator (around 1700 kWh/m2/year), and the Northern hemisphere, with the lowest irradiation (1400 kWh/m2/year).
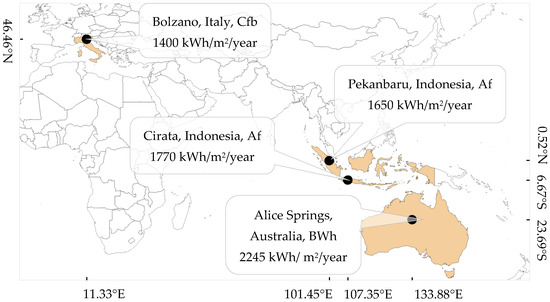
Figure 1.
The geographical distribution of the photovoltaic (PV) systems, climate locations, and annual global irradiation on a horizontal surface (kWh/m2/year). The map is based on [37], irradiation data are obtained from Global Solar Atlas 2.0, a free, web-based application developed and operated by Solargis s.r.o. on behalf of the World Bank Group, with funding provided by the Energy Sector Management Assistance Program (ESMAP). For additional information: https://globalsolaratlas.info.
Basic information about each system is given. The information includes rated power, module technical specification, mounting, tilt angle, and basic configuration. The PR calculation was possible with several months of data, but a minimum of 24 months of recording period is required for the calculation of PLR.
Irradiance on a horizontal surface in W/m2 is represented by several terms. They are beam or direct normal irradiance (DNI), diffuse horizontal irradiance (DHI), and ground-reflected irradiance on a horizontal surface (Eg). The sum of all irradiances is global horizontal irradiance (GHI). On the plane of array (POA), also in W/m2, we use the in-plane terms, namely, in-plane global irradiance (GPOA), in-plane beam irradiance (), in-plane diffuse irradiance (), and in-plane ground-reflected irradiance (). The terms used for irradiation in Watt-hours/m2 are horizontal irradiation (Hh) and POA irradiation (Hi), which are the irradiance aggregated. Other important variables include Tamb in °C, module temperature (Tm) in °C, and wind speed (ν) in m/s.
Global irradiance on the plane of array, GPOA, is mandatory for PR calculation. If GPOA was not available, it could be estimated from the global horizontal irradiance, GHI, using available decomposition and transposition models. Various empirical decomposition models that are commonly used have been tested by [38]. In general, they are used to estimate the diffuse horizontal irradiance, DHI, from measured GHI. Thereby, both parameters have the following relation.
Here, is the diffuse fraction and its value depends on the clearness index, , and the selected decomposition model. Furthermore, GHI, DHI, and the direct normal irradiance, DNI, can be described by Equation (3).
where θs is the solar elevation angle (°). All decomposition models use at least the clearness index, , as input for computing , while the other models require additional variables such as elevation angle, ambient temperature, or relative humidity (RH). All models can estimate both DHI and DNI effectively [38]. In this work, we use the Erbs decomposition model [39] due to simplicity because it requires only as the input variable to compute .
Next, a transposition model is used to determine GPOA using Equation (4).
where , with θ being the angle of incidence of the sunbeam on the plane of the array surface.
The calculation of is implemented using Equation (5) which is based on an isotropic model.
where ρ is the ground albedo, and β is the tilted angle of the PV array. Albedo is the fraction of and GHI on the ground that is reflected by a surface, with a value that can be significant, reaching up to 100 W/m2. Albedo is close to zero when the surface is very dark, and albedo is 1 when the surface is bright white, metallic, or a mirror. A ground albedo value of 0.2 is widely accepted and is used in the modeling of PV systems [40].
To estimate , Equation (6) is used by assuming that the sky is a uniform source of diffused irradiance [41]. Thus, can be found from DHI and the tilt angle of the PV array.
If the PV module temperature, Tm, was not available, it can be estimated using the Sandia module temperature model shown in Equation (7).
where ν is the wind speed in m/s, a and b are parameters that depend on the module construction and materials, as well as the mounting configuration of the module. The table that lists representative values for a and b for various common module types and configurations is provided in [42].
The estimations of and Tm were implemented using PVLIB Python, initiated by Sandia National Laboratories and developed by the PVLIB community [43]. PVLIB calculations are documented on Sandia’s PV Performance Modelling Collaborative (PVPMC).
If no meteorological data were available, the meteorological data from PVGIS were used [44]. PVGIS provides historical satellite data from many locations in the world and has been extensively used in scientific publications.
Monitoring sensors for PV systems in Alice Springs are cleaned fortnightly. The monitoring sensors in Italy are not cleaned periodically due to enough rain and low soiling rates. However, information regarding the sensors used in the monitoring system and maintenance of the sensors is not given for systems in Indonesia. The history of the plants and the record of the inverter failures are also available for systems in Alice Springs. Accordingly, we translated the moments of inverter failure into missing values and later dropped them from the analysis. Of all systems, only the system in Cirata is known to be free from any obstacles causing shading on the PV arrays throughout the year. The PV system in Italy has shading from the surrounding mountains, but that holds for the systems as well as for the irradiance sensors and simple filter-detected moments, where one is shaded but the others are not. For the other systems, there is no information available about shading.
The climates are classified according to Köppen–Geiger, which takes differences in temperature and rainfall as the basis for classification [45,46,47]. In the Köppen–Geiger classification, the Earth is classified into five main climate classes and 30 subtypes. The codification of the climate classes uses two or three letters (Figure 2). The first letter represents the five climate groups, where A is for equatorial or tropical, B is for arid, C is for warm temperate, D is for cold or snow, and E is for polar. Furthermore, subgroups are assigned as the second letter, which indicates the type of precipitation (water vapor condensation product in the atmosphere). The third letter, if applicable, represents the air temperature. Countries around the equator are covered by climate A. Climate B can be found in Australia, Southern and Northern Africa, Middle Southern America, the Middle-East, and Western parts of the US. Climate C dominates West Europe, Southern Australia, New Zealand, Japan, and South-East regions of the US, Southern America, Africa, and China. Climate D covers most of Russia, Canada, and the Northern US. Finally, climate E is over Northern Canada, Iceland, Northern Russia, and the North and South poles. Figure 2 shows a matrix of the complete and updated list of the 30 climate classes from Köppen–Geiger. The left axis represents the first letter, the top axis is for the second letter, and the bottom axis is for the third letter. For example, climate Aw is read as tropical, savannah; climate Dsc is read as cold, dry summer, cold summer.
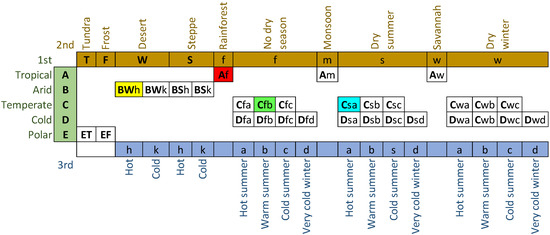
Figure 2.
Thirty climatic subclasses according to Köppen–Geiger [45] and updated by [46].
The PV systems are located in three different climates and countries: one system in climate Cfb in Italy, two systems in climate Af in Indonesia, and twelve systems in climate BWh in Australia. Table 1 summarizes the list of PV systems and the corresponding climatic information.
Most PV systems in Alice Springs are connected to identical SMA Sunny Mini Central 6-kW inverters. Only the PV systems in Site 17 (HIT modules) and Site 7 (CdTe) use differently sized inverters. Site 17 uses an SMA Sunny Mini Central 7-kW, and Site 7 uses a Fronius Primo 6 kW. The CdTe thin-film modules in Alice Springs Site 7 were originally rated by the manufacturer for installation in Europe. They were installed in Alice Springs without the installer, having gained approval from the manufacturer. PV systems in Site 3 and Site 11 in Alice Springs use p-Si modules with identical size and configuration. However, Site 3 is a roof installation, while Site 11 is ground-mounted. Therefore, it would be interesting to observe the performance difference between these two arrays and explain the impact of mounting an array on the roof.
Table 1 shows the mentioned parameter next to the total active area, Aa, of PV arrays and the temperature coefficient of the maximum output power (γPmp) of the PV modules. γPmp indicates how strongly the PV array power output depends on the cell temperature. It is a negative number because power output decreases with increasing cell temperature.
The PV system capacity ranges from 1.76 to 6.96 kWp, tilted 20° toward an orientation of 0° (North) for systems in Alice Springs. Systems in Pekanbaru and Cirata in Indonesia were tilted 10° toward an orientation of 180° (South) and 15°, respectively. The array angle of the system in Bolzano was 30°, with an orientation of 188.5° (South-West).
Figure 3 shows a chart of data availability for all PV systems and weather data. In general, data were available from September 2008 to January 2019. As shown, data from each PV and weather monitoring system were distributed over different periods. There was no period of time shared by all systems. Therefore, in this work, we analyzed each PV system according to the period of data availability rather than using the same period of time. The PV system in Bolzano had the longest period of available data of nine years, from February 2011 to January 2019. In contrast, the PV system in Cirata had the shortest period of two years of data, from March 2016 to March 2018. At a monthly level, most of the systems did not have missing values except for the PV systems in Site 27, which missed two months in total, and Site 7, which had a total of a half-year of missing data, both in Alice Springs. The weather data in Alice Springs are only available until October 2016. That is why all systems have the same end date.
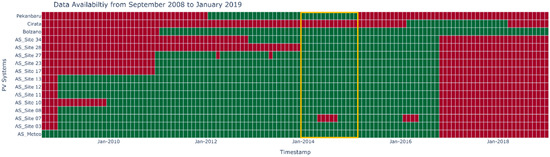
Figure 3.
The period of data availability for each PV system; green: data is available, red: data is not available.
3. Methods
3.1. Data Preparation
The measurement data should be as free from errors as possible. However, this is rarely the case. Data used in this work contain wrong values, gaps, outliers, spikes, drops, and other types of noise. Data also contain wrong or different formats of timestamps. These common problems affect the readiness of data for analysis, the quality of the time series, and, further, the quality of the analysis.
To ensure the systematic patterns of the time series data more salient, we applied a series of data preprocessing techniques to the raw data for each PV system. (1) Data were filtered according to standard IEC61724-1:2017 [48]. Namely, the daytime data were selected by eliminating irradiance values below 200 W/m2 and above 1500 W/m2. For Tamb, only values between −40 and 60 °C were used. For the module temperature, Tm, values between Tamb and Tamb plus 30 °C were included [49]. Wind speed values, ν, between 0 to 30 m/s were included. (2) The data were thoroughly checked to ensure consistency and to detect gaps. Duplicates in the data were detected and removed. (3) Further general outlier removal was applied based on predefined criteria depending on the characteristic of the data. If a variable value, X, minus the population mean, μ, is greater than two times the standard deviation, σ, then that specific X value is an outlier, and it will be excluded.
(4) Any abnormal value, such as largely negative and dead values that were stuck for one hour or longer, were removed. (5) Due to many incomplete records based on the previous treatments, we selected data with high monitoring fractions (MFs), either intrahours, intradays, or intramonth. A minimum MF of 85% was found to be optimal to keep the data quality high without losing too much data.
3.2. Calculation of the Performance Ratio
The monitoring standard IEC61724-1:2017 [48] was applied to calculate the PR. PR is defined by Equation (9) for the array-level DC performance ratio, PRA, and Equation (10) for the system level, PR. In this work, we use PR as one of the performance matrices to be evaluated.
where the array yield in kWh/kWp, YA, is the amount of energy produced by the array, Edc, from each installed rated power, P0, over the analysis period. YA is equivalent to the number of hours over which the PV array produces its rated power and is defined by Equation (11).
where the reference yield in kWh/kWp, Yr, is the total amount of available in-plane solar irradiance in kWh/m2, Hi, divided by the reference irradiance, Gref, of 1000 W/m2 (Equation (12).
where the final yield in kWh/kWp, Yf, is the annual, monthly, or daily net AC energy output in kWh, Eac, of the PV system per installed rated power, P0, given by Equation (13).
Three types of PR were calculated: PR, STC temperature-corrected PR, PRstc., and annual-averaged temperature-corrected PR, PRann.. For the calculation of PRstc. and PRann., the temperature coefficient of maximum power (γPmp) is a critical component.
3.3. Calculation of the Performance Loss Rate Using Linear Regression and STL
In this work, PLR was evaluated using linear regression (LR), STL decomposition, and the YoY approach. With the first approach, PLR was computed by evaluating the PRann. time series using linear regression. With the second approach, the calculation of PLR involved three main steps. First, the decomposition of continuous monthly PR time-series into its components using STL (see Equation (1)). We used the annual-averaged temperature-corrected PR, PRann., as the base data from which the PLR was calculated. PRann. was calculated using Equation (14) [50].
where i is a given point in time, Eac is the measured AC electrical generation (kWh).
The STL algorithm extracts Tt using a locally weighted polynomial fitting. The STL decomposition results in the “trend”, “seasonal”, and “residual” components of the original temperature-corrected PR time series. STL has been implemented in other PV performance studies using the software R [1,6,19,36]. Other studies such as [36,51] have also applied STL without mentioning the tools used to implement it in the analysis of PV systems’ time-series. In this work, the STL algorithm was implemented using a Python library named STLDecompose [52], according to the LOESS smoothing method [18]. The annual analysis period of 12 months is used, which represents the number of months in a year. To accommodate strong annual periodicity within the years of daily observations, if needed, a period of 365 days would be appropriate.
Second, the calculation of the linear least-squares regression values of the “trend” component, Tt, of the temperature-corrected PR follows, using Equation (15).
where x is an independent variable or the variable to make predictions, a is the slope of the regression line that represents the effect x has on Tt, and b is the Tt-intercept. The final PLR value, in percentage, is the rate of change, either positive or negative, of the regression of the trend component. From the regression parameters, the relative PLR is computed using Equation (16) [53].
where 12 is the number of months in a year. Further, removing the denominator b, if needed, will result in an absolute value of PLR, also known as PL.
As its name implies, the year-on-year (YoY) method uses performance time-series over year-on-year distributions. It aggregates the data points of the chosen metric between the same calendar days of subsequent years [54] by which the effects are minimized by comparing points at similar times of the year. The standard metric used in RdTools is renormalized power/energy values based on PVWatts.
3.4. Calculation of the Performance Loss Rate Using the YoY Approach
We calculated PLR based on monitoring data (using sensors) and a clear sky model using NREL’s RdTools. Figure 4 shows an example of degradation calculations taken from a CIGS PV module in Alice Springs in daily resolution. The time-series charts on the left-hand side show the year-on-year energy production normalized using baseline AC energy values from PVWatts calculation according to the following equation [55].
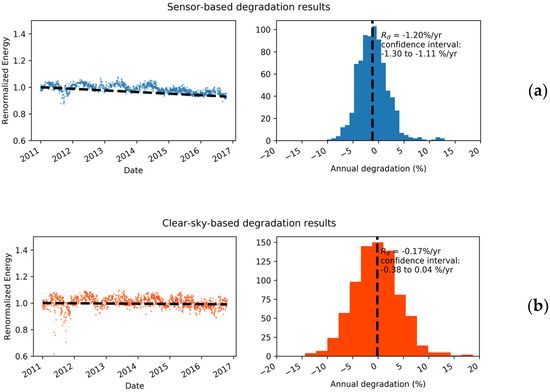
Figure 4.
Examples of the degradation rate of a copper indium gallium selenide (CIGS) PV system from Site 27 in Alice Springs. The degradation calculation based on (a) measurement sensors, and (b) a clear sky model.
PVWatts is a free software provided by NREL. It uses typical meteorological data to generate predicted energy production.
As shown, the annual PLR value was observed to be large enough to be visually detectable when calculated using sensor data compared to using the clear sky model. The histograms on the right-hand side present the distribution of the daily PLR values calculated by comparing a renormalized energy value of one particular date in a particular year to another PR value on the same date from the previous year. Depending on the comparison result of the energy output of two consecutive days, PLR values can be both positive and negative, as shown in the histograms. The median of the PLR values becomes the final single annual PLR value to be reported.
4. Results and Discussion
4.1. Performance Ratio
Figure 5 presents an example of daily performance ratios of a selected PV system, a p-Si system in Cirata, during the year of 2017. The performance ratio, PR, is shown in blue, PRstc. in orange, and PRann. in green. Scatter plots are the actual values, and the lines are the 30-day averaged values. As shown, the PR and PRann. values are close together while the PRstc. values are higher, about 0.1.
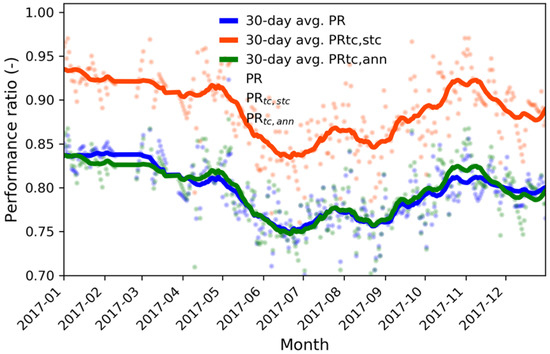
Figure 5.
Daily performance ratio of a p-Si system in Cirata in 2017.
In Figure 6, the performance ratios for each PV system, together with their mean values and standard deviation (std), are shown. In each subplot, the blue box plot to the left is the PR value. The middle orange plot is the PRstc. value. The right green plot is the PRann. value. As shown, the mean values of PR were slightly higher than PRann., with around a 0.4% difference. However, PRann. had a narrower standard deviation by 30% compared to the standard deviation of PR because its seasonal variations due to the temperature effect had been reduced using annual-averaged temperature values. The PRstc. values were always the biggest among the two other PRs (around 10% higher) because they were estimated with an STC temperature of 25 °C.
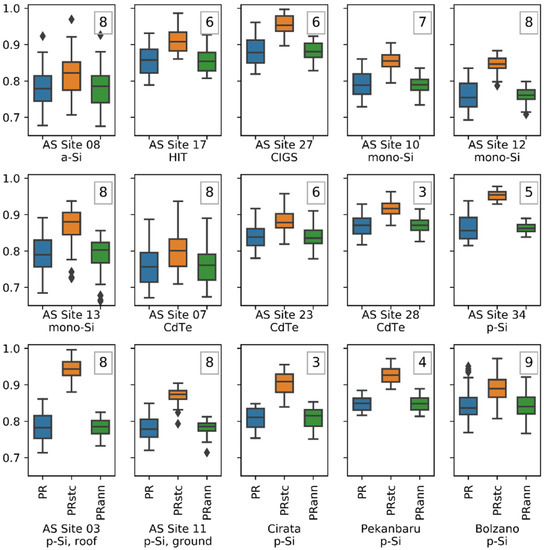
Figure 6.
Box plots of the performance ratio of each PV system. Left/blue: PR, middle/orange: temperature-corrected PR by STC, right/green: annual-averaged temperature-corrected PR. Numbers at the upper right corners in the boxes indicate the duration of the analyzed data in the number of years.
Figure 7 shows the mean performance ratio and its standard deviation by technology. The CIGS module has the highest values of all PR types, followed by HIT. The performance superiority of CIGS and HIT modules were also reported in Thailand, which has a tropical climate as well [12]. The p-Si and CdTe modules follow in terms of the values of PR and PRann.. However, when the temperature is closer to STC, p-Si modules performed better than CdTe modules. In addition, the performance range of p-Si modules is smaller than CdTe modules. A similar comparison was observed for mono-Si and a-Si modules in terms of STC temperature; the mono-Si modules had a higher PR than a-Si while their PR and PRann. were relatively similar.
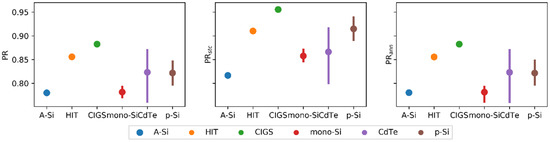
Figure 7.
Performance ratio by technology.
Table 2 shows the performance ratio and their standard deviation by climate. For the climatic comparison of PRs, we use p-Si modules because 50% of the evaluated PV systems fall in this category. In terms of PR and PRann., the p-Si system in climate Cfb of Italy has a higher performance of 0.84 than those in climates BWh (Australia) and Af (Indonesia) with the same value of 0.81. In contrast, PRstc. in climates BWh and Af were slightly higher than those in climate Cfb. The reason for this is because the average temperature in climates BWh and Af are closer to 25 °C.

Table 2.
Performance ratio of p-Si systems and their standard deviation by climate.
4.2. Performance Loss Rate Calculation Using LR and STL
PLR has been evaluated using linear regression and STL decomposition. Figure 8 shows the monthly PRann. time-series, their fitting lines, and trend components. As shown, the data do not have the same length, ranging from two to nine years. The grey lines are PRann., also shown in blue lines for PV systems with data less than a five-year period. The dashed orange lines are the applied linear regression fits of PRann., and the green lines are the STL-extracted “trend” component of the PRann. time-series. For almost all systems, the difference between the regression fits with the trends is very small, which means that the STL method is useful for an accurate calculation of changes in performance.
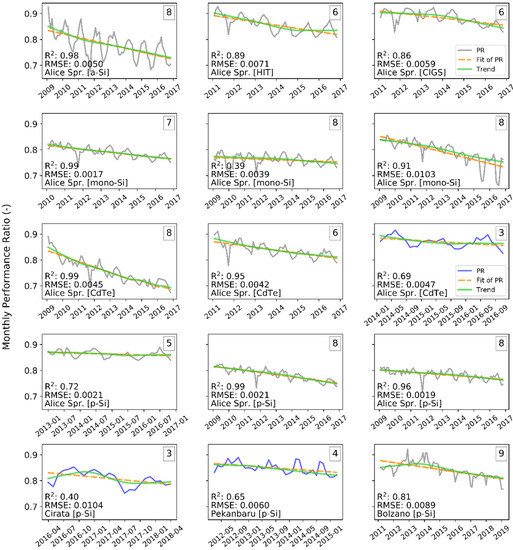
Figure 8.
Annual-averaged monthly temperature-corrected performance ratios, PRann., of the PV systems (grey or blue lines), their linear fit (dashed orange line), and trend components (green line) over the monitoring period. Numbers at the top right of the charts indicate the lengths of the data in years.
The quantities of PLR using STL are presented in Figure 9, grouped by module technologies and climate zones. The values of PLR are presented as relative values (chart on the left-hand side) and absolute values (chart on the right-hand side). Reading the mean of relative values, p-Si shows the lowest PLR of −0.6%/year, followed by CIGS at −0.8%/year, mono-Si at −0.84%/year, HIT at −1.01%/year, and CdTe at −1.18%/year. The strongest degradation was experienced by a-Si modules at −1.58%/year. CdTe systems have the largest range, from −0.38%/year to −2.20%/year. In contrast, the range of PLR values of p-Si systems was the smallest, from −0.19%/year to −0.97%/year. The results are in line with a previous similar study [6].
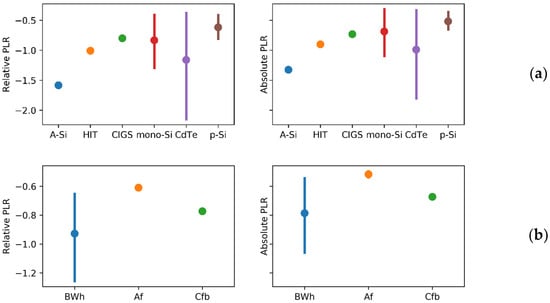
Figure 9.
Performance loss rate of the PV systems using STL. (a) Grouped by module technologies, (b) grouped by climate. Left: relative values, right: absolute values.
4.3. Comparison of PLR Values Using STL and YoY
While the methodology of calculating PR is widely accepted and standardized, the degradation of PV systems is estimated using different approaches. For that reason, in this section, we compare the PLR values presented in Section 4.2 with the ones retrieved using the YoY approach. For the YoY approach, the PLR calculation is mainly focused on using sensor-based data, but additional analysis is also performed using a clear sky model.
As shown in Figure 10a, the PLR calculation based on monitoring data showed that p-Si modules degraded the least while the highest rate was observed for the a-Si modules. On average, p-Si modules degrade at −0.93%/year, followed by mono-Si at −1.01%/year, HIT at −1.07%/year, CIGS at −1.2%/year, CdTe at −1.38%/year, and a-Si at −1.63%/year. If we apply the clear sky model for the calculation, the lowest PLR is observed for the HIT modules with −0.12%/year, while the a-Si system still experiences the highest PLR at −1.22%/year. In between, CIGS degrades at −0.17%/year, mono-Si at −0.28%/year, p-Si at −0.53%/year, and CdTe at −0.82%/year.
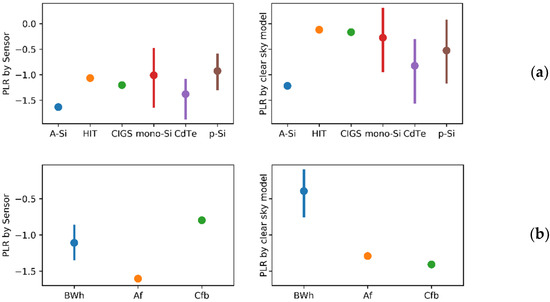
Figure 10.
Performance loss rate of the PV systems using YoY. (a) Grouped by module technologies, (b) grouped by climate. Left: based on monitoring sensors, right: based on the clear sky model.
When the PLR values were grouped by climate, as shown in Figure 10b. while using sensor data, the lowest PLR was observed in the Cfb climate of Bolzano at −0.8%/year, followed by Bwh in Alice Springs at −1.11%/year. The largest PLR was observed in the climate of Af in Indonesia at −1.6%/year. This confirms the previous study that higher PLR values occur in hotter climates compared to more moderate climates [8]. The annual average Tamb in Bolzano, Alice Springs, and Indonesia during their corresponding reporting periods were, respectively, 13, 26, and 31 °C. Moreover, calculations using the clear sky model showed different results, where the lowest PLR was in the BWh climate at −0.4%/year, followed by climate Af at −1.29%/year, and the highest rate was in the climate of Cfb at −1.41%/year. It has to be kept in mind, however, that clear sky modeling of irradiance data will inevitably result in higher uncertainties. It is usually used to cross-compare the quality of measured irradiance and as an alternative if no or corrupted irradiance measurements are available.
Appendix A, Table A1 shows a complete performance matrix of the PV systems. The PR and PRann. values of all systems fall between 76% and 88%, while the values of PRstc. are slightly higher. According to [56], the typical PR of present PV systems ranges from 80% to 90%. For most of the PV systems, the relative values of PLR using STL are smaller compared to the sensor-based PLR values using YoY, with a significant difference ranging from −12% to −20% for mono-Si in Alice Springs and −13% to −60% for p-Si in the same location. The differences in degradation values retrieved from STL and YoY were caused by the underlying differences in the methods themselves. The PLR using STL was calculated based on a decomposition of the temperature corrected PR while the YoY-based PLR was calculated using the differences in daily instances of PR and renormalized energy using PVWatts.
5. Conclusions
Two performance matrices of fifteen PV systems of six module technologies operating under real conditions in three climates were calculated. The PV systems consist of one amorphous silicon (a-Si) solar cell system, one heterojunction with intrinsic thin layer (HIT) hybrid silicon system, one copper indium gallium selenide (CIGS) system, three monocrystalline silicon (mono-Si) systems, three cadmium telluride (CdTe) systems, and six polycrystalline silicon (p-Si) systems. The PV systems are located in Australia, Indonesia, and Italy. The matrices include performance ratio (PR) and performance loss rate (PLR). PLR was calculated using two different approaches. Seasonal and trend decomposition using locally weighted scatterplot smoothing (STL decomposition) was applied to temperature-corrected PR time-series, while the Year-on-Year approach was applied to renormalized energy values based on the power predictive model PVWatts. The latter was furthermore applied to sensor-based irradiance data as well as clear-sky modeled data. The general conclusions of this work are
- The annual-averaged temperature-corrected performance ratio, PRann., with an average value of all systems from each technology. The CIGS system performed best with an average PR value of 0.88 ± 0.04. The least performing technology was the a-Si PV systems, with an average PR value of 0.78 ± 0.05. The p-Si systems in climate Cfb of Italy had a higher average PR of 0.84 than those operating in climates BWh (Australia) and Af (Indonesia), with the same value of 0.81.
- Performance loss rates based on the STL approach. For almost all systems, the use of STL for the calculation of PLR is helpful, especially if monitoring data of high quality was not available. The p-Si systems show the lowest PLR among the technologies with an average PLR value of −0.6%/year. The strongest performance loss was experienced by a-Si modules at −1.58%/year.
Results from Indonesia were appreciated because they provide the first study on the topic. However, they were based on only two PV systems with a data period of two and three years, which is not representative enough to draw a strong general conclusion and is subject to very high uncertainties. In addition, PV systems that used a-Si, CIGS, and HIT were represented by only one PV system each. More studies involving PV systems in South-East Asia and other climates are needed. Moreover, further investigations are required to show the nonlinear behavior in PV system performance, which is the actual case, while this work and many others assume a linear performance.
The differences in the calculation methods, in this case using STL and YoY, result in significant degradation values. STL employs a decomposition of the temperature corrected PR and the YoY was based on differences in daily instances of renormalized energy values. Distinct differences among the calculated PLR values between both approaches demand a standardization along the whole calculation chain from input data treatment to the application of statistical methods to calculate reliable PLR.
Author Contributions
Conceptualization, K.K. and A.R.; methodology, K.K., S.L., and A.R.; writing-original draft preparation, K.K.; writing-review and editing, K.K., A.R., S.L., D.M., M.J.; validation, S.L., D.M., A.R., M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Indonesia Endowment Fund for Education (LPDP).
Acknowledgments
This article/publication is based upon work from COST Action CA16235 PEARL PV supported by COST (European Cooperation in Science and Technology), including its Short Term Scientific Mission (STSM) grant conducted at EURAC Research in Bolzano, Italy. We also appreciate the expert support from Advanced Research on Innovations in Sustainability and Energy (ARISE) of the University of Twente.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The complete performance matrices of the PV systems.
Table A1.
The complete performance matrices of the PV systems.
| No. | City | Climate | Technology | PR | PRstc. | PRann. | PLR (%/year) YoY | PLR (%/year) STL | |
|---|---|---|---|---|---|---|---|---|---|
| Sensor | Clear Sky | Relative | |||||||
| 1 | Alice Springs | BWh | a-Si | 0.78 ± 0.05 | 0.82 ± 0.05 | 0.78 ± 0.05 | −1.63 | −1.22 | −1.58 |
| 2 | Alice Springs | BWh | HIT | 0.86 ± 0.04 | 0.91 ± 0.03 | 0.86 ± 0.03 | −1.07 | −0.12 | −1.01 |
| 3 | Alice Springs | BWh | CIGS | 0.88 ± 0.04 | 0.96 ± 0.03 | 0.88 ± 0.03 | −1.20 | −0.17 | −0.80 |
| 4 | Alice Springs | BWh | mono-Si | 0.79 ± 0.03 | 0.86 ± 0.02 | 0.79 ± 0.02 | −0.91 | −0.19 | −0.80 |
| 5 | Alice Springs | BWh | mono-Si | 0.76 ± 0.04 | 0.85 ± 0.02 | 0.76 ± 0.02 | −0.50 | +0.29 | −0.41 |
| 6 | Alice Springs | BWh | mono-Si | 0.79 ± 0.05 | 0.87 ± 0.05 | 0.79 ± 0.04 | −1.62 | −0.93 | −1.30 |
| 7 | Alice Springs | BWh | CdTe | 0.76 ± 0.05 | 0.80 ± 0.05 | 0.76 ± 0.05 | −1.85 | −1.55 | −2.20 |
| 8 | Alice Springs | BWh | CdTe | 0.84 ± 0.03 | 0.88 ± 0.03 | 0.84 ± 0.03 | −1.10 | −0.32 | −0.95 |
| 9 | Alice Springs | BWh | CdTe | 0.87 ± 0.03 | 0.92 ± 0.02 | 0.87 ± 0.02 | −1.19 | −0.60 | −0.38 |
| 10 | Alice Springs | BWh | p-Si | 0.86 ± 0.03 | 0.95 ± 0.01 | 0.86 ± 0.01 | −0.47 | +0.33 | −0.19 |
| 11 | Alice Springs | BWh | p-Si | 0.78 ± 0.04 | 0.94 ± 0.03 | 0.78 ± 0.02 | −1.12 | −0.36 | −0.97 |
| 12 | Alice Springs | BWh | p-Si | 0.78 ± 0.03 | 0.87 ± 0.02 | 0.78 ± 0.02 | −0.64 | +0.09 | −0.56 |
| 13 | Cirata | Af | p-Si | 0.81 ± 0.03 | 0.90 ± 0.03 | 0.81 ± 0.03 | n.a | n.a. | −0.60 |
| 14 | Pekanbaru | Af | p-Si | 0.85 ± 0.02 | 0.93 ± 0.02 | 0.85 ± 0.02 | −1.60 | −1.29 | −0.62 |
| 15 | Bolzano | Cfb | p-Si | 0.84 ± 0.04 | 0.89 ± 0.03 | 0.84 ± 0.03 | −0.80 | −1.41 | −0.77 |
References
- Ingenhoven, P.; Belluardo, G.; Moser, D. Comparison of statistical and deterministic smoothing methods to reduce the uncertainty of performance loss rate estimates. IEEE J. Photovolt. 2018, 8, 224–232. [Google Scholar] [CrossRef]
- Fouad, M.M.; Shihata, L.A.; Morgan, E.S.I. An integrated review of factors influencing the performance of photovoltaic panels. Renew. Sustain. Energy Rev. 2017, 80, 1499–1511. [Google Scholar] [CrossRef]
- De Graaf, L.E.; Van Der Weiden, T.C.J. Characteristics and performance of a PV-system consisting of 20 AC-modules. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Waikoloa, HI, USA, 5–9 December 1994; pp. 921–924. [Google Scholar]
- Fraunhofer ISE. Photovoltaics Report 2019; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg im Breisgau, Germany, 2019. [Google Scholar]
- Jordan, D.C.; Sarah, R. Kurtz Photovoltaic degradation rates—An Analytical Review. Prog. Photovolt. Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Ingenhoven, P.; Belluardo, G.; Makrides, G.; Georghiou, G.E.; Rodden, P.; Frearson, L.; Herteleer, B.; Bertani, D.; Moser, D. Analysis of Photovoltaic Performance Loss Rates of Six Module Types in Five Geographical Locations. IEEE J. Photovolt. 2019, 9, 1091–1096. [Google Scholar] [CrossRef]
- Jordan, D.C.; Deline, C.; Kurtz, S.R.; Kimball, G.M.; Anderson, M. Robust PV Degradation Methodology and Application. IEEE J. Photovolt. 2018, 8, 525–531. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R.; VanSant, K.; Newmiller, J. Compendium of photovoltaic degradation rates. Prog. Photovolt. 2016, 24, 978–989. [Google Scholar] [CrossRef]
- Makrides, G.; Zinsser, B.; Schubert, M.; Georghiou, G.E. Performance loss rate of twelve photovoltaic technologies under field conditions using statistical techniques. Sol. Energy 2014, 103, 28–42. [Google Scholar] [CrossRef]
- Larrivee, J. An Analysis of Degradation Rates of PV Power Plants at the System Level. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2013. [Google Scholar]
- Sharma, V.; Chandel, S.S. A novel study for determining early life degradation of multi-crystalline-silicon photovoltaic modules observed in western Himalayan Indian climatic conditions. Sol. Energy 2016, 134, 32–44. [Google Scholar] [CrossRef]
- Limmanee, A.; Udomdachanut, N.; Songtrai, S.; Kaewniyompanit, S.; Sato, Y.; Nakaishi, M.; Kittisontirak, S.; Sriprapha, K.; Sakamoto, Y. Field performance and degradation rates of different types of photovoltaic modules: A case study in Thailand. Renew. Energy 2016, 89, 12–17. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2013. [Google Scholar]
- Carr, A.J.; Pryor, T.L. A comparison of the performance of different PV module types in temperate climates. Sol. Energy 2004, 76, 285–294. [Google Scholar] [CrossRef]
- Phinikarides, A.; Makrides, G.; Zinsser, B.; Schubert, M.; Georghiou, G.E. Analysis of photovoltaic system performance time series: Seasonality and performance loss. Renew. Energy 2015, 77, 51–63. [Google Scholar] [CrossRef]
- Mills, T.C. Applied Time Series Analysis: A Practical Guide to Modeling and Forecasting; Elsevier: London, UK, 2019. [Google Scholar]
- Phinikarides, A.; Philippou, N.; Makrides, G.; Georghiou, G.E. Performance Loss Rates of Different Photovoltaic Technologies after Eight Years of Operation under Warm Climate Conditions. In Proceedings of the 29th EU-PVSEC Conference, Amsterdam, The Netherlands, 24–26 September 2014. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRae, J.E.; Terpenning, I. STL: A Seasonal-Trend Decomposition Procedure Based on Loss. J. Off. Stat. 1990, 6, 3–73. [Google Scholar]
- Lindig, S.; Kaaya, I.; Weis, K.A.; Moser, D.; Topic, M. Review of statistical and analytical degradation models for photovoltaic modules and systems as well as related improvements. IEEE J. Photovolt. 2018, 8, 1773–1786. [Google Scholar] [CrossRef]
- Srivastava, R.; Tiwari, A.N.; Giri, V.K. An overview on performance of PV plants commissioned at different places in the world. Energy Sustain. Dev. 2020, 54, 51–59. [Google Scholar] [CrossRef]
- Elibol, E.; Özmen, Ö.T.; Tutkun, N.; Köysal, O. Outdoor performance analysis of different PV panel types. Renew. Sustain. Energy Rev. 2017, 67, 651–661. [Google Scholar] [CrossRef]
- Li, C.; Zhou, D.; Zheng, Y. Techno-economic comparative study of grid-connected PV power systems in five climate zones, China. Energy 2018, 165, 1352–1369. [Google Scholar] [CrossRef]
- Oda, K.; Hakuta, K.; Nozaki, Y.; Ueda, Y. Characteristics evaluation of various types of PV modules in Japan and U.S. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016. [Google Scholar]
- Leloux, J.; Taylor, J.; Moretón, R.; Narvarte, L.; Trebosc, D.; Desportes, A.; Solar, S. Monitoring 30,000 PV systems in Europe: Performance, Faults, and State of the Art. In Proceedings of the 31st Eur. Photovolt. Sol. Energy Conf. Exhib., Hamburg, Germany, 14–18 September 2015; pp. 1574–1582. [Google Scholar]
- Haghdadi, N.; Copper, J.; Bruce, A.; Macgill, I. Operational performance analysis of distributed PV systems in Australia. In Proceedings of the Asia-pacific Sol. Res. Conf., Canberra, Australia, 29 November–1 December 2016. [Google Scholar]
- Burhan, M.; Ernest, C.K.J.; Choon, N.K. Electrical Rating of Concentrated Photovoltaic (CPV) Systems: Long-Term Performance Analysis and Comparison to Conventional PV Systems. Int. J. Technol. 2016, 2, 189–196. [Google Scholar] [CrossRef][Green Version]
- Limmanee, A.; Songtrai, S.; Udomdachanut, N.; Keawniyompanit, S.; Sato, Y.; Nakaishi, M.; Kittisontirak, S.; Sriprapha, K.; Sakamoto, Y. Comparison of Photovoltaic Degradation Rates in Tropical Climate Derived from Different Calculation Methods. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; pp. 735–738. [Google Scholar] [CrossRef]
- Veldhuis, A.J.; Nobre, A.M.; Peters, I.M.; Reindl, T.; Ruther, R.; Reinders, A.H.M.E. An Empirical Model for Rack-Mounted PV Module Temperatures for Southeast Asian Locations Evaluated for Minute Time Scales. IEEE J. Photovolt. 2015, 5, 774–782. [Google Scholar] [CrossRef]
- Lindig, S.; Moser, D.; Curran, A.J.; French, R.H. Performance Loss Rates of PV systems of Task 13 database. In Proceedings of the IEEE PVSC Chicago, Chicago, IL, USA, 16–21 June 2019. [Google Scholar]
- Kiefer, K.; Farnung, B.; Müller, B. Degradation in PV Power Plants: Theory and Practice. In Proceedings of the 36th European PV Solar Energy Conference and Exhibition, Marseille, France, 9–13 September 2018; pp. 9–13. [Google Scholar]
- Kyprianou, A.; Phinikarides, A.; Makrides, G.; Georghiou, G.E. Definition and Computation of the Degradation Rates of Photovoltaic Systems of Different Technologies With Robust Principal Component Analysis. IEEE J. Photovolt. 2015, 5, 1698–1705. [Google Scholar] [CrossRef]
- Phinikarides, A.; Makrides, G.; Georghiou, G.E. Estimation of annual performance loss rates of grid-connected photovoltaic systems using time series analysis and validation through indoor testing at standard test conditions. In Proceedings of the 2015 IEEE 42nd Photovolt. Spec. Conf., New Orleans, LA, USA, 14–19 June 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Kunaifi, K.; Reinders, A.; Kaharudin, D.; Harmanto, A.; Mudiarto, K. A Comparative Performance Analysis of A 1 MW CIS PV System and a 5 kW Crystalline-Si PV System under the Tropical Climate of Indonesia. Int. J. Technol. 2019, 10, 1082–1092. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A. Performance assessment and degradation analysis of solar photovoltaic technologies: A review. Renew. Sustain. Energy Rev. 2017, 78, 554–587. [Google Scholar] [CrossRef]
- Ye, J.Y.; Reindl, T.; Aberle, A.G.; Walsh, T.M. Performance Degradation of Various PV Module Technologies in Tropical Singapore. IEEE J. Photovolt. 2014, 4, 1288–1294. [Google Scholar] [CrossRef]
- Phinikarides, A.; Makrides, G.; Kindyni, N.; Georghiou, G.E. Comparison of trend extraction methods for calculating performance loss rates of different photovoltaic technologies. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference, Denver, CO, USA, 8–13 June 2014; pp. 3211–3215. [Google Scholar] [CrossRef]
- D-maps.com Map World (Pacific Ocean in the Center): States 2007. Available online: https://d-maps.com/carte.php?num_car=3227&lang=en (accessed on 14 January 2020).
- Lave, M.; Hayes, W.; Pohl, A.; Hansen, C.W. Evaluation of Global Horizontal Irradiance to Plane-of-Array Irradiance Models at Locations Across the United States. IEEE J. Photovolt. 2015, 5, 597–606. [Google Scholar] [CrossRef]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Gul, M.; Kotak, Y.; Muneer, T.; Ivanova, S. Enhancement of albedo for solar energy gain with particular emphasis on overcast skies. Energies 2018, 11, 2881. [Google Scholar] [CrossRef]
- Hottel, H.C.; Woertz, B.B. Evaluation of flat-plate solar heat collector. Trans. ASME 1942, 64, 91. [Google Scholar]
- Sandia National Laboratories. Sandia Module Temperature Model. 2018. Available online: https://pvpmc.sandia.gov/modeling-steps/2-dc-module-iv/module-temperature/sandia-module-temperature-model/ (accessed on 23 October 2019).
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. PVLIB Python: A Python Package for Modeling Solar Energy Systems. J. Open Source Softw. 2018. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Koppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Zeitschrift 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- The International Electrotechnical Commission. IEC 61724-1 Photovoltaic System Performance—Part 1: Monitoring; 2017. Available online: https://webstore.iec.ch/publication/33622 (accessed on 20 August 2019).
- Fthenakis, V.; Yu, Y. Analysis of the potential for a heat island effect in large solar farms. In Proceedings of the IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 3362–3366. [Google Scholar]
- Dierauf, T.; Growitz, A.; Kurtz, S.; Cruz, J.L.B.; Riley, E.; Hansen, C. Weather-Corrected Performance Ratio; NREL: Golden, CO, USA, 2013.
- Singh, R.; Sharma, M.; Rawat, R.; Banerjee, C. Field Analysis of three different silicon-based Technologies in Composite Climate Condition—Part II—Seasonal assessment and performance degradation rates using statistical tools. Renew. Energy 2020, 147, 2102–2117. [Google Scholar] [CrossRef]
- Montague, J. Stldecompose 0.0.5 2019. Available online: https://pypi.org/project/stldecompose/ (accessed on 20 December 2019).
- Belluardo, G.; Ingenhoven, P.; Sparber, W.; Wagner, J.; Weihs, P.; Moser, D. Novel method for the improvement in the evaluation of outdoor performance loss rate in different PV technologies and comparison with two other methods. Sol. Energy 2015, 117, 139–152. [Google Scholar] [CrossRef]
- Hasselbrink, E.; Anderson, M.; Defreitas, Z.; Mikofski, M.; Shen, Y.C.; Caldwell, S.; Terao, A.; Kavulak, D.; Campeau, Z.; Degraaff, D. Validation of the PVLife model using 3 million module-years of live site data. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference, Tampa, FL, USA, 16–21 June 2013; pp. 7–12. [Google Scholar] [CrossRef]
- NREL PVWatts Calculator. Available online: https://pvwatts.nrel.gov/ (accessed on 12 December 2019).
- Fraunhofer-ISE. Photovoltaics Report; Fraunhofer Institute for Solar Energy Systems ISE: Freiburg im Breisgau, Germany, 2020. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).