A Novel Grid and Place Neuron’s Computational Modeling to Learn Spatial Semantics of an Environment
Abstract
1. Introduction
2. Issue and Modeling Challenges
3. Proposed Mechanism
3.1. Movement Representation
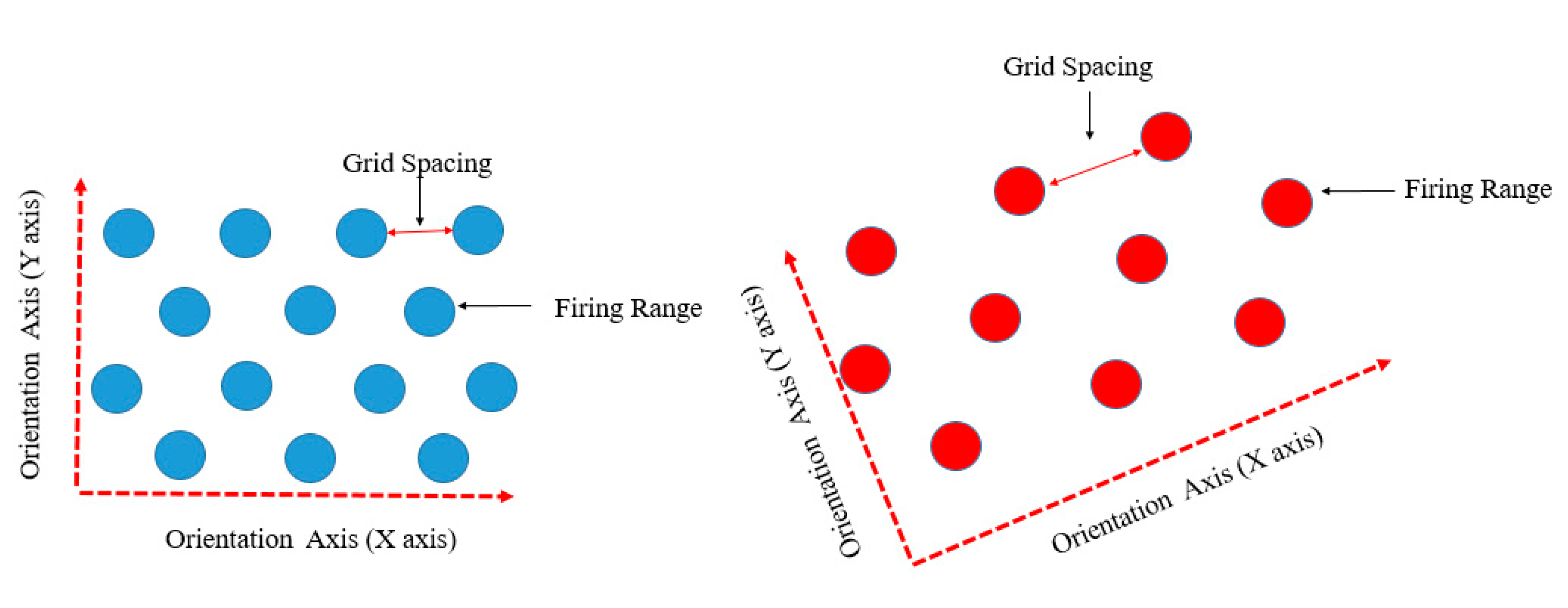
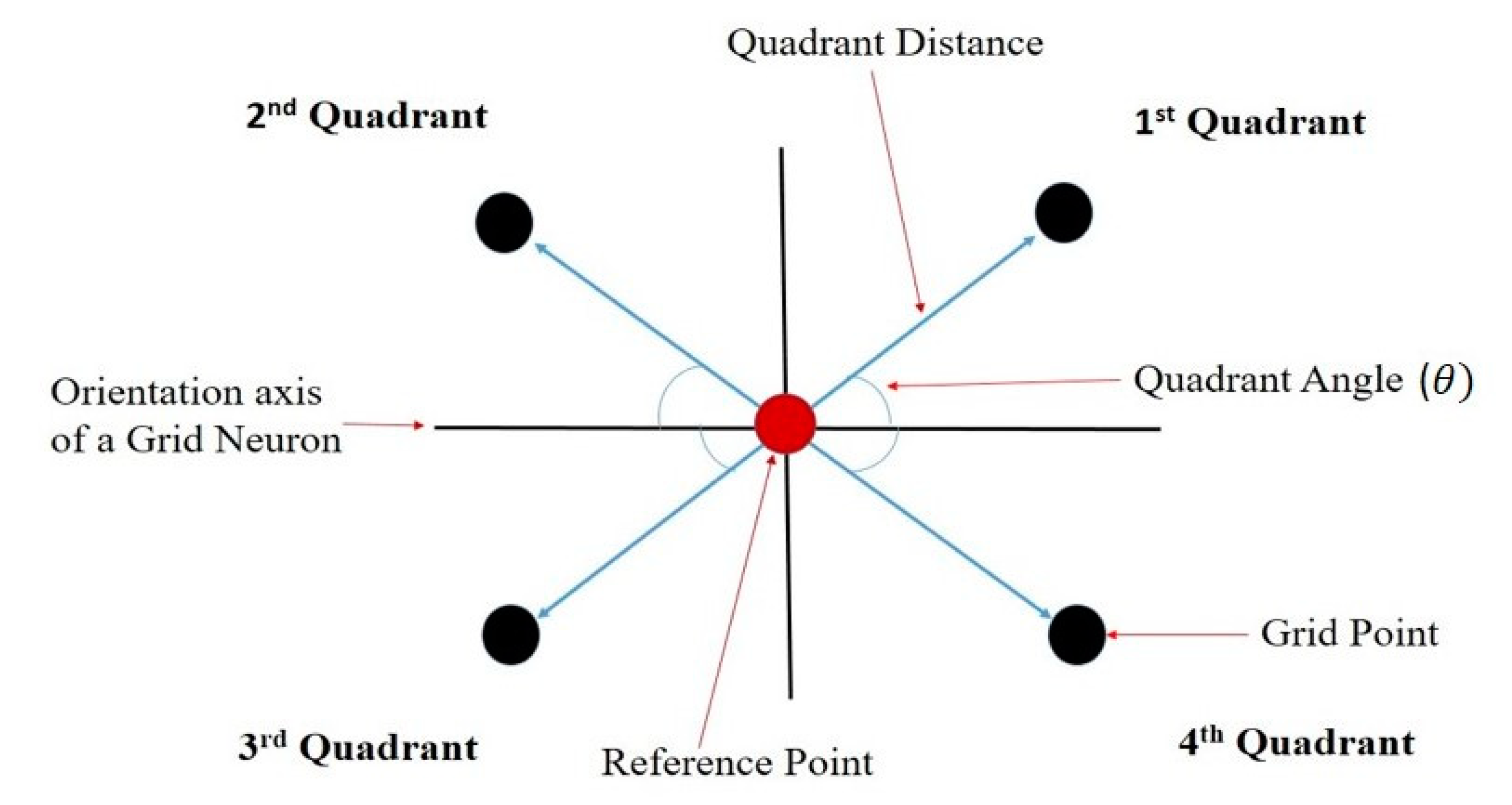
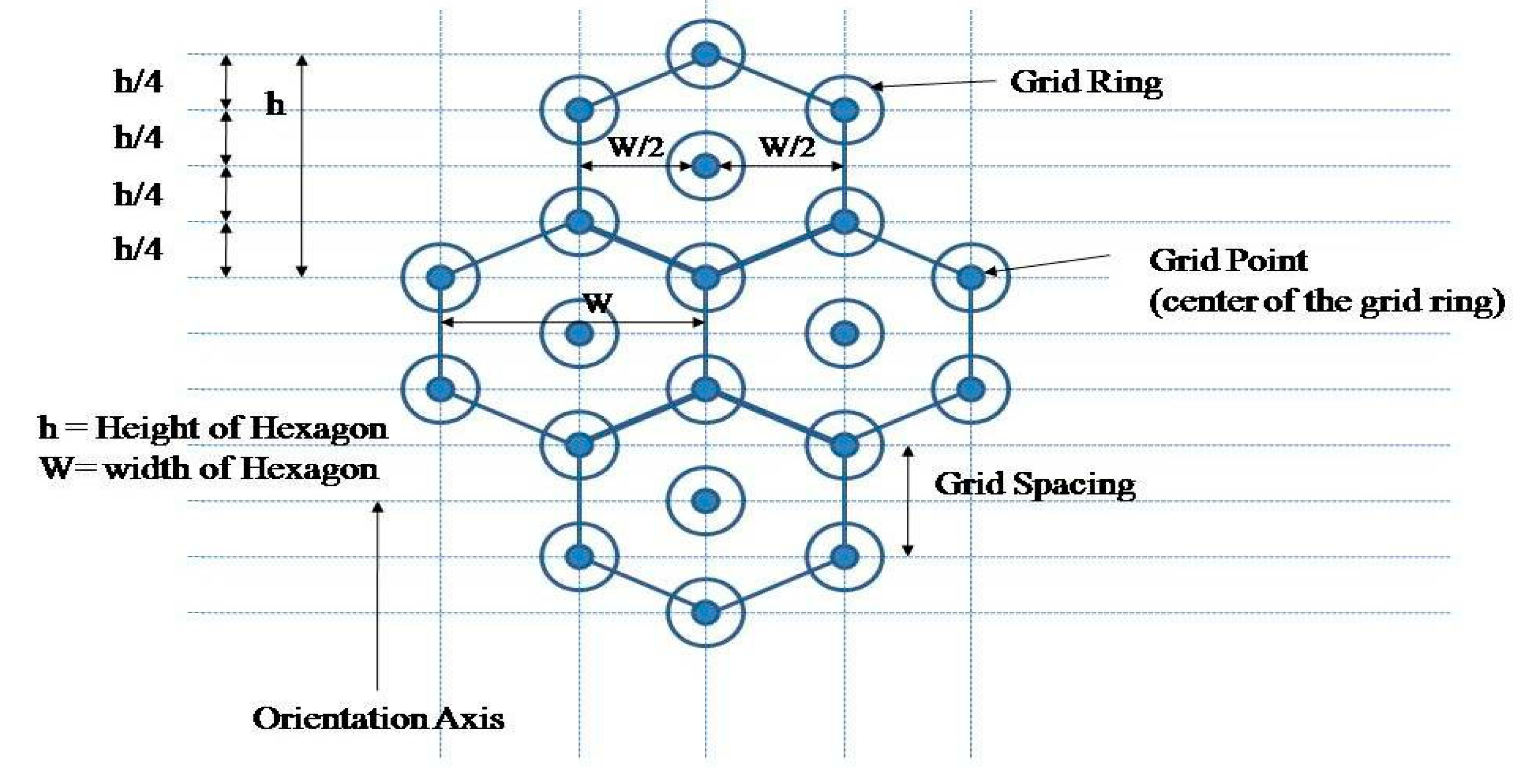
3.2. Quadrant Model for Grid Pattern Generation from the Body Movement
3.2.1. Finding the Coordinates of the Agent Based on the Magnitude and the Current Direction of Movement from a Reference Point
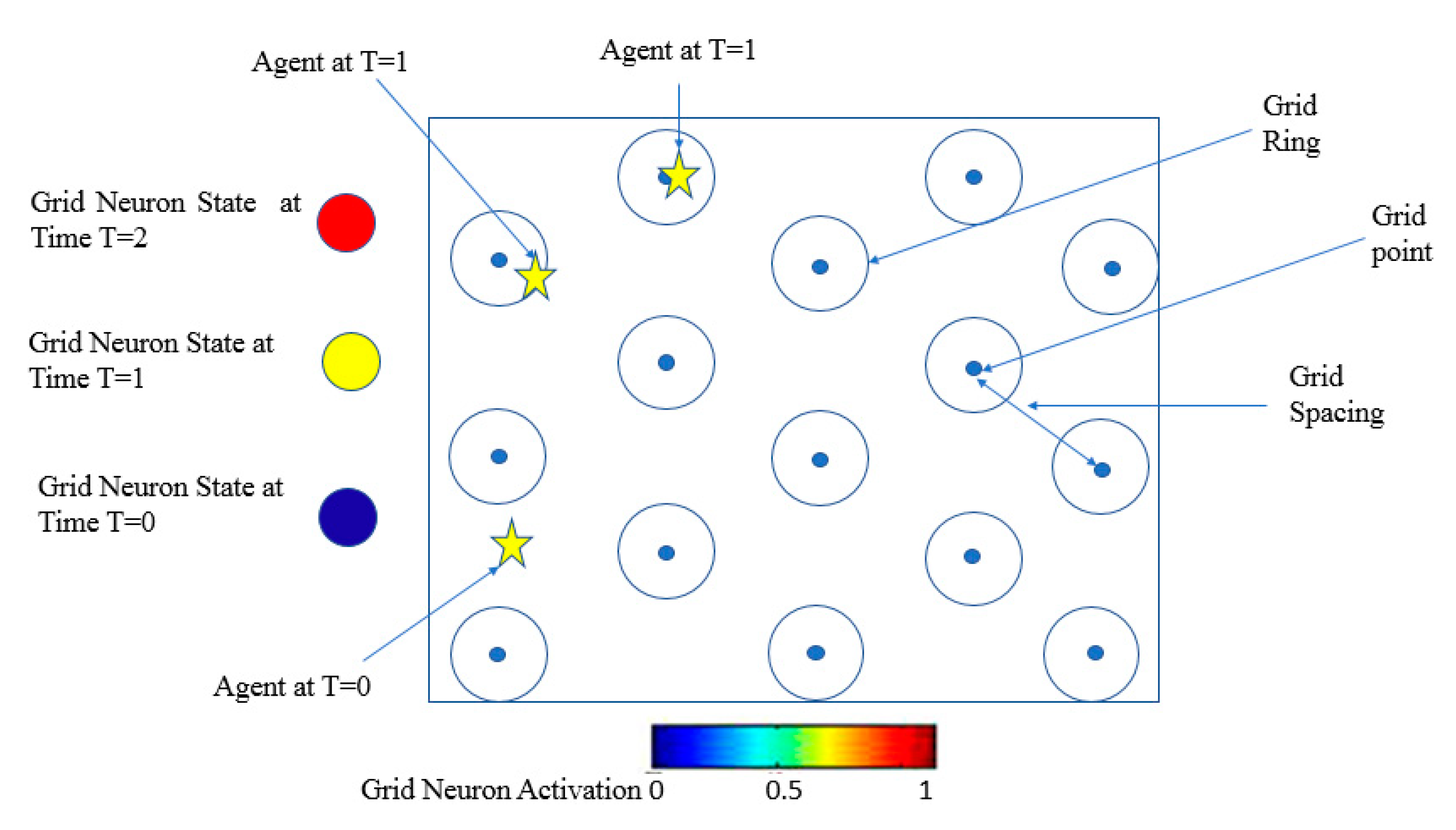
3.2.2. Grid Neuron Activation
| Algorithm 1: Calculation for the grid neuron activation |
| 1: I ← ROUND (XCORD/width) // ROUND is the round off function |
| 2: J ← CEIL (YCORD/ H) −1 // CEIL is ceiling function |
| 3: while J < CEIL (YCORD/H) do |
| 4: J ← J +0.5; |
| 5: Gx ← I × W// Gx is the X coordinate of the chosen grid point; |
| 6: Gy ← J × H// Gy is the Y coordinate of the chosen grid point; |
| 7: D ← EUCLIDEAN ((XCORD,YCORD), (Gx, Gy)); |
| 8: // Euclidean to find the distance between agent and the chosen grid point |
| 9: if D < R then |
| 10: activation ← 1 − (D/R); |
| 11: else |
| 12: activation ← 0; |
| 13: end |
| 14: if Y is the 0.5 multiple of the height (h) then |
| 15: activation ← 1; |
| 16: else if X is the 0.5 multiple of the W(width) then |
| 17: If Y is the 0.25 multiple of the height (h) then |
| 18: activation ← 1; |
| 19: else |
| 20: activation ← 0; |
| 21: end |
| 22: end |
| 23: end |
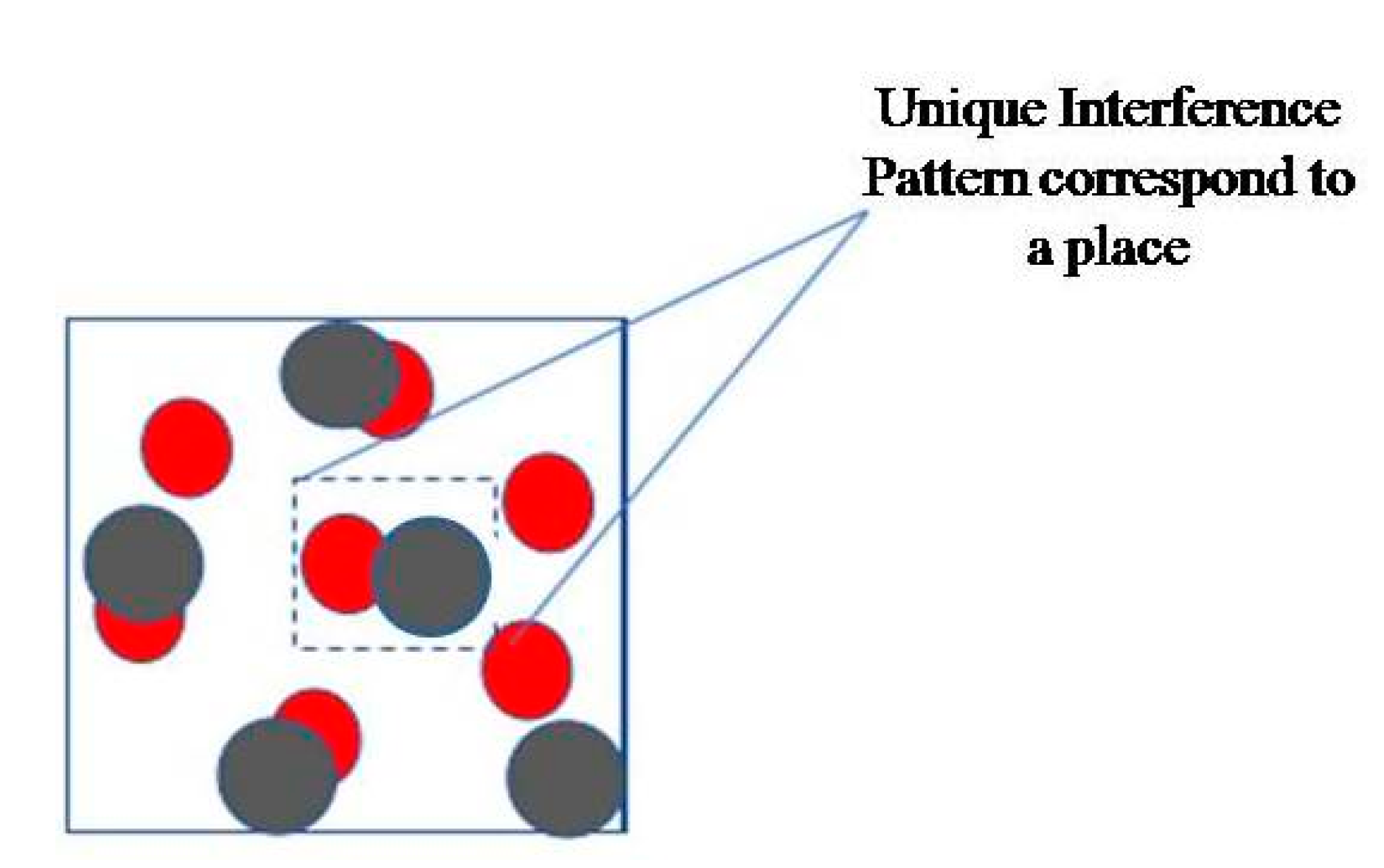
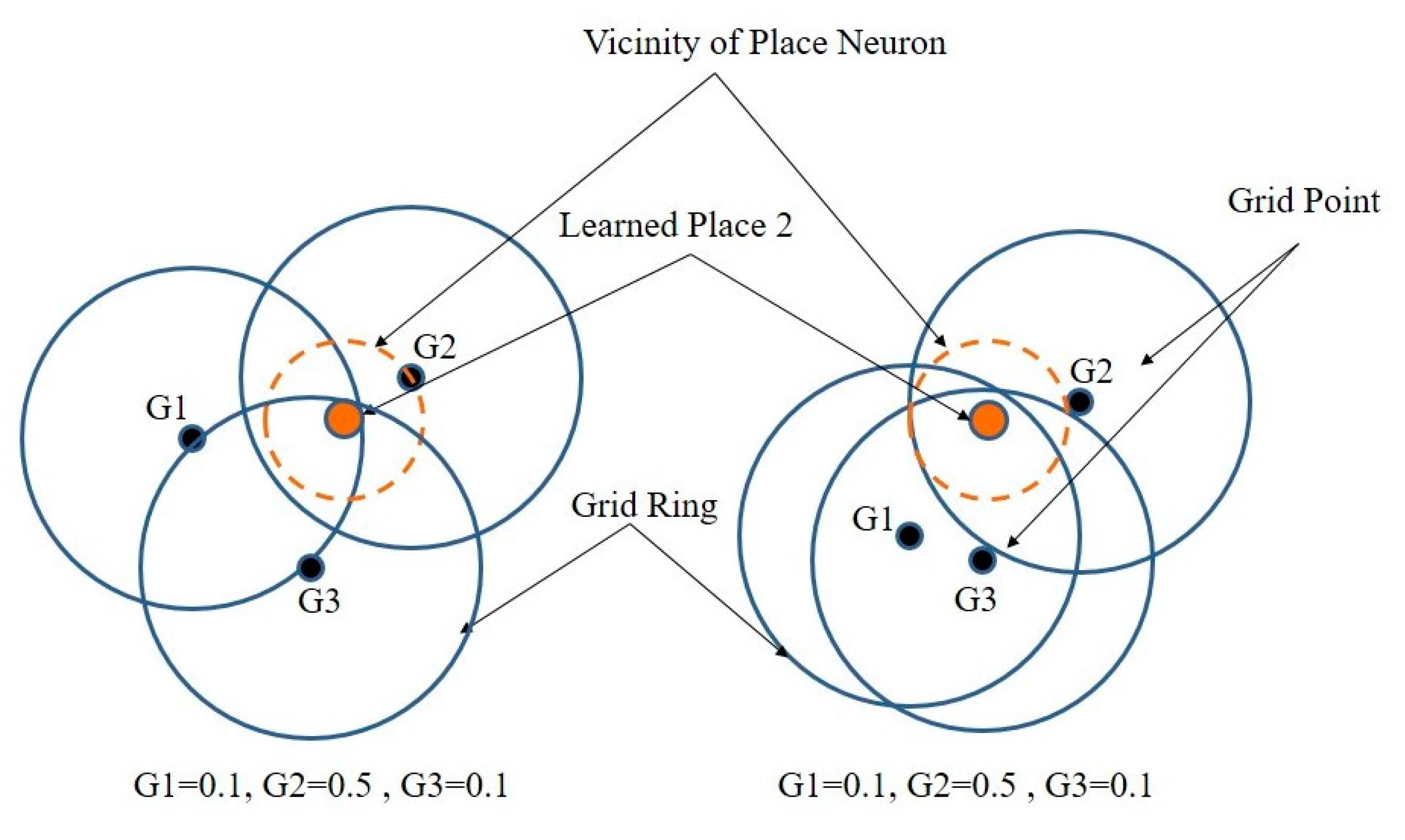
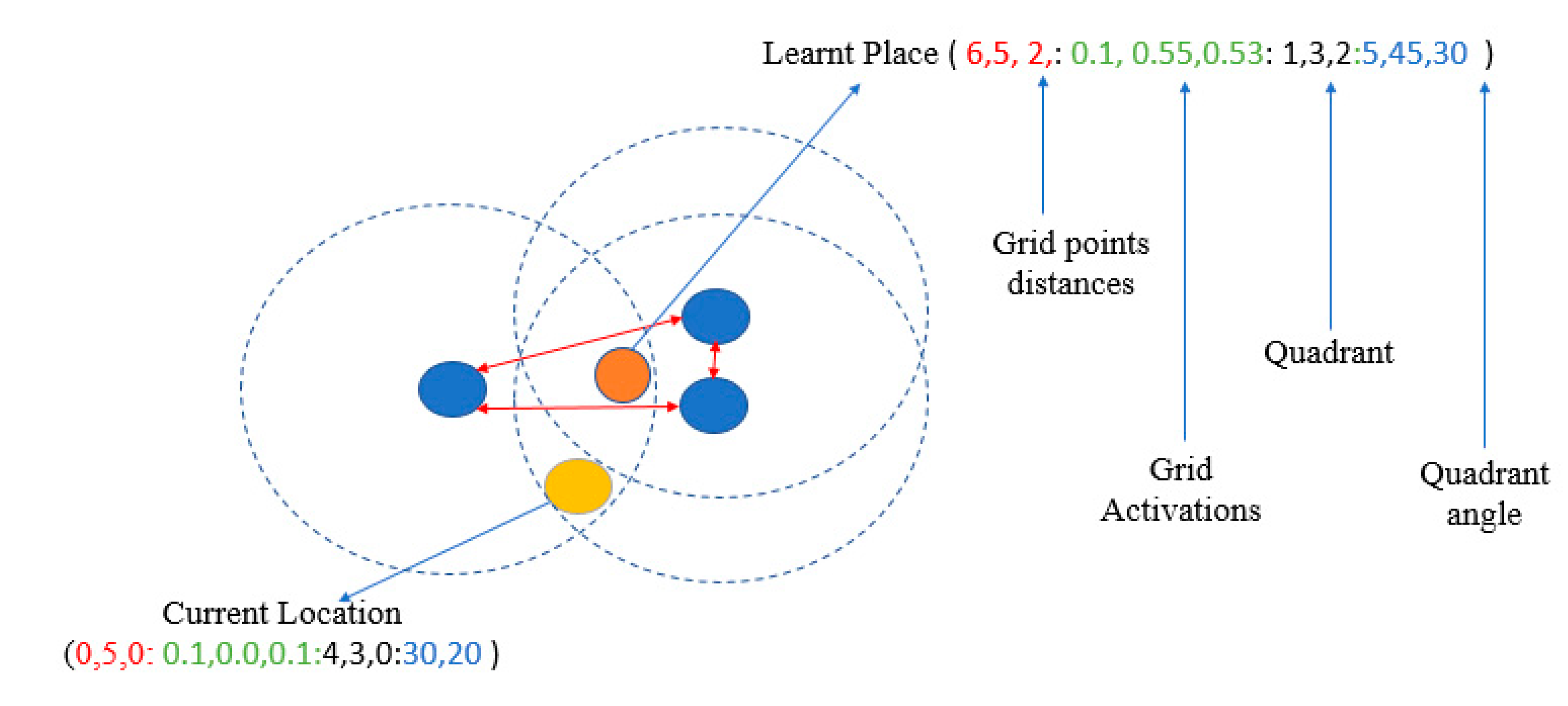
3.3. Grid Code Learning and ItsRecalling
3.3.1. Calculation of Grid Point Distances of the Interfered Rings
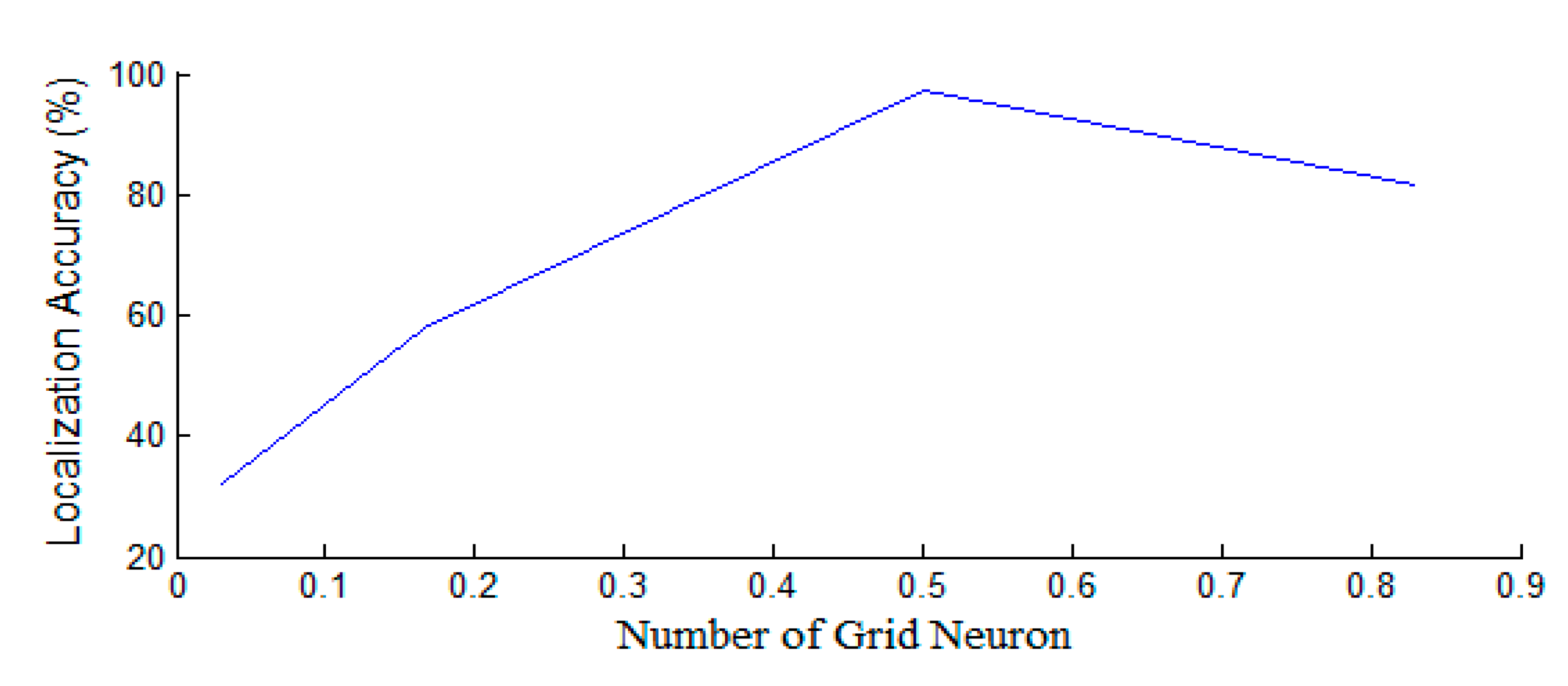
3.3.2. Role of Grid Spacing in the Localization Accuracy
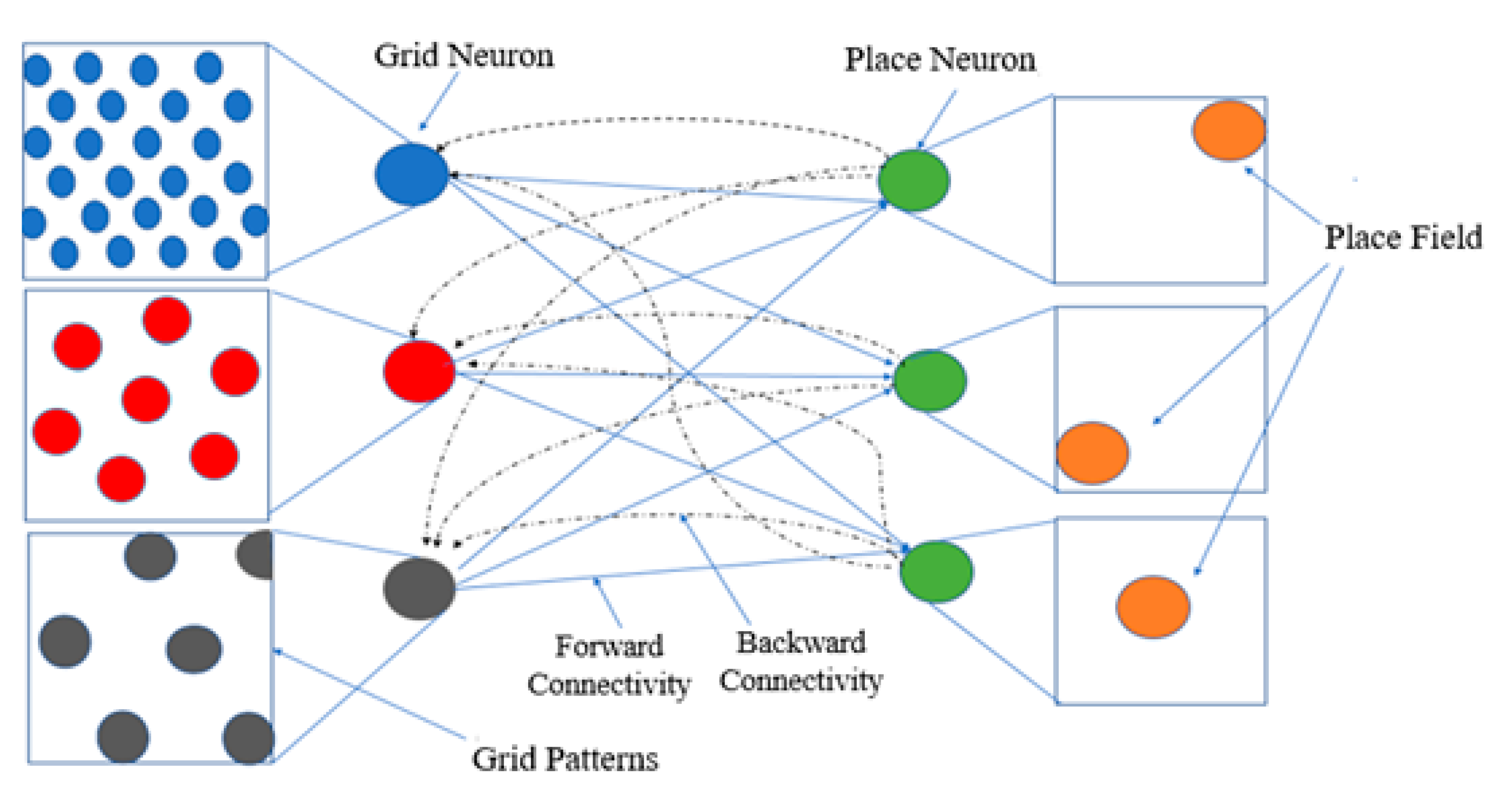
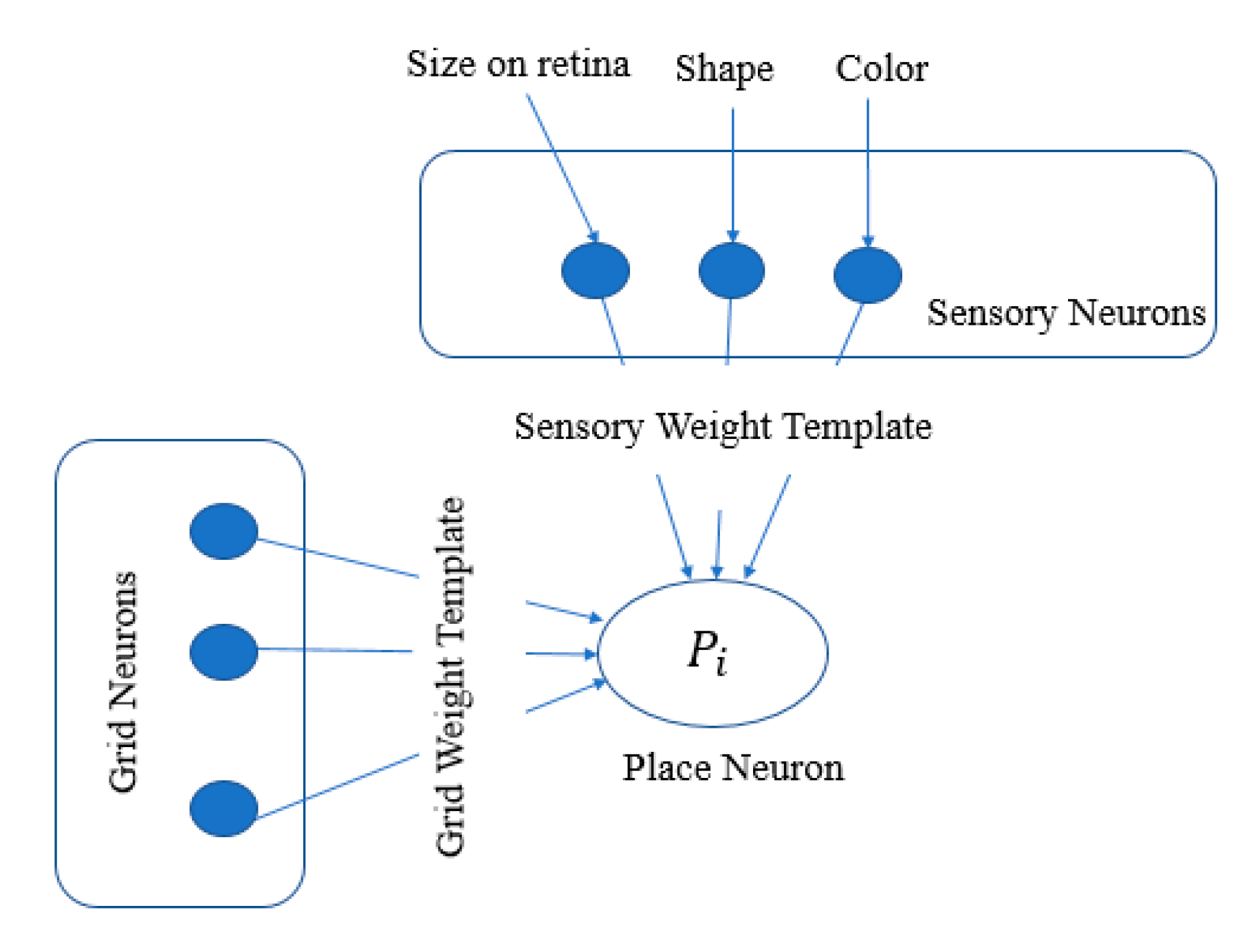
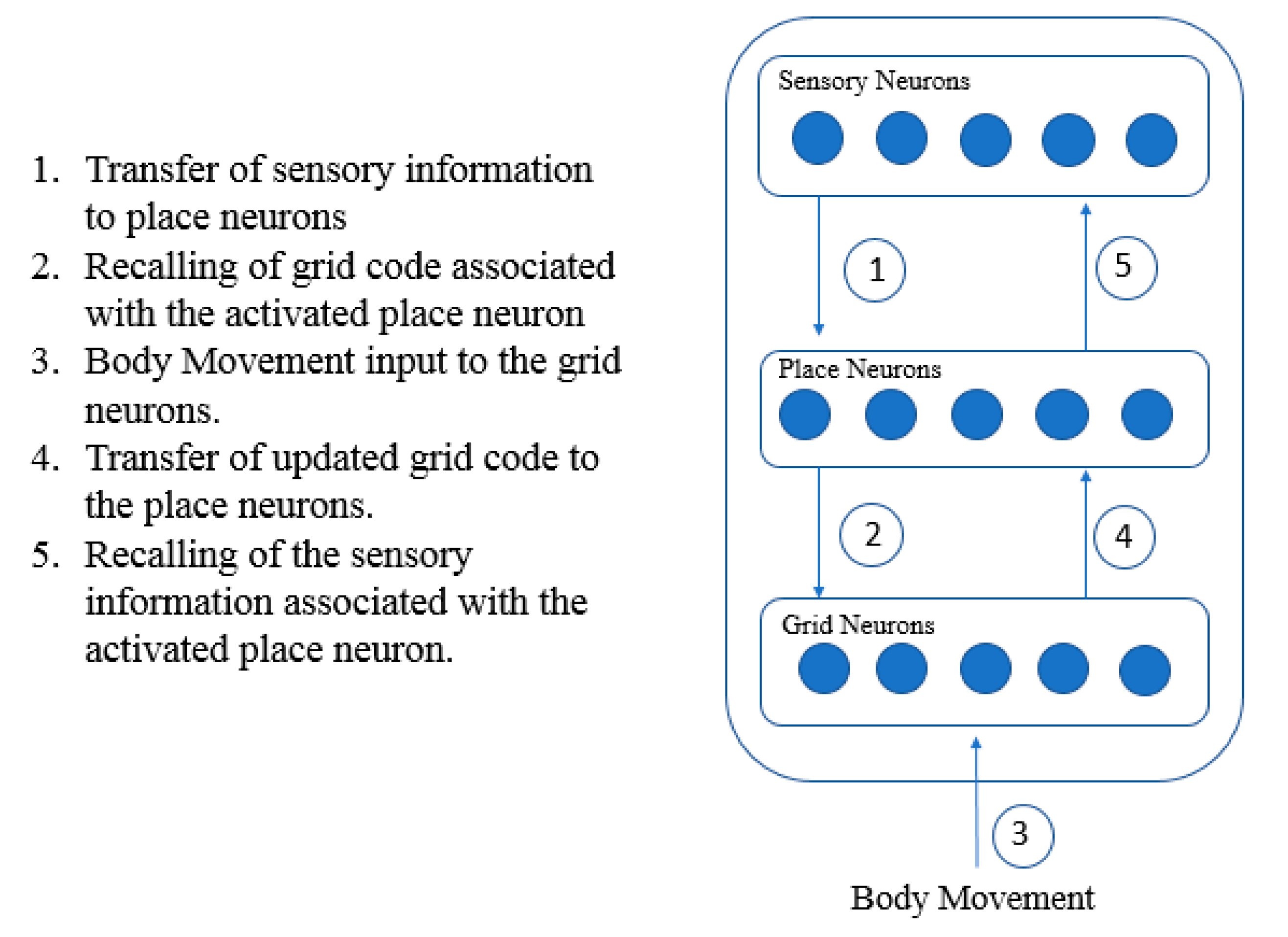
3.4. Modelling of Place and Grid Neuron Interaction System to Perform Predictions and Recognition
3.5. Place Sequence Learning
4. Experimental Detail
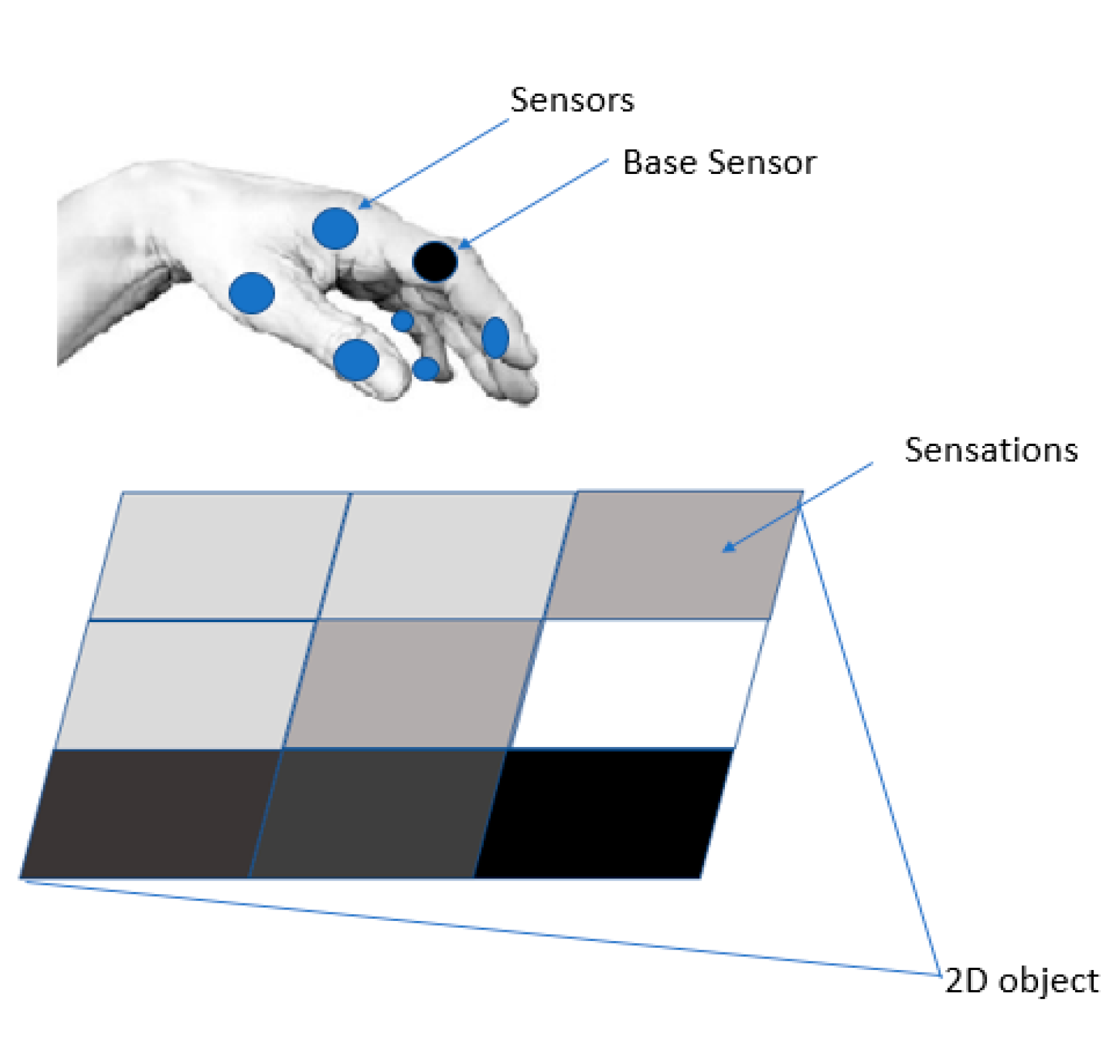
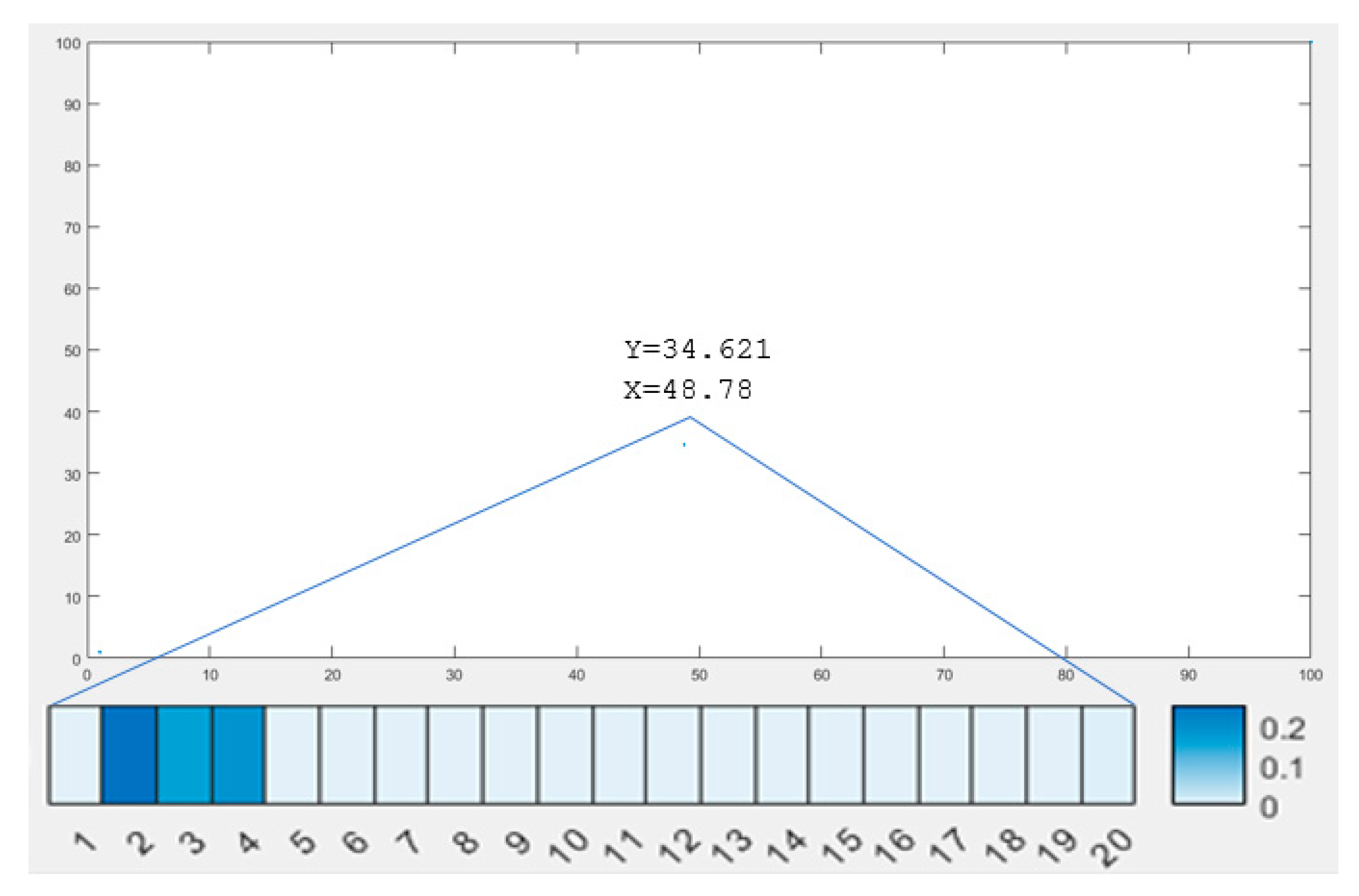
4.1. Object Identification
- Observe the sensation of the base sensor, and recall the grid code corresponds to the observed sensation.
- Other sensors observe their sensations and recall their corresponding grid codes called sensed grid code.
- Next, each sensor integrates their relative position of the base sensor with the grid codes of base sensors to generate new grid codes called path integrated grid code.
- The next comparison will be made between the path integrated grid codes and the sensed grid codes. Those sensed grid codes found similar will be chosen to activate their associated place neurons.
- The objects which are associated with the activated place neurons will be in the list of the active object, and others will be inhibited for future activation.
- A similar process will be repeated again and again until a single object survives in the activation list.
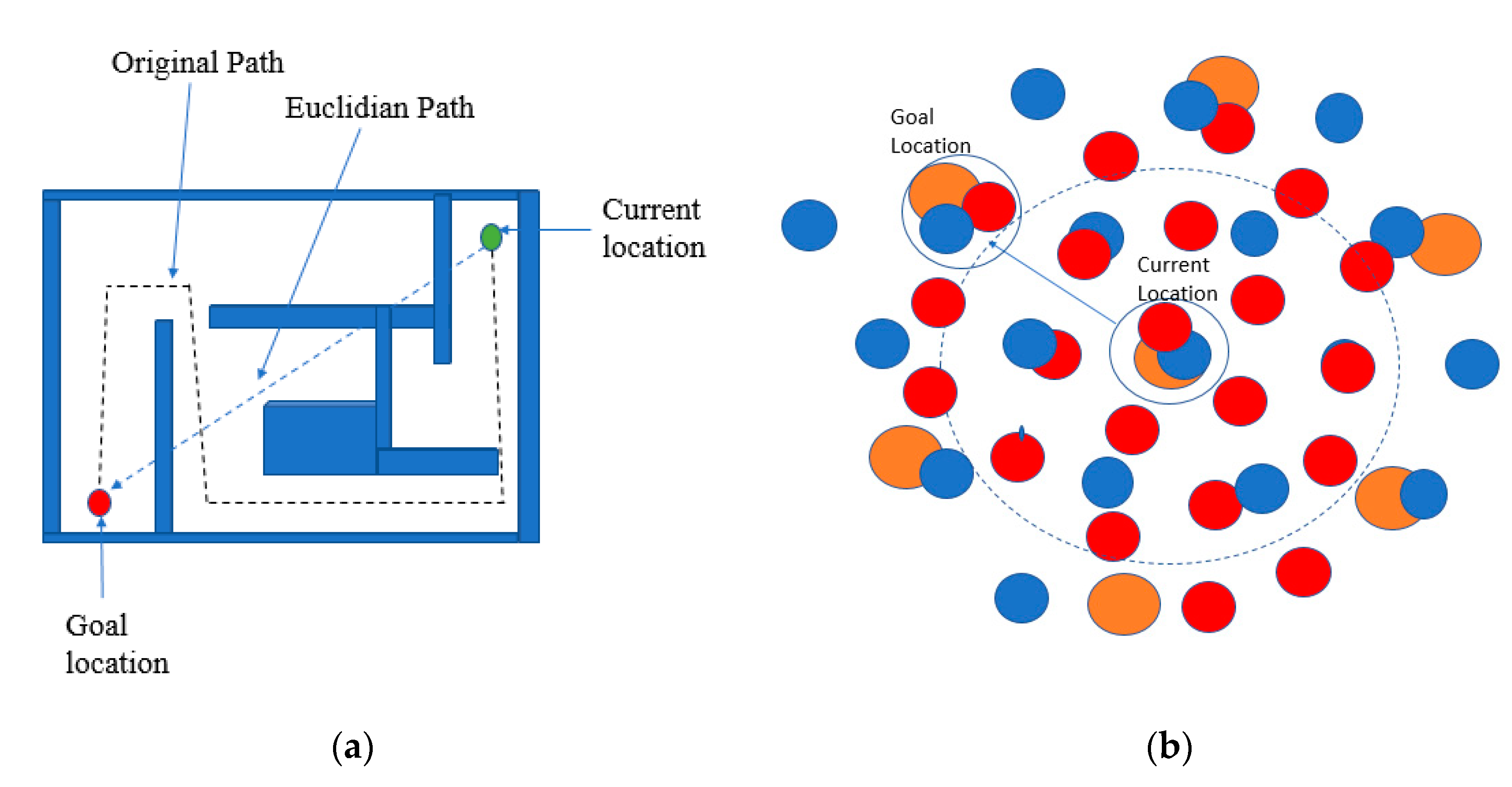
4.2. Prediction during Navigation, and Navigation towards a Goal Location
4.2.1. Finding the Direction of a Goal Location
4.2.2. Navigation Using Place Learner
5. Results and Discussion
5.1. Results of Object Recognition
5.2. Self-Localization Accuracy
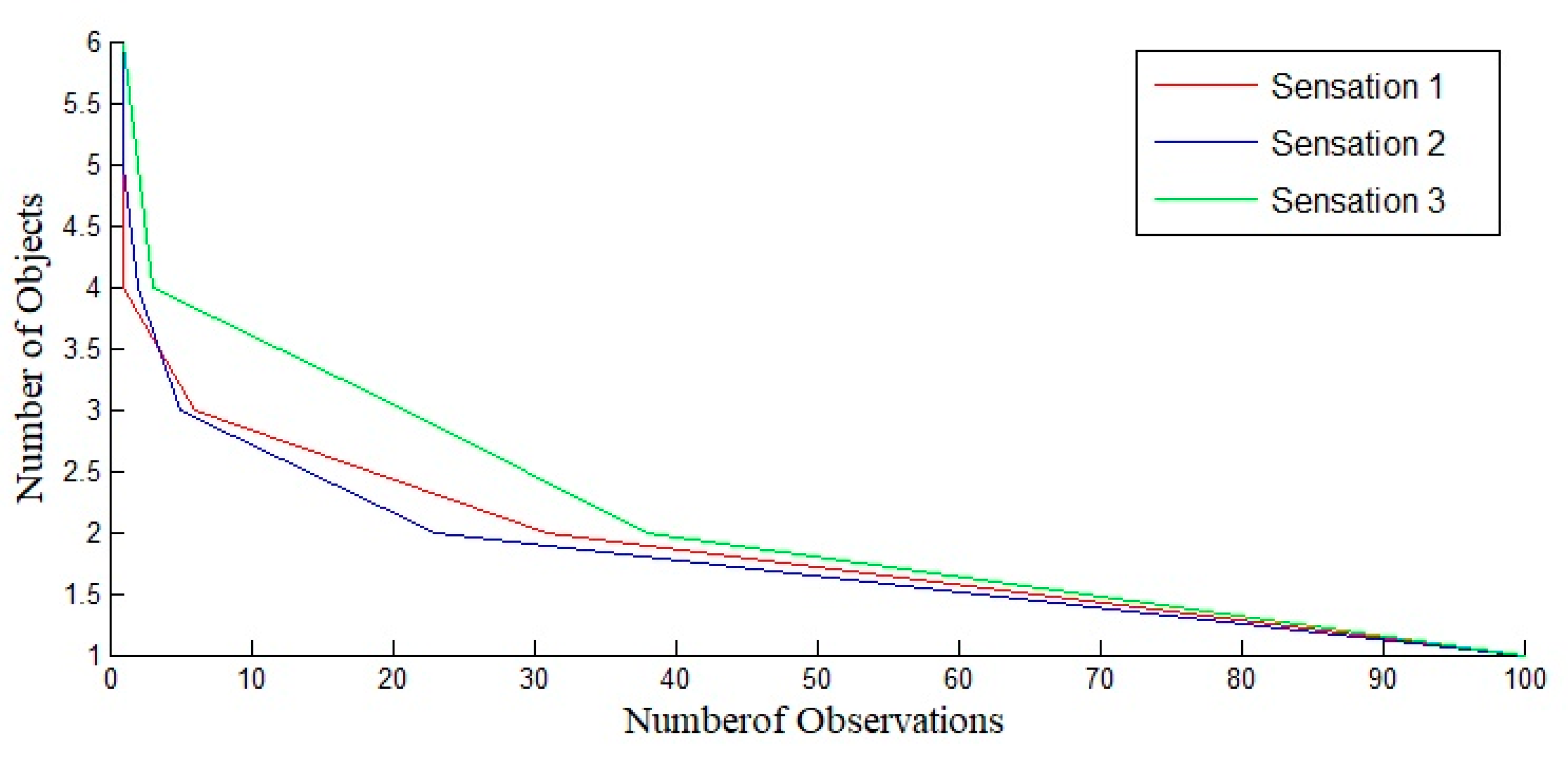
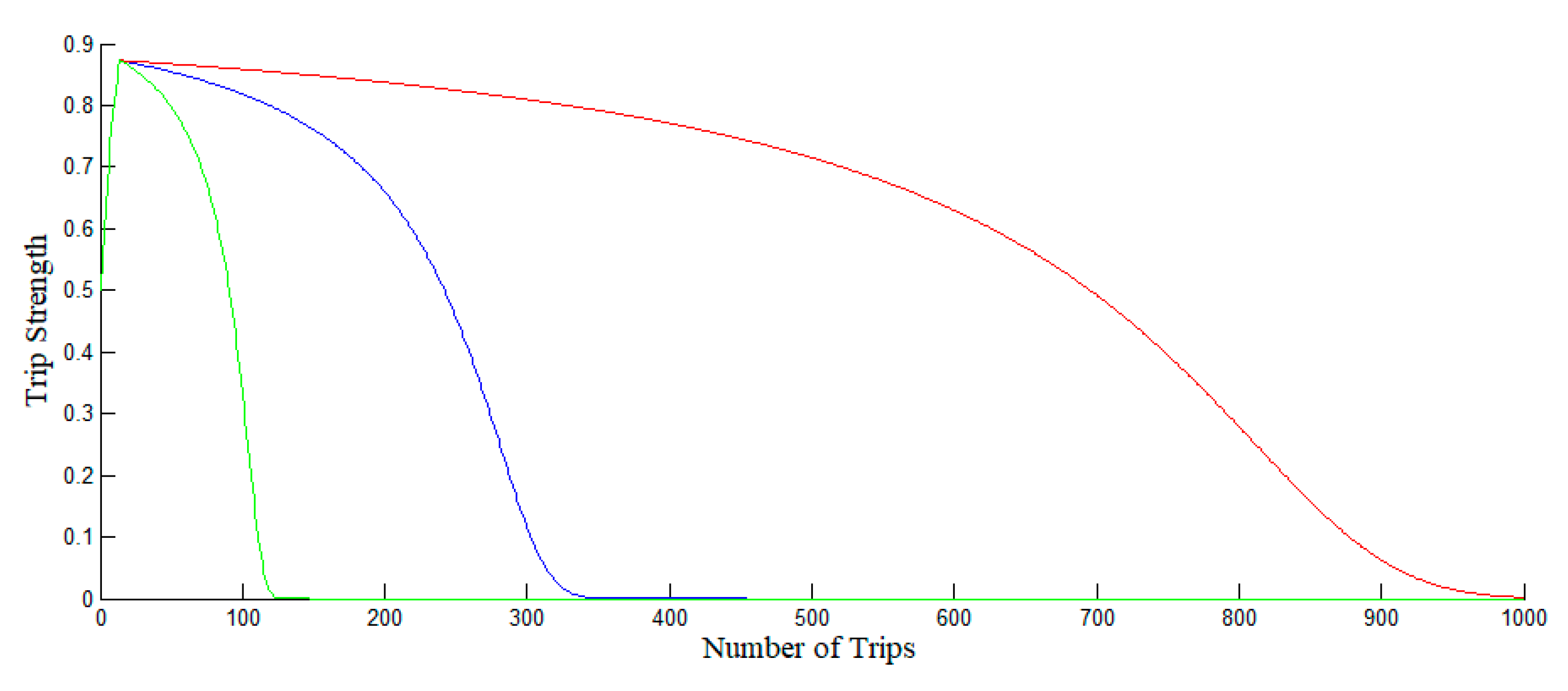
5.3. Trip Forgetting
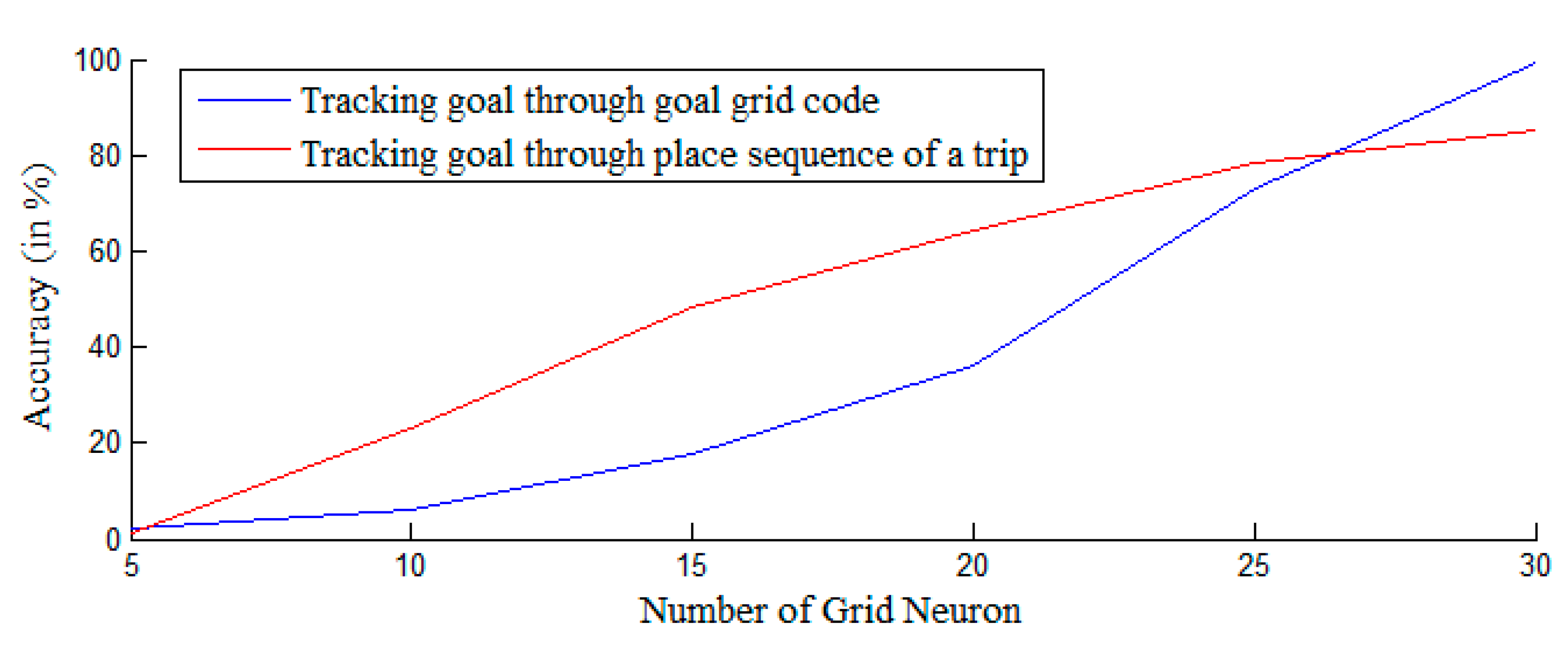
5.4. Comparison between the Navigation Using Tracking Goal Grid Code and Using the Place Sequence (Trip)
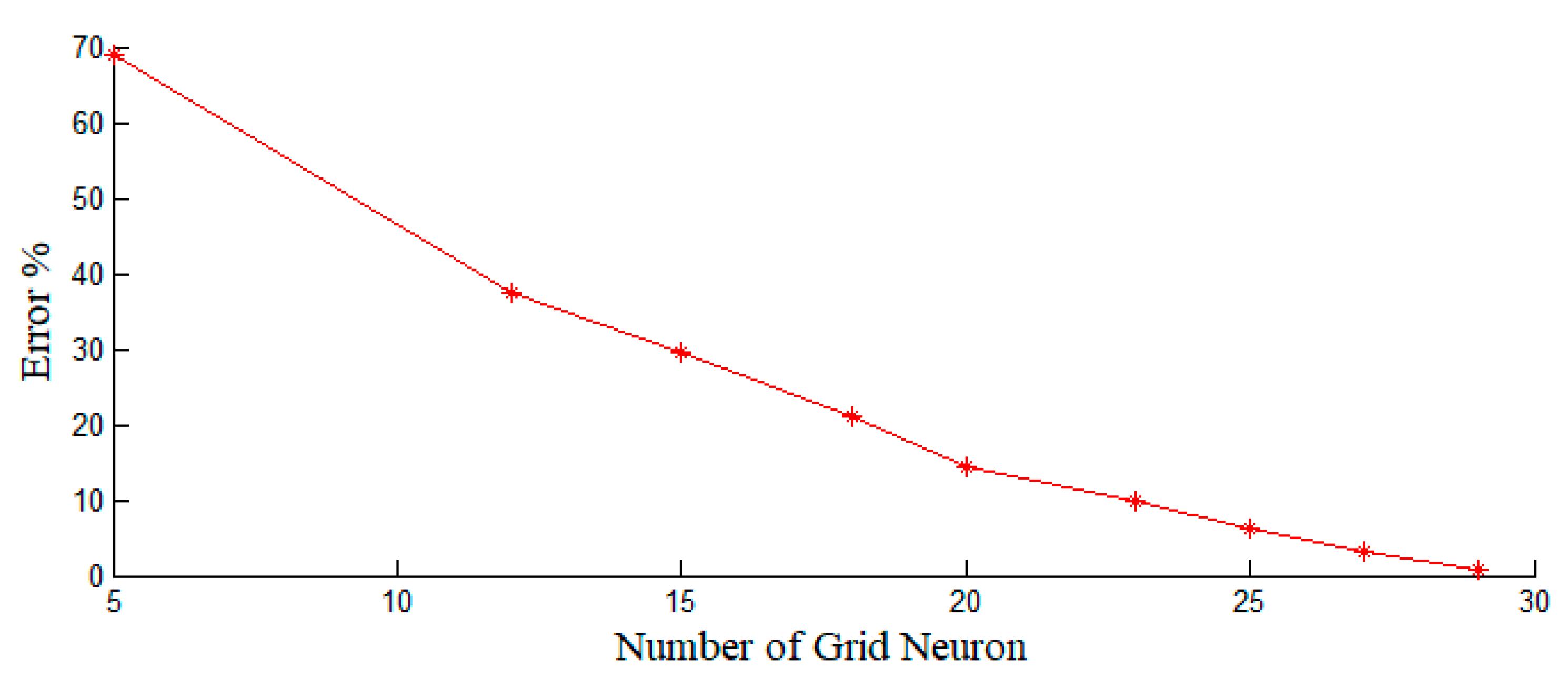
5.5. Accuracy Results on Different Grid Spacings and Size of the Activation Field
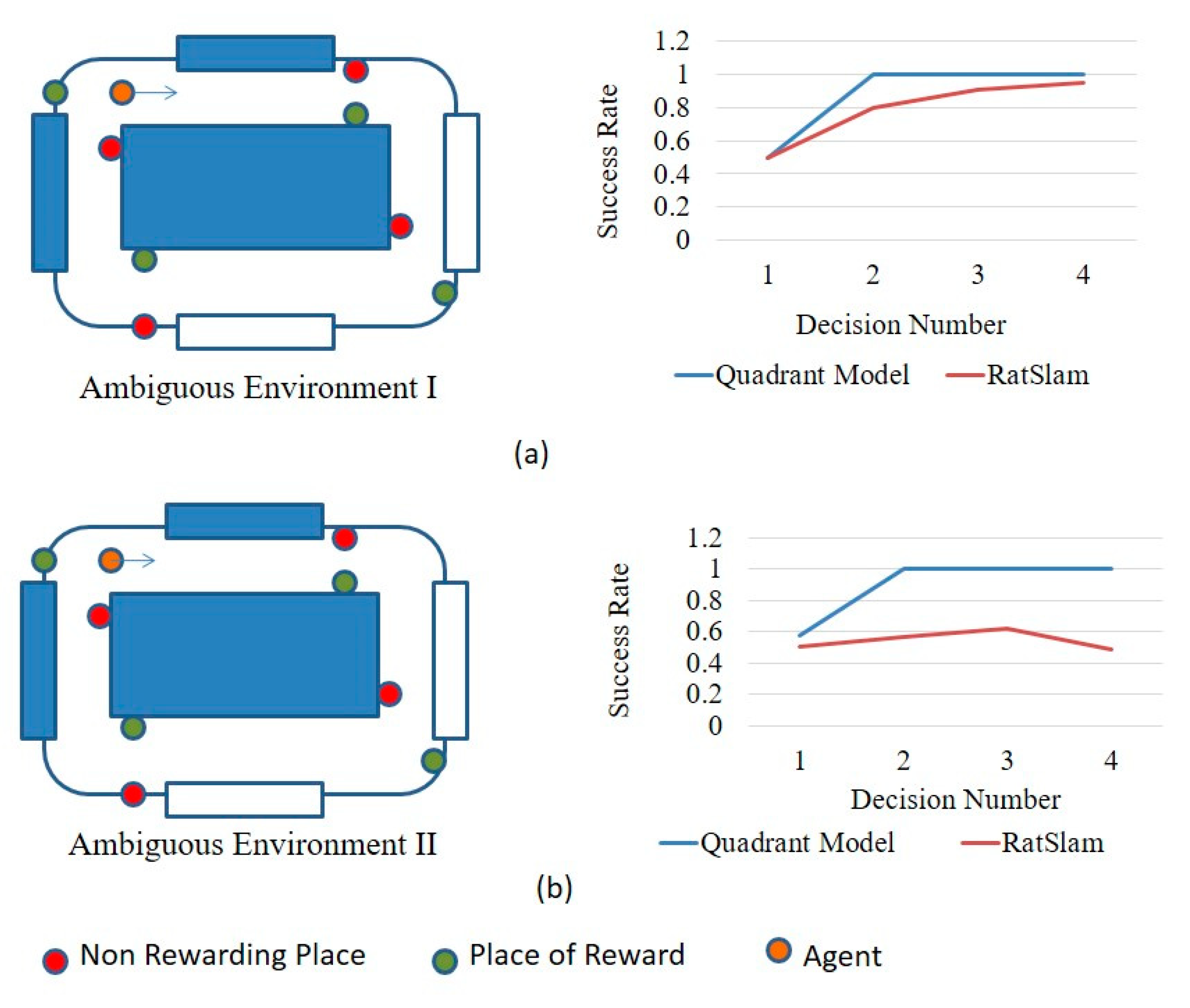
5.6. Localization Accuracy in Ambiguous Field
5.7. Space and Time Complexity
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chatila, R.; Laumond, J.-P. Position referencing and consistent world modeling for mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 138–145. [Google Scholar]
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Rodríguez, F.J.S.; Moreno, V.; Curto, B.; Álves, R. Semantic Localization System for Robots at Large Indoor Environments Based on Environmental Stimuli. Sensors 2020, 20, 2116. [Google Scholar] [CrossRef]
- Mcelhoe, B.A. An Assessment of the Navigation and Course Corrections for a Manned Flyby of Mars or Venus. IEEE Trans. Aerosp. Electron. Syst. 1966, 2, 613–623. [Google Scholar] [CrossRef]
- Jauffret, A.; Cuperlier, N.; Gaussier, P. From grid cells and visual place cells to multimodal place cell: A new robotic architecture. Front. Neurorobot. 2015, 9, 1. [Google Scholar] [CrossRef]
- O’Keefe, J.; Burgess, N.; Donnett, J.G.; Jeffery, K.J.; Maguire, E.A. Place cells, navigational accuracy, and the human hippocampus. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1998, 353, 1333–1340. [Google Scholar] [CrossRef] [PubMed]
- O’Keefe, J.; Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971, 34, 171–175. [Google Scholar] [CrossRef]
- Hafting, T.; Fyhn, M.; Molden, S.; Moser, E.I.; Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. Nature 2005, 436, 801–806. [Google Scholar] [CrossRef]
- Fyhn, M.; Hafting, T.; Witter, M.P.; Moser, E.I.; Moser, M.-B. Grid cells in mice. Hippocampus 2008, 18, 1230–1238. [Google Scholar] [CrossRef]
- Yartsev, M.M.; Witter, M.P.; Ulanovsky, N. Grid cells without theta oscillations in the entorhinal cortex of bats. Nature 2011, 479, 103–107. [Google Scholar] [CrossRef]
- Killian, N.J.; Jutras, M.J.; Buffalo, E.A. A map of visual space in the primate entorhinal cortex. Nature 2012, 491, 761–764. [Google Scholar] [CrossRef]
- Jacobs, J.; Weidemann, C.T.; Miller, J.F.; Solway, A.; Burke, J.F.; Wei, X.-X.; Suthana, N.; Sperling, M.R.; Sharan, A.D.; Fried, I.; et al. Direct recordings of grid-like neuronal activity in human spatial navigation. Nat. Neurosci. 2013, 16, 1188–1190. [Google Scholar] [CrossRef] [PubMed]
- Doeller, C.F.; Barry, C.; Burgess, N. Evidence for grid cells in a human memory network. Nature 2010, 463, 657–661. [Google Scholar] [CrossRef] [PubMed]
- Moser, E.I.; Kropff, E.; Moser, M.B. Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci. 2008, 31, 69–89. [Google Scholar] [CrossRef] [PubMed]
- Bush, D.; Barry, C.; Burgess, N. What do grid cells contribute to place cell firing? Trends Neurosci. 2014, 37, 136–145. [Google Scholar] [CrossRef] [PubMed]
- McNaughton, B.L.; Battaglia, F.P.; Jensen, O.; Moser, E.I.; Moser, M.-B. Path integration and the neural basis of the’cognitivemap. Nat. Rev. Neurosci. 2006, 7, 663–678. [Google Scholar] [CrossRef] [PubMed]
- Milford, M.; Wiles, J.; Wyeth, G.F. Solving Navigational Uncertainty Using Grid Cells on Robots. PLoS Comput. Biol. 2010, 6, e1000995. [Google Scholar] [CrossRef]
- Burgess, N.; Barry, C.; O’Keefe, J. An oscillatory interference model of grid cell firing. Hippocampus 2007, 17, 801–812. [Google Scholar] [CrossRef] [PubMed]
- Bush, D.; Burgess, N. A hybrid oscillatory interference/continuous attractor network model of grid cell firing. J. Neurosci. 2014, 34, 5065–5079. [Google Scholar] [CrossRef] [PubMed]
- Savelli, F.; Knierim, J.J. Origin and role of path integration in the cognitive representations of the hippocampus: Computational insights into open questions. J. Exp. Biol. 2019, 222 (Suppl. 1). [Google Scholar] [CrossRef]
- O’Keefe, J.; Lynn, N. The Hippocampus as a Cognitive Map; Clarendon Press: Oxford, UK, 1978. [Google Scholar]
- Leutgeb, S.; Leutgeb, J.K.; Barnes, C.A.; Moser, E.I.; McNaughton, B.L.; Moser, M.B. Independent Codes for Spatial and Episodic Memory in Hippocampal Neuronal Ensembles. Science 2005, 309, 619–623. [Google Scholar] [CrossRef] [PubMed]
- Rolls, E.T.; Stringer, S.M.; Trappenberg, T.P. A unified model of spatial and episodic memory. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2002, 269, 1087–1093. [Google Scholar] [CrossRef] [PubMed]
- Shrivastava, R.; Tripathi, S. Computational Model of Episodic Memory Formation, Recalling, and Forgetting. In Proceedings of the International Conference on Recent Advancement on Computer and Communication; Springer: Singapore, 2018; Volume 34, pp. 395–403. [Google Scholar]
- Kolisetty, V.; Rajput, D. A Review on the Significance of Machine Learning for Data Analysis in Big Data. Jordanian J. Comput. Inf. Technol. 2019, 6. [Google Scholar] [CrossRef]
- Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Kaluri, R.; Rajput, D.S.; Srivastava, G.; Baker, T. Analysis of Dimensionality Reduction Techniques on Big Data. IEEE Access 2020, 8, 54776–54788. [Google Scholar] [CrossRef]
- Tiwari, V.; Thakur, R.S. Pattern Warehouse: Context Based Modeling and Quality Issues. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2016, 86, 417–431. [Google Scholar] [CrossRef]
- Tiwari, V.; Thakur, R.S. Contextual snowflake modelling for pattern warehouse logical design. Sadhana 2015, 40, 15–33. [Google Scholar] [CrossRef]
- Iwendi, C.; AlQarni, M.A.; Anajemba, J.H.; Alfakeeh, A.S.; Zhang, Z.; Bashir, A.K. Robust Navigational Control of a Two-Wheeled Self-Balancing Robot in a Sensed Environment. IEEE Access 2019, 7, 82337–82348. [Google Scholar] [CrossRef]
- Patel, H.; Rajput, D.S.; Reddy, G.T.; Iwendi, C.; Bashir, A.K.; Jo, O. A review on classification of imbalanced data for wireless sensor networks. Int. J. Distrib. Sens. Netw. 2020, 16. [Google Scholar] [CrossRef]
- Deepa, N.; Prabadevi, B.; Maddikunta, P.K.R.; Gadekallu, T.R.; Baker, T.; Khan, M.A.; Tariq, U. An AI-based intelligent system for healthcare analysis using Ridge-Adaline Stochastic Gradient Descent Classifier. J. Supercomput. 2020. [Google Scholar] [CrossRef]
- Godard, C.; Mac Aodha, O.; Brostow, G.J. Unsupervised Monocular Depth Estimation with Left-Right Consistency. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6602–6611. [Google Scholar]
- Poluru, R.K.; Reddy, M.P.K.; Kaluri, R.; Lakshmanna, K.; Reddy, G.T. Agribot. In Advances in Computer and Electrical Engineering; IGI Global: Hershey, PA, USA, 2020; pp. 151–157. [Google Scholar]
- Tang, Q.; Yang, K.; Zhou, D.; Luo, Y.-S.; Yu, F. A Real-Time Dynamic Pricing Algorithm for Smart Grid With Unstable Energy Providers and Malicious Users. IEEE Internet Things J. 2015, 3, 554–562. [Google Scholar] [CrossRef]
- He, S.; Zeng, W.; Xie, K.; Yang, H.; Lai, M.; Su, X. PPNC: Privacy Preserving Scheme for Random Linear Network Coding in Smart Grid. KSII Trans. Internet Inf. Syst. 2017, 11, 1510–1532. [Google Scholar] [CrossRef]
- Xia, Z.; Tan, J.; Wang, J.; Zhu, R.; Xiao, H.; Sangaiah, A.K. Research on Fair Trading Mechanism of Surplus Power Based on Blockchain. J. UCS 2019, 25, 1240–1260. [Google Scholar]
- Tu, Y.; Lin, Y.; Wang, J. Semi-supervised Learning with Generative Adversarial Networks on Digital Signal Mod-ulation Classification. Comput. Mater. Contin. 2018, 55, 243–254. [Google Scholar]
- Liu, M.; Cheng, L.; Qian, K.; Wang, J.; Wang, J.; Liu, Y. Indoor acoustic localization: A survey. Hum. Cent. Comput. Inf. Sci. 2020, 10, 2. [Google Scholar] [CrossRef]
- Chen, Y.; Xiong, J.; Xu, W.; Zuo, J. A novel online incremental and decremental learning algorithm based on variable support vector machine. Clust. Comput. 2018, 22, 7435–7445. [Google Scholar] [CrossRef]
- Li, H.; Li, W.; Zhang, S.; Wang, H.; Pan, Y.; Wang, J. Page-sharing-based virtual machine packing with multi-resource constraints to reduce network traffic in migration for clouds. Future Gener. Comput. Syst. 2019, 96, 462–471. [Google Scholar] [CrossRef]
- Singh, S.; Ra, I.-H.; Meng, W.; Kaur, M.; Cho, G.H. SH-BlockCC: A secure and efficient Internet of things smart home architecture based on cloud computing and blockchain technology. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719844159. [Google Scholar] [CrossRef]
- Zhang, D.; Yin, T.; Yang, G.; Xia, M.; Li, L.; Sun, X. Detecting image seam carving with low scaling ratio using multi-scale spatial and spectral entropies. J. Vis. Commun. Image Represent. 2017, 48, 281–291. [Google Scholar] [CrossRef]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrivastava, R.; Kumar, P.; Tripathi, S.; Tiwari, V.; Rajput, D.S.; Gadekallu, T.R.; Suthar, B.; Singh, S.; Ra, I.-H. A Novel Grid and Place Neuron’s Computational Modeling to Learn Spatial Semantics of an Environment. Appl. Sci. 2020, 10, 5147. https://doi.org/10.3390/app10155147
Shrivastava R, Kumar P, Tripathi S, Tiwari V, Rajput DS, Gadekallu TR, Suthar B, Singh S, Ra I-H. A Novel Grid and Place Neuron’s Computational Modeling to Learn Spatial Semantics of an Environment. Applied Sciences. 2020; 10(15):5147. https://doi.org/10.3390/app10155147
Chicago/Turabian StyleShrivastava, Rahul, Prabhat Kumar, Sudhakar Tripathi, Vivek Tiwari, Dharmendra Singh Rajput, Thippa Reddy Gadekallu, Bhivraj Suthar, Saurabh Singh, and In-Ho Ra. 2020. "A Novel Grid and Place Neuron’s Computational Modeling to Learn Spatial Semantics of an Environment" Applied Sciences 10, no. 15: 5147. https://doi.org/10.3390/app10155147
APA StyleShrivastava, R., Kumar, P., Tripathi, S., Tiwari, V., Rajput, D. S., Gadekallu, T. R., Suthar, B., Singh, S., & Ra, I.-H. (2020). A Novel Grid and Place Neuron’s Computational Modeling to Learn Spatial Semantics of an Environment. Applied Sciences, 10(15), 5147. https://doi.org/10.3390/app10155147







