Seismic AVOA Inversion for Weak Anisotropy Parameters and Fracture Density in a Monoclinic Medium
Abstract
1. Introduction
2. Methods
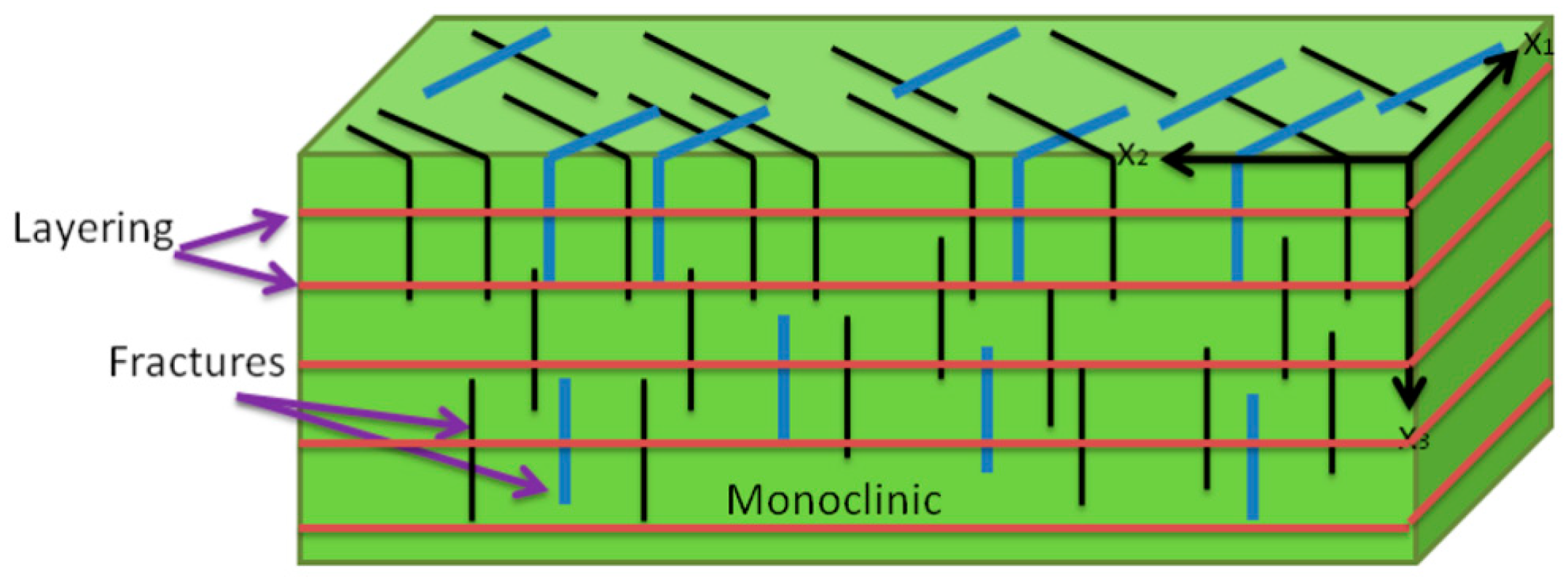
2.1. Elastic Compliance Tensor of Fractured Medium
2.2. PP-Wave Reflection Coefficient and Generalized Anisotropy Parameters
2.3. Bayesian Inversion for Weak Anisotropy Parameters and Fracture Density
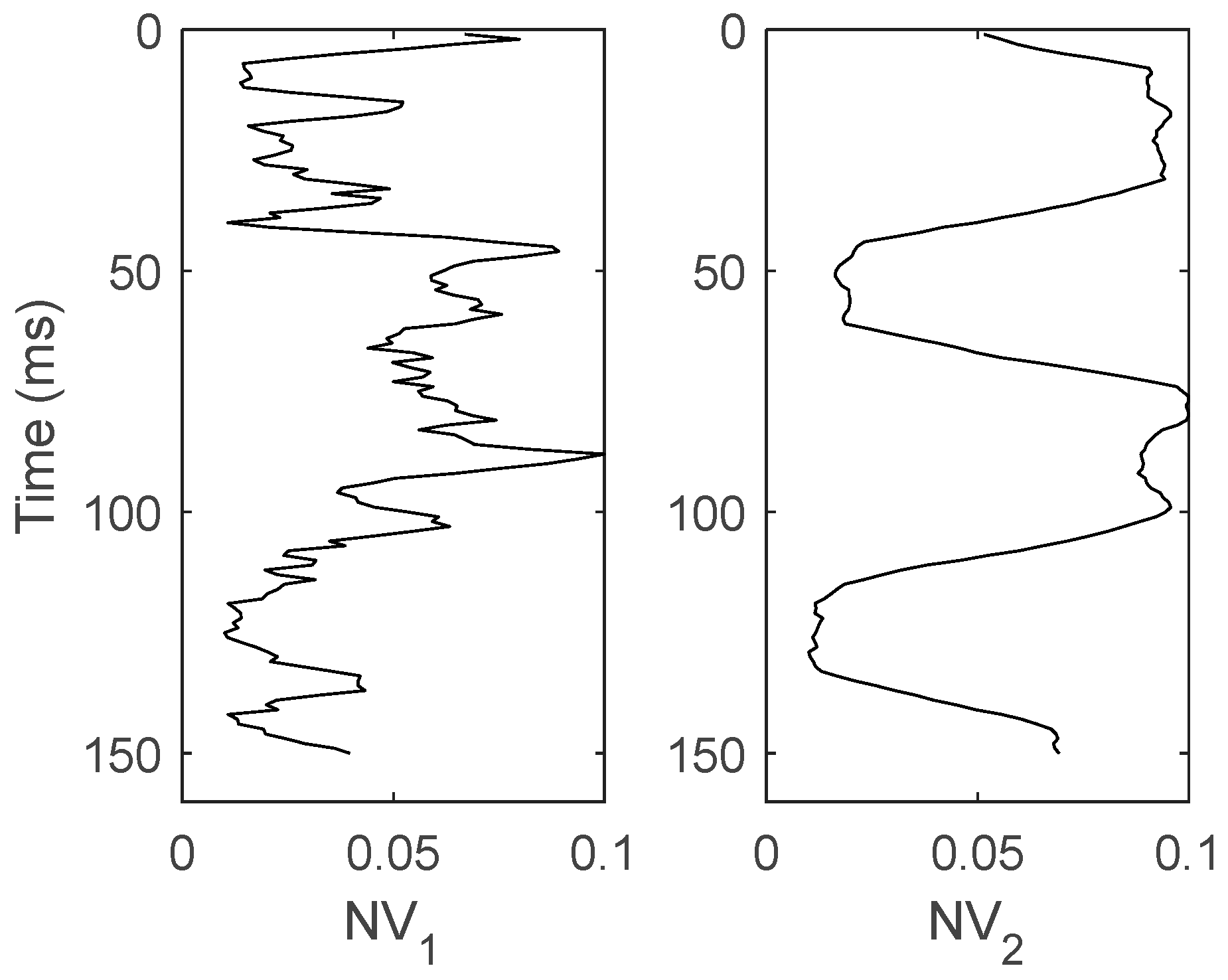
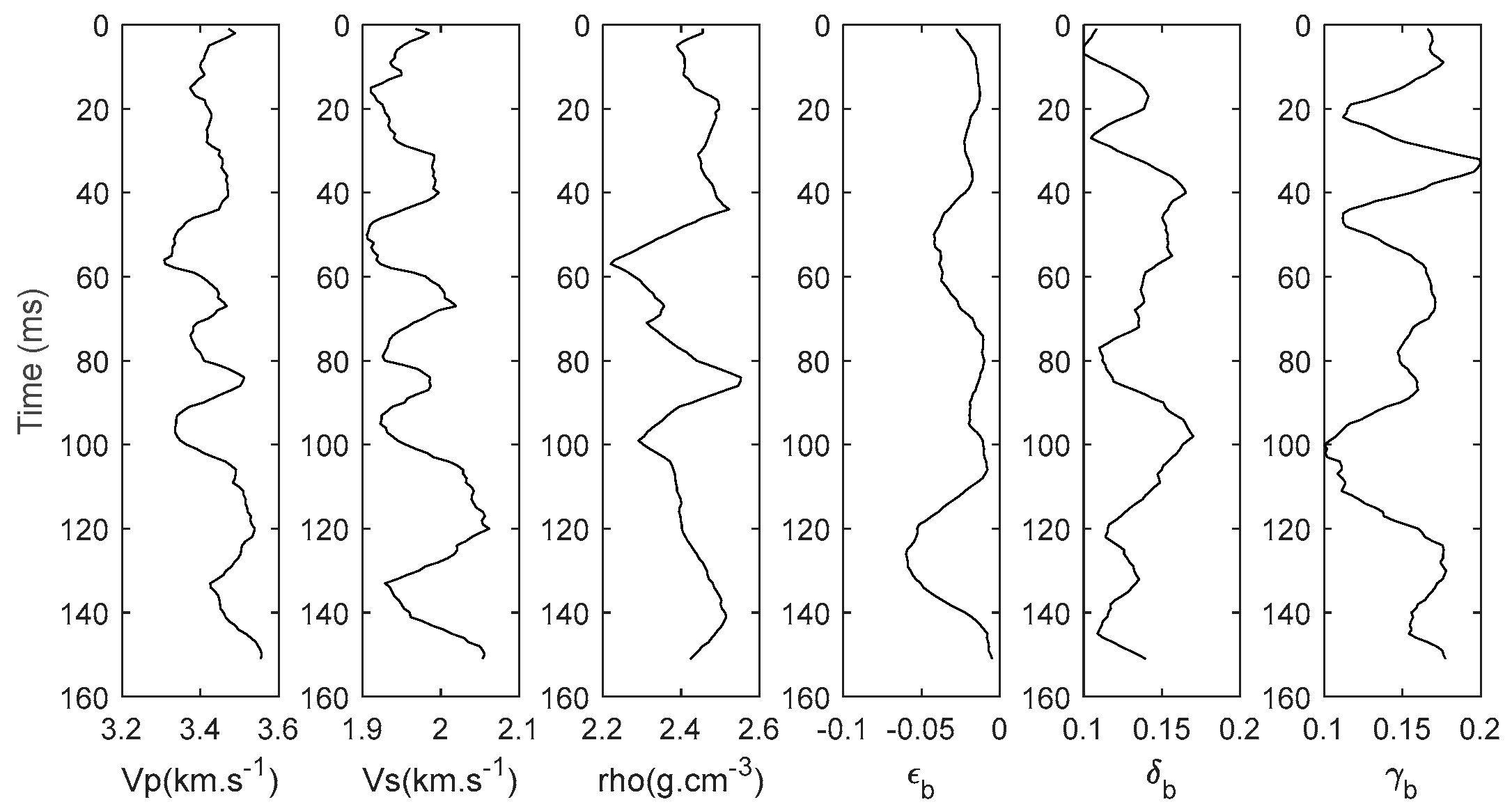
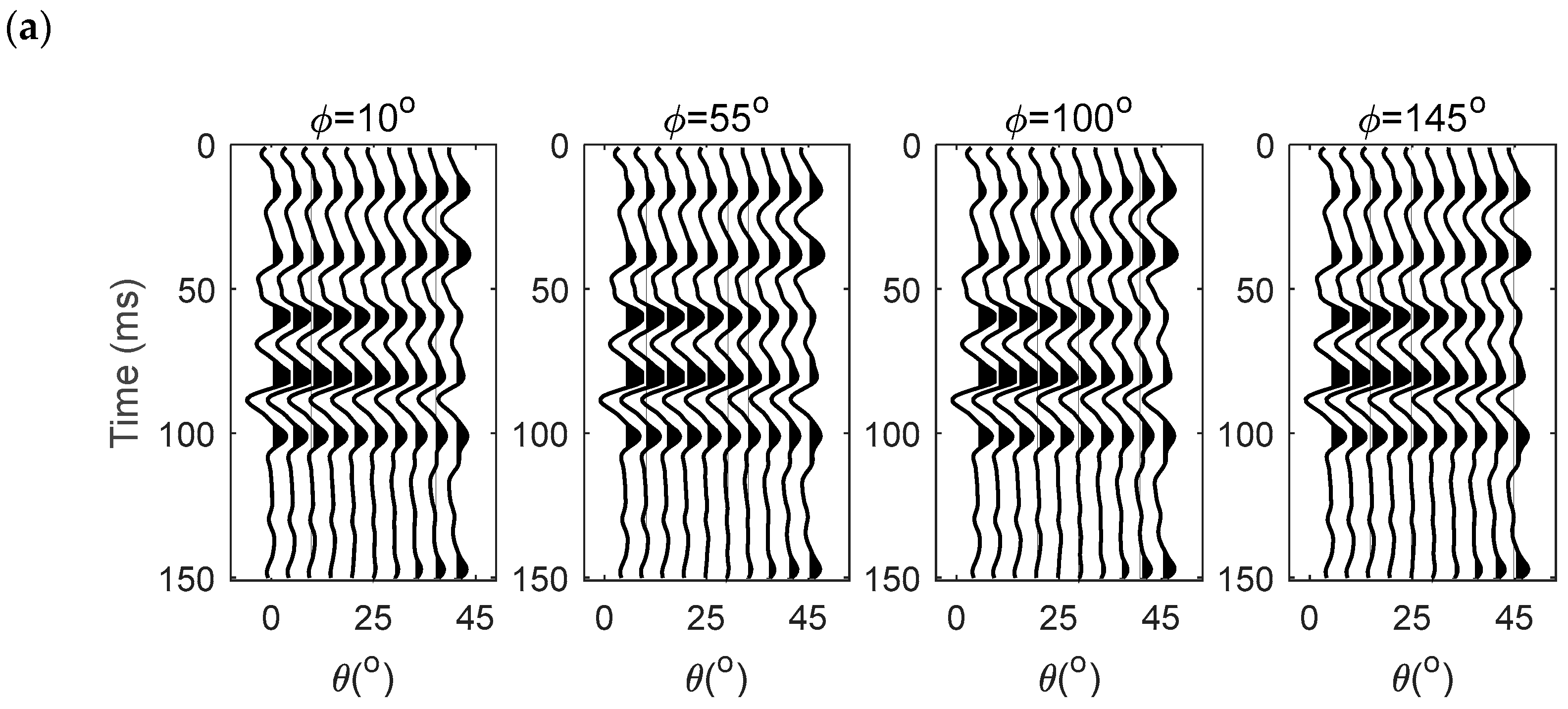
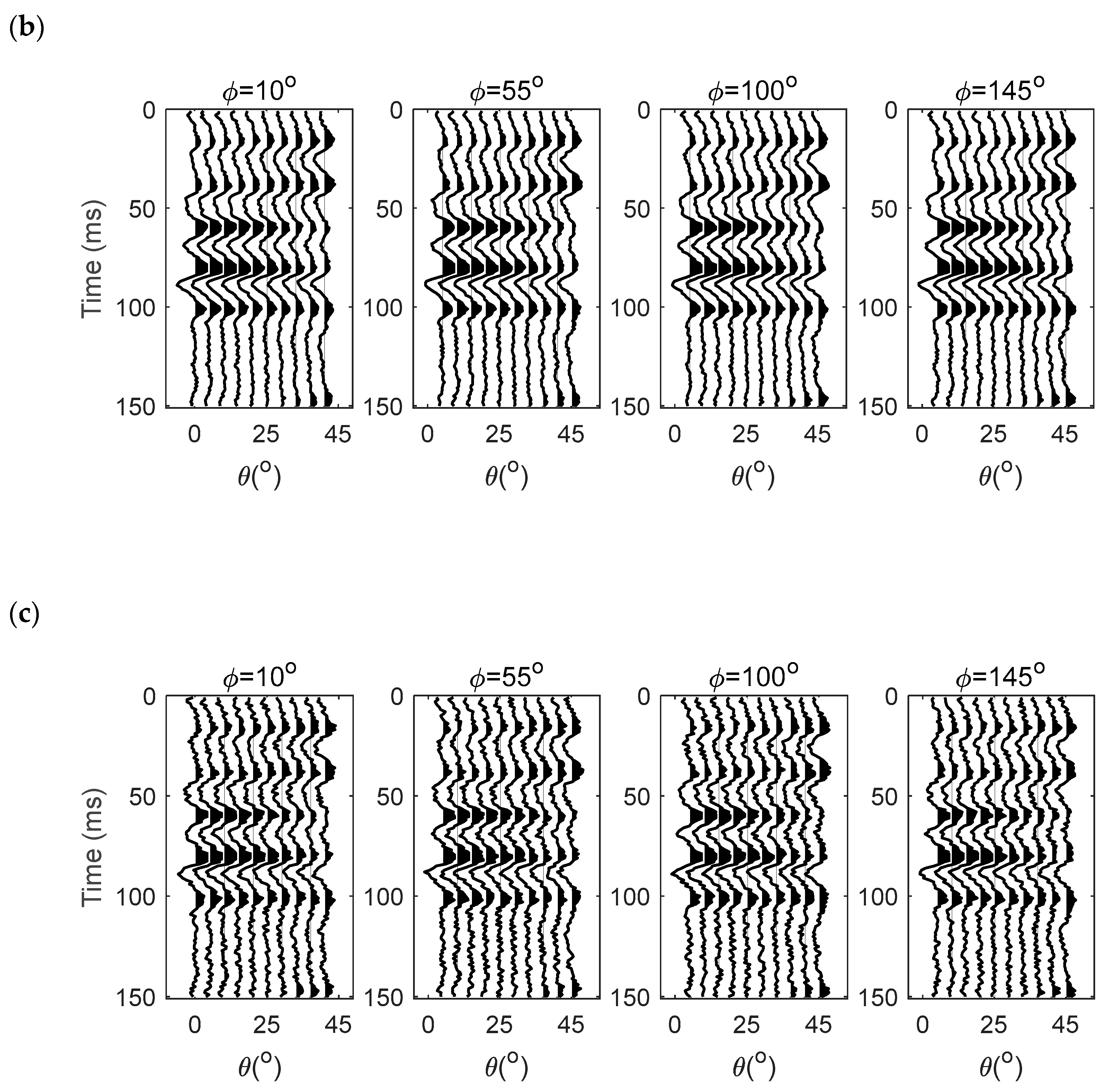
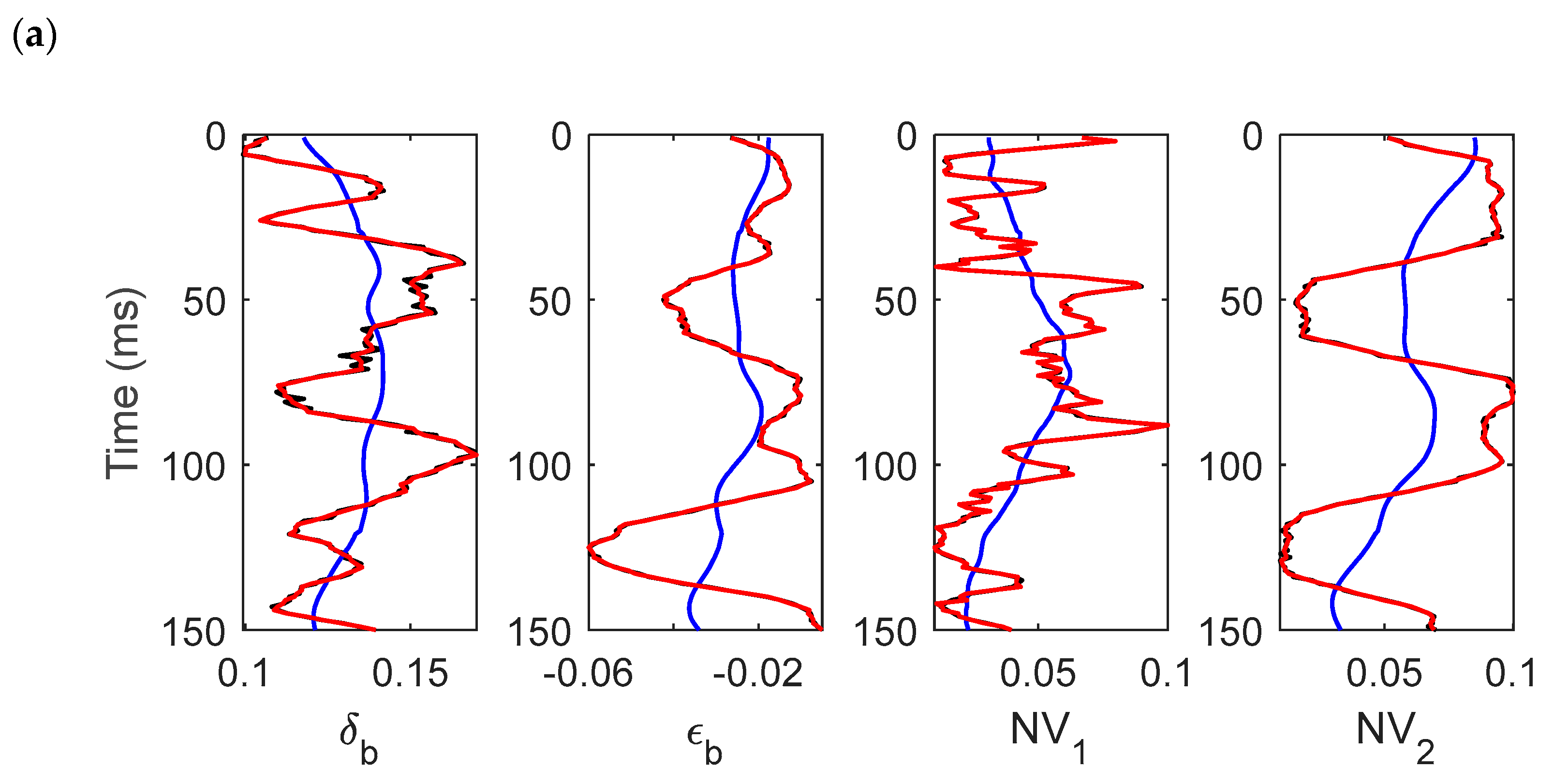
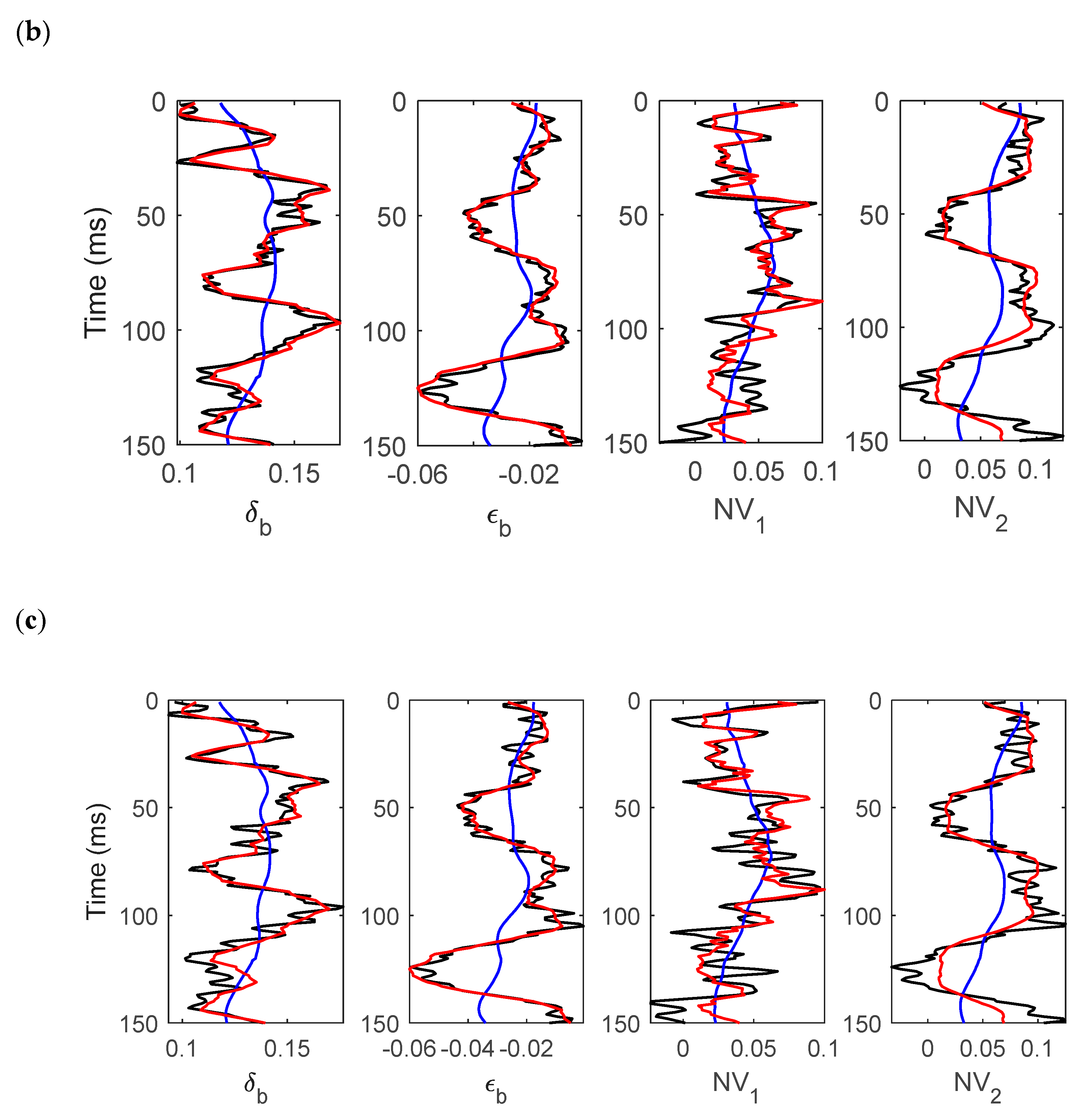
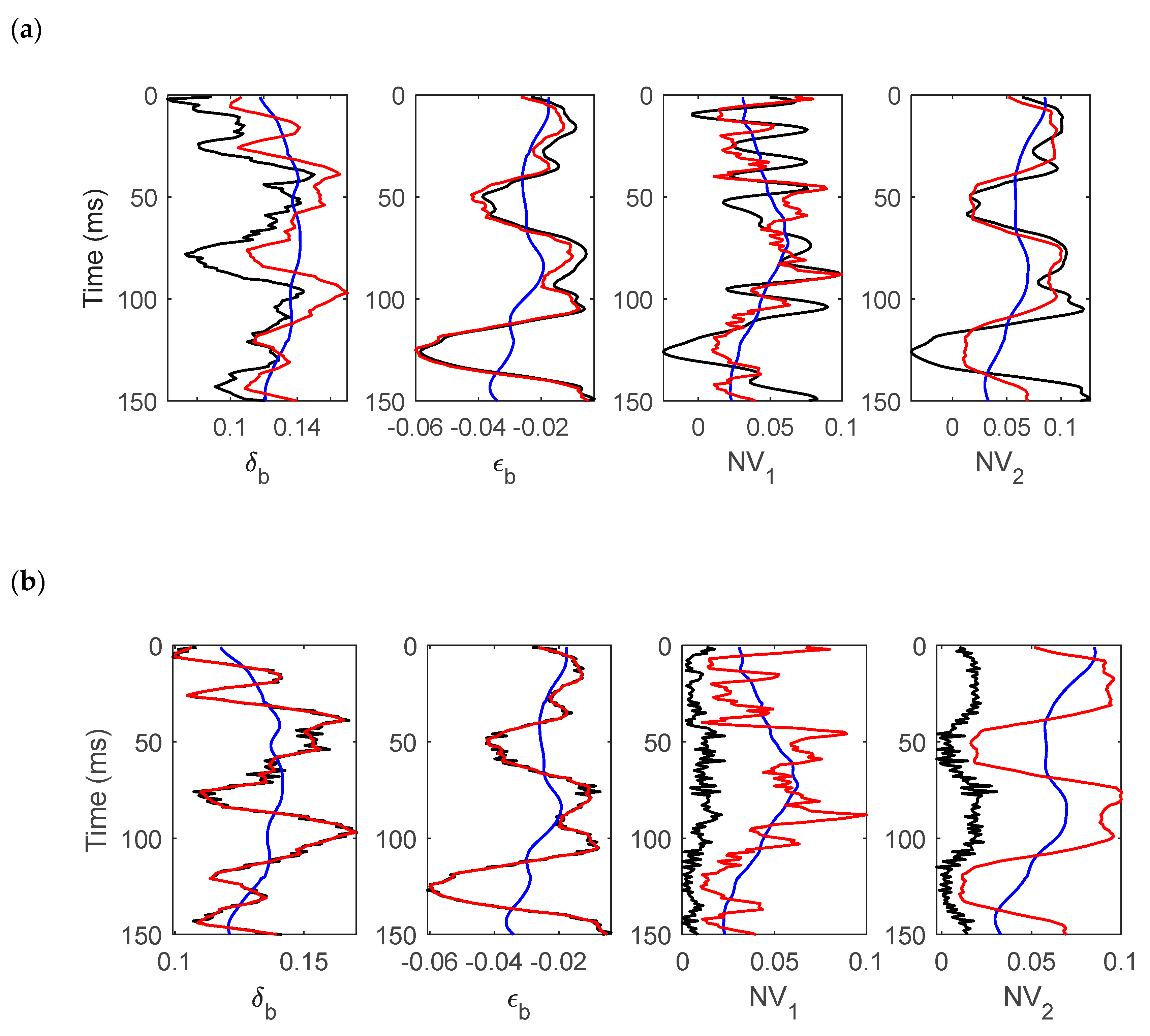
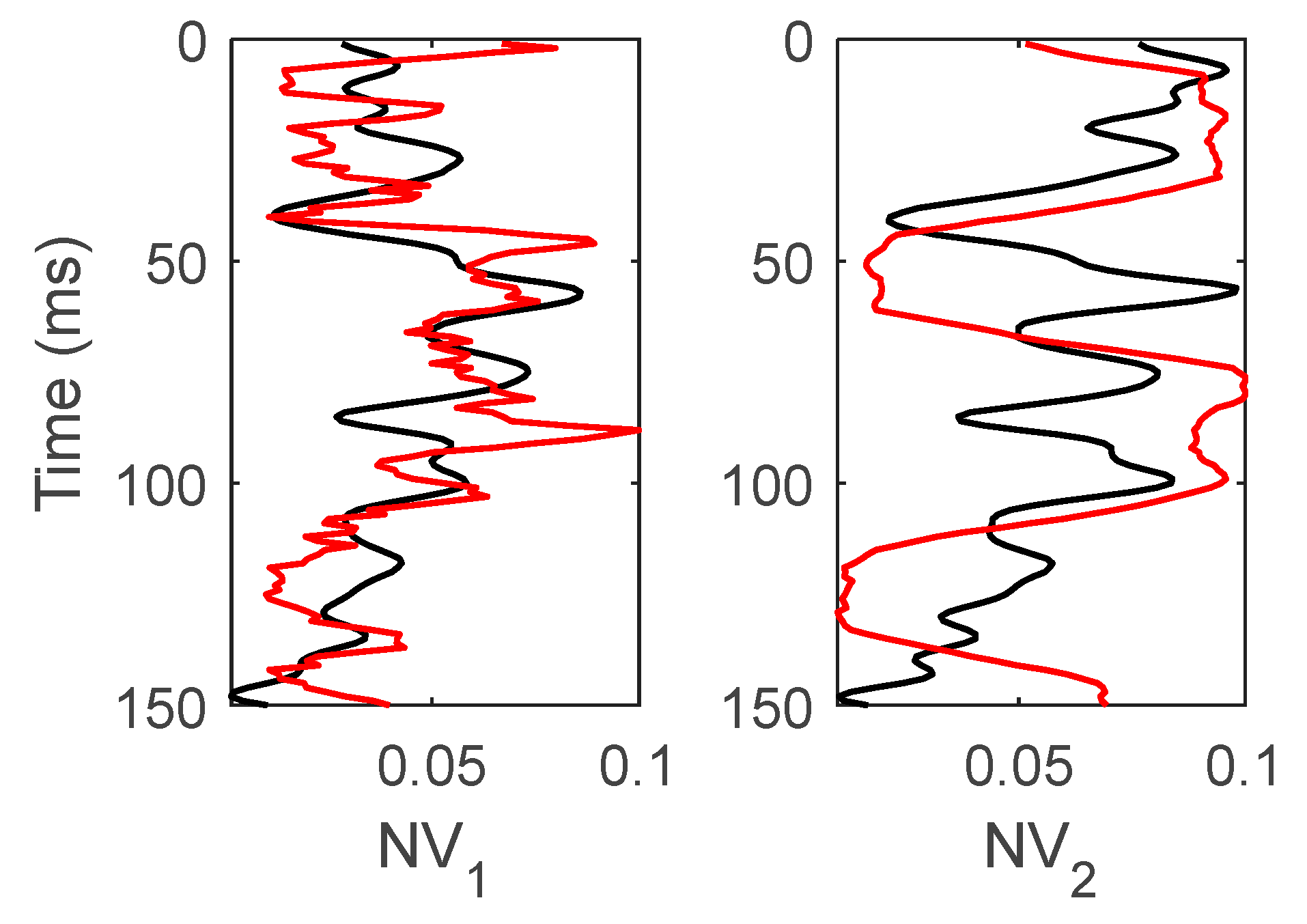
3. Numerical Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Nelson, R.A. Geologic Analysis of Naturally Fractured Reservoirs; Gulf Publishing Company: Houston, TX, USA, 1985. [Google Scholar]
- Sayers, C.M. Seismic characterization of reservoirs containing multiple fracture sets. Geophys. Prospect. 2009, 57, 187–192. [Google Scholar] [CrossRef]
- Dvorkin, J.; Mavko, G.; Nur, A. Squirt flow in fully saturated rocks. Geophysics 1995, 60, 97–107. [Google Scholar] [CrossRef]
- Rubino, J.; Holliger, K. Research note: Seismic attenuation due to wave-induced fluid flow at microscopic and mesoscopic scales. Geophys. Prospect. 2013, 61, 882–889. [Google Scholar] [CrossRef]
- Chen, H.; Innanen, K.A.; Chen, T. Estimating P-and S-wave inverse quality factors from observed seismic data using an attenuative elastic impedance. Geophysics 2018, 83, R173–R187. [Google Scholar] [CrossRef]
- Far, M.E.; Sayers, C.M.; Thomsen, L.; Han, D.; Castagna, J.P. Seismic characterization of naturally fractured reservoirs using amplitude versus offset and azimuth analysis. Geophys. Prospect. 2013, 61, 427–447. [Google Scholar] [CrossRef]
- Wright, J. The effects of transverse isotropy on reflection amplitude versus offset. Geophysics 1987, 52, 564–567. [Google Scholar] [CrossRef]
- Banik, N.C. An effective anisotropy parameter in transversely isotropic media. Geophysics 1987, 52, 1654–1664. [Google Scholar] [CrossRef]
- Kim, K.Y.; Wrolstad, K.H.; Aminzadeh, F. Effects of transverse isotropy on P-wave AVO for gas sands. Geophysics 1993, 58, 883–888. [Google Scholar] [CrossRef]
- Rahimian, M.; Eskandari-Ghadi, M.; Pak, R.Y.; Khojasteh, A. Elastodynamic Potential Method for Transversely Isotropic Solid. J. Eng. Mech. 2007, 133, 1134–1145. [Google Scholar] [CrossRef]
- Shahbodagh, B.; Ashari, M.; Khalili, N. A hybrid element method for dynamics of piles and pile groups in transversely isotropic media. Comput. Geotech. 2017, 85, 249–261. [Google Scholar] [CrossRef]
- Moghaddasi, H.; Shahbodagh, B.; Khalili, N. Lateral Vibration of Piles and Pile Groups in Nonhomogeneous Transversely Isotropic Media. Int. J. Geomech. 2020, 20, 04020124. [Google Scholar] [CrossRef]
- Rüger, A. P-wave reflection coefficients for transversely isotropic media with vertical and horizontal axis of symmetry. Geophysics 1997, 62, 713–722. [Google Scholar] [CrossRef]
- Sayers, C.M.; Rickett, J.E. Azimuthal variation in AVO response for fractured gas sands. Geophys. Prospect. 1997, 45, 165–182. [Google Scholar] [CrossRef]
- Bakulin, A.V.; Grechka, V.; Tsvankin, I. Estimation of fracture parameters from reflection seismic data. Part III: Fractured models with monoclinic symmetry. Geophysics 2000, 65, 1818–1830. [Google Scholar] [CrossRef]
- Sayers, C.M.; Dean, S. Azimuth-dependent AVO in reservoirs containing non-orthogonal fracture sets. Geophys. Prospect. 2001, 49, 100–106. [Google Scholar] [CrossRef]
- Far, M.E. Seismic Characterization of Naturally Fractured Reservoirs. Ph.D. Dissertation, University of Houston, Houston, TX, USA, 2011. [Google Scholar]
- Sil, S.; Davidson, M.; Zhou, C.; Olson, R.; Swan, H.; Howell, J.; Chiu, S.; Willis, M. Effect of near-surface anisotropy on a deep anisotropic target layer. In Proceedings of the 81st Annual International Meeting, SEG, Expanded Abstracts, San Antonio, TX, USA, 18–23 September 2011; pp. 305–309. [Google Scholar]
- Far, M.E.; Hardage, B.; Wagner, D. Fracture parameter inversion for Marcellus Shale. Geophysics 2014, 79, C55–C63. [Google Scholar] [CrossRef]
- Chen, H.; Yin, X.; Qu, S.; Zhang, G. AVAZ inversion for fracture weakness parameters based on the rock physics model. J. Geophys. Eng. 2014, 11, 65–70. [Google Scholar] [CrossRef]
- Chen, H.; Pan, X.; Ji, Y.; Zhang, G. Bayesian Markov Chain Monte Carlo inversion for weak anisotropy parameters and fracture weaknesses using azimuthal elastic impedance. Geophys. J. Int. 2017, 210, 801–818. [Google Scholar] [CrossRef]
- Chaveste, A.; Hall, M.; Verm, R.; Gaiser, J.E. Estimation of fracture density and orientation through azimuthal processing and interpretation of seismic data. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2011. [Google Scholar]
- Cortes-Gómez, D.-M.; Agudelo-Zambrano, W.-M.; Montes-Vides, L.-A. Estimation of density and fracture orientation in HTI media through azimuthal analysis of P-waves. CT F-Cienc. Tecnol. y Futuro 2013, 5, 5–18. [Google Scholar] [CrossRef]
- Shahraini, A.; Jakobsen, M.; Ali, A. Non linear Bayesian inversion of seismic AVAZ and production data with respect to the fracture aperture and density. In Proceedings of the 11th International Congress of the Brazilian Geophysical Society & EXPOGEF, Salvador, Bahia, Brazil, 24–28 August 2009. [Google Scholar]
- Mahmoudian, F.; Margrave, G.F.; Wong, J.; Henley, D.C. Fracture orientation and intensity from AVAz inversion. A physical modeling study. In Proceedings of the 83rd Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 22–27 September 2013. [Google Scholar]
- Shulin, P.; Ke, Y.; Hai-Qiang, L.; José, B.; Ziyu, Q. Adaptive step-size fast iterative shrinkage-thresholding algorithm and sparse-spike deconvolution. Comput. Geosci. 2020, 134, 104343. [Google Scholar]
- Shulin, P.; Ke, Y.; Hai-Qiang, L.; Ziyu, Q. A Bregman adaptive sparse-spike deconvolution method in the frequency domain. Appl. Geophys. 2019, 16, 463–472. [Google Scholar]
- Shulin, P.; Ke, Y.; Hai-Qiang, L.; José, B.; Ziyu, Q. A Sparse Spike Deconvolution Algorithm Based on a Recurrent Neural Network and the Iterative Shrinkage-Thresholding Algorithm. Energies 2020, 13, 3074. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Sayers, C.M.; Kachanov, M. Microcrack-induced elastic wave anisotropy of brittle rocks. J. Geophys. Res. 1995, 100, 4149–4156. [Google Scholar] [CrossRef]
- Thomsen, L. Weak elastic anisotropy. Geophysics 1986, 51, 1954–1966. [Google Scholar] [CrossRef]
- Pšencík, I.; Martins, J.L. Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media. Studia Geophys. Geod. 2001, 45, 176–199. [Google Scholar] [CrossRef]
- Worthington, M.H. Interpreting seismic anisotropy in fractured reservoirs. First Break 2008, 26, 57–63. [Google Scholar] [CrossRef]
- Backus, G.E. Long-wave elastic anisotropy produced by horizontal layering. J. Geophys. Res. 1962, 67, 4427–4440. [Google Scholar] [CrossRef]
- Buland, A.; Omre, H. Bayesian linearized AVO inversion. Geophysics 2003, 68, 185–198. [Google Scholar] [CrossRef]
- Birch, F. The velocity of compressional waves in rocks to 10 kilobars. J. Geophys. Res. 1961, 66, 2199–2224. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Z.; Pan, S.; Li, J. Seismic AVOA Inversion for Weak Anisotropy Parameters and Fracture Density in a Monoclinic Medium. Appl. Sci. 2020, 10, 5136. https://doi.org/10.3390/app10155136
Ge Z, Pan S, Li J. Seismic AVOA Inversion for Weak Anisotropy Parameters and Fracture Density in a Monoclinic Medium. Applied Sciences. 2020; 10(15):5136. https://doi.org/10.3390/app10155136
Chicago/Turabian StyleGe, Zijian, Shulin Pan, and Jingye Li. 2020. "Seismic AVOA Inversion for Weak Anisotropy Parameters and Fracture Density in a Monoclinic Medium" Applied Sciences 10, no. 15: 5136. https://doi.org/10.3390/app10155136
APA StyleGe, Z., Pan, S., & Li, J. (2020). Seismic AVOA Inversion for Weak Anisotropy Parameters and Fracture Density in a Monoclinic Medium. Applied Sciences, 10(15), 5136. https://doi.org/10.3390/app10155136




