Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique
Abstract
1. Introduction
1.1. CPU Scheduling
1.2. Clustering Technique
| Algorithm 1 K-Means | |
| Input | -Dataset -number of clusters |
| Output | -K clusters |
| Step-1: | -Initialize K centers of the cluster |
| Step-2: | -Repeat -Calculate the mean of all the objects belonging to that cluster where is the mean of cluster k and Nk is the number of points belonging to that cluster -Assign objects to the closest cluster centroid -Update cluster centroids based on the assignment -Until centroids do not change |
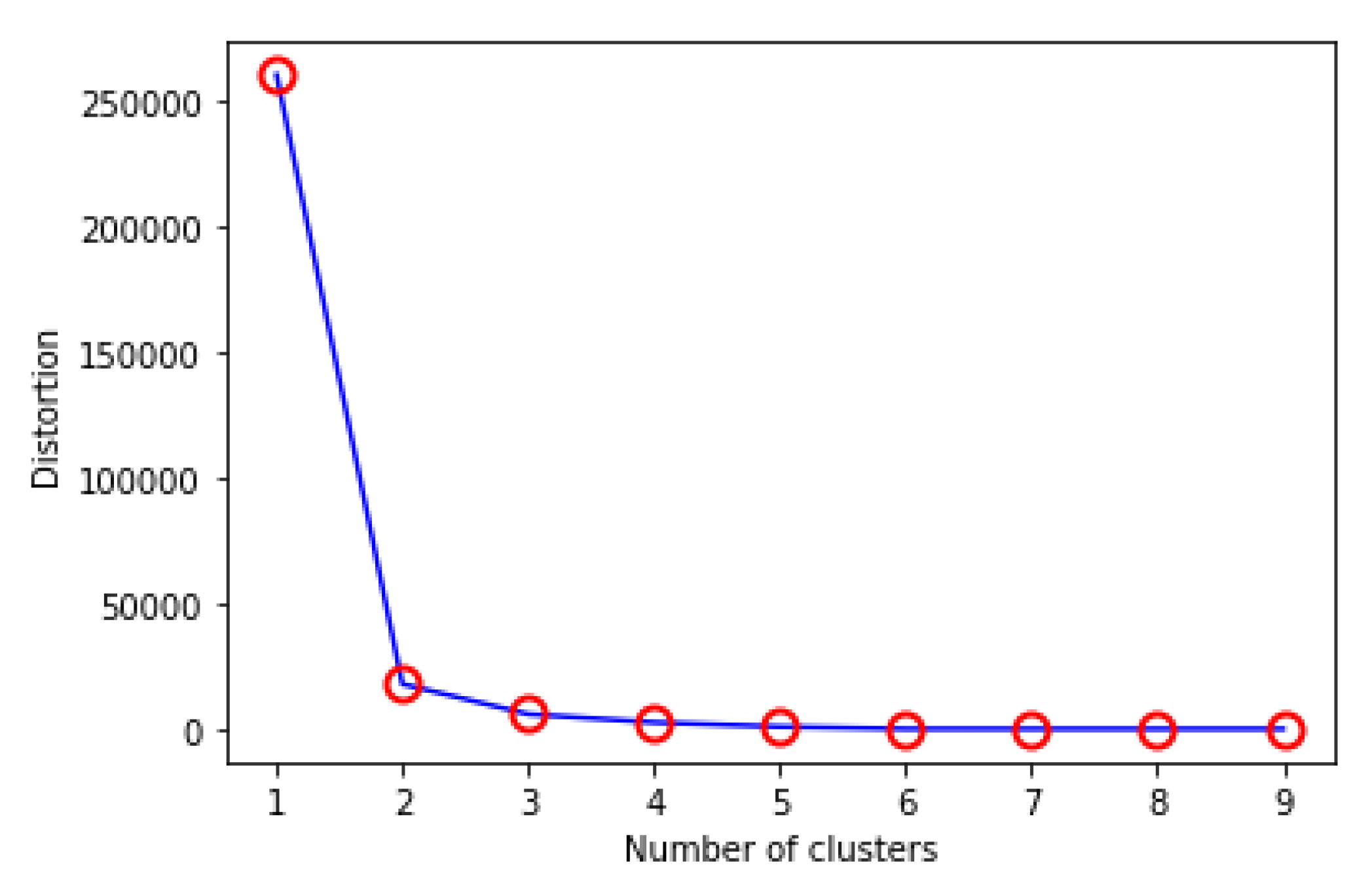
- Compute clustering algorithm for different values of k. For instance, by varying k from 1 to 10 clusters.
- For each k, calculate total Within-cluster Sum of Square (WSS).
- Plot the curve of WSS according to the value of k.
- The location of a knee in the curve indicates the appropriate number of clusters.
2. Related Works
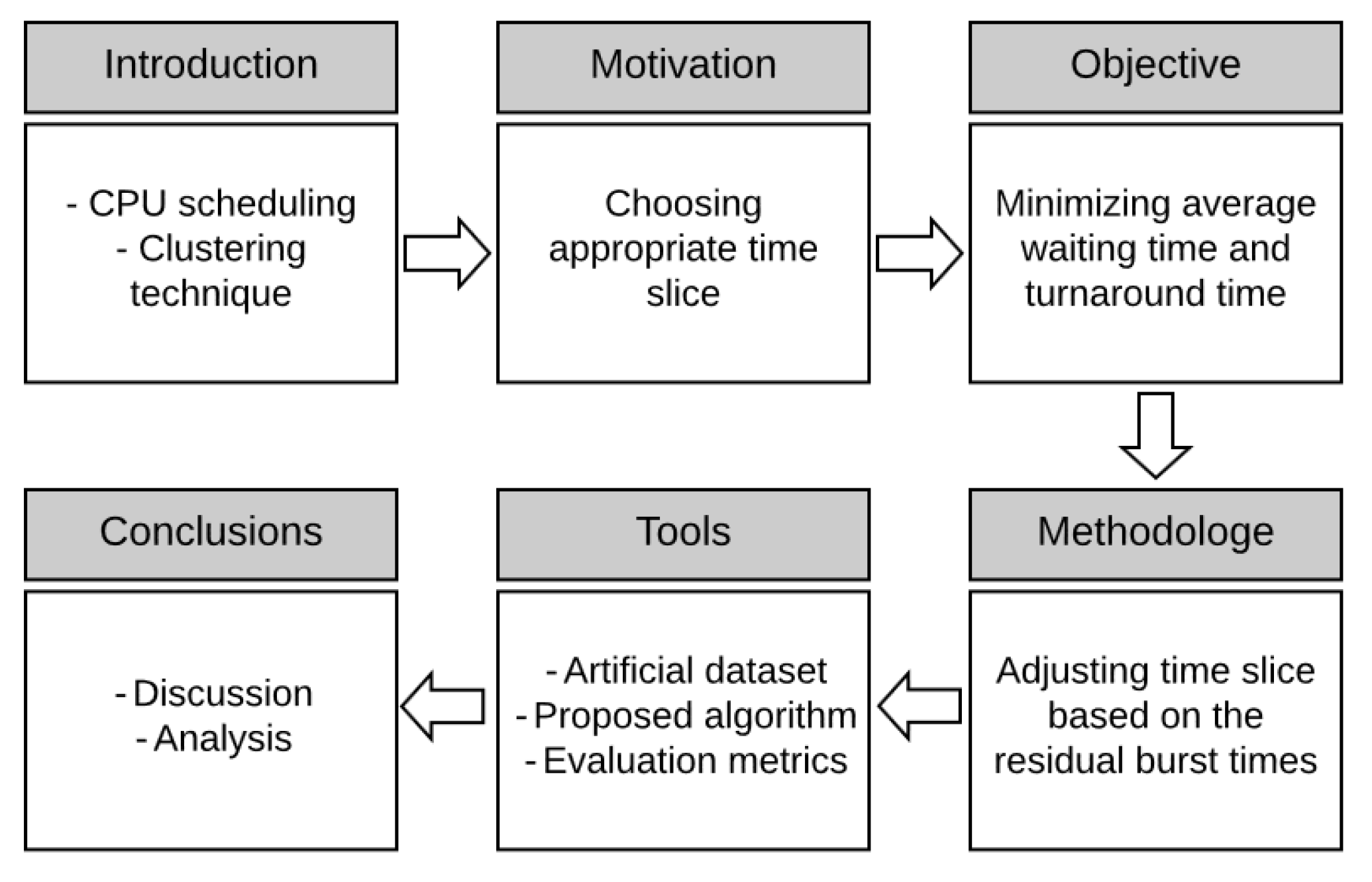
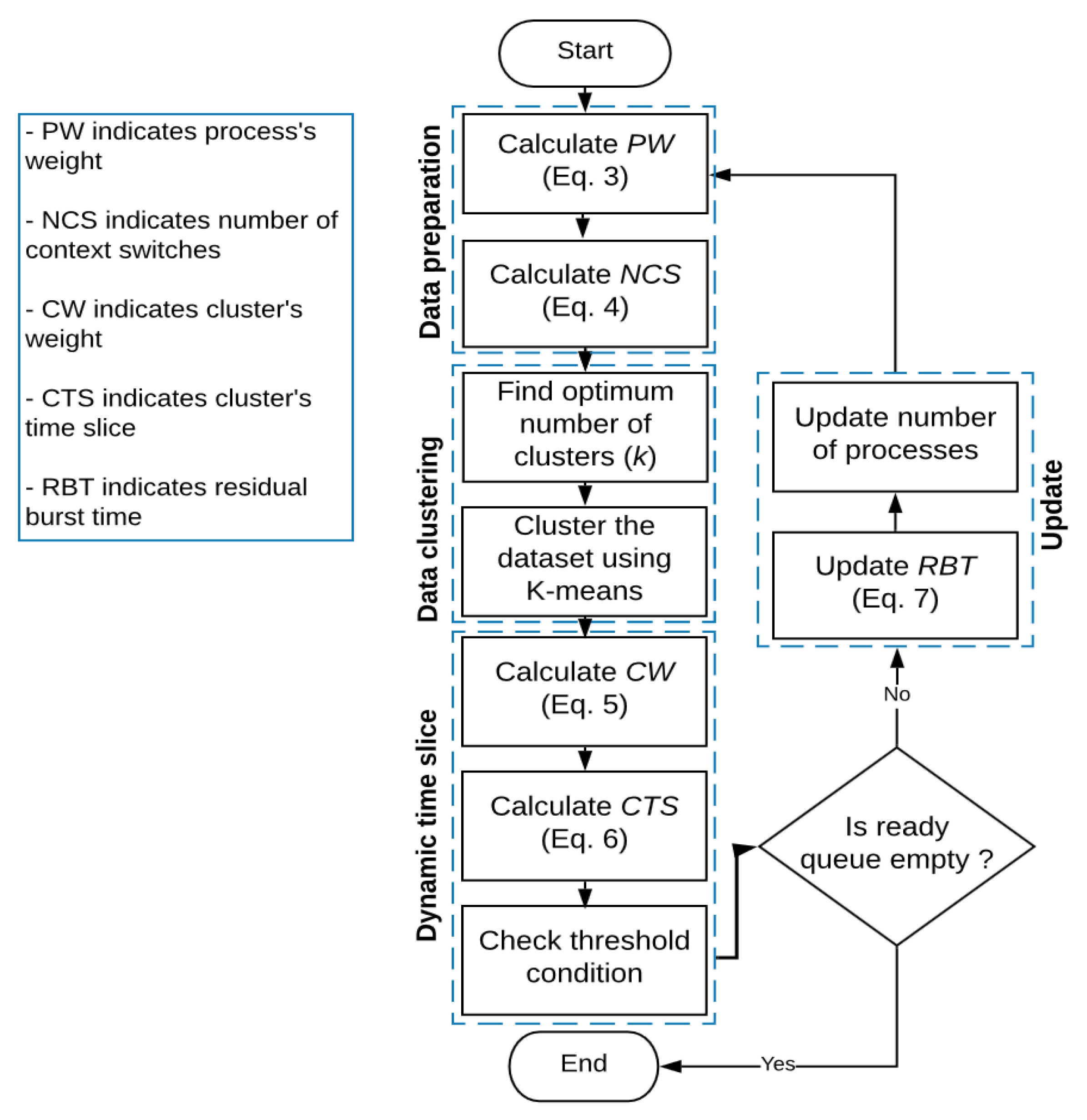
3. The Proposed Algorithm
3.1. Data Preparation
3.2. Data Clustering
3.3. Dynamic Time Slice Implementation
3.4. Illustrative Examples
3.4.1. Example 1
3.4.2. Example 2

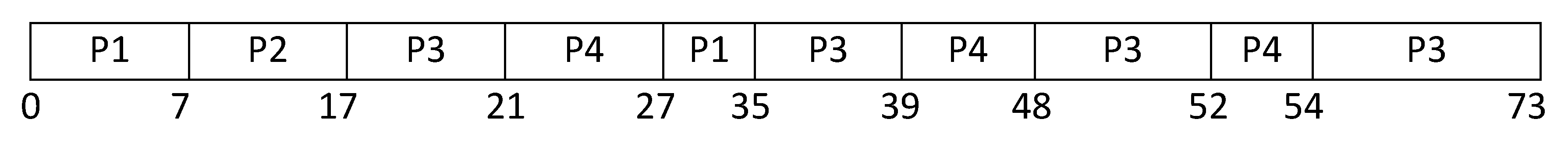
4. Experimental Implementation
4.1. Benchmark Datasets
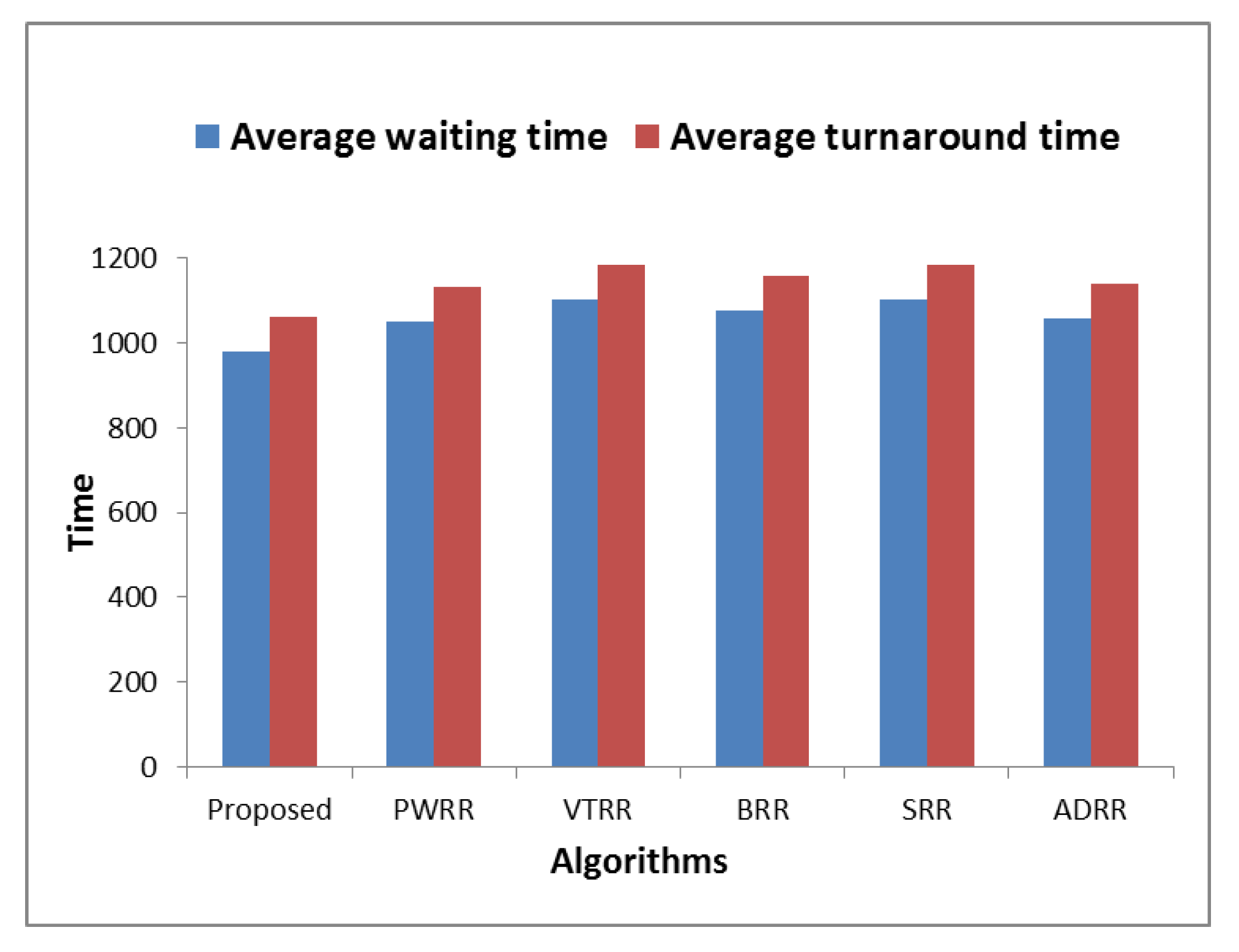
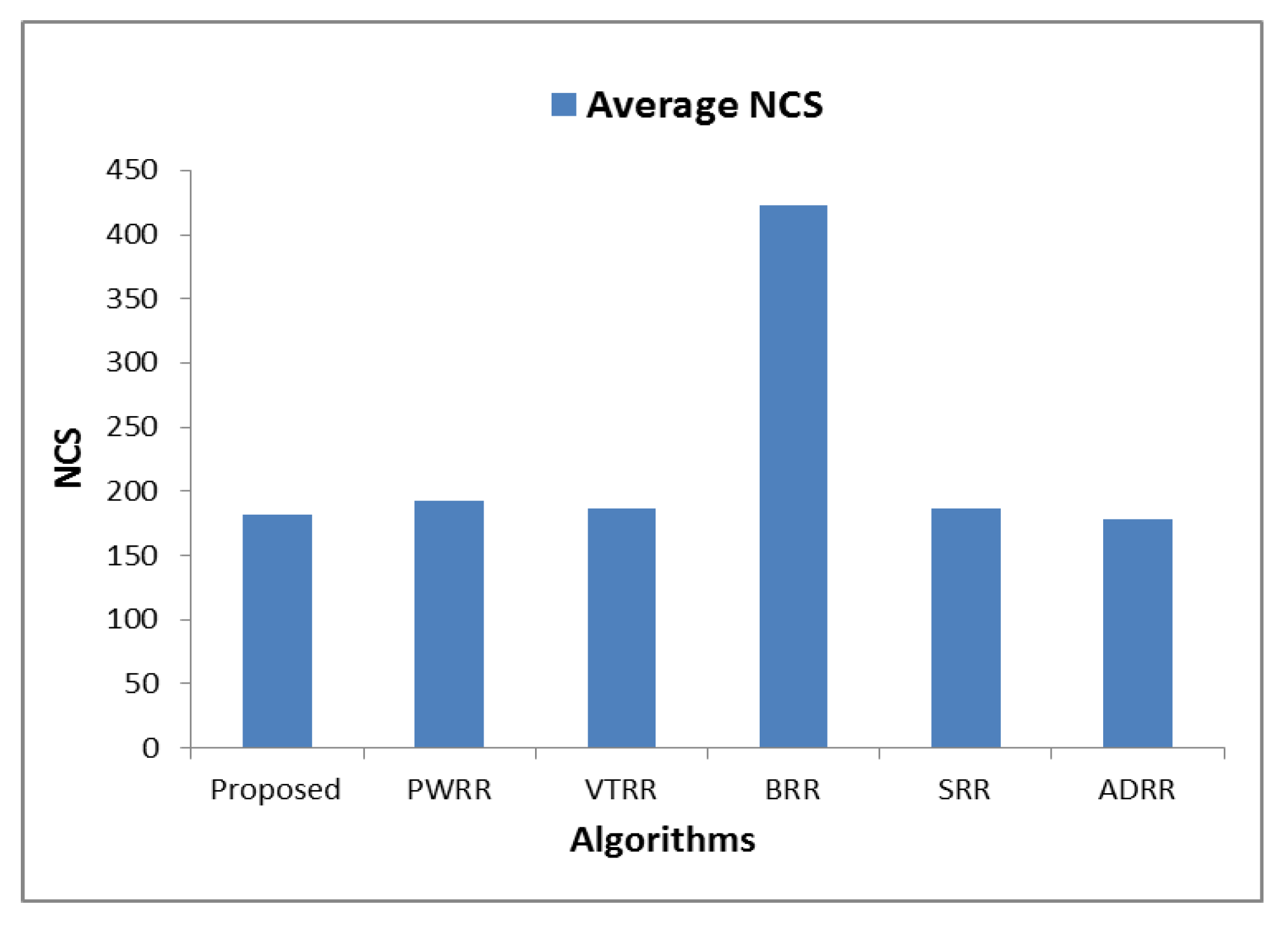
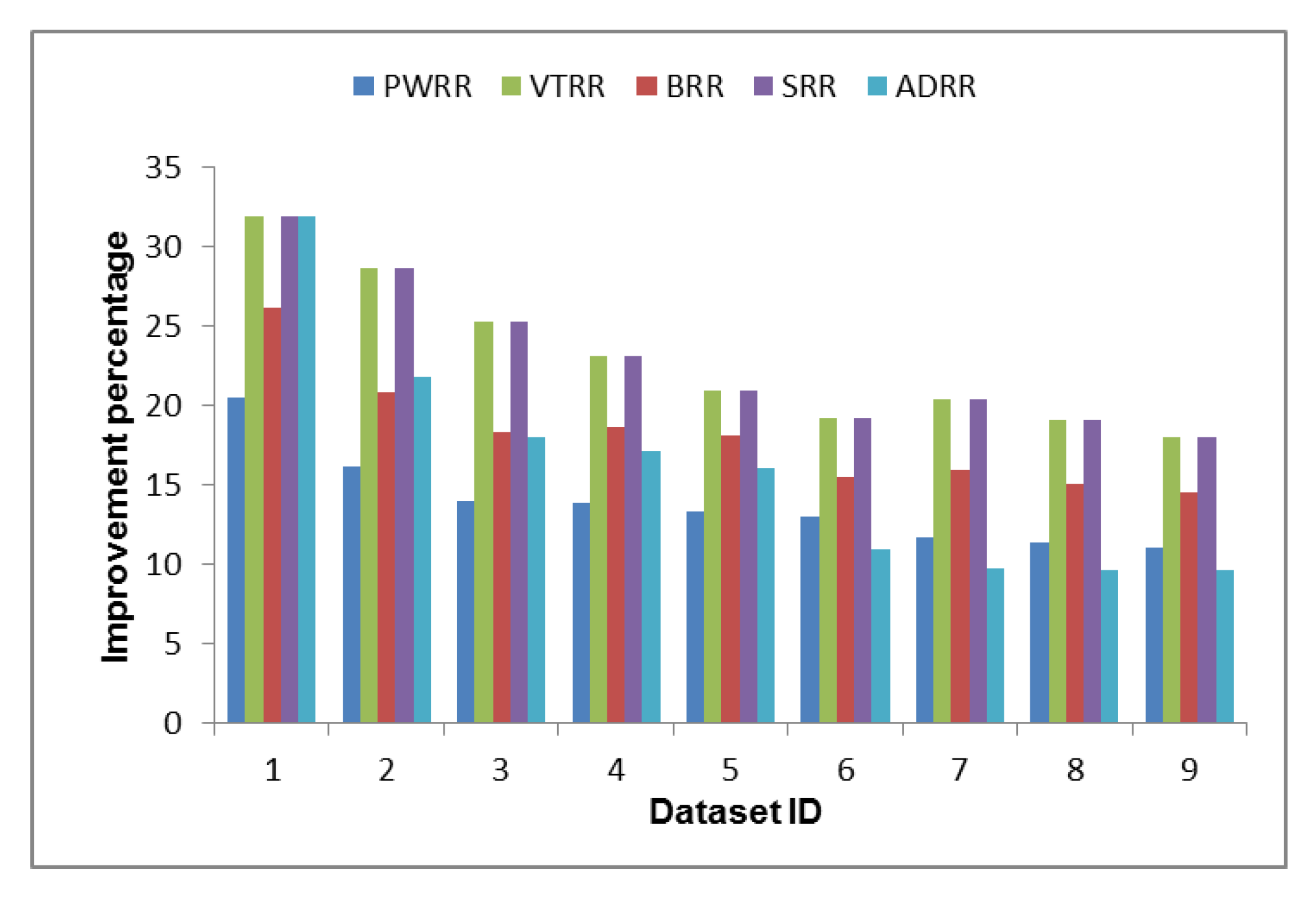
4.2. Performance Evaluation
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Dataset | Proposed | PWRR | VTRR | BRR | SRR | ADRR |
|---|---|---|---|---|---|---|
| 1 | 0.04 | 0.01 | 0.01 | 0.017 | 0.008 | 0.01 |
| 2 | 0.042 | 0.01 | 0.01 | 0.018 | 0.008 | 0.01 |
| 3 | 0.042 | 0.012 | 0.011 | 0.018 | 0.009 | 0.011 |
| 4 | 0.046 | 0.02 | 0.021 | 0.022 | 0.01 | 0.02 |
| 5 | 0.048 | 0.02 | 0.021 | 0.023 | 0.011 | 0.02 |
| 6 | 0.05 | 0.021 | 0.022 | 0.023 | 0.011 | 0.021 |
| 7 | 0.05 | 0.02 | 0.022 | 0.025 | 0.012 | 0.022 |
| 8 | 0.06 | 0.024 | 0.024 | 0.027 | 0.013 | 0.024 |
| 9 | 0.062 | 0.026 | 0.025 | 0.027 | 0.013 | 0.025 |
| Dataset | Proposed | PWRR | VTRR | BRR | SRR | ADRR | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | |
| 1 | 398.41 | 538.61 | 124 | 450.85 | 591.05 | 141 | 485.90 | 626.10 | 124 | 467.60 | 607.80 | 306 | 485.90 | 626.10 | 124 | 485.9 | 626.1 | 124 |
| 2 | 552.37 | 660.44 | 140 | 605.22 | 713.28 | 154 | 653.27 | 761.33 | 144 | 622.20 | 730.27 | 341 | 653.27 | 761.33 | 144 | 625.933 | 734 | 139 |
| 3 | 704.30 | 795.40 | 156 | 760.63 | 851.73 | 169 | 812.35 | 903.45 | 160 | 779.50 | 870.60 | 371 | 812.35 | 903.45 | 160 | 778.3 | 869.4 | 154 |
| 4 | 852.07 | 932.59 | 171 | 918.54 | 999.06 | 182 | 968.24 | 1048.76 | 175 | 943.52 | 1024.04 | 401 | 968.24 | 1048.76 | 175 | 935.36 | 1015.88 | 169 |
| 5 | 1004.37 | 1077.63 | 185 | 1078.26 | 1151.53 | 195 | 1125.67 | 1198.93 | 190 | 1107.80 | 1181.07 | 430 | 1125.67 | 1198.93 | 190 | 1094.77 | 1168.03 | 184 |
| 6 | 1154.23 | 1222.00 | 199 | 1236.42 | 1304.20 | 210 | 1280.57 | 1348.34 | 205 | 1254.31 | 1322.09 | 455 | 1280.57 | 1348.34 | 205 | 1222.97 | 1290.74 | 194 |
| 7 | 1275.34 | 1338.61 | 210 | 1356.38 | 1419.65 | 220 | 1423.53 | 1486.80 | 219 | 1388.58 | 1451.85 | 479 | 1423.53 | 1486.80 | 219 | 1341.85 | 1405.13 | 204 |
| 8 | 1383.72 | 1443.23 | 221 | 1468.75 | 1528.26 | 230 | 1533.09 | 1592.60 | 229 | 1498.91 | 1558.42 | 499 | 1533.09 | 1592.60 | 229 | 1454.76 | 1514.27 | 214 |
| 9 | 1487.44 | 1543.74 | 228 | 1575.99 | 1632.29 | 238 | 1637.48 | 1693.78 | 239 | 1605.92 | 1662.22 | 519 | 1637.48 | 1693.78 | 239 | 1563.62 | 1619.92 | 224 |
| Average | 979.14 | 1061.36 | 181.56 | 1050.11 | 1132.34 | 193.22 | 1102.23 | 1184.45 | 187.22 | 1074.26 | 1156.48 | 422.33 | 1102.23 | 1184.45 | 187.22 | 1055.94 | 1138.16 | 178.44 |
| Improvement% | 6.76 | 6.27 | 5.87 | 11.17 | 10.39 | 2.85 | 8.85 | 8.23 | 56.93 | 11.17 | 10.39 | 2.85 | 7.27 | 6.75 | −1.74 | |||
| PWRR | VTRR | BRR | SRR | ADRR | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | WT | TT | NCS | |
| 1 | 11.63 | 8.87 | 12.06 | 18.01 | 13.97 | 0.00 | 14.80 | 11.38 | 59.48 | 18.01 | 13.97 | 0.00 | 18.01 | 13.97 | 0.00 |
| 2 | 8.73 | 7.41 | 9.09 | 15.45 | 13.25 | 2.78 | 11.22 | 9.56 | 58.94 | 15.45 | 13.25 | 2.78 | 11.75 | 10.02 | −0.72 |
| 3 | 7.41 | 6.61 | 7.69 | 13.30 | 11.96 | 2.50 | 9.65 | 8.64 | 57.95 | 13.30 | 11.96 | 2.50 | 9.51 | 8.51 | −1.30 |
| 4 | 7.24 | 6.65 | 6.04 | 12.00 | 11.08 | 2.29 | 9.69 | 8.93 | 57.36 | 12.00 | 11.08 | 2.29 | 8.90 | 8.20 | −1.18 |
| 5 | 6.85 | 6.42 | 5.13 | 10.78 | 10.12 | 2.63 | 9.34 | 8.76 | 56.98 | 10.78 | 10.12 | 2.63 | 8.26 | 7.74 | −0.54 |
| 6 | 6.65 | 6.30 | 5.24 | 9.87 | 9.37 | 2.93 | 7.98 | 7.57 | 56.26 | 9.87 | 9.37 | 2.93 | 5.62 | 5.33 | −2.58 |
| 7 | 5.97 | 5.71 | 4.55 | 10.41 | 9.97 | 4.11 | 8.16 | 7.80 | 56.16 | 10.41 | 9.97 | 4.11 | 4.96 | 4.73 | −2.94 |
| 8 | 5.79 | 5.56 | 3.91 | 9.74 | 9.38 | 3.49 | 7.68 | 7.39 | 55.71 | 9.74 | 9.38 | 3.49 | 4.88 | 4.69 | −3.27 |
| 9 | 5.62 | 5.42 | 4.20 | 9.16 | 8.86 | 4.60 | 7.38 | 7.13 | 56.07 | 9.16 | 8.86 | 4.60 | 4.87 | 4.70 | −1.79 |
References
- Chandiramani, K.; Verma, R.; Sivagami, M. A Modified Priority Preemptive Algorithm for CPU Scheduling. Procedia Comput. Sci. 2019, 165, 363–369. [Google Scholar] [CrossRef]
- Rajput, I.S.; Gupta, D. A Priority based Round Robin CPU Scheduling Algorithm for Real Time Systems. J. Adv. Eng. Technol. 2012, 1, 1–11. [Google Scholar]
- Reddy, M.R.; Ganesh, V.; Lakshmi, S.; Sireesha, Y. Comparative Analysis of CPU Scheduling Algorithms and Their Optimal Solutions. In Proceedings of the 2019 3rd International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 27–29 March 2019; pp. 255–260. [Google Scholar] [CrossRef]
- Silberschatz, A.; Galvin, P.B.; Gagne, G. Operating System Concepts, 10th ed.; Wiley Publ.: Hoboken, NJ, USA, 2018. [Google Scholar]
- Sunil, J.G.; Anisha Gnana, V.T.; Karthija, V. Fundamentals of Operating Systems Concepts; Lambert Academic Publications: Saarbrucken, Germany, 2018. [Google Scholar]
- Silberschatz, A.; Gagne, G.B.; Galvin, P. Operating Systems Concepts, 9th ed.; Wiley Publ.: Hoboken, NJ, USA, 2012. [Google Scholar]
- McGuire, C.; Lee, J. The Adaptive80 Round Robin Scheduling Algorithm. Trans. Eng. Technol. 2015, 243–258. [Google Scholar]
- Wilmshurst, T. Designing Embedded Systems with PIC Microcontrollers; Elsevier BV: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Singh, P.; Pandey, A.; Mekonnen, A. Varying Response Ratio Priority: A Preemptive CPU Scheduling Algorithm (VRRP). J. Comput. Commun. 2015, 3, 40–51. [Google Scholar] [CrossRef][Green Version]
- Farooq, M.U.; Shakoor, A.; Siddique, A.B. An Efficient Dynamic Round Robin algorithm for CPU scheduling. In Proceedings of the 2017 International Conference on Communication, Computing and Digital Systems (C-CODE), Islamabad, Pakistan, 8–9 March 2017; 2017; pp. 244–248. [Google Scholar] [CrossRef]
- Alsulami, A.A.; Abu Al-Haija, Q.; Thanoon, M.I.; Mao, Q. Performance Evaluation of Dynamic Round Robin Algorithms for CPU Scheduling. In Proceedings of the 2019 SoutheastCon, Huntsville, AL, USA, 11–14 April 2019; pp. 1–5. [Google Scholar]
- Singh, A.; Goyal, P.; Batra, S. An optimized round robin scheduling algorithm for CPU scheduling. Int. J. Comput. Sci. Eng. 2010, 2, 2383–2385. [Google Scholar]
- Shafi, U.; Shah, M.; Wahid, A.; Abbasi, K.; Javaid, Q.; Asghar, M.; Haider, M. A Novel Amended Dynamic Round Robin Scheduling Algorithm for Timeshared Systems. Int. Arab. J. Inf. Technol. 2019, 17, 90–98. [Google Scholar] [CrossRef]
- Garrido, J.M. Performance Modeling of Operating Systems Using Object-Oriented Simulation, 1st ed.; Series in Computer Science; Springer US: New York, NY, USA, 2002. [Google Scholar]
- Tajwar, M.M.; Pathan, N.; Hussaini, L.; Abubakar, A. CPU Scheduling with a Round Robin Algorithm Based on an Effective Time Slice. J. Inf. Process. Syst. 2017, 13, 941–950. [Google Scholar] [CrossRef]
- Saidu, I.; Subramaniam, S.; Jaafar, A.; Zukarnain, Z.A. Open Access A load-aware weighted round-robin algorithm for IEEE 802. 16 networks. EURASIP J. Wirel. Commun. Netw. 2014, 1–12. [Google Scholar]
- Mostafa, S.M.; Amano, H. An Adjustable Round Robin Scheduling Algorithm in Interactive Systems. Inf. Eng. Express 2019, 5, 11–18. [Google Scholar]
- Mostafa, S.M.; Rida, S.Z.; Hamad, S.H. Finding Time Quantum of Round Robin CPU Scheduling Algorithm in General Computing Systems Using Integer Programming. Int. J. New Comput. Archit. Appl. 2010, 5, 64–71. [Google Scholar]
- Mostafa, S.M. Proportional Weighted Round Robin: A Proportional Share CPU Scheduler in Time Sharing Systems. Int. J. New Comput. Arch. Appl. 2018, 8, 142–147. [Google Scholar] [CrossRef]
- Lasek, P.; Gryz, J. Density-based clustering with constraints. Comput. Sci. Inf. Syst. 2019, 16, 469–489. [Google Scholar] [CrossRef]
- Lengyel, A.; Botta-Dukát, Z. Silhouette width using generalized mean—A flexible method for assessing clustering efficiency. Ecol. Evol. 2019, 9, 13231–13243. [Google Scholar] [CrossRef] [PubMed]
- Starczewski, A.; Krzyżak, A. Performance Evaluation of the Silhouette Index BT. In Artificial Intelligence and Soft Computing; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9120, pp. 49–58. [Google Scholar]
- Al-Dhaafri, H.; Alosani, M. Closing the strategic planning and implementation gap through excellence in the public sector: Empirical investigation using SEM. Meas. Bus. Excel. 2020, 35–47. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Wu, J. Cluster Analysis and K-means Clustering: An Introduction; Springer Science and Business Media LLC: Berlin, Germany, 2012; pp. 1–16. [Google Scholar]
- Yuan, C.; Yang, H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J. Multidiscip. Sci. J. 2019, 2, 16. [Google Scholar] [CrossRef]
- Guan, C.; Yuen, K.K.F.; Coenen, F. Particle swarm Optimized Density-based Clustering and Classification: Supervised and unsupervised learning approaches. Swarm Evol. Comput. 2019, 44, 876–896. [Google Scholar] [CrossRef]
- Mostafa, S.M.; Amano, H. Effect of clustering data in improving machine learning model accuracy. J. Theor. Appl. Inf. Technol. 2019, 97, 2973–2981. [Google Scholar]
- Kassambara, A. Practical Guide to Cluster Analysis in R: Unsupervised Machine Learning; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2017. [Google Scholar]
- Inyang, U.G.; Obot, O.O.; Ekpenyong, M.E.; Bolanle, A.M. Unsupervised Learning Framework for Customer Requisition and Behavioral Pattern Classification. Mod. Appl. Sci. 2017, 11, 151. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of Internal Clustering Validation Measures. In Proceedings of the 2010 IEEE International Conference on Data Mining, Sydney, Australia, 13–17 December 2010; Institute of Electrical and Electronics Engineers (IEEE): Sydney, Australia; pp. 911–916. [Google Scholar]
- Harwood, A.; Shen, H. Using fundamental electrical theory for varying time quantum uni-processor scheduling. J. Syst. Arch. 2001, 47, 181–192. [Google Scholar] [CrossRef]
- Helmy, T. Burst Round Robin as a Proportional-Share Scheduling Algorithm. Proceedings of The Fourth IEEE-GCC Conference on Towards Techno-Industrial Innovations, Bahrain, Manama, 11–14 November 2007; pp. 424–428. [Google Scholar]
- Datta, L. Efficient Round Robin Scheduling Algorithm with Dynamic Time Slice. Int. J. Educ. Manag. Eng. 2015, 5, 10–19. [Google Scholar] [CrossRef]
- Zouaoui, S.; Boussaid, L.; Mtibaa, A. Improved time quantum length estimation for round robin scheduling algorithm using neural network. Indones. J. Electr. Eng. Inform. 2019, 7, 190–202. [Google Scholar]
- Pandey, A.; Singh, P.; Gebreegziabher, N.H.; Kemal, A. Chronically Evaluated Highest Instantaneous Priority Next: A Novel Algorithm for Processor Scheduling. J. Comput. Commun. 2016, 4, 146–159. [Google Scholar] [CrossRef][Green Version]
- Srinivasu, N.; Balakrishna, A.S.V.; Lakshmi, R.D. An Augmented Dynamic Round Robin CPU. J. Theor. Appl. Inf. Technol. 2015, 76. [Google Scholar]
- El Mougy, S.; Sarhan, S.; Joundy, M. A novel hybrid of Shortest job first and round Robin with dynamic variable quantum time task scheduling technique. J. Cloud Comput. 2017, 6, 1–12. [Google Scholar] [CrossRef]
| Typical Clustering Algorithm | Based on (Category) |
|---|---|
| K-medoids, CLARA, CLARANS, PAM, K-means | Partition |
| Chameleon, ROCK, CURE, BIRCH | Hierarchy |
| MM, FCS, FCM | Fuzzy theory |
| GMM, DBCLASD | Distribution |
| Mean-shift, OPTICS, DBSCAN | Density |
| MST, CLICK | Graph theory |
| CLIQUE, STING | Grid |
| FC | Fractal theory |
| ART, SOM, GMM, COBWEB, | Model |
| Researchers | Year | Technique Name | Technique Type | Based on | Performance Metrics | ||
|---|---|---|---|---|---|---|---|
| WT | TT | NCS | |||||
| Aaron and Hong | 2001 | VTRR | Dynamic | SRR | √ | √ | √ |
| Tarek and Abdelkader | 2007 | BRR | Dynamic | SRR | √ | √ | √ |
| Samih et al. | 2010 | CTQ | Dynamic | SRR | √ | √ | √ |
| Lipika Datta | 2015 | - | Dynamic | SRR and SJF | √ | √ | √ |
| Christoph and Jeonghw | 2015 | Adaptive80 RR | Dynamic | SRR and SJF | √ | √ | √ |
| Samir et al. | 2017 | SRDQ | Dynamic | SRR and SJF | √ | √ | √ |
| Samih | 2018 | PWRR | Dynamic | SRR | √ | √ | √ |
| Samih and Hirofumi | 2019 | ARR | Dynamic based on threshold | SRR | √ | √ | √ |
| Uferah et al. | 2020 | ADRR | Dynamic | SRR and SJF | √ | √ | √ |
| BT | Weight | NCS | |
|---|---|---|---|
| 0 | 109 | 0.077746 | 10 |
| 1 | 150 | 0.10699 | 15 |
| 2 | 3 | 0.00214 | 0 |
| 3 | 50 | 0.035663 | 4 |
| 4 | 4 | 0.03495 | 4 |
| 5 | 49 | 0.03495 | 4 |
| 6 | 409 | 0.291726 | 48 |
| 7 | 490 | 0.349501 | 48 |
| 8 | 47 | 0.033524 | 4 |
| 9 | 46 | 0.03281 | 4 |
| BT | Weight | NCS | y | |
|---|---|---|---|---|
| 0 | 109 | 0.077746 | 10 | 0 |
| 1 | 150 | 0.10699 | 15 | 0 |
| 2 | 3 | 0.00214 | 0 | 0 |
| 3 | 50 | 0.035663 | 4 | 0 |
| 4 | 49 | 0.03495 | 4 | 0 |
| 5 | 49 | 0.03495 | 4 | 0 |
| 6 | 409 | 0.291726 | 48 | 1 |
| 7 | 490 | 0.349501 | 48 | 1 |
| 8 | 47 | 0.033524 | 4 | 0 |
| 9 | 46 | 0.03281 | 4 | 0 |
| Process ID | BT |
|---|---|
| P1 | 15 |
| P2 | 10 |
| P3 | 31 |
| P4 | 17 |
| Round 1 | Round 2 | Round 3 | Round 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Process ID | BT | TS | RBT | TS | RBT | TS | RBT | TS |
| P1 | 15 | 7 | 8 | 12.5 terminates after 8 tu | --- | --- | --- | --- |
| P2 | 10 | 10 terminates | --- | --- | --- | --- | --- | --- |
| P3 | 31 | 4 | 27 | 4 | 23 | 4 | 19 | 19 |
| P4 | 17 | 6 | 11 | 9 | 2 | 50 terminates after 2 tu | --- | --- |
| Dataset ID | Number of Processes | Number of Attributes | Standard Deviation |
|---|---|---|---|
| 1 | 10 | 3 | 160.2615 |
| 2 | 15 | 3 | 83.1789 |
| 3 | 20 | 3 | 123.5103 |
| 4 | 25 | 3 | 112.4794 |
| 5 | 30 | 3 | 103.9525 |
| 6 | 35 | 3 | 97.17821 |
| 7 | 40 | 3 | 91.67769 |
| 8 | 45 | 3 | 87.08785 |
| 9 | 50 | 3 | 83.1789 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mostafa, S.M.; Amano, H. Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique. Appl. Sci. 2020, 10, 5134. https://doi.org/10.3390/app10155134
Mostafa SM, Amano H. Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique. Applied Sciences. 2020; 10(15):5134. https://doi.org/10.3390/app10155134
Chicago/Turabian StyleMostafa, Samih M., and Hirofumi Amano. 2020. "Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique" Applied Sciences 10, no. 15: 5134. https://doi.org/10.3390/app10155134
APA StyleMostafa, S. M., & Amano, H. (2020). Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique. Applied Sciences, 10(15), 5134. https://doi.org/10.3390/app10155134





