Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran
Abstract
1. Introduction
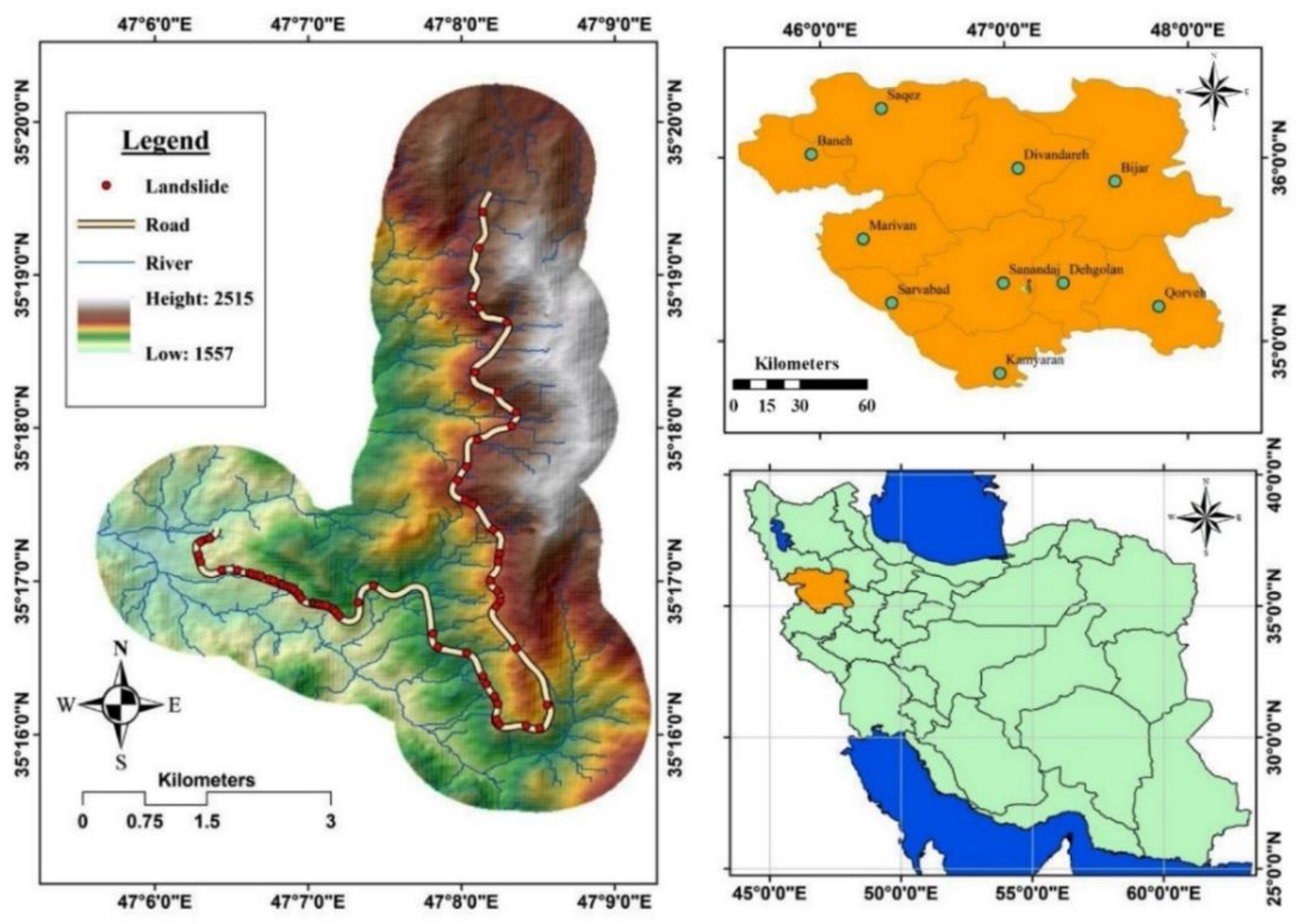
2. Study Area
3. Data Acquisition
3.1. Landslide Inventory Map
3.2. Landslide Conditioning Factors
3.2.1. Slope Angle
3.2.2. Slope Aspect
3.2.3. Elevation
3.2.4. Distance to Road
3.2.5. Topographic Wetness Index
3.2.6. Normalized Difference Vegetation Index
3.2.7. Lithology
3.2.8. Land Cover/Land Use
3.2.9. Rainfall
3.2.10. Distance to Fault
3.2.11. Plan Curvature
3.2.12. Profile Curvature
3.2.13. Slope Length-Angle Index (LS)
3.2.14. Solar Radiation
3.2.15. Stream Power Index (SPI)
3.2.16. Distance to the River
3.2.17. River Density
3.2.18. Fault Density
4. Machine Learning Algorithms
4.1. Support Vector Machine
4.2. Bayesian Logistic Regression
- (1)
- Determine the prior probability of parameters
- (2)
- Determine the likelihood function for data
- (3)
- Create a posterior distribution function for parameters
4.3. Alternating Decision Tree
- 1-
- Initialization
- 2-
- Pre-adjustment
- -
- Create a C group of rules by the weak algorithm using the weight-related to each training sample .
- -
- For each main precondition and each condition calculate:
- -
- Select with minima and run and through the adding rule so that the precondition and condition are equal to, respectively, and . Then predict the two prediction amounts:
- -
- Establish and by adding and
- -
- Update the weights based on the following equation for each repeat:
- 3-
- Output
4.4. Multicollinearity Tests
4.5. Selecting the Most Important Conditioning Factors by IGR
4.6. Validation and Comparison of the Models
5. Results and Analysis
5.1. Correlation between the Conditioning Factors
5.2. The Most Important Landslide Conditioning Factors in the Study Area
5.3. Landslide Modeling and Evaluation Process
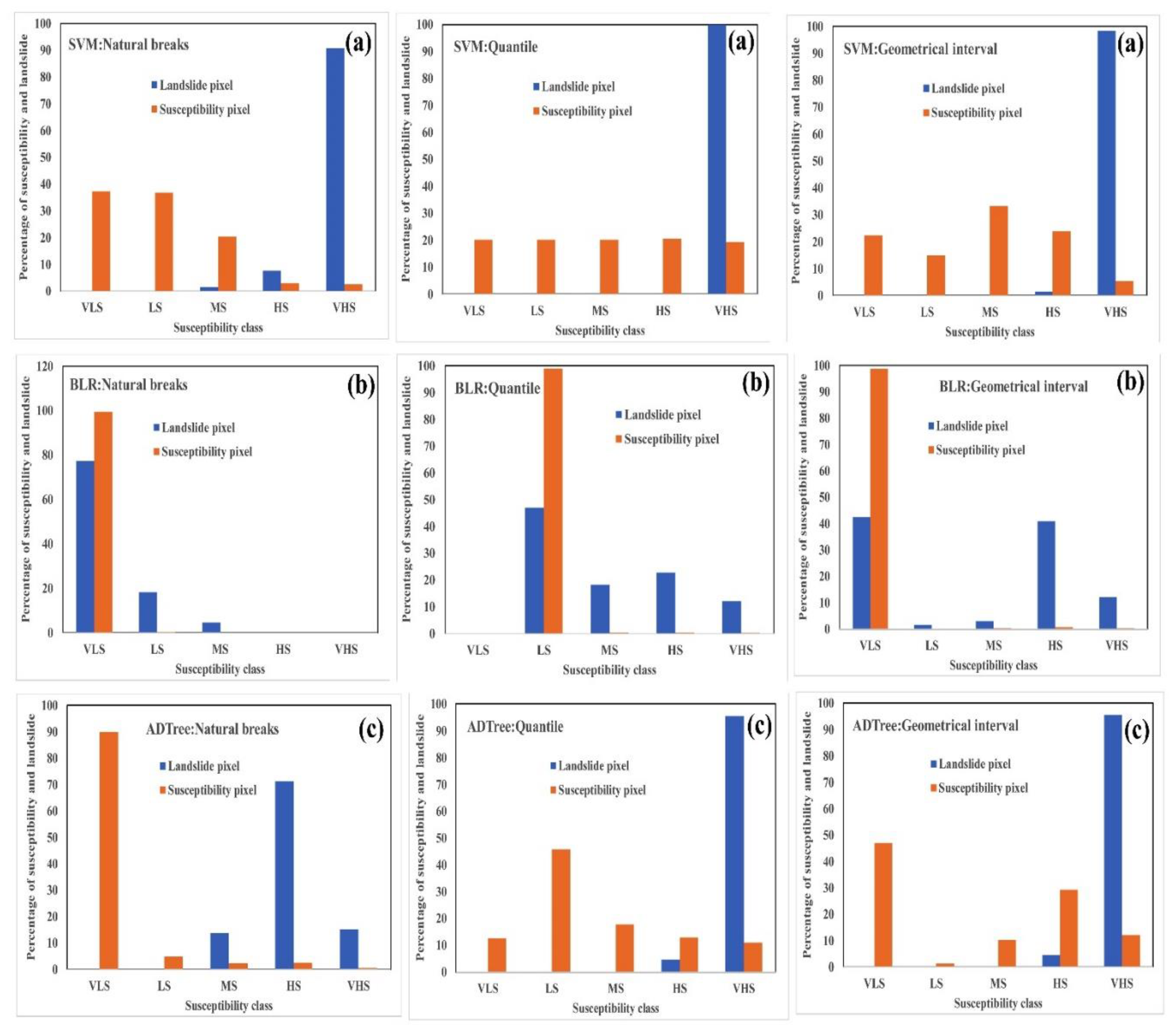
5.4. Development of Landslide Susceptibility Maps
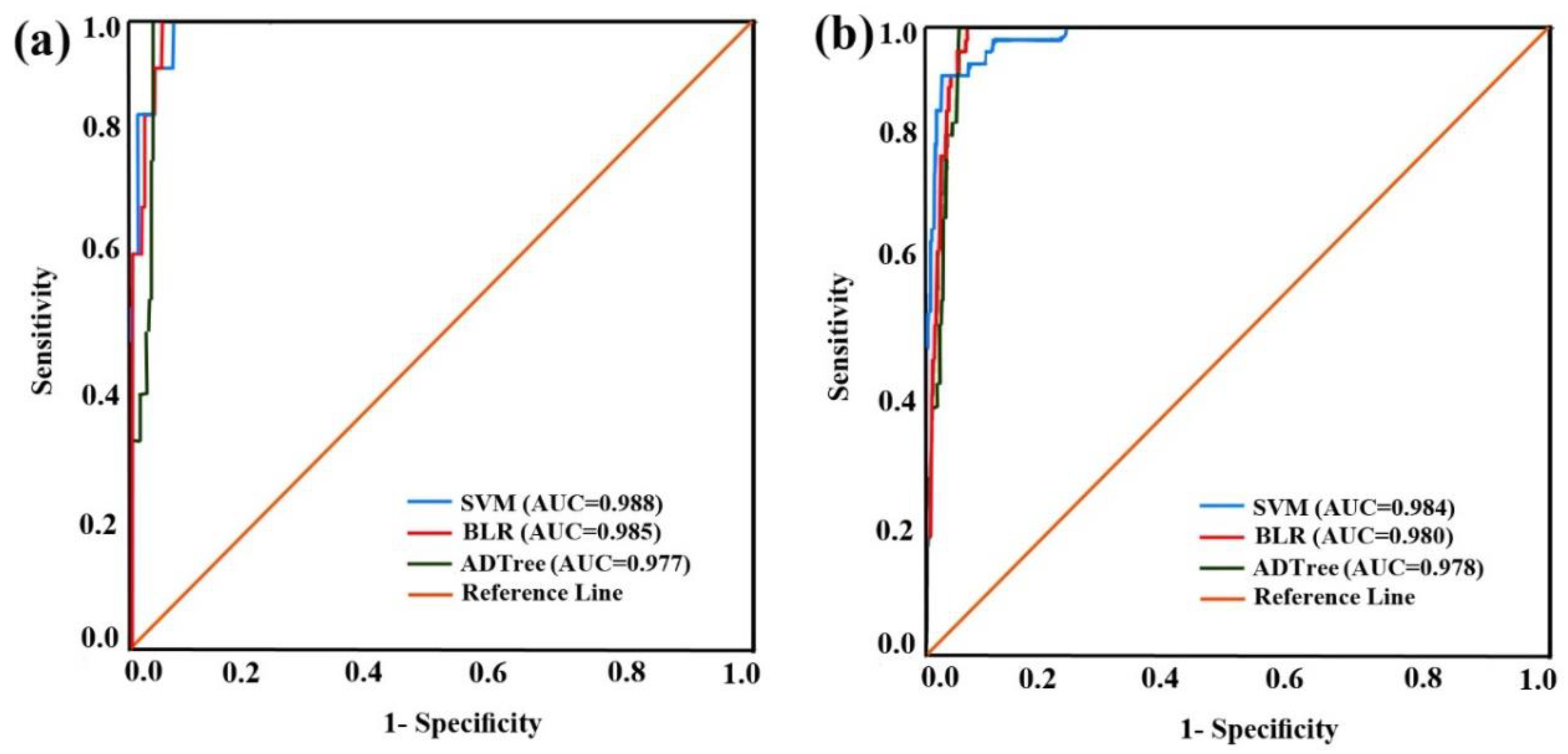
5.5. Evaluation of Landslide Susceptibility Maps
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Varnes, D.J. The international association of engineering geology commission on landslides and other mass movements on slopes. 1984. Landslide hazard zonation: A review of principles and practice. Nat. Hazards 1984, 3, 63–79. [Google Scholar]
- Nadim, F.; Kjekstad, O.; Peduzzi, P.; Herold, C.; Jaedicke, C. Global landslide and avalanche hotspots. Landslides 2006, 3, 159–173. [Google Scholar] [CrossRef]
- Assilzadeh, H.; Levy, J.K.; Wang, X. Landslide catastrophes and disaster risk reduction: A gis framework for landslide prevention and management. Remote Sens. 2010, 2, 2259–2273. [Google Scholar] [CrossRef]
- Rezaei, S.; Shooshpasha, I.; Rezaei, H. Reconstruction of landslide model from ert, geotechnical, and field data, nargeschal landslide, iran. Bull. Eng. Geol. Environ. 2019, 78, 3223–3237. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Tien Bui, D. Landslide susceptibility evaluation and management using different machine learning methods in the gallicash river watershed, iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in gis: Safarood basin, iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Kornejady, A.; Pourghasemi, H.R.; Afzali, S.F. Presentation of rffr new ensemble model for landslide susceptibility assessment in iran. In Landslides: Theory, Practice and Modelling; Springer: Berlin/Heidelberg, Germany, 2019; pp. 123–143. [Google Scholar]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C.; Mohammadi, M.; Moradi, H.R. Application of weights-of-evidence and certainty factor models and their comparison in landslide susceptibility mapping at haraz watershed, iran. Arab. J. Geosci. 2013, 6, 2351–2365. [Google Scholar] [CrossRef]
- Ehteshami-Moinabadi, M. On the historical landslide fatalities in the iranian plateau. In NHAQ97; Geographical Organization of Iran: Tehran, Iran, 2019. [Google Scholar]
- Aghda, S.F.; Bagheri, V.; Razifard, M. Landslide susceptibility mapping using fuzzy logic system and its influences on mainlines in lashgarak region, tehran, iran. Geotech. Geol. Eng. 2018, 36, 915–937. [Google Scholar]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Party, I.L.W. Iranian Landslides List; Forest, Rangeland and Watershed Association: Tehran, Iran, 2007; Volume 60. [Google Scholar]
- Duncan, C.; Norman, I. Stabilization of Rock Slopes; Landslides investigations and mitigation, special report 247; Transportation Research Board, National Research Council: Washington, DC, USA, 1996; pp. 474–506. [Google Scholar]
- Wang, G.; Lei, X.; Chen, W.; Shahabi, H.; Shirzadi, A. Hybrid computational intelligence methods for landslide susceptibility mapping. Symmetry 2020, 12, 325. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J. Shallow landslide susceptibility mapping: A comparison between logistic model tree, logistic regression, naïve bayes tree, artificial neural network, and support vector machine algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef] [PubMed]
- Nhu, V.H.; Mohammadi, A.; Shahabi, H.; Ahmad, B.B.; Al-Ansari, N.; Shirzadi, A.; Clague, J.J.; Jaafari, A.; Chen, W.; Nguyen, H. Landslide Susceptibility Mapping Using Machine Learning Algorithms and Remote Sensing Data in a Tropical Environment. Int. J. Environ. Res. Public Health 2020, 17, 4933. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Anbalagan, R. Landslide susceptibility mapping using analytical hierarchy process (ahp) in tehri reservoir rim region, uttarakhand. J. Geol. Soc. India 2016, 87, 271–286. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Rahimi, S.; Beglou, M.J. Promethee ii and fuzzy ahp: An enhanced gis-based landslide susceptibility mapping. Nat. Hazards 2014, 73, 77–95. [Google Scholar] [CrossRef]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Ahmad, B.B. Rock fall susceptibility assessment along a mountainous road: An evaluation of bivariate statistic, analytical hierarchy process and frequency ratio. Environ. Earth Sci. 2017, 76, 152. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and gis-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the central zab basin, iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at central zab basin, iran: A comparison between analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.B.; Panahi, M.; Hong, H. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in cameron highlands, malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Hong, H.; Shahabi, H.; Shirzadi, A.; Chen, W.; Chapi, K.; Ahmad, B.B.; Roodposhti, M.S.; Hesar, A.Y.; Tian, Y.; Bui, D.T. Landslide susceptibility assessment at the wuning area, china: A comparison between multi-criteria decision making, bivariate statistical and machine learning methods. Nat. Hazards 2019, 96, 173–212. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Peng, J.; Shahabi, H.; Hong, H.; Bui, D.T.; Duan, Z.; Li, S.; Zhu, A.-X. Gis-based landslide susceptibility evaluation using a novel hybrid integration approach of bivariate statistical based random forest method. Catena 2018, 164, 135–149. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using gis-based statistical models and remote sensing data in tropical environment. Sci. Rep. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Rahmati, O.; Falah, F.; Shojaei, S.; Al-Ansari, N.; Shahabi, H.; Shirzadi, A.; Górski, K.; Nguyen, H.; Ahmad, B.B. Mapping of groundwater spring potential in karst aquifer system using novel ensemble bivariate and multivariate models. Water 2020, 12, 985. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B.B. Modelling gully-erosion susceptibility in a semi-arid region, iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
- Shirzadi, A.; Saro, L.; Joo, O.H.; Chapi, K. A gis-based logistic regression model in rock-fall susceptibility mapping along a mountainous road: Salavat abad case study, kurdistan, iran. Nat. Hazards 2012, 64, 1639–1656. [Google Scholar] [CrossRef]
- Pack, R.T.; Tarboton, D.; Goodwin, C. Sinmap 2.0-a Stability Index Approach to Terrain Stability Hazard Mapping, User’s Manual; U.S. Forest Service, Rocky Mountain Research Station: Logan, UT, USA, 1999. [Google Scholar]
- Dietrich, W.E.; de Asua, R.R.; Coyle, J.; Orr, B.; Trso, M. A validation study of the shallow slope stability model, shalstab, in forested lands of northern california. Stillwater Ecosyst. Watershed Riverine Sci. Berkeley CA 1998, 11, 16–60. [Google Scholar]
- Cohen, D.; Schwarz, M. Effects of tree roots on shallow landslides distribution and frequency in the european alps using a new physically-based discrete element model. EGUGA 2017, 19, 6154. [Google Scholar]
- Cislaghi, A.; Bischetti, G.B. Source areas, connectivity, and delivery rate of sediments in mountainous-forested hillslopes: A probabilistic approach. Sci. Total Environ. 2019, 652, 1168–1186. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.; Parkin, G.; O’Connell, P.E. Shetran: Distributed river basin flow and transport modeling system. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. Trigrs—A fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. US Geol. Surv. Open File Rep. 2002, 424, 38. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using gis-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Moradi, H.; Aghda, S.F. Landslide susceptibility mapping by binary logistic regression, analytical hierarchy process, and statistical index models and assessment of their performances. Nat. Hazards 2013, 69, 749–779. [Google Scholar] [CrossRef]
- Thiery, Y.; Malet, J.-P.; Sterlacchini, S.; Puissant, A.; Maquaire, O. Landslide susceptibility assessment by bivariate methods at large scales: Application to a complex mountainous environment. Geomorphology 2007, 92, 38–59. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in lianhua county (china): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Shirzadi, A.; Shahabi, H.; Chapi, K.; Bui, D.T.; Pham, B.T.; Shahedi, K.; Ahmad, B.B. A comparative study between popular statistical and machine learning methods for simulating volume of landslides. Catena 2017, 157, 213–226. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Hong, H.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ann) models: An example of the 2013 minxian (china) mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef]
- Rahmati, O.; Panahi, M.; Ghiasi, S.S.; Deo, R.C.; Tiefenbacher, J.P.; Pradhan, B.; Jahani, A.; Goshtasb, H.; Kornejady, A.; Shahabi, H.; et al. Hybridized neural fuzzy ensembles for dust source modeling and prediction. Atmos. Environ. 2020, 224, 117320. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (china) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Panahi, S.; Li, S.; Jaafari, A.; Ahmad, B.B. Applying population-based evolutionary algorithms and a neuro-fuzzy system for modeling landslide susceptibility. Catena 2019, 172, 212–231. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.P.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Tran, H.T.; Le, T.M.; Van Phong, T.; Khoi, D.K.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modelling using rotation forest ensemble and different base classifiers. Geocarto Int. 2019, 1–25. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.J.; Pham, B.T.; Dou, J.; Asl, D.T.; Ahmad, B.B. New ensemble models for shallow landslide susceptibility modeling in a semi-arid watershed. Forests 2019, 10, 743. [Google Scholar]
- Shahabi, H.; Shirzadi, A.; Ghaderi, K.; Omidvar, E.; Al-Ansari, N.; Clague, J.J.; Geertsema, M.; Khosravi, K.; Amini, A.; Bahrami, S. Flood detection and susceptibility mapping using sentinel-1 remote sensing data and a machine learning approach: Hybrid intelligence of bagging ensemble based on k-nearest neighbor classifier. Remote Sens. 2020, 12, 266. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Shahabi, H.; Shirzadi, A.; Khosravi, K.; Chai, H.; Zhang, S.; Zhang, L.; Ma, J.; Chen, Y. Spatial prediction of landslide susceptibility by combining evidential belief function, logistic regression and logistic model tree. Geocarto Int. 2019, 34, 1177–1201. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Omidavr, E.; Pham, B.T.; Asl, D.T.; Khaledian, H.; Pradhan, B.; Panahi, M. A novel ensemble artificial intelligence approach for gully erosion mapping in a semi-arid watershed (iran). Sensors 2019, 19, 2444. [Google Scholar]
- Pham, B.T.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Asl, D.T.; Ahmad, B.B.; Kim Quoc, N.; Lee, S. Landslide susceptibility assessment by novel hybrid machine learning algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Ahmad, B.B. A hybrid computational intelligence approach to groundwater spring potential mapping. Water 2019, 11, 2013. [Google Scholar]
- Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. Catena 2019, 178, 172–188. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Wang, X.; Ahmad, B.B. Evaluating the usage of tree-based ensemble methods in groundwater spring potential mapping. J. Hydrol. 2020, 583, 124602. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and uneec methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, jiangxi province, china. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using j48 decision tree with adaboost, bagging and rotation forest ensembles in the guangchang area (china). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using reduced error pruning trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Amini, A.; Shahabi, H.; Al-Ansari, N.; Hamidi, S.; Singh, S.K.; Pham, B.T.; Ahmad, B.B.; Ghazvinei, P.T. A hybrid intelligence approach to enhance the prediction accuracy of local scour depth at complex bridge piers. Sustainability 2020, 12, 1063. [Google Scholar]
- Nhu, V.-H.; Janizadeh, S.; Avand, M.; Chen, W.; Farzin, M.; Omidvar, E.; Shirzadi, A.; Shahabi, H.; Clague, J.J.; Jaafari, A. Gis-based gully erosion susceptibility mapping: A comparison of computational ensemble data mining models. Appl. Sci. 2020, 10, 2039. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Chen, W.; Clague, J.J.; Geertsema, M.; Jaafari, A.; Avand, M.; Miraki, S.; Asl, D.T. Shallow landslide susceptibility mapping by random forest base classifier and its ensembles in a semi-arid region of iran. Forests 2020, 11, 421. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of bayesian logistic regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2019, 34, 1427–1457. [Google Scholar] [CrossRef]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat. Resour. Res. 2019, 28, 1239–1258. [Google Scholar] [CrossRef]
- Taheri, K.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Gutiérrez, F.; Khosravi, K. Sinkhole susceptibility mapping: A comparison between bayes-based machine learning algorithms. Land Degrad. Dev. 2019, 30, 730–745. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Panahi, M.; Shahabi, H.; Wang, Y.; Shirzadi, A.; Pirasteh, S.; Alesheikh, A.A.; Khosravi, K.; Panahi, S. Spatial prediction of landslide susceptibility using gis-based data mining techniques of anfis with whale optimization algorithm (woa) and grey wolf optimizer (gwo). Appl. Sci. 2019, 9, 3755. [Google Scholar] [CrossRef]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based naïve bayes, rbf classifier, and rbf network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B. Modeling flood susceptibility using data-driven approaches of naïve bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef]
- Nguyen, P.T.; Tuyen, T.T.; Shirzadi, A.; Pham, B.T.; Shahabi, H.; Omidvar, E.; Amini, A.; Entezami, H.; Prakash, I.; Phong, T.V. Development of a novel hybrid intelligence approach for landslide spatial prediction. Appl. Sci. 2019, 9, 2824. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve bayes tree classifiers for a landslide susceptibility assessment in langao county, china. Geomat. Nat. Hazards Risk. 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Shahabi, H.; Daggupati, P.; Adamowski, J.F.; Melesse, A.M.; Thai Pham, B.; Pourghasemi, H.R.; Mahmoudi, M.; Bahrami, S. Flood spatial modeling in northern iran using remote sensing and gis: A comparison between evidential belief functions and its ensemble with a multivariate logistic regression model. Remote Sens. 2019, 11, 1589. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Xu, C.; Bui, D.T. Spatial prediction of landslide hazard at the yihuang area (china) using two-class kernel logistic regression, alternating decision tree and support vector machines. Catena 2015, 133, 266–281. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I. Landslide susceptibility assessment using bagging ensemble based alternating decision trees, logistic regression and j48 decision trees methods: A comparative study. Geotech. Geol. Eng. 2017, 35, 2597–2611. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel gis based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Fam, P.S.; Tay, L.; Low, H. An overview and comparison on recent landslide susceptibility mapping methods. Disaster Adv. 2019, 12, 46–64. [Google Scholar]
- Samadian, B.; Fakher, A. Proposing a framework to combine geological and geotechnical information for city planning in sanandaj (iran). Eng. Geol. 2016, 209, 1–11. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. Gis-based support vector machine modeling of earthquake-triggered landslide susceptibility in the jianjiang river watershed, china. Geomorphology 2012, 145, 70–80. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Gokceoglu, C. Assessment of landslide susceptibility for a landslide-prone area (north of yenice, nw turkey) by fuzzy approach. Environ. Geol. 2002, 41, 720–730. [Google Scholar]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the revised universal soil loss equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Bui, D.T.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.T.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Ahmad, B.B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar]
- Hong, H.; Liu, J.; Zhu, A.-X.; Shahabi, H.; Pham, B.T.; Chen, W.; Pradhan, B.; Bui, D.T. A novel hybrid integration model using support vector machines and random subspace for weather-triggered landslide susceptibility assessment in the wuning area (china). Environ. Earth Sci. 2017, 76, 652. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Safarrad, T.; Shahabi, H. Drought sensitivity mapping using two one-class support vector machine algorithms. Atmos. Res. 2017, 193, 73–82. [Google Scholar] [CrossRef]
- Das, I.; Stein, A.; Kerle, N.; Dadhwal, V.K. Landslide susceptibility mapping along road corridors in the indian himalayas using bayesian logistic regression models. Geomorphology 2012, 179, 116–125. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Freund, Y.; Mason, L. The Alternating Decision Tree Learning Algorithm; icml: San Francisco, CA, USA, 1999; pp. 124–133. [Google Scholar]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater spring potential mapping using artificial intelligence approach based on kernel logistic regression, random forest, and alternating decision tree models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Pradhan, B.; Chen, W.; Khosravi, K.; Panahi, M.; Bin Ahmad, B.; Saro, L. Land subsidence susceptibility mapping in south korea using machine learning algorithms. Sensors 2018, 18, 2464. [Google Scholar] [CrossRef] [PubMed]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (lidar) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Moosavi, V.; Talebi, A.; Shirmohammadi, B. Producing a landslide inventory map using pixel-based and object-oriented approaches optimized by taguchi method. Geomorphology 2014, 204, 646–656. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Sameen, M.I.; Sarkar, R.; Pradhan, B.; Drukpa, D.; Alamri, A.M.; Park, H.-J. Landslide spatial modelling using unsupervised factor optimisation and regularised greedy forests. Comput. Geosci. 2020, 134, 104336. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the izu-oshima volcanic island, japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Quinlan, J.R. Improved use of continuous attributes in c4. 5. J. Artif. Intell. Res. 1996, 4, 77–90. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems. In Inference in Possibilistic Hypergraphs; Springer: Berlin/Heidelberg, Germany, 1990; pp. 249–259. [Google Scholar]
- Kononenko, I. European conference on machine learning. In Estimating Attributes: Analysis and Extensions of Relief; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Ayalew, L.; Yamagishi, H. The application of gis-based logistic regression for landslide susceptibility mapping in the kakuda-yahiko mountains, central japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Schicker, R.; Moon, V. Comparison of bivariate and multivariate statistical approaches in landslide susceptibility mapping at a regional scale. Geomorphology 2012, 161, 40–57. [Google Scholar] [CrossRef]
- Meng, Q.; Miao, F.; Zhen, J.; Wang, X.; Wang, A.; Peng, Y.; Fan, Q. Gis-based landslide susceptibility mapping with logistic regression, analytical hierarchy process, and combined fuzzy and support vector machine methods: A case study from wolong giant panda natural reserve, china. Bull. Eng. Geol. Environ. 2016, 75, 923–944. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using gis. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Falaschi, F.; Giacomelli, F.; Federici, P.; Puccinelli, A.; Avanzi, G.A.; Pochini, A.; Ribolini, A. Logistic regression versus artificial neural networks: Landslide susceptibility evaluation in a sample area of the serchio river valley, italy. Nat. Hazards 2009, 50, 551–569. [Google Scholar] [CrossRef]
- Bednarik, M.; Magulová, B.; Matys, M.; Marschalko, M. Landslide susceptibility assessment of the kraľovany–liptovský mikuláš railway case study. Physics Chem. Earth Parts A/B/C 2010, 35, 162–171. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H.S.B. Improvement of statistical landslide susceptibility mapping by using spatial and global regression methods in the case of more and romsdal (norway). Landslides 2010, 7, 55–68. [Google Scholar] [CrossRef]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the sibiciu basin (romania). Environ. Earth Sci. 2011, 63, 397–406. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X. Controlling parameter analyses and hazard mapping for earthquake-triggered landslides: An example from a square region in beichuan county, sichuan province, china. Arab. J. Geosci. 2013, 6, 3827–3839. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Jebur, M.N.; Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in west sumatera province, indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Yao, X.; Tham, L.; Dai, F. Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of hong kong, china. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using svm machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support vector machines for landslide susceptibility mapping: The staffora river basin case study, italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (svm), logistic regression (lr) and artificial neural networks (ann). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Bui, D.T. A comparative study of support vector machine and logistic model tree classifiers for shallow landslide susceptibility modeling. Environ. Earth Sci. 2019, 78, 560. [Google Scholar] [CrossRef]
- Pandey, V.K.; Pourghasemi, H.R.; Sharma, M.C. Landslide susceptibility mapping using maximum entropy and support vector machine models along the highway corridor, garhwal himalaya. Geocarto Int. 2020, 35, 168–187. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Hoang, N.-D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the lao cai area (vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on random subspace and classification and regression trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Dunson, D.B. Commentary: Practical advantages of bayesian analysis of epidemiologic data. Am. J. Epidemiol. 2001, 153, 1222–1226. [Google Scholar] [CrossRef] [PubMed]
- Rose, C.E.; Pan, Y.; Baughman, A.L. Bayesian logistic regression modeling as a flexible alternative for estimating adjusted risk ratios in studies with common outcomes. J. Biom. Biostat. 2015, 6, 1–6. [Google Scholar]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at haraz watershed, northern iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Sok, H.K.; Ooi, M.P.-L.; Kuang, Y.C.; Demidenko, S. Multivariate alternating decision trees. Pattern Recognit. 2016, 50, 195–209. [Google Scholar] [CrossRef]
- Mahalingam, R.; Olsen, M.J.; O’Banion, M.S. Evaluation of landslide susceptibility mapping techniques using lidar-derived conditioning factors (oregon case study). Geomat. Nat. Hazards Risk 2016, 7, 1884–1907. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Brown, M.K.; Panter, K.; Onasch, C.M.; Simic, A.; Snyder, J. Landslide detection and susceptibility mapping using lidar and an artificial neural network approach: A case study in the cuyahoga valley national park, ohio. Landslides 2016, 13, 467–484. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Manifestation of lidar-derived parameters in the spatial prediction of landslides using novel ensemble evidential belief functions and support vector machine models in gis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 674–690. [Google Scholar] [CrossRef]


| Lithological Unit | Description | Age Era | Age Period | |
|---|---|---|---|---|
| 1 | Kll1 | Gray and light gray, thick-bedded to massive, fetid orbitolina bearing limestone. | MESOZOIC | Early Cretaceous |
| 2 | Kll2 | Thick-bedded, gray to dark gray, rudist and orbitolina bearing limestone. | MESOZOIC | Early Cretaceous |
| 3 | Klv,12 | Basaltic and andesitic volcanics, tuff, volcanic breccia and calcareous shale with intercalations of limestone. | MESOZOIC | Early Cretaceous |
| 4 | K213 | Gray and light gray micritic limestone and radioarian limestone with calcschiste structure. | MESOZOIC | Late Cretaceous |
| 5 | K2v | Basalt, andesite, spilitic basalte and pyroclastic rocks with developed layering and climbing. | MESOZOIC | Late Cretaceous |
| 6 | Klv,13 | Spilitic basalt, basalt and andesite lava with intercalation of red, blue, gray limestone, red shale and sandstone. | MESOZOIC | Early Cretaceous |
| 7 | Klv,14 | Tuff, green tuff, andesite and andesitic dacite, shale, limestone and sandstone. | MESOZOIC | Early Cretaceous |
| 8 | Kls | Purpel to red medium to thick-bedded sandstone with intercalation of polymictic conglomerate and silty shale. | MESOZOIC | Early Cretaceous |
| 9 | K2sh | Black, dark gray, yellow shale, silty shale and phillitic shale with minor sandstone and micritic limestone intercalations. (Sanandaj shale) | MESOZOIC | Late Cretaceous |
| 10 | Qal | Recent alluvium (alluvial channel deposits). | CENOZOIC | Quaternary |
| 11 | Residential area | Salavat Saddle |
| Factors | TOL | VIF |
|---|---|---|
| Slope angle | 0.520 | 1.587 |
| Aspect | 0.322 | 2.184 |
| Elevation | 0.212 | 1.135 |
| Profile curvature | 0.825 | 2.381 |
| Plan curvature | 0.705 | 1.843 |
| Distance to road | 0.553 | 2.529 |
| NDVI | 0.498 | 1.814 |
| Land use | 0.340 | 2.321 |
| Lithology | 0.263 | 1.311 |
| LS | 0.541 | 1.849 |
| Rainfall | 0.887 | 1.552 |
| Solar radiation | 0.670 | 2.698 |
| TWI | 0.776 | 1.541 |
| SPI | 0.732 | 1.873 |
| Distance to river | 0.820 | 2.987 |
| River density | 0.922 | 1.784 |
| Distance to fault | 0.712 | 2.835 |
| Fault density | 0.825 | 2.781 |
| Conditioning Factor | Rank | AMIGR |
|---|---|---|
| Distance to road | 1 | 0.1434 |
| NDVI | 2 | 0.0725 |
| Land use | 3 | 0.0187 |
| Aspect | 4 | 0.0139 |
| Lithology | 5 | 0.0097 |
| Slope angle | 6 | 0.0091 |
| Rainfall | 7 | 0.0090 |
| Distance to fault | 8 | 0.0087 |
| Elevation | 9 | 0.0078 |
| TWI | 10 | 0.0040 |
| Parameter | SVM | BLR | ADTree |
|---|---|---|---|
| TP | 50 | 48 | 47 |
| TN | 52 | 52 | 50 |
| FP | 1 | 1 | 3 |
| FN | 3 | 5 | 6 |
| Sensitivity | 0.943 | 0.906 | 0.887 |
| Specificity | 0.981 | 0.981 | 0.943 |
| Accuracy | 0.962 | 0.943 | 0.915 |
| Kappa | 0.924 | 0.886 | 0.846 |
| RMSE | 0.192 | 0.237 | 0.245 |
| AUC | 0.986 | 0.943 | 0.912 |
| Parameter | SVM | BLR | ADTree |
|---|---|---|---|
| TP | 12 | 11 | 11 |
| TN | 11 | 10 | 9 |
| FP | 1 | 2 | 2 |
| FN | 2 | 3 | 4 |
| Sensitivity | 0.857 | 0.786 | 0.714 |
| Specificity | 0.917 | 0.833 | 0.818 |
| Accuracy | 0.885 | 0.808 | 0.760 |
| Kappa | 0.869 | 0.846 | 0.751 |
| RMSE | 0.251 | 0.277 | 0.343 |
| AUC | 0.976 | 0.923 | 0.910 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nhu, V.-H.; Zandi, D.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Al-Ansari, N.; Singh, S.K.; Dou, J.; Nguyen, H. Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran. Appl. Sci. 2020, 10, 5047. https://doi.org/10.3390/app10155047
Nhu V-H, Zandi D, Shahabi H, Chapi K, Shirzadi A, Al-Ansari N, Singh SK, Dou J, Nguyen H. Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran. Applied Sciences. 2020; 10(15):5047. https://doi.org/10.3390/app10155047
Chicago/Turabian StyleNhu, Viet-Ha, Danesh Zandi, Himan Shahabi, Kamran Chapi, Ataollah Shirzadi, Nadhir Al-Ansari, Sushant K. Singh, Jie Dou, and Hoang Nguyen. 2020. "Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran" Applied Sciences 10, no. 15: 5047. https://doi.org/10.3390/app10155047
APA StyleNhu, V.-H., Zandi, D., Shahabi, H., Chapi, K., Shirzadi, A., Al-Ansari, N., Singh, S. K., Dou, J., & Nguyen, H. (2020). Comparison of Support Vector Machine, Bayesian Logistic Regression, and Alternating Decision Tree Algorithms for Shallow Landslide Susceptibility Mapping along a Mountainous Road in the West of Iran. Applied Sciences, 10(15), 5047. https://doi.org/10.3390/app10155047










