H2/H∞ Output Tracking Control with a Performance Compensator for Aeroengines
Abstract
1. Introduction
2. Problem Formulation
- (1)
- the controlled system with is asymptotically stable;
- (2)
- are constant variables and such that and hold.
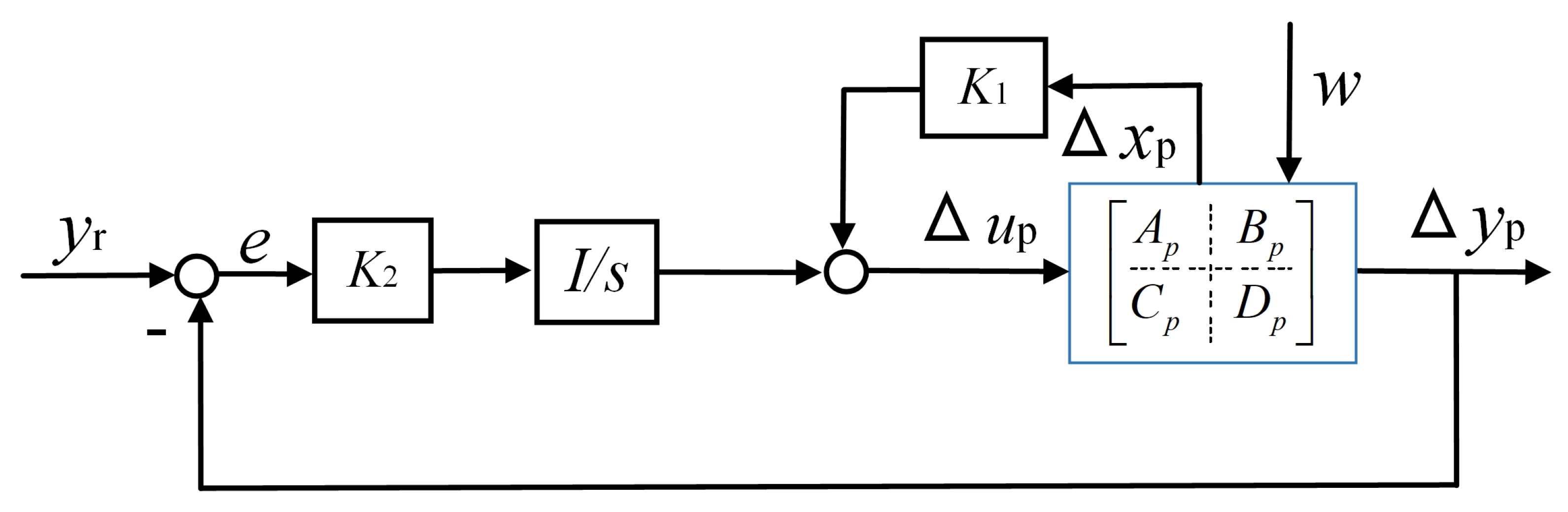
3. Nominal Controller Design
- (a)
- ;
- (b)
- there is such that and .
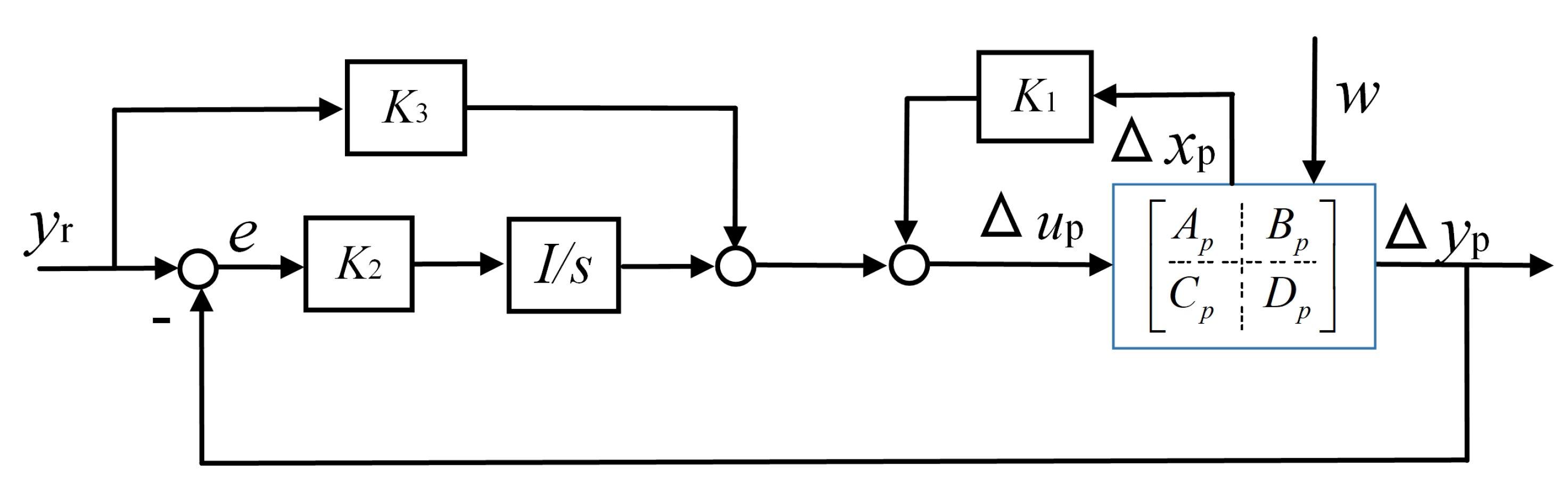
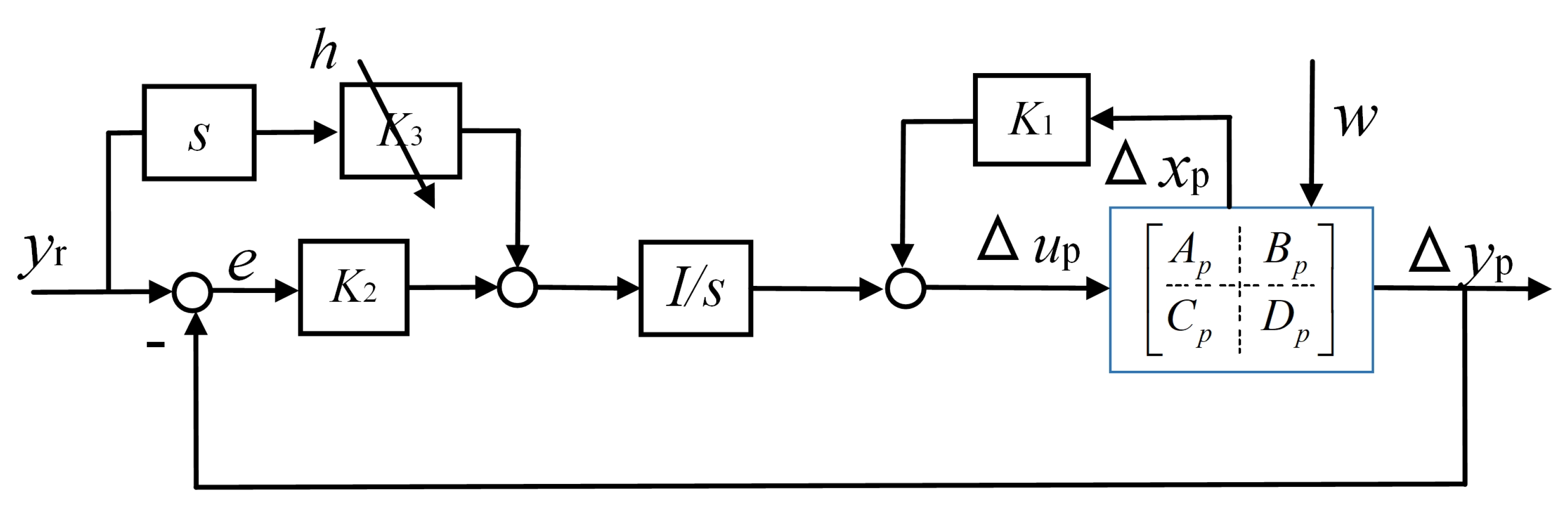
4. Compensator Design
4.1. Compensator for Nominal Controller
4.2. Compensator Design for Stable Reference
4.3. Compensator Design for Bounded Reference
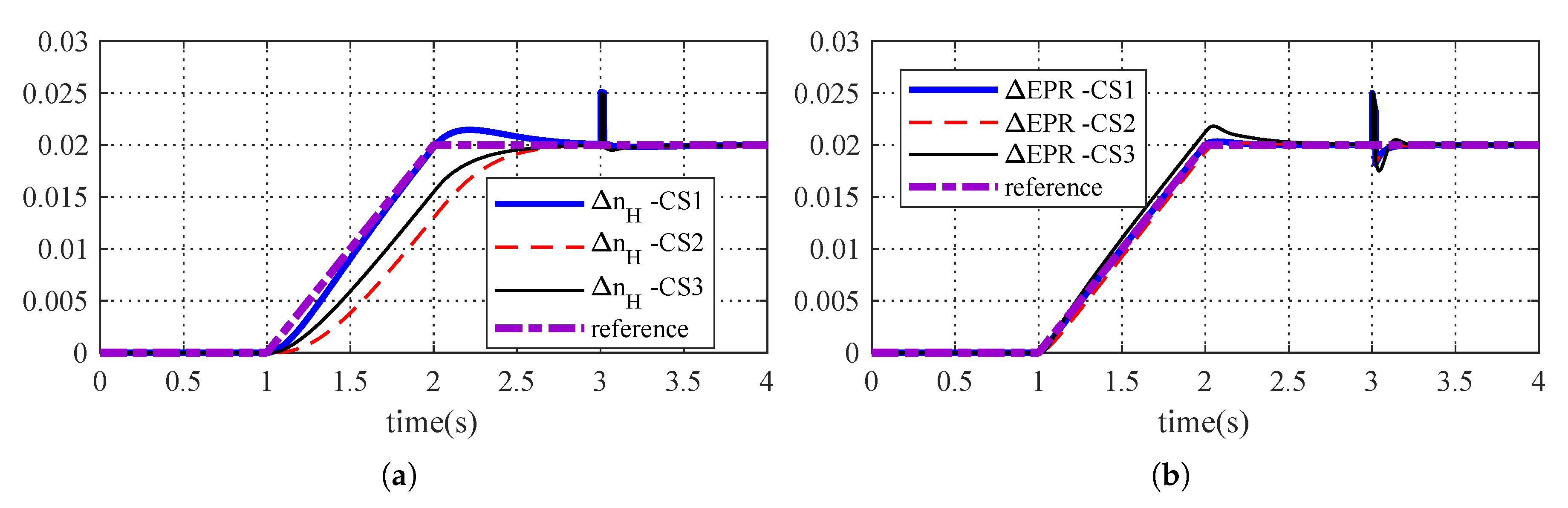
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coro, A.; Abasolo, M.; Aguirrebeitia, J.; Lopez De Lacalle, L. Inspection scheduling based on reliability updating of gas turbine welded structures. Adv. Mech. Eng. 2019, 11, 1–20. [Google Scholar] [CrossRef]
- Coro, A.; Macareno, L.; Aguirrebeitia, J.; Lopez de Lacalle, L. A methodology to evaluate the reliability impact of the replacement of welded components by additive manufacturing spare parts. Metals 2019, 9, 932. [Google Scholar] [CrossRef]
- Bhattacharyya, S.P.; Keel, L.H. Robust control: The parametric approach. In Advances in Control Education 1994; Elsevier: Amsterdam, The Netherlands, 1995; pp. 49–52. [Google Scholar]
- Wu, L.; Zhao, R.; Li, Y.; Chen, Y.H. Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach. Appl. Sci. 2020, 10, 3472. [Google Scholar] [CrossRef]
- Szuch, J.; Soeder, J.; Skira, C. Evaluation of an F100 Multivariable Control Using a Real-Time Enginesimulation; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1977. [Google Scholar]
- Athans, M.; Kapasouris, P.; Kappos, E.; Spang, H., I. Multivariable Control for the F-100 Engine Using the LQG/LTR Methodology; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1984; pp. 435–444. [Google Scholar]
- Zames, G. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms, and approximate inverses. IEEE Trans. Autom. Control 1981, 26, 301–320. [Google Scholar] [CrossRef]
- Bernstein, D.S.; Haddad, W.M. LQG control with an H∞ performance bound: A riccati equation approach. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988; pp. 796–802. [Google Scholar]
- Moriwaki, K. Autonomous steering control for electric vehicles using nonlinear state feedback control. Nonlinear Anal. 2005, 63, e2257–e2268. [Google Scholar] [CrossRef]
- Kurishige, M.; Nishihara, O.; Kumamoto, H. A new control strategy to reduce steering torque without perceptible vibration for vehicles equipped with electric power steering. Automob. Technol. 2010, 132, 054504. [Google Scholar] [CrossRef]
- Härefors, M. Application of H∞ robust control to the RM12 jet engine. Control Eng. Pract. 1997, 5, 1189–1201. [Google Scholar] [CrossRef]
- Ben, N.; Bacem, B.; Khaled, D.; Michael, D.; Mohamed, H.; Mohamed, A. State feedback stabilization of a class of uncertain nonlinear systems on non-uniform time domains. Syst. Control Lett. 2016, 97, 18–26. [Google Scholar]
- Wu, H.; Feng, S.; Liu, Z.; Guo, L. Disturbance observer based robust mixed H2/H∞ fuzzy tracking control for hypersonic vehicles. Fuzzy Sets Syst. 2017, 306, 118–136. [Google Scholar] [CrossRef]
- Liu, M.; Dong, Z. Multiobjective robust H2/H∞ fuzzy tracking control for thermal system of power plant. J. Process Control 2018, 70, 47–64. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, J. H infinity output tracking control for a class of switched LPV systems and its application to an aero-engine model. Int. J. Robust Nonlinear Control 2017, 27, 2102–2120. [Google Scholar] [CrossRef]
- Liao, F.; Wang, J.L.; Yang, G.H. Reliable robust flight tracking control: An LMI approach. IEEE Trans. Control Syst. Technol. 2002, 10, 76–89. [Google Scholar] [CrossRef]
- Athans, M.; Falb, P. Optimal control: An introduction to theory and its applications. In SERBIULA (Sistema Librum 2.0); Wiley: Hoboken, NJ, USA, 1966. [Google Scholar]
- Lewis, F.; Vrabie, D.; Syrmos, V. Optimal Control, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Bauer, P.; Bokor, J. Development and performance evaluation of an infinite horizon LQ optimal tracker. Eur. J. Control 2018, 39, 8–20. [Google Scholar] [CrossRef]
- Ahmed, H.; Ríos, H.; Ayalew, B.; Wang, Y. Robust Output Tracking Control for Van der Pol Oscillator: A Sliding-Mode Differentiator Approach. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Deng, S. A novel emergent state control law for an integrated helicopter/turboshaft engine system. Math. Probl. Eng. 2014, 2014, 385807. [Google Scholar] [CrossRef]
- Bruzelius, F.; Breitholtz, C.; Pettersson, S. LPV-based gain scheduling technique applied to a turbo fan engine model. Int. Conf. Control Appl. 2002, 2, 713–718. [Google Scholar]
- Modares, H.; Lewis, F.L.; Jiang, Z. H∞ tracking control of completely unknown continuous-time systems via Off-Policy Reinforcement Learning. IEEE Trans. Neural Netw. 2015, 26, 2550–2562. [Google Scholar] [CrossRef] [PubMed]
- Yu, L. Robust Control-Linear Matrix Inequalities Approach; Tsinghua University Press: Beijing, China, 2002; Chapter 2; pp. 31–32. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat. No.04CH37508), New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Chen, Q.; Huang, J.; Pan, M.; Lu, F. A novel real-time mechanism modeling approach for turbofan engine. Energies 2019, 12, 3791. [Google Scholar] [CrossRef]

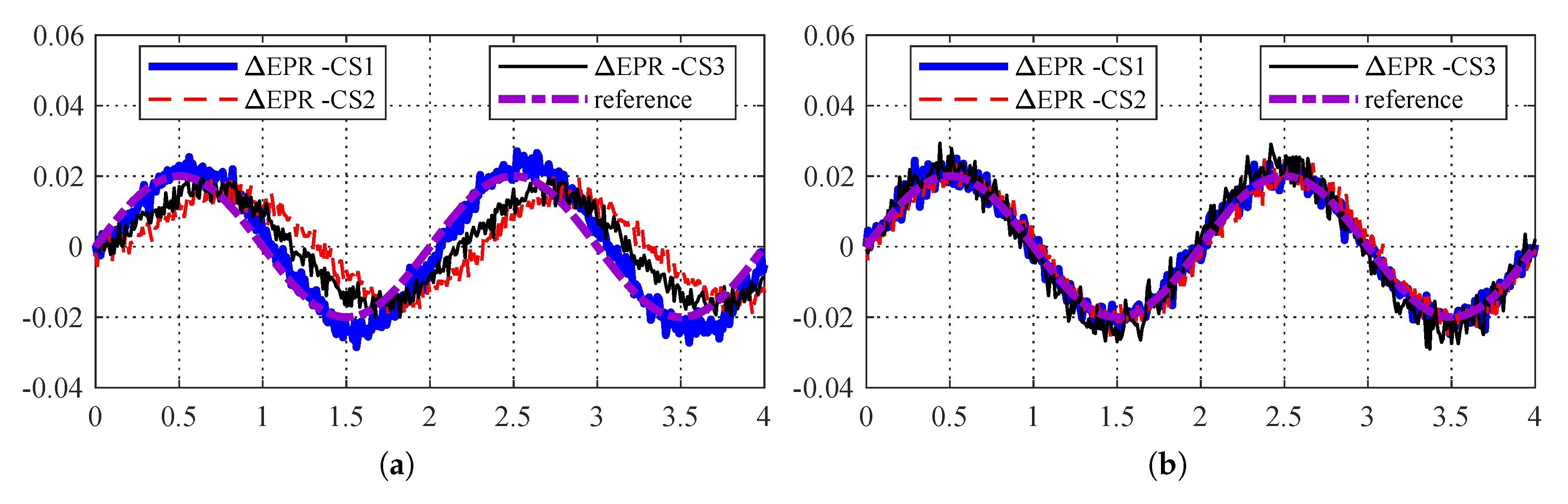
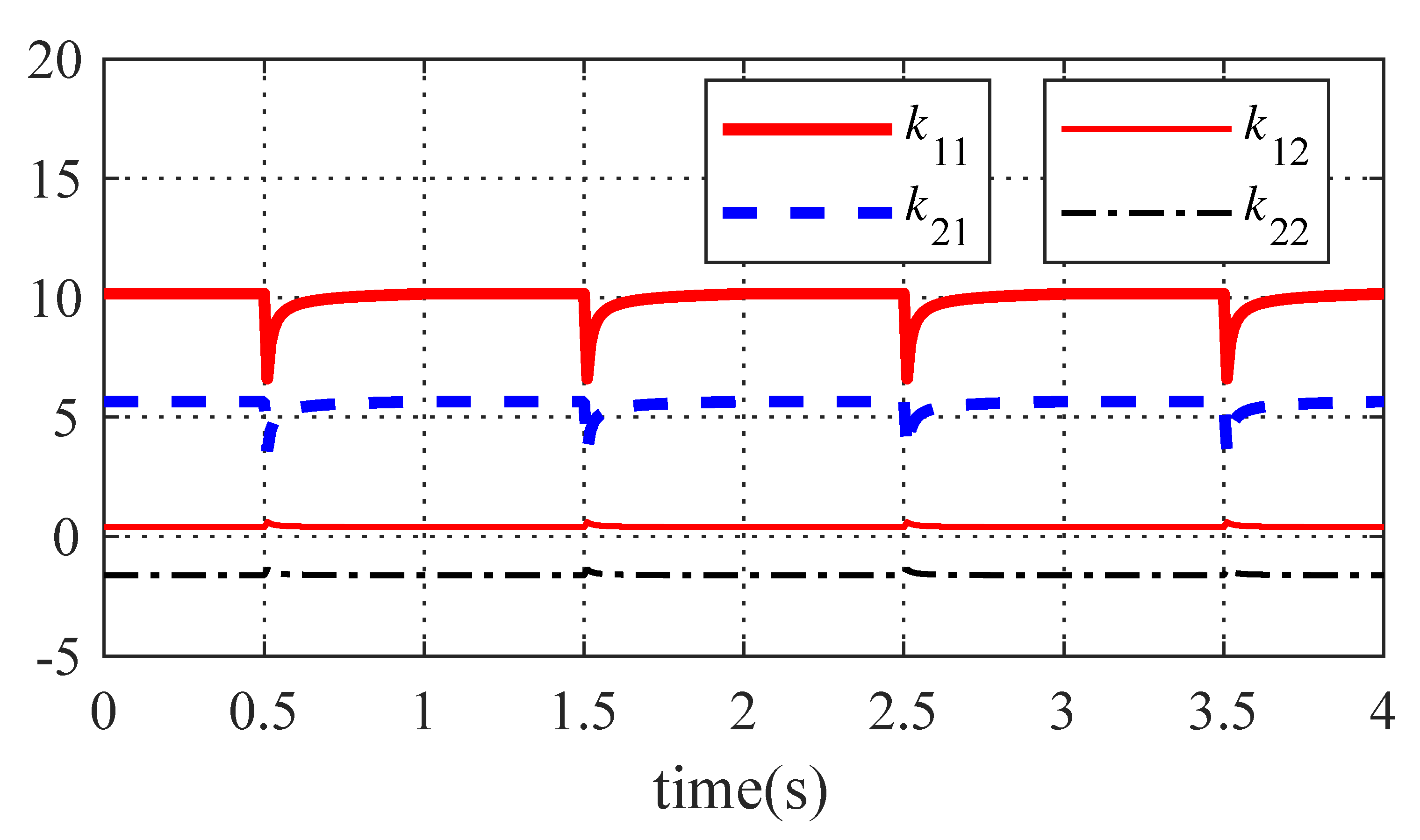
| Reference | Image Function | Primitive Function | h | |
|---|---|---|---|---|
| step | ∞ | |||
| ramp | t | 1 | 0 | |
| exponential | a |
| Ramp | Exponential | Sine | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CS1 | CS2 | CS3 | CS1 | CS2 | CS3 | CS1 | CS2 | CS3 | |
| 0.75 | 3.12 | 2.05 | 1.78 | 3.29 | 2.17 | 7.33 | 15.45 | 10.41 | |
| 0.32 | 0.49 | 0.72 | 0.25 | 0.52 | 0.71 | 2.31 | 3.33 | 4.48 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Huang, J.; Pan, M.; Lu, F. H2/H∞ Output Tracking Control with a Performance Compensator for Aeroengines. Appl. Sci. 2020, 10, 4929. https://doi.org/10.3390/app10144929
Chen Q, Huang J, Pan M, Lu F. H2/H∞ Output Tracking Control with a Performance Compensator for Aeroengines. Applied Sciences. 2020; 10(14):4929. https://doi.org/10.3390/app10144929
Chicago/Turabian StyleChen, Qianjing, Jinquan Huang, Muxuan Pan, and Feng Lu. 2020. "H2/H∞ Output Tracking Control with a Performance Compensator for Aeroengines" Applied Sciences 10, no. 14: 4929. https://doi.org/10.3390/app10144929
APA StyleChen, Q., Huang, J., Pan, M., & Lu, F. (2020). H2/H∞ Output Tracking Control with a Performance Compensator for Aeroengines. Applied Sciences, 10(14), 4929. https://doi.org/10.3390/app10144929





