Improved Epidemic Dynamics Model and Its Prediction for COVID-19 in Italy

Abstract

The outbreak of coronavirus disease 2019 (COVID-19) has become a global public health crisis due to its high contagious characteristics. In this article, we propose a new epidemic-dynamics model combining the transmission characteristics of COVID-19 and then use the reported epidemic data from 15 February to 30 June to simulate the spread of the Italian epidemic. Numerical simulations showed that (1) there was a remarkable amount of asymptomatic individuals; (2) the lockdown measures implemented by Italy effectively controlled the spread of the outbreak; (3) the Italian epidemic has been effectively controlled, but SARS-CoV-2 will still exist for a long time; and (4) the intervention of the government is an important factor that affects the spread of the epidemic.

1. Introduction

In December 2019, a new type of coronavirus pneumonia (COVID-19) broke out in Wuhan, China. Since then, there have been cases of infected individuals in various regions of the world. On 30 January 2020, the WHO listed COVID-19 as an “emergency public health event of international concern” [1]. According to the official statistics of the World Health Organization, as of 30 June 2020, the outbreak of COVID-19 has caused 10,193,723 confirmed cases and 503,867 fatalities globally [2]. The epidemic-prevention situation is extremely severe, and the number of confirmed cases in South Korea, Iran, the United States, and other countries continues to increase, while in Europe, Italy has become the “severe disaster country” of the epidemic. The collapse of the medical system [3] and the high proportion of the elderly population [4] make the mortality rate in Italy much higher than in other regions. According to the official report of the Italian Ministry of Health, as of 30 June 2020, the outbreak of COVID-19 has caused 240,578 confirmed cases and 34,767 fatalities in Italy, and the mortality rate is approximately 14% [5]. In view of the rapid spread of the epidemic nationwide, the Italian government took proactive prevention and control measures. On 10 March 2020, Italy implemented a lockdown measure nationwide.

Scientific and effective calculation of the spread tendency of the epidemic is crucial to the decision on epidemic prevention and restriction. It should rely on theoretically perfect models, reasonable parameters, and accurate predictions. The mathematical models generally advocated to describe the spread of infectious diseases include the Susceptible–Infectious–Recovered model (the SIR model), Susceptible–Exposed–Infectious–Recovered model (the SEIR model), and Susceptible–Infectious–Diagnosed–Recovered model (the SEIJR model). The main idea is to divide the population into groups such as susceptible, latent, infectious, diagnosed, and recovered ones. We have established differential equations according to the propagation mechanism among various groups and then revealed the spreading laws of the epidemic. The dynamic model is modeled according to the transmission of disease, and the model is interpretable and expandable. Game theory continues to be an effective tool to model intervention decision making by individuals [6]. Chang et al. used game theory to introduce the decision making of individuals into the SIR model and then get the effect of the vaccination on the epidemic [7]. Over the years, numerous research projects and promotions have been built on the original SIR model to meet different epidemic characteristics. As the global epidemic becomes more severe, a more complete infectious-disease model is urgently needed. Many scholars have adopted the infectious-disease-dynamics model for COVID-19 [8,9,10,11,12,13,14]. Based on the traditional SEIR model, the population is divided more concretely. Here, we will briefly review the following articles.

The recent work of Tang et al. [8] proposed a deterministic compartment model containing isolation measures and epidemiological conditions, but this model implied that the latent patients are not infectious and therefore does not reflect the dynamics of COVID-19. Yan et al. [9] proposed an infectious-disease-dynamics model based on the time-delay dynamic system, which introduced the time-delayed processes of incubation, recovery, and fatality. However, they did not consider the different types of infected people (symptomatic or asymptomatic), and the definition of patients during the infectious incubation period was not clear. Wu et al. [10] considered traffic factors based on the traditional SEIR model and predicted the number of total cases imported from Wuhan, China, but they did not explicitly consider the impact of quarantine measures in the dynamic. Chen et al. [11] presented an improved epidemic-dynamics model. They combined the multiple characteristics of the new coronavirus but ignored the death process and the difference in the infectiousness of the patients with different symptoms, which cannot be applied to some areas with a high mortality rate. Wang et al. analyzed the impact of the resumption of work on the epidemic in each city by controlling the regeneration number [12]. Due to the uniqueness of COVID-19 and the diversity of outbreaks in different countries, different types of infected individuals require different prevention and control measures, which in turn lead to different fitness and predictions. In addition, most scholars model under the assumption that prevention and control measures are unchanged, but, in fact, different measures will affect the spread of the epidemic to varying degrees [13], so the simulation results will deviate from the actual situation.

To meet the aforementioned issues and realistically reflect the transmission mechanism of COVID-19, we comprehensively consider the characteristics of COVID-19 (numerous asymptomatically infected individuals, different infectious carriers have different infectiousness) and government intervention measures based on the traditional SEIR model and propose a new epidemic model. The model divides the incubation period into quarantined and nonquarantined, adding asymptomatically infected individuals (IA). Meanwhile, we take the difference between asymptomatically and symptomatically infected individuals into account as well as the death process of infected individuals. We build a model called the SEIR_QJD model (SEIR with Quarantined, Dead, and Diagnosed) based on the Italian epidemic data and parameterize it with public data. Parameter analysis can reflect the effects of policy interventions and reveal the inherent laws of epidemic transmission. With these parameters, the modified model may renovate the development of the epidemic analysis and accurately predict the trend of the epidemic. Simultaneously, we simulate the time when the government takes measures and further explore the impact of the government response on the scale of the epidemic.

2. SEIR_QJD Model

The traditional SEIR model (Figure 1) only divides the population into four categories: susceptible (S), exposed (E), infected (I), and recovered (R), which could not describe the transmission law of COVID-19 well.

Figure 1. Susceptible–Exposed–Infectious–Recovered (SEIR) epidemic-dynamics model.

In view of the uniqueness of the disease, we designed a new dynamic model to characterize COVID-19:

①

Infected individuals during the incubation period are infectious [14].

②

There is a large proportion of asymptomatic infected individuals [15].

③

The rate of infection is different between symptomatic and asymptomatic individuals [15].

The new dynamic model comprehensively covers the government’s containment measures (lockdown of key epidemic areas, school suspension, and suspension of noncritical production activities) and the classification of infected people (symptomatic and asymptomatic). The model consists of eight objects in the proposed model: susceptible (S), exposed (E), quarantine-exposed ($E_Q$), asymptomatic infected (IA), symptomatic infected (I), diagnosed (J), recovered (R), and dead (D); we call it the SEIR_QJD for short, and the process is shown in Figure 2.

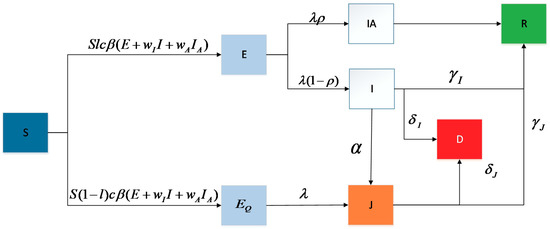
Figure 2. Process illustration.

For the purpose of conciseness, we denote $S(t),$ $E(t),$ $E_Q(t)$, and so on as the amount in the corresponding states at time $t$. The specific process is described as follows:

• Infection: Every primary case (including $E$, $IA$, and $I$ status) with infectiousness will transmit the virus to its secondary cases at time $t$; that is, if a primary case contacts a susceptible individual, the susceptible individual will be infected with a certain probability.
• Quarantine: Due to the government’s prevention and control measures (suspension, work stoppages, restrictions on the diagnosed individuals, etc.) and people’s self-precautionary awareness (self-isolation), each individual in status $E_Q$ and $J$ will be isolated. Note: we assume that the quarantined individuals cannot contact the susceptible ones; namely, it is not contagious.
• Symptom Onset: Individuals in states $E,$ $E_Q$ will become symptomatic after the infectious incubation period and will transition to states $I$ and $J$ at the rate of $\lambda$.
• Recovery: Individuals in states ${\mathrm{I}}_A,$ $I,$ and $J$ will recover at rates of ${\gamma }_A,$ ${\gamma }_I,$ and ${\gamma }_J$, respectively.
• Death: Individuals in states $I$ and $J$ will die at rates of ${\delta }_I$ and ${\delta }_J$, respectively. Note: as the mortality rates of asymptomatic and mild-symptomatic individuals are extremely low, the death of asymptomatic infections is not included.

Meanwhile, we get the dynamic model defined by the following differential equations:

$$\frac{dS\left(t\right)}{dt}=-S\left(t\right)l\beta \left(E\left(t\right)+{\omega }_{I}I\left(t\right)+I_A\left(t\right)\right)-S\left(t\right)\left(1-l\right)\beta \left(E\left(t\right)+{\omega }_{I}I\left(t\right)+I_A\left(t\right)\right)$$

(1)

$$\frac{dE\left(t\right)}{dt}=S\left(t\right)\left(1-l\right)\beta \left(t\right)\left(E\left(t\right)+{\omega }_{I}I\left(t\right)+I_A\left(t\right)\right)-\lambda E\left(t\right)$$

(2)

$$\frac{d{E}_Q\left(t\right)}{dt}=S\left(t\right)l\beta \left(t\right)\left(E\left(t\right)+{\omega }_{I}I\left(t\right)+I_A\left(t\right)\right)-\lambda E_Q\left(t\right)$$

(3)

$$\frac{d{I}_A\left(t\right)}{dt}=\lambda \rho E\left(t\right)-{\gamma }_A{I}_A\left(t\right)$$

(4)

$$\frac{dI\left(t\right)}{dt}=\lambda \left(1-\rho \right)E\left(t\right)-\left({\delta }_I+{\gamma }_I+\alpha \right)I\left(t\right)$$

(5)

$$\frac{dJ\left(t\right)}{dt}=\alpha I\left(t\right)+\lambda E_Q\left(t\right)-\left({\delta }_J+{\gamma }_J\right)J\left(t\right)$$

(6)

$$\frac{dR\left(t\right)}{dt}={\gamma }_A{I}_A\left(t\right)+{\gamma }_{I}I\left(t\right)+{\gamma }_{J}J\left(t\right)$$

(7)

$$\frac{dD\left(t\right)}{dt}={\delta }_{I}I\left(t\right)+{\delta }_{J}J\left(t\right)$$

(8)

3. Estimation of Model Parameters

Given the values of parameters $l,\beta ,w_I,\lambda ,\rho ,\alpha ,{\gamma }_A,{\gamma }_I,{\gamma }_J,{\delta }_I,{\delta }_J$ and the initial conditions $\{S(t_0),E(t_0),E_Q(t_0),I(t_0),I_A(t_0),J(t_0),R(t_0),D(t_0)\}$ of each group, the evolution of the epidemic can be simulated by Equations (1)–(8). The initial state $t_0$ represents the time when the first batch of infected people appeared (according to roughly 40% of asymptomatic individuals among infected ones [14], we assume that five patients are symptomatic and three patients are asymptomatic). Because the first cases discovered in Italy were all imported cases, we assume that $E(t_0)=0,E_Q(t_0)=0$, and $J(t_0),R(t_0),D(t_0)$ can be obtained from the reporting data. Besides, we set the initial value of the susceptible $E(t_0)$ to unknown and estimate it together with other model parameters as described below. Since the number of exposures available to susceptible people is limited, we do not consider the total population of Italy as susceptible.

Since the SEIR_QJD model contains a relatively large number of parameters, the model could be overfitted while the available data are limited, which will affect the results and mislead the epidemic judgment. The proposed model consists of 11 parameters: $l,\beta ,w_I,\lambda ,\rho ,\alpha ,{\gamma }_A,{\gamma }_I,{\gamma }_J,{\delta }_I,{\delta }_J$, of which ${\gamma }_A,{\gamma }_I,{\gamma }_J,{\delta }_I,{\delta }_J$ are related to the clinical characteristics of the disease and can be prefixed by relevant studies. Since the official report data show that $R(t)$ and $D(t)$ are only related to the diagnosed individuals $J(t)$, we can roughly estimate them from the related data with the approximate equation ${\gamma }_J\approx \left(R(t+1)-R(t)\right)/J(t)$, ${\delta }_J\approx \left(D(t+1)-D(t)\right)/J(t)$. The remaining parameters will be estimated according to the model. By observing the trend chart of ${\gamma }_J$ and ${\delta }_J$, in Figure 3 and Figure 4, respectively, it can be found that the change in ${\gamma }_J$ over time is not significant, while that of ${\delta }_J$ decreases continuously over time. Meanwhile, in order to reflect the effects of government interventions and medical investment, we will consider $\beta$ and ${\delta }_J$ as time-varying parameters, that is, $\beta (t)=1_{\{t<T_1+t’\}}{\beta }_0+1_{\{t>T_1+t’\}}c{\beta }_0$ and ${\delta }_J=f(t)$; see Figure 4 for specific functions of $f(t)$. The time $T_1$ is set to be the time when Italy implemented the nationwide lockdown measure, $t’$ is the lag time of the implementation, and the time $T_2$ is set to the end of Italy’s lockdown measure.

Figure 3. The plot of the recovery rate of diagnosed patients.

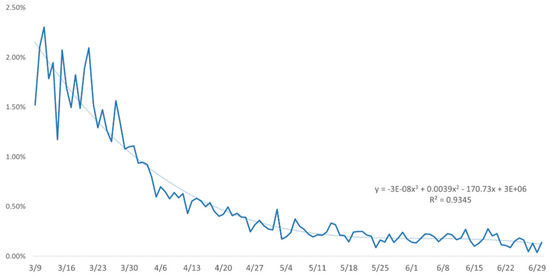
Figure 4. The plot of the fatality rate for diagnosed patients.

The likelihood function is obtained by assuming that daily confirmed cases are independent Poisson random variables [10], that is:

$$L(l,\beta ,w_I,\rho ,a)={\displaystyle \sum _{i=1}^k\log \frac{e^{-{\lambda }_i}{\lambda }_i{}^{\Delta J_i}}{\Delta J_i!}}$$

(9)

where $\Delta J$ is the newly confirmed cases per day and ${\lambda }_i$ is the functions of model parameters $l,\beta ,w_I,\rho ,a,S(0)$ based on the differential Equations (1)–(8). We use the Markov chain Monte Carlo (MCMC) algorithm to fit the model based on Italian epidemic data from 15 February to 30 June (see Appendix A), where noninformative uniform distributions are chosen as the prior distributions; the specific information is in Table 1.

Table 1. SEIR_QJD parameter setting (Italy).

Parameter	Definitions	Search Range	Estimated Mean Value
$S\left(t_0\right)$	The initial value of susceptible individuals	$5\times {10}^5\sim 1\times {10}^6$	$\mathrm{714,253}$
$l$	The probability of incubation individuals being detected	$0.10~0.90$	$0.2495$
$\beta$	The contact rate between susceptible and incubation individuals (roughly estimated by $R_0$)	$1.0\times {10}^{-7}~1.0\times {10}^{-6}$	$4.01\times {10}^{-7}$
$c_1$	Adjustment coefficient of $\beta$ with the government’s lockdown measures	$0.20\sim 0.80$	$0.3068$
$c_2$	Adjustment coefficient of $\beta$ with the government lifting the blockade	$1.00~2.00$	$1.0949$
$w_I$	The infectiousness of symptomatic individuals relative to incubation ones	$2.0$	$2.0\left[12\right]$
$\lambda$	The speed of individuals from exposed to infected, which is the reciprocal of the incubation period	$1/5.3$	$1/5.9$
$\rho$	The proportion of asymptomatic individuals among all infected ones	$0.10\sim 0.60$	$0.4099$
$\alpha$	The diagnosed speed of symptomatic individuals	$0.0\sim 0.5$	$0.0788$
${\gamma }_A,{\gamma }_I$	The recovery rate of infected individuals	$0.1$	$0.1\left[9\right]$
${\gamma }_J$	The recovery rate of diagnosed individuals	0.01887	$0.01887$
${\delta }_I,{\delta }_J$	The mortality rate of infected and diagnosed individuals	$f\left(t\right)$	$f\left(t\right)$

4. Empirical Analysis

1. Fitting Effect: Based on the cumulative number of confirmed cases in Italy as of 30 June 2020, we used the SEIR_QJD model for data fitting. The fitting effect of the model is measured by calculating the average deviation between the actual and simulated cumulative number of confirmed cases (Table 2). The curve fitting of Italian epidemic cases is shown in Figure 5.

Table 2. Model fitting effect.

Region	Evaluation Index	Distribution Range
Italy	The estimated deviation in the past 30 days. (%)	−0.33~0.20%
	The estimated deviation in the past 60 days. (%)	−1.73~0.20%
	The estimated deviation in the past 90 days. (%)	−1.73~2.95%

Figure 5. Simulation of epidemic-situation development trend. Simulation of the epidemic spread in Italy. Fitting curves: cumulative incidence (a), prevalence (b), incidence (c).

This paper evaluates the fitting effect of the model by calculating the deviation between the simulated value and the real value (Table 2). The average deviation of the model in the past 90 days was 0.86%, and the maximum deviation was controlled within 2.95%. Overall, the fitting effect of the model was very good and, to a great extent, largely simulated the development of the Italian epidemic.

2. The duration of the epidemic is relatively long. With the change in government control, people’s awareness of epidemic prevention, medical level, and other factors, the contact rate between susceptible and infected people will also change accordingly. This paper describes the change by constructing a time-varying function of the contact rate. During the implementation of the nationwide “lockdown measures” in Italy, the time-varying parameters changed significantly (adjustment coefficient c_1 was 0.4364), while after the closure measures, the change of time-varying parameters was insignificant, indicating that the epidemic situation in Italy was basically under control and there was no secondary outbreak. Furthermore, according to the model (1–8), we used the regeneration matrix to get the formula of the regeneration number:

$$R_c=[\frac{\beta (1-\rho )w_I(1-l)}{{\delta }_I+{\gamma }_I+a}+\frac{\beta \rho w_A(1-l)}{{\gamma }_A}+\frac{\beta (1-l)}{\lambda }]S_0$$

(10)

The regeneration numbers of the three stages were $R_{c0}=2.9527$, $R_{c1}=0.7064$, and $R_{c2}=0.8204$, respectively, indicating that the government’s prevention and control measures suppressed the spread of the epidemic effectively.

3. COVID-19 is a disease with strong spreading ability, which can be effectively controlled under good public health conditions and quarantine measures. In order to analyze the impact of the government’s response on the epidemic, this paper simulates four different situations by changing the time of the government interventions, which is based on time-varying parameters (Figure 6). The analysis showed that the government’s timely intervention measures could reduce the scale of the disease significantly. This paper only takes Italy’s “closure measures” into account; in practice, it still needs to be comprehensively considered according to the local epidemic situation.

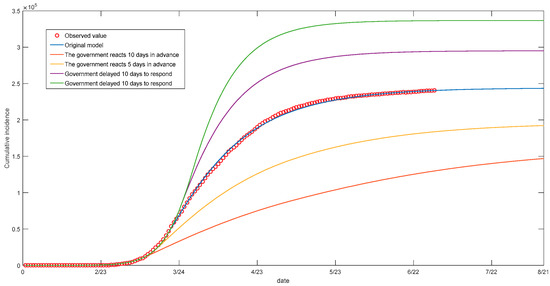
Figure 6. Simulation of the spread of the epidemic.

4. The proportion of asymptomatic and undetected patients in Italy is approximately 40%, which accounts for a relatively high proportion of total infected people. Therefore, the government needs to strengthen the detection of close contacts of cases.

Overall, the model has good generalizability and can change the parameters according to the different regions to simulate the spread of the epidemic and provide scientific judgment for epidemic prevention and control decisions.

5. Discussion

In response to the characteristics of coronavirus disease 2019 (COVID-19), the infectiousness during the incubation period, the specificity of a large proportion of asymptomatic infections, and the strong government interventions, we proposed a SEIR_QJD epidemic-dynamics model that comprehensively considers the characteristics of infectious diseases and the impact of overall prevention and control measures to make it closely related to the reality.

According to the analysis results, the government intervention in Italy has effectively contained the spread of the epidemic. At the same time, after the lifting of the blockade, the Italian epidemic has not rebounded, indicating that the epidemic was controlled effectively. However, there is still a long time until the epidemic is completely over, so the government should continue to strengthen the prevention and control of the epidemic to avoid a second outbreak. In addition, due to the existence of a large number of asymptomatic infected people, which has increased the difficulty of controlling the epidemic, the government should strengthen the detection of the individuals who are asymptomatic and strengthen the isolation of confirmed patients and the medical observation of close contacts.

Recently, the number of new confirmed cases per day in Italy has shown a slight increase, so the maintenance of the current prevention and control measures is of great importance. Both the infection rate and isolation rate measure the ability of the virus to spread, so blocking transmission is the key. However, Italy’s restrictions have now been lifted; we advise citizens to reduce public activities, strengthen self-protection, and wear masks when going out. People should seek medical treatment or self-quarantine after developing symptoms such as fever and dry cough so as not to spread the virus to others.