GBCNet: In-Field Grape Berries Counting for Yield Estimation by Dilated CNNs
Abstract
Featured Application
Abstract
1. Introduction
2. Preliminaries
3. Materials and Methods
3.1. From Crowd to Berries Counting
3.2. In-Field Images
3.3. Performance Metrics
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| CNN | Convolutional Neural Network |
| CV | Cross-Validation |
| CSRNet | Congested Scene Recognition Network |
| DL | Deep Learning |
| VGG-16 | Oxford Visual Geometry Group v.16 |
| MAE | Mean Absolute Error |
| MCNN | Multi-scale Convolutional Neural Network |
| MSE | Mean Squared Error |
References
- Schrijver, R. Precision Agriculture and the Future of Farming in Europe; Technical Report Scientific Foresight Study IP/G/STOA/FWC/2013-1/Lot 7/SC5; European Parliament Research Series; Scientific Foresight Unit (STOA): Brussels, Belgium, 2016. [Google Scholar]
- Seng, K.P.; Ang, L.M.; Schmidtke, L.M.; Rogiers, S.Y. Computer Vision and Machine Learning for Viticulture Technology. IEEE Access 2018, 6, 67494–67510. [Google Scholar] [CrossRef]
- Lüttich, F.R. Predictive Models for Smart Vineyards. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2019. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). The Future of Food and Agriculture. Trends and Challenges; Technical Report; FAO: Rome, Italy, 2017. [Google Scholar]
- Zabawa, L.; Kicherer, A.; Klingbeil, L.; Milioto, A.; Töpfer, R.; Kuhlmann, H.; Roscher, R. Detection of Single Grapevine Berries in Images Using Fully Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–21 June 2019; pp. 2571–2579. [Google Scholar]
- Zabawa, L.; Kicherer, A.; Klingbeil, L.; Töpfer, R.; Kuhlmann, H.; Roscher, R. Counting of grapevine berries in images via semantic segmentation using convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2020, 164, 73–83. [Google Scholar] [CrossRef]
- Nellithimaru, A.K.; Kantor, G.A. ROLS: Robust Object-Level SLAM for Grape Counting. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–21 June 2019; pp. 2648–2656. [Google Scholar]
- Millan, B.; Velasco-Forero, S.; Aquino, A.; Tardaguila, J. On-the-Go Grapevine Yield Estimation Using Image Analysis and Boolean Model. J. Sens. 2018, 2018, 9634752. [Google Scholar] [CrossRef]
- Kurtser, P.; Ringdahl, O.; Rotstein, N.; Berenstein, R.; Edan, Y. In-Field Grape Cluster Size Assessment for Vine Yield Estimation Using a Mobile Robot and a Consumer Level RGB-D Camera. IEEE Robot. Autom. Lett. 2020, 5, 2031–2038. [Google Scholar] [CrossRef]
- Hacking, C.; Poona, N.; Manzan, N.; Poblete-Echeverría, C. Investigating 2-D and 3-D Proximal Remote Sensing Techniques for Vineyard Yield Estimation. Sensors 2019, 19, 3652. [Google Scholar] [CrossRef] [PubMed]
- Aquino, A.; Millan, B.; Gaston, D.; Diago, M.P.; Tardaguila, J. vitisFlower®: Development and testing of a novel Android-smartphone application for assessing the number of grapevine flowers per inflorescence using artificial vision techniques. Sensors 2015, 15, 21204–21218. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Toscano, P.; Cinat, P.; Berton, A.; Matese, A. A Low-Cost and Unsupervised Image Recognition Methodology for Yield Estimation in a Vineyard. Front. Plant Sci. 2019, 10, 559. [Google Scholar] [CrossRef]
- Silver, D.L.; Monga, T. In Vino Veritas: Estimating Vineyard Grape Yield from Images Using Deep Learning. In Proceedings of the 2019 Canadian Conference on Artificial Intelligence: Advances in Artificial Intelligence, Kingston, ON, Canada, 28–31 May 2019; Volume 11489, pp. 212–224. [Google Scholar]
- Liu, S.; Zeng, X.; Whitty, M. 3DBunch: A novel iOS-smartphone application to evaluate the number of grape berries per bunch using image analysis techniques. IEEE Access 2020, 8, 114663–114674. [Google Scholar] [CrossRef]
- Nuske, S.; Achar, S.; Bates, T.; Narasimhan, S.; Singh, S. Yield estimation in vineyards by visual grape detection. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 2352–2358. [Google Scholar]
- Nuske, S.; Wilshusen, K.; Achar, S.; Yoder, L.; Narasimhan, S.; Singh, S. Automated Visual Yield Estimation in Vineyards. J. Field Robot. 2014, 31, 837–860. [Google Scholar] [CrossRef]
- Liu, S.; Zeng, X.; Whitty, M. A vision-based robust grape berry counting algorithm for fast calibration-free bunch weight estimation in the field. Comput. Electron. Agric. 2020, 173, 105360. [Google Scholar] [CrossRef]
- Pizer, S.M.; Amburn, E.P.; Austin, J.D.; Cromartie, R.; Geselowitz, A.; Greer, T.; ter Haar Romeny, B.; Zimmerman, J.B.; Zuiderveld, K. Adaptive histogram equalization and its variations. Comput. Vision, Graph. Image Process. 1987, 39, 355–368. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zissermann, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Tabb, A.; Holguín, G.A.; Naegele, R. Using cameras for precise measurement of two-dimensional plant features: CASS. arXiv 2020, arXiv:1904.13187v2. [Google Scholar]
- Pérez-Zavala, R.; Torres-Torriti, M.; Cheein, F.A.; Troni, G. A pattern recognition strategy for visual grape bunch detection in vineyards. Comput. Electron. Agric. 2018, 151, 136–149. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Toscano, P.; Cinat, P.; Berton, A.; Matese, A. A precision viticulture UAV-based approach for early yield prediction in vineyard. In Precision Agriculture ’19; Wageningen Academic Publishers: Gelderland, The Netherlands, 2019; pp. 373–379. [Google Scholar]
- Schmidtke, L.M. Developing a Phone-Based Imaging Tool to Inform on Fruit Volume and Potential Optimal Harvest Time; Technical Report CSU 1501; Charles Sturt University for Australian Grape and Wine Authority trading as Wine Australia (Australian Government): Bathurst, Australia, 2018.
- Sa, I.; Ge, Z.; Dayoub, F.; Upcroft, B.; Perez, T.; McCool, C. Deepfruits: A fruit detection system using deep neural networks. Sensors 2016, 16, 1222. [Google Scholar] [CrossRef]
- Keresztes, B.; Abdelghafour, F.; Randriamanga, D.; Da Costa, J.P.; Germain, C. Real-time Fruit Detection Using Deep Neural Networks. In Proceedings of the 14th International Conference on Precision Agriculture (ICPA), Montreal, QC, Canada, 24–27 June 2018; pp. 1–10. [Google Scholar]
- Pereira, C.S.; Morais, R.; Reis, M.J.C.S. Deep Learning Techniques for Grape Plant Species Identification in Natural Images. Sensors 2019, 19, 4850. [Google Scholar] [CrossRef] [PubMed]
- Rahnemoonfar, M.; Sheppard, C. Deep count: Fruit counting based on deep simulated learning. Sensors 2017, 17, 905. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Śkrabánek, P. DeepGrapes: Precise Detection of Grapes in Low-resolution Images. In Proceedings of the 15th IFAC Conference on Programmable Devices and Embedded Systems (PDeS), Ostrava, Czech Republic, 23–25 May 2018; Volume 51, pp. 185–189. [Google Scholar]
- Cecotti, H.; Rivera, A.; Farhadloo, M.; Pedroza, M.A. Grape detection with convolutional neural networks. Expert Syst. Appl. 2020, 159, 113588. [Google Scholar] [CrossRef]
- Santos, T.T.; de Souza, L.L.; dos Santos, A.A.; Avila, S. Grape detection, segmentation, and tracking using deep neural networks and three-dimensional association. Comput. Electron. Agric. 2020, 170, 105247. [Google Scholar] [CrossRef]
- Bresilla, K.; Perulli, G.D.; Boini, A.; Morandi, B.; Corelli Grappadelli, L.; Manfrini, L. Single-Shot Convolution Neural Networks for Real-Time Fruit Detection Within the Tree. Front. Plant Sci. 2019, 10, 611. [Google Scholar] [CrossRef]
- Araya-Alman, M.; Leroux, C.; Acevedo-Opazo, C.; Guillaume, S.; Valdés-Gómez, H.; Verdugo-Vásquez, N.; Pañitrur-De la Fuente, C.; Tisseyre, B. A new localized sampling method to improve grape yield estimation of the current season using yield historical data. Precis. Agric. 2019, 20, 445–459. [Google Scholar] [CrossRef]
- Guerrero-Gómez-Olmedo, R.; Torre-Jiménez, B.; López-Sastre, R.; Maldonado Bascón, S.; Oñoro-Rubio, D. Extremely Overlapping Vehicle Counting. In Proceedings of the 2015 Iberian Conference on Pattern Recognition and Image Analysis (IbPRIA), Santiago de Compostela, Spain, 10–12 June 2015; Volume 9117, pp. 423–431. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS), Montreal, QC, Canada, 7–12 December 2015; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; 2015; pp. 91–99. [Google Scholar]
- Girshick, R. Fast R-CNN Object detection with Caffe. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Acuna, D.; Ling, H.; Kar, A.; Fidler, S. Efficient Interactive Annotation of Segmentation Datasets with Polygon-RNN++. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 859–868. [Google Scholar]
- Xie, W.; Noble, J.A.; Zisserman, A. Microscopy cell counting and detection with fully convolutional regression networks. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 283–292. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Wang, X.; Yang, X. Cross-scene crowd counting via deep convolutional neural networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 833–841. [Google Scholar]
- Poni, S.; Casalini, L.; Bernizzoni, F.; Civardi, S.; Intrieri, C. Effects of early defoliation on shoot photosynthesis, yield components, and grape composition. Am. J. Enol. Vitic. 2006, 57, 397–407. [Google Scholar]
- Liu, S.; Whitty, M.; Cossell, S. A Lightweight Method for Grape Berry Counting based on Automated 3D Bunch Reconstruction from a Single Image. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Font, D.; Tresanchez, M.; Martínez, D.; Moreno, J.; Clotet, E.; Palacín, J. Vineyard Yield Estimation Based on the Analysis of High Resolution Images Obtained with Artificial Illumination at Night. Sensors 2015, 15, 8284–8301. [Google Scholar] [CrossRef] [PubMed]
- Aquino, A.; Barrio, I.; Diago, M.P.; Millan, B.; Tardaguila, J. vitisBerry: An Android-smartphone application to early evaluate the number of grapevine berries by means of image analysis. Comput. Electron. Agric. 2018, 148, 19–28. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Chen, D. CSRNet: Dilated convolutional neural networks for understanding the highly congested scenes. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 1091–1100. [Google Scholar]
- Zhang, Y.; Zhou, D.; Chen, S.; Gao, S.; Ma, Y. Single-Image Crowd Counting Via Multi-Column Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 589–597. [Google Scholar]
- Heinrich, K.; Roth, A.; Breithaupt, L.; Möller, B.; Maresch, J. Yield Prognosis for the Agrarian Management of Vineyards using Deep Learning for Object Counting. In Proceedings of the 14th International Conference on Wirtschaftsinformatik (WI), Siegen, Germany, 24–27 February 2019; pp. 407–421. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 2015 International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F.-F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Dumoulin, V.; Visin, F. A guide to convolution arithmetic for deep learning. arXiv 2016, arXiv:1603.07285. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Lempitsky, V.; Zisserman, A. Learning to count objects in images. In Proceedings of the Advances in Neural Information Processing Systems 23 (NIPS), Vancouver, BC, Canada, 6–9 December 2010; Lafferty, J.D., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; 2010; pp. 1324–1332. [Google Scholar]
- Van der Walt, S.; Schönberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T. scikit-image: Image processing in Python. PeerJ 2014, 2, e453. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Wiltschko, A., van Merriënboer, B., Lamblin, P., Eds.; 2017; pp. 1–4. [Google Scholar]
- Sloth Development Team. Sloth. 2017. Available online: https://github.com/cvhciKIT/sloth (accessed on 11 July 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 2015 International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]






| 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | V | |
|---|---|---|---|---|---|---|---|
| [g] | [g] | [g] | [g] | [g] | [g] | ||
| Chardonnay | 170 | 184 | 176 | 172 | 172 | 208 | 0.06 |
| Lagrein | 280 | 279 | 325 | 265 | 259 | 264 | 0.06 |
| Marzemino | 308 | 311 | 336 | 326 | 350 | 318 | 0.04 |
| Pinot Gris | 164 | 177 | 181 | 141 | 167 | 205 | 0.09 |
| Pinot Noir | 149 | 174 | 159 | 155 | 158 | 175 | 0.05 |
| Sauvignon Blanc | 169 | 208 | 173 | 163 | 178 | 205 | 0.09 |
| Traminer | 138 | 155 | 174 | 143 | 157 | 151 | 0.06 |
| 2016 | 2017 | 2018 | V | |
|---|---|---|---|---|
| [g] | [g] | [g] | ||
| Chardonnay | 1.6 | 1.6 | 1.7 | 0.03 |
| Lagrein | 1.9 | 2.2 | 2.0 | 0.06 |
| Marzemino | 2.1 | 2.3 | - | 0.05 |
| Pinot Gris | 1.4 | 1.6 | 1.6 | 0.06 |
| Pinot Noir | 1.5 | 1.6 | 1.6 | 0.03 |
| Sauvignon Blanc | - | 1.8 | 1.6 | 0.06 |
| Traminer | 1.4 | 1.7 | 1.7 | 0.08 |
| Dataset | Variety | Images | Max | Min | Mean | Total |
|---|---|---|---|---|---|---|
| Chardonnay | 7 | 172 | 51 | 104.71 | 733 | |
| Lagrein | 9 | 211 | 117 | 163.22 | 1469 | |
| Marzemino | 16 | 244 | 53 | 114.81 | 1837 | |
| CR1 | Pinot Gris | 34 | 322 | 86 | 150.91 | 5131 |
| Pinot Noir | 21 | 269 | 93 | 142.00 | 2982 | |
| Sauvignon | 21 | 167 | 42 | 110.38 | 2318 | |
| Traminer | 20 | 207 | 61 | 126.80 | 2536 | |
| Total | 128 | 322 | 42 | 132.90 | 17,006 | |
| CR2 | Teroldego | 17 | 1764 | 535 | 1095.41 | 18,622 |
| n | MAE | MAE (%) | MSE | ||
|---|---|---|---|---|---|
| 5-CV | Per Image | 20.4 | 13.66 ± 4.70 | 11.16% ± 2.70% | 18.33 ± 6.33 |
| Overall | 2670.6 | 56.48 ± 60.08 | 2.13% ± 1.97% | ||
| Test | Per Image | 26 | 13.25 | 10.32% | 16.07 |
| Overall | 3653 | 10.65 | 0.29% |
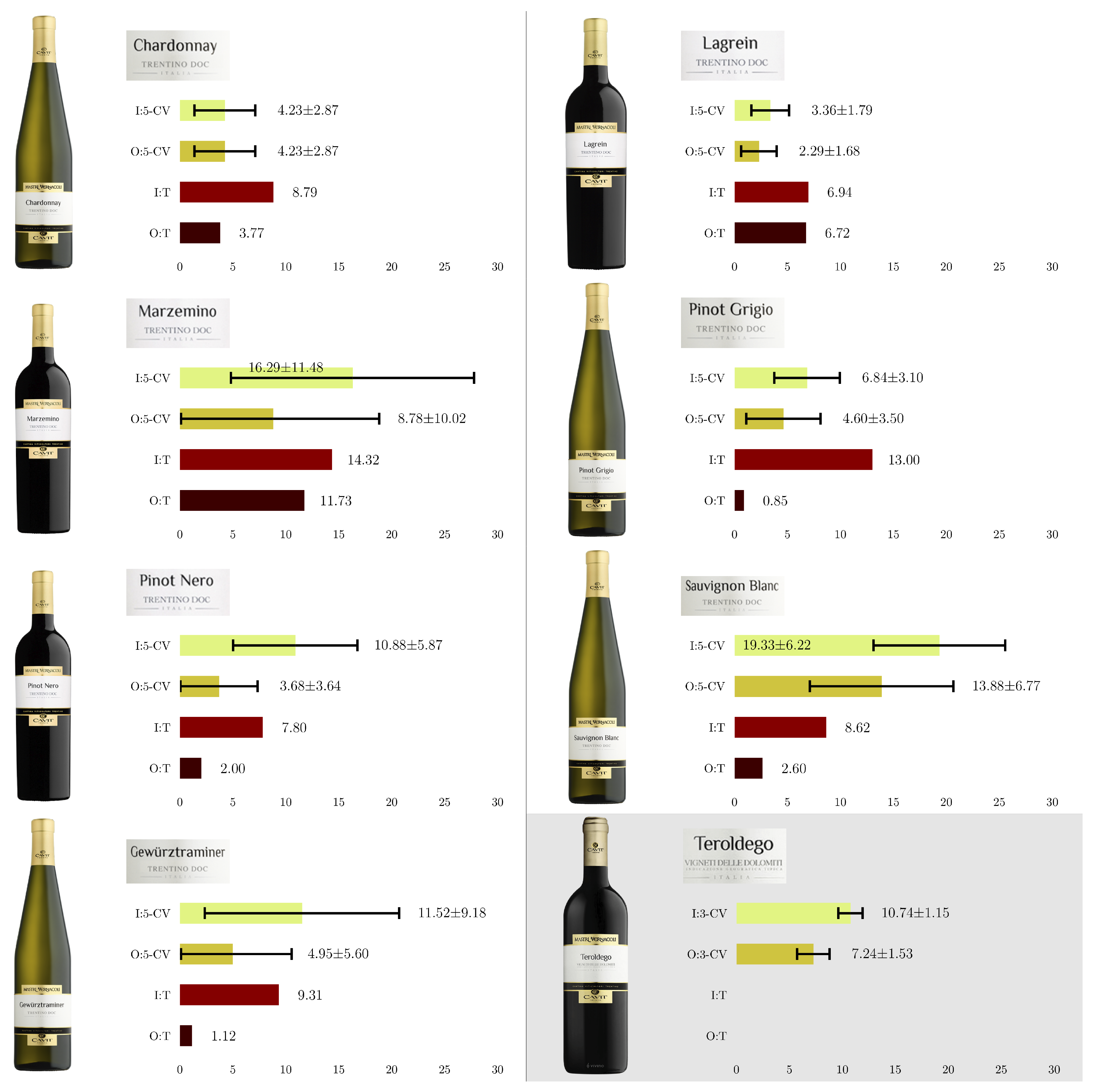
| Per Image | Overall | ||||||
|---|---|---|---|---|---|---|---|
| n | MAE | MAE (%) | MSE | N | MAE | MAE (%) | |
| Chardonnay | 1.0 | 4.69 ± 3.53 | 4.23% ± 2.87% | 4.69 ± 3.53 | 112.8 | 4.69 ± 3.53 | 4.23% ± 2.87% |
| Lagrein | 1.4 | 5.41 ± 3.23 | 3.36% ± 1.79% | 5.61 ± 3.51 | 228.2 | 4.63 ± 3.22 | 2.29% ± 1.68% |
| Marzemino | 2.6 | 18.48 ± 17.43 | 16.29% ± 11.48% | 21.29 ± 18.71 | 307.2 | 19.20 ± 16.00 | 8.78% ± 10.02% |
| Pinot Gris | 5.4 | 9.57 ± 3.75 | 6.84% ± 3.10% | 11.59 ± 4.39 | 766.6 | 36.60 ± 27.58 | 4.60% ± 3.50% |
| Pinot Noir | 3.4 | 14.30 ± 8.48 | 10.88% ± 5.87% | 16.08 ± 9.33 | 480.0 | 16.37 ± 13.82 | 3.68% ± 3.64% |
| Sauvignon | 3.4 | 21.35 ± 7.03 | 19.33% ± 6.22% | 25.08 ± 8.51 | 367.0 | 50.55 ± 28.15 | 13.88% ± 6.77% |
| Traminer | 3.2 | 14.02 ± 11.28 | 11.52% ± 9.18% | 15.88 ± 12.72 | 408.8 | 24.02 ± 32.51 | 4.95% ± 5.60% |
| Per Image | Overall | ||||||
|---|---|---|---|---|---|---|---|
| n | MAE | MAE (%) | MSE | N | MAE | MAE (%) | |
| Chardonnay | 2 | 7.74 | 8.79% | 8.38 | 169 | 6.38 | 3.77% |
| Lagrein | 2 | 11.03 | 6.94% | 11.88 | 328 | 22.05 | 6.72% |
| Marzemino | 3 | 13.77 | 14.32% | 16.99 | 301 | 35.31 | 11.73% |
| Pinot Gris | 7 | 19.86 | 13.00% | 22.98 | 1298 | 11.08 | 0.85% |
| Pinot Noir | 4 | 10.36 | 7.80% | 10.91 | 582 | 11.62 | 2.00% |
| Sauvignon | 4 | 10.35 | 8.62% | 12.79 | 483 | 12.54 | 2.60% |
| Traminer | 4 | 10.95 | 9.31% | 12.22 | 492 | 5.52 | 1.12% |
| n | MAE | MAE (%) | MSE | |
|---|---|---|---|---|
| Per Image | 5.7 | 117.36 ± 14.07 | 10.74 ± 1.15 | 137.81 ± 18.19 |
| Overall | 6207.3 | 466.53 ± 182.99 | 7.24 ± 1.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coviello, L.; Cristoforetti, M.; Jurman, G.; Furlanello, C. GBCNet: In-Field Grape Berries Counting for Yield Estimation by Dilated CNNs. Appl. Sci. 2020, 10, 4870. https://doi.org/10.3390/app10144870
Coviello L, Cristoforetti M, Jurman G, Furlanello C. GBCNet: In-Field Grape Berries Counting for Yield Estimation by Dilated CNNs. Applied Sciences. 2020; 10(14):4870. https://doi.org/10.3390/app10144870
Chicago/Turabian StyleCoviello, Luca, Marco Cristoforetti, Giuseppe Jurman, and Cesare Furlanello. 2020. "GBCNet: In-Field Grape Berries Counting for Yield Estimation by Dilated CNNs" Applied Sciences 10, no. 14: 4870. https://doi.org/10.3390/app10144870
APA StyleCoviello, L., Cristoforetti, M., Jurman, G., & Furlanello, C. (2020). GBCNet: In-Field Grape Berries Counting for Yield Estimation by Dilated CNNs. Applied Sciences, 10(14), 4870. https://doi.org/10.3390/app10144870






