Abstract
The Coulomb focusing effect on the electron–atom bremsstrahlung spectrum is investigated in nonthermal Lorentzian plasmas. The universal expression of the cross section of nonrelativistic electron–atom bremsstrahlung process is obtained by the solution of the Thomas-Fermi equation with the effective atomic charge. The effective Coulomb focusing for the electron–atom bremsstrahlung cross section near the threshold domain is also investigated by adopting the modified Elwert-Sommerfeld factor with the mean effective charge for the bremsstrahlung process. In addition, the bremsstrahlung emission rates are obtained by considering encounters between nonthermal electrons and atoms such as Fe and W atoms. We found that the bremsstrahlung emission rates for nonthermal electron–atoms are lower than those for thermal plasmas. Various nonthermal effects on the bremsstrahlung emission rates in Lorentzian plasmas are also discussed.
1. Introduction
The bremsstrahlung processes [1,2,3,4,5,6,7,8,9,10,11,12] in thermal and nonthermal plasmas have received considerable attention in astrophysics and plasma physics since the continuum X-ray spectra due to the electron–nucleus and electron–atom bremsstrahlung processes have long been used for plasma diagnostics in various weakly coupled astrophysical plasmas. Most research papers have considered the bremsstrahlung process for the electron-ion collision rather than for the electron–atom process, because of the smaller population of neutral atoms in highly ionized plasmas. Especially the electron–nucleus bremsstrahlung cross section [13] in weakly coupled plasmas has been extensively investigated by using the Yukawa-type Debye-Hückel potential. The electron–atom bremsstrahlung process [9,14,15] is quite important in weakly ionized plasmas, i.e., where the scattering of electrons by neutral atoms is important. In the electron–atom bremsstrahlung or scattering case, the screening [1,9] by the bound atomic electrons plays a crucial role in the cross section and the spectrum of the bremsstrahlung process. The influence of atomic screening on the electron–atom bremsstrahlung cross section can be studied with the Thomas-Fermi statistical model [16] for many-electron atoms. In addition, the doubly differential electron–atom bremsstrahlung cross section with form factor based on the approximate self-consistent Dirac-Hartree-Fock-Slater calculations has been obtained at high energies [15]. It is obvious that the Coulomb focusing factor for the electron-ion bremsstrahlung process is not the same with the electron–atom bremsstrahlung process because the effective charge of the bound atomic electrons is different from the total charge of the nucleus. However, the influence of Coulomb focusing on the electron–atom bremsstrahlung cross section and the radiation spectrum has not been investigated yet. In many plasmas, the coupling of the thermal plasma with the external radiation field produces the nonthermal plasma whose distribution is quite different from that of a Maxwellian plasma [17,18]. It has also been shown that the plasma electrons that deviated from the Maxwellian distribution are well represented by the Lorentzian distribution since the interaction potential in nonthermal plasmas cannot be appropriately obtained by using the conventional Debye-Hückel potential [18,19,20,21]. Therefore, we are motivated to study the bremsstrahlung process for electron–atom collision under the influence of atomic screening and Coulomb focusing correction in nonthermal plasmas. In this work, we derive the bremsstrahlung cross section for the electron–atom system by employing the Thomas-Fermi method with the effective charge of the atom. The Coulomb focusing correction for the electron–atom bremsstrahlung cross section near the threshold domain is also obtained by the modified Elwert-Sommerfeld factor with the mean effective charge for the electron–atom interaction based on the Thomas-Fermi solution. In addition, we obtain the Coulomb focused bremsstrahlung emission rates by encounters of nonthermal electrons and neutral atoms such as Fe (iron) and W (tungsten) atoms.
This paper is composed as follows: in Section 2, we introduce the Thomas-Fermi model for atoms and discuss the solution of the Thomas-Fermi model. We also obtain the mean effective charge based on the Thomas-Fermi method. In Section 3, we discuss the nonrelativistic electron–atom bremsstrahlung process and the Elwert-Sommerfeld Coulomb focusing factor. In Section 4, we obtain the modified electron–atom bremsstrahlung cross section by using the Thomas-Fermi solution including the Coulomb focusing factor with the mean effective charge of many-electron atoms. In Section 5, we obtain the closed form of the bremsstrahlung emission rates in nonthermal plasmas using the Lorentzian distribution function. In Section 6, the influence of nonthermal plasma on the electron–atom bremsstrahlung spectrum is investigated in nonthermal plasmas represented by the Lorentzian distribution function. Finally, the conclusions are given in Section 7.
2. Mean Effective Charge
The electron–atom interaction potential for the electron–atom bremsstrahlung process is represented by:
where r and denote the position of the projectile electron with respect to the center of the target atom and the position of the bound electron, respectively, Z is the charge number of the nucleus, e is the electron charge, and is the bound electron density of the target atom with being the bound electron number density. Then, the Fourier transformation of Equation (1) is obtained as:
where denote the atomic form factor due to the distribution of bound atomic electrons given by . It is obvious that is zero in the electron-ion bremsstrahlung process since there are no atomic electrons in the target ion. The Thomas-Fermi model [22] is very useful to study the process in the many-electron atoms and the collision dynamics in the neutral atoms. Using the typical parameters in the Thomas-Fermi model, is represented by:
where the parameter , is the Bohr radius of the hydrogen atom, is the Planck constant divided by , m is the electron mass, is the dimensionless momentum transfer, is the dimensionless distance, and is the Thomas-Fermi number density given by:
with being the solution of the Thomas-Fermi equation, (with the boundary condition ), and is the screening function of the atomic electrons in the Thomas-Fermi scheme defined by:
The approximate Thomas-Fermi solution can be often given in the form of single-exponential Mott-Massey solution [9,16], such as:
where . Since the boundary conditions [16] for the Thomas-Fermi equation, , are known as and , the single-exponential approximate Mott-Massey solution, would be reasonably reliable to investigate the atomic collision and radiation processes including many-electron neutral atoms. By taking of the Mott-Massey’s Thomas-Fermi solution given by Equation (6), the atomic form factor is obtained as:
Now, Equation (2) based on Mott-Massey’s single-exponential Thomas-Fermi solution becomes:
Hence, the effective charge of the target atom can take the form:
The mean effective charge for the electron–atom bremsstrahlung process is then given by:
where is defined by and is the maximum momentum transfer given by , with being the Bohr radius of the hydrogenic ion and Ze being the nuclear charge. Here, it is expected that Equation (10) is the universal expression of the mean effective charge for the bremsstrahlung and collision processes with many electron atoms since the effective charge is obtained by the Thomas-Fermi solution and the maximum momentum transfer is given by the main contribution region for the binary-encounter. Since the mean effective charge has a universal expression, Equation (10) can be the general expression of the effective charge for collision and radiation processes including neutral atoms with nuclear charge Ze.
3. Electron–Atom Bremsstrahlung and Coulomb Focusing
Using the second-order nonrelativistic perturbation analysis [8,14], the differential electron-ion bremsstrahlung cross section can be written as:
where is the differential elastic scattering cross section:
is the initial velocity of the projectile electron, is the Fourier transformation of the interaction potential :
where is the momentum transfer, and and are the wave vectors of the initial and final states of the projectile electron, respectively. Here, is the differential probability of emitting a photon of frequency between and in the solid angle :
where is the Compton wave number given by , is the fine structure constant, and is the unit photon polarization vector. By integrating over the directions of the radiation photon in Equation (14), we obtain the bremsstrahlung cross section in the form:
since the summation over polarizations gives the angular distribution factor , where is the angle between and q. In Equation (15), the quantity is defined as . In the nonrelativistic Born approximation, it is known that the domain of applicability is since the projectile energy is greater than , where is the Rydberg constant. It has been also known that the nonrelativistic Bethe-Heitler formula is invalid for the final state of the projectile electron near the cutoff region owing to the inaccuracy of the Born approximation for . Therefore, the nonrelativistic Bethe-Heitler formula must be corrected for hard spectral photon energies. In order to correct the Bethe-Heitler cross section, we must consider the motion of the initial and final states of the projectile electron in the external field of the target ion using a continuum wave function for the Coulomb potential since the final Coulomb wave function must be different from the initial Coulomb wave function due to the momentum transfer and the energy loss of the initial projectile electron. It has been shown that the Coulomb correction to the nonrelativistic Bethe-Heitler bremsstrahlung formula [1,3] using the Born approximation is obtained by the Elwert-Sommerfeld factor which is given by the ratio of the absolute square of the Coulomb wave functions at infinity and at the origin . The Coulomb correction in the Hamiltonian transition matrix element can be well approximated by the ratio of the absolute square of the final Coulomb s-wave function [22] to the initial Coulomb s-wave wave function at the origin, since survives for and the mutual Coulomb interaction between the electron and the target ion is quite effective for the small separation due to the Coulomb focusing effect, where and . Therefore, the square of the Coulomb wave function at the origin, , when the incident amplitude of the wave normalized to unity at infinity, , is given by . It is quite obvious that the main contribution to emission due to the bremsstrahlung process comes from the wave near the center of the scattering system since the acceleration of the projectile electron is largest near the scattering center. Hence, the Coulomb correction known as the Elwert-Sommerfeld Coulomb focusing factor [3,14,23] is represented by:
and in the Born limit, i.e., and . It has been also shown that the Elwert-Sommerfeld factor can correctly modified the electron-impact excitation cross section near the threshold domain [23]. As we see in Equation (15), the Coulomb focusing factor diverges at the spectral cutoff. However, this divergence compensates for the vanishing of the nonrelativistic Bethe-Heitler cross section at the cutoff, correctly resulting in a finite Bethe-Heitler cross section at the cutoff spectrum. The detailed discussion of the Coulomb correction using the Elwert-Sommerfeld Coulomb focusing factor is given in a recent work of Gould [14]. In the nonrelativistic electron–atom bremsstrahlung process, the charge number Z can be replaced by the effective charge number [Equation (10)], including the influence of screening by bound electrons.
4. Coulomb Focused Bremsstrahlung Cross Section
Using Equations (4) and (15) with the integration over the momentum transfer q for the domain , the electron–atom bremsstrahlung cross section [9] per photon energy using Mott-Massey’s single-exponential Thomas-Fermi solution is given by:
where is the bremsstrahlung photon energy, is the classical electron radius, , , , and . For the electron-ion bremsstrahlung process [14], the expression of the bremsstrahlung cross section is rather simple due to the omission of the screening effects:
However, the Coulomb focusing effect in the electron–atom bremsstrahlung process has not been investigated in the previous work of Jung and Lee [9], thus, the electron–atom bremsstrahlung cross section has to be corrected in the low-energy region. It is expected that Equations (6) and (15) provide the Coulomb focusing for the bremsstrahlung with neutral atoms since describes the effective charge of the neutral atom by the electron-encounter since the Coulomb focusing factor is needed for the modification of the bremsstrahlung cross section near the threshold region. The modified Elwert-Sommerfeld Coulomb focusing factor for the electron–atom bremsstrahlung process is then given by:
since the expression of the standard Elwert-Sommerfeld factor [14] is given by . Hence, Equation (19) is the universal formula for the Coulomb focusing factor for the bremsstrahlung process with neutral atoms. The scaled form of the Coulomb focused nonrelativistic electron–atom bremsstrahlung cross section per photon energy in units of including the influence of bound atomic electrons and Coulomb focusing at the spectral cutoff is then represented by:
Since the electron–atom bremsstrahlung cross section [Equation (20)] has been obtained by the Thomas-Fermi solution and the modified Elwert-Sommerfeld Coulomb focusing factor with the mean effective charge for the electron–atom interaction, the modified electron–atom bremsstrahlung cross section would be quite reliable for investigating the physical properties of atomic bremsstrahlung spectra over wide range of electron energy including the spectral cutoff region. The bremsstrahlung emission rates in nonthermal Lorentzian astrophysical plasmas will also be discussed in the following section.
5. Bremsstrahlung Emission Rates in Lorentzian Kappa Plasmas
In most astrophysical and space plasmas, the external disturbances in thermal plasmas would produce the high-energy tail in the distribution of plasma electrons so that the deviations from the thermal Maxwellian distribution is expected due to the interaction between the plasma and the external perturbations. A pioneering work by Hasegawa, Mima, and Duong-van [17] showed that the nonthermal distribution due to the entropy generalization mechanism in the presence of external radiation field in astrophysical plasmas obeys the Lorentzian (kappa) velocity distribution function [17,18,24] in the form:
where and are the velocity and the density of electron, is the spectral index in the Lorentzian distribution, is the effective energy of the Lorentzian electrons, , is the Boltzmann constant, T is the electron temperature, and represents the gamma function with the argument z. Then, the differential Lorentzian electron distribution function can be represented by . It has been also shown that the radiation interaction modifies the conventional diffusion process in astrophysical plasmas so that the correction on the total diffusion coefficient can be represented by the factor , where is a constant related to the external radiation field intensity, since the non-Coulombic diffusion coefficient is found to be proportional to the square of the electron velocity and can be also induced by the interaction with the field [17]. It is also interesting to note that the Lorentzian distribution acquiesces a simple power-law form at high energies, i.e., we have when . Moreover, the nonthermal astrophysical Lorentzian distribution with the infinity spectral index , equivalent to the absence of the external interaction, turns out to be the thermal distribution for all velocities such as owing to the mathematical limiting relation: , where corresponds to the thermal energy in the Maxwellian plasmas, i.e., [17]. Hence, we have found that the Lorentzian distribution encompasses a wide range of plasma velocity distributions from the Maxwellian distribution to the inverse power law distribution. In addition, the effective Debye length in nonthermal Lorentzian plasmas can be represented by [18] where is the conventional Debye length in Maxwellian plasmas and stands for the fractional measure of the nonthermal population in astrophysical Lorentzian plasmas. Hence, the bremsstrahlung emission rate for a given differential Lorentzian electron density distribution can be written by:
where is the bremsstrahlung radiation energy and is the atom density. Then, the scaled bremsstrahlung emission rate in units of is represented by:
where in the lower bound of the integral represents the cutoff, i.e., , , and . The nonthermal effects on the bremsstrahlung emission rate as well as the electron–atom bremsstrahlung cross sections will be discussed in the following section.
6. Nonthermal and Coulomb Focusing Effects in Lorentzian (Kappa) Plasmas
The neutral elements in a plasma can be detected by using spatially resolved plasma spectroscopy [25]. Since Fe and W atoms are important elements in astrophysical and laboratory plasmas, we shall consider the electron–atom bremsstrahlung process with those elements in nonthermal Lorentzian plasmas. In order to investigate the behavior of the electron–atom bremsstrahlung in wide spectral ranges such as the soft- and hard-photon ranges, we choose , i.e., .
Figure 1 shows the electron-ion bremsstrahlung cross sections and the electron–atom bremsstrahlung cross sections per photon energy in units of as functions of the scaled photon energy for W and Fe atoms. In this figure, we see that the electron–atom bremsstrahlung cross section is quite different from the electron-ion bremsstrahlung cross section due to the screening effect caused by the bound electrons in the atom. We also see that the bremsstrahlung cross section is suppressed by the influence of bound atomic electrons. Figure 2 represents the scaled form of the electron–atom bremsstrahlung cross sections per photon energy in units of as functions of the scaled photon energy for W and Fe atoms. As shown in this figure, the Coulomb focusing enhances the bremsstrahlung cross section, especially for high-energy photons, for example, about 30% at . In addition, we see that the Coulomb focusing effect on the electron–atom bremsstrahlung cross section increases with an increase of the radiation photon energy. Hence, the Coulomb focused electron–atom bremsstrahlung cross sections including the influence of Coulomb focusing would be especially accurate for high-energy photons since the Coulomb focusing effect is significant near the cutoff spectral domain. Figure 3 shows the bremsstrahlung emission rate in units of as a function of for W atom with different values of when the Coulomb focusing is not considered. Figure 4 shows the Coulomb focused bremsstrahlung emission rate in units of as a function of for W atom with different including the Coulomb focusing effect. Figure 5 shows as a function of for Fe atom with different excluding the Coulomb focusing effect. Figure 6 shows as a function of for Fe atom with different including the effect of Coulomb focusing. As shown in Figure 3, Figure 4, Figure 5 and Figure 6, the bremsstrahlung emission rates for the electron–atom bremsstrahlung process in Maxwellian plasmas are always greater than those in nonthermal plasmas. In addition, the nonthermal effects on the bremsstrahlung emission rate for the soft photon case are found to be more significant than those for the hard photon case. Moreover, the influence of Coulomb focusing on the bremsstrahlung emission rate decreases with a decrease of the spectral index . Therefore, the Coulomb focusing effect on the bremsstrahlung emission rate is more significant in thermal plasmas and in hard spectral ranges. As shown in these figures, the nonthermal effect on decreases with decreasing . Hence, the classification of the nonthermal character of plasmas by using the bremsstrahlung spectrum would be quite significant in hard spectral regions. It is known that the states of free-electron in a dense plasma would be blocked by electrons occupying a quantum state by using the blocking factor [26,27]. The quantum blocking effect on the bremsstrahlung spectrum in dense quantum plasmas will be treated elsewhere.
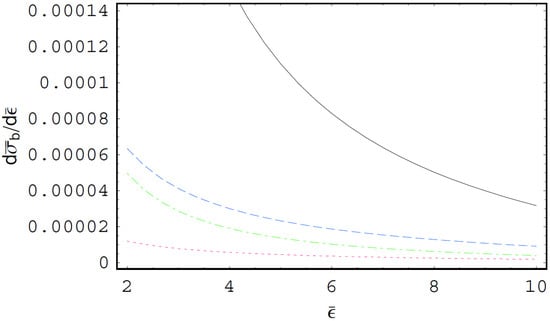
Figure 1.
The scaled form of the bremsstrahlung cross section per photon energy in units of as a function of the scaled photon energy for W and Fe atoms when . The black solid line is the electron-ion bremsstrahlung cross section for the W atom. The blue dashed line is the electron–atom bremsstrahlung cross section for the W atom including the influence of Coulomb focusing. The green dot-dashed line is the electron-ion bremsstrahlung cross section for the Fe atom. The red dotted line is the electron–atom bremsstrahlung cross section for the Fe atom including the influence of Coulomb focusing.
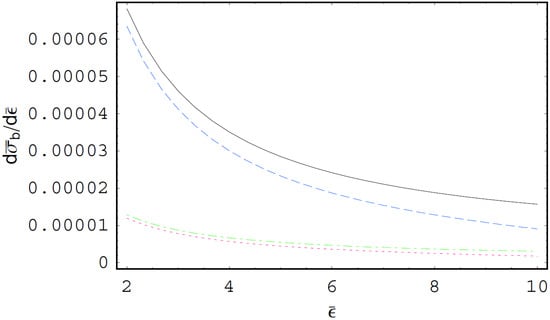
Figure 2.
The scaled form of the electron–atom bremsstrahlung cross section per photon energy in units of as a function of the scaled photon energy for W and Fe atoms when . The black solid line is the Coulomb focused electron–atom bremsstrahlung cross section for the W atom including the influence of Coulomb focusing. The blue dashed line is the electron–atom bremsstrahlung cross section for the W atom without the Coulomb focusing effect. The green dot-dashed line is the Coulomb focused electron–atom bremsstrahlung cross section for the Fe atom including the influence of Coulomb focusing. The red dotted line is the electron–atom bremsstrahlung cross section for the Fe atom without the Coulomb focusing effect.
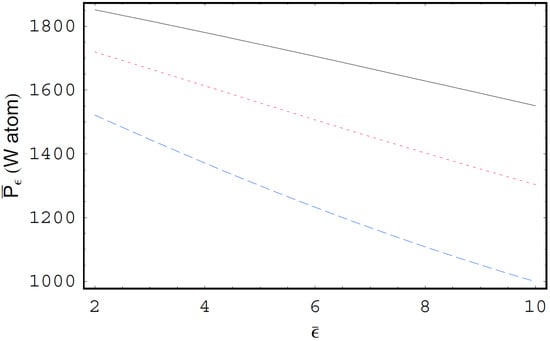
Figure 3.
The bremsstrahlung emission rate in units of as a function of the scaled photon energy for the W atom when without the Coulomb focusing effect. The solid line is the case of the thermal case, i.e., . The dotted line is the case of . The dashed is the case of .
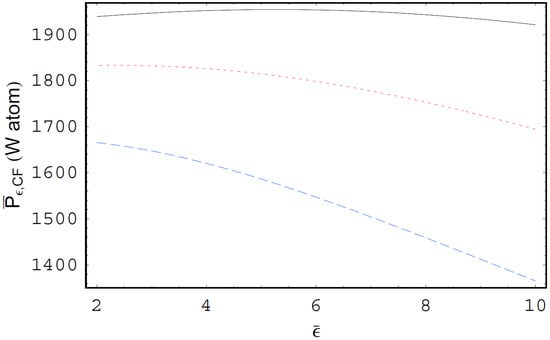
Figure 4.
The Coulomb focused bremsstrahlung emission rate in units of as a function of the scaled photon energy for the W atom when including the influence of Coulomb focusing. The solid line is the case of the thermal case, i.e., . The dotted line is the case of . The dashed is the case of .
Figure 5.
The bremsstrahlung emission rate in units of as a function of the scaled photon energy for the Fe atom when without the Coulomb focusing effect. The solid line is the case of the thermal case, i.e., . The dotted line is the case of . The dashed is the case of .
Figure 6.
The Coulomb focused bremsstrahlung emission rate in units of as a function of the scaled photon energy for the W atom when including the influence of Coulomb focusing. The solid line is the case of the thermal case, i.e., . The dotted line is the case of . The dashed is the case of .
7. Conclusions
In this work, we have investigated the Coulomb focused bremsstrahlung spectrum due to the electron–atom bremsstrahlung process in nonthermal plasmas. We derived the universal expression of the electron–atom bremsstrahlung cross section by using the Thomas-Fermi model with the effective charge method. We also derived the effective Coulomb focusing factor for the electron–atom bremsstrahlung process by using the modified Elwert-Sommerfeld factor with the mean effective charge for the binary-encounter. The Coulomb focused electron–atom bremsstrahlung cross section and the Coulomb focused bremsstrahlung emission rates in Lorentzian plasmas with Fe and W atoms were also obtained. The Coulomb focusing is found to increase the bremsstrahlung cross section. The effect of the Coulomb focusing on the electron–atom bremsstrahlung cross section becomes bigger with an increase of the radiation photon energy. Moreover, the bremsstrahlung emission rates for the electron–atom bremsstrahlung process in thermal Maxwellian plasmas are always greater than those in nonthermal Lorentzian plasmas. The nonthermal effect on the bremsstrahlung emission rate for the soft photon case is more significant than those for the hard photon case. Hence, it is expected that the hard-photon X-ray spectroscopy of the electron–atom bremsstrahlung process would be useful to explore the physical properties of nonthermal plasmas. In addition, we have found that the Coulomb focusing effect on the bremsstrahlung emission rate is important in thermal plasmas and in hard spectral ranges. It was shown that the synchrotron radiation image would be important for the investigation of the degree of anisotropy in fusion plasmas [28]. It was also shown that the screening effect plays a significant role in the photoionization process in weakly coupled plasmas [29,30]. Hence, the Coulomb focusing effects on the bremsstrahlung process in magnetized plasmas and on the photoionization process will also be investigated elsewhere by using the modified effective charge method [31,32]. Recently, the physical significance of dusty plasmas has received a considerable attention since the dusty plasmas can be found in various astrophysical complex plasmas as well as in laboratory plasma devices [33,34,35,36,37,38]. The investigation of the influence of Coulomb focusing on the bremsstrahlung process in dusty plasmas will also be treated elsewhere since the charging of the dust grains takes a crucial role in the bremsstrahlung spectrum. It is quite obvious that the simple universal theoretical model such as the Thomas-Fermi model [39] provides a necessary intellectual framework for the collision and radiation processes as well as the geometrical configurations of the physical system. In addition, the simple analytical model can be used to understand simulations and experiments [40,41], and to extract more physical information from them. Hence, our results for the analytic expressions of the Coulomb focused electron–atom bremsstrahlung cross section and the Coulomb focused bremsstrahlung emission rates in Lorentzian plasmas would provide the useful information on the astrophysical and laboratory nonthermal X-ray radiations. In this work, we have found that the nonthermal character of the plasma as well as the Coulomb focusing effect plays a very important role in the electron–atom bremsstrahlung process in Lorentzian plasma. These results should be useful for the investigation of radiation processes in nonthermal plasmas.
Author Contributions
Conceptualization, N.A.; Formal analysis, M.-J.L., Y.-D.J.; Funding acquisition, M.-J.L.; Investigation, Y.-D.J.; Methodology, Y.-D.J.; Project administration, M.-J.L.; Resources, N.A.; Validation, N.A.; Writing–original draft, M.-J.L., Y.-D.J.; Writing–review & editing, M.-J.L., N.A., Y.-D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Foundation of Korea (NRF-2019M1A7A1A03088471).
Acknowledgments
Two of the authors (M.-J. Lee and Y.-D. Jung) gratefully acknowledge I. Murakami and D. Kato for their warm hospitality while visiting the National Institute for Fusion Science (NIFS), Japan. This research was carried out while two of the authors (M.-J. Lee and Y.-D. Jung) were visiting the NIFS as visiting professors. The work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (NRF-2019M1A7A1A03088471).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One-and Two-Electron Atoms; Springer: Berlin/Heidelberg, Germany, 1957. [Google Scholar]
- Bekefi, G. Radiation Processes in Plasmas; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, synchrotron radiation, and Compton scattering of high-energy electrons traversing dilute gases. Rev. Mod. Phys. 1970, 42, 237. [Google Scholar] [CrossRef]
- Gould, R.J. Low-Frequency Bremsstrahlung in Coulomb Scatterings of Nonrelativistic Electrons. Am. J. Phys. 1970, 38, 189. [Google Scholar] [CrossRef]
- Gould, R.J. Thermal bremsstrahlung from high-temperature plasmas. Astrophys. J. 1980, 238, 1026. [Google Scholar] [CrossRef]
- Gould, R.J. Low-energy electron-atom bremsstrahlung. Astrophys. J. 1986, 302, 205. [Google Scholar] [CrossRef]
- Kawakami, R.; Mima, K.; Totsuji, H.; Yokoyama, Y. Bremsstrahlung from hot, dense, partially ionized plasmas. Phys. Rev. A 1988, 38, 3618. [Google Scholar] [CrossRef]
- Gould, R.J. Multipole radiation in charged-particle scattering. Astrophys. J. 1990, 362, 284. [Google Scholar] [CrossRef]
- Jung, Y.-D.; Lee, K.-S. Screening Effects on Nonrelativistic Bremsstrahlung in the Scattering of Electrons by Neutral Atoms. Astrophys. J. 1995, 440, 830. [Google Scholar] [CrossRef][Green Version]
- Jung, Y.-D.; Jeong, H.-D. Bremsstrahlung in electron-ion Coulomb scattering in strongly coupled plasma using the hyperbolic-orbit trajectory method. Phys. Rev. E 1996, 54, 1912. [Google Scholar] [CrossRef]
- Krainov, V.P.; Reiss, H.R.; Smirnovi, B.M. Radiative Processes in Atomic Physics; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Riffert, H.; Klingler, M.; Ruder, H. Bremsstrahlung Emissivity of a Proton-Electron Plasma in a Strong Magnetic Field. Phys. Rev. Lett. 1999, 87, 3432. [Google Scholar] [CrossRef]
- Jung, Y.-D.; Yang, K.-S. Classical Electron-Ion Coulomb Bremsstrahlung in Weakly Coupled Plasmas. Astrophys. J. 1997, 479, 912. [Google Scholar] [CrossRef][Green Version]
- Gould, R.J. Electromagnetic Processes; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Haug, E. Bremsstrahlung cross-section with screening and Coulomb corrections at high energies. Rad. Phys. Chem. 2008, 77, 207. [Google Scholar] [CrossRef]
- Mott, N.F.; Massey, H.S.W. The Theory of Atomic Collisions, 3rd ed.; Oxford University Press: Oxford, UK, 1987; Volume II. [Google Scholar]
- Hasegawa, A.; Mima, K.; Duong-van, M. Plasma Distribution Function in a Superthermal Radiation Field. Phys. Rev. Lett. 1985, 54, 2608. [Google Scholar] [CrossRef]
- Hasegawa, A.; Sato, T. Space Plasma Physics; Stationary Processes; Springer: Berlin/Heidelberg, Germany, 1989; Volume 1. [Google Scholar]
- Rubab, N.; Murtaza, G. Dust-charge fluctuations with non-Maxwellian distribution functions. Phys. Scr. 2006, 73, 178. [Google Scholar] [CrossRef]
- Rubab, N.; Murtaza, G. Debye length in non-Maxwellian plasmas. Phys. Scr. 2006, 74, 145. [Google Scholar] [CrossRef]
- Mendis, D.A.; Rosenberg, M. Cosmic dusty plasma. Annu. Rev. Astron. Astrophys. 1994, 32, 419. [Google Scholar] [CrossRef]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules, 2nd ed.; Prentice Hall: Harlow, UK, 2003. [Google Scholar]
- Jung, Y.-D. A simple correction for the Born approximation for electron impact excitation of hydrogenic ions. Astrophys. J. 1992, 396, 725. [Google Scholar] [CrossRef]
- Summers, D.; Thorne, R.M. Landau damping in space plasmas. Phys. Fluids B 1991, 3, 2117. [Google Scholar]
- Park, S.; Choe, W.; Moon, S.Y.; Park, J. Electron density and temperature measurement by continuum radiation emitted from weakly ionized atmospheric pressure plasmas. Appl. Phys. Lett. 2014, 104, 084103. [Google Scholar] [CrossRef]
- Ebeling, W.; Fortov, V.E.; Filinov, V. Quantum Statistics of Dense Gases and Nonideal Plasmas; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Tallents, G.J. An Introduction to the Atomic and Radiation Physics of Plasmas; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Hoppe, M.; Embréus, O.; Paz-Soldan, C.; Moyer, R.A.; Fülöp, T. Interpretation of runaway electron synchrotron and bremsstrahlung images. Nucl. Fusion 2018, 58, 082001. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Influence of Debye plasmas on photoionization of Li-like ions: Emergence of Cooper minima. Phys. Rev. A 2010, 81, 033405. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Photoionization cross sections of hydrogen impurities in spherical quantum dots using the finite-element discrete-variable representation. Phys. Rev. A 2011, 84, 023407. [Google Scholar] [CrossRef]
- Jung, Y.-D.; Gould, R.J. Energies and wave functions for many-electron atoms. Phys. Rev. A 1991, 44, 111. [Google Scholar] [CrossRef]
- Jung, Y.-D. Screening effects for transition probabilities in collisions of charged particles with an atom or stripped ion. Phys. Rev. A 1994, 50, 3895. [Google Scholar] [CrossRef]
- Kim, S.-H.; Merlino, R.L. Electron attachment to C7F14 and SF6 in a thermally ionized potassium plasma. Phys. Rev. E 2007, 76, 035401(R). [Google Scholar] [CrossRef] [PubMed]
- Heinrich, J.; Kim, S.-H.; Merlino, R.L. Observations of a structure-forming instability in a dc-glow-discharge dusty plasma. Phys. Rev. E 2011, 84, 026403. [Google Scholar] [CrossRef] [PubMed]
- Akbari-Moghanjoughi, M.; Shukla, P.K. Theory for large-amplitude electrostatic ion shocks in quantum plasmas. Phys. Rev. E 2012, 86, 066401. [Google Scholar] [CrossRef]
- Shukla, P.K.; Akbari-Moghanjoughi, M. Hydrodynamic theory for ion structure and stopping power in quantum plasmas. Phys. Rev. E 2013, 87, 043106. [Google Scholar] [CrossRef]
- Dzhumagulova, K.N.; Masheeva, R.U.; Ramazanov, T.S.; Donkó, Z. Effect of magnetic field on the velocity autocorrelation and the caging of particles in two-dimensional Yukawa liquids. Phys. Rev. E 2014, 89, 033104. [Google Scholar] [CrossRef] [PubMed]
- Ramazanov, T.S.; Moldabekov, Z.A.; Gabdullin, M.T. Multipole expansion in plasmas: Effective interaction potentials between compound particles. Phys. Rev. E 2016, 93, 053204. [Google Scholar] [CrossRef]
- Lee, M.-J.; Jung, Y.-D. Eikonal-Glauber Thomas-Fermi model for atomic collisions with many-electron atoms for plasma applications. J. Plasma Phys. 2018, 84, 905840313. [Google Scholar] [CrossRef]
- Griem, H. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).