Abstract
With the increasing number of population and the rising demand for electricity, providing safe and secure energy to consumers is getting more and more important. Adding dispersed products to the distribution network is one of the key factors in achieving this goal. However, factors such as the amount of investment and the return on the investment on one side, and the power grid conditions, such as loss rates, voltage profiles, reliability, and maintenance costs, on the other hand, make it more vital to provide optimal annual planning methods concerning network development. Accordingly, in this paper, a multilevel method is presented for optimal network power expansion planning based on the binary dragonfly optimization algorithm, taking into account the distributed generation. The proposed objective function involves the minimization of the cost of investment, operation, repair, and the cost of reliability for the development of the network. The effectiveness of the proposed model to solve the multiyear network expansion planning problem is illustrated by applying them on the 33-bus distribution network and comparing the acquired results with the results of other solution methods such as GA, PSO, and TS.
1. Introduction
In traditional networks, the transmission and distribution unit was utilized only to transfer the energy from the production unit to consumers, but with an increase in the use of a distributed generation, a part of the production was also assigned to the distribution system. According to definition [1], the distributed generations (DGs) are small production units associated with the distribution network. There are also other definitions describing the DGs, for example, [2,3,4]. On the other hand, the use of DGs changes the features of the distribution network [5].
With the increase in the population and the demand for electricity load, the need to supply safe and secure energy for consumers is becoming necessary more than ever. Adding DGs to the distribution network is one of the key factors to achieve this aim, which has several benefits such as preventing a sudden change in prices in the restructured markets [6], shorter production times duration than in comparison with large power plants, emission reduction, etc. [7]. To maximize the use of DGs, they should be placed at the optimum size and location [8,9]. Solving the multiyear network expansion planning (MNEP) problem is difficult due to the existence of large variables and complex mathematical model [10]. Therefore, a comprehensive model to solve the problem is highly needed. The objective function of the problem could include different factors such as investment cost, operating and maintenance cost, and reliability cost. These factors could be integrated with the coefficients weight or be solved through multi-objective models such as the dynamic ant colony search algorithm [11,12]. Several methods are utilized to solve this problem; for instance, integer linear programming [13,14], nonlinear programming [15,16], and dynamic programming [17,18]. Due to the complexity of the problem and the large number of its variables, the use of metaheuristic to obtain the best objective function value has been widely considered. The genetic algorithm (GA), particle swarm optimization algorithm (PSO), simulated annealing algorithm (SA), and other algorithms [19,20,21,22] show a small fraction of the application of metaheuristic to solve the problem. Favuzza et al. believe that it would be better to place the DGs and improve the feeders simultaneously, rather than separately solving these two problems. In this research, an intelligent method is proposed in which the DGs are employed as the alternatives [11]. Ouyang et al. proposed a method to develop a distribution network along with the DGs. In this research, the problem is solved taking into account the growth of prices and the uncertainty of DGs [23]. Peker et al. proposed a two-step stochastic programming model for the reliability constrained power system expansion planning. The model has been applied on the IEEE 118-bus power system and IEEE reliability test system [24]. Sharma and Balachandra have provided a model for solving the problem considering the uncertainty of the renewable resources [25]. Ahmadigorji and Amjady used the binary whale optimization algorithm to solve the expansion planning of distribution networks based on the multiyear DG-incorporated framework [26]. Essallah et al. presented a new model for the sizing and placement of distributed generation in order to ensure the reduction in total power losses and voltage stability in the power grid [27]. Vita provided a new model based on the decision-making algorithm in order to optimize the size and placement of distributed generation [28].
The main contributions and innovations of this paper are considered as follows:
- (a)
- A multilevel optimization method for optimal network power expansion planning has been proposed.
- (b)
- A new version of binary dragonfly’s algorithm has been proposed.
- (c)
- Considering distributed generation as renewable energies in power expansion planning.
- (d)
- The proposed objective function involves the minimization of the cost of investment, operation, and repair, plus the cost of reliability for the development of the network.
The structure of this study is summarized as follows: The mathematical formulation for multiyear network expansion planning is provided in Section 2. Section 3 presents the dragonfly optimization algorithm. The simulation and results are denoted in Section 4. The conclusion is summarized in Section 5.
2. Mathematical Formulation for Multiyear Network Expansion Planning
2.1. Problem Assumptions
In the present paper, each distributed generator could produce separately. The cost of investment and maintenance has been considered too.
2.2. Objective Function
In this study, the objective function is defined in a way that the cost of investment, operation and repair, along with the reliability cost are minimized in the presence of the DGs and its impact on the network. The main goal is to provide the best schedule for installing the DGs and network development within a specified time. The first phase of the objective function is the cost of investment including the installation cost of DGs and reinforcement of the feeder. The second phase is the operating cost, which includes the cost of purchasing power from the upstream grid, the operating cost of the DGs, the maintenance cost, and the cost of losses. The third phase of the objective function is the reliability value consisting of the unsupplied energy of the consumer. Finally, the mathematical model of the objective function is shown as follows:
where IC and OC are the investment cost and operation cost, respectively. The mathematical formulations are as follows:
Moreover, the converting function γ(t) to return the net present value of future cost is computed as follows:
where Dr is the discount rate, InvDG is the investment cost of the DG, and IC is the installation capacity. Kg,i and kr,i are binary variables to represent the installation decision of DG at bus i and the decision for reinforcement of the feeder section before bus i, respectively. U(t) is the unit step function (). FR is the reinforcement cost of the feeder section. πi,ls is the electricity price for purchasing power from the upstream grid at load level ls of year i. PUi,ls is the generated active power from the upstream grid at load level ls of year i. TDls is the time duration of load level ls. OpeDG is the operation and maintenance cost of the DG. PGi,j,ls is the generated active power of DG in bus j and load level ls of year i. Ny, Nb, and Nls are the number of years of the planning period, number of load buses, and number of load levels, respectively.
where is the electricity price for purchasing power from the upstream grid at load level ls of year 0.
where Demandi,ls is the total load demand of the distribution network at load level ls of year i. The reliability cost (RC) is calculated through Equation (7) [26]:
where EENSi is the expected energy not supplied of the distribution network in year i. VOLL0 is the value of lost load in the base year. σj is the average failure rate of the feeder section located before bus i. FLj is the length of the feeder section located before bus i. SP is the set of loads which can be restored by DG. UP is the set of loads which cannot be restored by DG. TPP is the set of loads which are shed after the fault occurrence on the ith feeder section and can be restored by the upstream grid. Trs is the required time to detect the fault location and isolating in the faulted feeder section. Trp is the required time to repair the faulted feeder section.
2.3. Problem Constraints
The nodal power balance for all buses should be satisfied by the following equations:
where Equations (10) and (11) demonstrate the constraints of power balance in the reference bus. Equations (12) and (13) illustrate the constraints of power balance for different load buses (from 1 to N).
2.3.1. Voltage Constraint
The voltage magnitude of each bus should be within the secure and admissible operating range:
In order to increase the performance of the optimization algorithm, the voltage constraint has been added to the objective function as a penalty part. The new version of the objective function is calculated as the following equation:
where Vj is the voltage of jth bus.
2.3.2. Thermal Capacity of Feeders
The feeders’ power must be less than their rated capacity:
In this study, the feeders’ reinforcement is supposed as doubling their thermal capacity. The total capacity of distributed generation on the grid should not exceed its maximum capacity:
where IL is a factor that determines the capacity constraints of the DGs per year.
3. Dragonfly Optimization Algorithm
In this paper, the dragonfly algorithm (DA) is utilized to solve the MNEP problem. The dragonfly is an insect of the dragonfly or Odonata. This insect is claimed to be one of the oldest winged insects. The fastest insect is Odonata, which is a kind of Australian dragonfly. Dragonflies have special conditions and special predator organs in terms of larvae and puberty, as well as the predatory features, and spend most of their life in a neonatal period [29]. In static groups, the dragonflies form a small group to cover a small area for hunting their own food [30].
However, in dynamic groups, a large number of dragonflies form a large group and go a long way in hunting [31]. The shape of the legs of this insect is in the form of a basket to make hunting easier, and the mouthpieces of the insect are also very powerfully rodent. Dragonflies are fast hunters that hunt their prey in the air. They have exceptionally high vision powers and can track the hunter’s insects and easily hunt with their blubber legs. Mirjalili introduced the dragonfly algorithm in 2016 [32]. The group behavior of dragonflies consists of three primitive principles [33]: (I) Separation, which implies the static collision avoidance of the neighbourhood individuals. (II) Alignment, which represents the velocity matching of neighbourhood individuals. (III) Cohesion, which refers to the tendency of neighbourhood individuals towards the center of the mass.
Figure 1 indicates the main factors in position updating of individuals in swarms. Each of these five factors is mathematically formulated as follows:
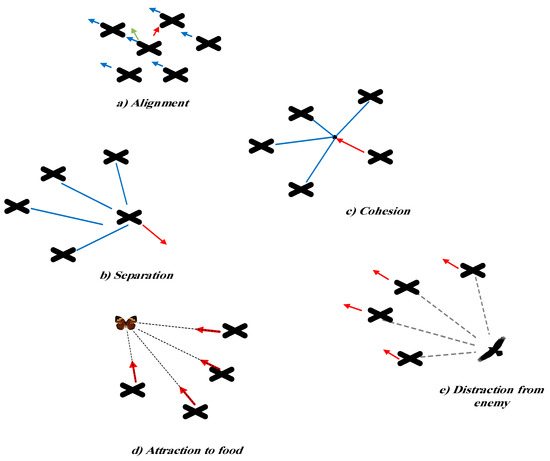
Figure 1.
Five factors in position updating of individuals in swarms.
The separation equation:
where Xi and Xn are the position of the current individual and the position nth neighbouring individual, respectively. N is the number of neighbouring individuals.
The alignment equation:
where Vn presents the velocity of nth neighbouring individual.
The cohesion equation:
The attraction towards a food source equation:
is the position of the food source.
The distraction outwards of an enemy equation:
is the position of the enemy.
In this paper, it is assumed that the behaviour of the dragonflies is a combination of these five corrective patterns.
where s, a, c, f, e are weight coefficients of the five main factors (separation, alignment, cohesion, attraction food, and the position of enemy). In addition, Si, Ai, Ci, Fi, Ei are the separation, alignment, cohesion, food source, and position of enemy of ith individual, respectively. w is the inertia weight, and t is the iteration counter.
To improve the performance of the algorithm, the position of dragonflies is updated based on the following equation:
where t and d are the iteration and the dimension of the position vectors, respectively. The dragonflies are required to fly around the search space using a random walk called Levy flight [32]. L is the Levy flight that can be calculated as follows:
where r1, r2 are two random numbers in [0, 1], β is a constant, and σ is calculated as follows:
The dragonfly algorithm flowchart is presented in Figure 2 [34].
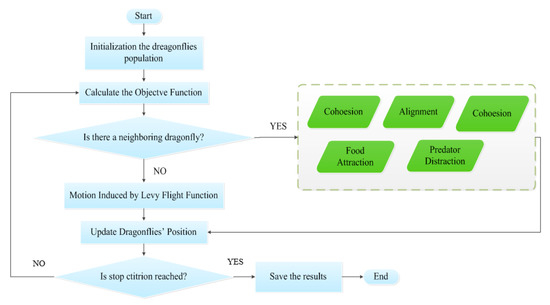
Figure 2.
Flowchart of the dragonfly algorithm.
Binary Version of the Dragonfly Algorithm
In continuous search spaces of the dragonfly algorithm, the search agents of DA get a new position by adding the step vectors. However, in the binary space, search agents can only obtain either 0 or 1.
The reference [35] concluded that the best way to solve this problem is to use the conversion function. Reference [36] showed that the v-shaped transfer functions are better than the s-shaped transfer functions in terms of exploitation. The following function has been used in this study:
The search position is updated as follows:
where r is a random number in the interval [0, 1].
4. Simulation and Results
The proposed optimization method is tested on a 33-bus IEEE-standard network to solve the multiyear network expansion planning problem. The single-line diagram of this network is shown in Figure 3. The network consists of 32 load buses, a reference bus, and 32 lines. The data of this network is visible in Table 1. The active and reactive load of the network are 3715 kW and 2300 kVAR, respectively.
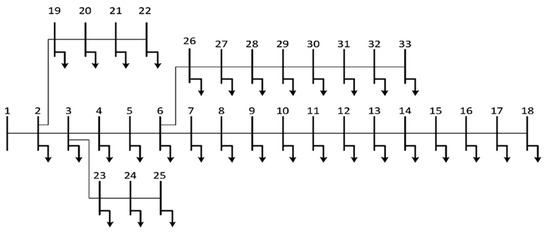
Figure 3.
The diagram of the IEEE 33-bus radial distribution system.

Table 1.
The data of the IEEE 33-bus distribution network [37].
In addition, the annual growth of the network 0.05 is assumed. Table 2 reports the required data for simulation, which are used from [26]. For this network, the three-level load is assumed based on which size of the load, the duration of load level, and the price of electricity at each level are shown in Table 3. The problem is solved by the proposed method and the details of the best solution are presented in Table 4. In this scenario, four DGs in the first and second years, two DGs in the third year, and one DG in the fourth year are installed.

Table 2.
The simulation data [26].

Table 3.
The details of the load duration curve [26].

Table 4.
The results of the best solution based on the proposed method.
Figure 4 represents the average network voltage before (without DG) and after (with DG) simulation. According to Figure 4, the voltage improvement rate could be clearly seen. As shown in the diagram, the base year of the program is also below the rated voltage (0.95) and, in order to improve the network voltage in the first year, it is necessary to add the DGs to the network. The voltage in the fourth year, due to the annual increase in load, gets the worst value, with an average of less than 0.93. Nevertheless, at the end of the planning, the network would no longer have this problem and therefore the voltage would increase significantly.
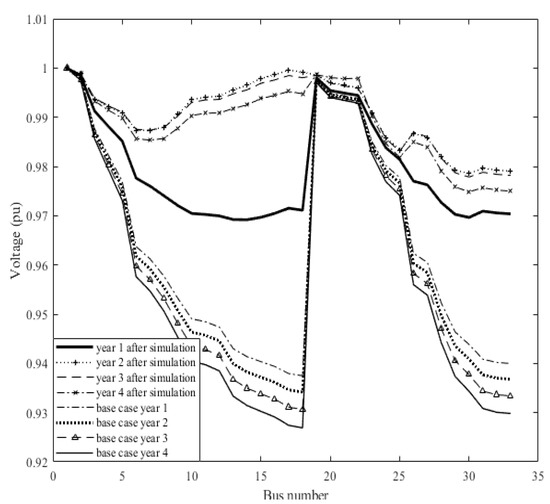
Figure 4.
The average network voltage in different years.
The problem solution has a great impact on the reliability of the network. Table 5 indicates the size of the EENS index before and after solving the problem (without DG and with DG). As it is shown in the Table, the expected reduction in unsupplied energy is significant. In the fourth year, this amount has reached from 21,058.9 to 11,579.8. The run times of each optimization method for 33-bus test systems are indicated in Table 6.

Table 5.
The EENSt values for each year of the planning period.

Table 6.
The run times of the proposed method and other optimization methods to solve the multiyear network expansion planning problem on 33-bus distribution networks.
5. Conclusions
According to some issues such as the amount of investment and the rate of return investment, and the power network conditions such as losses, voltage profiles, reliability, and maintenance, providing optimal annual planning methods for the development of the power system is essential. In this paper, a multilevel method is presented for optimal network power development planning based on the binary dragonfly optimization algorithm considering the DGs. The proposed objective function involves minimizing the cost of investment, operating and repairs, and the reliability cost for the network development by considering the presence of DGs. Additionally, the results indicate that considering DG decreases the EENS of the 33-bus test system by 29.37%, 37.64%, 41.45%, and 45.01% in the first, second, third, and fourth years, respectively. The proposed optimization method has been analyzed on a standard network, which has significantly improved the results compared with other benchmark methods such as GA, PSO, and TS.
Author Contributions
Conceptualization, M.H.K. and A.H.; investigation and methodology, all authors; validation, A.H., M.A., and F.K.; writing—original draft, M.H.K. and A.H.; writing—review and editing, A.H. and F.K., supervision, F.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| IC | Installation capacity | EENSi | Expected energy not supplied of distribution network in year i |
| OC | Operation cost | VOLL0 | Value of lost load in base year |
| RC | Reliability cost | σj | Average failure rate of feeder section located before bus i |
| γ(t) | Converting function | FLj | Length of feeder section located before bus i |
| Dr | Discount rate (%) | SP | Set of loads which can be restored by DG |
| U(t) | Unit step function | UP | Set of loads which cannot be restored by DG |
| InvDG | Investment Cost of DG | TPP | Set of loads which are shed after the fault occurrence on the ith feeder section and can be restored by the upstream grid |
| Kg,i | Binary variables to represent the installation decision of DG at bus i | Trs | Required time to detect the fault location and isolating in the faulted feeder section |
| kr,i | Binary variables to represent the decision for reinforcement of the feeder section before bus i | Trp | Required time to repair the faulted feeder section |
| FR | Reinforcement cost of the feeder section | Vj | Voltage of jth bus |
| πi,ls | Electricity price for purchasing power from the upstream grid at load level ls of year i | IL | A factor that determines the DGs capacity constraints per year |
| PUi,ls | Generated active power from the upstream grid at load level ls of year i | ||
| Abbreviations | |||
| TDls | Time duration of load level ls | MNEP | Multiyear Network Expansion Planning |
| OpeDG | DGs operation and maintenance cost | DG | Distributed Generation |
| PGi,j,ls | Generated active power of DG in bus j and load level ls of year i | GA | Genetic Algorithm |
| Ny | Number of years of the planning period | SA | Simulated Annealing Algorithm |
| Nb | Number of load buses | PSO | Particle Swarm Optimization Algorithm |
| Nls | Number of load levels | TS | Tabu Search |
| π0,ls | Electricity price for purchasing power from the upstream grid at load level ls of year 0 | DA | Dragonfly Algorithm |
| Demandi,ls | Total load demand of distribution network at load level ls of year i | ||
References
- Willis, H.L. Analytical methods and rules of thumb for modeling dg-distribution interaction. In Proceedings of the 2000 Power Engineering Society Summer Meeting (Cat. No. 00CH37134), Seattle, WA, USA, 16–20 July 2000; Volume 3, pp. 1643–1644. [Google Scholar] [CrossRef]
- Cardell, J.; Tabors, R. Operation and Control in a Competitive Market: Distributed Generation in a Restructured Industry. Energy J. 1997, 18, 111–136. [Google Scholar] [CrossRef]
- Sharma, D.; Bartels, R. Distributed electricity generation in competitive energy markets: A case study in Australia. Energy J. 1997, 18, 17–39. [Google Scholar] [CrossRef]
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation—A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Pesaran, M.H.A.; Huy, P.D. Ramachandaramurthy VK. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy Rev. 2017, 75, 293–312. [Google Scholar] [CrossRef]
- Capuder, T.; Mancarella, P. Techno-economic and environmental modelling and optimization of flexible distributed multi-generation options. Energy 2014, 71, 516–533. [Google Scholar] [CrossRef]
- Zangiabadi, M.; Feuillet, R.; Lesani, H.; Hadj-Said, N.; Kvaløy, J.T. Assessing the performance and benefits of customer distributed generation developers under uncertainties. Energy 2010, 36, 1703–1712. [Google Scholar] [CrossRef]
- Celli, G.; Ghiani, E.; Mocci, S.; Pilo, F. A multiobjective evolutionary algorithm for the sizing and siting of distributed generation. IEEE Trans. Power Syst. 2005, 20, 750–757. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Gorien, T.; Foote, B.L. Distribution-system planning using mixed-integer programming. IEE Proc. C Gener. Transm. Distrib. 1981, 128, 70–79. [Google Scholar]
- Favuzza, S.; Graditi, G.; Ippolito, M.G.; Sanseverino, E.R. Optimal electrical distribution systems reinforcement planning using gas micro turbines by dynamic ant colony search algorithm. IEEE Trans. Power Syst. 2007, 22, 580–587. [Google Scholar] [CrossRef]
- Pilo, F.; Celli, G.; Mocci, S.; Soma, G.G. Multi-objective programming for optimal DG integration in active distribution systems. In Proceedings of the IEEE PES General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Kang, X.; Fang, Z.; Kong, L.; Cheng, H.; Yao, X.; Lu, G.; Wang, P. Ammonia borane destabilized by lithium hydride: An advanced on-board hydrogen storage material. Adv. Mater. 2008, 20, 2756–2759. [Google Scholar] [CrossRef] [PubMed]
- Shu, J.; Wu, L.; Li, Z.; Shahidehpour, M.; Zhang, L.; Han, B. A new method for spatial power network planning in complicated environments. IEEE Trans. Power Syst. 2012, 27, 381–389. [Google Scholar] [CrossRef]
- Khodr, H.M.; Vale, Z.A.; Ramos, C. A benders decomposition and fuzzy multicriteria approach for distribution networks remuneration considering dg. IEEE Trans. Power Syst. 2009, 24, 1091–1101. [Google Scholar] [CrossRef]
- Wong, S.; Bhattacharya, K.; Fuller, J.D. Electric power distribution system design and planning in a deregulated environment. IET Gener. Transm. Distrib. 2009, 3, 1061–1078. [Google Scholar] [CrossRef]
- Popović, Z.N.; Popović, D.S. Graph theory based formulation of multi-period distribution expansion problems. Electr. Power Syst. Res. 2010, 80, 1256–1266. [Google Scholar] [CrossRef]
- Ganguly, S.; Sahoo, N.C.; Das, D. Multi-objective particle swarm optimization based on fuzzy-Pareto-dominance for possibilistic planning of electrical distribution systems incorporating distributed generation. Fuzzy Sets Syst. 2013, 213, 47–73. [Google Scholar] [CrossRef]
- Salehi, J.; Haghifam, M.R. Long term distribution network planning considering urbanity uncertainties. Int. J. Electr. Power Energy Syst. 2012, 42, 321–333. [Google Scholar] [CrossRef]
- Chen, T.H.; Lin, E.H.; Yang, N.C.; Hsieh, T.Y. Multi-objective optimization for upgrading primary feeders with distributed generators from normally closed loop to mesh arrangement. Int. J. Electr. Power Energy Syst. 2013, 45, 413–419. [Google Scholar] [CrossRef]
- Popović, Z.N.; Kerleta, V.D.; Popović, D.S. Hybrid simulated annealing and mixed integer linear programming algorithm for optimal planning of radial distribution networks with distributed generation. Electr. Power Syst. Res. 2014, 108, 211–222. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Georgilakis, P.S.; Hatziargyriou, N.D. A Tabu search method for distribution network planning considering distributed generation and uncertainties. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7–10 July 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ouyang, W.; Cheng, H.; Zhang, X.; Yao, L.; Bazargan, M. Distribution network planning considering distributed generation by genetic algorithm combined with graph theory. Electr. Power Compon. Syst. 2010, 38, 325–339. [Google Scholar] [CrossRef]
- Peker, M.; Kocaman, A.S.; Kara, B.Y. A two-stage stochastic programming approach for reliability constrained power system expansion planning. Int. J. Electr. Power Energy Syst. 2018, 103, 458–469. [Google Scholar] [CrossRef]
- Sharma, T.; Balachandra, P. Model based approach for planning dynamic integration of renewable energy in a transitioning electricity system. Int. J. Electr. Power Energy Syst. 2019, 105, 642–659. [Google Scholar] [CrossRef]
- Ahmadigorji, M.; Amjady, N. A multiyear DG-incorporated framework for expansion planning of distribution networks using binary chaotic shark smell optimization algorithm. Energy 2016, 102, 199–215. [Google Scholar] [CrossRef]
- Essallah, S.; Khedher, A.; Bouallegue, A. Integration of distributed generation in electrical grid: Optimal placement and sizing under different load conditions. Comput. Electr. Eng. 2019, 79, 106461. [Google Scholar] [CrossRef]
- Vita, V. Development of a decision-making algorithm for the optimum size and placement of distributed generation units in distribution networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Thorp, J.H.; Rogers, D.C. Thorp and Covich’s Freshwater Invertebrates: Ecology and General Biology; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Wikelski, M.; Moskowitz, D.; Adelman, J.S.; Cochran, J.; Wilcove, D.S.; May, M.L. Simple rules guide dragonfly migration. Biol. Lett. 2006, 2, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Russell, R.W.; May, M.L.; Soltesz, K.L.; Fitzpatrick, J.W. Massive Swarm Migrations of Dragonflies (Odonata) in Eastern North America. Am. Midl. Nat. 1998, 140, 325–342. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, Herds, and Schools: A Distributed Behavioral Model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Association for Computing Machinery, New York, NY, USA, 1 January 1987; pp. 25–34. [Google Scholar] [CrossRef]
- Zolghadr-Asli, B.; Bozorg-Haddad, O.; Chu, X. Dragonfly Algorithm (DA), Advanced Optimization by Nature-Inspired Algorithms; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary Particle Swarm Optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. How important is a transfer function in discrete heuristic algorithms. Neural Comput. Appl. 2015, 26, 625–640. [Google Scholar] [CrossRef]
- Das, D.; Kothari, D.P.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).