Hybrid Forecasting Models Based on the Neural Networks for the Volatility of Bitcoin
Abstract
1. Introduction and Review of Models
1.1. Introduction
1.2. Review of Models
1.2.1. GARCH Model
1.2.2. EGARCH Model
1.2.3. GJR-GARCH Model
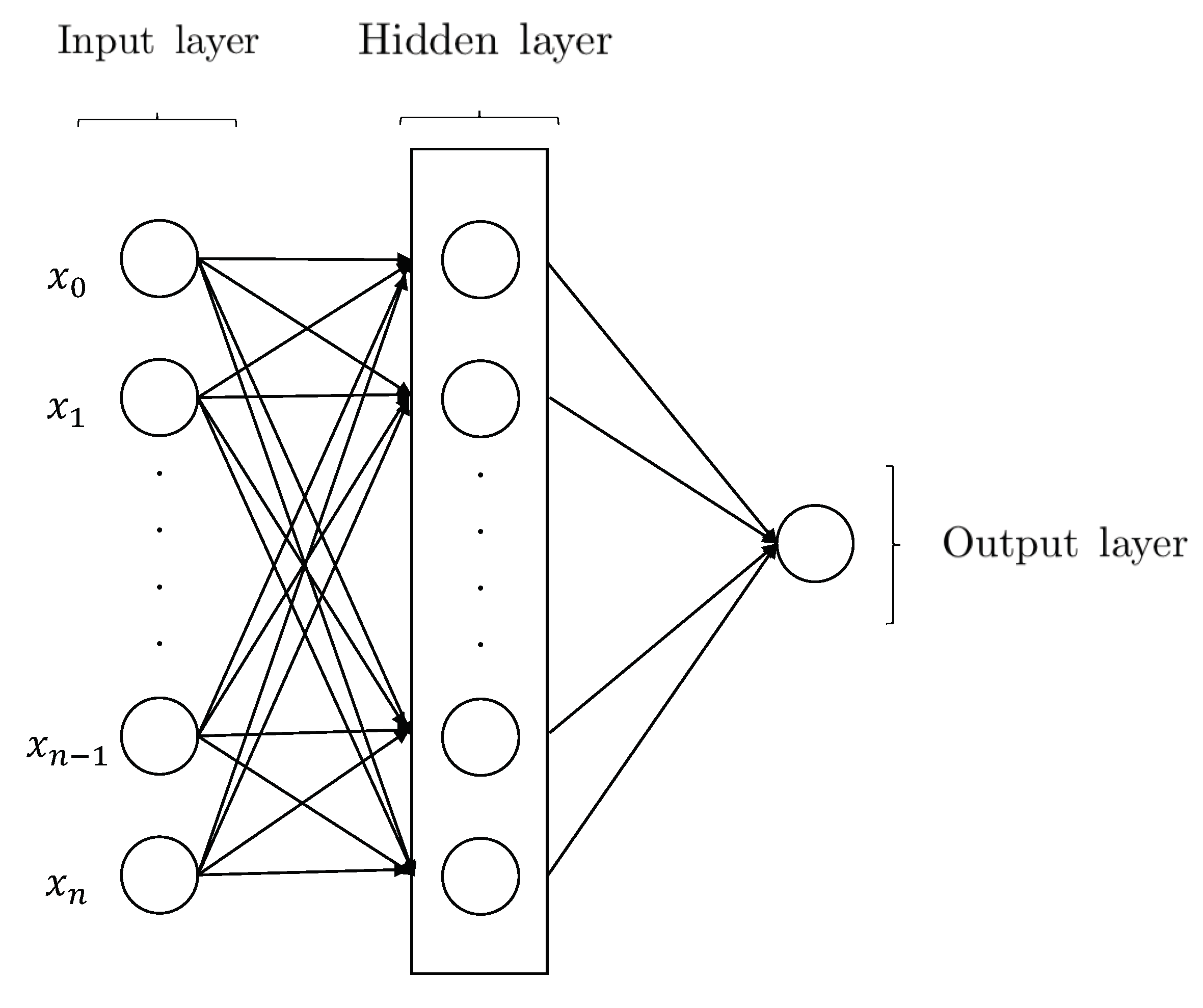
1.2.4. Artificial Neural Network (ANN)
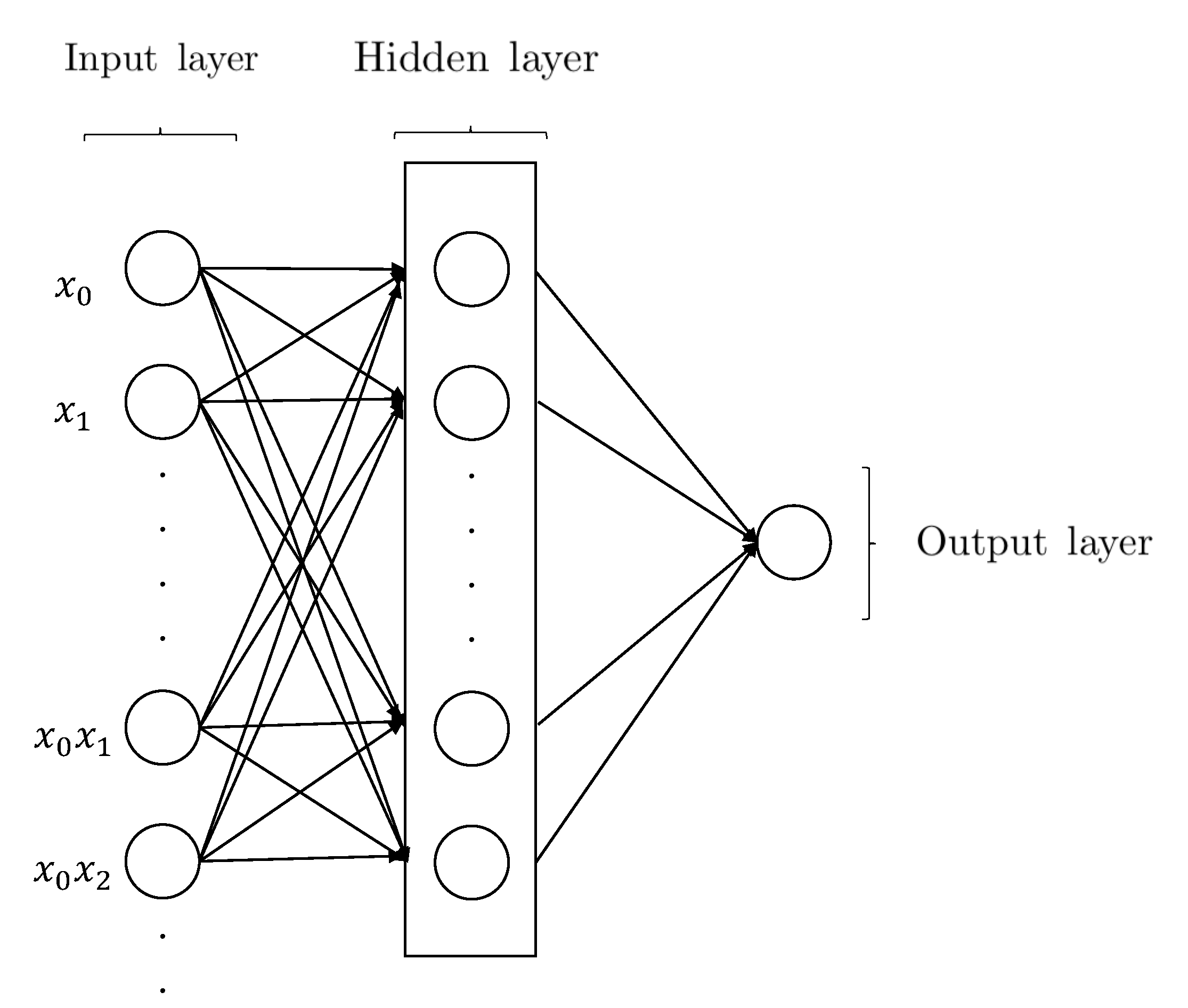
1.2.5. Higher Order Neural Network (HONN)
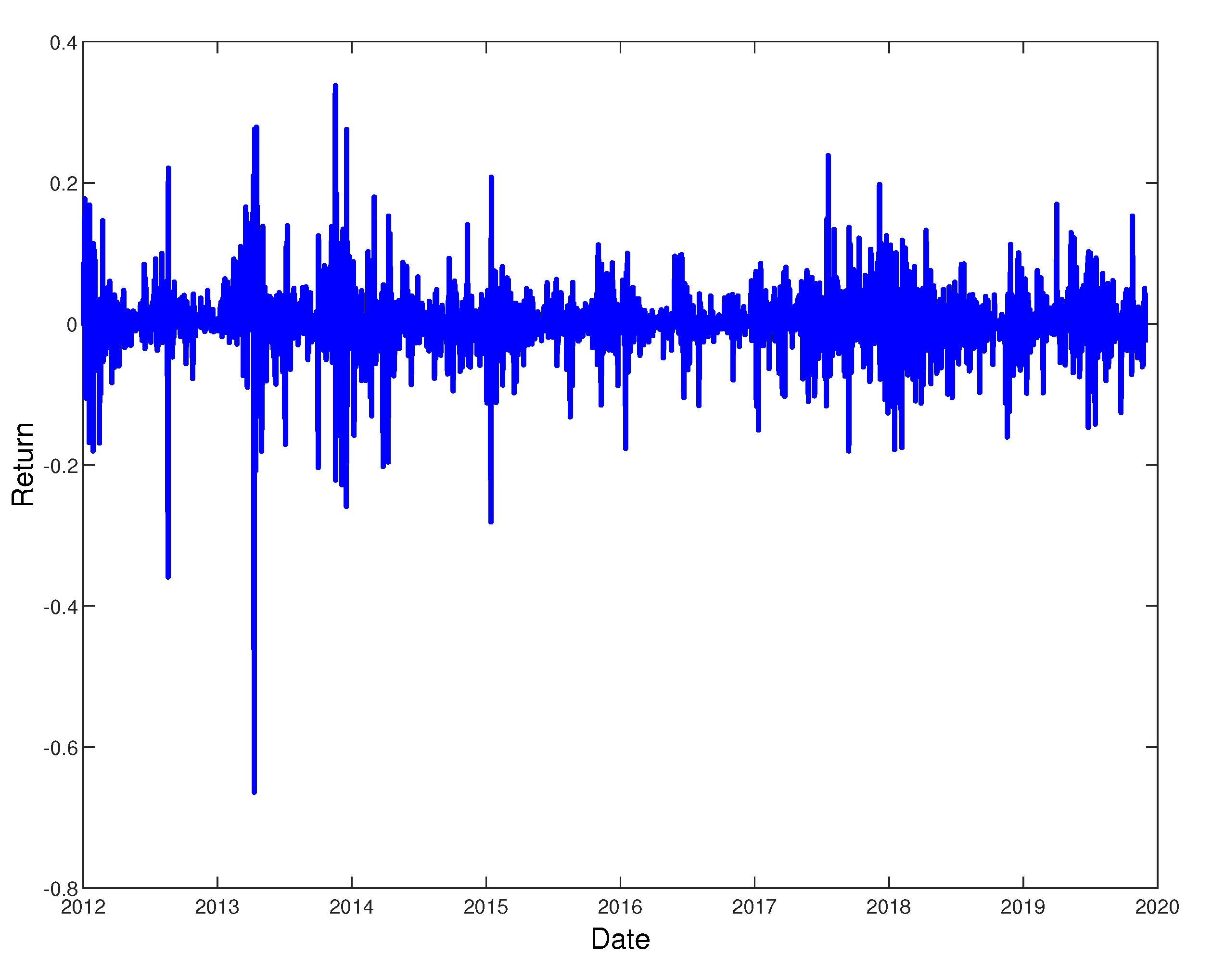
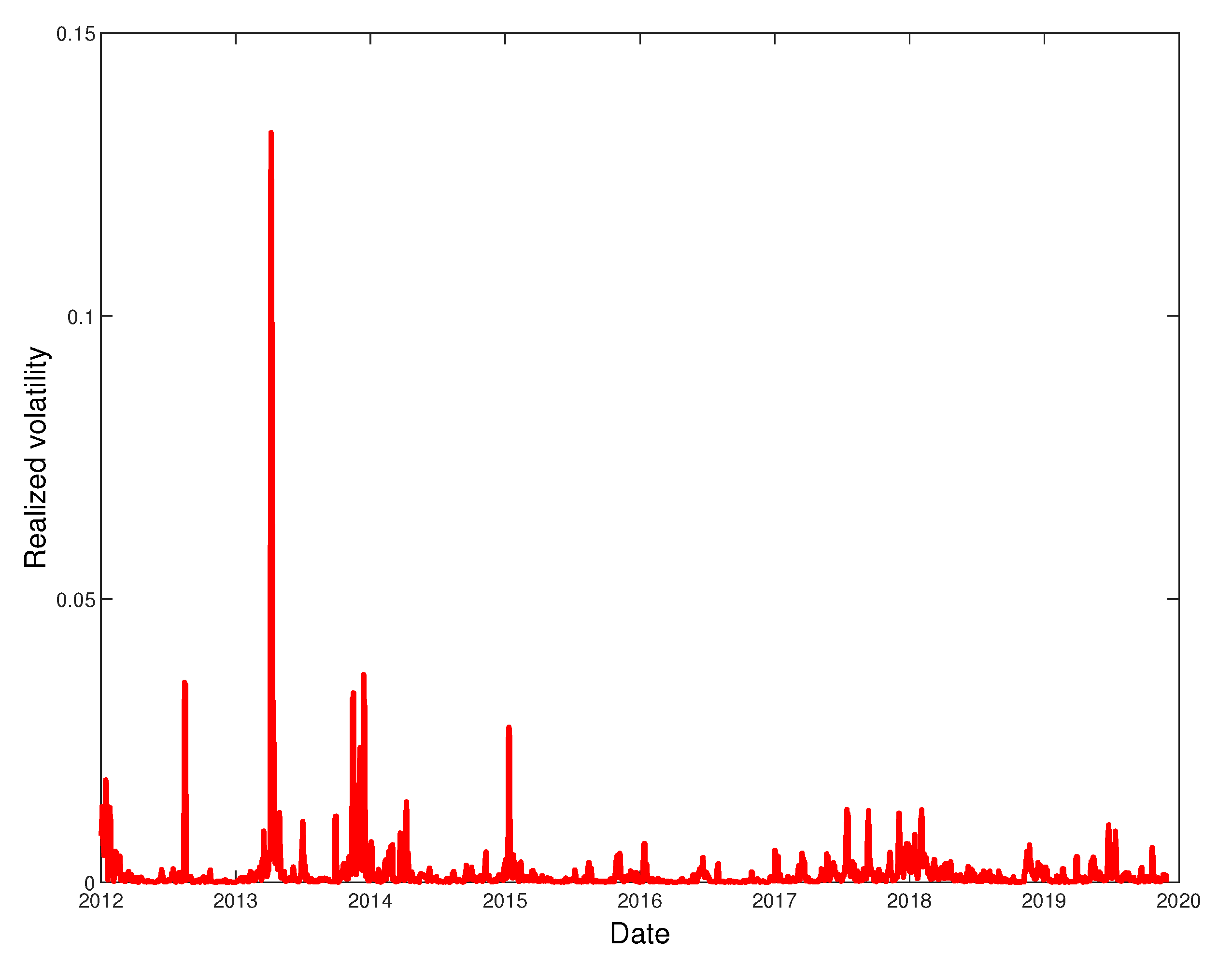
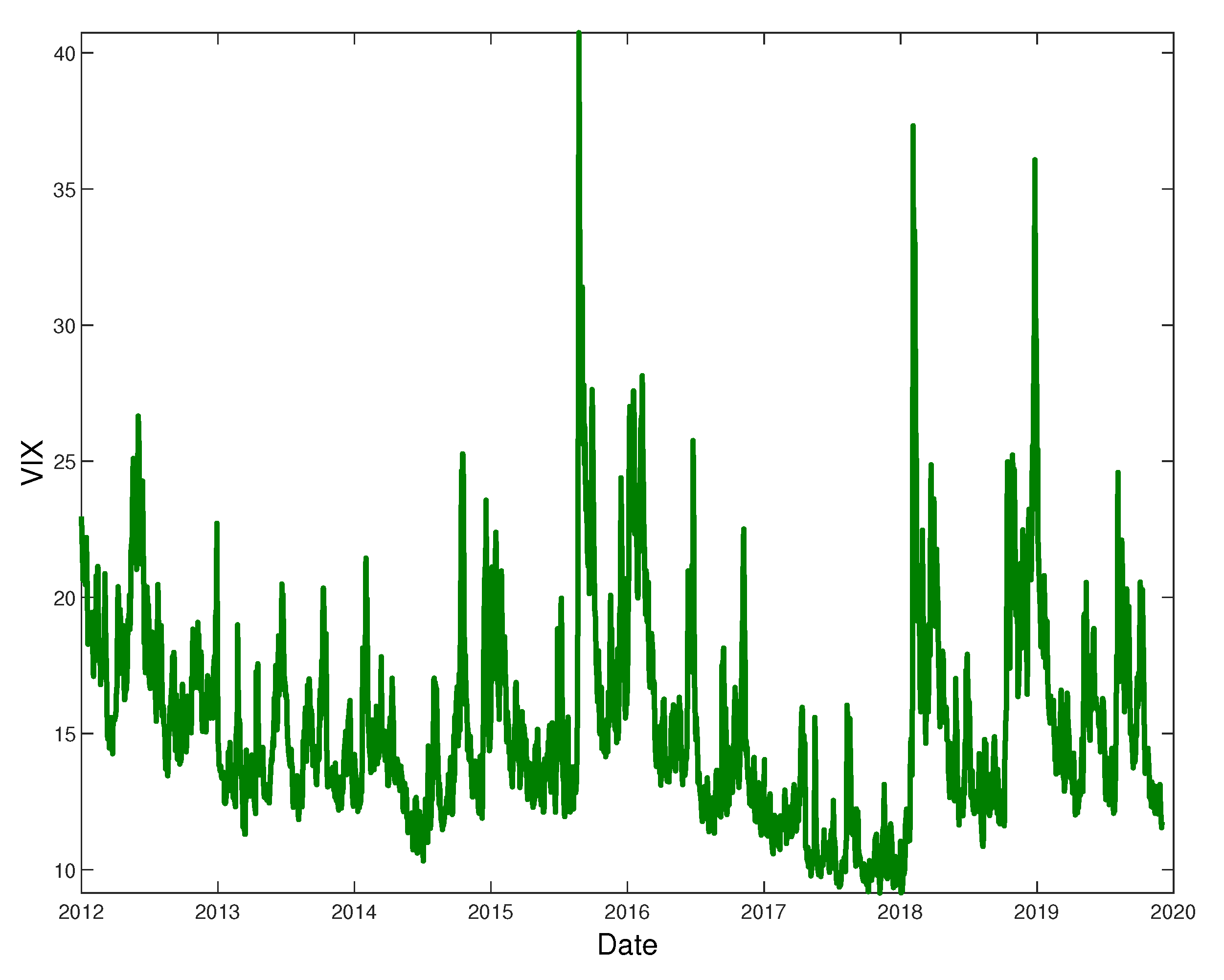
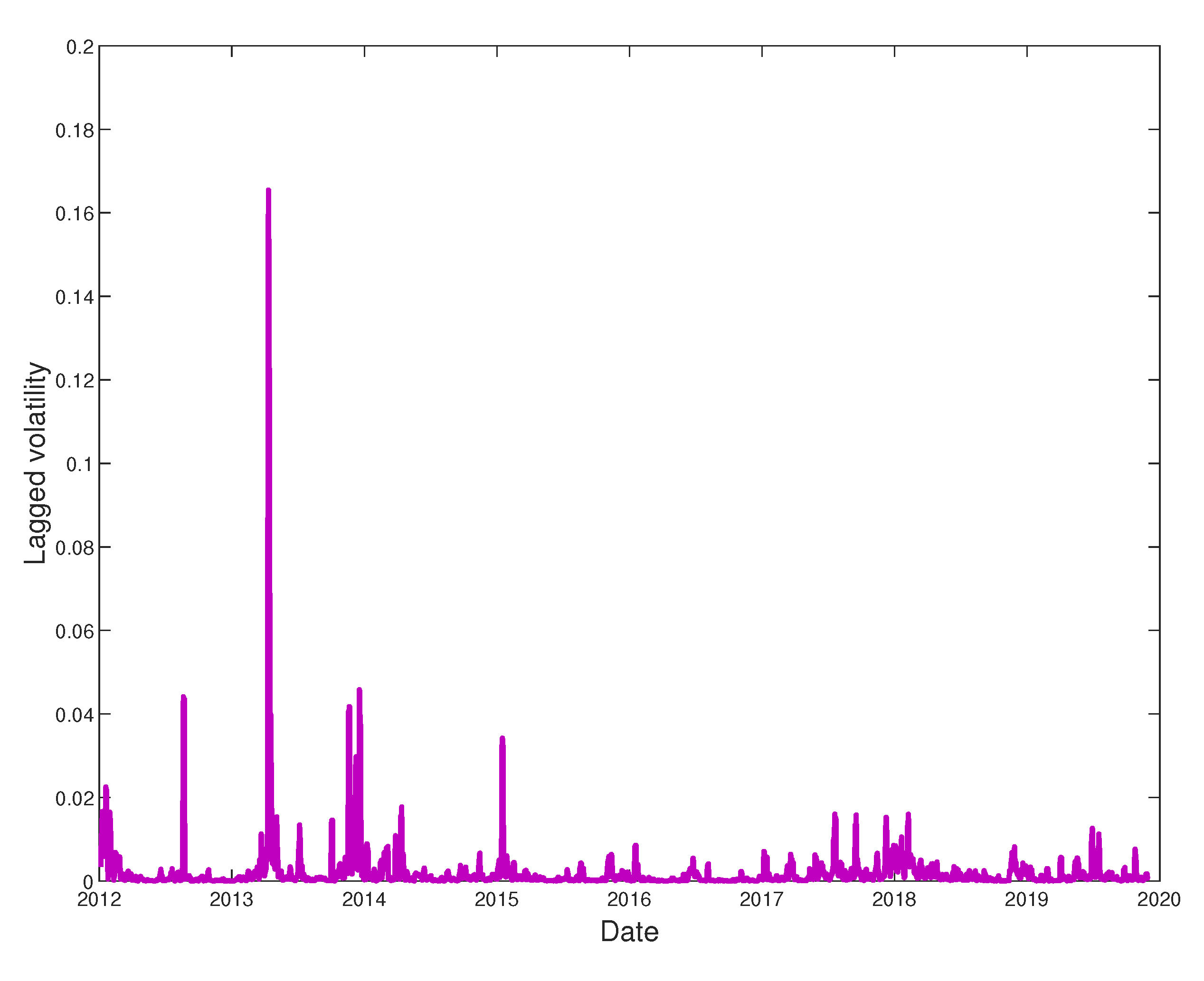
2. Material and Methods
3. Hybrid Models and Results
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System; ReadLiberty.Org: Chicago, IL, USA, 2008. [Google Scholar]
- Urquhart, A. The inefficiency of Bitcoin. Econ. Lett. 2016, 148, 80–82. [Google Scholar] [CrossRef]
- Stavroyiannis, S.; Babalos, V.; Bekiros, S.; Lahmiri, S.; Uddin, G.S. The high frequency multifractal properties of Bitcoin. Physica A 2019, 520, 62–71. [Google Scholar] [CrossRef]
- Gajardo, G.; Kristjanpoller, W.D.; Minutolo, M. Does bitcoin exhibit the same asymmetric multifractal cross-correlations with crude oil, gold and DJIA as the Euro, Great British Pound and Yen. Chaos Solitons Fractals 2018, 109, 195–205. [Google Scholar] [CrossRef]
- Yonghong, J.; He, N.; Weihua, R. Time-varying long-term memory in Bitcoin market. Financ. Res. Lett. 2018, 25, 280–284. [Google Scholar]
- Dyhrberg, A.H. Bitcoin, gold and the dollar–a garch volatility analysis. Financ. Res. Lett. 2016, 16, 85–92. [Google Scholar] [CrossRef]
- Dyhrberg, A.H. Hedging capabilities of bitcoin. is it the virtual gold? Financ. Res. Lett. 2016, 16, 139–144. [Google Scholar] [CrossRef]
- Marie, B.; Kim, O.; Ariane, S. Virtual currency, tangible return: Portfolio diversification with bitcoin. J. Asset Manag. 2015, 16, 365–373. [Google Scholar]
- Hong, K. Bitcoin as an alternative investment vehicle. Inf. Technol. Manag. 2017, 18, 265–275. [Google Scholar] [CrossRef]
- Chuen, D.L.K.; Guo, L.; Wang, Y. Cryptocurrency: A new investment opportunity? J. Altern. Invest. 2017, 20, 16–40. [Google Scholar] [CrossRef]
- Iwamura, M.; Kitamura, Y.; Matsumoto, T.; Saito, K. Can we stabilize the price of a Cryptocurrency?: Understanding the design of Bitcoin and its potential to compete with Central Bank money. Hitotsub. J. Econ. 2019, 60, 41–60. [Google Scholar] [CrossRef][Green Version]
- Yermack, D. Is Bitcoin a Real Currency? An Economic Appraisal. In Handbook of Digital Currency; Academic Press: Cambridge, MA, USA, 2015; pp. 31–44. [Google Scholar]
- Baur, D.G.; Hong, K.H.; Lee, A.D. Bitcoin: Medium of exchange or speculative assets? J. Int. Financ. Mark. Inst. Money 2018, 54, 177–189. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. Asymmetric volatility in cryptocurrencies. Econ. Lett. 2018, 173, 148–151. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Chaos, randomness and multi-fractality in bitcoin market. Chaos Solitons Fractals 2018, 106, 28–34. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S.; Salvi, A. Long-range memory, distributional variation and randomness of bitcoin volatility. Chaos Solitons Fractals 2018, 107, 43–48. [Google Scholar] [CrossRef]
- Balcilar, M.; Bouri, E.; Gupta, R.; Roubaud, D. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Econ. Model 2017, 64, 74–81. [Google Scholar] [CrossRef]
- Katsiampa, P. Volatility estimation for bitcoin: A comparison of GARCH models. Econ. Lett. 2017, 158, 3–6. [Google Scholar] [CrossRef]
- Chu, J.; Chan, S.; Nadarajah, S.; Osterrieder, J. GARCH modelling of cryptocurrencies. J. Risk Financ. Manag 2017, 10, 17. [Google Scholar] [CrossRef]
- Conrad, C.; Custovic, A.; Ghysels, E. Long-and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. J. Risk Financ. Manag. 2018, 11, 23. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. A hybrid volatility forecasting framework integrating GARCH, artificial neural network, technical analysis and principal components analysis. Expert Syst. Appl. 2018, 109, 1–11. [Google Scholar] [CrossRef]
- Peng, Y.; Albuquerque, P.H.M.; Sá, J.M.C.; Padula, A.J.A.; Montenegro, M.R. The best of two worlds: Forecasting high frequency volatility for cryptocurrencies and traditional currencies with Support Vector Regression. Expert Syst. Appl. 2018, 97, 177–192. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Cryptocurrency forecasting with deep learning chaotic neural networks. Chaos Solitons Fractals 2019, 118, 35–40. [Google Scholar] [CrossRef]
- Tseng, C.H.; Cheng, S.T.; Wang, Y.H.; Peng, J.T. Artificial neural network model of the hybrid EGARCH volatility of the Taiwan stock index option prices. Physica A 2008, 387, 3192–3200. [Google Scholar] [CrossRef]
- Tseng, C.H.; Cheng, S.T.; Wang, Y.H. New hybrid methodology for stock volatility prediction. Expert Syst. Appl. 2009, 36, 1833–1839. [Google Scholar] [CrossRef]
- Zahedi, J.; Rounaghi, M.M. Application of artificial neural network models and principal component analysis method in predicting stock prices on Tehran Stock Exchange. Physica A 2015, 438, 178–187. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Gold price volatility: A forecasting approach using the Artificial neural network-GARCH model. Expert Syst. Appl. 2015, 42, 7245–7251. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Forecasting volatility of oil price using an artificial neural network-GARCH model. Expert Syst. Appl. 2016, 65, 233–241. [Google Scholar] [CrossRef]
- Lahmiri, S. Modeling and predicting historical volatility in exchange rate markets. Physica A 2017, 471, 387–395. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Hernández, E. Volatility of main metals forecasted by a hybrid ANN-GARCH model with regressors. Expert Syst. Appl. 2017, 84, 290–300. [Google Scholar] [CrossRef]
- Hajizadeh, E.; Seifi, A.; Zarandi, M.F.; Turksen, I.B. A hybrid modeling approach for forecasting the volatility of S&P 500 index return. Expert Syst. Appl. 2012, 39, 431–436. [Google Scholar]
- Kristjanpoller, W.; Fadic, A.; Minutolo, M.C. Volatility forecast using hybrid Neural Network models. Expert Syst. Appl. 2014, 41, 2437–2442. [Google Scholar] [CrossRef]
- Lahmiri, S.; Boukadoum, M. An ensemble system based on hybrid EGARCH-ANN with different distributional assumptions to predict S&P500 intraday volatility. Fluct. Noise Lett. 2015, 14, 1550001. [Google Scholar]
- Seo, M.; Lee, S.; Kim, G. Forecasting the Volatility of Stock Market Index Using the Hybrid Models with Google Domestic Trends. Fluct. Noise Lett. 2019, 18, 1950006. [Google Scholar] [CrossRef]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Nelson, D.B. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Glosten, L.; Jagannathan, R.; Runkle, D. On the relation between the expected value and the volatility nominal excess return on stocks. J. Financ. 1993, 46, 1779–1801. [Google Scholar] [CrossRef]
- Brownlees, C.; Engle, R.; Kelly, B. A practical guide to volatility forecasting through calm and storm. J. Risk 2011, 14, 3–22. [Google Scholar] [CrossRef]
- Giles, L.; Maxwell, T. Learning, invariance and generalization in higher order neural networks. Appl. Opt. 1987, 26, 4972–4978. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, S.; Fulcher, J. Neuron-adaptive higher order neural-network models for automated financial data modelling. IEEE Trans. Neural Netw. 2002, 3, 188–204. [Google Scholar] [CrossRef]
- Xiong, R.; Nichols, E.P.; Shen, Y. Deep learning stock volatility with Google domestic trends. arXiv 2015, arXiv:1512.04916. [Google Scholar]
- Hamid, A.; Heiden, M. Forecasting volatility with empirical similarity and Google Trends. J. Econ. Behav. Organ. 2015, 117, 62–81. [Google Scholar] [CrossRef]
- Dimpfl, T.; Jank, S. Can Internet search queries help to predict stock market volatility? Eur. Financ. Manag. 2016, 22, 171–192. [Google Scholar] [CrossRef]
- Kristoufek, L. BitCoin Meets Google Trends and Wikipedia: Quantifying the Relationship between Phenomena of the Internet Era. Sci. Rep. 2013, 3, 3415. [Google Scholar] [CrossRef] [PubMed]
- Kjærland, F.; Khazal, A.; Krogstad, E.A.; Nordstrøm, F.B.; Oust, A. An Analysis of Bitcoin’s Price Dynamics. J. Risk Financ. Manag. 2018, 11, 63. [Google Scholar] [CrossRef]
- Aalborg, H.A.; Molnár, P.; Vries, J.E. What can explain the price, volatility and trading volume of Bitcoin? Financ. Res. Lett. 2019, 29, 255–265. [Google Scholar] [CrossRef]
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018, arXiv:1809.03006. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Hansen, P.R.; Lunde, A.; Nason, J.M. The model confidence set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef]
| Name | Activation Function |
|---|---|
| Sigmoid | |
| Hyperbolic Tangent (Tanh) | |
| Rectified Linear Unit (ReLU) | |
| Exponential Linear Unit (ELU) |
| Models | |||
|---|---|---|---|
| (1,1) | −7593.56 | −7570.83 | |
| (2,2) | −7633.38 | −7599.30 | |
| (3,3) | −7630.73 | −7585.28 | |
| (1,1) | −7589.75 | −7561.34 | |
| (2,2) | −7577.91 | −7538.14 | |
| (3,3) | −7558.42 | −7507.29 | |
| (1,1) | −7646.91 | −7618.51 | |
| (2,2) | −7665.96 | −7626.19 | |
| (3,3) | −7687.68 | −7636.55 |
| Models | ||||
|---|---|---|---|---|
| (1,1) | 0.01820086 | 0.022997082 | 60.71728437 | |
| (2,2) | 0.018615039 | 0.023244302 | 62.97792289 | |
| (3,3) | 0.031275112 | 0.274933282 | 104.4275052 | |
| (1,1) | 0.018100989 | 0.022782066 | 59.57816469 | |
| (2,2) | 0.018273329 | 0.022976453 | 61.3172729 | |
| (3,3) | 0.018353907 | 0.023128309 | 61.44172661 | |
| (1,1) | 0.021923047 | 0.025916869 | 80.21691954 | |
| (2,2) | 0.021758949 | 0.025850653 | 79.23566863 | |
| (3,3) | 0.022439612 | 0.026596278 | 81.70952727 |
| Models | Selected Input Variables | |
|---|---|---|
| {GARCH(1,1), GARCH(2,2), GARCH(3,3), GJR-GARCH(1,1), GJR-GARCH(2,2), | ||
| GJR-GARCH(3,3), EGARCH(1,1), EGARCH(2,2), EGARCH(3,3), GT, } | ||
| {GARCH(1,1), GARCH(2,2), GARCH(3,3), GJR-GARCH(1,1), GJR-GARCH(2,2), | ||
| GJR-GARCH(3,3), EGARCH(1,1), EGARCH(2,2), EGARCH(3,3), GT, , VIX } |
| Model | Activation Function | Nodes | |||
|---|---|---|---|---|---|
| GT-GARCH | Relu | 10 | 0.016455061 | 0.0228628 | 44.03939302 |
| 20 | 0.016455761 | 0.02286762 | 44.01794052 | ||
| 30 | 0.016456899 | 0.022870071 | 44.01377941 | ||
| 40 | 0.016457765 | 0.02287134 | 44.01490369 | ||
| 50 | 0.016456698 | 0.022868367 | 44.01481934 | ||
| Tanh | 10 | 0.01645589 | 0.022866914 | 44.02158481 | |
| 20 | 0.016456046 | 0.022867024 | 44.02205182 | ||
| 30 | 0.016457015 | 0.022869247 | 44.01766755 | ||
| 40 | 0.016457969 | 0.022870135 | 44.0273439 | ||
| 50 | 0.016457073 | 0.022869712 | 44.01422672 | ||
| Elu | 10 | 0.016456301 | 0.022867778 | 44.01894413 | |
| 20 | 0.016451684 | 0.02284573 | 44.10871 | ||
| 30 | 0.016456961 | 0.022866742 | 44.03292253 | ||
| 40 | 0.016455294 | 0.022864722 | 44.02362704 | ||
| 50 | 0.016456115 | 0.022866339 | 44.0296898 | ||
| Sigmoid | 10 | 0.016456811 | 0.02286878 | 44.02080023 | |
| 20 | 0.016457144 | 0.022869732 | 44.01885011 | ||
| 30 | 0.016456885 | 0.022867327 | 44.02887424 | ||
| 40 | 0.016456888 | 0.022870528 | 44.01028107 | ||
| 50 | 0.016457102 | 0.022868327 | 44.02443017 |
| Model | Activation Function | Nodes | |||
|---|---|---|---|---|---|
| GT-VIX-GARCH | Relu | 10 | 0.016464618 | 0.022961953 | 43.6754142 |
| 20 | 0.016463169 | 0.022961503 | 43.66309023 | ||
| 30 | 0.016464239 | 0.022963376 | 43.66271481 | ||
| 40 | 0.016464096 | 0.022965466 | 43.65610286 | ||
| 50 | 0.016468159 | 0.022966994 | 43.68492065 | ||
| Tanh | 10 | 0.016465239 | 0.022964124 | 43.67126798 | |
| 20 | 0.016463913 | 0.022960066 | 43.67926114 | ||
| 30 | 0.016464939 | 0.022962888 | 43.67179649 | ||
| 40 | 0.01646529 | 0.022962936 | 43.68079538 | ||
| 50 | 0.016463781 | 0.022958457 | 43.68308928 | ||
| Elu | 10 | 0.016464796 | 0.022964955 | 43.66256389 | |
| 20 | 0.016465883 | 0.02296502 | 43.67128545 | ||
| 30 | 0.016464635 | 0.022962084 | 43.67544449 | ||
| 40 | 0.016466452 | 0.022966505 | 43.66998111 | ||
| 50 | 0.016462585 | 0.022957731 | 43.67119374 | ||
| Sigmoid | 10 | 0.01646477 | 0.022963578 | 43.67003712 | |
| 20 | 0.016461495 | 0.022957864 | 43.67131767 | ||
| 30 | 0.016464624 | 0.022961432 | 43.67831534 | ||
| 40 | 0.016464975 | 0.022965387 | 43.66149144 | ||
| 50 | 0.01647861 | 0.02302727 | 43.4274305 |
| Model | Activation Function | Nodes | |||
|---|---|---|---|---|---|
| GT-H | Relu | 10 | 0.016941584 | 0.022027929 | 52.70636488 |
| 20 | 0.016941599 | 0.02202816 | 52.70680583 | ||
| 30 | 0.016941163 | 0.022027678 | 52.70298093 | ||
| 40 | 0.016940914 | 0.022027074 | 52.70274993 | ||
| 50 | 0.016941279 | 0.022027853 | 52.70347102 | ||
| Tanh | 10 | 0.016941714 | 0.022027935 | 52.70708064 | |
| 20 | 0.016942079 | 0.022028228 | 52.70821739 | ||
| 30 | 0.016941977 | 0.022028122 | 52.70722389 | ||
| 40 | 0.016941485 | 0.022028033 | 52.70475844 | ||
| 50 | 0.016940999 | 0.022027369 | 52.70261778 | ||
| Elu | 10 | 0.01694181 | 0.022028066 | 52.70750404 | |
| 20 | 0.016941503 | 0.022027574 | 52.70587155 | ||
| 30 | 0.016942019 | 0.022027821 | 52.7097488 | ||
| 40 | 0.01694203 | 0.022027968 | 52.70826475 | ||
| 50 | 0.01694185 | 0.022027961 | 52.71021157 | ||
| Sigmoid | 10 | 0.016941511 | 0.022027945 | 52.70543218 | |
| 20 | 0.016941295 | 0.022027628 | 52.70568077 | ||
| 30 | 0.016941514 | 0.022028015 | 52.70581447 | ||
| 40 | 0.016942199 | 0.022028407 | 52.70889483 | ||
| 50 | 0.016941966 | 0.022027852 | 52.70746498 |
| Model | Activation Function | Nodes | |||
|---|---|---|---|---|---|
| GT-VIX-H | Relu | 10 | 0.016745304 | 0.022489019 | 48.02497968 |
| 20 | 0.01674541 | 0.02248914 | 48.0246867 | ||
| 30 | 0.016746443 | 0.022489882 | 48.02759455 | ||
| 40 | 0.016745041 | 0.022488647 | 48.02404413 | ||
| 50 | 0.016748236 | 0.022522086 | 47.82463374 | ||
| Tanh | 10 | 0.016745657 | 0.022489571 | 48.02533742 | |
| 20 | 0.016745787 | 0.02248942 | 48.02683015 | ||
| 30 | 0.016745458 | 0.02248931 | 48.02374776 | ||
| 40 | 0.016744942 | 0.022489028 | 48.0238152 | ||
| 50 | 0.01674544 | 0.022489515 | 48.02256555 | ||
| Elu | 10 | 0.01674516 | 0.02248885 | 48.02508728 | |
| 20 | 0.016745349 | 0.022488898 | 48.02401028 | ||
| 30 | 0.016745336 | 0.022489 | 48.02517194 | ||
| 40 | 0.016745663 | 0.022488933 | 48.02556819 | ||
| 50 | 0.016745491 | 0.022489525 | 48.02760086 | ||
| Sigmoid | 10 | 0.016745208 | 0.022489047 | 48.02402778 | |
| 20 | 0.016745744 | 0.022489067 | 48.02780298 | ||
| 30 | 0.0167453 | 0.022489284 | 48.0246795 | ||
| 40 | 0.016745533 | 0.022488691 | 48.02600782 | ||
| 50 | 0.016745073 | 0.022489534 | 48.02441867 |
| Model | Activation Function | Nodes | |||
|---|---|---|---|---|---|
| GT-VIX-GARCH-H | Relu | 10 | 0.016099377 | 0.022304876 | 41.97126277 |
| 20 | 0.016101827 | 0.02228648 | 42.07658833 | ||
| 30 | 0.016095555 | 0.022284853 | 42.03342476 | ||
| 40 | 0.016109686 | 0.022277813 | 42.13001676 | ||
| 50 | 0.016097934 | 0.02228606 | 42.05669279 | ||
| Tanh | 10 | 0.016098348 | 0.022302633 | 41.964812188 | |
| 20 | 0.01609808 | 0.022231812 | 42.38508374 | ||
| 30 | 0.016094577 | 0.022298402 | 42.01919185 | ||
| 40 | 0.016098404 | 0.022302775 | 42.04282541 | ||
| 50 | 0.016096921 | 0.022285756 | 42.04785915 | ||
| Elu | 10 | 0.016108832 | 0.02236164 | 41.71558473 | |
| 20 | 0.016100976 | 0.022290669 | 42.06674165 | ||
| 30 | 0.016098687 | 0.022285274 | 42.06192355 | ||
| 40 | 0.016101002 | 0.022291082 | 42.06727282 | ||
| 50 | 0.016105162 | 0.022295976 | 42.088699 | ||
| Sigmoid | 10 | 0.016099661 | 0.022292957 | 42.06001306 | |
| 20 | 0.016099905 | 0.022281962 | 42.06856524 | ||
| 30 | 0.016100028 | 0.022278299 | 42.07671847 | ||
| 40 | 0.016105448 | 0.022285267 | 42.1902812 | ||
| 50 | 0.016096398 | 0.02229977 | 42.03760228 |
| Input Variables | |||||
|---|---|---|---|---|---|
| Models | |||||
| O | O | X | X | X | |
| O | O | O | X | X | |
| O | O | O | O | O |
| Loss Function | |||||
|---|---|---|---|---|---|
| Ranking | Model | Activation Function | Nodes | MCS | |
| 1 | GT-VIX-GARCH-H | Relu | 30 | 0.016095555 | 1.000 |
| 2 | GT-VIX-GARCH-H | Tanh | 20 | 0.01609808 | 0.991 |
| 3 | GT-VIX-GARCH-H | Tanh | 30 | 0.016094577 | 0.991 |
| 4 | GT-VIX-GARCH-H | Relu | 50 | 0.016097934 | 0.991 |
| 5 | GT-VIX-GARCH-H | Tanh | 40 | 0.016098404 | 0.991 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, M.; Kim, G. Hybrid Forecasting Models Based on the Neural Networks for the Volatility of Bitcoin. Appl. Sci. 2020, 10, 4768. https://doi.org/10.3390/app10144768
Seo M, Kim G. Hybrid Forecasting Models Based on the Neural Networks for the Volatility of Bitcoin. Applied Sciences. 2020; 10(14):4768. https://doi.org/10.3390/app10144768
Chicago/Turabian StyleSeo, Monghwan, and Geonwoo Kim. 2020. "Hybrid Forecasting Models Based on the Neural Networks for the Volatility of Bitcoin" Applied Sciences 10, no. 14: 4768. https://doi.org/10.3390/app10144768
APA StyleSeo, M., & Kim, G. (2020). Hybrid Forecasting Models Based on the Neural Networks for the Volatility of Bitcoin. Applied Sciences, 10(14), 4768. https://doi.org/10.3390/app10144768





