1. Introduction
A robot swarm [
1,
2] is a group of robots that operate autonomously without relying on a leader robot or on external infrastructures. By cooperating, the robots of a swarm can collectively accomplish missions that individual robots could not accomplish alone. The collective behavior of a robot swarm—and hence its ability to accomplish a particular mission—is the result of the interactions that the robots have with the environment and with their peers [
3].
Unfortunately, conceiving and implementing a collective behavior for a robot swarm is particularly challenging. Indeed, to obtain a collective behavior, one must conceive and implement the control software of the individual robots. The problem is that no generally applicable method exists to tell what an individual robot should do so that the desired behavior is obtained [
4]. Automatic design is a promising approach to address this problem. An automatic design method produces control software via an optimization algorithm that maximizes an appropriate mission-dependent objective function. For a recent literature review on the automatic design of robot swarms, see Francesca et al. [
5].
Traditionally, research on the automatic design of robot swarms adopts the neuro-evolutionary approach [
6,
7]. Design methods based on neuro-evolution produce control software in the form of artificial neural networks. The architecture and parameters of the network are selected by an evolutionary algorithm. As an alternative to neuro-evolution, some modular methods have been proposed [
8,
9,
10,
11,
12,
13,
14]. In the modular approach, preexisting software modules are combined and tuned by an optimization algorithm. Results show that modular methods are more suitable to produce communication-based behaviors [
14] and are more robust to the so-called reality gap [
8,
15], that is, the possibly subtle but unavoidable differences between reality and the simulation models used in the design process.
In this paper, we present
TuttiFrutti: a method for the automatic design of swarms of e-pucks (extended with an omnidirectional vision turret [
16]) that can display and perceive colors.
TuttiFrutti designs control software for the individual robots in the swarm by selecting, tuning, and assembling preexisting software modules into probabilistic finite state machines.
TuttiFrutti is an instance of AutoMoDe [
8]—a family of modular methods for the realization of robot swarms.
TuttiFrutti differentiates from previous instances of AutoMoDe by enabling the production of control software that operates with information expressed in the form of colors. More precisely,
TuttiFrutti is intended to solve classes of missions in which robots shall act according to colors displayed by objects in their environment and/or their peers. With
TuttiFrutti, we significantly enlarge the variety of collective behaviors that can be obtained by AutoMoDe. The study we present in this paper is framed within the tenets of the automatic off-line design of robot swarms, as recently defined by Birattari et al. [
17]: (i)
TuttiFrutti is not intended to solve a specific design problem but rather a class thereof, without the need to undergo any problem-specific modification or adjustment; (ii) once a design problem is specified, human intervention is not provided for in any phase of the design process.
In our research, we address the following questions: Is TuttiFrutti capable of deciding whether a color displayed in the environment provides information useful to accomplish a mission? Can TuttiFrutti produce collective behaviors that exhibit color-based communication between robots? Do the extended capabilities of the e-puck increase the difficulty of automatically designing control software for the robot swarm? How could these new resources be used to create more complex missions?
We consider a model of the e-puck that can use its RGB LEDs for emitting color signals, and its omnidirectional vision turret [
16] for detecting robots or other objects that display colors in the environment. We conduct our study to demonstrate that e-pucks that display and perceive colors enable the automatic design of collective behaviors with event-handling, communication and navigation properties. As a proof of concept, we assess
TuttiFrutti in three missions in which colors displayed in the environment play a different role:
stop, AGGREGATION, and
foraging. In
stop, the robots must
stop moving as soon as a color signal appears in the environment. In AGGREGATION, the robots must aggregate in a region where a specific color is displayed. In
foraging, the robots must forage in an environment that has two sources of items—the sources differ in the profit they provide and in the color displayed at their location. We report a statistical analysis of results obtained with realistic computer simulations and with a swarm of e-puck robots.
Alongside the results of TuttiFrutti, we report the results obtained by EvoColor—a design method based on neuro-evolution. EvoColor is a straightforward implementation of the neuro-evolutionary approach that, likewise TuttiFrutti, produces control software for swarms of e-pucks that can display and perceive colors. We report these results as a reference for appraising the complexity of the missions considered in our study. In the absence of a well established state-of-the-art off-line design method for the missions proposed here, we consider EvoColor as a reasonably appropriate yardstick against which we can assess the performance of TuttiFrutti. A thorough comparison of TuttiFrutti against any possible declination of the neuro-evolutionary approach is well beyond the scope of this paper.
The paper is structured as follows:
Section 2 discusses previous related work;
Section 3 introduces
TuttiFrutti;
Section 4 describes the experimental set-up;
Section 5 presents the results; and
Section 6 concludes the paper and highlights future work.
2. Related Work
In this section, we first introduce studies in which the robots of a swarm have the capabilities of displaying and perceiving colors. After, we revise related works on automatic design of robot swarms. Finally, we compare TuttiFrutti with the other existing instances of AutoMoDe.
Robots that can display or perceive colors have been largely used to demonstrate collective behaviors in swarm robotics. The literature on robot swarms that use visual information is extensive and it is not our intention to provide an exhaustive review. We exclude from our discussion any system in which robots only perceive visual information but do not display it—such as [
18,
19,
20,
21,
22]. Instead, we focus on studies in which the robots both display and perceive colors to achieve collective behaviors [
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47].
Designers of robot swarms commonly use color lights to represent specific information that robots in the swarm must identify, process and/or transmit—the nature of the information varies from one study to another and is used ad hoc to obtain a particular behavior. For example, Nouyan et al. [
35] designed a swarm that connects locations by establishing a chain of robots that act as waypoints for their peers. They conducted two experiments in which robots use colors differently: in the first experiment, robots repeat a pattern of 3 colors along the chain to indicate the sense in which the peers should move; in the second one, robots use colors to inform their peers about a location of interest. Mathews et al. [
25] designed a swarm in which robots self-organize in mergeable structures. In their experiments, robots react to colored objects in their environment and display color signals that indicate their location. Garattoni and Birattari [
31] designed a robot swarm that autonomously identifies and perform sequences of tasks. In their experiments, robots emit color signals to coordinate their collective action and associate each task in a sequence with objects that display a particular color. In a more general sense, one can find a similar approach in swarms that exhibit self-assembly and morphogenesis [
23,
24,
25,
26], collective fault detection [
25,
27], collective exploration [
28,
29,
30,
31], collective transport [
28,
30], coordinated motion [
25,
26,
32], human-swarm interaction [
33,
34], chain formation [
28,
31,
35], group size regulation [
36], task allocation [
31,
37,
38,
39,
40], object clustering [
39,
41], and foraging [
42]—according to the taxonomy proposed by Brambilla et al. [
4]. In these studies [
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42], designers manually established ad hoc relationships between the colors that a robot can perceive and the corresponding behavior that a robot must adopt when it perceives them. The research question we address in the present paper is whether automatic design methods [
5,
17] can establish similar relationships.
It is our contention that classes of missions that require the robots to communicate and react to color-based information are an appropriate benchmark to assess automatic design methods. First, the capability of displaying and perceiving colors is platform-independent and generalizes across different design methods—robot platforms used in swarm robotics often include LEDs and cameras [
48]. Second, colors facilitate the conception and realization of complex missions—colored environments can be created in various manners [
40,
41,
49,
50,
51]. Finally, colors simplify the visualization and monitoring of robot swarms [
48]—a property relevant to the human understandability of collective behaviors, an open research area in swarm robotics [
52]. Yet, no existing method for the automatic design of robot swarms targets classes of missions that require the robots to operate with color-based information. Specifically, we refer to methods that can be framed within the tenets of the automatic off-line design of robot swarms [
17].
Few related studies have been conducted following the neuro-evolutionary approach [
43,
44,
45,
46,
47]. Floreano et al. [
43] evolved communication behaviors for a swarm performing a foraging mission. Ampatzis et al. [
44] evolved self-assembly behaviors with a team of two robots. Sperati et al. [
45,
46] evolved behaviors for coordinated motion with a group of three robots, and later, evolved a dynamic chain of robots that perform a foraging-like mission. Trianni and López-Ibañez [
47] used multi-objective optimization to evolve flocking and a two-robot collaborative behavior within a robot swarm. In the studies mentioned above, the methods under analysis have not been tested for their ability to generate control software autonomously. As a consequence, these studies belong in semi-automatic design rather than in automatic design [
17]. Indeed, in these studies, researchers either focused a single mission [
43,
44,
46] or modify the design methods and/or robot platform when they applied the methods under analysis to more than one [
45,
47]. In addition, we argue that mission-specific bias was manually introduced in the way the robots display and perceive colors: robots display colors that are manually defined at the beginning of the experiment [
44]; robots display color-based information that is encoded by the researchers [
46,
47]; and the perception capabilities of the robots are adjusted to ease the emergence of a specific behavior [
45,
46]. We contend that these studies do not expose the full potential of using color-based information in the automatic design of collective behaviors. As a matter of fact, previous works were limited to produce control software for robots than can display and perceive a single [
43,
44,
45] or at most two simultaneous colors [
46,
47].
Our research belongs in the family of modular design methods known as AutoMoDe [
8]. In the rest of the section, we restrict our attention to this family. Francesca and Birattari [
5] discussed how the capabilities of robot platforms limit the variety of collective behaviors that automatic design methods can produce. Methods conceived for e-puck robots with equal capabilities—such as
Vanilla [
8],
Chocolate [
9],
Maple [
10],
Waffle [
11],
Coconut [
12] and
IcePop [
13]—are restricted to address the same class of missions: robots in the swarm must position themselves regarding their peers [
9,
15] or few static environmental features [
8,
9,
10,
11,
12,
13,
15,
53], and they can only use a single global reference for navigation [
8,
9,
10,
11,
12,
13,
15,
53]. In contrast, Hasselmann et al. [
14] obtained a larger variety of collective behaviors by considering an extended set of capabilities with respect to those considered in
Chocolate. They introduced
Gianduja—a method for the automatic design of swarms of e-pucks that can selectively broadcast binary messages. Hasselmann et al. showed that by broadcasting and reacting to messages, the robots can perform missions that
Chocolate cannot address—for example, missions that require event-handling collective behaviors.
The approach we follow in our research is similar to the one of Hasselmann et al. [
14]. We conceived
TuttiFrutti as an instance of AutoMoDe that designs control software for e-pucks with the extended capability of communicating by displaying and perceiving colors. As we will see in
Section 3,
TuttiFrutti can address missions that require the robots to act according to color-based information—a class of missions that existing instances of AutoMoDe can not address.
4. Experimental Set-Up
In this section, we describe our experiments in the design of collective behaviors for robots that can display and perceive colors. The study evaluates the capabilities of TuttiFrutti to address a class of missions in which colors displayed by objects in the environment provide relevant information to the robots. In the following, we first introduce the missions we consider in our study. Then, we present EvoColor—a baseline design method that serves as a reference to appraise the complexity of the missions. Finally, at the end of the section we describe the protocol we follow to assess TuttiFrutti.
4.1. Missions
We conceived three missions in which robot swarms operate in arenas surrounded by modular RGB blocks:
stop,
aggregation, and
foraging.
stop and
aggregation are adaptations we make from the equivalent missions proposed by Hasselmann et al. to study
Gianduja [
14].
foraging is an abstraction of a foraging task, in a
best-of-n fashion [
63]—similar to the experiment of Valentini et al. [
64]. The performance of the swarm is evaluated according to a mission-dependent objective function. We selected these missions because we conjecture that, to successfully perform them, the robots need to identify, process and/or transmit color-based information. In all missions, the time available to the robots is
. The RGB blocks are arranged in walls that display colors on a per-mission basis—each RGB block is
length and can display the colors red, green and blue
. In the context of these missions, when we reference to colored walls we imply that the RGB blocks arranged in the wall display the named color—for example,
“the green wall” stands for a wall in which the RGB blocks composing it display the color green. In the following, we describe the scenario, the objective function, and the role of the colors for each mission.
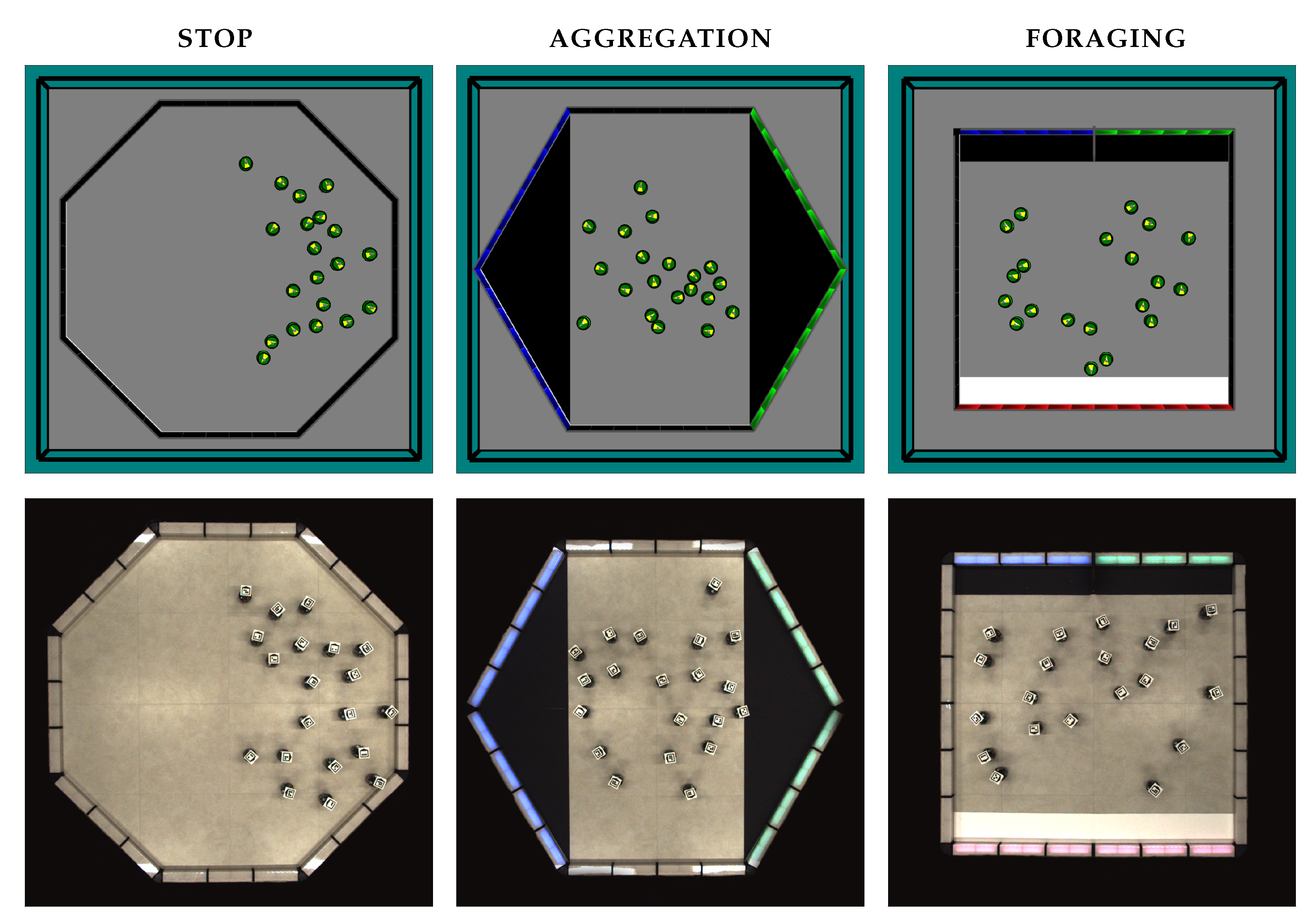
Figure 2 shows the arenas for the three missions.
4.1.1. stop
The robots must move until one of the walls that surrounds the arena emits a
stop signal by turning green. Once the wall turns green, all the robots in the swarm must
stop moving as soon as possible. The swarm operates in an octagonal arena of 2.75 m
2 and gray floor. The wall that emits the
stop signal is selected randomly. At the beginning of each run, the robots are positioned in the right side of the arena.
Figure 2 (left) shows the arena for
stop.
The performance of the swarm
is measured by the objective function described by Equation (
1); the lower the better.
measures the amount of time during which the robots do not perform the intended behavior—before and after the stop signal. N and T represent respectively the number of robots and the duration of the mission. indicates the time at which the stop signal is displayed. The time is uniformly sampled between [40, 60] s. We expect that TuttiFrutti produces collective behaviors with event-handling capabilities that allow the swarm to react when the stop signal appears.
4.1.2. aggregation
The robots must aggregate in the left black region of the arena as soon as possible. The swarm operates in a hexagonal arena of about 2.60 m
2 and gray floor. Triangular black regions of about 0.45 m
2 are located at the left and right side of the arena. The walls lining the left black region are blue and those lining the right black region are green—the colors do not change during the mission. Each black region is characterized by the color of the walls that lines it. That is, the
blue zone refers to the black region lined by blue walls and the
green zone refers to the black region lined by green walls. At the beginning of each run, the robots are randomly positioned in the center of the arena—between the black regions.
Figure 2 (center) shows the arena for
aggregation.
The performance of the swarm
is measured by the objective function described by Equation (
2); the lower the better.
indicates the time that the robots spend outside of the blue zone.
N and
T represent the number of robots and the duration of the mission, respectively. We expect that
TuttiFrutti produces collective behaviors in which the swarm uses the blue walls as a reference to navigate and aggregate in the blue zone.
4.1.3. foraging
The robots must select and forage from the most profitable of two sources of items. The swarm operates in a squared arena of 2.25 m
2 and gray floor. A rectangular white region of about 0.23 m
2 is located at the bottom of the arena and represents the nest of the swarm. A rectangular black region of 0.23 m
2 is located at the top of the arena and represents the two sources of items—the sources are separated by a short wall segment that does not display any color. This wall segment divides the black region in half. We account that an item is transported and successfully delivered when a robot travels from any of the sources to the nest. The walls lining the nest are red, the walls lining the left source are blue, and the walls lining the right source are green—the colors do not change during the mission. We consider then two types of sources of items: the
blue source—the black region lined by blue walls; and the
green source—the black region lined by green walls. At the beginning of each run, the robots are randomly positioned in the center of the arena—between the white and black areas.
Figure 2 (right) shows the arena for
foraging.
The performance of the swarm
is measured by the objective function described by Equation (
3); the higher the better.
indicates the aggregate profit of the total of items collected from the two sources.
corresponds to the number of items collected from the blue source, and
corresponds number of items collected from the green one. We added the factor
to balance the profit of the items available in each source. In our study
. Items from the blue source account for a profit of
and items from the green source account for a penalization of
. We expect that
TuttiFrutti produces collective behaviors in which swarms use the blue walls as a reference to navigate towards the blue source, the green walls for avoiding the green source, and the red walls to navigate towards the nest.
4.2. Baseline Method: EvoColor
No standard design method exists to address the class of missions we consider in this study. Little related work exists—see
Section 2—and refers only to mission-specific methods that follow the neuro-evolutionary approach. Indeed, as no extensive comparison has ever been performed between neuro-evolutionary methods across multiple missions, a state of the art in neuro-evolutionary robotics has not been identified, yet. Together with the results obtained with
TuttiFrutti, in the following we will present also those obtained by
EvoColor—a method based on neuro-evolution for the automatic design of swarms of e-pucks that can display and perceive colors. The results we will present should not therefore be considered as a comparison between
TuttiFrutti and the state of the art in neuro-evolutionary robotics. In this context, our results should rather be considered as a comparison between
TuttiFrutti and a reasonable instance of the neuro-evolutionary approach.
EvoColor is an adaptation of
EvoStick [
65]—a standard neuro-evolutionary method previously used as a yardstick in studies on the automatic design of robot swarms [
8,
10,
15,
53]. To the best of our knowledge,
EvoStick is the only neuro-evolutionary method that has been tested via simulations and robot experiments on multiple missions without undergoing any per-mission modification.
EvoColor produces control software for swarms of e-pucks that operate with RM 3—see
Section 3.1. The control software has the form of a fully connected feed-forward artificial neural network with 41 input nodes
, 8 output nodes
and no hidden layers. In this topology, the input nodes and output nodes are directly connected by synaptic connections (
) with weights
in a range of
. The activation of each output node is determined by the weighted sum of all inputs nodes filtered through a standard logistic function.
EvoColor selects appropriate synaptic weights using an evolutionary process based on elitism and mutation. Just as in
TuttiFrutti, the evolutionary process is conducted through simulations performed in ARGoS3, version beta 48, together with the argos3-epuck library. The evolution ends when an
a priori defined budget of simulations is exhausted.
Table 3 summarizes the topology of the neural network, the novelties with respect to
EvoStick and the parameters used in the evolutionary process.
The readings of the proximity and ground sensors are passed directly to the network. Information about the number of neighboring peers is provided through the function , with . The vector and each vector in are translated into scalar projections onto four unit vectors that point at 45°, 135°, 225°, and 315° with respect to the front of the robot. Then, each projection is passed to the network through an independent input node. The last input of the network comes from a bias node. Four output nodes encode tuples of negative and positive components of the velocity of the wheels. Each tuple is obtained from two independent output nodes and is defined as . The velocity of a wheel is computed as the sum of the two elements in a tuple . Similarly, the color displayed by the RGB LEDs of the robot is selected by comparing the value of the output nodes that correspond to colors in the set . The color displayed corresponds to the maximum value found across the four colors.
EvoColor differs from EvoStick in two aspects: the reference model and how the output of the neural network is mapped to the velocity of the robots. First, EvoColor is based on RM 3 and EvoStick on RM 1.1. In accordance to RM 3, EvoColor does not integrate the capability of the e-pucks for sensing the intensity of ambiance light—originally integrated in EvoStick. The second difference between EvoColor and EvoStick is how the output of the neural network is mapped to the velocity of the e-pucks. In EvoColor, we introduce a velocity mapping based on tuples to facilitate the evolution of standstill behaviors—as we expect robots need them to perform stop and aggregation.
In EvoStick, the control software maps directly a single output node of the neural network into velocity commands for each wheel —a robot can stand still only if the velocity of the two wheels is set exactly to 0. A standstill behavior is then difficult to achieve since only one pair of values in the output nodes maps exactly to and ; Moreover, the output nodes can not maintain a steady value because they are subject to the injection of sensory noise. In EvoColor, the control software maps the sum of elements of a tuple into velocity commands for each wheel —each tuple is defined by two output nodes and provides a negative and a positive component to compute the velocity. We expect that this mapping facilitates the evolution of standstill behaviors: first, robots can stand still if the elements of each tuple are any pair of values of equal magnitude—steady values are not required provided that the output nodes that encode the same tuple vary proportionally; second, the sum of the positive and negative components can cancel out the sensory noise injected in the output nodes that encode a tuple—given a proper tuning of the synaptic weights. If one compares EvoColor with EvoStick, the first has more freedom to tune neural networks that lead to standstill behaviors.
4.3. Protocol
We conduct experiments with twenty e-pucks on the missions described in
Section 4.1. For each mission, we produce ten designs of control software with
TuttiFrutti and ten with
EvoColor. We assess the effectiveness of the methods by testing each design once in simulation and once with physical robots.
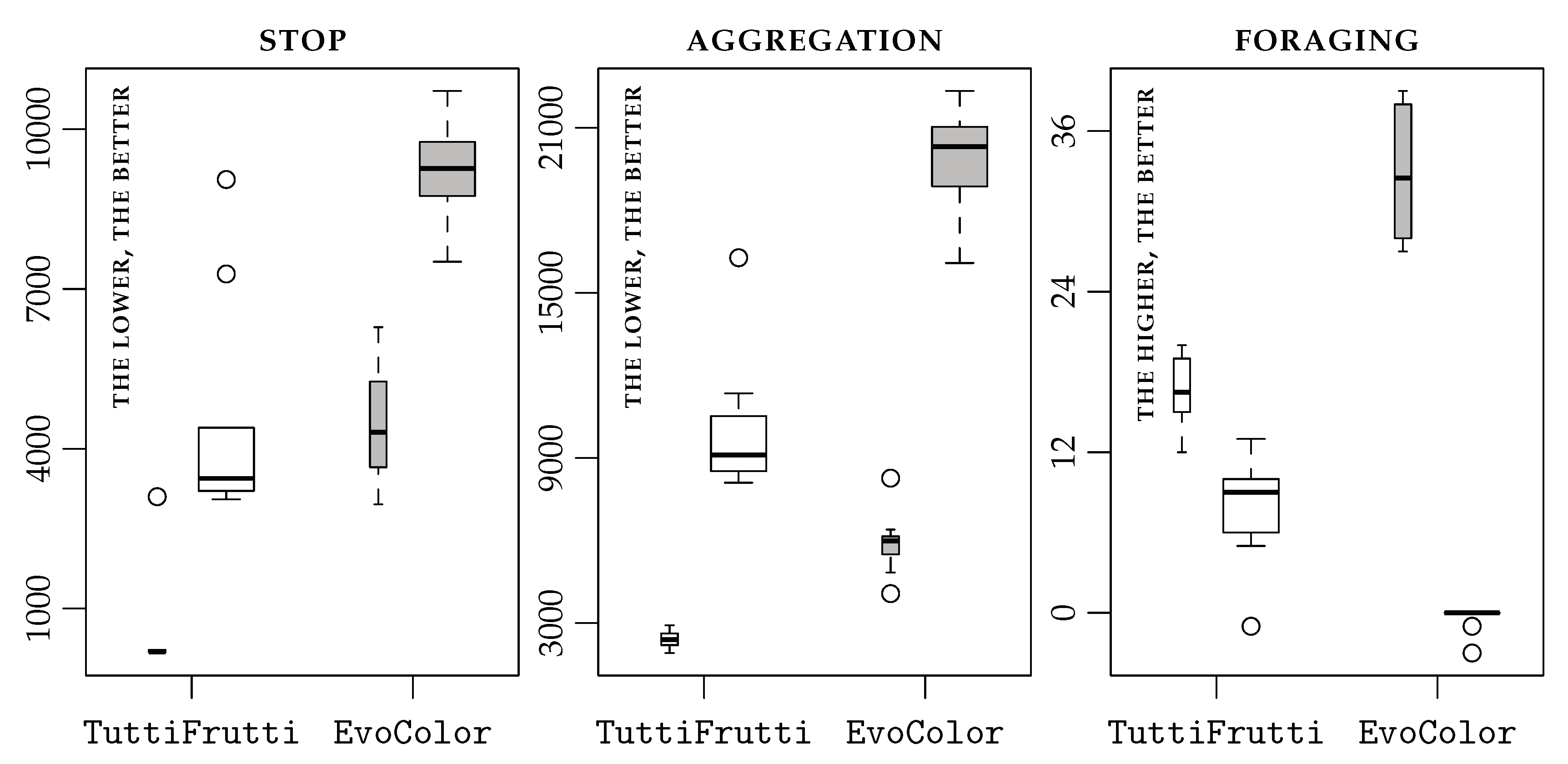
Statistics
We use box-plots to represent the performance of the control software we produce. For each method, we report the performance obtained in simulation (thin boxes) and with physical robots (thick ones). In all cases, we support comparative statements with an exact binomial test, at 95% confidence [
66]: statements like “
A performs
significantly better/worse than
B” imply that the comparison is supported by a an exact binomial test, at 95% confidence. In addition, we estimate the overall performance of
TuttiFrutti with respect to
EvoColor. To this purpose, we aggregate the results by comparing the performance of the two design methods across each mission. In the context of the overall performance of the design methods, any statement like “
A performs
significantly better/worse than
B” also implies that the comparison is supported by an exact binomial test, at 95% confidence [
66].
5. Results and Discussion
We present the qualitative and quantitative analysis of the results obtained with
TuttiFrutti and
EvoColor. We discuss first the behavior and performance of the swarms on a per-mission basis. Then, we elaborate on the aggregate performance across the three missions. In the end, we address the research questions presented in
Section 1 and we discuss our findings. The code, control software and demonstrative videos are provided as
Supplementary Material [
67]. In the context of these results, references to colored robots imply that the robots display the named color—for example,
“cyan robots” stands for robots that display the color cyan.
5.1. stop
Figure 3 (left) shows the performance of
TuttiFrutti and
EvoColor in
stop. In this mission,
TuttiFrutti performs significantly better than
EvoColor.
From visual inspection,
TuttiFrutti produced control software that effectively uses the capabilities of the robots for displaying and perceiving colors. The swarm first disperses and homogeneously covers the arena—aiming to rapidly detect the
stop signal. If a robot detects the
stop signal, it stands still and disseminates the information by emitting a signal of an arbitrary color. When other robots perceive the signal emitted by their peer, they also transition to a standstill behavior and relay the signal. The process continues until all robots in the swarm are standing still. We consider that this behavior shows the potential of
TuttiFrutti for producing event-handling collective behaviors. The swarm collectively transitions from coverage to standstill when the
stop signal appears. As we expected,
TuttiFrutti produces control software that establishes communication protocols by correctly pairing the color of the signals that robots emit and the behavior other robots must adopt when they perceive them—similarly to the results obtained by Hasselmann et al. [
14] with
Gianduja.
EvoColor, unlike TuttiFrutti, designed collective behaviors that do not respond to the stop signal. The swarm adopts a rather simplistic behavior in which robots move until stopped by the walls. They remain then in a standstill behavior because they persistently push against the walls—no reaction can be appreciated in the swarms when the stop signal appears. This behavior was observed too in the experiments with physical robots, and in many cases, robots maintained standing-still behaviors by pushing against other robots too.
In the experiments with physical robots, both TuttiFrutti and EvoColor showed a significant drop in performance with respect to the simulations. However, the difference in mean performance between simulations and experiments with physical robots is larger for EvoColor than TuttiFrutti. Swarms deployed with the control software produced by TuttiFrutti showed the same collective behavior observed in simulation, although the rapidness in discovering the stop signal and disseminating the information decreased. In the case of EvoColor, robots often do not reach the walls and they push against each other to remain still in place.
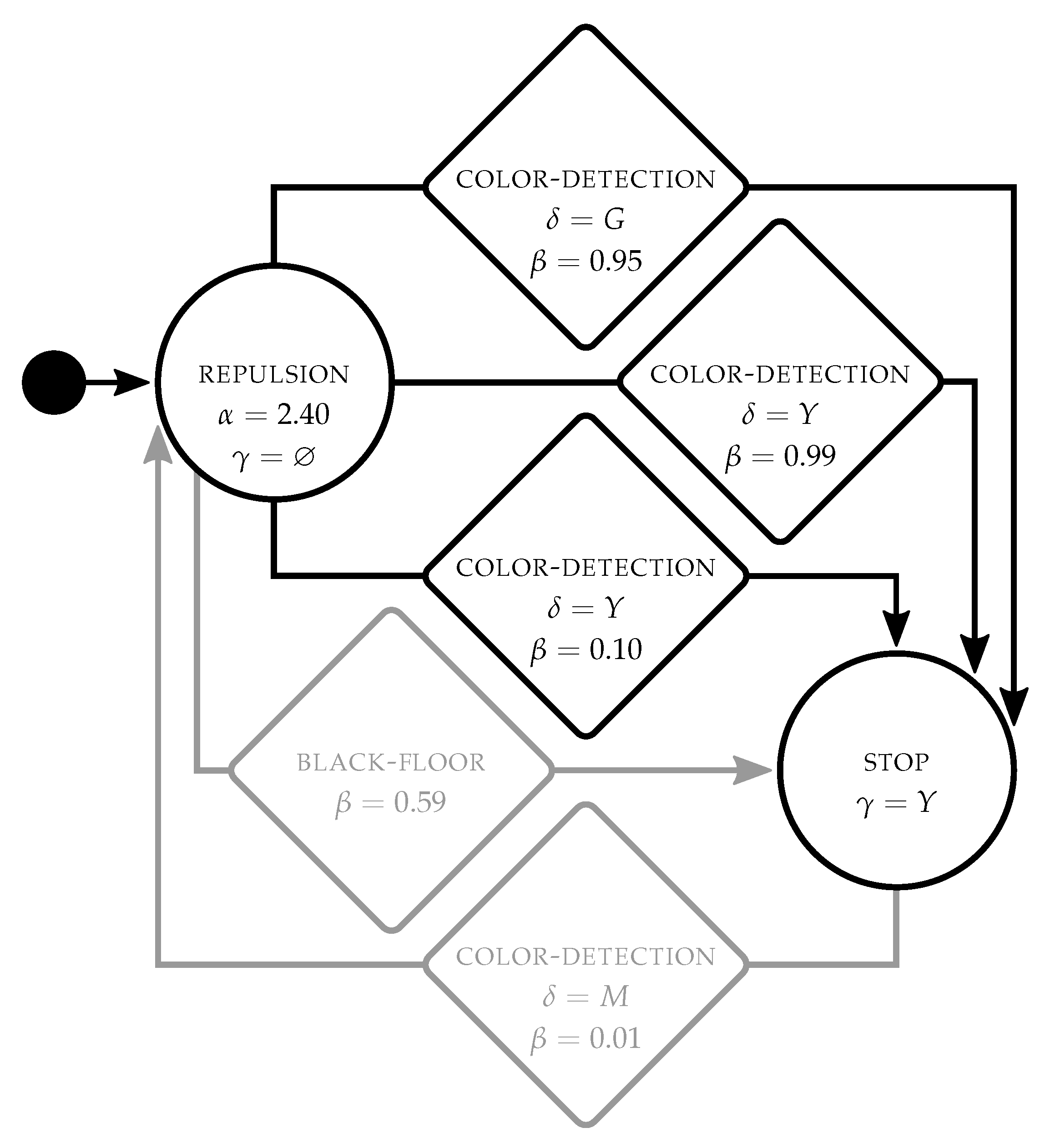
Figure 4 shows an example of the control software produced by
TuttiFrutti for
stop. Robots start in
repulsion with no color displayed
. They transition to
stop and turn yellow
when
color-detection is triggered either by a green wall
or by yellow robots
. In this sense, robots change their behavior when they either perceive the
stop signal or the yellow signals that other robots emit.
5.2. aggregation
Figure 3 (center) shows the performance of
TuttiFrutti and
EvoColor in
aggregation. In this mission,
TuttiFrutti performs significantly better than
EvoColor.
Also in this case, from visual inspection, TuttiFrutti produced control software that effectively uses the capabilities that the robots have of displaying and perceiving colors. As we expected, TuttiFrutti designs collective behaviors in which robots reach and remain in the blue zone by moving towards blue walls. This behavior is often complemented with navigation or communication strategies that boost the efficiency of the swarm. For example, some instances of control software include a repulsion behavior that drives robots away from the green walls—robots reach the blue zone faster by avoiding unnecessary exploration in the green zone. In other instances, robots that step in the blue zone, or perceive the blue walls, emit a signal of an arbitrary color—other robots then follow this signal to reach the blue zone. In this sense, robots communicate and collectively navigate to aggregate faster. Finally, some instances combine the two strategies.
EvoColor designed collective behaviors in which robots use the colors displayed in the arena. Robots explore the arena until they step in one of the black regions—either at the blue or green zone. If robots step in the green zone, they move away from the green walls and reach the blue zone. If robots step in the blue zone, they attempt to stand still. In this sense, robots react and avoid the green walls as a strategy to aggregate in the blue zone.
The control software produced by TuttiFrutti and EvoColor showed a significant drop in performance when ported to the physical robots. As observed in stop, the difference in mean performance between simulations and experiments with physical robots is larger for EvoColor than TuttiFrutti. Robot swarms that use the control software produced by TuttiFrutti display the same collective behaviors observed in simulation. The decrease in performance occurs because few robots that leave the blue zone do not return as fast as observed in the simulations. The control software produced by EvoColor does not port well to the physical robots—that is, robots appear to be unable to reproduce the behaviors observed in the simulation. Robots ramble in the arena and seem to react to the presence of their peers, however, no specific meaningful behavior could be identified by visual inspection.
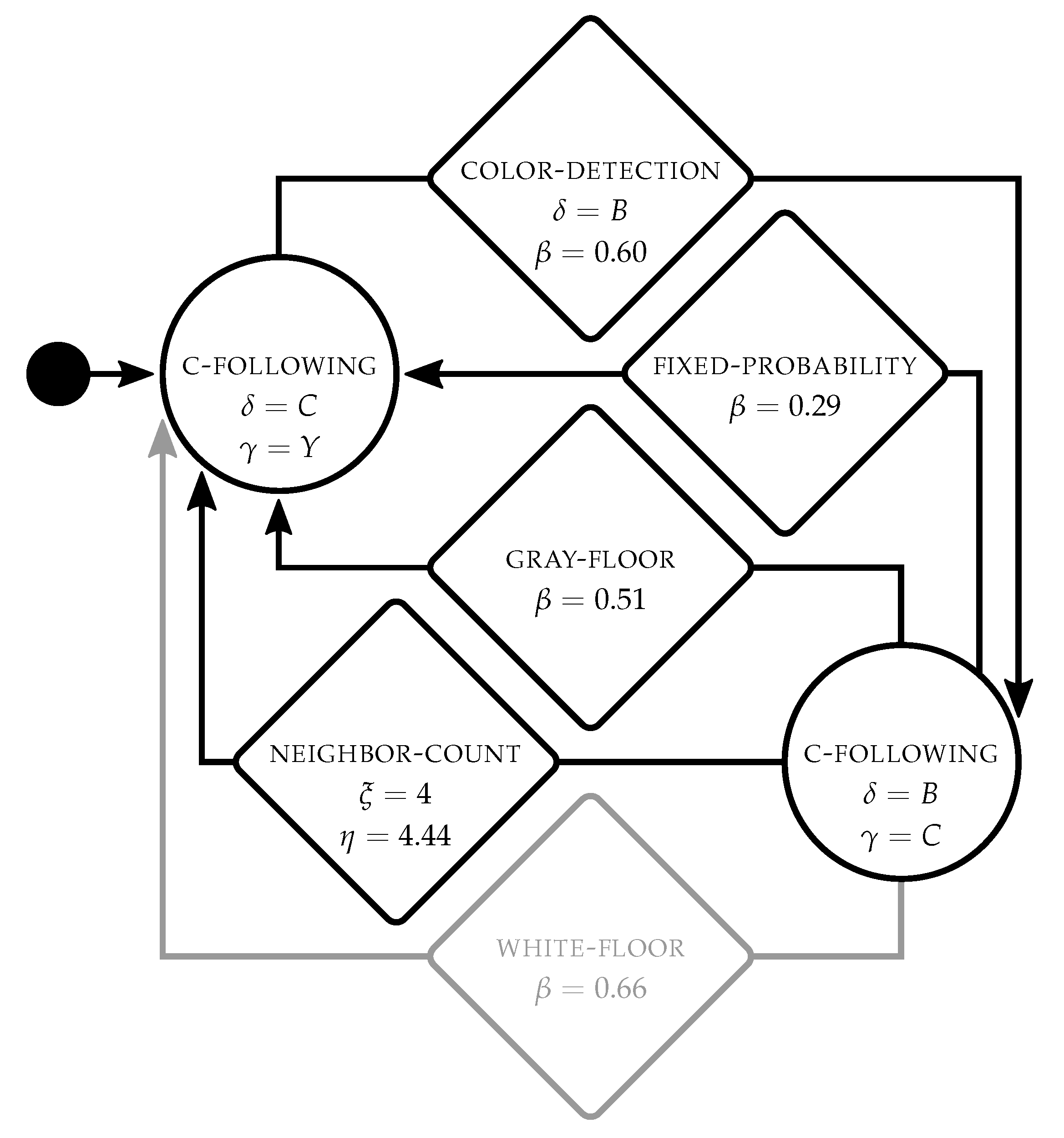
Figure 5 shows an example of the control software produced by
TuttiFrutti for
aggregation. Robots start in
color-following displaying yellow
and move towards cyan robots
. When they perceive the blue walls
,
color-detection triggers and the robots transition to a second module
color-following in which they move towards the blue walls
while emitting a cyan signal
. By cycling in these behaviors, robots can navigate to the blue zone either by moving towards the blue walls or by following the cyan signals that other robots emit. The transition conditions
fixed-probablity,
gray-floor and
neighbor-count trigger the
color-following behavior that allows the robot to return to the aggregation area.
5.3. foraging
Figure 3 (right) shows the performance of
TuttiFrutti and
EvoColor in
foraging. In this mission,
EvoColor performs significantly better than
TuttiFrutti in simulation. However,
TuttiFrutti performs significantly better than
EvoColor in the experiments with physical robots.
As in the other missions, from visual inspection,
TuttiFrutti produced control software that effectively uses the capabilities that the robots have of displaying and perceiving colors. Robots explore the arena and forage only from the profitable source. However, contrary to what we expected,
TuttiFrutti designed collective behaviors that do not use all the colors displayed in the arena. In fact, robots mostly forage by randomly exploring the arena while moving away from the green wall—in other words, they only avoid to step in the green source. Although the swarm can perform the mission with this behavior, we expected that robots could navigate faster by moving towards the blue and red walls. Still,
TuttiFrutti produced only few instances of control software in which robots react to more than one color—see
Figure 6. We conjecture that
TuttiFrutti exploits the convex shape of the arena to produce solutions that are effective at the minimal complexity—that is, the performance of a swarm in this mission might not improve even if robots react to all three colors.
EvoColor designed collective behaviors in which the swarm does not react to the colors displayed in the arena. Robots forage from the blue source by following the walls of the arena in a clockwise direction. This behavior efficiently drives the robots around the arena and across the blue source. When the robots reach the intersection that divides the blue and green source, they continue moving straight and effectively reach the nest. By cycling in this behavior, the swarm maintains an efficient stream of foraging robots.
TuttiFrutti and EvoColor showed a significant drop in performance in the experiments with physical robots, in comparison to the performance obtained in the simulations. Likewise the other two missions, the difference in mean performance between simulations and experiments with physical robots is larger for EvoColor than TuttiFrutti. In the case of TuttiFrutti, we did not observe any difference in the behavior of the swarms with respect to the simulations. Conversely, the collective behaviors designed by EvoColor are affected to the point that the swarm is unable to complete the mission. In the control software produced by EvoColor, the ability of the robots to follow the walls strongly depends on the fine-tuning of the synaptic weights in the neural network—more precisely, it requires a precise mapping between the proximity sensors and wheels of the robots. In the physical robots, the noise of the proximity sensors and wheels differs from the original design model, and a fine-tuned neural network is less effective. Indeed, the swarm is not any more able to maintain the stream of foraging robots, and on the contrary, robots stick to each other and to the walls.
We also observe a
rank inversion of the performance of the two methods in this mission. As defined by Ligot and Birattari [
53], a rank inversion is a phenomenon that manifests when an instance of control software outperforms another in simulation, but it is outperformed by the latter when it is evaluated on physical robots. In our experiments,
TuttiFrutti is outperformed by
EvoColor in simulation, but it outperforms
EvoColor when it is ported to the physical robots. These results are consistent with the ones reported by Francesca et al. [
8], and further discussed by Birattari et al. [
68] and Ligot and Birattari [
53], for comparisons between the modular and the neuro-evolutionary approach to the automatic design of robot swarms.
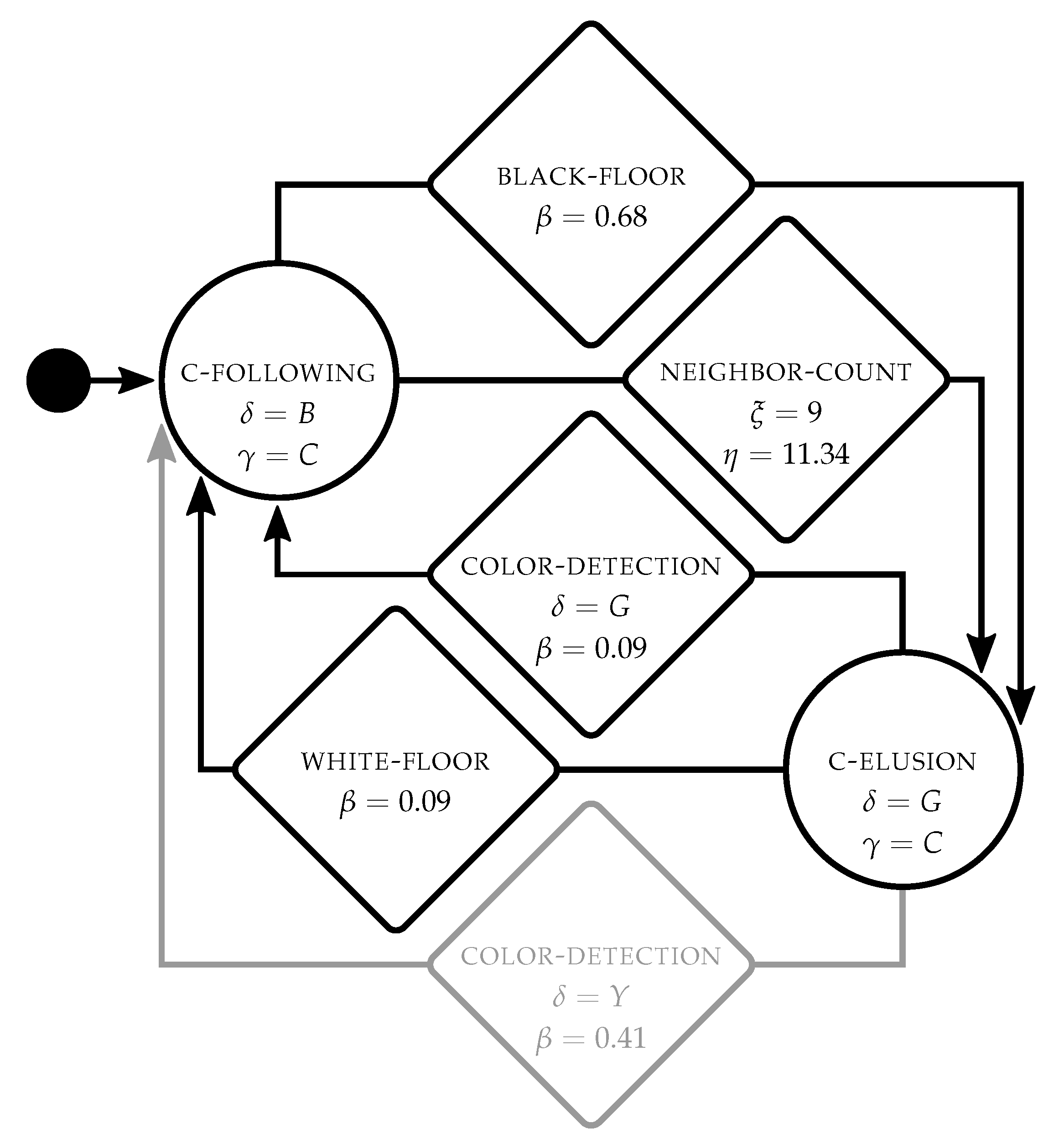
Figure 6 shows an example of the control software produced by
TuttiFrutti for
foraging. Robots start in
color-following displaying cyan
and moving towards the blue wall
. If a robot steps in one of the two sources,
black-floor triggers and the robot transitions to
color-elusion—it then becomes cyan
and moves away from the green wall
. When the robot steps in the nest,
white-floor triggers and the robot transitions back to
color-following. By cycling this behavior, robots move back and forth between the blue source and the nest. When robots are in
color-elusion,
color-detection can trigger with a low probability
if robots perceive the green wall
. This transition mitigates the penalty caused by robots that step in the green source. If a robot steps in the green source, it transitions back to
color-following and moves towards the blue wall. Finally, the transition condition
neighbor-count can trigger when the robot perceives more than four neighboring robots. Yet, we do not find a clear effect of this transition in the overall behavior of the robots.
5.4. Aggregate Results
TuttiFrutti and
EvoColor obtain similar results when the control software is evaluated with simulations. On the other hand,
TuttiFrutti is significantly better than
EvoColor when the control software is ported to the physical robots. It has already been pointed out that when control software developed in simulation is ported to a real-world platform, due to the reality gap one might observe both a drop in performance [
53] and a substantial modification of the collective behavior [
69]. The entity of these effects might depend on the design method, and some design methods might be more robust than others [
53]. Our results indicate that
EvoColor is more affected by the reality gap than
TuttiFrutti across the three missions considered. This is apparent both in the entity of the performance drop we measured and in the fact that the collective behaviors of the control software generated by
EvoColor are often dramatically differently in simulation and in the real world, while the ones of the control software generated by
TuttiFrutti are essentially unchanged.
By introducing
TuttiFrutti, we also investigated the impact of an extended design space in the optimization process of AutoMoDe. The size of the design space in
Vanilla and
Chocolate is
, as estimated by Kuckling et al. [
70].
B and
C represent, respectively, the number of modules in low-level behaviors and transition conditions. Using the same method as Kuckling et al., we estimate the design space in
TuttiFrutti to be
—that is, 256 times larger than the one searched by
Chocolate. Notwithstanding the larger design space, we do not find evidence that
TuttiFrutti is affected by the increased number of parameters to tune. Indeed,
TuttiFrutti produced effective control software for all missions considered.
5.5. Discussion
In the following, we first address the research questions defined in
Section 1 and then we discuss our findings.
TuttiFrutti selects, tunes and assembles control software that operates with information that is available in the environment in the form of colors. In the three missions, the robot swarm reacts to these colors and act according to the information they provide in each case—both for handling events and navigating. Additionally, we observed that TuttiFrutti can design collective behaviors that exhibit color-based communication between robots. For example, TuttiFrutti designed collective behaviors with color-based communication in stop and aggregation—missions in which communication can influence the performance of the robot swarm. These collective behaviors are feasible thanks to the extended capabilities of the e-puck, capabilities that translated into a larger space of possible control software than the one considered by Vanilla and Chocolate—early versions of AutoMoDe. As the design space of TuttiFrutti is larger than the one of Vanilla and Chocolate, one could have expected that the automatic design process would have difficulties in producing meaningful control software. Still, we did not find evidence that TuttiFrutti suffers from an increased difficulty to design collective behaviors for robot swarms. The reference model RM 3 and the set of modules introduced with TuttiFrutti allowed it to conceive stop and aggregation—variants of missions already studied with AutoMoDe, and foraging—a new mission framed within the best-of-n problem. By introducing TuttiFrutti, we enlarged the variety of collective behaviors that can be produced with the AutoMoDe family.
We argue that the experiments we conducted with
TuttiFrutti show evidence that automatic modular design methods can establish a mission-specific relationship between the colors that the robots perceive and the behavior that they must adopt. In
Section 2, we described experiments in which this relationship enabled the design of complex collective behaviors [
25,
31,
35]. We find that these collective behaviors have similarities with those designed by
TuttiFrutti—for example, robots react to colored objects in the environment and use colors signals to communicate with their peers. We conjecture that
TuttiFrutti, or design methods that might share its characteristics, can produce a wider range and more complex collective behaviors than those described in this paper. In this sense, we believe that research with robot swarms that can perceive and display colors has the potential to close the gap between the complexity of the missions performed with manual design methods, and those performed with automatic design.
6. Conclusions
In this paper, we introduced AutoMoDe-TuttiFrutti—an automatic method to design collective behaviors for robots that can perceive and communicate color-based information. We designed control software for swarms of e-pucks that comply with RM 3—e-pucks can use their LEDs to display colors and their omnidirectional vision turret to perceive them. The capability of the robots to act upon different colors translated into an increased variety of collective behaviors compared to previous instances of AutoMoDe. We assessed TuttiFrutti on a class of missions in which the performance of the swarm depends on its ability to use color-based information for handling events, communicating, and navigating.
We conducted experiments in simulation and with physical robot swarms performing three missions: stop, aggregation and foraging. In all cases, TuttiFrutti designed collective behaviors that effectively use color-based information. In stop, the swarm collectively changes its behavior when a specific color signal appears. In stop and aggregation, the swarm exhibits communication behaviors in which robots pair the color signals they emit and the colors to which they react. In aggregation and foraging, robots use the colors they perceive as a reference to navigate the environment. In foraging, swarms differentiate two sources of items and forage from the profitable one. Alongside the results obtained with TuttiFrutti, we assessed a method based on neuro-evolution: EvoColor. In stop and foraging, EvoColor designed collective behaviors that do not use color-based information. In aggregation, EvoColor designed collective behaviors in which robots use the colors they perceive to navigate the environment—likewise TuttiFrutti. The aggregated results showed that TuttiFrutti performs better than EvoColor in the class of missions we considered. Results with physical robots suggest that TuttiFrutti crosses the reality gap better than EvoColor—result partially sustained by the visual inspection of the behavior of the robots.
Automatic design methods can effectively produce control software for swarms of robots that can display and perceive colors. We demonstrated that TuttiFrutti establishes an appropriate relationship between the colors that the robots perceive and the behavior they must adopt. In our experiments, this relationship was established on a per-mission basis and responded to the specifications of each mission. Yet, the set of missions on which we assess TuttiFrutti is far from being exhaustive, and more research work is needed to define the limitations of the design method. Future work will be devoted to assess TuttiFrutti in a larger and more complex class of missions. It is our contention that TuttiFrutti can design collective behaviors to address missions that involve a larger number of features in the environment and time-varying conditions. As observed in stop, robots can effectively transition between two collective behaviors. We foresee that this ability enables the design of swarms that can perform missions with two or more sequential tasks. To the best of our knowledge, the design of collective behaviors to address this class of missions has not been studied in the context of automatic off-line design of robot swarms.