Real Geometrical Imperfection of Bow-String Arches—Measurement and Global Analysis
Abstract
1. Introduction
2. Imperfections
2.1. Application of Imperfections in Bridge Arch Analysis
2.2. Innovative Geometric Imperfections Measurement
2.3. Comment on the Structural Imperfections
3. Pilot Study
3.1. Selected Bridge
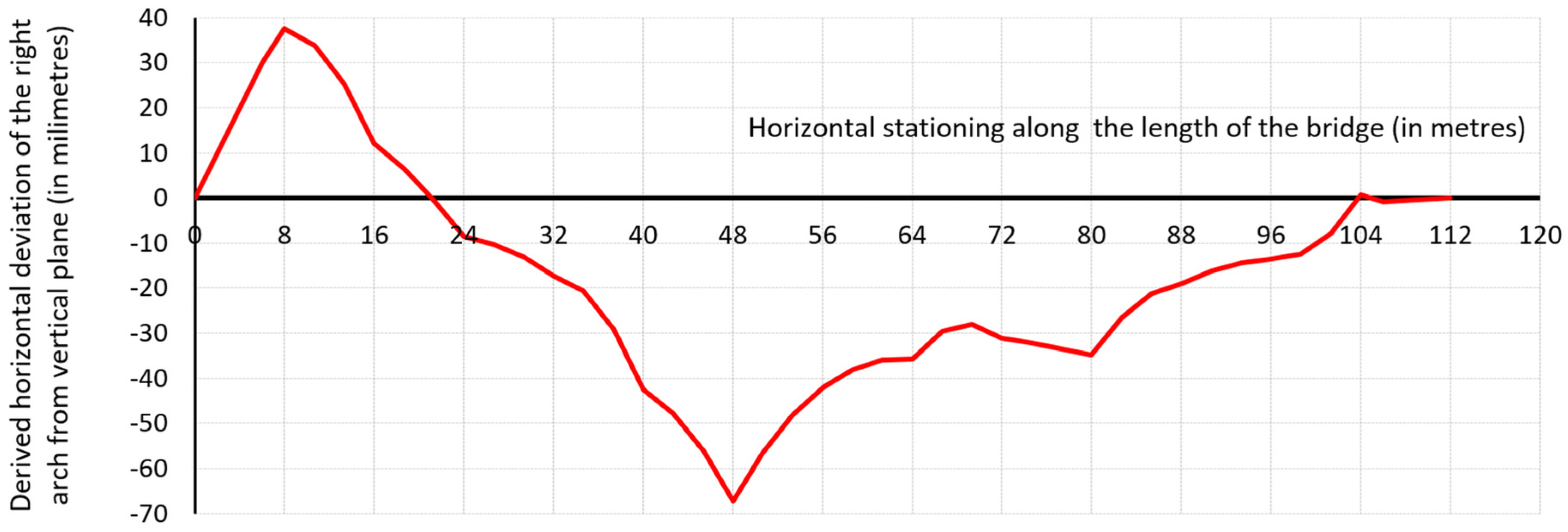
3.2. Laser Scanning
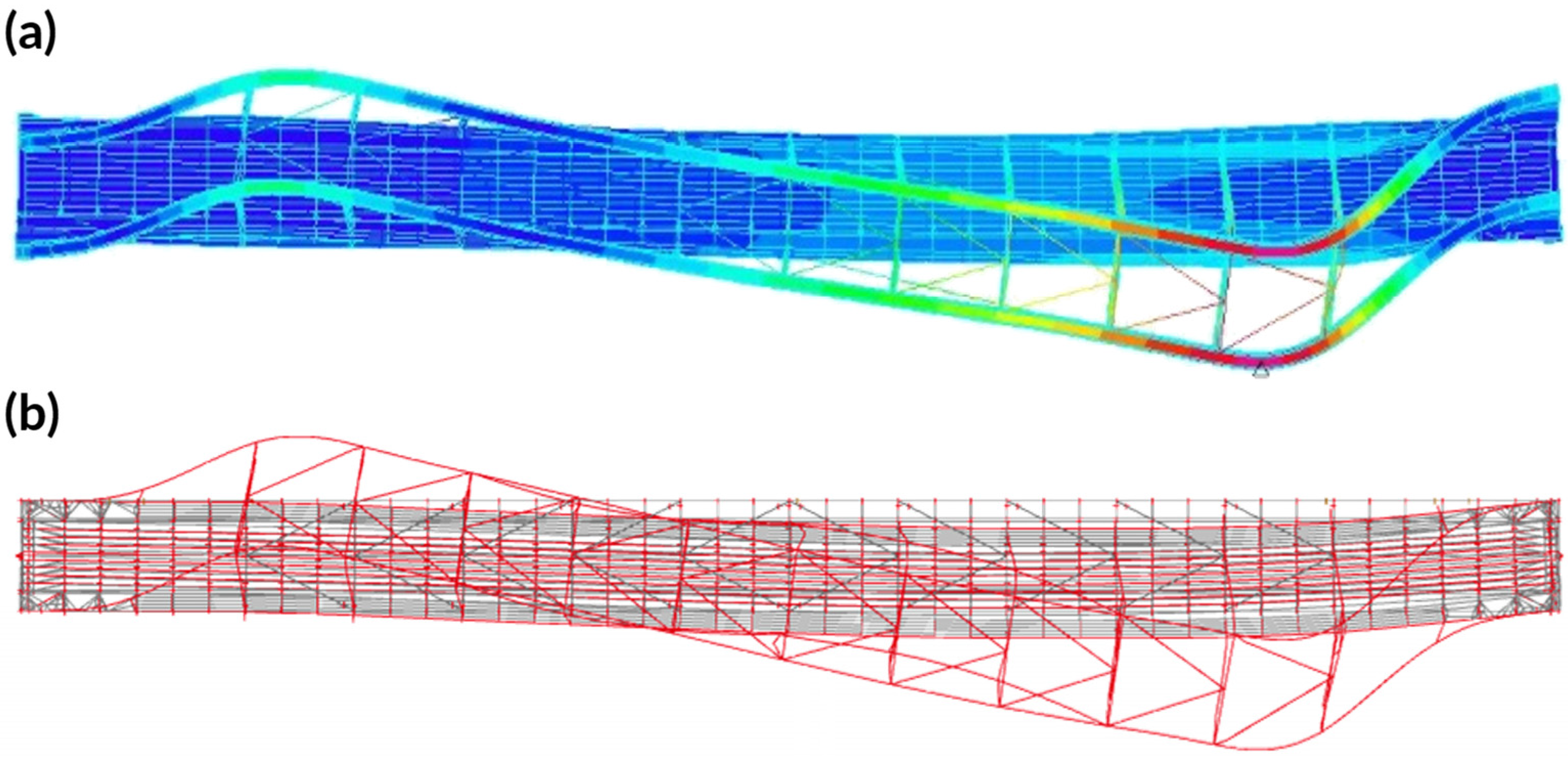
3.3. Finite Element Method Analyses
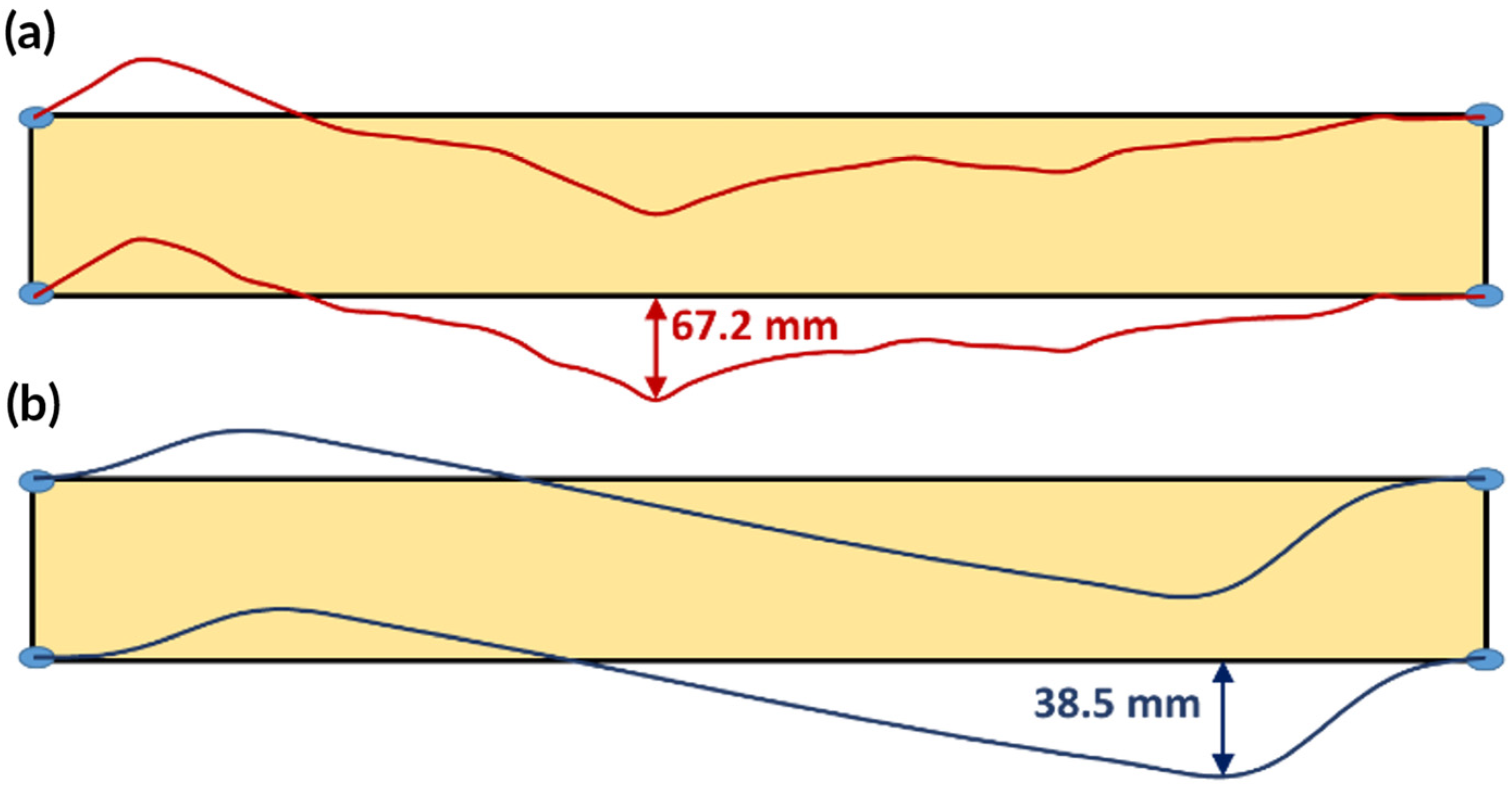
3.4. Comparison of Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vičan, J.; Odrobiňák, J.; Gocál, J. Recently designed bow-string railway bridges in Slovakia. In Proceedings of the 7th International Conference on Arch Bridges (ARCH 2013), Split, Croatia, 2–4 October 2013; pp. 427–434. [Google Scholar]
- Vičan, J.; Odrobiňák, J.; Gocál, J.; Hlinka, R. Design of the two-line railway bridge with the longest span in Slovakia. In Proceedings of the 8th International Conference “Bridges in Danube Basin”, Timişoara, Romania, 4–5 October 2013; pp. 267–278. [Google Scholar]
- Chladný, E.; (Slovak University of Technology, Bratislava, Slovakia). Comments to EN 1993-1-1: Draft 2000. Comments sent to J. Brozetti, accepted by G. Sedlacek from TC 250/SC3, CEN Brussels. Personal Communication, 2000. [Google Scholar]
- Baláž, I. Determination of flexural buckling resistance of frames with members with non-uniform cross-sections and non-uniform axial compression forces. In Proceedings of the 34th Slovak Meeting of Experts on Steel Structures, Pezinok, Slovakia, 16–17 October 2008; pp. 17–22. [Google Scholar]
- Baláž, I.; Koleková, Y. Structures with UGLI imperfections. In Proceedings of the 18th International Conference “Engineering Mechanics 2012”, Svratka, Czech Republic, 14–17 May 2012; pp. 61–86. [Google Scholar]
- Chladný, E.; Štujberová, M. Frames with unique global and local imperfection in the shape of the elastic buckling mode (Part 1). Stahlbau 2013, 82, 609–617. [Google Scholar] [CrossRef]
- Chladný, E.; Štujberová, M. Frames with unique global and local imperfection in the shape of the elastic buckling mode (Part 2). Stahlbau 2013, 82, 684–694. [Google Scholar] [CrossRef]
- Chladný, E.; Chladná, M. The application of initial bow imperfection in the designs of new Danube Bridges in Slovakia. In Proceedings of the 4th International Conference “Bridges across the Danube”, Bratislava, Slovakia, 13–15 September 2001; pp. 179–184. [Google Scholar]
- Vičan, J.; Odrobiňák, J.; Gocál, J. Analysis of out-of-plane stability of bow-string arches. Communications 2016, 18, 3–9. [Google Scholar]
- Aguero, A.; Pallares, L.; Pallares, F.J. Equivalent geometric imperfection definition in steel structures sensitive to lateral torsional buckling due to compression. Eng. Struct. 2015, 96, 41–55. [Google Scholar] [CrossRef]
- Aguero, A.; Pallares, L.; Pallares, F.J. Equivalent geometric imperfection definition in steel structures sensitive to flexural and/or torsional buckling due to compression. Eng. Struct. 2015, 96, 160–177. [Google Scholar] [CrossRef]
- Farbák, M.; Chromčák, J.; Jošt, J. Meranie reálnych geometrických imperfekcií na oceľových oblúkových mostoch/Measurement of real geometric imperfections on steel arch bridges. In Proceedings of the 43th Slovak Meeting of Experts on Steel Structures, Bešeňová, Slovakia, 16–17 October 2013; pp. 47–52. [Google Scholar]
- Ižvoltová, J.; Pisca, P.; Koťka, V.; Mancovič, M. 3D laser scanning of railway line. Communications 2013, 15, 80–84. [Google Scholar]
- Ižvoltová, J.; Villim, A.; Kozák, P. Determination of geometrical track position by robotic total station. Procedia Eng. 2014, 91, 322–327. [Google Scholar] [CrossRef]
- Alpsten, G.A.; Tall, L. Residual Stresses in Heavy Welded Shapes. Weld. Res. Suppl. 1970, 49, 3–105. [Google Scholar]
- Gkatzogiannis, S.; Knoedel, P.; Ummenhofer, T. Simulation of welding residual Stresses—from theory to practice. In Mathematical Modelling of Weld Phenomena 12; Verlag der Technischen Universität Graz: Graz, Austria, 2019; pp. 383–400. [Google Scholar]
- Szalai, J.; Papp, F. On the probabilistic evaluation of the stability resistance of steel columns and beams. J. Constr. Steel Res. 2009, 65, 569–577. [Google Scholar] [CrossRef]
- Young, B.W. Residual Stresses in Hot Rolled Members; Iabse Reports of the Working Commissions; Ein Dienst der ETH-Bibliothek: Zürich, Switzerland, 2019; 15p, Available online: https://www.e-periodica.ch/cntmng?pid=bse-re-001:1975:23::41 (accessed on 29 June 2020).
- Prokop, J.; Vičan, J. Pinned-fixed beam-column resistance verification according to European standards. Civ. Environ. Eng. 2018, 14, 28–36. [Google Scholar] [CrossRef]
- Koubova, L.; Janas, P.; Markopoulos, A.; Krejsa, M. Nonlinear analyses of steel beams and arches using virtual unit moments and effective rigidity. Steel. Compos. Struct. 2019, 33, 755–765. [Google Scholar]





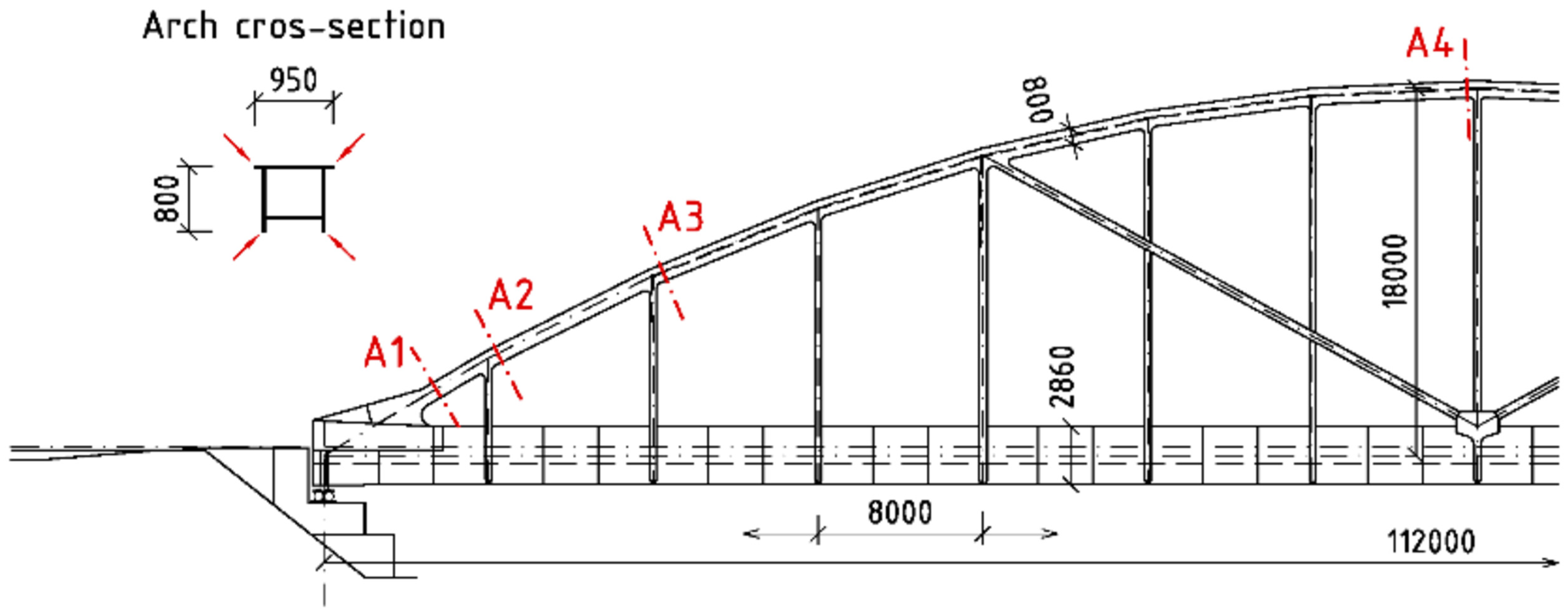
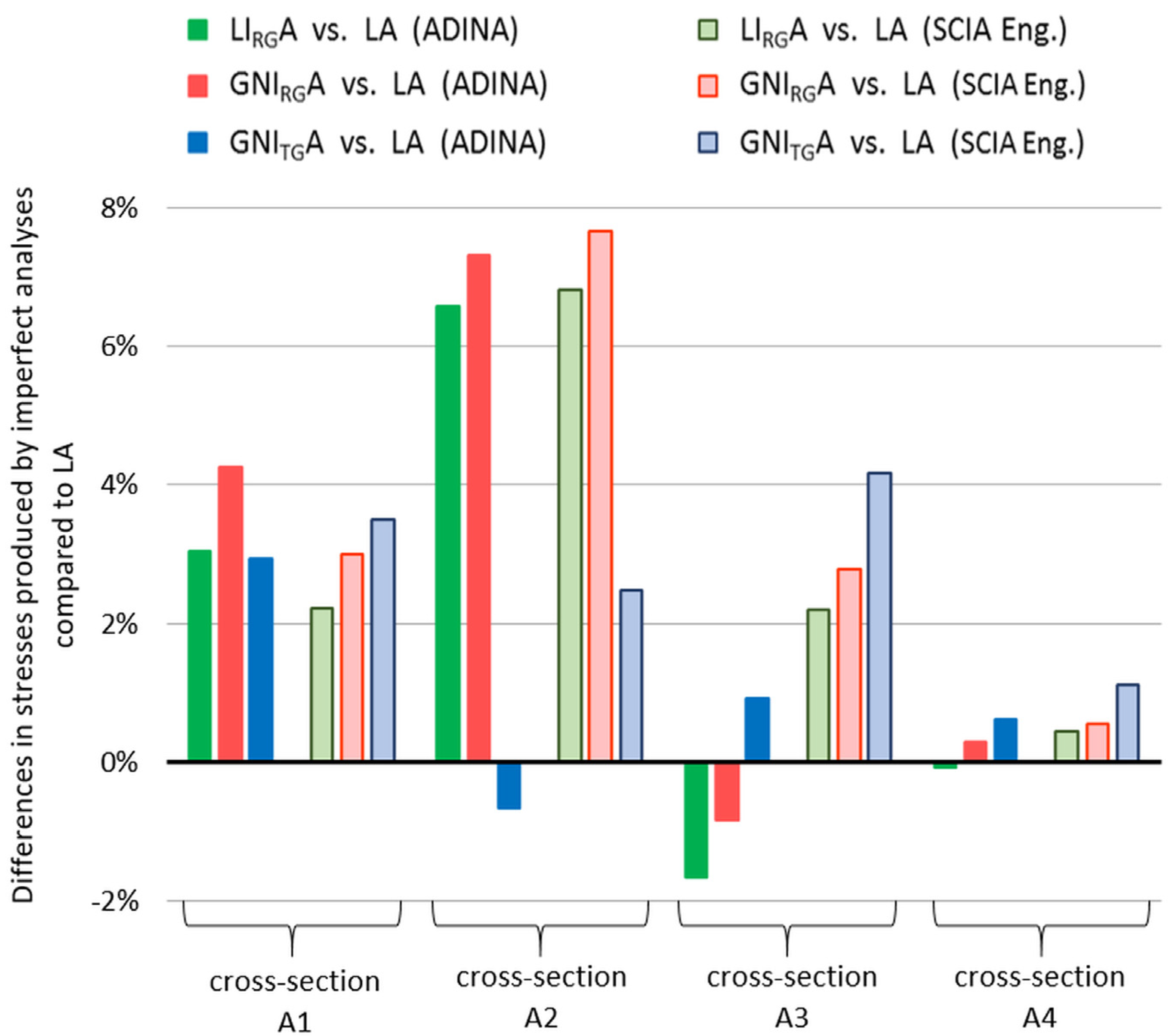
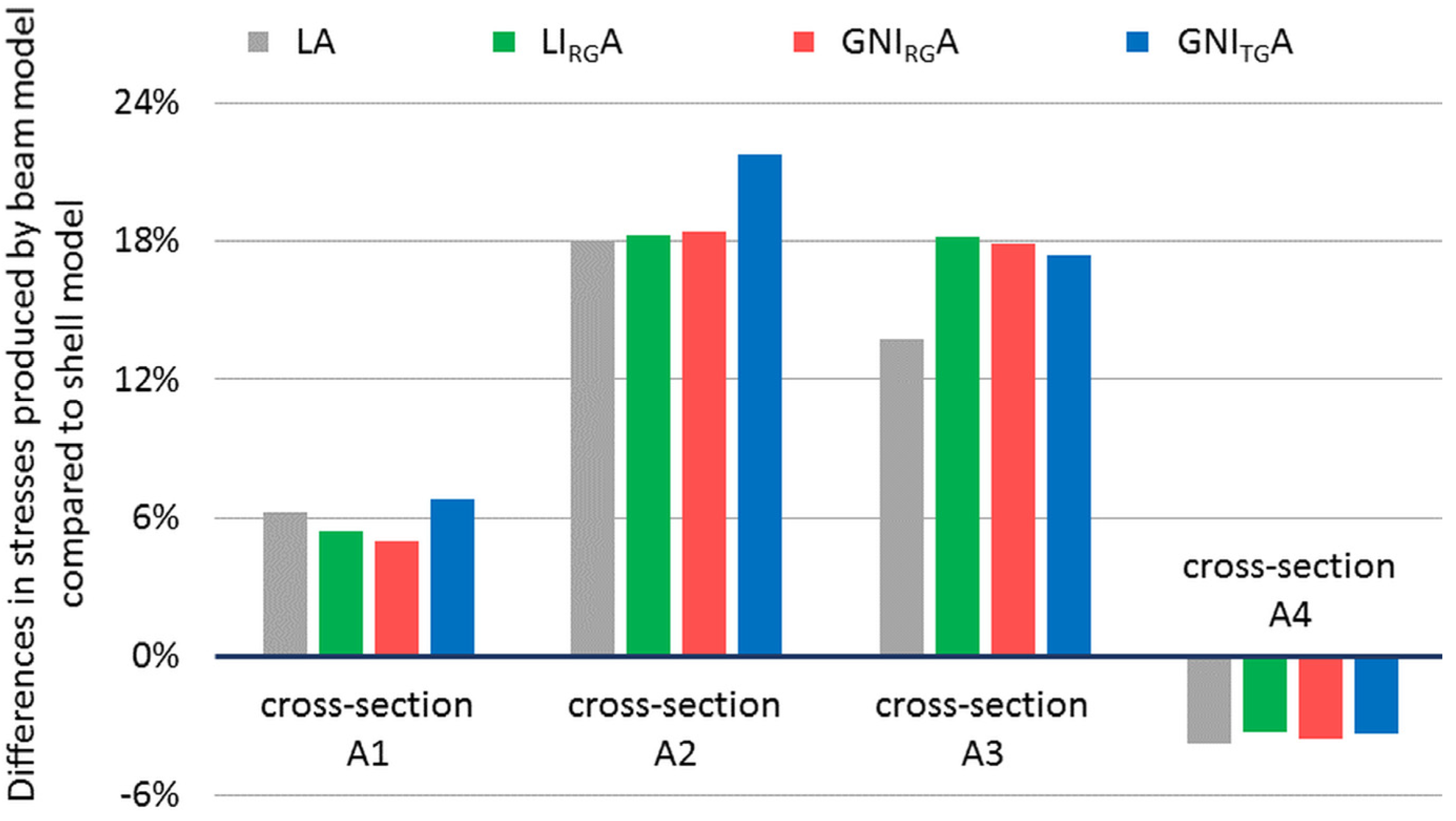
| Arch Cross- Section | Dominant Elements/Software | Type of FEM Analysis | |||
|---|---|---|---|---|---|
| LA | LIRGA | GNIRGA | GNITGA | ||
| A1 | shells/ADINA | −190.8 | −196.6 | −198.9 | −196.4 |
| beams/SCIA Eng. | −202.7 | −207.2 | −208.8 | −209.8 | |
| A2 | shells/ADINA | −181.5 | −193.5 | −194.8 | −180.3 |
| beams/SCIA Eng. | −214.2 | −228.8 | −230.6 | −219.5 | |
| A3 | shells/ADINA | −183.6 | −180.5 | −182.0 | −185.3 |
| beams/SCIA Eng. | −208.8 | −213.4 | −214.6 | −217.5 | |
| A4 | shells/ADINA | −186.1 | −185.9 | −186.6 | −187.2 |
| beams/SCIA Eng. | −179.0 | −179.8 | −180.0 | −181.0 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odrobiňák, J.; Farbák, M.; Chromčák, J.; Kortiš, J.; Gocál, J. Real Geometrical Imperfection of Bow-String Arches—Measurement and Global Analysis. Appl. Sci. 2020, 10, 4530. https://doi.org/10.3390/app10134530
Odrobiňák J, Farbák M, Chromčák J, Kortiš J, Gocál J. Real Geometrical Imperfection of Bow-String Arches—Measurement and Global Analysis. Applied Sciences. 2020; 10(13):4530. https://doi.org/10.3390/app10134530
Chicago/Turabian StyleOdrobiňák, Jaroslav, Matúš Farbák, Jakub Chromčák, Ján Kortiš, and Jozef Gocál. 2020. "Real Geometrical Imperfection of Bow-String Arches—Measurement and Global Analysis" Applied Sciences 10, no. 13: 4530. https://doi.org/10.3390/app10134530
APA StyleOdrobiňák, J., Farbák, M., Chromčák, J., Kortiš, J., & Gocál, J. (2020). Real Geometrical Imperfection of Bow-String Arches—Measurement and Global Analysis. Applied Sciences, 10(13), 4530. https://doi.org/10.3390/app10134530




