A New Semi-Analytical Method for Elasto-Plastic Analysis of a Deep Circular Tunnel Reinforced by Fully Grouted Passive Bolts
Abstract
:Featured Application
Abstract
1. Introduction
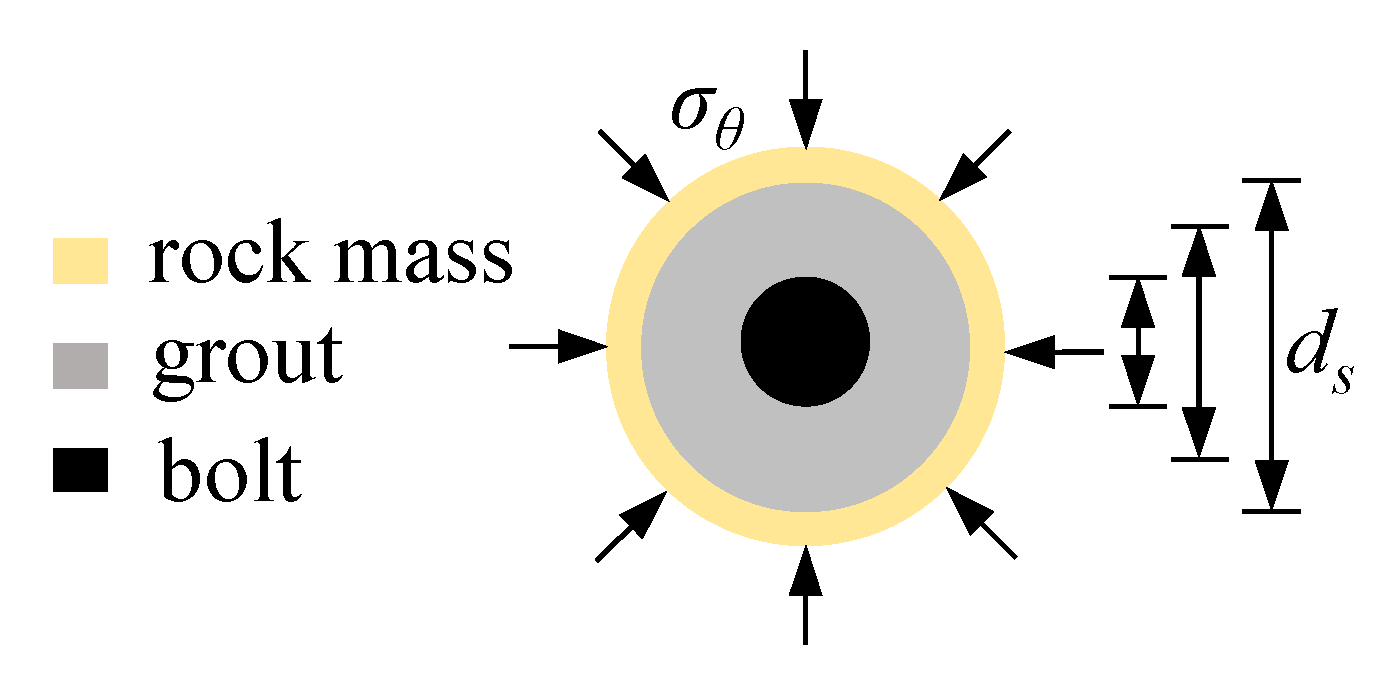
2. Definition of the Problem
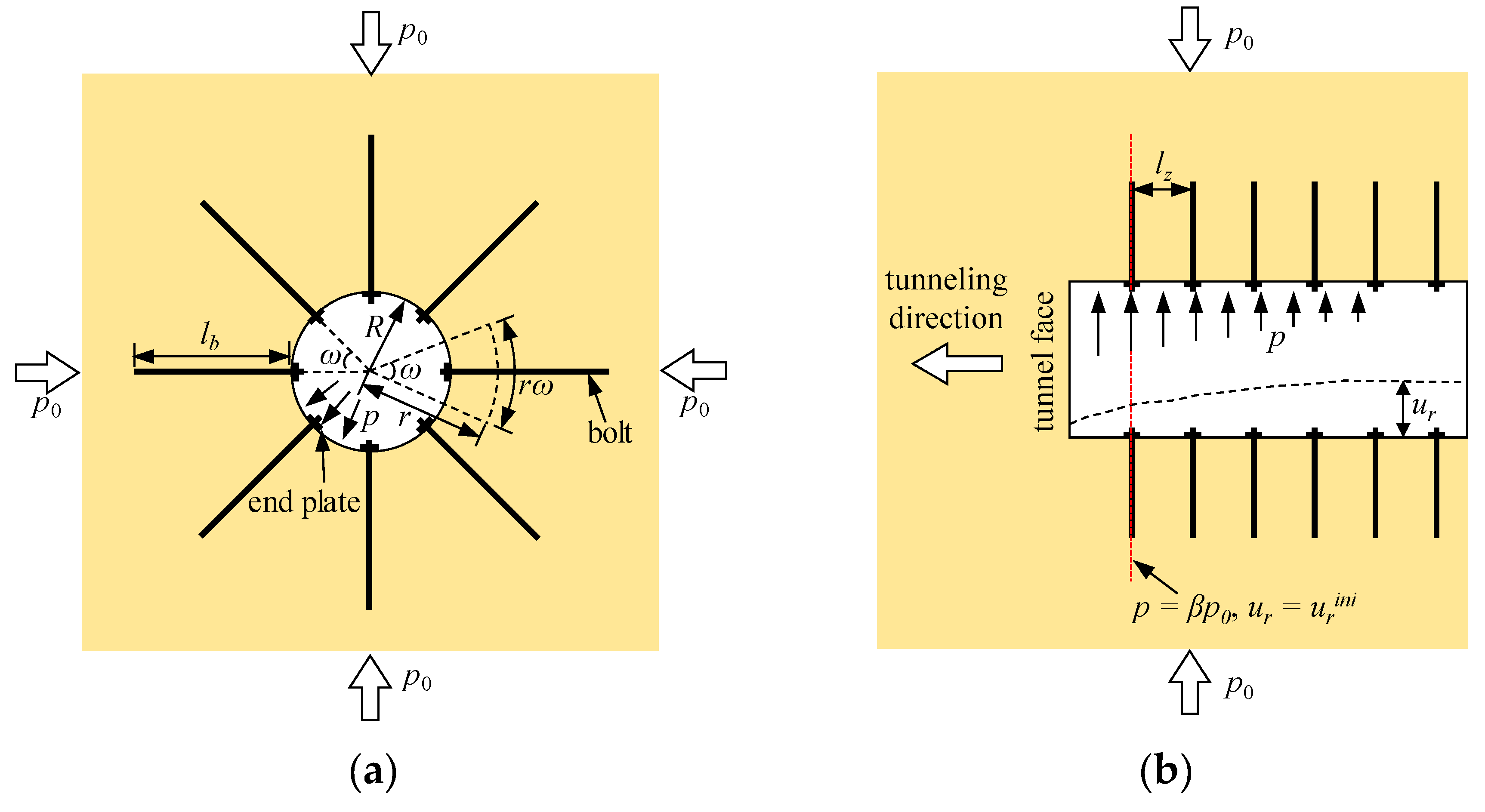
2.1. Basic Assumptions
2.2. Tunnel Face Effect during Tunneling
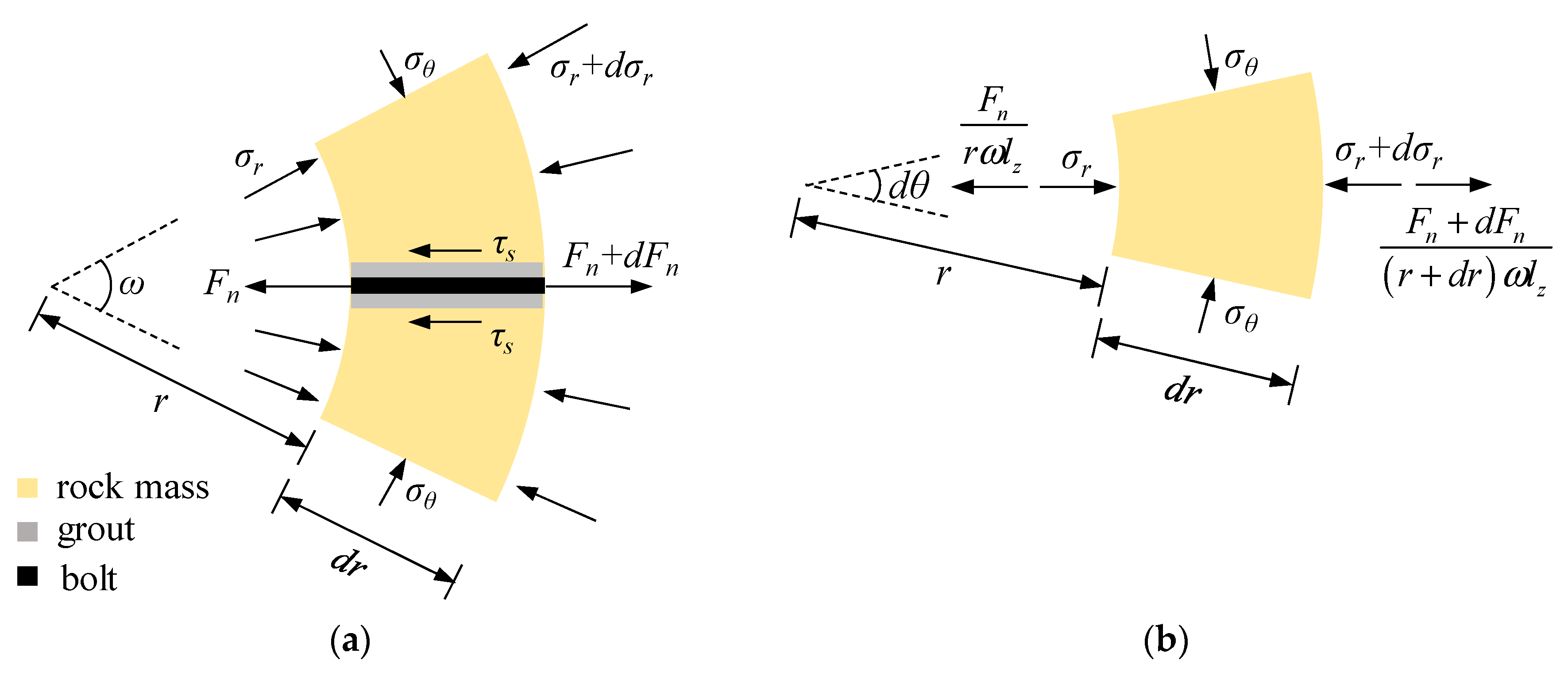
2.3. Equation of Equilibrium
2.4. Failure Criterions
2.4.1. Mohr–Coulomb Criterion
2.4.2. Generalized Hoek–Brown Criterion
2.5. Plastic Potential Equation
2.6. Equations of Strains and Displacements
2.6.1. In an Elastic Region
2.6.2. In a Plastic Region
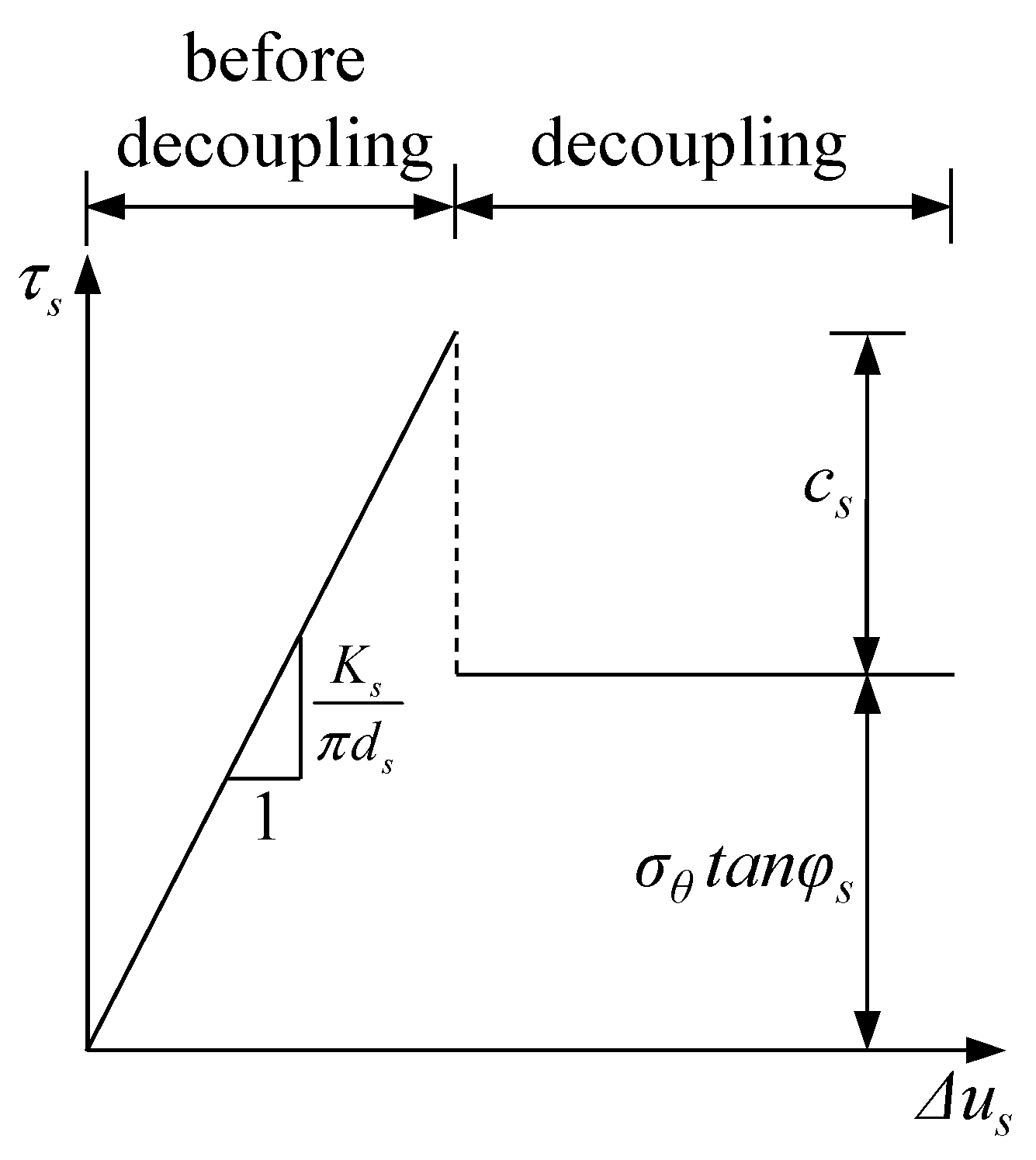
2.7. Interaction between the Rock Mass and the Passive Bolts
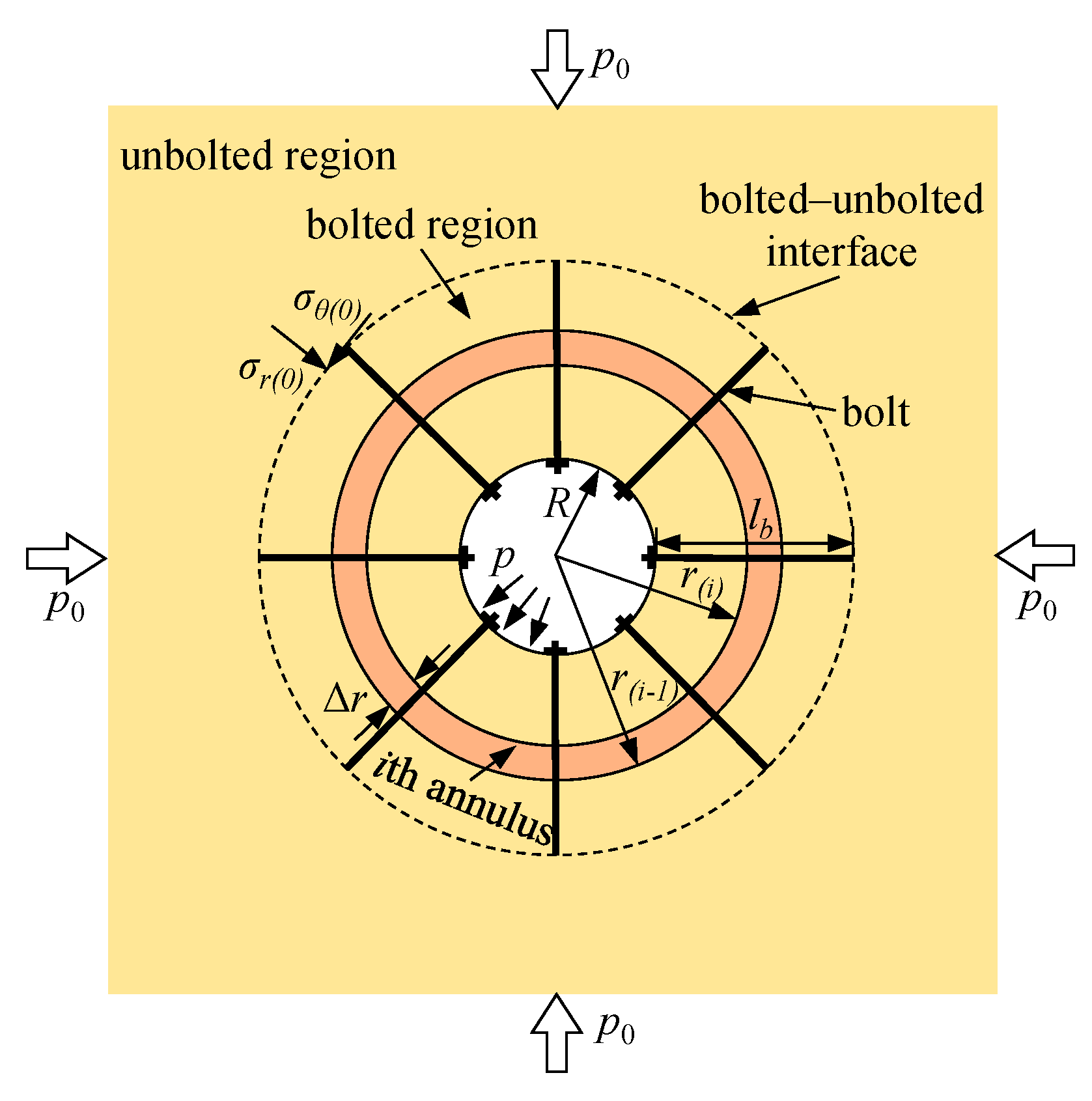
3. Stress–Strain Analysis of the Rock Mass and Passive Bolts Using the Finite Difference Method
3.1. Stress–Strain Analysis in an Unbolted Region
3.2. Stress–Strain Analysis in a Bolted Region
3.2.1. Stress–Strain Analysis in an Elastic Region
3.2.2. Stress–Strain Analysis in a Plastic Region
3.2.3. Behaviors of the Passive Bolts
4. Verification
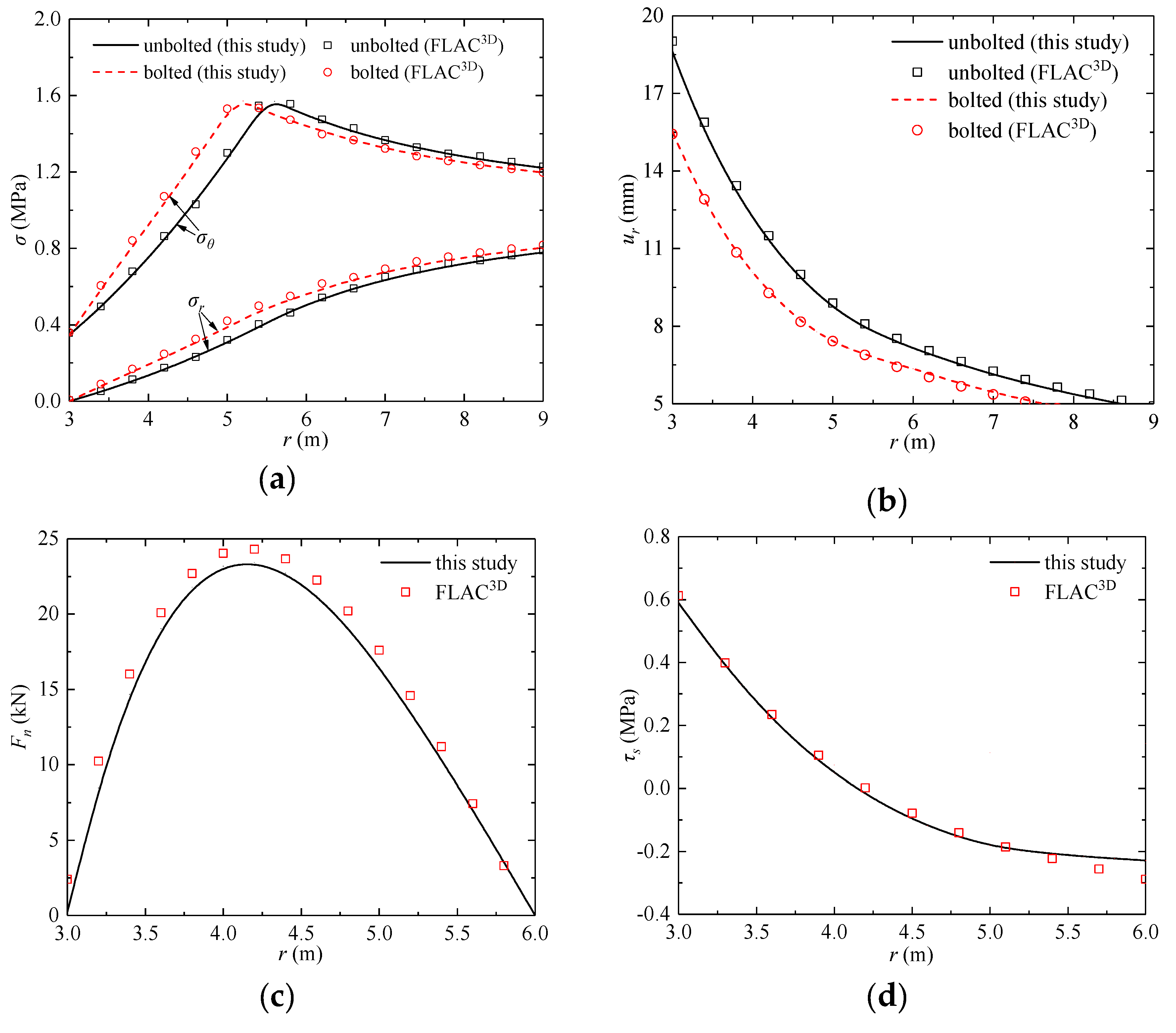
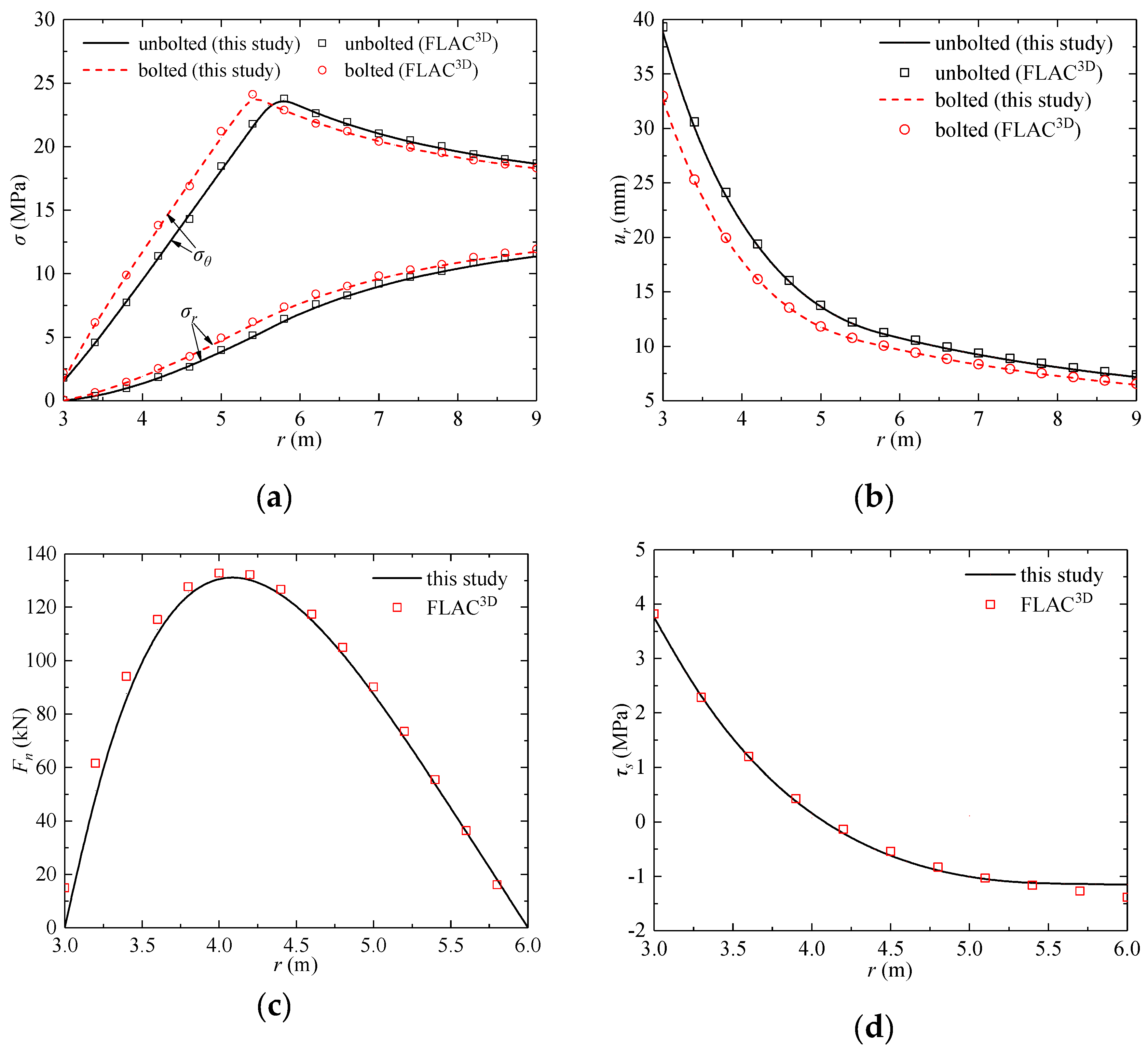
4.1. Comparison with the Results from the Commercial Numerical Software
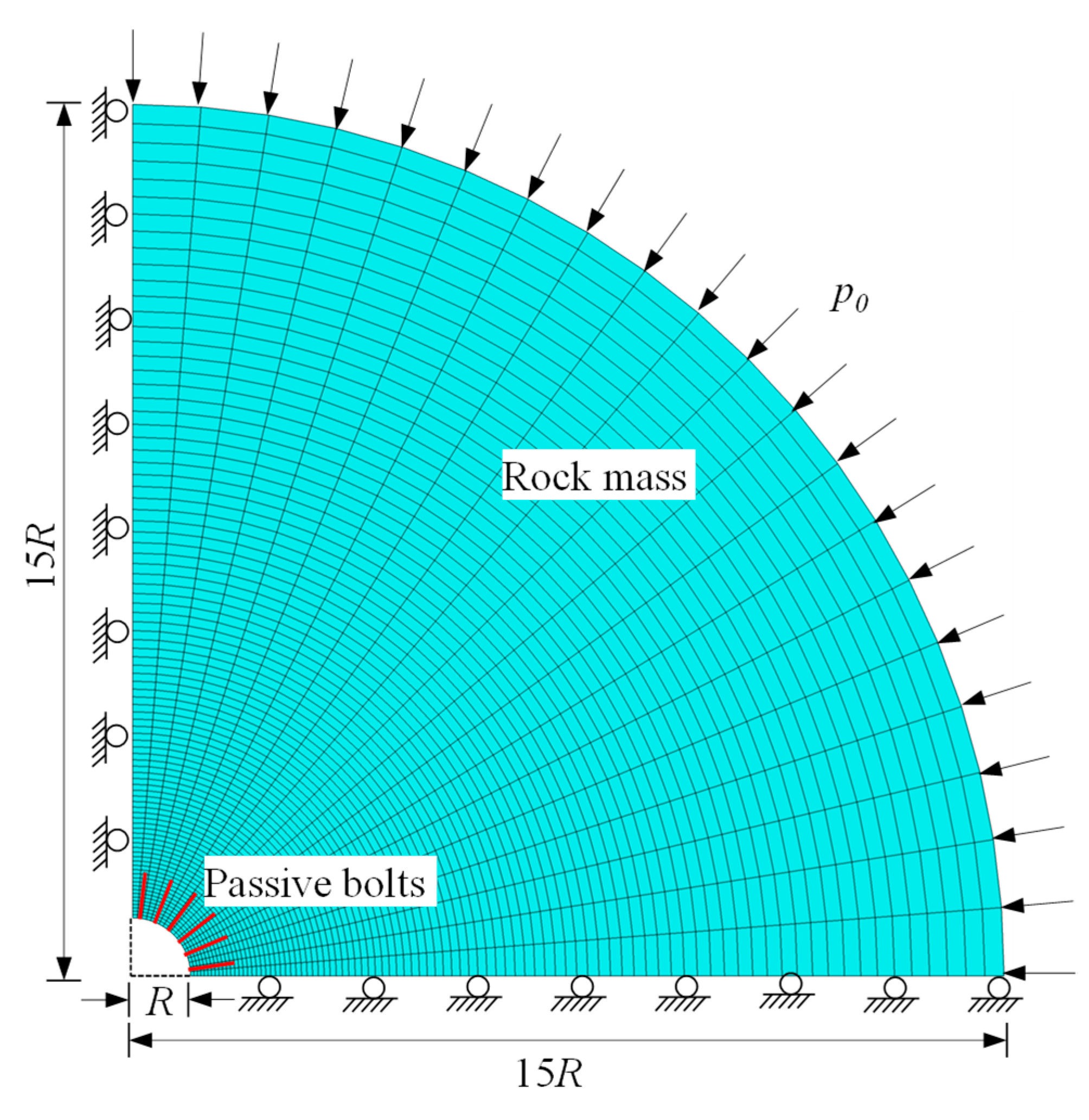
4.1.1. Establishment of the Numerical Model
4.1.2. Mohr–Coulomb Criterion
4.1.3. Generalized Hoek–Brown Criterion
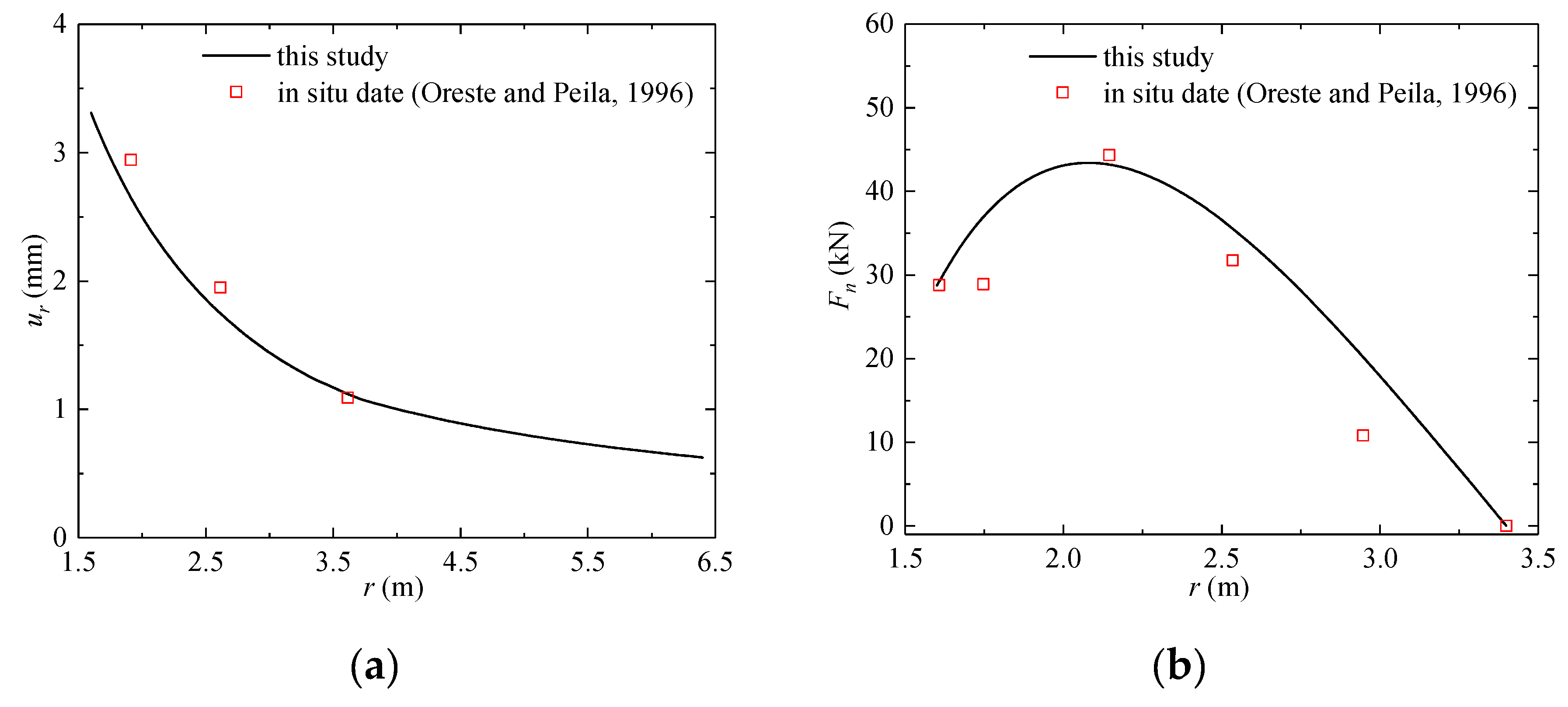
4.2. Comparison with the In Situ Test Results from the Kielder Experimental Tunnel
5. Discussion
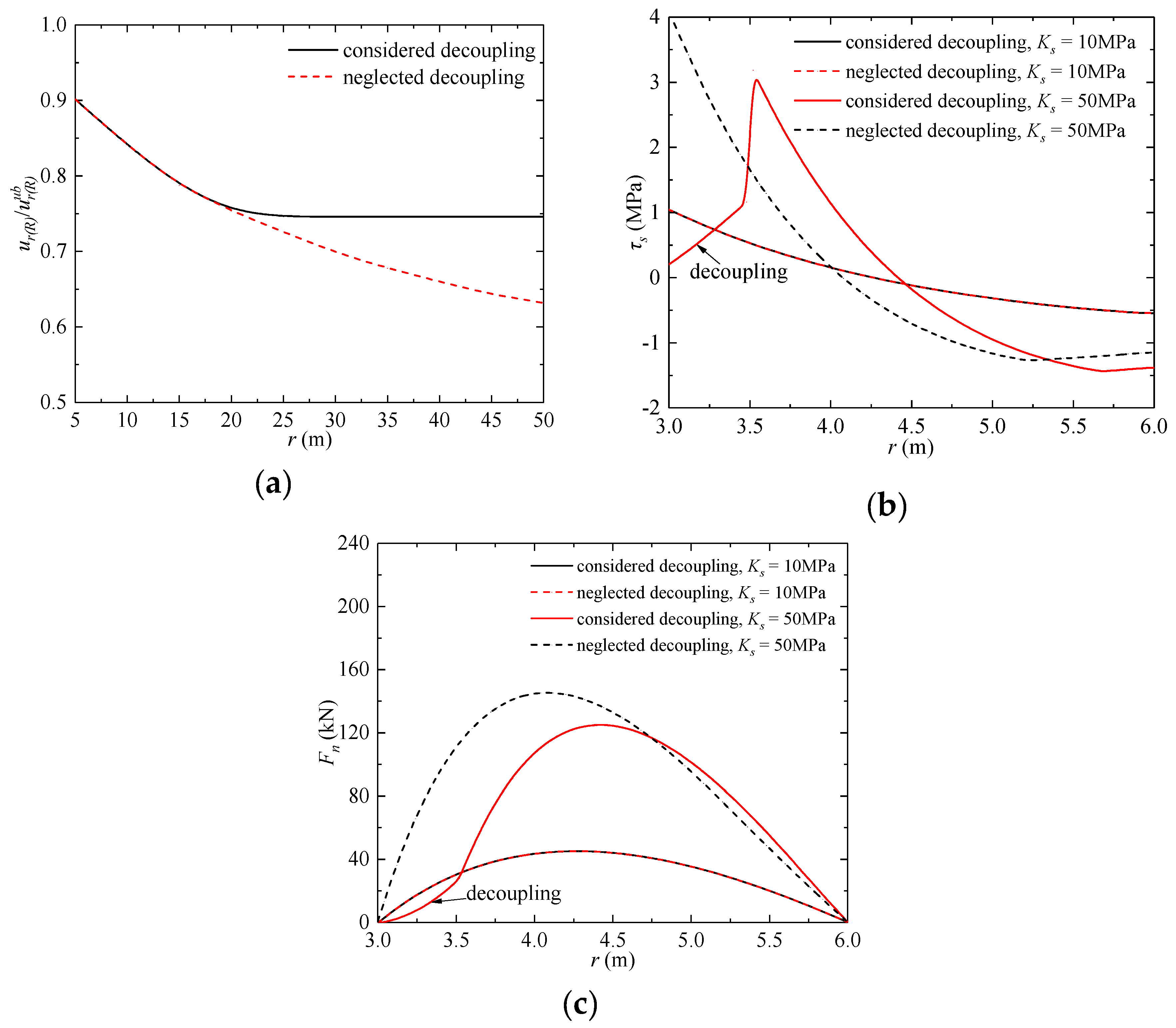
5.1. Comparison of the Solutions That Considered or Neglected Decoupling at the Bolt–Rock Interface
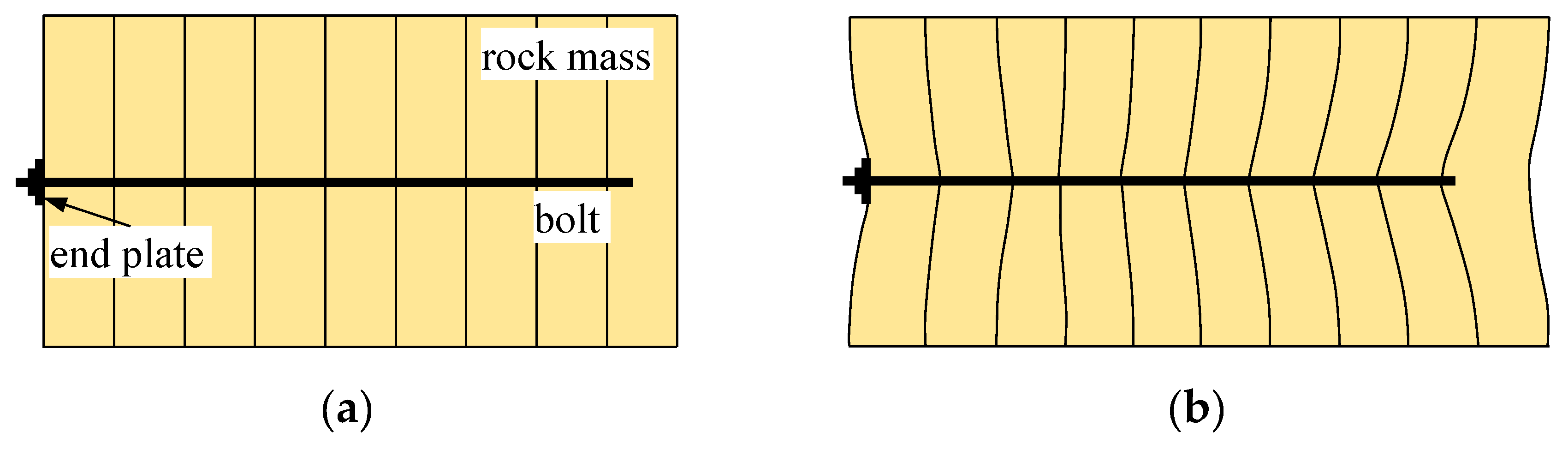
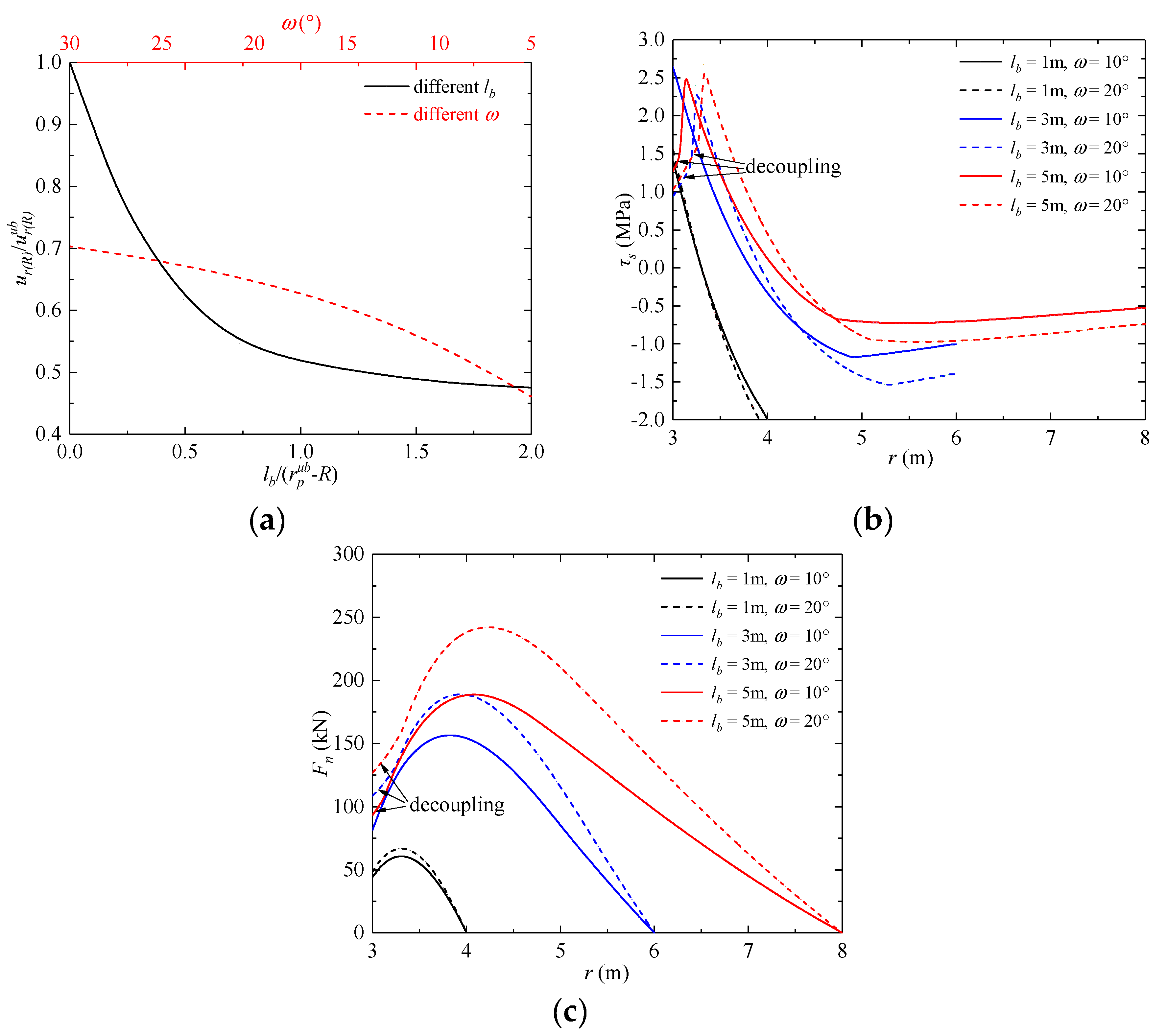
5.2. Effect of the End Plate and Shear Stiffness at the Bolt–Rock Interface
5.3. Effect of Bolt Length and Density
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Stress–Strain Analysis in an Unbolted Tunnel
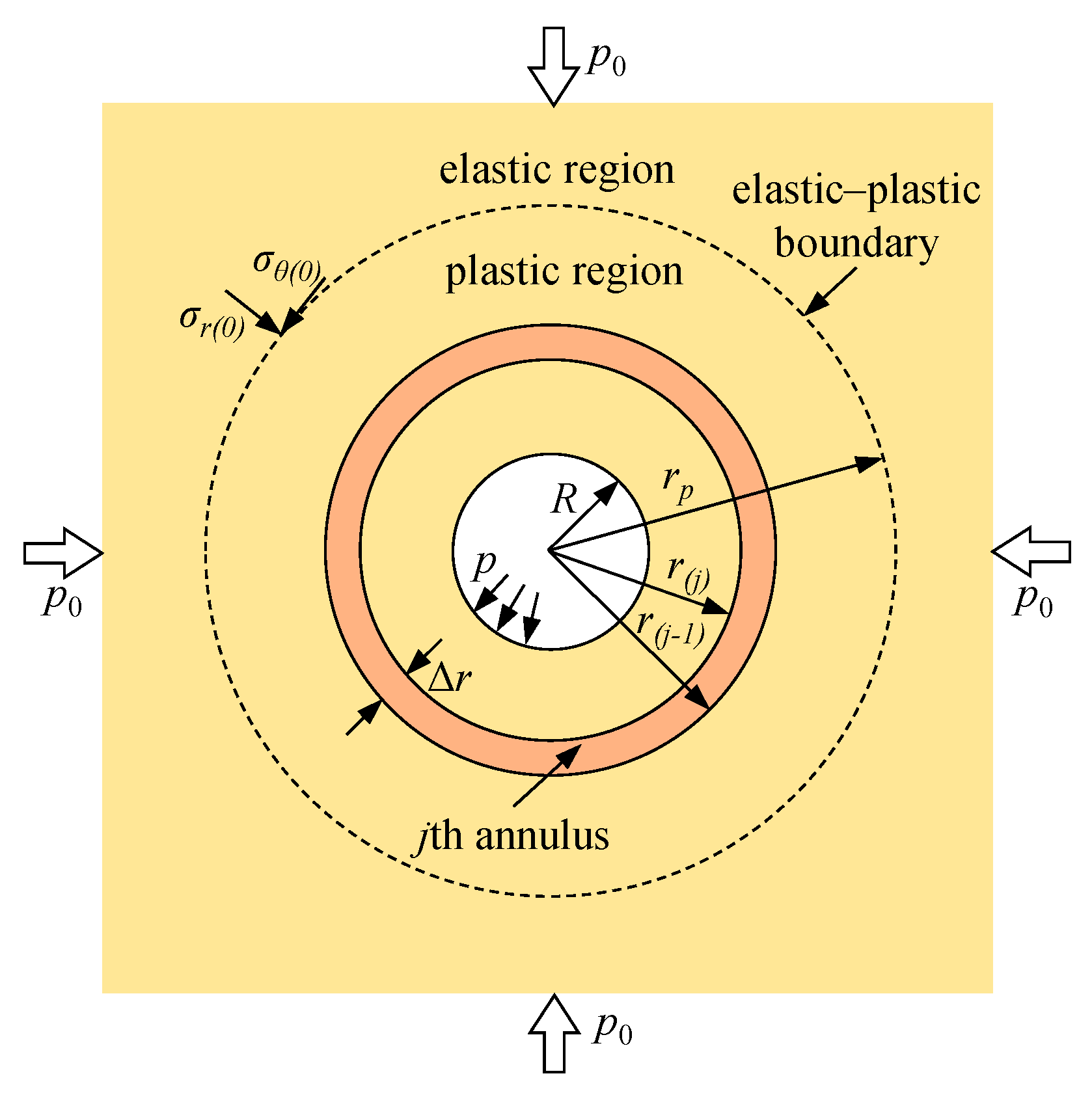
Appendix A.1. Stress–Strain Analysis in an Unbolted Elastic Region
Appendix A.2. Stress–Strain Analysis in an Unbolted Elastic Region
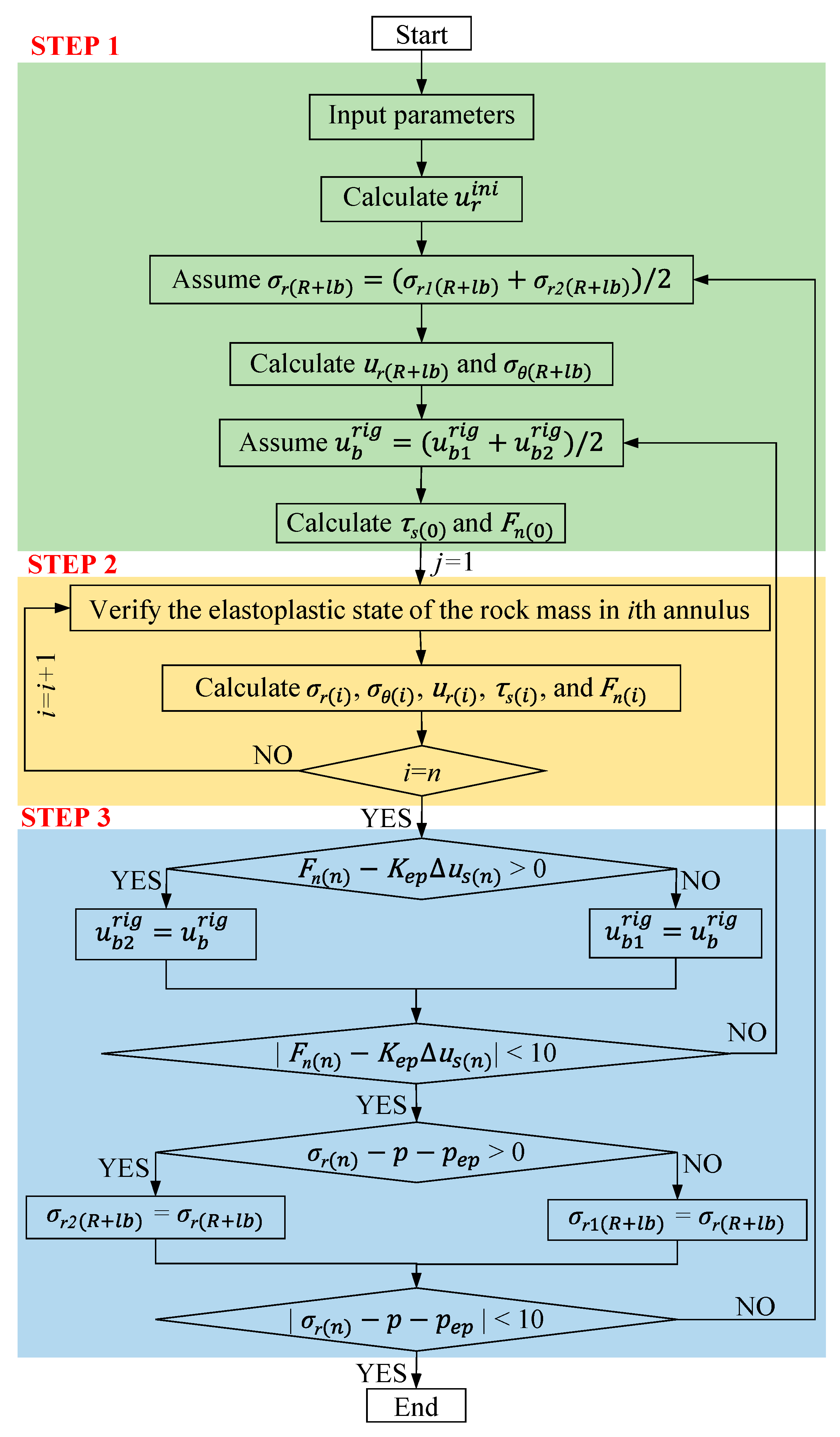
Appendix B. Calculation Procedure
- (1)
- Input parameters: R, p0, β, p, E, μ, ψ, Eb, lb, ds, Ab, lz, ω, Ks, Kep, cs, φs, Δr, cp, cr, φp, φr, σci,p, σci,r, mb,p, mb,r, sp, sr, ap, and ar.
- (2)
- (3)
- Assume an initial value of σr(R+lb) = (σr1(R+lb)+σr2(R+lb))/2, where σr1(R+lb) = 0 and σr2(R+lb) = p0.
- (4)
- Calculate ur(R+lb) and σθ(R+lb) by replacing p and R in the equations in Appendix A with σr(R+lb) and R+lb, respectively.
- (5)
- Assume an initial value of = (+)/2, where = 0 and= 10.
- (6)
- Calculate τs(0) and Fn(0) using Equations (32) and (33), respectively.
- (1)
- Verify the elastoplastic state of the rock mass in the ith annulus using Equation (4) (M–C rock mass) or Equation (5) (H–B rock mass).
- (2)
- Calculate σr(i) using Equation (24) (elastic state), or Equation (27) (plastic state, M–C rock mass) or Equation (29) (plastic state, H–B rock mass).
- (3)
- Calculate σθ(i) using Equation (25) (elastic state), or Equation (28) (plastic state, M–C rock mass) or Equation (30) (plastic state, H–B rock mass).
- (4)
- Calculate ur(i) using Equation (26) (elastic state) or Equation (31) (plastic state).
- (5)
- Calculate τb(i) and Fn(i) using Equations (32) and (33), respectively.
References
- Kovári, K. History of the sprayed concrete lining method—Part I: Milestones up to the 1960s. Tunn. Undergr. Space Technol. 2003, 18, 57–69. [Google Scholar] [CrossRef]
- Bobet, A.; Einstein, H. Tunnel reinforcement with rockbolts. Tunn. Undergr. Space Technol. 2011, 26, 100–123. [Google Scholar] [CrossRef]
- Li, P.F.; Wang, F.; Fang, Q. Undrained analysis of ground reaction curves for deep tunnels in saturated ground considering the effect of ground reinforcement. Tunn. Undergr. Space Technol. 2018, 71, 579–590. [Google Scholar] [CrossRef]
- Bobet, A. Elastic solution for deep tunnels. Application to excavation damage zone and rockbolt support. Rock Mech. Rock Eng. 2009, 42, 147–174. [Google Scholar] [CrossRef]
- Carranza-Torres, C. Analytical and numerical study of the mechanics of rockbolt reinforcement around tunnels in rock masses. Rock Mech. Rock Eng. 2009, 42, 175–228. [Google Scholar] [CrossRef]
- Fahimifar, A.; Ranjbarnia, M. Analytical approach for the design of active grouted rockbolts in tunnel stability based on convergence-confinement method. Tunn. Undergr. Space Technol. 2009, 24, 363–375. [Google Scholar] [CrossRef]
- Fahimifar, A.; Soroush, H. A theoretical approach for analysis of the interaction between grouted rockbolts and rock masses. Tunn. Undergr. Space Technol. 2005, 20, 333–343. [Google Scholar] [CrossRef]
- Oreste, P.; Peila, D. Radial passive rockbolting in tunnelling design with a new convergence-confinement model. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1996; pp. 443–454. [Google Scholar]
- Stille, H.; Holmberg, M.; Nord, G. Support of weak rock with grouted bolts and shotcrete. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1989; pp. 99–113. [Google Scholar]
- Zou, J.; Chen, K.; Pan, Q. An improved numerical approach in surrounding rock incorporating rockbolt effectiveness and seepage force. Acta Geotech. 2018, 13, 707–727. [Google Scholar] [CrossRef]
- Wang, G.; Liu, C.; Jiang, Y.; Wu, X.; Wang, S. Rheological model of DMFC rockbolt and rock mass in a circular tunnel. Rock Mech. Rock Eng. 2015, 48, 2319–2357. [Google Scholar] [CrossRef]
- Wang, G.; Han, W.; Jiang, Y.; Luan, H.; Wang, K. Coupling analysis for rock mass supported with CMC or CFC rockbolts based on viscoelastic method. Rock Mech. Rock Eng. 2019, 52, 4565–4588. [Google Scholar] [CrossRef]
- Zou, J.F.; Xia, Z.Q.; Dan, H.C. Theoretical solutions for displacement and stress of a circular opening reinforced by grouted rock bolt. Geomech. Eng. 2016, 11, 439–455. [Google Scholar] [CrossRef]
- Freeman, T. The behaviour of fully-bonded rock bolts in the Kielder experimental tunnel. Tunn. Tunn. Int. 1978, 10, 37–40. [Google Scholar]
- Cui, L.; Dong, Y.-K.; Sheng, Q.; Shen, Q. New numerical procedures for fully-grouted bolt in the rock mass with slip and non-slip cases at the rock-bolt interface. Constr. Build. Mater. 2019, 204, 849–863. [Google Scholar] [CrossRef]
- Indraratna, B.; Kaiser, P. Analytical model for the design of grouted rock bolts. Int. J. Numer. Anal. Methods Geomech. 1990, 14, 227–251. [Google Scholar] [CrossRef]
- Indraratna, B.; Kaiser, P. Design for grouted rock bolts based on the convergence control method. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1990; pp. 269–281. [Google Scholar]
- Osgoui, R.R.; Oreste, P. Convergence-control approach for rock tunnels reinforced by grouted bolts, using the homogenization concept. Geotech. Geol. Eng. 2007, 25, 431–440. [Google Scholar] [CrossRef]
- Osgoui, R.R.; Oreste, P. Elasto-plastic analytical model for the design of grouted bolts in a Hoek–Brown medium. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1651–1686. [Google Scholar] [CrossRef]
- Osgoui, R.R.; Ünal, E. An empirical method for design of grouted bolts in rock tunnels based on the Geological Strength Index (GSI). Eng. Geol. 2009, 107, 154–166. [Google Scholar] [CrossRef]
- Yu, T.Z.; Xian, C.J. Behaviour of rock bolting as tunnelling support. In Proceedings of the International Symposium on Rock Bolting; Abisko: Abisko, Sweden, 1983; pp. 87–92. [Google Scholar]
- Cai, Y.; Esaki, T.; Jiang, Y. A rock bolt and rock mass interaction model. Int. J. Rock Mech. Min. Sci. 2004, 41, 1055–1067. [Google Scholar] [CrossRef]
- Cai, Y.; Esaki, T.; Jiang, Y. An analytical model to predict axial load in grouted rock bolt for soft rock tunnelling. Tunn. Undergr. Space Technol. 2004, 19, 607–618. [Google Scholar] [CrossRef]
- Li, C.; Stillborg, B. Analytical models for rock bolts. Int. J. Rock Mech. Min. Sci. 1999, 36, 1013–1029. [Google Scholar] [CrossRef]
- Guan, Z.; Jiang, Y.; Tanabasi, Y.; Huang, H. Reinforcement mechanics of passive bolts in conventional tunnelling. Int. J. Rock Mech. Min. Sci. 2007, 44, 625–636. [Google Scholar] [CrossRef]
- Oreste, P. Distinct analysis of fully grouted bolts around a circular tunnel considering the congruence of displacements between the bar and the rock. Int. J. Rock Mech. Min. Sci. 2008, 45, 1052–1067. [Google Scholar] [CrossRef]
- Tan, C.H. Difference solution of passive bolts reinforcement around a circular opening in elastoplastic rock mass. Int. J. Rock Mech. Min. Sci. 2016, 81, 28–38. [Google Scholar] [CrossRef]
- Tan, C.H. Passive bolts reinforcement around a circular opening in strain-softening elastoplastic rock mass. Int. J. Rock Mech. Min. Sci. 2016, 88, 221–234. [Google Scholar] [CrossRef]
- Cui, L.; Zheng, J.-J.; Sheng, Q.; Pan, Y. A simplified procedure for the interaction between fully-grouted bolts and rock mass for circular tunnels. Comput. Geotech. 2019, 106, 177–192. [Google Scholar] [CrossRef]
- Möller, S.C. Tunnel Induced Settlements and Structural Forces in Linings; Univ. Stuttgart, Inst. f. Geotechnik: Stuttgart, Germany, 2006. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion-2002 edition. Proc. Narms-Tac. 2002, 1, 267–273. [Google Scholar]
- Jafari, A. A Laboratory Study of Bond Failure Mechanism in Deformed Rock Bolts Using a Modified Hoek Cell. In Proceedings of the Frontiers of Rock Mechanics & Sustainable Development in the Century—Isrm International Symposium-asian Rock Mechanics Symposium, Beijing, China, 11–14 September 2001. [Google Scholar]
- Malvar, L.J. Bond of Reinforcement Under Controlled Confinement. Aci. Mater. J. 1991, 89, 47. [Google Scholar]
- Itasca. FLAC3D V5. 0, Fast Lagrangian Analysis of Continua in 3 Dimensions; User’s Guide; Itasca Consulting Group: Minneapolis, MN, USA, 2011. [Google Scholar]
- Lee, Y.-K.; Pietruszczak, S. A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass. Tunn. Undergr. Space Technol. 2008, 23, 588–599. [Google Scholar] [CrossRef]
- Brady, B.H.; Brown, E.T. Rock Mechanics: For Underground Mining: Springer Science & Business Media; Springer: New York, NY, USA, 1993. [Google Scholar]
- Sharan, S. Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek–Brown rock. Int. J. Rock Mech. Min. Sci. 2008, 1, 78–85. [Google Scholar] [CrossRef]

| Rock Mass | Passive Bolts | ||
|---|---|---|---|
| Symbol (Unit) | Value | Symbol (Unit) | Value |
| R (m) | 3 | Eb (GPa) | 210 |
| p0 (MPa) | 1 | lb (m) | 3 |
| E (GPa) | 0.5 | ds (mm) | 25 |
| μ | 0.2 | Ab (mm2) | 491 |
| cp (MPa) | 0.1 | lz (m) | 1 |
| cr (MPa) | 0.1 | ω (°) | 10 |
| φp (°) | 30 | Ks (MPa) | 10 |
| φr (°) | 30 | Kep (MN/m) | 0 |
| ψ (°) | 0 | β | 0.3 |
| p (MPa) | 0 | ||
| cs (kPa) | ∞ | ||
| φs (°) | 0 | ||
| Symbol (Unit) | Value | Symbol (Unit) | Value |
|---|---|---|---|
| R (m) | 3 | mb,r | 2 |
| p0 (MPa) | 15 | sp | 4 × 10−3 |
| E (GPa) | 5.7 | sr | 4 × 10−3 |
| μ | 0.25 | ap | 0.55 |
| σci,p (MPa) | 30 | ar | 0.55 |
| σci,r (MPa) | 30 | ψ (°) | 15 |
| mb,p | 2 |
| Rock Mass | Passive Bolts | ||
|---|---|---|---|
| Symbol (Unit) | Value | Symbol (Unit) | Value |
| R (m) | 1.6 | Eb (GPa) | 210 |
| p0 (MPa) | 2.6 | lb (m) | 1.8 |
| E (GPa) | 5 | ds (mm) | 25 |
| μ | 0.25 | Ab (mm2) | 491 |
| σci,p (MPa) | 37 | lz (m) | 0.9 |
| σci,r (MPa) | 37 | ω (°) | 32 |
| mb,p | 0.1 | Ks (MPa) | 70 |
| mb,r | 0.05 | Kep (MN/m) | 30 |
| sp | 8 × 10−5 | β | 0.3 |
| sr | 1 × 10−5 | p (MPa) | 0 |
| ap | 0.5 | cs (kPa) | ∞ |
| ar | 0.5 | φs (°) | 0 |
| ψ (°) | 0 | ||
| Symbol (Unit) | Value | Symbol (Unit) | Value |
|---|---|---|---|
| R (m) | 3 | mb,r | 0.615 |
| p0 (MPa) | 5 | sp | 7.3 × 10−4 |
| E (GPa) | 2.57 | sr | 1.7 × 10−4 |
| μ | 0.25 | ap | 0.516 |
| σci,p (MPa) | 30 | ar | 0.538 |
| σci,r (MPa) | 24 | ψ (°) | 0 |
| mb,p | 0.981 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, X.; Tong, J.; Yi, W.; Wang, Z.; Liu, D. A New Semi-Analytical Method for Elasto-Plastic Analysis of a Deep Circular Tunnel Reinforced by Fully Grouted Passive Bolts. Appl. Sci. 2020, 10, 4402. https://doi.org/10.3390/app10124402
Wang M, Zhang X, Tong J, Yi W, Wang Z, Liu D. A New Semi-Analytical Method for Elasto-Plastic Analysis of a Deep Circular Tunnel Reinforced by Fully Grouted Passive Bolts. Applied Sciences. 2020; 10(12):4402. https://doi.org/10.3390/app10124402
Chicago/Turabian StyleWang, Mingnian, Xiao Zhang, Jianjun Tong, Wenhao Yi, Zhilong Wang, and Dagang Liu. 2020. "A New Semi-Analytical Method for Elasto-Plastic Analysis of a Deep Circular Tunnel Reinforced by Fully Grouted Passive Bolts" Applied Sciences 10, no. 12: 4402. https://doi.org/10.3390/app10124402
APA StyleWang, M., Zhang, X., Tong, J., Yi, W., Wang, Z., & Liu, D. (2020). A New Semi-Analytical Method for Elasto-Plastic Analysis of a Deep Circular Tunnel Reinforced by Fully Grouted Passive Bolts. Applied Sciences, 10(12), 4402. https://doi.org/10.3390/app10124402




