IMPAβ: Incremental Modal Pushover Analysis for Bridges
Abstract
1. Introduction
2. Nonlinear Static Analysis for Bridges
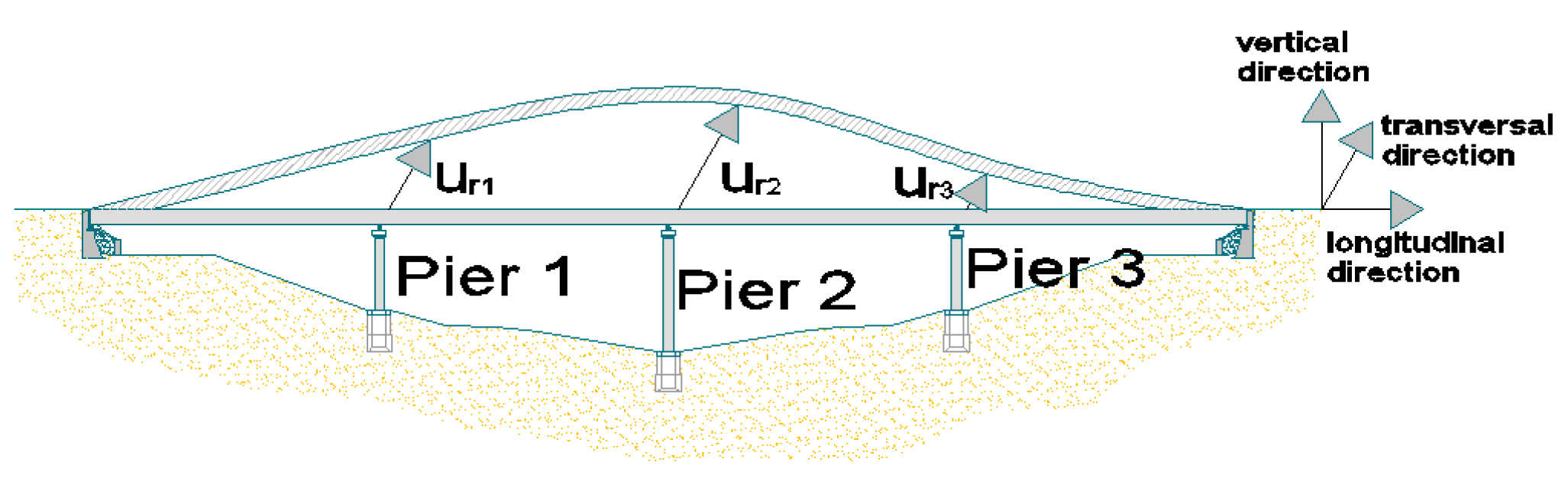
2.1. General Considerations for Bridges
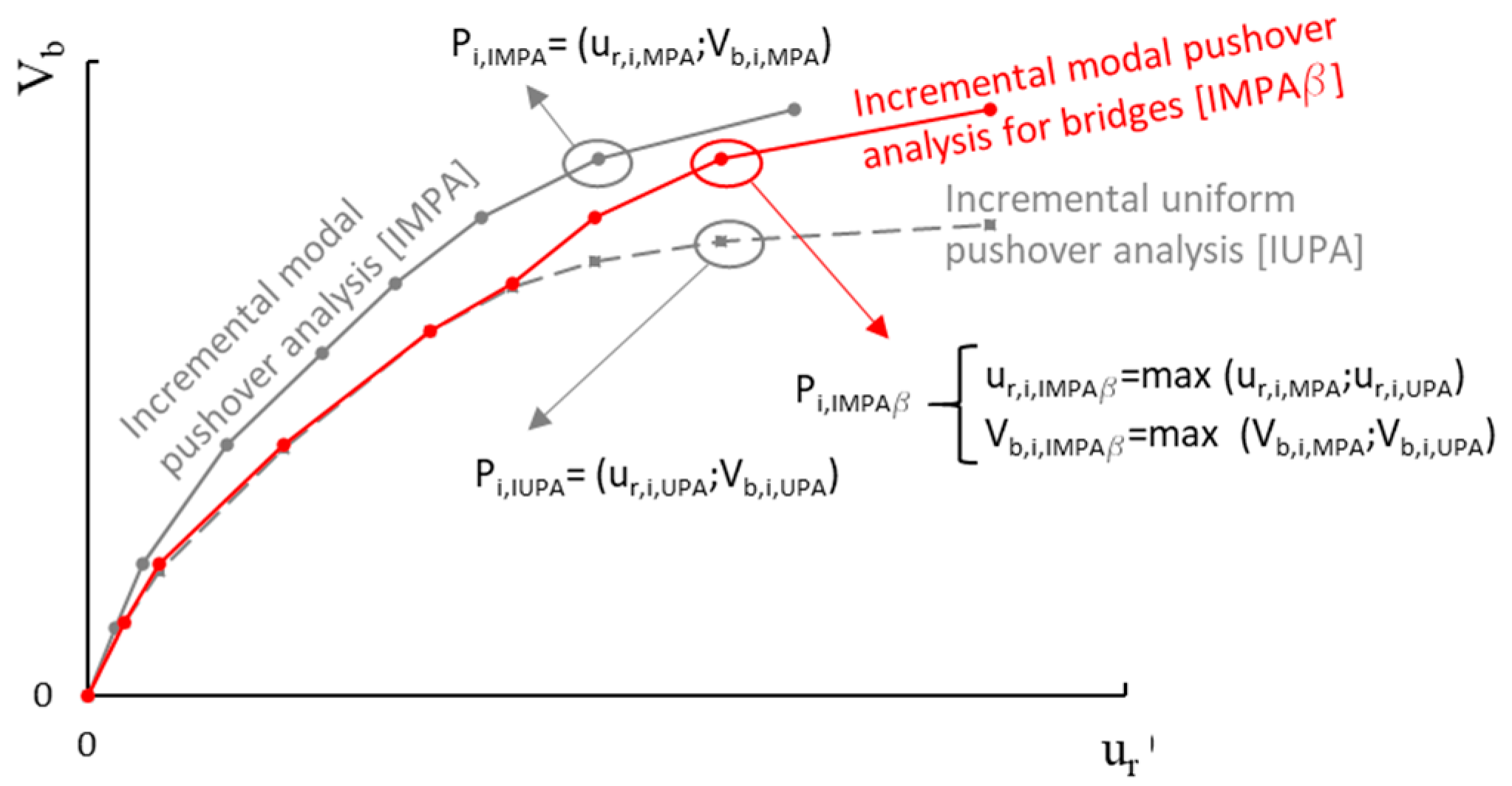
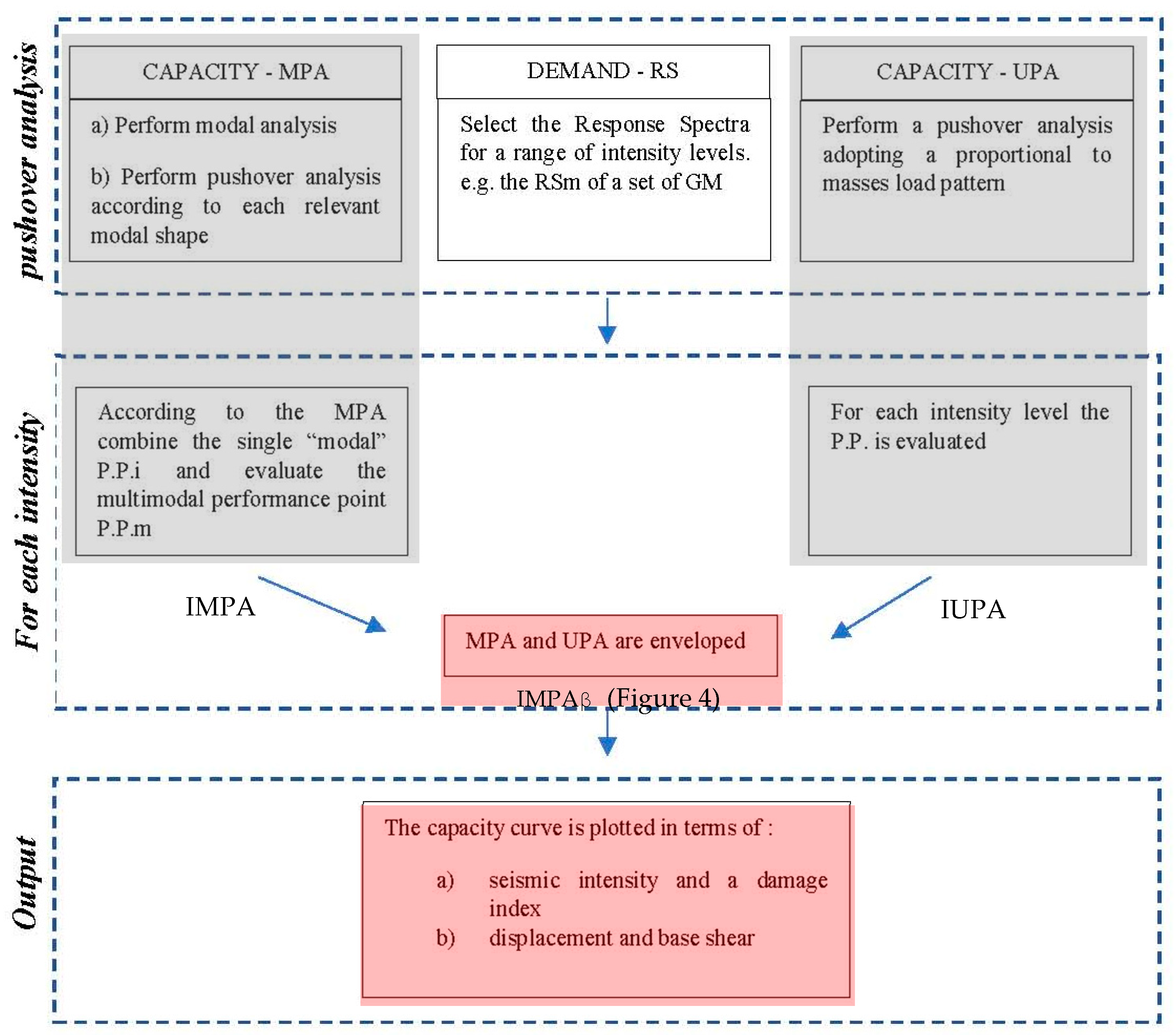
2.2. The Incremental Modal Pushover Analysis for Bridges (IMPAβ)
- Compute the natural frequencies, wn and modes, n for the linear elastic vibration of the bridge. The modal properties of the bridge model are obtained from the linear dynamic modal analysis, and the relevant modes of the bridge are selected;
- Define the seismic demand in terms of response spectra (RS) for a defined range of intensity levels;
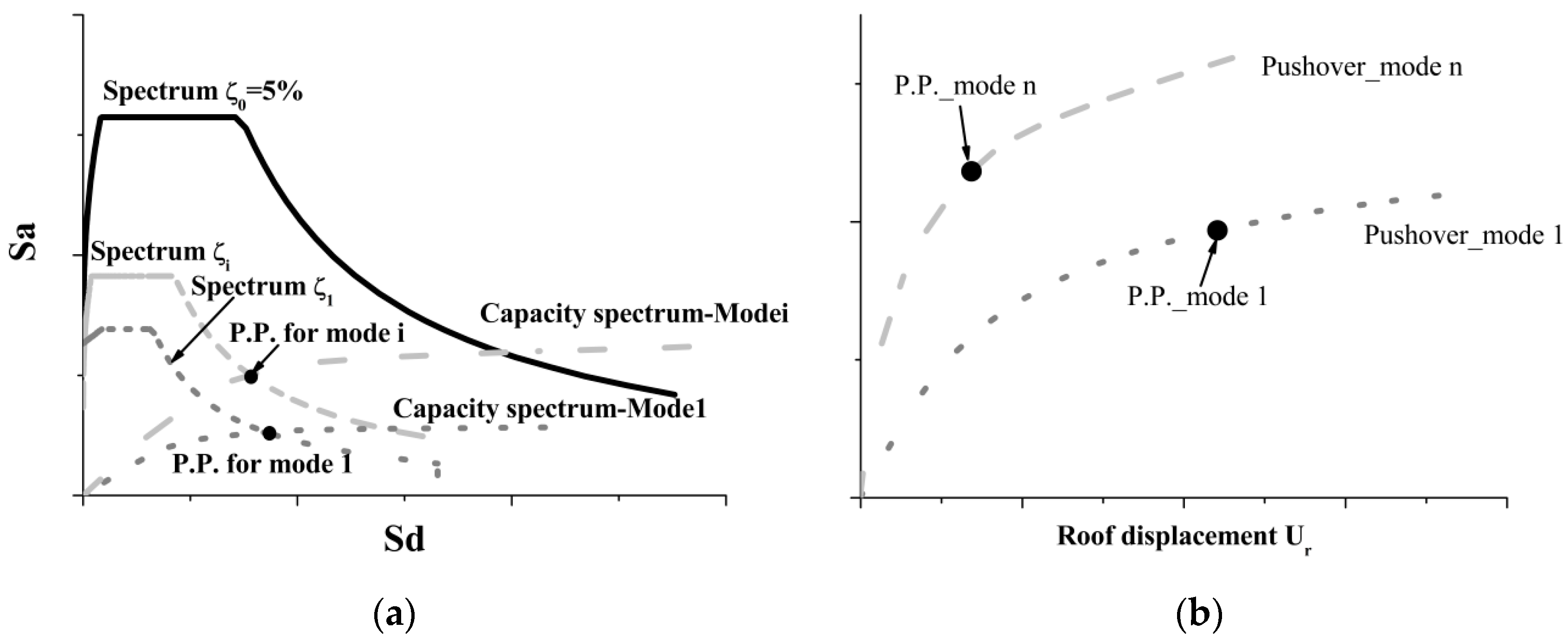
- For the intensity level, i, represented by peak ground motion acceleration (PGA), the performance point (P.P.) for the selected (predominant) modes can be determined (Figure 1a);
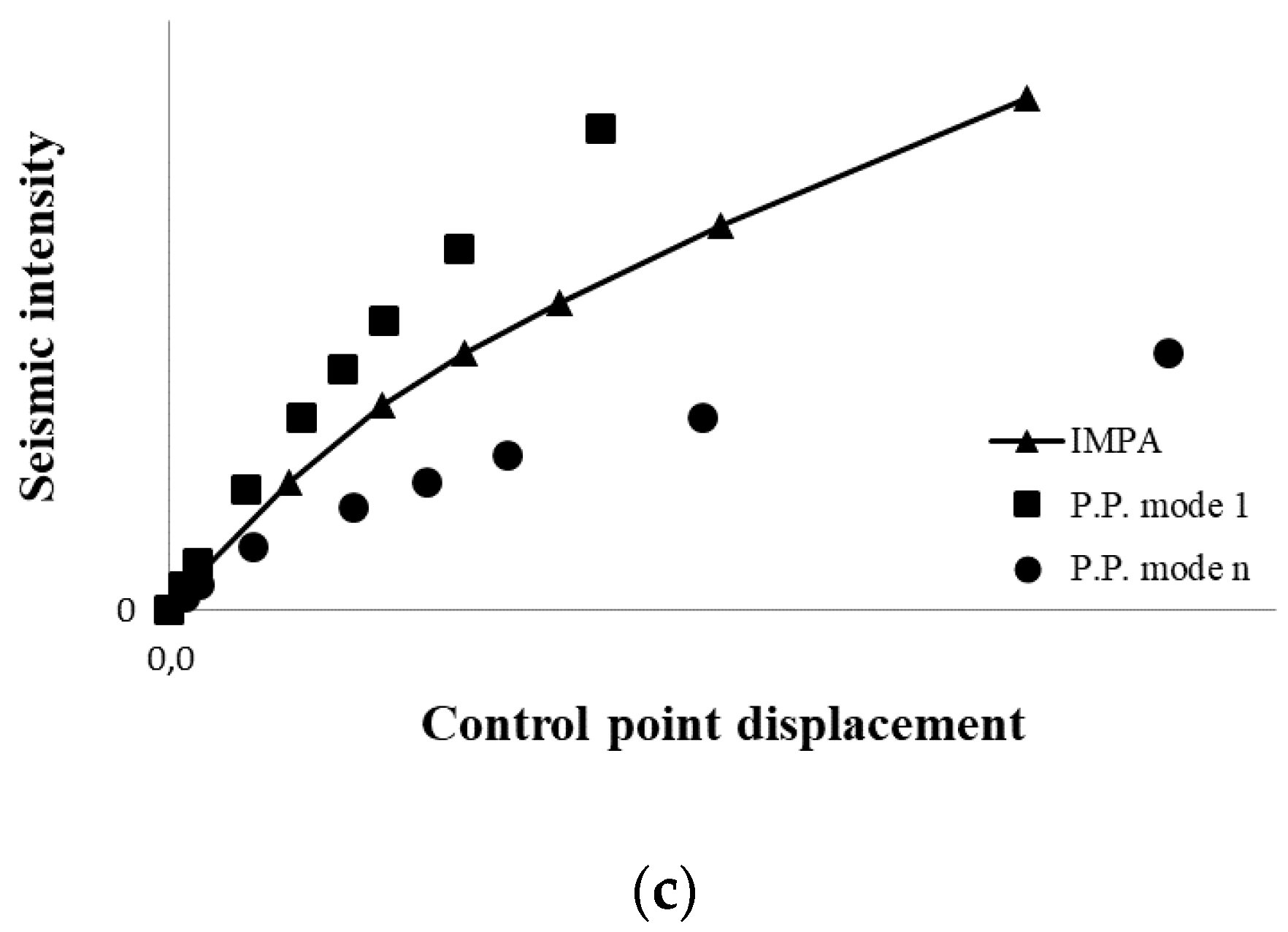
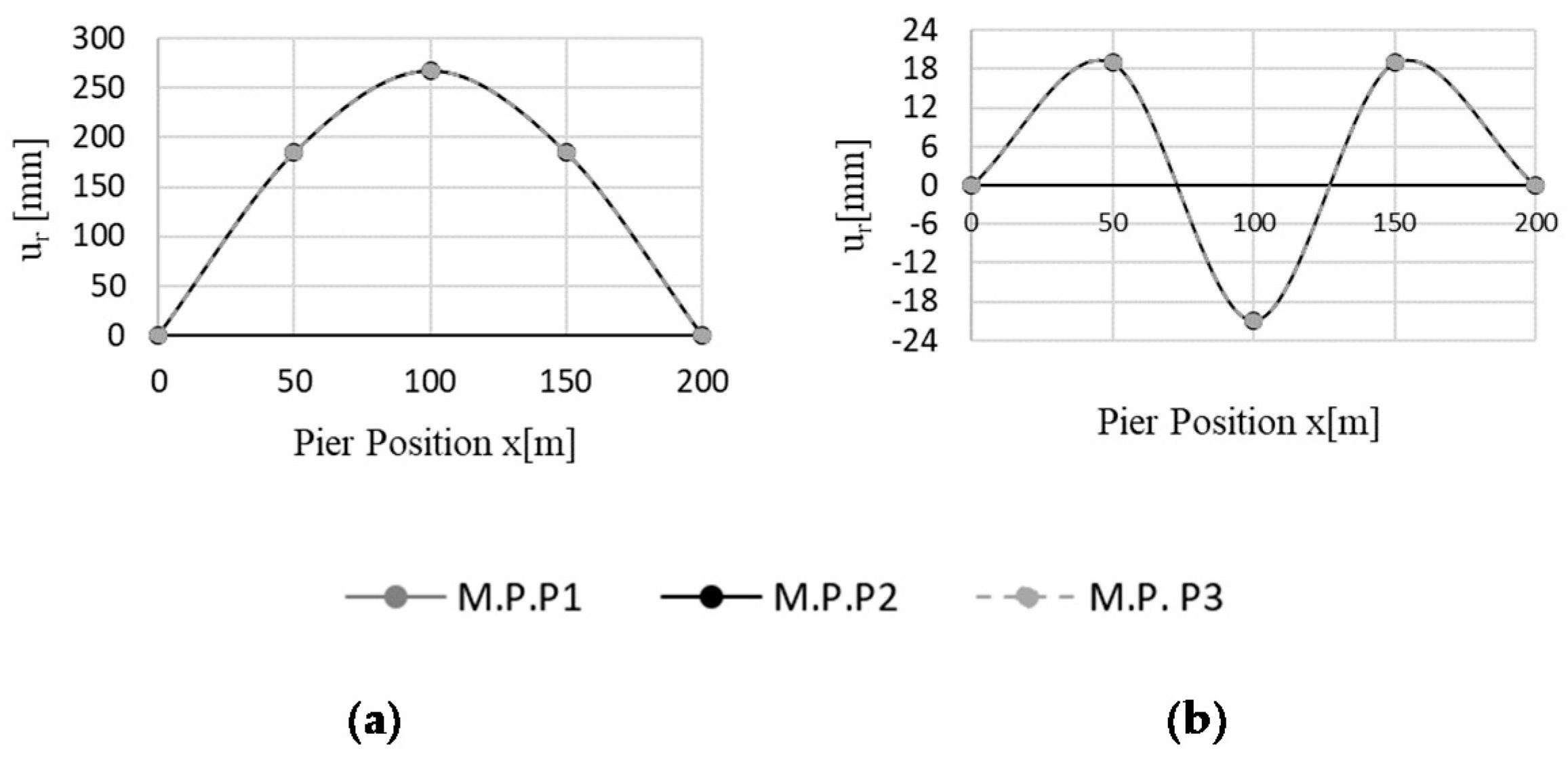
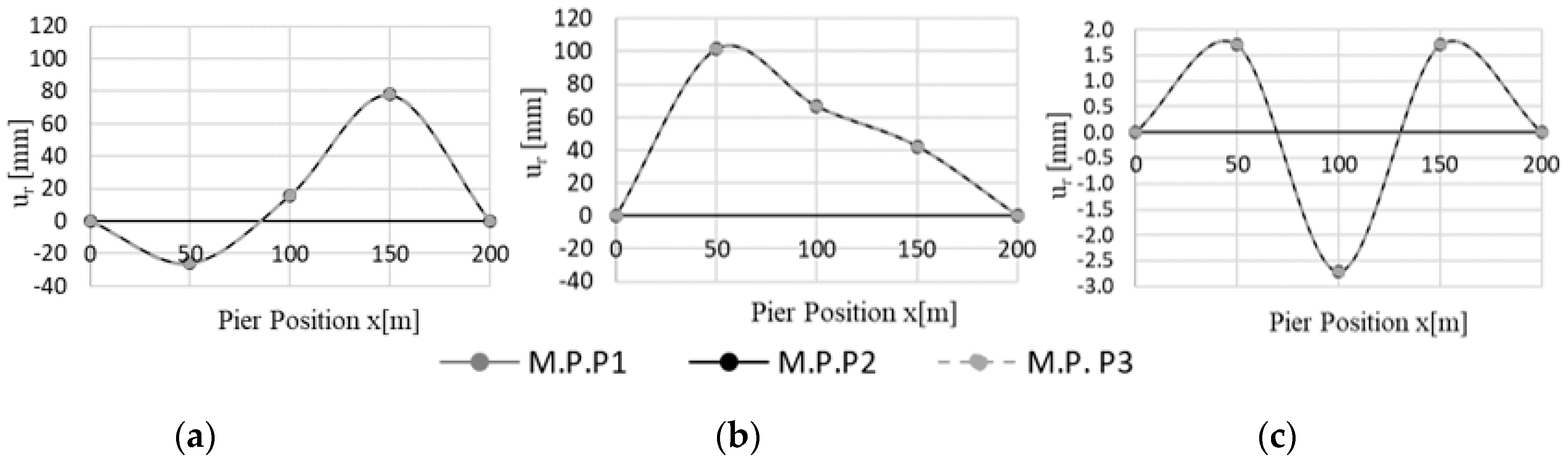
- Using a combination rule to combine the P.P. corresponding to each mode for each intensity, i, the “multimodal performance point” (P.P.m,i) can be determined (Figure 1b). The P.P.m,i is expressed in terms of monitoring point displacement, urmmi, and corresponding global base shear, Vb,i, for each intensity level considered: being urni the modal displacements of the monitoring point, in this paper, the transverse direction is considered.
3. Case Studies
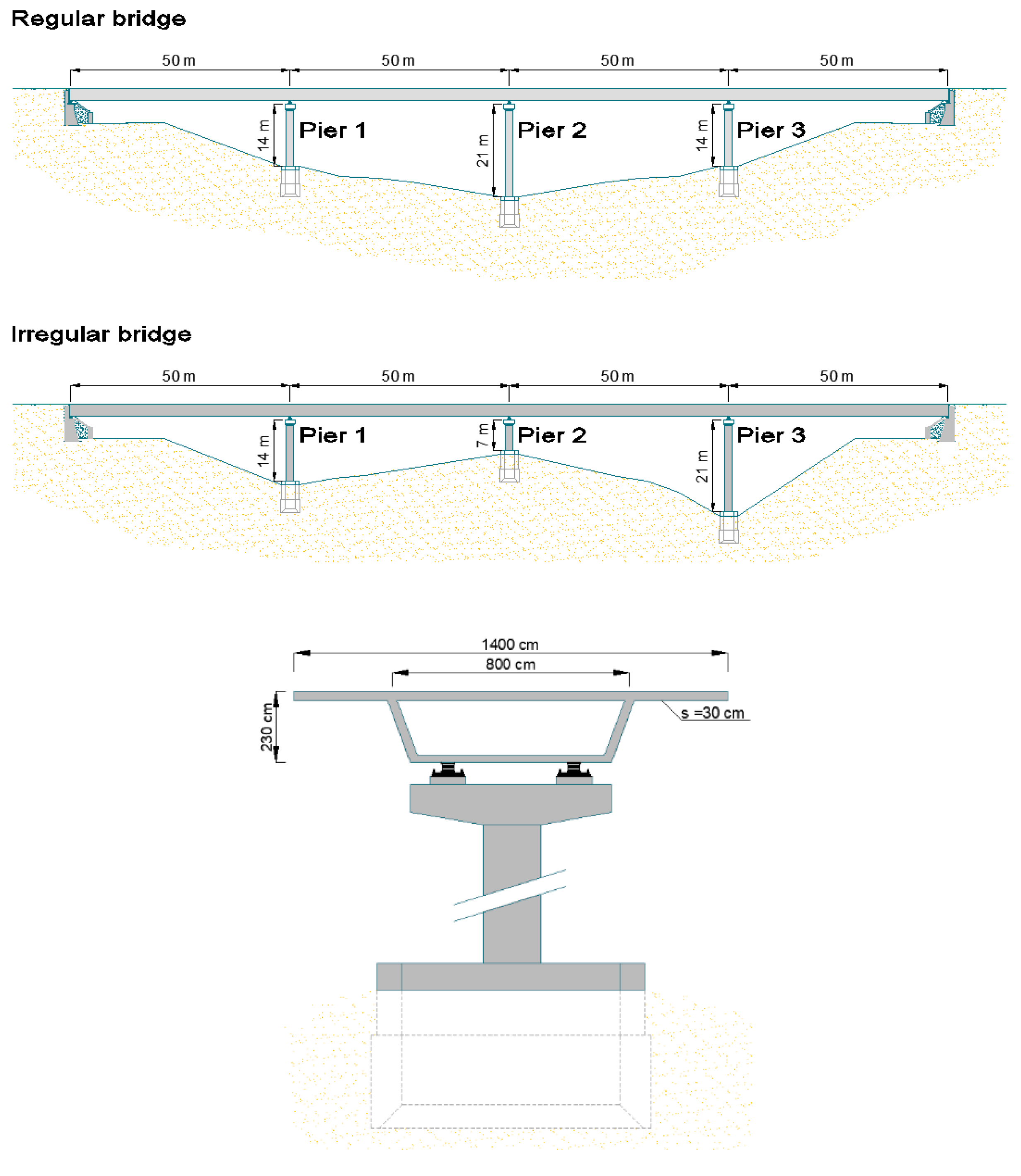
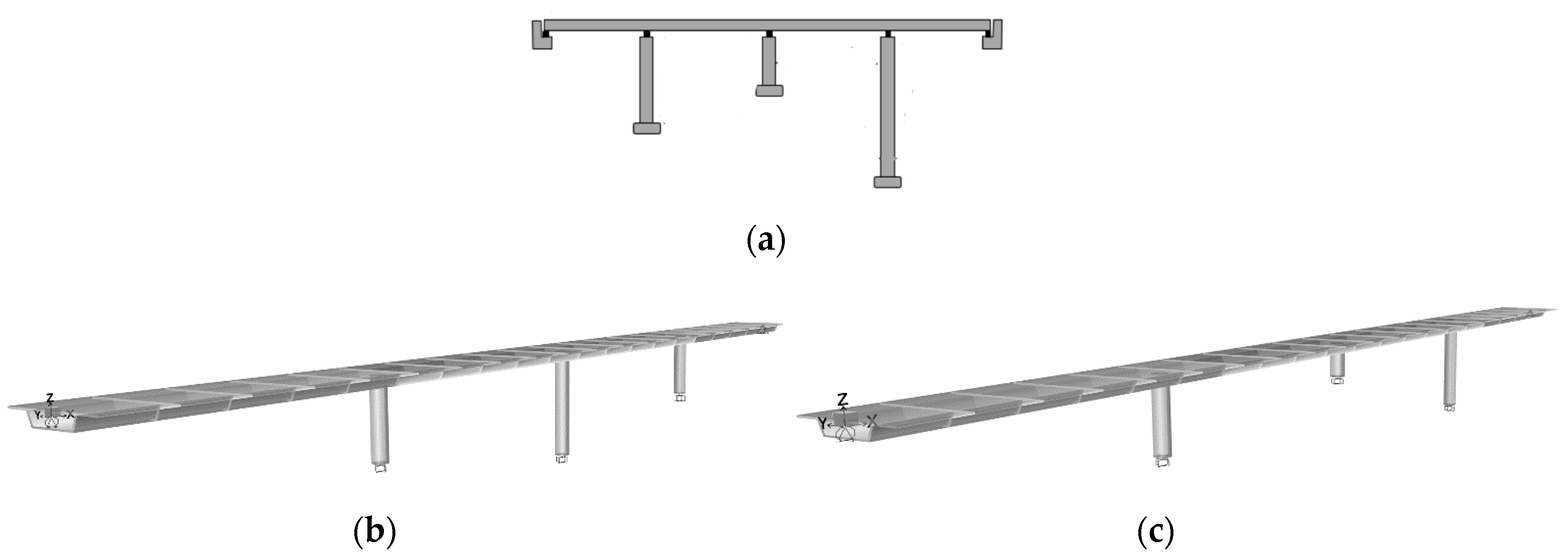
3.1. Bridges
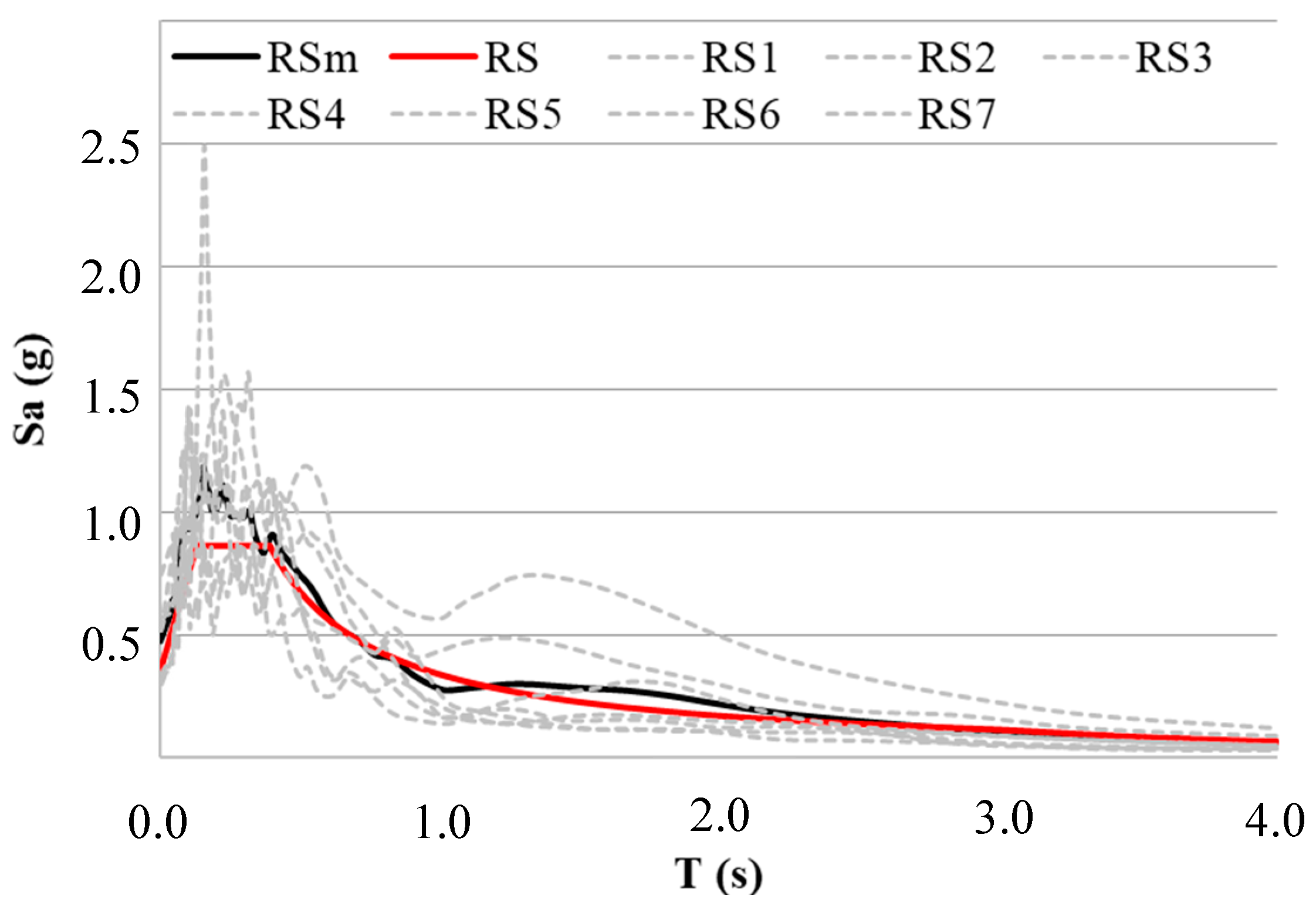
3.2. Seismic Input
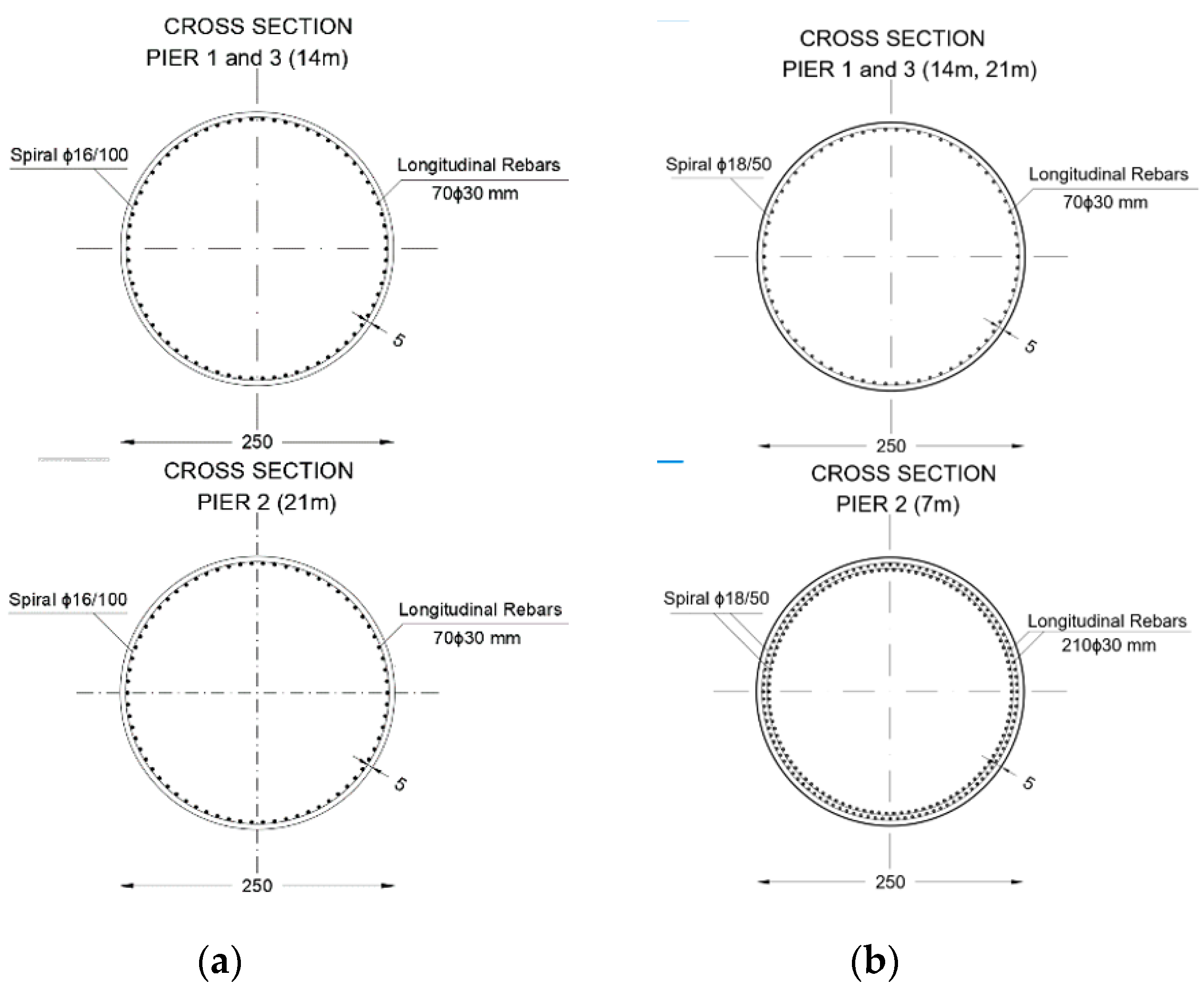
3.3. Numerical Models
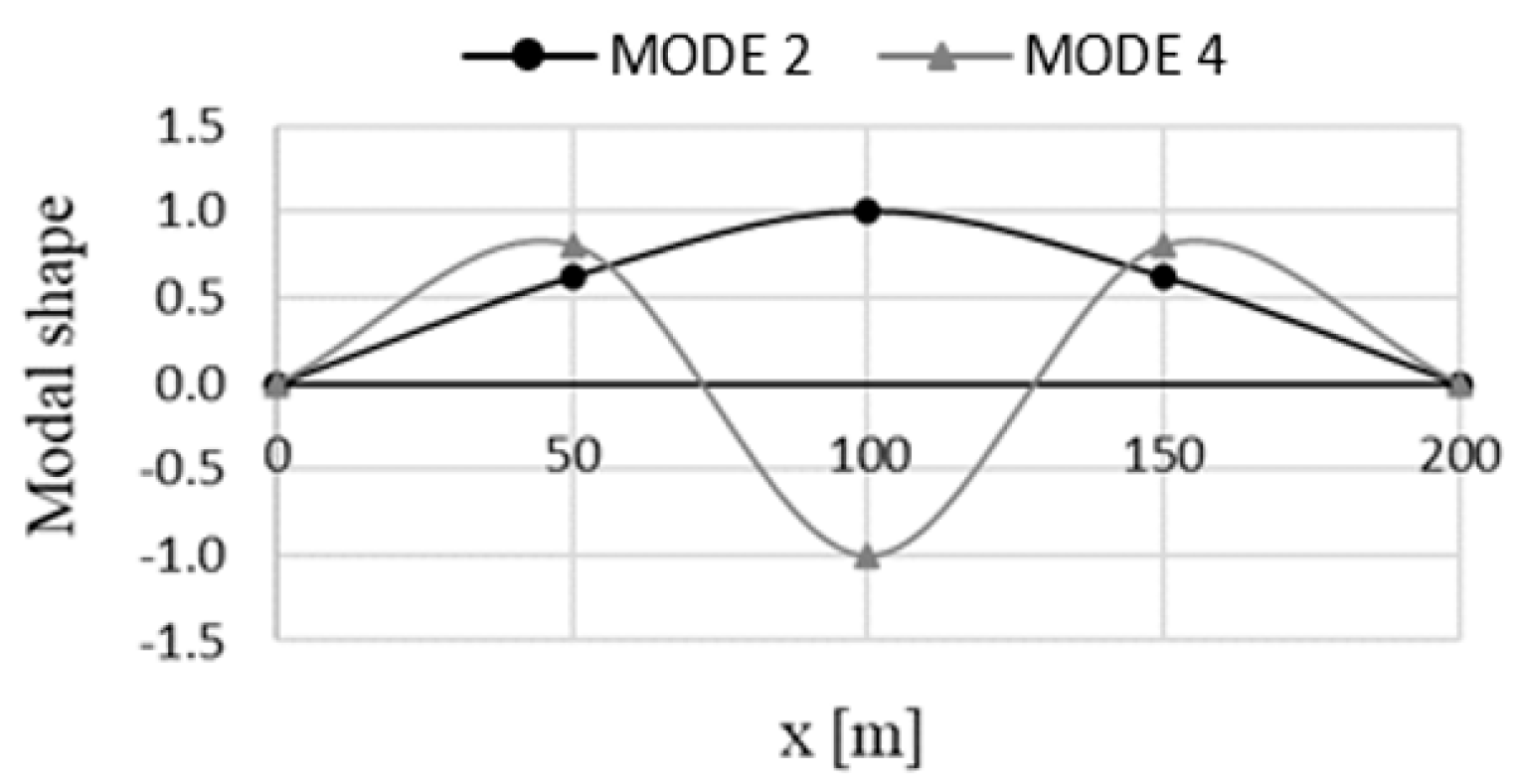
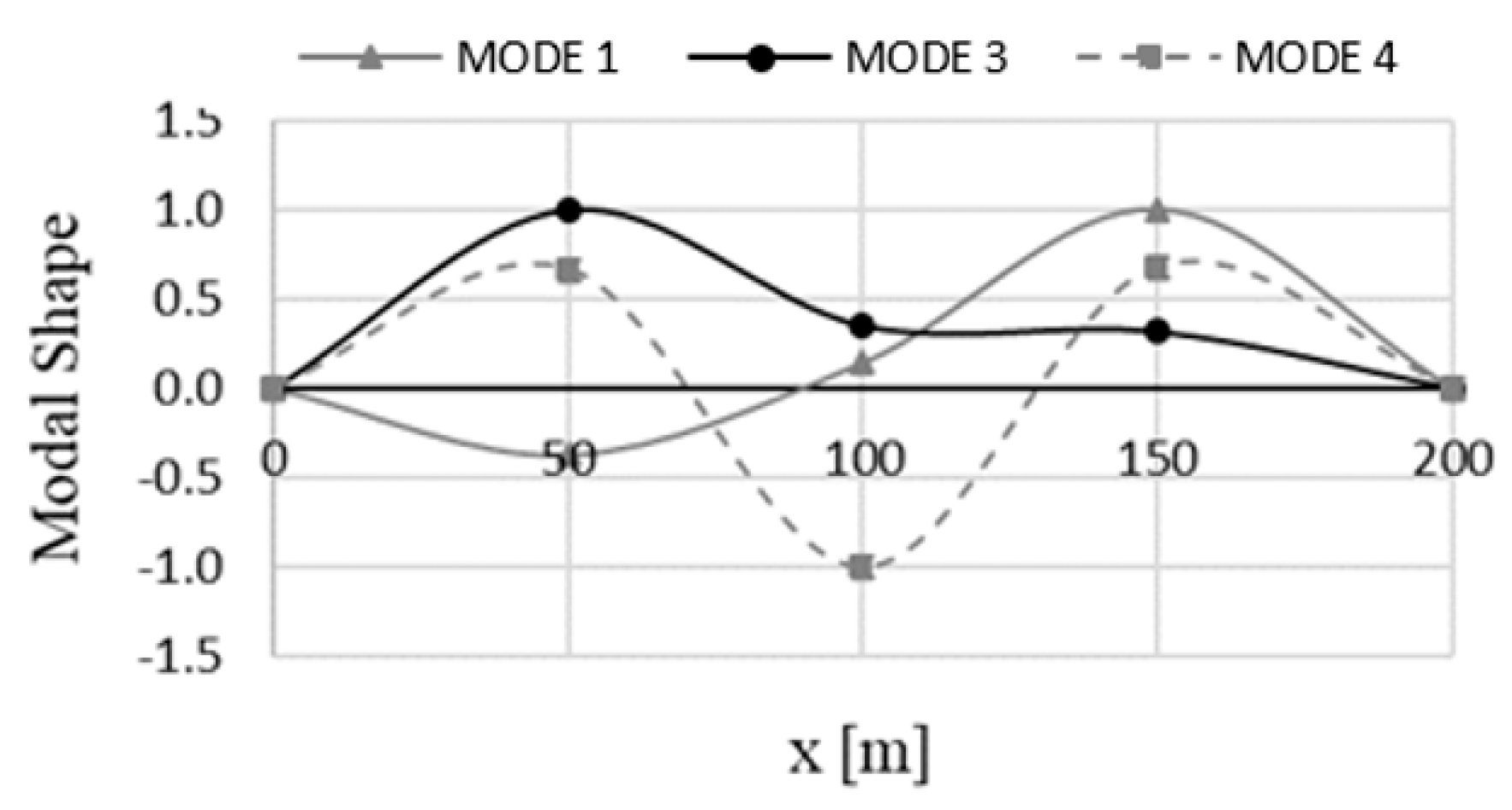
3.4. Modal Properties
4. Nonlinear Analyses
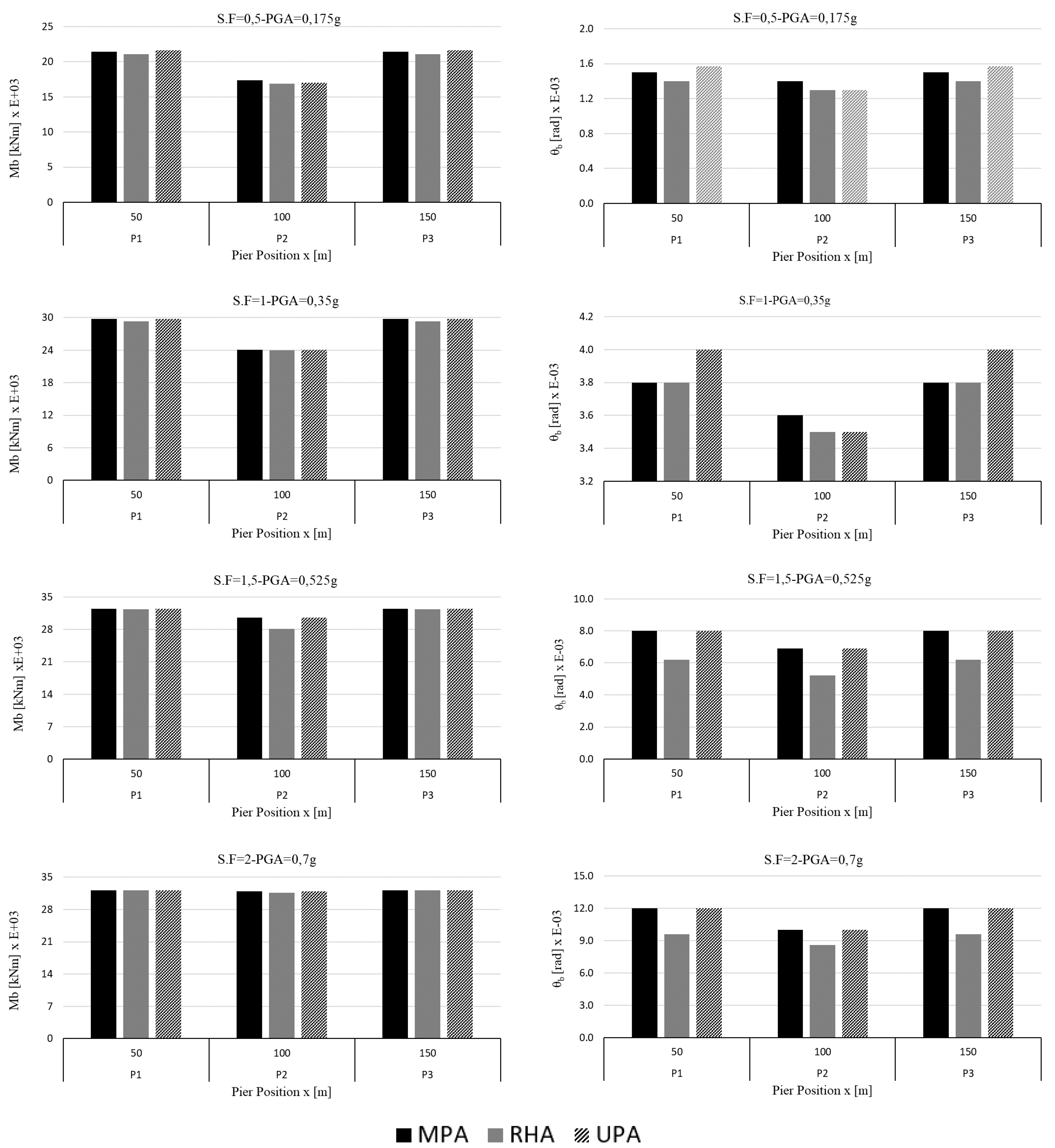
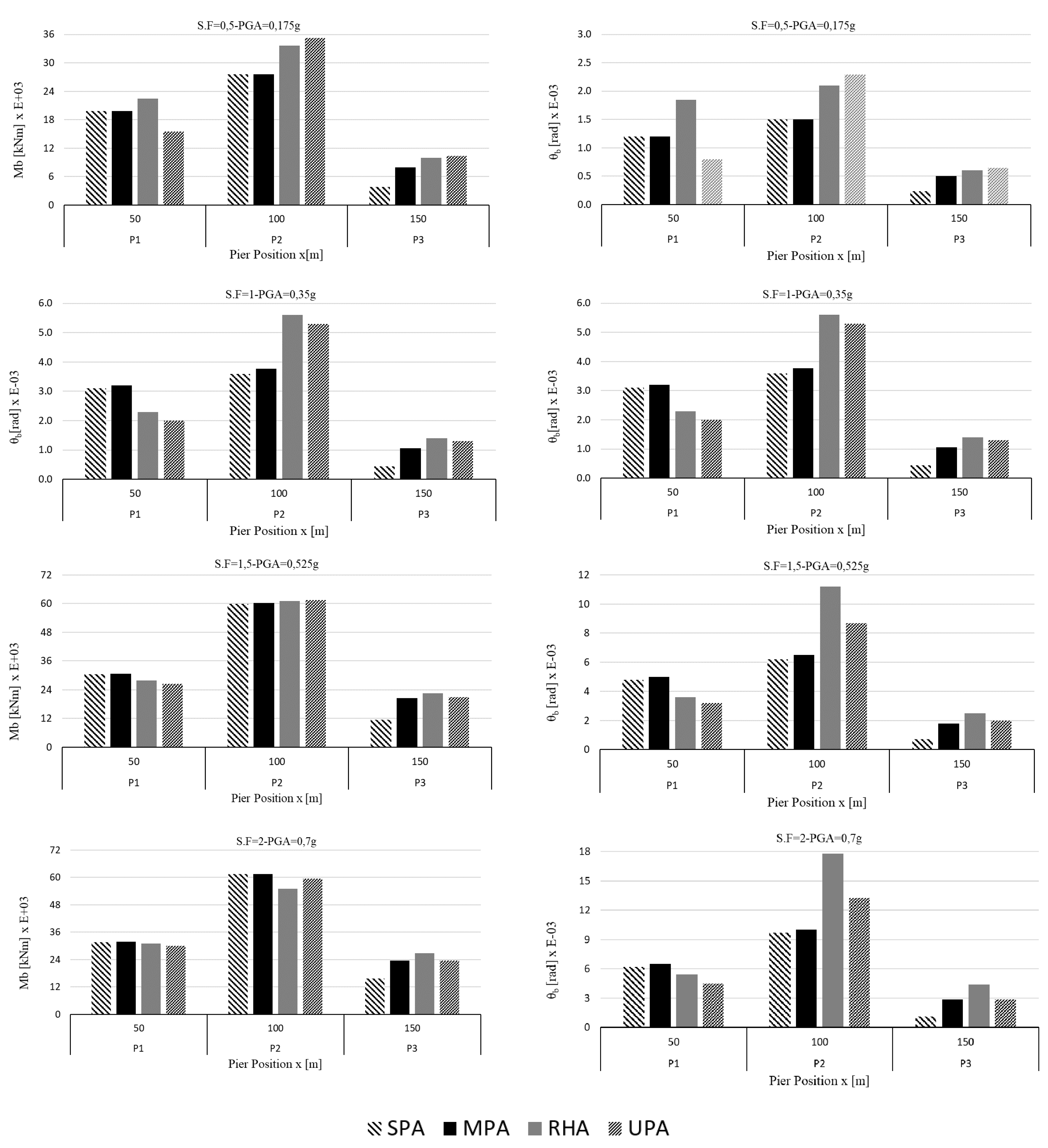
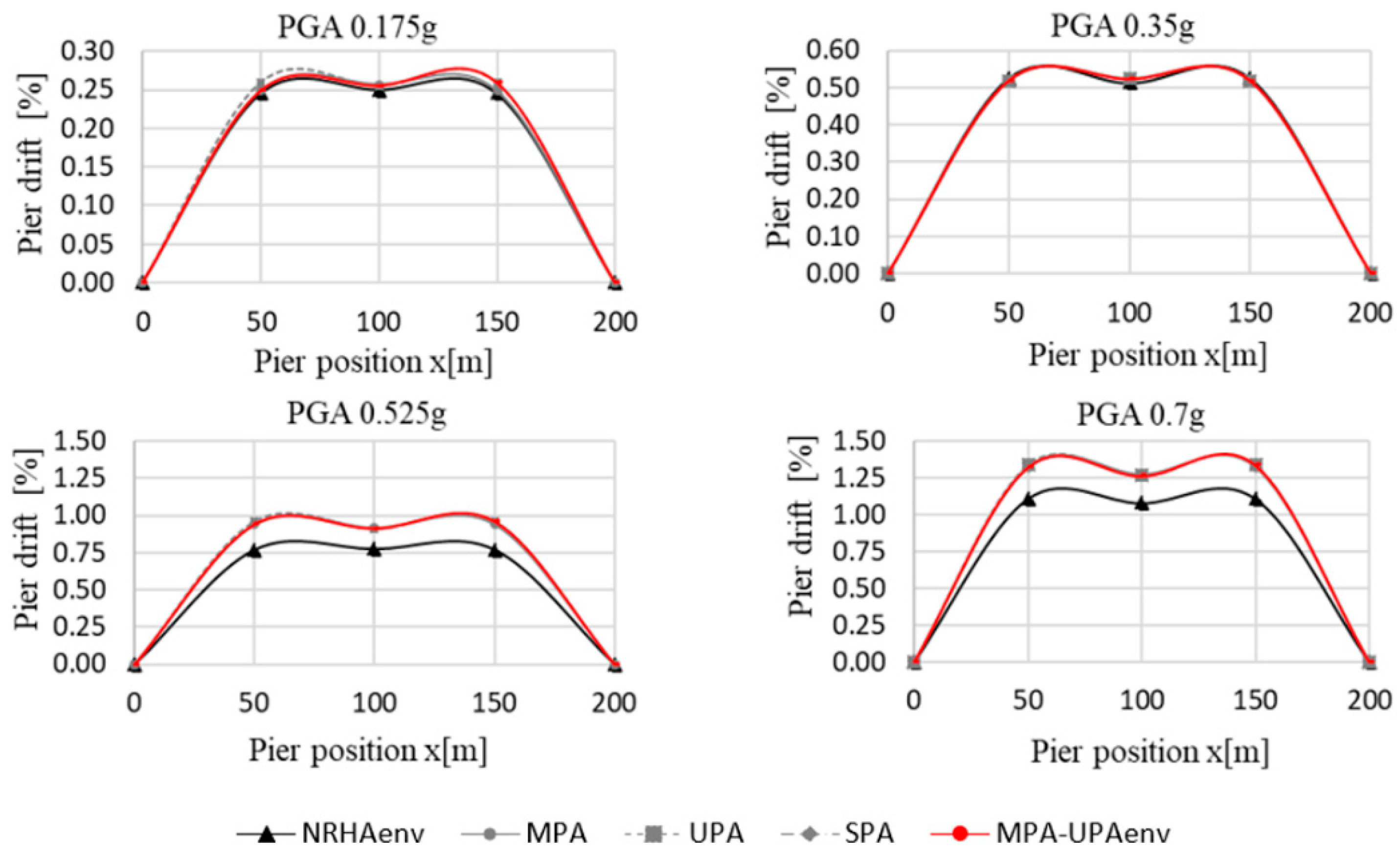
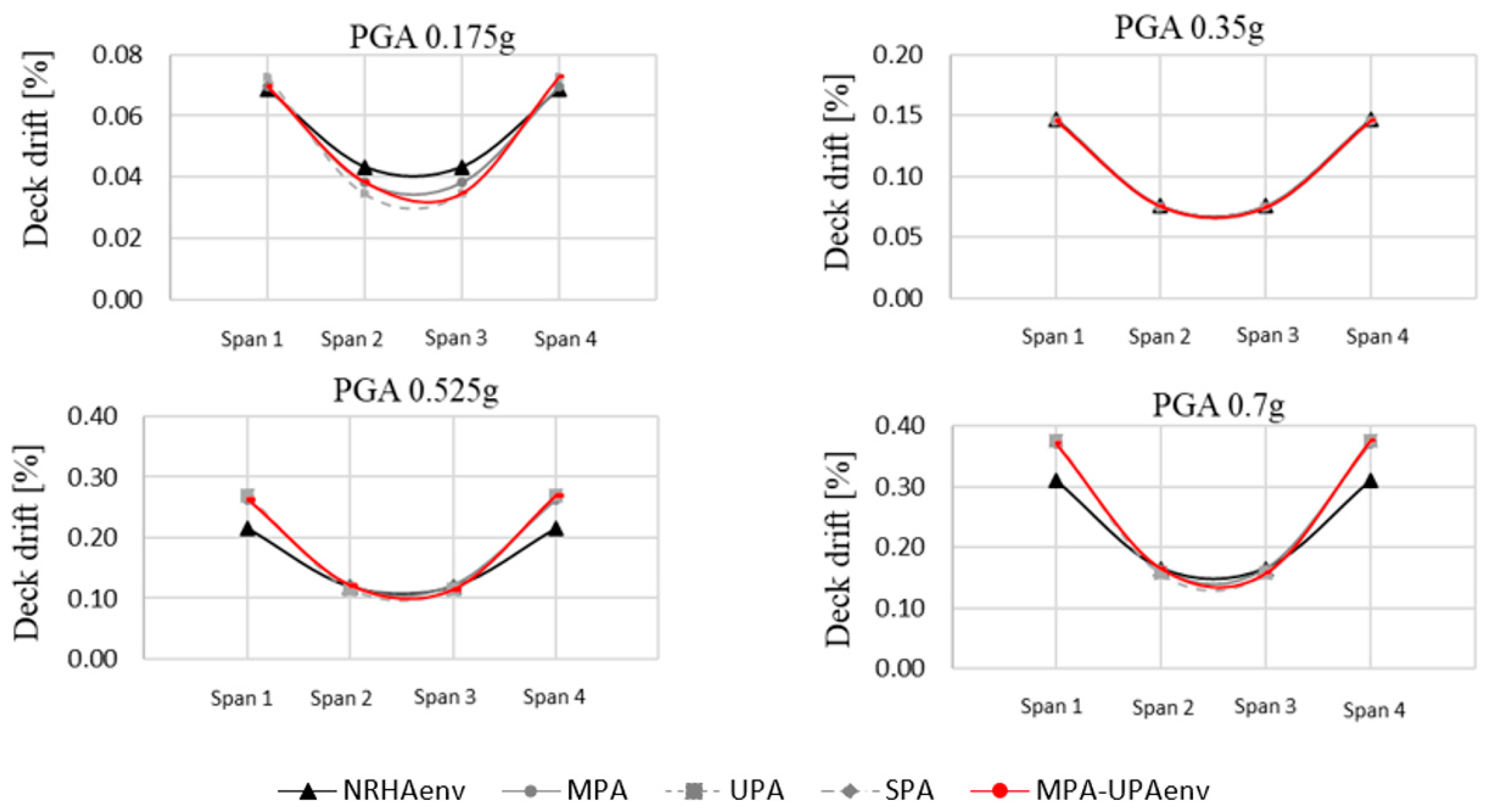
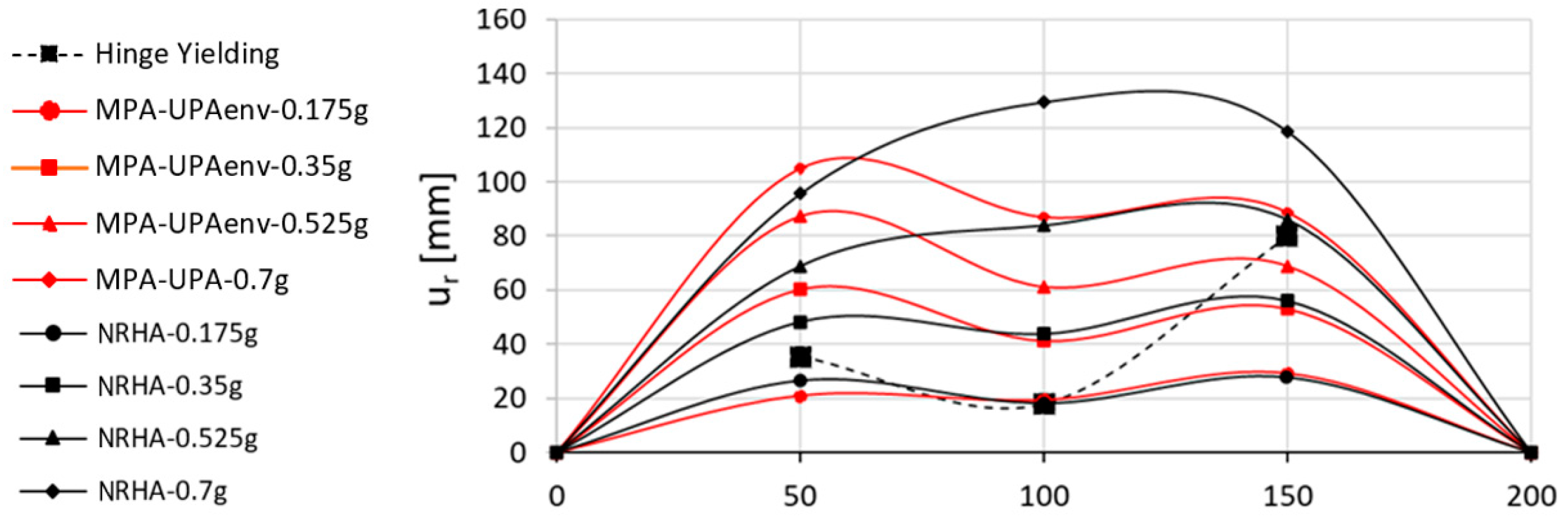
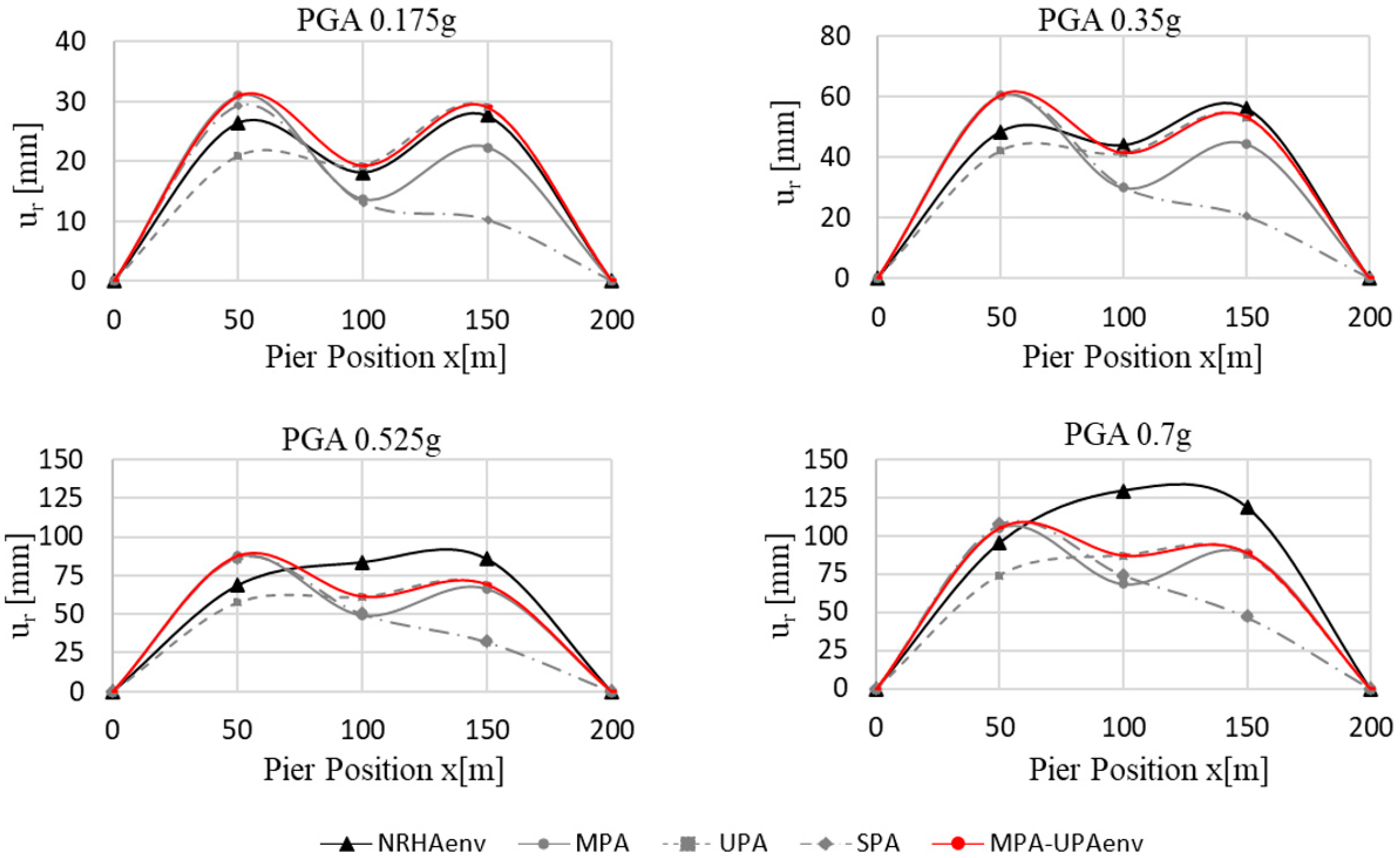
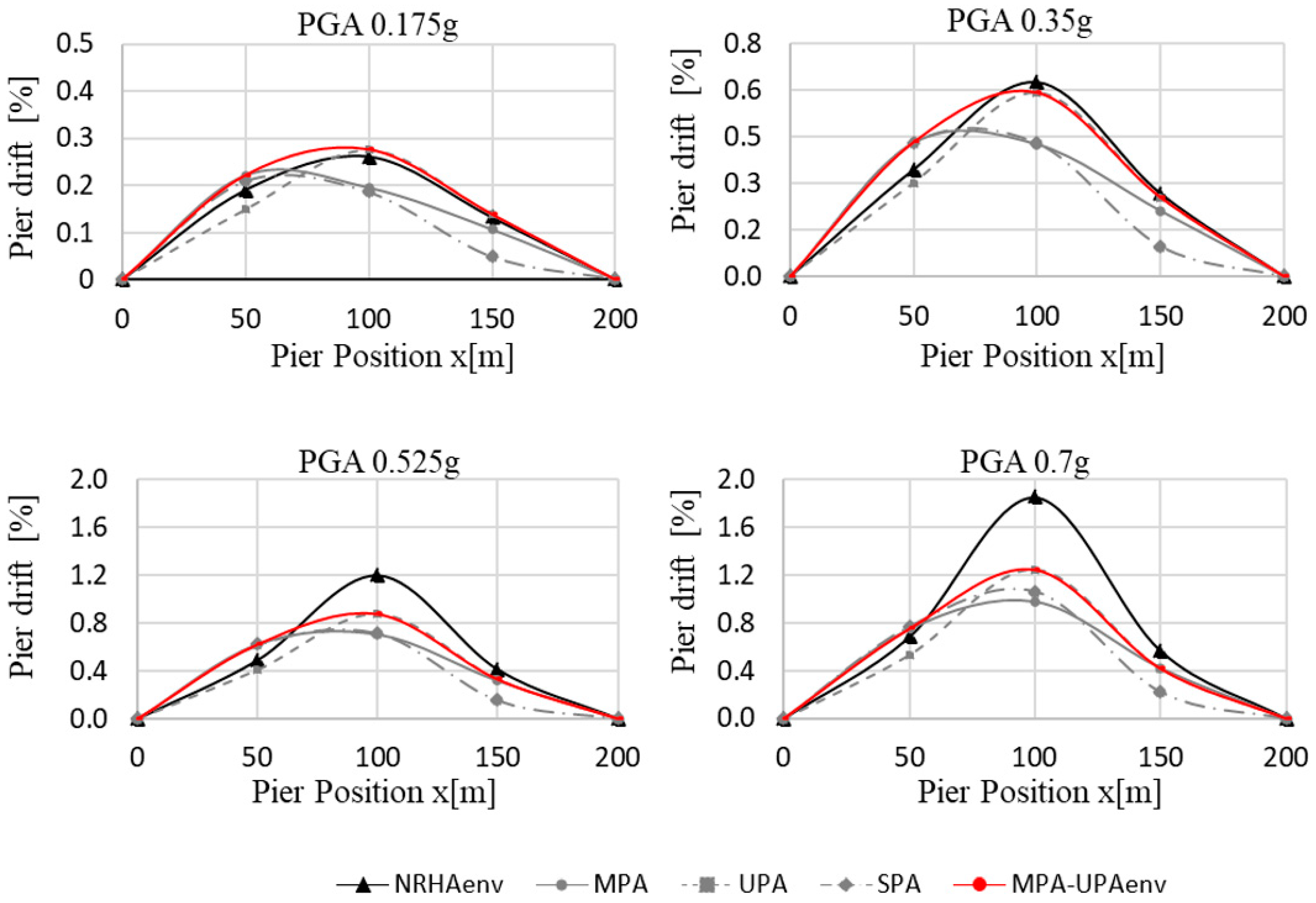
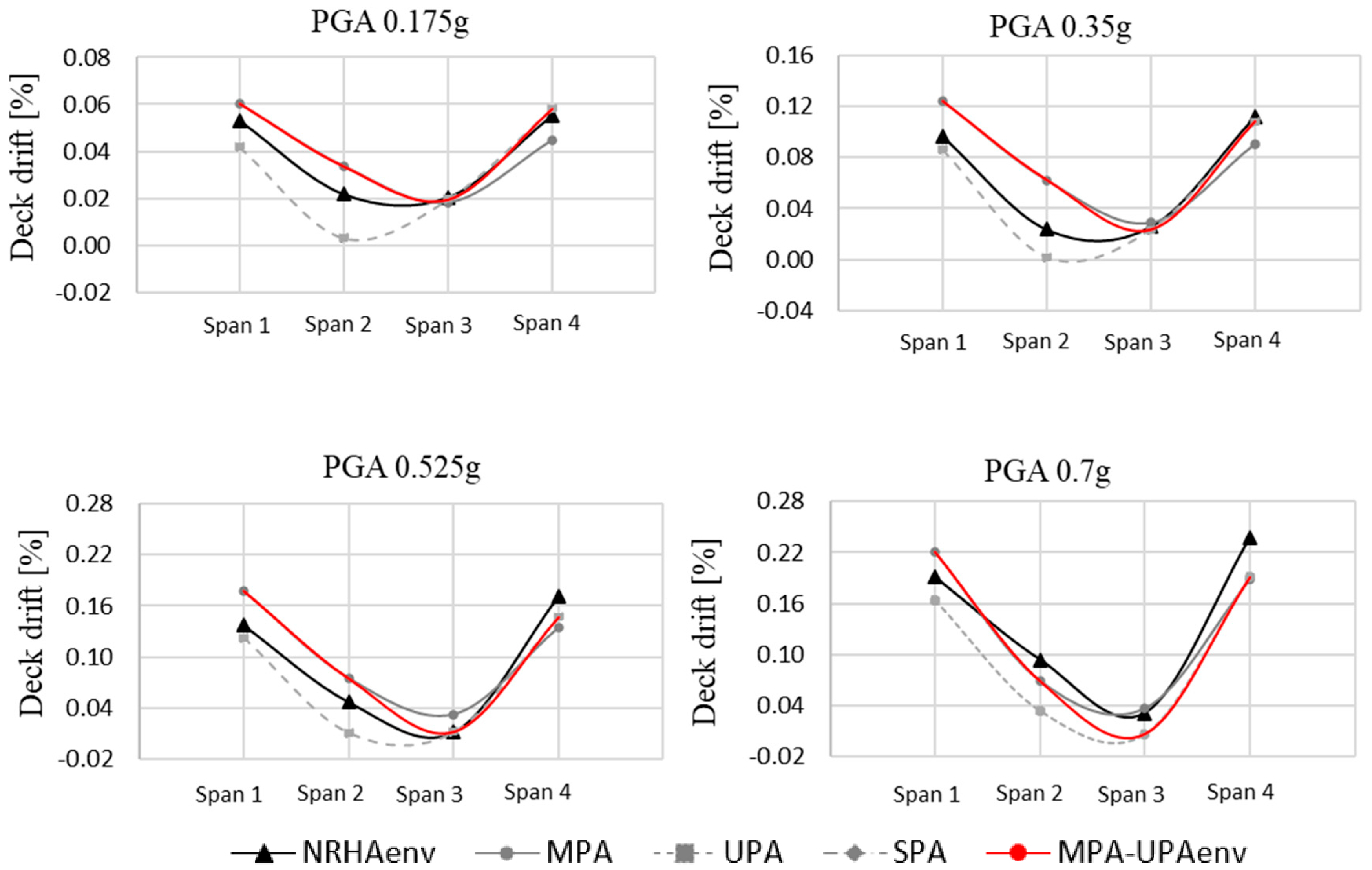
4.1. Analysis of the Regular Bridge (RB)
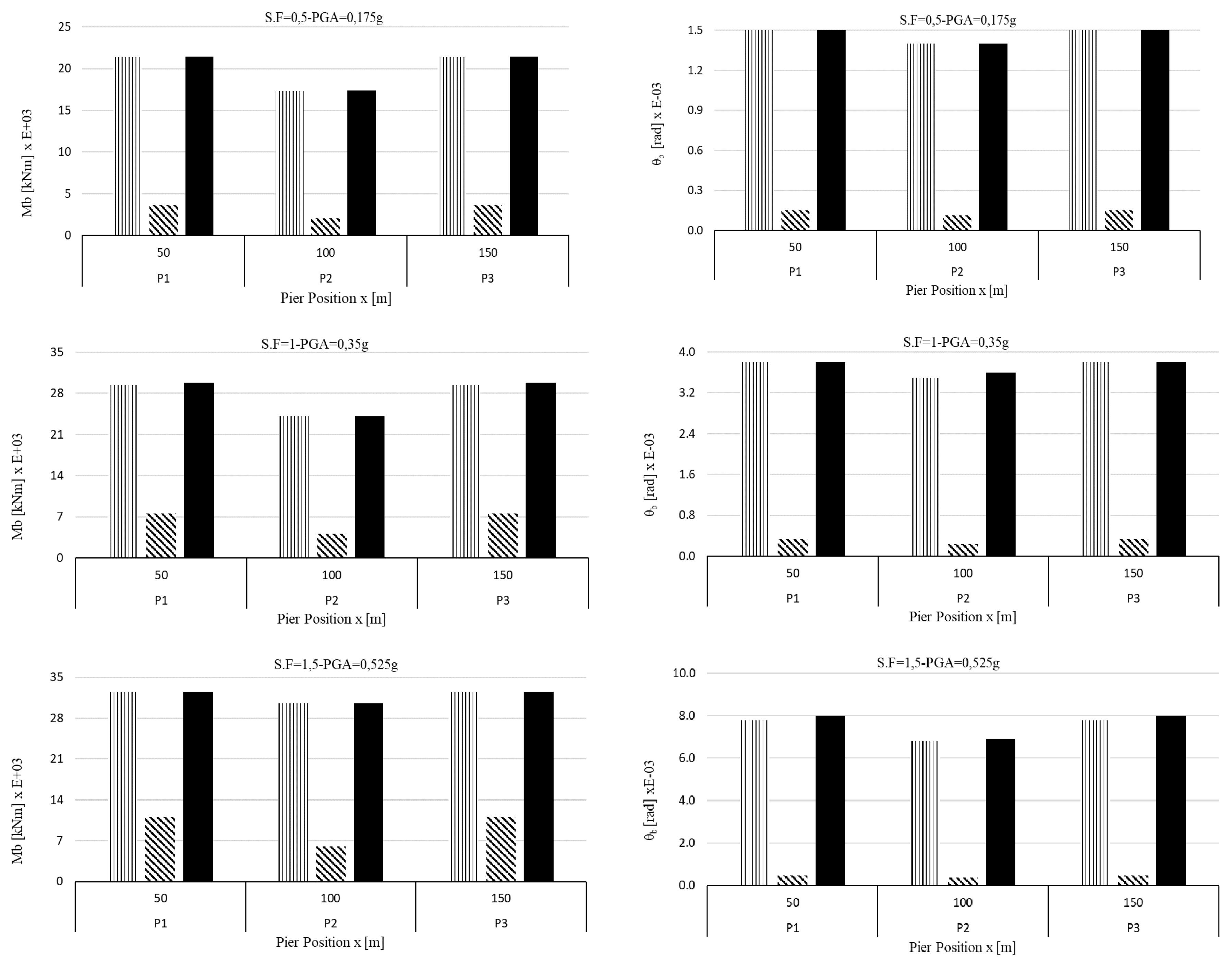
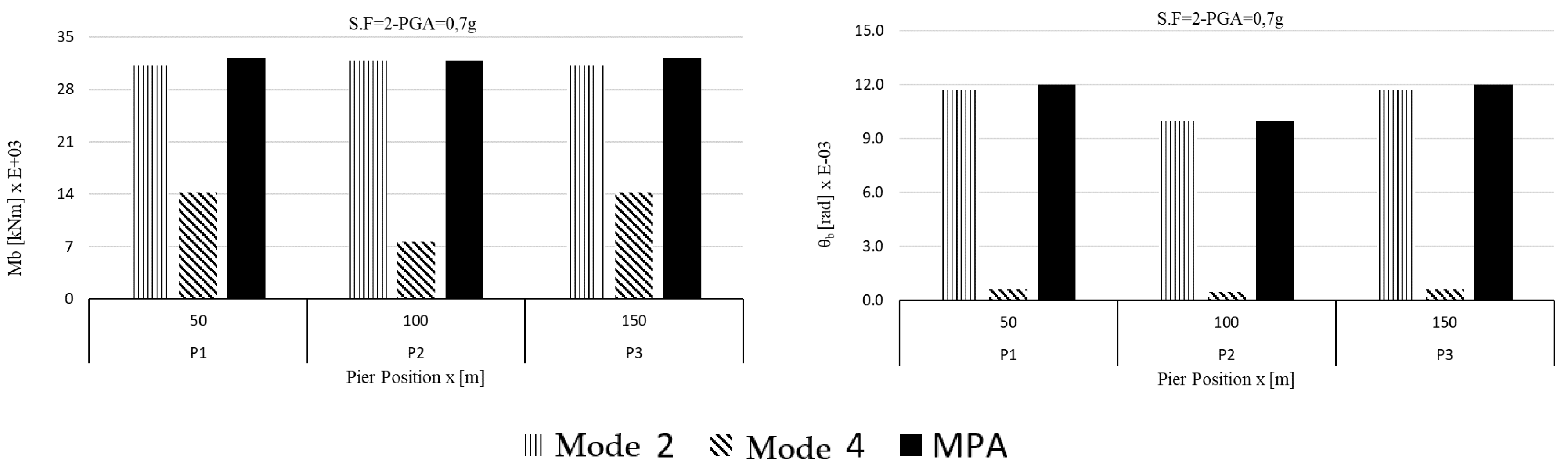
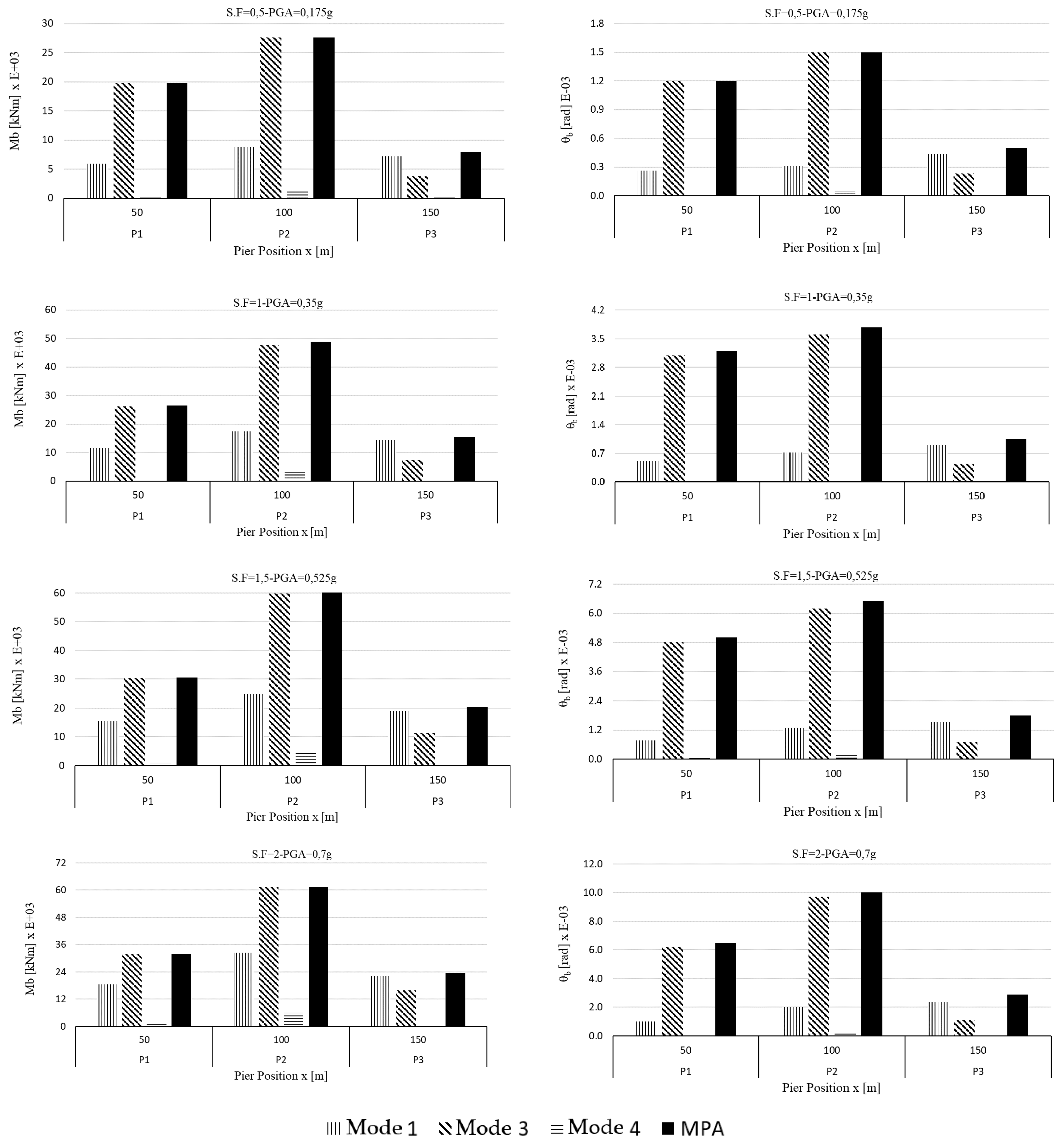
4.2. Analysis of the Irregular Bridge (IB)
5. Discussion
6. Conclusions and Future Developments
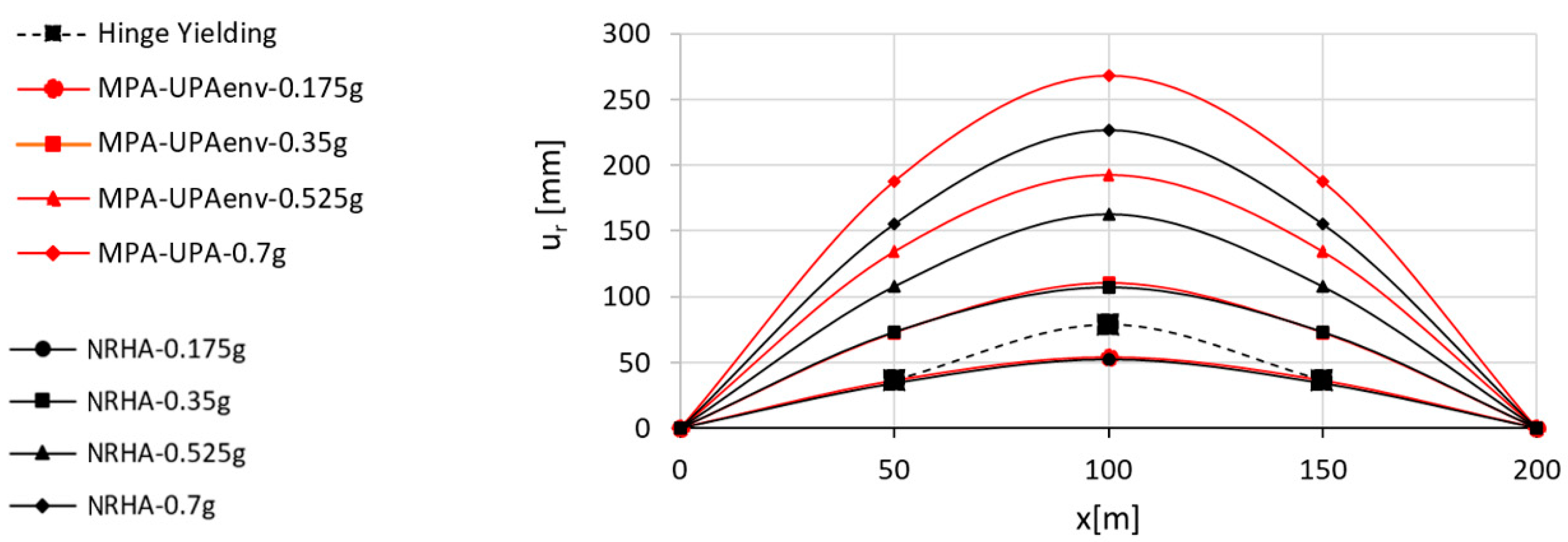
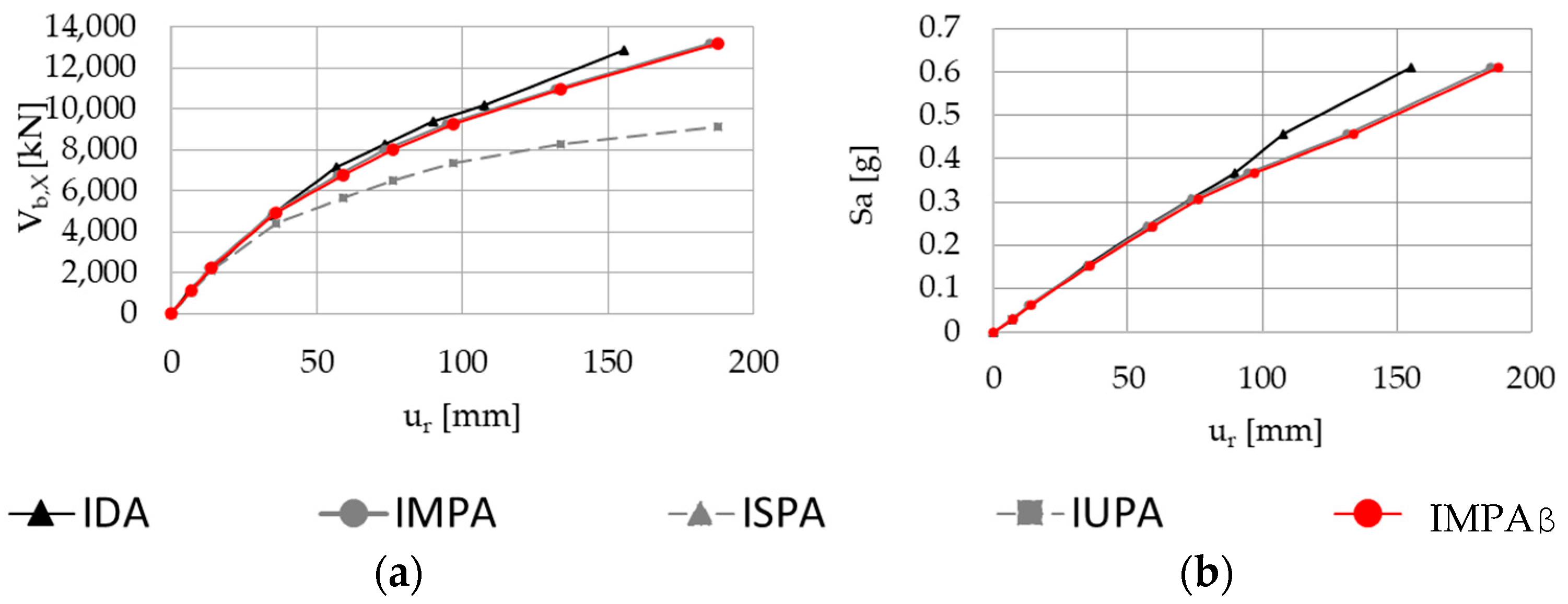
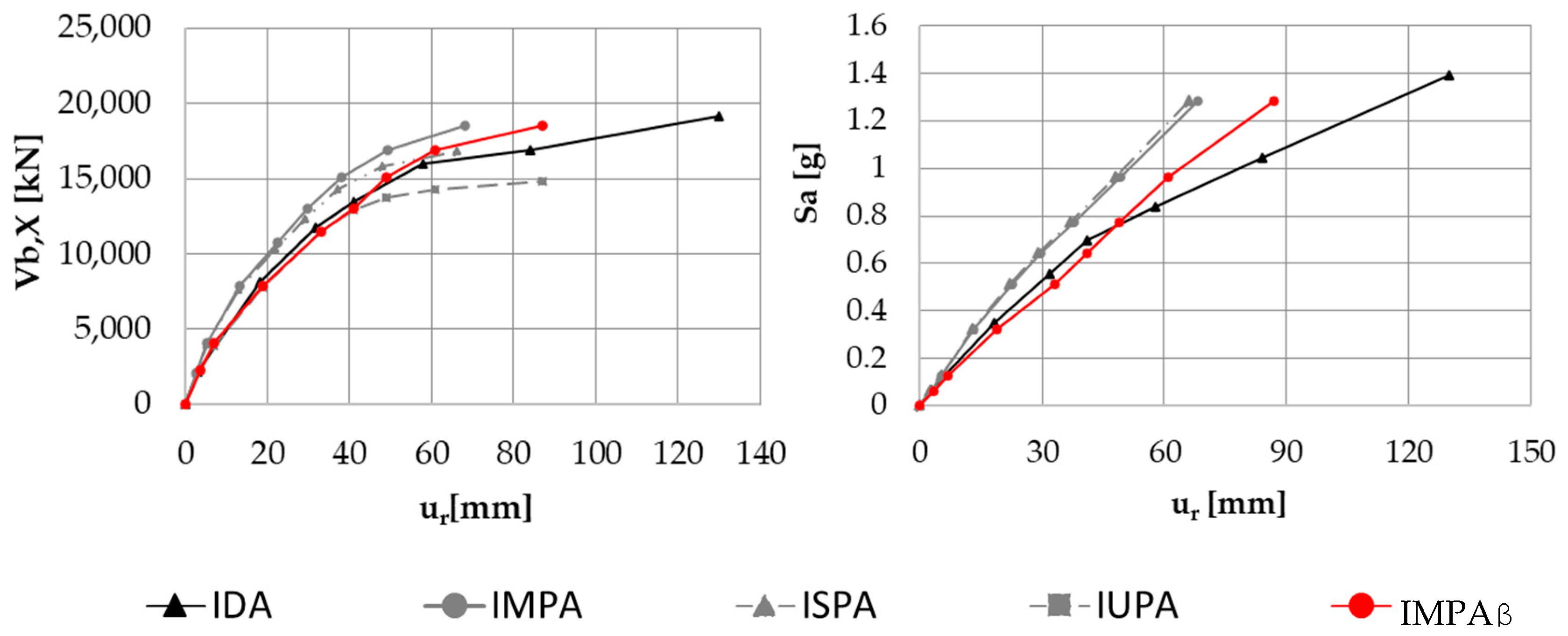
- The procedure keeps the simplicity and low computational effort typical of a standard pushover analysis. In fact, IMPAβ implies the execution of one nonlinear static analysis for each loading pattern, while performing IDA, several nonlinear response history analyses have to be performed, i.e., one for each of the seven ground motions, and it has to be repeated for every intensity level considered.
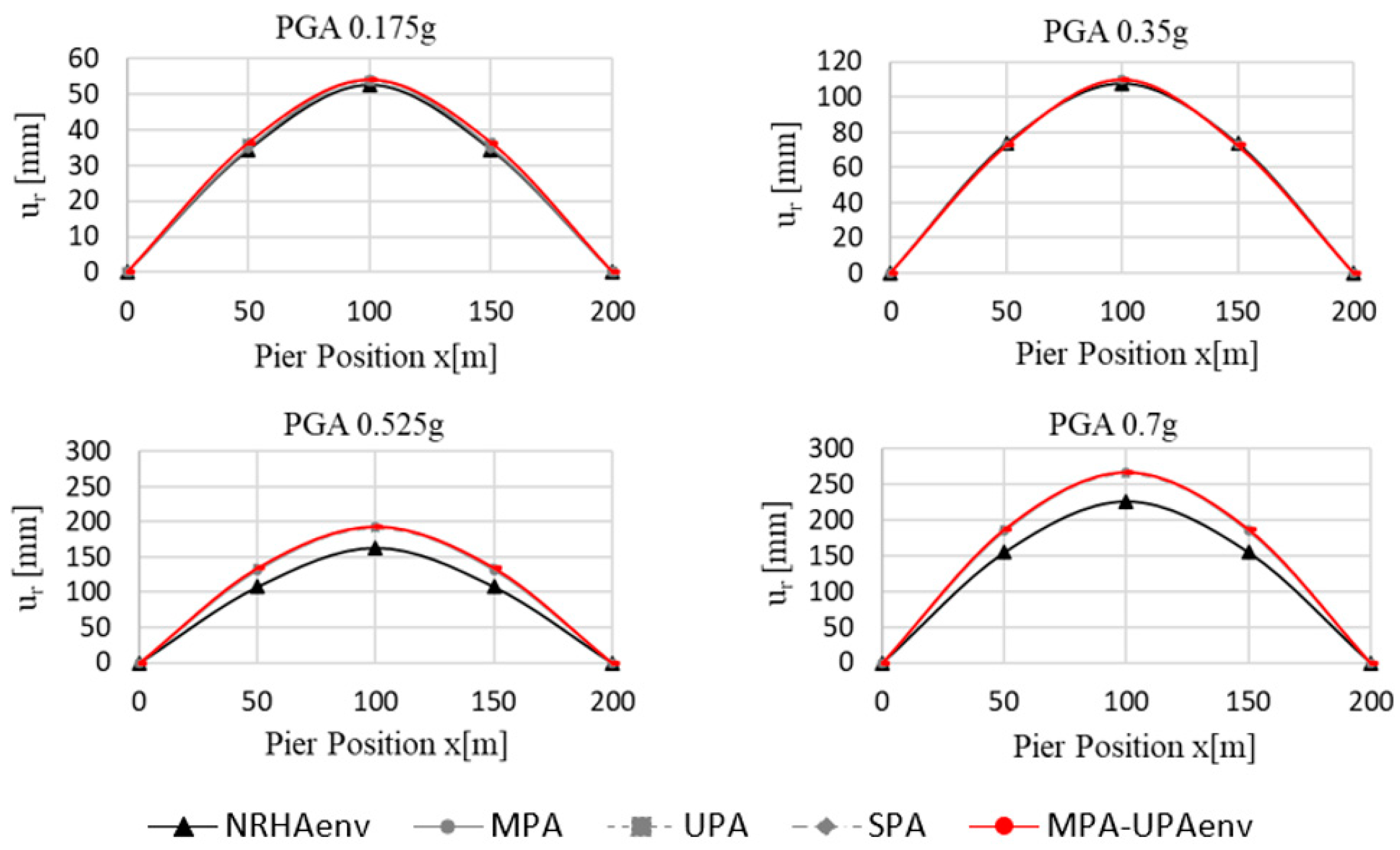
- If the capacity curve is obtained by using a multimodal load pattern only, it well matches the IDA curve, for both the regular and irregular bridge, up to the seismic design intensity only, while the present proposal allows us to analyze even higher intensities.
- IMPAβ produces a capacity curve very similar to what derived with IDA also beyond the seismic design intensity (0.35 g), and, for very high seismic intensities (beyond 0.6 g), the capacity curve of IMPAβ is conservative.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| C.S.M. | capacity spectrum method |
| GM | ground motion |
| IDA | incremental dynamic analysis |
| IMPA | incremental modal pushover analysis |
| IMPAβ | incremental modal pushover analysis for bridges |
| ISPA | incremental standard pushover |
| IUPA | incremental uniform pushover analysis |
| NSA | nonlinear static analysis |
| NRHA | nonlinear response history analysis |
| M.P. | monitoring point |
| MPA | modal pushover analysis |
| P.P. | performance point |
| RS | response spectrum |
| RSm | mean response spectrum |
| SPA | standard pushover analysis—loading pattern proportional to 1st modal shape |
| UPA | uniform pushover analysis—loading pattern proportional to masses |
| ur | monitored displacement |
| Vb | base shear |
Appendix A
References
- FEMA-356. Applied Technology Council (Report no 40); Applied Technology Council (ATC): Redwood City, CA, USA, 2000; Volume 1. [Google Scholar]
- ATC, Applied Technology Council. Seismic Evaluation and Retrofit of Concrete Buildings; ATC 40 Report; ATC: Redwood City, CA, USA, 1996. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Vamvatisikos, D.; Cornell, C.A. Direct estimation of seismic demand and capacity of multi-degree of freedom systems through incremental dynamic analysis of single degree of freedom approximation. J. Struct. Eng. ASCE 2005, 131, 589–599. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance-based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Antoniou, S.; Pinho, R. Development and verification of a displacement-based adaptive pushover procedure. J. Earthq. Eng. 2004, 8, 643–661. [Google Scholar] [CrossRef]
- Bento, R.; Bhatt, C.; Pinho, R. Using nonlinear static procedures for seismic assessment of the 3D irregular SPEAR building. Earthq. Struct. 2010, 1, 177–195. [Google Scholar] [CrossRef]
- Bhatt, C.; Bento, R. Assessing the seismic response of existing RC buildings using the extended N2 method. Bull. Earthq. Eng. 2011, 9, 1183–1201. [Google Scholar] [CrossRef]
- Bhatt, C.; Bento, R. Extension of the CSM-FEMA440 to plan-asymmetric real building structures. Earthq. Eng. Struct. Dyn. 2011, 40, 1263–1282. [Google Scholar] [CrossRef]
- Kappos, A.J.; Saiidi, M.S.; Aydınoğlu, M.N.; Isaković, T. Seismic Design and Assessment of Bridges: Inelastic Methods of Analysis and Case Studies; Kappos, A.J., Saiidi, M.S., Aydınoğlu, M.N., Isaković, T., Eds.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 21. [Google Scholar]
- Pinho, R.; Casarotti, C.; Antoniou, S. A comparison of single-run pushover analysis techniques for seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2007, 36, 1347–1362. [Google Scholar] [CrossRef]
- Muljati, I.; Warnitchai, P. A modal pushover analysis on multi-span concrete bridges to estimate inelastic seismic responses. Civil. Eng. Dimens. 2007, 9, 33–41. [Google Scholar]
- Kappos, A.J.; Goutzika, E.D.; Stefanidou, S.P.; Sextos, A.G. Problems in pushover analysis of bridges sensitive to torsion. In Computational Methods in Earthquake Engineering; Springer: Dordrecht, The Netherlands, 2010; Volume 21. [Google Scholar] [CrossRef]
- Kappos, A.J.; Paraskeva, T.S. Nonlinear static analysis of bridges accounting for higher mode effects. In Workshop on Nonlinear Static Methods for Design/Assessment of 3D Structures; Springer: Lisbon, Portugal, 2008. [Google Scholar]
- Goel, R.K.; Chopra, A.K. Evaluation of modal and FEMA pushover analyses: SAC buildings. Earthq. Spectra 2004, 20, 225–254. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Han, S.W.; Chopra, A.K. Approximate incremental dynamic analysis using the modal pushover analysis procedure. Earthq. Eng. Struct. Dyn. 2006, 35, 1853–1873. [Google Scholar] [CrossRef]
- Fajfar, P.; Marusic, D.; Perus, I. The extension of the N2 method to asymmetric buildings, In Proceedings of the 4th European Workshop on the Seismic Behaviour of Irregular and Complex Structures, Thessaloniki, Greece, 26–27 August 2005.
- Bergami, A.V.; Nuti, C.; Liu, X. Proposal and application of the Incremental Modal Pushover Analysis (IMPA). In Proceedings of the IABSE Conference, Geneva 2015: Structural Engineering: Providing Solutions to Global Challenges—Report, Geneva, Switzerland, 23–25 September 2015; pp. 1695–1700. [Google Scholar]
- Bergami, A.V.; Forte, A.; Lavorato, D.; Nuti, C. Proposal of an Incremental Modal Pushover Analysis (IMPA); Earthquake & Structures; Techno Press: Daejeon, Korea, 2017; Volume 13, pp. 539–549. ISSN 2092-7614. [Google Scholar]
- Bergami, A.V.; Nuti, C. A Design Procedure of Dissipative Braces for Seismic Upgrading Structures; Earthquake & Structures; Techno Press: Daejeon, Korea, 2013; Volume 4, pp. 85–108. ISSN 2092-7614. [Google Scholar]
- Bergami, A.V.; Forte, A.; Lavorato, D.; Nuti, C. Non-linear static analysis: Application of existing concrete building. In Proceedings of the Italian Concrete Days, Rome, Italy, 27–28 October 2016. [Google Scholar]
- Bommer, J.; Acevedo, A. The use of real earthquake accelerograms as input to dynamic analysis. J. Earthq. Eng. 2004, 8, 43–91. [Google Scholar] [CrossRef]
- Calvi, G.M.; Priestley, M.J.N. Seismic design and retrofitting of reinforced concrete bridges. In Proceedings of the International Workshop, LitoLine Arti Grafiche, Pavia, 2–5 April 1991. [Google Scholar]
- European Committee for Standardization. Eurocode 8—Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- European Committee for Standardization. Eurocode 8—Design of Structures for Earthquake Resistance—Part 2: Bridges; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Isaković, T.; Fischinger, M. Higher modes in simplified inelastic seismic analysis of single column bent viaducts. Earthq. Eng. Struct. Dyn. 2006, 35, 95–114. [Google Scholar] [CrossRef]
- Isaković, T.; Lazaro, M.P.N.; Fischinger, M. Applicability of pushover methods for the seismic analysis of single-column bent viaducts. Earthq. Eng. Struct. Dyn. 2008, 37, 1185–1202. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.J.; Sextos, A.G. Extension of modal pushover analysis to seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2006, 35, 1269–1293. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.J. Further development of a multimodal pushover analysis procedure for seismic assessment of bridges. Earthq. Eng. Struct. Dyn. 2010, 39, 211–222. [Google Scholar] [CrossRef]
- Paraskeva, T.S.; Kappos, A.J. Seismic assessment of complex bridges using an improved modal pushover analysis procedure. In Proceedings of the Fifth European Workshop on the Seismic Behaviour of Irregular and Complex Structures, Catania, Italy, 16–17 September 2008; pp. 335–348. [Google Scholar]
- Mohtashami, E.; Shooshtari, A. A multimode adaptive pushover procedure for seismic assessment of integral bridges. Adv. Civ. Eng. 2013, 2013, 941905. [Google Scholar] [CrossRef][Green Version]
- Isakovic, T.; Fischinger, M.; Kante, P. Bridges: When is single mode seismic analysis adequate? Struct. Build. 2003, 156, 163–173. [Google Scholar] [CrossRef]
- Decreto 17 gennaio 2018 Aggiornamento delle «Norme tecniche per le costruzioni». (18A00716) (GU Serie Generale n.42 del 20-02-2018—Suppl. Ordinario n. 8). In Italian. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 22 June 2020).
- Beyer, K.; Bommer, J. Selection and scaling of real accelerograms for bi-directional loading: A review of current practice and code provisions. J. Earthq. Eng. 2006, 11, 13–45. [Google Scholar] [CrossRef]
- Kastanos, E.I.; Sextos, A.G.; Manolis, G.D. Selection of earthquake ground motion records: A state of the art review from a structural perspective. Soil Dyn. Earthq. Eng. 2010, 30, 157–169. [Google Scholar]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]
- Computers and Structures Inc. SAP2000 Nonlinear Version 10 (2005) User’s Reference Manual; Computers and Structures Inc.: Berkeley, CA, USA, 2005. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress–strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Forte, A.; Santini, S.; Fiorentino, G.; Lavorato, D.; Bergami, A.V.; Nuti, C. Influence of materials knowledge level on the assessment of the shear strength characteristic value of existing RC beams. In Proceedings of the 12th FIB International PhD Symposium in Civ. Engineering, Prague, Czech Republic, 29–31 August 2018; pp. 979–986. [Google Scholar]
- Lavorato, D.; Fiorentino, G.; Bergami, A.V.; Ma, H.-B.; Nuti, C.; Briseghella, B.; Vanzi, I.; Zhou, W. Surface generation of asynchronous seismic signals for the seismic response analysis of bridges. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; Volume 1, pp. 2203–2213. [Google Scholar]
- Lavorato, D.; Bergami, A.V.; Rago, C.; Ma, H.-B.; Nuti, C.; Vanzi, I.; Briseghella, B.; Zhuo, W.-D. Seismic behaviour of isolated RC bridges subjected to asynchronous seismic input. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; Volume 1, pp. 2214–2216. [Google Scholar]
- Lavorato, D.; Fiorentino, G.; Pelle, A.; Rasulo, A.; Bergami, A.V.; Briseghella, B.; Nuti, C. A corrosion model for the interpretation of cyclic behavior of reinforced concrete sections. Struct. Concr. 2019, 1–15. [Google Scholar] [CrossRef]
- Liu, T.; Zordan, T.; Zhang, Q.; Briseghella, B. Equivalent viscous damping of bilinear hysteretic oscillators. J. Struct. Eng. 2015, 141, 06015002. [Google Scholar] [CrossRef]
- Aviram, A.; Mackie, K.R.; Stojadinović, B. Guidelines for Nonlinear Analysis of Bridge Structures in California; Report No. UCB/PEER 2008/03; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2008. [Google Scholar]

| Load | kN/m | kN | |
|---|---|---|---|
| Dead | Self-weight | 200 | - |
| Live | Vehicle loads (Qik) | - | 1200 |
| Live | Distributed load (qik) | 54.5 | - |
| Etq ID | Earthquake Name | Waveform | Date | PGA (g) |
|---|---|---|---|---|
| 1635 | South Iceland | 4674-xa | 17/06/2000 | 0.31 |
| 1635 | South Iceland | 4674-ya | 17/06/2000 | 0.31 |
| 2309 | Bingol | 7142-xa | 01/05/2003 | 0.50 |
| 2309 | Bingol | 7142-ya | 01/05/2003 | 0.50 |
| 2142 | South Iceland (aftershock) | 6349-xa | 21/06/2000 | 0.72 |
| 2142 | South Iceland (aftershock) | 6332-ya | 21/06/2000 | 0.51 |
| 1635 | South Iceland | 6277-ya | 17/06/2000 | 0.35 |
| - | Mean | - | 0.46 |
| Mode | Period | Participating Mass |
|---|---|---|
| N° | S | % |
| 2 | 1.02 | 78.0 |
| 4 | 0.33 | 12.0 |
| Mode | Period | Participating Mass |
|---|---|---|
| N° | S | % |
| 1 | 0.65 | 16.9 |
| 3 | 0.53 | 71.3 |
| 4 | 0.13 | 4.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergami, A.V.; Nuti, C.; Lavorato, D.; Fiorentino, G.; Briseghella, B. IMPAβ: Incremental Modal Pushover Analysis for Bridges. Appl. Sci. 2020, 10, 4287. https://doi.org/10.3390/app10124287
Bergami AV, Nuti C, Lavorato D, Fiorentino G, Briseghella B. IMPAβ: Incremental Modal Pushover Analysis for Bridges. Applied Sciences. 2020; 10(12):4287. https://doi.org/10.3390/app10124287
Chicago/Turabian StyleBergami, Alessandro Vittorio, Camillo Nuti, Davide Lavorato, Gabriele Fiorentino, and Bruno Briseghella. 2020. "IMPAβ: Incremental Modal Pushover Analysis for Bridges" Applied Sciences 10, no. 12: 4287. https://doi.org/10.3390/app10124287
APA StyleBergami, A. V., Nuti, C., Lavorato, D., Fiorentino, G., & Briseghella, B. (2020). IMPAβ: Incremental Modal Pushover Analysis for Bridges. Applied Sciences, 10(12), 4287. https://doi.org/10.3390/app10124287









