Featured Application
Damage fracture for engineering materials.
Abstract
The evaluation of energy release rate with angle is still a challenging task in metal crack propagation analysis, especially for the mixed Mode I-II-III loading situation. In this paper, the energy release rate associated with stress intensity factors at an arbitrary angle under mixed mode loadings has been investigated using both a numerical method and theoretical derivation. A relatively simple and precise numerical method was established through a series of spatial-inclined ellipses in Mode I-II and ellipsoids in Mode I-II-III, with different propagation angles computed from simulation. Meanwhile, a theoretical expression of the energy release rate with angle for a crack tip under a I-II-III mixed mode crack was deduced based on the propagation mechanism of the crack tip under the influence of a stress field. It is confirmed that the theoretical expression deduced could provide results as accurately as the present numerical method. The present results were confirmed to be effective and accurate by comparison with experimental data and other literature.
1. Introduction
The understanding of mixed-mode fracture is an important subject in fracture mechanics, as material flaws or pre-cracks may inevitably occur in the manufacturing process. To describe crack propagation under mixed-mode loading, the classical formula of energy release rate was expanded in this hypothesis that crack extends collinearly with the initial crack:
where is stress intensity factor, is shear modulus, and for plane strain, elastic modulus must be replaced by , is Poisson’s ratio. While much research shows that the actual expanding direction is not collinear with its initial path, Formula (1) cannot be applied to a mixed-mode crack [1,2,3,4,5,6,7,8,9,10,11]. For a I-II mixed-mode crack, the analytic method is widely used in the early development of fracture mechanics; Hussian’s [12] work as a founder is also worth mentioning, which simplified the star-shaped crack to an L-shaped crack and used a mapping function to solve the elastic problem. However, some inaccuracy in Hussain’s equation can be found as the derivatives of two stress functions in the mapping function during the “simultaneous expansion” procedure are incorrect. Meanwhile, complex numerical calculations were used. Wu, C. H [13] gave the numerical relationship of for non-crack-parallel propagations by using explicit asymptotic analysis. K. Hayashi and S. Nemat-Nasser [14] obtained the energy release rate in the form of a quadratic of stress intensity factors with the coefficients tabulated for various kink angles by the method that models a kink as a continuous distribution of edge dislocations. Antonin Chambolle [15] revisited energy release rate using the expansion of Amestoy and Leblond [16]. In addition, the validity of Irwin’s formula for the energy release rate for any kink angle, material anisotropy and loading condition was proved by Abbas Azhdari and Sia Nemat-Nasser [17]. G.C. Sih, P. C. Paris and F. Erdogan [18] used a complex variable method to evaluate the strength of stress singularities at crack tips in plane problems and plate bending problems, which can extend the Griffith–Irwin fracture theory to arbitrary crack extension. F. Erdogan and G.C. Sih [19] analyzed the stresses of a plate crack in cylindrical coordinates and discussed the experimental results of plane stress and transverse bending of plates, respectively.
Although many achievements have been made for energy release rate, the validity of conclusions reached through a complex process cannot be evaluated. Most of the researches are aimed at cracks under two kinds of loading situation, the mixed-mode I-II-III loading situation is rarely mentioned, and the methods they used neither analytical method nor numerical method is complex; therefore, they are difficult to generalize to other crack problems.
The objective of this paper was to evaluate the energy release rate associated with stress intensity factors at any angle under mixed mode loading. In this paper, a more uncomplicated and precise numerical method was established based on the concept that the energy release rate is equal to the change rate of the energy difference before and after crack kinking. A series of spatial inclined ellipses in Mode I-II and ellipsoids in Mode I-II-III with different propagation angles computed from non-dimensional value () were fitted by MATLAB. Meanwhile, a theoretical expression of energy release rate with angle for a crack tip under I-II-III mixed mode crack was deduced based on the propagation mechanism of the crack tip under the influence of a stress field. It was confirmed that the theoretical expression deduced could provide results as accurately as the present numerical method. The validity of the present methods will be shown by comparing them with experimental data and other literature.
2. Determining G for I-II Mixed Mode Crack
2.1. Numerical Analysis of 2D Crack
2.1.1. Crack Simulation with ABAQUS
To find the relationship between the stress intensity factors and energy release rate under the I-II combined loading situation, finite element technology was applied to research the problem.
As shown in Figure 1a, a rectangular plate with crack was under combined Mode I and Mode II loading on the top side, and fixed on the bottom side, , . the finite element model was shown in Figure 1b,c shows the meshes around the crack tip, the type of which is a collapsed element side, and duplicate nodes configure the mid-side node parameter to its 1/4 position to simulate the singularity of displacement of the crack tip region. The material is linear elastic homogeneous isotropic aluminum alloy, . The and are obtained by changing the value of .
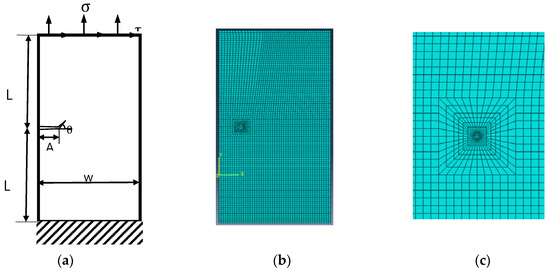
Figure 1.
Crack model in ABAQUS. (a) A rectangular plate with crack; (b) The finite element model; (c) Drawing of partial enlargement for crack.
When , the value of changes from 20 to 100 , with a step of 20. The result is shown in Figure 2. The simulation value output from ABAQUS is basically consistent with the reference value calculated by the literature [20], and the errors between the two values of each loading presented in Figure 2b are about 0.53%. This verified simulation method will be applied in the following sections.
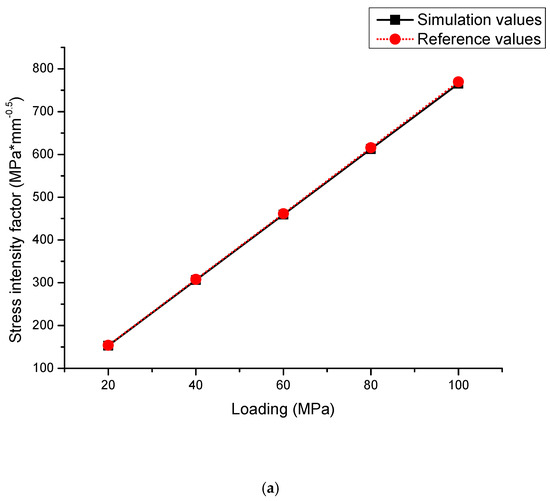
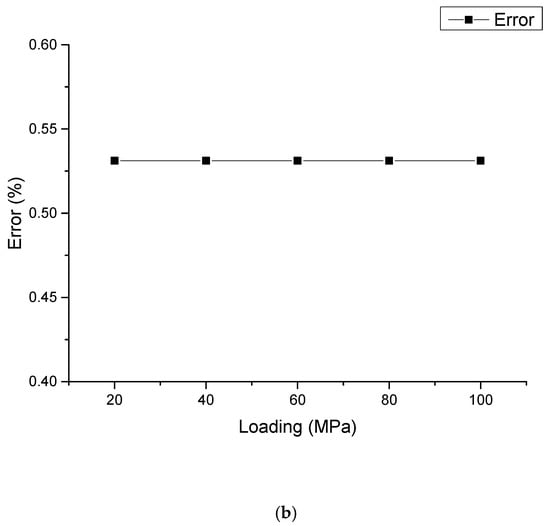
Figure 2.
Verification of simulation accuracy. (a) Verification of simulation value output from ABAQUS; (b) Errors between the two values of each loading.
2.1.2. The Theoretical Basis of Energy Release Rate Definition
A cracked plate in plane stress has an infinitesimal kink at an angle from the plane of the crack, as illustrated in Figure 3a–c. The energy release rate , as a crack extension force, is a measure of the energy available for an increment of crack extension, which can be calculated approximately as:
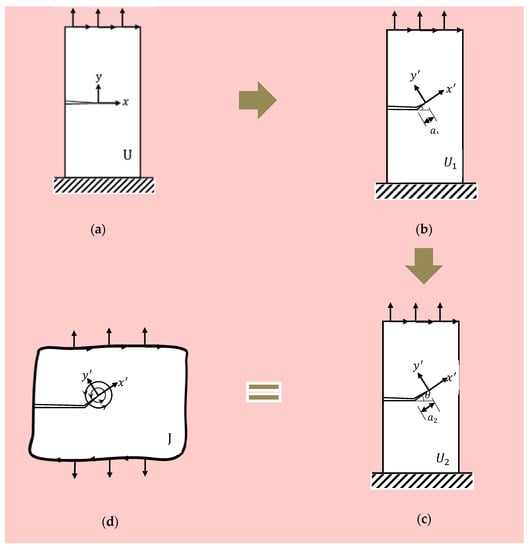
Figure 3.
Cracked plane with kink extension. (a) Initial crack; (b) Kink crack ; (c) Kink crack ; (d) J integral.
Irrespective of whether the crack extension is in its initial plane or kinked, the angle is , where and are the strain energy before and after kink extension, respectively, and is the length of the kink, which is measured from the original crack tip.
For an edge crack in the linear elastic body, the J-integral computed along a contour surrounding the crack tip is equal to the energy release rate (Figure 3d), which is revalidated by simulation work. The strain energy release rate and -integral for a kink can be evaluated based on the output data of ABAQUS, as shown in Figure 4. It shows that energy release rate is in good agreement with the -integral evaluated along the contour starting at one kink’s crack surface and ending at the other kink’s crack surface under arbitrary loading and kink angle conditions.
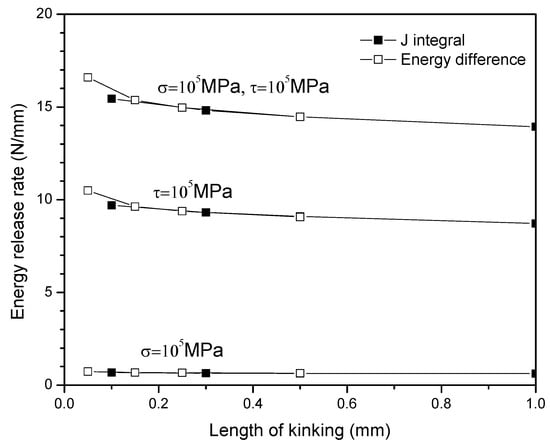
Figure 4.
Determination of energy release rates as the length of kink crack approaches zero.
- (1)
- Obtain the values of and strain energy at the points
- (2)
- The energy differences between are calculated and divided by It represents the energy release rate for the crack at 0.05 mm, 0.15 mm, 0.25 mm, 0.5 mm.
- (3)
- Determine that the minimum value of kink length for calculation is 0.1 mm; since the kink crack becomes infinitesimally small, the values from the energy difference deviate from the integral.
This validates the assumption made in the connection with strain energy release rate. -integral will be used in the following research as it is reliable and convenient.
2.1.3. Computational Analysis
From the output data of the simulation, the energy release rate and stress intensity factors can be obtained corresponding to the required condition. The method developed in the present study is described as follows:
- (1)
- Determine and under arbitrary combined Mode and Mode loading conditions with the initial crack.
- (2)
- Determine for kink cracks repeatedly, varying the kink length from to with four data points . Then, compute energy release rate as the kink propagation vanishes on the curve of versus kink length by the method of fitting.
- (3)
- Plot the non-dimensional value () for each kink angle ()
- (4)
- Determine the parameters of inclined ellipses that fit the above data points using the curve fitting algorithm by MATLAB, and the corresponding ellipse equation is presented as follows:where , , are the semi-major axis, semi-minor axis and inclination of ellipse, respectively.
- (5)
- Obtain the coefficients of quadratic of energy release rate in terms of stress intensity factors, and defined as
As shown in Figure 5, the non-dimensional value () for each kink angle can be calculated through the technique proposed above. By fitting the database, a series of inclined ellipses are presented with a certain angle and size. Figure 6 shows the inclined angle of Iso-energy release rate ellipses with kink angle . The variation of inclination for ellipses drops linearly with the increase of the kink angle. The trend of semi-major axis and semi-minor axis of ellipses according to the variation of kink angle has been shown in Figure 7. The coefficients of quadratics for energy release rate in terms of stress intensity factors are calculated for each kink angle based on the ellipse equations (Figure 8).
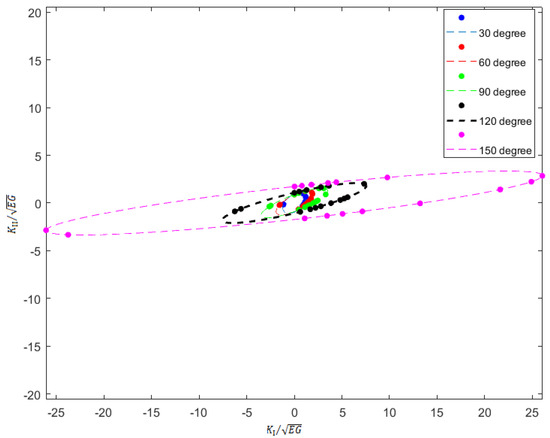
Figure 5.
Iso-energy release rate ellipses on normalized mixed mode stress intensity factors.
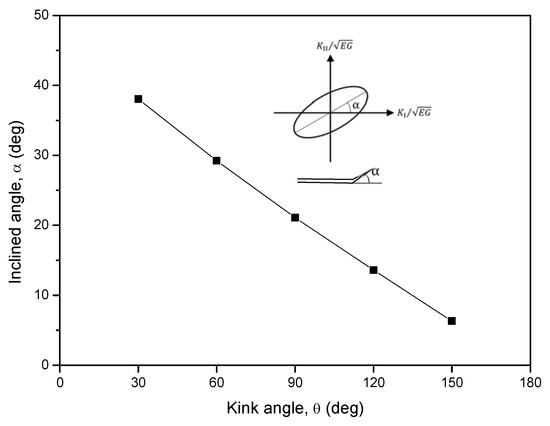
Figure 6.
Inclined angle of the Iso-energy release rate.
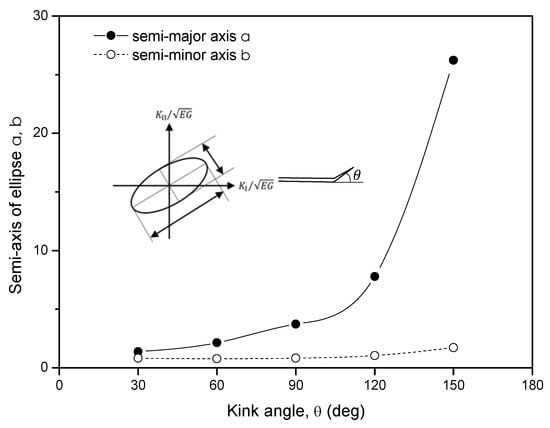
Figure 7.
Semi-major and semi-minor axis of the Iso-energy release rate.
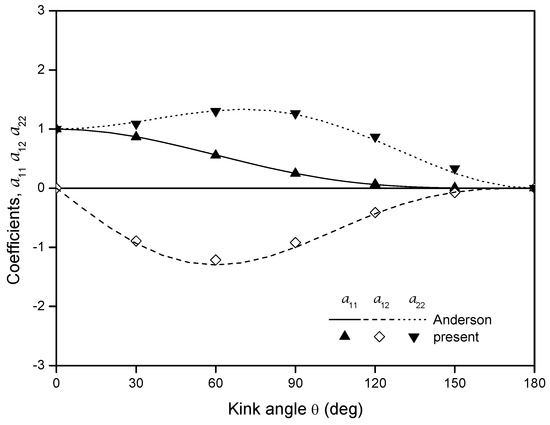
Figure 8.
Coefficients of energy release rate.
2.2. Discussion of Numerical Results
2.2.1. Comparison with References
The results obtained by the present method are more evident through the comparison with Anderson [21]. Anderson’s analytic work introduced the local SIFs, which are functions of nominal SIFs—the local SIFs represent the true stress strength in front of a kink crack. Figure 9a shows the coefficients calculated by Anderson’s theory and the present method.
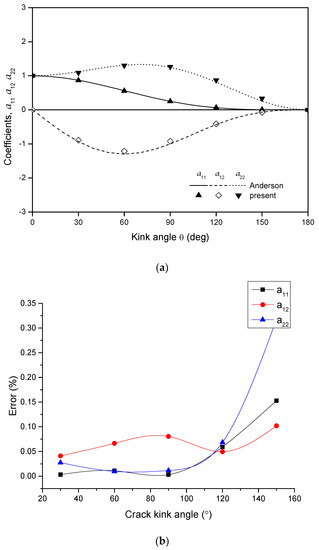
Figure 9.
Energy release rate coefficients of the present work compared with Anderson. (a) The energy release rate coefficients of the present work compared with Anderson; (b) Error.
The values of coefficients and calculated by Anderson and the present method are surprisingly consistent. Figure 9b presents the errors between the two results for each kink angle; the average error between each kink angle is less than 1%, which illustrates that the results obtained by the present work agree well with Anderson’s.
Moreover, the validity of extended Irwin’s formula is reiterated by the numerical simulation under two arbitrary loading conditions, as shown in Table 1. Stress intensity factors and energy release rate with the limiting process as the propagation kink goes to zero are obtained from the output of the ABAQUS. The calculated value of obtained from Equation (3) is very consistent with the value from ABAQUS.

Table 1.
Comparison of G for two different methods.
2.2.2. Experiment Verification
To research the law of crack propagation under combined loading, the uniaxial oblique crack experiment was carried out. For an oblique crack under a tensile loading shown in Figure 10, the stress intensity factors can be calculated by Formula (5):
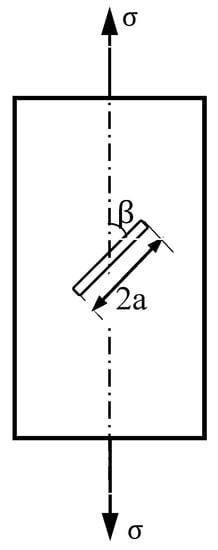
Figure 10.
Uniaxial oblique crack.
Reference [22] verified the validity of specimen for mixed mode fracture experiment. The composition of the 6061-T6 aluminum alloy which is used to manufacture test specimens is shown in Table 2. Three groups were divided by inclination angle (30°, 60°, 90°), and each group has three samples, as shown in Figure 11a. Samples are processed by middle-speed WEDM, and the accuracy is 0.2 mm. Figure 11b shows the Universal Hydraulic Testing Machine, type LD26.105. The samples with oblique crack were of the exerted displacement boundary condition on the top end at a speed of 0.2 mm/s, and fixed on the bottom end until the crack started propagation.

Table 2.
Composition of 6061-T6 aluminum alloy.

Figure 11.
Samples and Universal Hydraulic Testing Machine. (a) Three groups samples; (b) Universal Hydraulic Testing Machine.
As shown in Figure 12a, it was revealed that when the inclination angle was 90°(Mode I crack), the crack extended in a self-similar manner that propagated along the direction of the initial crack. While the phenomenon was unsuitable to describe 30° and 60° (mixed I-II crack) extension situations, crack propagation under these two angles deviated from the initial direction, which illustrated that the assumption for the mixed-mode crack extension path of Formula (1) was wrong.
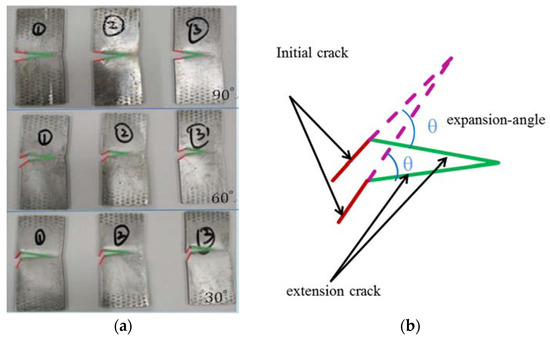
Figure 12.
Crack propagation path. (a) Samples with extension crack; (b) The actual extension angles.
From the experimental results, the actual extension angles were measured as shown in Figure 12b; besides, the value , calculated by expression (5) for a inclined crack, was plugged into the arbitrary angle energy release rate formula obtained by numerical fitting. Therefore, the extension angles were deduced by the -criterion, and Table 3 shows the results:

Table 3.
Calculated extension angle and experimental extension angle.
The results between the calculated extension angle and experimental extension angle are extraordinary similar. The error value, considering the specimens are not manufactured by ideal elastic material, was lower than the 5% that can be accepted. Consequently, the validity of the numerical method can be verified by the two comparison results above, which can be applied for the I-II-III mixed mode crack.
3. Fracture Parameters for 3D Crack
3.1. The Theoretical Derivation of Energy Release Rate for I-II-III Mixed Mode Crack
Considering the meaning of SIFs, denote the intensity of tensile stress, in-plane stress and out-of-plane stress, as shown in Figure 13. When crack kink occurs, the local SIFs should be recalculated. A local coordinate system at the tip of the kink is defined and assumes that the remote stress fields in polar coordinates defined the local stress field. The transformation of the plane is shown in Figure 14.
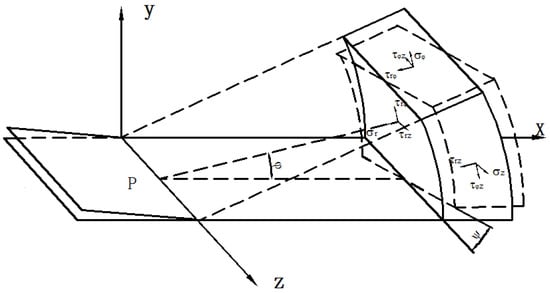
Figure 13.
Stress field at crack tip.

Figure 14.
Infinitesimal kink at the tip in different coordinates. (a) The crack-tip stress fields in polar; (b) The local stress fields in coordinates.
Stress fields ahead of the crack front for Mode I, Mode II and Mode III at an angle in polar coordinates are shown in Formula (6).
The directions of the local stress field for the crack tip in a local coordinate system are consistent with those of the polar coordinate, as shown in Figure 14. Thus, the stress at the crack tip between the polar coordinate and local coordinate has the following relationship:
The local stress intensity factors at the arbitrary extend angle were deduced by summing the normal and shear stresses, respectively:
Combining Formula (6)–(8), the coefficients can be calculated using Formula (9):
Reviewing the expression of the classical energy release rate, the new expression for the I-II-III mixed mode crack can be modified as (10):
3.2. Numerical Analysis of 3D Crack
3.2.1. 3D Model of Crack Simulation
A 3D model with a mixed mode I-II-III crack is considered here: ; the bottom is fixed, and normal stress and shear stress are applied at the top. The 20-nodes collapsed element used in the crack tip region is used to simulate the singularity of the displacement at the crack tip (Figure 15).
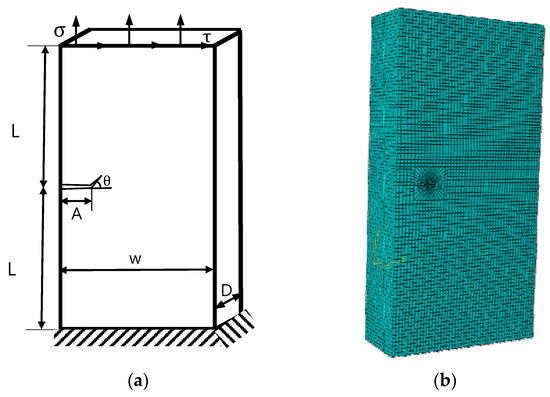
Figure 15.
Crack model with mixed mode I-II-III in ABAQUS. (a) A 3D model with a mixed mode I-II-III crack; (b) The finite element model.
3.2.2. Computational Analysis
The data processing for and outputted by the I-II-III mixed mode crack simulation is more complex than for the I-II mixed mode crack—not only for the value added, but also for much more data on the crack tip line. To obtain the fracture parameter , the present study is described as follows:
- (1)
- Determine and for kink cracks repeatedly, varying the kink length from to with four data points . Then, compute the energy release rate as the kink propagation vanishes on the curve of and versus kink length through fitting each node on the crack tip line.
- (2)
- Plot the non-dimensional value () for each kink angle ()
- (3)
- Determine the parameters of inclined ellipses that fit the above data points using a fitting method for quadric surfaces in space by MATLAB, and the corresponding ellipse equation is presented as follows:where , , , are the semi-major axis, semi-middle axis, semi-minor axis and inclination of ellipse, respectively.
- (4)
- Obtain the coefficients of quadratic of energy release rate in terms of stress intensity factors, and defined as
The results of fitting the non-dimensional value are shown in Figure 16; a series of conclusions can be summarized as follows:
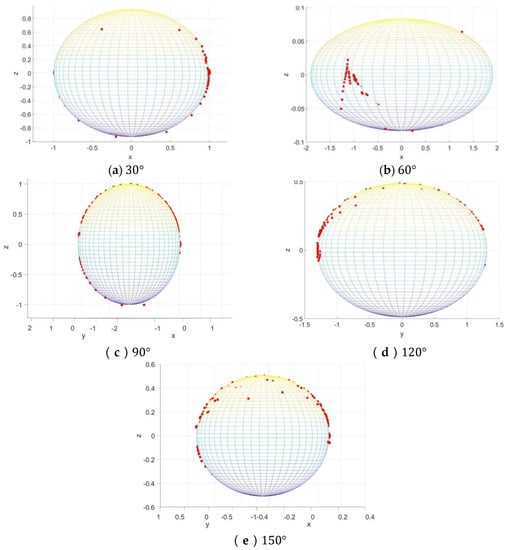
Figure 16.
Iso-energy release rate ellipsoids on normalized mixed mode stress intensity factors. (a) ; (b) ; (c) ; (d) ; (e) .
- (1)
- The non-dimensional value ( ) transformed from the data output by ABAQUS forms a series of ellipsoids.
- (2)
- At each presupposed extended angle (30°~150°), the scattered points of dimensionless data output by ABAQUS under different loadings are all on the surface of the same tilted ellipsoid.
- (3)
- The coefficients of quadratics for energy release rate in terms of stress intensity factors are calculated for each kink angle based on the ellipsoid equations.
3.3. Discussion of Theoretical and Numerical Results
This section expanded the I-II mixed mode crack to the I-II-III mixed mode crack, not only added out-of-plane loading, but also considered the thickness factor. Therefore, the nodes along the thickness direction in a finite element model can output multi group values of and . Based on the result of (12), an arbitrary loading had been imposed on the crack model, and the output data of and were obtained. is calculated with the obtained from the theoretical expression (10). Figure 17 shows the along the thickness direction, the values at node 4~17 are at about a constant value of 1.1, while the values at node 1, 2, 3 and 18, 19, 20 which are adjacent to the free surface are offset highly from 1.1. It is confirmed that the theoretical expression deduced could provide the results as accurately as the present numerical method. The reason of deviation for the two solutions is not only the influence of the free surface at both ends of the crack front, but also the stress coupling effect.
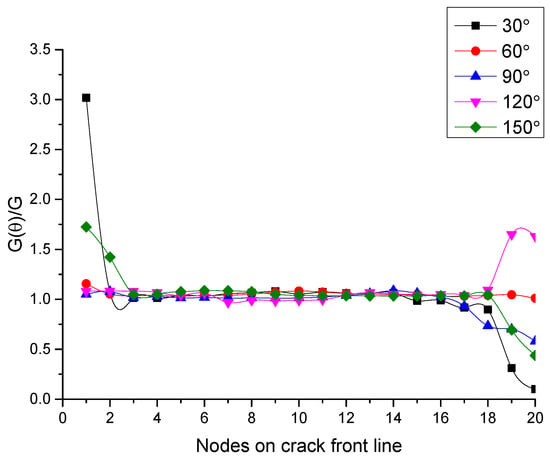
Figure 17.
for each expansion angle.
The case to be considered is the specimen subject to in-plane shear loading. In this case the generated values are rather constant in the inner part of the specimen, as shown in Figure 18, but for nodes near the free surface, they increase remarkably, which means that the singularity changed in the vicinity of the free surface. The stress intensity factor was generated, even if the external loading of the specimen does not include an out-of-plane shear component. This phenomenon is defined as the stress coupling effect [23,24]. The absolute values of were enlarged gradually from the middle node of crack tip to both sides, which illustrated the coupling effect enhanced by the free surface. Due to the absolute values of being less than , especially in the inner part of the specimen, the coupling effect is called weak coupling.
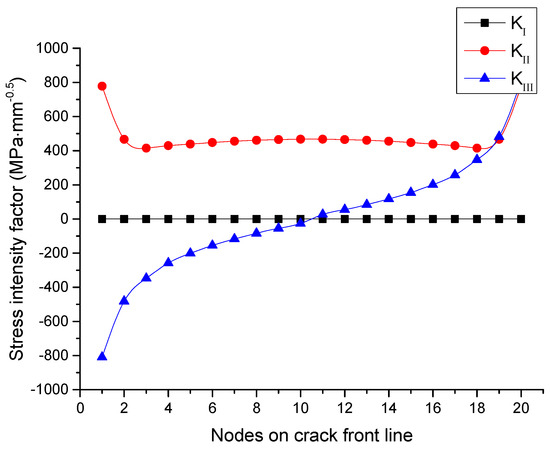
Figure 18.
Distribution of Stress Intensity Factor on the crack tip line under mode II loading.
Figure 19 shows the out-of-plane shear loading case. In this case, the pure III mode loading generated and , and the absolute value of nodes adjacent to the free surfaces exceeds the value of , which is called the strong coupling effect. Regarding the I-II-III mixed mode crack simulation, the induced and have a significant influence on their theoretical value due to the coupling effect, which can result in the deviation between and .
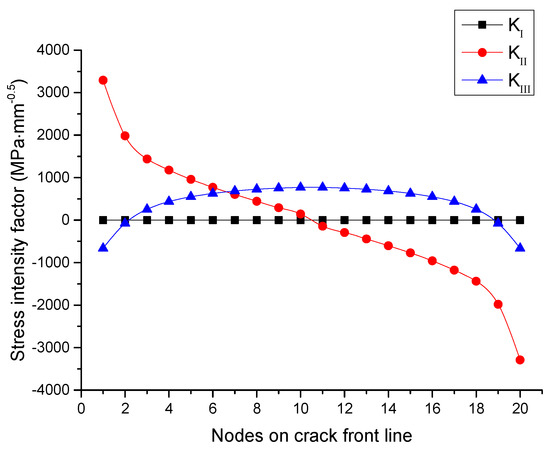
Figure 19.
Distribution of Stress Intensity Factor on the crack tip line under mode III loading.
4. Conclusions
The energy release rate associated with stress intensity factors under mixed mode loading for aluminum alloy material has been investigated using both a numerical method and theoretical derivation. The present results demonstrate the simpler, accurate calculation process and accurate evaluation of the energy release rate. The following conclusions can be drawn:
- (1)
- A relatively simple and precise numerical method was established to evaluate the energy release rate associated with the stress intensity factors under mixed mode loading based on the concept that the energy release rate is equal to the change rate of the energy difference before and after crack kinking.
- (2)
- Based on the numerical method, a series of spatial inclined ellipses in Mode I-II and ellipsoids in Mode I-II-III with different propagation angles computed from non-dimensional value () were fitted by MATLAB, and the expression of the energy release rate with the crack propagation angle was obtained.
- (3)
- A theoretical expression of energy release rate at any propagation angle for a crack tip under I-II-III mixed mode crack was deduced based on the propagation mechanism of the crack tip under the influence of a stress field. It is confirmed that the theoretical expression deduced could provide results as accurately as the present numerical method.
- (4)
- The present results are consistent with the experimental data. The error, which is lower than 5%, can be accepted considering that the specimens are not manufactured using ideal elastic material. Consequently, the present results demonstrate the simpler, accurate calculation process and the accurate evaluation of energy release rate.
Author Contributions
Conceptualization, S.J.C. and Y.Y.; methodology, S.J.C. and Y.Y.; software, W.s.H.; validation, S.J.C. and. W.s.H.; formal analysis, S.J.C. and Y.Y.; investigation, H.C.; resources, H.C.; data curation, Y.Y. and W.s.H.; writing—original draft preparation, Y.Y. and W.s.H.; writing—review and editing, S.J.C. and Y.Y.; visualization, S.J.C. and Y.Y.; supervision, S.J.C.; project administration, S.J.C.; funding acquisition, S.J.C. and H.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Shanghai (18ZR1416500); Development Fund for Shanghai Talents (2018053); and “Shuguang Program” supported by the Shanghai Education Development Foundation and Shanghai Municipal Education Commission (19SG51).
Conflicts of Interest
The Authors declare no conflicts of interest.
Nomenclature
| Energy release rate | |
| and | Stress intensity factor, and for Mode I, Mode II, Mode III. |
| Elastic modulus | |
| Poisson’s ratio | |
| Shear modulus | |
| Length of rectangular plate | |
| Wide of rectangular plate | |
| Thickness of rectangular plate | |
| Length of initial crack | |
| Kinking angel of crack | |
| Normal stress | |
| Shear stress | |
| Length of kink crack | |
| , | Strain energy before kink extension and after kink extension |
| Integral for a kink | |
| , , | Semi-major axis, semi-minor axis and inclination of ellipse |
| Oblique angle of crack | |
| Stress fields in polar coordinate | |
| Local stress intensity factors |
References
- Irwin, G.R. Onset of Fast Crack Propagation in High Strength Steel and Aluminum Alloys; Naval Research Lab: Washington, DC, USA, 1956; Sagamore Research Conference Proceedings; Volume 2, pp. 289–305. [Google Scholar]
- Chatterjee, S.N. The stress field in the neighborhood of a branched crack in an infinite elastic sheet. Int. J. Solids Struct. 1975, 11, 521–538. [Google Scholar] [CrossRef]
- Yukio, U.; Kazuo, I.; Tetsuya, Y.; Mitsuru, A. Characteristics of brittle fracture under general combined modes including those under bi-axial tensile loads. Eng. Fract. Mech. 1983, 18, 1131–1158. [Google Scholar] [CrossRef]
- Melin, S. Fracture from a straight crack subjected to mixed mode loading. Int. J. Fract. 1987, 32, 257–263. [Google Scholar]
- He, M.Y.; Bartlett, A.; Evans, A.G.; Hutchinson, J.W. Kinking of a crack out of an interface: Role of in-plane stress. J. Am. Ceram. Soc. 1991, 74, 767–771. [Google Scholar] [CrossRef]
- Kishen, J.M.C.; Singh, K.D. Stress intensity factors based fracture criteria for kinking and branching of interface crack: Application to dams. Eng. Fract. Mechan. 2001, 68, 201–219. [Google Scholar] [CrossRef]
- Hammouda, M.M.; Fayed, A.S.; Sallam, H.E. Simulation of mixed mode I/II cyclic deformation at the tip of a short kinked inclined crack with frictional surfaces. Int. J. Fatigue 2003, 25, 743–753. [Google Scholar] [CrossRef]
- Pantano, A. Cohesive model for the simulation of crack initiation and propagation in mixed-mode I/II in composite materials. Appl. Compos. Mater. 2019, 26, 1207–1225. [Google Scholar] [CrossRef]
- Li, X.F.; Lee, K.Y.; Tang, G.J. Kink angle and fracture load for an angled crack subjected to far-field compressive loading. Eng. Fract. Mech. 2012, 82, 172–184. [Google Scholar] [CrossRef]
- Fajdiga, G.; Zafošnik, B. Determining a kink angle of a crack in mixed mode fracture using maximum energy release rate, SED and MTS criteria. J. Multidiscip. Eng. Sci. Technol. 2015, 2, 356–362. [Google Scholar]
- Guo, B.K.; Yan, H.H.; Zhang, L. Cracking angle of an arbitrary oriented crack embedded in a strip under I-II mixed mode loading. Int. J. Mater. Sci. 2016, 6, 52–57. [Google Scholar] [CrossRef]
- Hussain, M.; Pu, S.; Underwood, J. Strain Energy Release Rate for a Crack under Combined Mode I and Mode II. In Fracture Analysis: Proceedings of the 1973 National Symposium on Fracture Mechanics, Part II; Irwin, G., Ed.; ASTM International: West Conshohocken, PA, USA, 1974; pp. 2–28. [Google Scholar]
- Wu, C.H. Fracture under Combined Loads by Maximum-Energy-Release-Rate Criterion. J. Appl. Mech. 1978, 45, 553–558. [Google Scholar] [CrossRef]
- Hayashi, K.; Nemat-Nasser, S. Energy-Release Rate and Crack Kinking Under Combined Loading. Trans. ASME 1981, 48, 520–524. [Google Scholar] [CrossRef]
- Chambolle, A.; Francfort, G.A.; Marigo, J.J. Revisiting energy release rates in brittle fracture. Nonlinear Sci. 2010, 20, 395–424. [Google Scholar] [CrossRef]
- Amestoy, M.; Leblond, J.B. Crack path in plane situations-II. Detailed form of the expansion of the stress intensity factors. Int. J. Solids Struct. 1992, 29, 465–501. [Google Scholar] [CrossRef]
- Azhdari, A.; Nemat-Nasser, S. Energy-Release Rate and Crack Kinking in Anisotropic Brittle Solids. J. Mech. Phys. Solids 1996, 44, 929–951. [Google Scholar] [CrossRef]
- Sih, G.C.; Paris, P.C.; Erdogan, F. Crack-Tip, Stress-Intensity Factors for Plane Extension and Plate Bending Problems. J. Appl. Mech. 1962, 29, 306–312. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G.C. On the Crack Extension in Plates Under Plane Loading and Transverse Shear. J. Basic Eng. 1997, 12, 527. [Google Scholar] [CrossRef]
- Qizhi, W.; Xing, Z.; Qingzhi, H. Stress Intensity Factor; Springer Netherlands: Berlin, Germany, 2008. [Google Scholar]
- Anderson, T.L. Fracture Mechanics Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Richard, H.A. Specimens for Investigating Biaxial Fracture and Fatigue Process. In Biaxial and Multiaxial Fatigue; Brown, M.W., Miller, K.J., Eds.; Mechanical Engineering Publications: London, UK, 1989; pp. 217–229. [Google Scholar]
- Luca, S.; John, Y.; Alfredo, N.; Thierry, P.-L. Fracture and Structural Integrity: Annals 2014; Gruppo Italiano Frattura: Cassino, Italy, 2014. [Google Scholar]
- Pantano, A.; Averill, R.C. A Penalty-Based Interface Technology for Coupling Independently Modeled Three-Dimensional Finite Element Meshes. Finite Elem. Anal. Des. 2007, 43, 271–286. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).