Featured Application
Private data mining.
Abstract
The oblivious transfer primitive is sufficient to implement secure multiparty computation. However, secure multiparty computation based on public-key cryptography is limited by the security and efficiency of the oblivious transfer implementation. We present a method to generate and distribute oblivious keys by exchanging qubits and by performing commitments using classical hash functions. With the presented hybrid approach of quantum and classical, we obtain a practical and high-speed oblivious transfer protocol. We analyse the security and efficiency features of the technique and conclude that it presents advantages in both areas when compared to public-key based techniques.
1. Introduction
In Secure Multiparty Computation (SMC), several agents compute a function that depends on their own inputs, while maintaining them private [1]. Privacy is critical in the context of an information society, where data is collected from multiple devices (smartphones, home appliances, computers, street cameras, sensors, …) and subjected to intensive analysis through data mining. This data collection and exploration paradigm offers great opportunities, but it also raises serious concerns. A technology able to protect the privacy of citizens, while simultaneously allowing to profit from extensive data mining, is going to be of utmost importance. SMC has the potential to be that technology if it can be made practical, secure and ubiquitous.
Current SMC protocols rely on the use of asymmetric cryptography algorithms [2], which are considered significantly more computationally complex compared with symmetric cryptography algorithms [3]. Besides being more computationally intensive, in its current standards, asymmetric cryptography cannot be considered secure anymore due to the expected increase of computational power that a large-scale quantum computer will bring [4]. Identifying these shortcomings in efficiency and security motivates the search for alternative techniques for implementing SMC without the need of public key cryptography.
1.1. Secure Multiparty Computation and Oblivious Transfer
Consider a set of N agents and a multivariate function. For , a SMC service (see Figure 1) receives the input from the i-th agent and outputs back the value in such a way that no additional information is revealed about the remaining , for . Additionally, this definition can be strengthened by requiring that for some number of corrupt agents working together, no information about the remaining agents gets revealed (secrecy). It can also be imposed that if at most agents do not compute the function correctly, the protocol identifies it and aborts (authenticity).
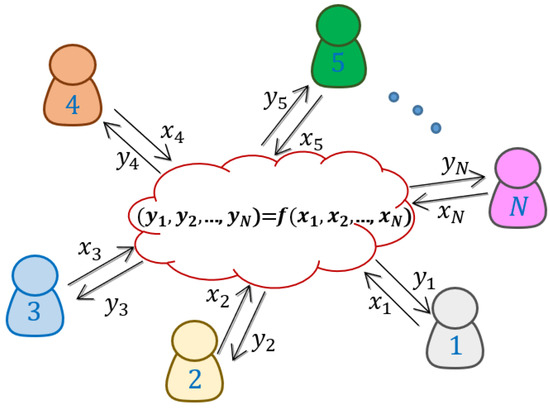
Figure 1.
In secure multiparty computation, N parties compute a function preserving the privacy of their own input. Each party only has access to their own input–output pair.
Some of the most promising approaches towards implementing SMC are based on oblivious circuit evaluation techniques such as Yao’s garbled circuits for the two party case [5] and the GMW or BMR protocols for the general case [2,6,7,8]. It has been shown that to achieve SMC it is enough to implement the Oblivious Transfer (OT) primitive and, without additional assumptions, the security of the resulting SMC depends only on that of the OT [9]. In the worst case, this requires each party to perform one OT with every other party for each gate of the circuit being evaluated. This number can be reduced by weakening the security or by increasing the amount of exchanged data [10]. Either way, the OT cost of SMC represents a major bottleneck for its practical implementation. Finding fast and secure OT protocols, hence, is a very relevant task in the context of implementing SMC.
Let Alice and Bob be two agents. A 1-out-of-2 OT service receives bits as input from Alice and a bit c as input from Bob, then outputs to Bob. This is done in a way that Bob gets no information about the other message, i.e., , and Alice gets no information about Bob’s choice, i.e., the value of c [11].
1.2. State of the Art
Classical OT implementations are based on the use of asymmetric keys, and suffer from two types of problems. The first one is the efficiency: asymmetric cryptography relies on relatively complex key generation, encryption, and decryption algorithms [12] (Chapter 1) and [13] (Chapter 6). This limits achievable rates of OTs, and since implementations of SMC require a very large number of OTs [3,10], this has hindered the development of SMC-based applications. The other serious drawback is that asymmetric cryptography, based on integer number factorization or discrete-logarithm problems, is insecure in the presence of quantum computers, and therefore, it has to be progressively abandoned. There are strong research efforts in order to find other hard problems that can support asymmetric cryptography [4]. However, the security of these novel solutions is still not fully understood.
A possible way to circumvent this problem is by using quantum cryptography to improve the efficiency and security of current techniques. Quantum solutions for secure key distribution, Bit Commitment (BC) and OT have been already proposed [14]. The former was proved to be unconditionally secure (assuming an authenticated channel) and realizable using current technology. Although, it was shown to be impossible to achieve unconditionally secure quantum BC and OT [15,16,17], one can impose restrictions on the power of adversaries in order to obtain practically secure versions of these protocols [18,19]. These assumptions include physical limitations on the apparatuses, such as noisy or bounded quantum memories [20,21,22]. For instance, quantum OT and BC protocols have been developed and implemented (see [23,24,25]) under the noisy storage model. Nevertheless, solutions based on hardware limitations may not last for long, because as quantum technology improves the rate of secure OT instances will decrease. Other solutions include exploring relativistic scenarios using the fact that no information can travel faster than light [26,27,28]. However, at the moment, these solutions do not seem to be practical enough to allow the large dissemination of SMC.
In this work, we explore the resulting security and efficiency features of implementing oblivious transfer using a well known quantum protocol [5] supported by using a cryptographic hash based commitment scheme [29]. We call it a hybrid approach, since it mixes both classical and quantum cryptography. We analyse the protocol stand alone security, as well as its composable security in the random oracle model. Additionally, we study its computational complexity and compare it with the complexity of alternative public key based protocols. Furthermore, we show that, while unconditional information-theoretic security cannot be achieved, there is an advantage (both in terms of security and efficiency) of using quantum resources in computationally secure protocols, and as such, they are worth consideration for practical tasks in the near future.
This paper is organized as follows. In Section 2, we present a quantum protocol to produce OT given access to a collision resistant hash function, define the concept of oblivious keys, and explain how having pre-shared oblivious keys can significantly decrease the computational cost of OT during SMC. The security and efficiency of the protocol is discussed in Section 3. Finally, in Section 4 we summarize the main conclusions of this work.
2. Methods
2.1. Generating the OTs
In this section, we describe how to perform oblivious transfer by exchanging qubits. The protocol shown in Figure 2 is the well known quantum oblivious transfer protocol first introduced by Yao, which assumes access to secure commitments. The two logical qubit states and represent the computational basis, and the states , represent the Hadamard basis. We also define the states for according to the following rule:

Figure 2.
Quantum OT protocol based on secure commitments. The ⨁ denotes the bit XOR of all the elements in the family.
Note that these states can be physically instantiated using, for instance, a polarization encoding fiber optic quantum communication system, provided that a fast polarization encoding/decoding process and an algorithm to control random polarization drifts in optical fibers are available [30,31].
Intuitively, this protocol works because the computational and the Hadamard are conjugate bases. Performing a measurement in the preparation basis of a state, given by , yields a deterministic outcome, whereas measuring in the conjugate basis, given by , results in a completely random outcome. By preparing and measuring in random bases, as shown in steps 1 and 2, approximately half of the measurement outcomes will be equal to the prepared states, and half of them will have no correlation. As Alice sends the information of preparation bases to Bob in step 6, he gets to know which of his bits are correlated with Alice’s. During steps 3 to 6, Bob commits the information of his measurement basis and outcomes to Alice, who then chooses a random subset of them to test for correlations. Passing this test (statistically) ensures that Bob measured his qubits as stated in the protocol as opposed to performing a different (potentially joint) measurement. Such strategy may extract additional information from Alice’s strings, but would fail to pass the specific correlation check in step 6. At step 8, Bob separates his non-tested measurement outcomes in two groups: where he measured in the same basis as the preparation one, and , in which he measured in the different basis. He then inputs his bit choice c by selecting the order in which he sends the two sets to Alice. During step 9, Alice encrypts her first and second input bits with the preparation bits associated with the first and second second sets sent by Bob respectively. This effectively hides Bob’s input bit because she is ignorant about the measurements that were not opened by Bob (by the security of the commitment scheme). Finally, Bob can decrypt only the bit encrypted with the preparation bits associated to .
In real implementations of the protocol one should consider imperfect sources, noisy channels, and measurement errors. Thus, in step 6 Alice should perform parameter estimation for the statistics of the measurements, and pass whenever the error parameter es below some previously fixed value. Following this, Alice and Bob perform standard post-processing techniques of information reconciliation and privacy amplification before continuing to step 7. These techniques indeed work even in the presence of a dishonest Bob. As long as he has some minimal amount of uncertainty about Alice’s preparation string s, an adequate privacy amplification scheme can be used to maximize Bob’s uncertainty of one of Alice’s input bits. This comes at the cost of increasing the amount of qubits shared per OT [32]. An example of these techniques applied in the context of the noisy storage model (where the commitment based check is replaced by a time delay under noisy memories) can be found in [19].
2.2. Oblivious Key Distribution
In order to make the quantum implementation of OT more practical during SMC we introduce the concept of oblivious keys. The protocol can be separated in two phases: the Oblivious Key Distribution phase which consists of steps 1 to 7 and forms the subprotocol, and the Oblivious Transfer phase which takes steps 8 to 10 and we denote as the subprotocol. Note that after step 7 of the subsets have not been revealed to Alice, so she has no information yet on how the correlated and uncorrelated bits between k and are distributed (recall that k and are the result of removing the tested bits from the strings s and respectively). On the other hand, after receiving Alice’s preparation bases, Bob does know the distribution of correlated and uncorrelated bits between k and , which is recorded in the string x ( if , otherwise ). Note that until step 7 of the protocol all computation is independent of the input bits . Furthermore, from step 8, only the strings , and x are needed to finish the protocol (in addition to the input bits). We call these three strings collectively an oblivious key, depicted in Figure 3. Formally, let Alice and Bob be two agents. Oblivious Key Distribution (OKD) is a service that outputs to Alice the string and to Bob the string together with the bit string , such that whenever and does not give any information about k whenever . All of the strings are chosen at random for every invocation of the service. A pair distributed as above is what we call an oblivious key pair. Alice, who knows k, is referred to as the sender, and Bob, who holds and x, is the receiver. In other words, when two parties share an oblivious key, the sender holds a string k, while the receiver has only approximately half of the bits of k, but knows exactly which of those bits he has.
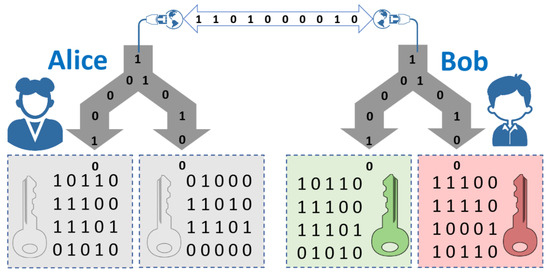
Figure 3.
Oblivious keys. Alice has the string k and Bob the string . For each party, the boxes in the left and right represent the bits of their string associated to the indices i for which equals 0 (left box) or 1 (right box). Alice knows the entire key, Bob only knows half of the key, but Alice does not know which half Bob knows.
When two parties have previously shared an oblivious key pair, they can securely produce OT by performing the steps of . This is significantly faster than current implementations of OT without any previous shared resource and does not require quantum communication during SMC. Note that the agents can perform, previously or concurrently, an OKD protocol to share a sufficiently large oblivious key, which can be then partitioned and used to perform as many instances of OT as needed for SMC.
Fortunately, it is possible to achieve fast oblivious key exchange if the parties have access to fast and reliable quantum communications and classical commitments. In order to use this QOT protocol, the commitment scheme must be instantiated. Consider the commitment protocol shown in Figure 4, first introduced by Halevi and Micali. It uses a combination of universal and cryptographic hashing, the former to ensure statistical uniformity on the commitments, and the latter to hide the committed message. The motivation for the choice of this protocol for this task will become more apparent during the following sections as we discuss the security and efficiency characteristics of the composition of with , henceforth referred as the (for Hybrid Oblivious Key) protocol for OT.

Figure 4.
Commitment protocol based on collision resistant hash functions.
The existence of a reduction from OT to commitments, while proven within quantum cryptography through the protocol, is an open problem in classical cryptography. The existence of commitment schemes such as , which do not rely on asymmetric cryptography, provides a way to obtain OT in the quantum setting while circumventing the disadvantages of asymmetric cryptography.
3. Results and Discussion
3.1. Security
In this section, we analyse the security of the proposed composition of protocols. The main result is encapsulated in the following theorem.
Theorem 1.
The protocol is secure as long as the hash function is collision resistant. Moreover, if the hash function models a Random Oracle, a simple modification of the protocol can make it universally-composable secure.
Proof.
The security proof relies on several well-established results in cryptography. First, notice that the protocol is closely related to the standard Quantum OT protocol , which is proven statistically secure in Yao’s original paper [33] and later universally composable in the quantum composability framework [34]. The difference between the two is that uses ideal commitments, as opposed to the hash-based commitments in . We start by showing that the protocol is standalone secure. For this case, we only need to replace the ideal commitment of with a standalone secure commitment protocol, such as the Halevi and Micali [29], which is depicted in . Since the latter is secure whenever the hash function is collision resistant, we conclude that is secure whenever the hash function is collision resistant.
Finally, we provide the simple modification of that makes it universally-composable secure when the hash function models a Random Oracle. The modification is only required to improve upon the commitment protocol, as Yao’s protocol with ideal commitments is universally-composable [34]. Indeed, we need to consider universally composable commitment scheme instead of . This is achieved by the HMQ construction [35] which, given a standalone secure commitment scheme and a Random Oracle, outputs a universally-composable commitment scheme, which is perfectly hiding and computationally binding, that is, secure as far as collisions cannot be found. So we just need to replace with the output of the HMQ construction, when and H are given as inputs and H models a Random Oracle. ☐
Regarding the above theorem we note that, for the composable security, the HMQ construction mentioned in the proof formally requires access to a random oracle, which is an abstract object used for studying security and cannot be realized in the real world. Hence, we leave it as an additional security property, as hash functions are traditionally modelled as random oracles. Stand alone security of the protocol does not require the hash function to be a random oracle.
The use of collision resistant hash functions is acceptable in the quantum setting, as it has been shown that there exist functions for which a quantum computer does not have any significant advantage in finding collisions when compared with a classical one [36]. One point to note about the security of is that it is not susceptible to intercept now-decrypt later style of attacks. Bob can attempt an attack in which he does not properly measure the qubits sent by Alice at step 2, and instead waits until Alice reveals the test subset in step 4 to measure honestly only those qubits. For that he must be able to control the openings of the commitment scheme such that Alice opens the values of his measurement outcomes for those qubits. In order to do this, he must be able find collisions for H before step 5. This means that attacking the protocol by finding collisions of the hash function is only effective if it is done in real time, that is, between steps 3 and 5 of the protocol. This is in contrast to asymmetric cryptography based OT, in which Bob can obtain both bits if he is able to overcome the computational security at a later stage.
Finally, we point out that the OT extension algorithms that are used during SMC often rely only on collision resistant hash functions [37] anyway. If those protocols are used to extend the base OTs produced by , we can effectively speed up the OT rates without introducing any additional computational complexity assumption.
3.2. Efficiency
Complexity-wise, the main problem with public-key based OT protocols is that they require a public/private key generation, encryption, and decryption per transfer. In the case of RSA and ElGamal based algorithms, this has complexity (where is the size of the group), using Karatsuba multiplication and Berett reduction for Euclidian division [38]. Post-quantum protocols are still ongoing optimization, but recent results show RLWE key genereration and encryption in time [39].
To study the time complexity of the protocol, consider first the complexity of . It requires two calls of H and one call of the universal hash family F, bit comparisons (if using the technique proposed in [29] to find the required f), and one additional evaluation of f. Cryptographic hash functions are designed so that their time complexity is linear on the size of the input, which in this case is . To compute the universal hashing, the construction in [29] requires binary multiplications. Thus, the running time of is linear on the security parameter k. On the other hand, has two security parameters: n, associated to the size of the keys used to encrypt the transferred bits, and m, associated to the security of the measurement test done by Alice. The protocol requires qubit preparations and measurements, calls of the commitment scheme, and n bit comparisons. This leads to an overall time complexity of for the protocol, which is linear in all of its security parameters.
In realistic scenarios, however, error correction and privacy amplification must be implemented during the . For the former, LDPC codes [40] or the cascade algorithm [41] can be used, and the latter can be done with universal hashing. For a given channel error parameter, these algorithms have time complexity linear in the size of the input string, which in our case is n. Hence, stays efficient when considering channel losses and preparation/measurement errors.
One of the major bottlenecks in the GMW protocol for SMC is the number of instances of OT required (it is worth noting that GMW uses 1-out-of-4 OT, which can efficiently be obtained from two instances of the 1-out-of-2 OT presented here [42]). A single Advanced Encryption Standard (AES) circuit can be obtained with the order of instances of OT. However, with current solutions, i.e., with computational implementations of OT based on asymmetric classical cryptography, one can generate secure OTs per second in standard devices [43]. It is possible to use OT extension algorithms to increase its size up to rates of the order of OT per second [3]. Several of such techniques are based on symmetric cryptography primitives [43], such as hash functions, and could also be used to extend the OTs generated by .
Due to the popularity of crypto-currencies, fast and efficient hashing machines have recently become more accessible. Dedicated hashing devices are able to compute SHA-256 at rates of hashes per second (see Bitfury, Ebit, and WhatsMiner, for example). In addition, existent standard Quantum Key Distribution (QKD) setups can be adapted to implement OKD, since both protocols share the same requirements for the generation and measurement of photons. Notably, QKD setups have already demonstrated secret key rates of the order of bits per second [44,45,46,47,48]. It is also worth mentioning that, as opposed to QKD, OKD is useful even in the case when Alice and Bob are at the same location. This is because in standard key distribution the parties trust each other and, if at the same location, they can just exchange hard drives with the shared key, whereas when sharing oblivious keys, the parties do not trust each other and need a protocol that enforces security. Thus, for the cases in which both parties being at the same location is not an inconvenience, the oblivious key rates can be further raised, as the effects of channel noise are minimized.
Direct comparisons of OT generation speed between asymmetric cryptography techniques and quantum techniques are difficult because the algorithms run on different hardware. Nevertheless, as quantum technologies keep improving, the size and cost of devices capable of implementing quantum protocols will decrease and their use can result in significant improvements of OT efficiency, in the short-to-medium term future.
4. Conclusions
Motivated by the usefulness of SMC as a privacy-protecting data mining tool, and identifying its OT cost as its main implementation challenge, we have proposed a potential solution for practical implementation of OT as a subroutine SMC. The scheme consists on pre-sharing an oblivious key pair and then using it to compute fast OT during the execution of the SMC protocol. We call this approach hybrid because it uses resources traditionally associated with classical symmetric cryptography (cryptographic hash functions), as well as quantum state communication and measurements on conjugate observables, resources associated with quantum cryptography. The scheme is secure as far as the chosen hash function is secure against quantum attacks. In addition, we showed that the overall time complexity of is linear on all its security parameters, as opposed to the public-key based alternatives, whose time complexities are at least quadratic on their respective parameters. Finally, by comparing the state of current technology with the protocol requirements, we concluded that it has the potential to surpass current asymmetric cryptography based techniques.
It was also noted that current experimental implementations of standard discrete-variable QKD can be adapted to perform . The same post-processing techniques of error correction and privacy amplification apply, however, fast hashing subroutines should be added for commitments during the parameter estimation step. Future work includes designing an experimental setup, meeting the implementation challenges, and experimentally testing the speed, correctness, and security of the resulting oblivious key pairs. This includes computing oblivious key rate bounds for realistic scenarios and comparing them with current alternative technologies. Real world key rate comparisons can help us understand better the position of quantum technologies in the modern cryptographic landscape.
Regarding the use of quantum cryptography during the commitment phase; because of the impossibility theorem for unconditionally secure commitments in the quantum setting [17], one must always work with an additional assumption on top of needing quantum resources. The noisy storage model provides an example in which the commitments are achieved by noisy quantum memories [21,22,49]. The drawback of this particular assumption is the fact that advances in quantum storage technology work against the performance of the protocol, which is not a desired feature. The added cost of using quantum communication is a disadvantage. So far, to the knowledge of the authors, there are no additional practical quantum bit commitment protocols that provide advantages in security or efficiency compared to classical ones once additional assumptions (such as random oracles, common reference strings, computational hardness, etc.,) are introduced. Nevertheless, we are optimistic that such protocols can be found in the future, perhaps by clever design, or by considering a different a kind of assumption outside of the standard ones.
Author Contributions
Conceptualization, P.M. and A.N.P.; methodology, M.F.R., N.A.S. and N.J.M.; validation, M.L., N.P., and A.S.; formal analysis, M.L., P.Y., N.P., A.S. and P.M.; investigation, M.L., M.F.R., N.A.S. and N.J.M.; writing—original draft preparation, M.L., N.P., P.Y., M.F.R., N.A.S., N.J.M. and A.N.P.; writing—review and editing, M.L. and P.M.; visualization, M.F.R., N.A.S., N.J.M. and A.N.P.; supervision, P.M. and A.N.P.; project administration, P.M., A.S. and A.N.P.; funding acquisition, P.M., A.S. and A.N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Fundação para a Ciência e a Tecnologia (FCT) through national funds, by FEDER, COMPETE 2020, and by Regional Operational Program of Lisbon, under UIDB/50008/2020, UIDP/50008/2020, UID/CEC/00408/2013, POCI-01-0145-FEDER-031826, POCI-01-0247-FEDER-039728, PTDC/CCI-CIF/29877/2017, PD/BD/114334/2016, PD/BD/113648/2015, and CEECIND/04594/2017/CP1393/CT0006A.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lindell, Y.; Pinkas, B. Secure Multiparty Computation for Privacy-Preserving Data Mining. J. Priv. Confid. 2009, 59–98. [Google Scholar] [CrossRef]
- Laud, P.; Kamm, L. Applications of Secure Multiparty Computation; IOS Press: Amsterdam, The Netherlands, 2015; Volume 13. [Google Scholar]
- Asharov, G.; Lindell, Y.; Schneider, T.; Zohner, M. More Efficient Oblivious Transfer Extensions. J. Cryptol. 2017, 30, 805–858. [Google Scholar] [CrossRef]
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188. [Google Scholar] [CrossRef] [PubMed]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar] [CrossRef]
- Goldreich, O.; Micali, S.; Wigderson, A. How to Play ANY Mental Game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, New York, NY, USA, 25–27 May 1987; ACM: New York, NY, USA, 1987; pp. 218–229. [Google Scholar] [CrossRef]
- Schneider, T.; Zohner, M. GMW vs. Yao? Efficient Secure Two-Party Computation with Low Depth Circuits. In Financial Cryptography and Data Security, Proceedings of the 17th International Conference, FC 2013, Okinawa, Japan, 1–5 April 2013; Revised Selected Papers; Sadeghi, A.R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 275–292. [Google Scholar]
- Beaver, D.; Micali, S.; Rogaway, P. The round complexity of secure protocols. In Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 14–16 May 1990; pp. 503–513. [Google Scholar]
- Kilian, J. Founding Cryptography on Oblivious Transfer. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; ACM: New York, NY, USA, 1988; pp. 20–31. [Google Scholar]
- Harnik, D.; Ishai, Y.; Kushilevitz, E. How many oblivious transfers are needed for secure multiparty computation? In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2007; pp. 284–302. [Google Scholar]
- Rabin, M.O. How To Exchange Secrets; Technical Report TR-81; Aiken Computation Laboratory, Harvad University: Cambridge, MA, USA, 1981. [Google Scholar]
- Goldreich, O. Foundations of Cryptography, Volume I Basic Techniques; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Paar, C.; Pelzl, J. Understanding Cryptography; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Broadbent, A.; Schaffner, C. Quantum cryptography beyond quantum key distribution. Des. Codes Cryptogr. 2016, 78, 351–382. [Google Scholar] [CrossRef]
- Shenoy-Hejamadi, A.; Pathak, A.; Radhakrishna, S. Quantum cryptography: Key distribution and beyond. Quanta 2017, 6, 1–47. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Is Quantum Bit Commitment Really Possible? Phys. Rev. Lett. 1997, 78, 3410–3413. [Google Scholar] [CrossRef]
- Mayers, D. Unconditionally Secure Quantum Bit Commitment is Impossible. Phys. Rev. Lett. 1997, 78, 3414–3417. [Google Scholar] [CrossRef]
- Wehner, S.; Schaffner, C.; Terhal, B.M. Cryptography from Noisy Storage. Phys. Rev. Lett. 2008, 100, 220502. [Google Scholar] [CrossRef]
- Wehner, S.; Curty, M.; Schaffner, C.; Lo, H.K. Implementation of two-party protocols in the noisy-storage model. Phys. Rev. A 2010, 81, 052336. [Google Scholar] [CrossRef]
- Konig, R.; Wehner, S.; Wullschleger, J. Unconditional Security From Noisy Quantum Storage. IEEE Trans. Inf. Theory 2012, 58, 1962–1984. [Google Scholar] [CrossRef]
- Loura, R.; Almeida, Á.J.; André, P.; Pinto, A.; Mateus, P.; Paunković, N. Noise and measurement errors in a practical two-state quantum bit commitment protocol. Phys. Rev. A 2014, 89, 052336. [Google Scholar] [CrossRef]
- Almeida, Á.J.; Stojanovic, A.D.; Paunković, N.; Loura, R.; Muga, N.J.; Silva, N.A.; Mateus, P.; André, P.S.; Pinto, A.N. Implementation of a two-state quantum bit commitment protocol in optical fibers. J. Opt. 2015, 18, 015202. [Google Scholar] [CrossRef]
- Erven, C.; Ng, N.; Gigov, N.; Laflamme, R.; Wehner, S.; Weihs, G. An experimental implementation of oblivious transfer in the noisy storage model. Nat. Commun. 2014, 5, 3418. [Google Scholar] [CrossRef] [PubMed]
- Furrer, F.; Gehring, T.; Schaffner, C.; Pacher, C.; Schnabel, R.; Wehner, S. Continuous-variable protocol for oblivious transfer in the noisy-storage model. Nat. Commun. 2018, 9, 1450. [Google Scholar] [CrossRef] [PubMed]
- Ng, N.H.Y.; Joshi, S.K.; Chen Ming, C.; Kurtsiefer, C.; Wehner, S. Experimental implementation of bit commitment in the noisy-storage model. Nat. Commun. 2012, 3, 1326. [Google Scholar] [CrossRef] [PubMed]
- Lunghi, T.; Kaniewski, J.; Bussières, F.; Houlmann, R.; Tomamichel, M.; Wehner, S.; Zbinden, H. Practical Relativistic Bit Commitment. Phys. Rev. Lett. 2015, 115, 030502. [Google Scholar] [CrossRef] [PubMed]
- Verbanis, E.; Martin, A.; Houlmann, R.; Boso, G.; Bussières, F.; Zbinden, H. 24-Hour Relativistic Bit Commitment. Phys. Rev. Lett. 2016, 117, 140506. [Google Scholar] [CrossRef]
- Pitalúa-García, D.; Kerenidis, I. Practical and unconditionally secure spacetime-constrained oblivious transfer. Phys. Rev. A 2018, 98, 032327. [Google Scholar] [CrossRef]
- Halevi, S.; Micali, S. Practical and Provably-Secure Commitment Schemes from Collision-Free Hashing. In Advances in Cryptology—CRYPTO ’96, Proceedings of the 16th Annual International Cryptology Conference Santa Barbara, California, CA, USA, 18–22 August 1996; Koblitz, N., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 201–215. [Google Scholar]
- Pinto, A.N.; Ramos, M.F.; Silva, N.A.; Muga, N.J. Generation and Distribution of Oblivious Keys through Quantum Communications. In Proceedings of the 2018 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Ramos, M.F.; Silva, N.A.; Muga, N.J.; Pinto, A.N. Reversal operator to compensate polarization random drifts in quantum communications. Opt. Express 2020, 28, 5035–5049. [Google Scholar] [CrossRef]
- Lindell, Y.; Pinkas, B. An efficient protocol for secure two-party computation in the presence of malicious adversaries. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Barcelona, Spain, 20–24 May 2007; pp. 52–78. [Google Scholar]
- Yao, A.C.C. Security of Quantum Protocols Against Coherent Measurements. In Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, Las Vegas, NV, USA, 29 May–1 June 1995; ACM: New York, NY, USA, 1995; pp. 67–75. [Google Scholar]
- Unruh, D. Universally composable quantum multi-party computation. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, French Riviera, France, 30 May–3 June 2010; pp. 486–505. [Google Scholar]
- Hofheinz, D.; Müller-Quade, J. Universally Composable Commitments Using Random Oracles. In Theory of Cryptography; Naor, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 58–76. [Google Scholar]
- Aaronson, S.; Shi, Y. Quantum Lower Bounds for the Collision and the Element Distinctness Problems. J. ACM 2004, 51, 595–605. [Google Scholar] [CrossRef]
- Asharov, G.; Lindell, Y.; Schneider, T.; Zohner, M. More Efficient Oblivious Transfer and Extensions for Faster Secure Computation. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 4–8 November 2013; ACM: New York, NY, USA, 2013; pp. 535–548. [Google Scholar] [CrossRef]
- Menezes, A.J.; Katz, J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press, Inc.: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ding, J.; Xie, X.; Lin, X. A Simple Provably Secure Key Exchange Scheme Based on the Learning with Errors Problem. Iacr Cryptol. Eprint Arch. 2012, 2012, 688. [Google Scholar]
- Martinez-Mateo, J.; Elkouss, D.; Martin, V. Key reconciliation for high performance quantum key distribution. Sci. Rep. 2013, 3, 1576. [Google Scholar] [CrossRef] [PubMed]
- Brassard, G.; Salvail, L. Secret-key reconciliation by public discussion. In Workshop on the Theory and Application of of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1993; pp. 410–423. [Google Scholar]
- Naor, M.; Pinkas, B. Computationally secure oblivious transfer. J. Cryptol. 2005, 18, 1–35. [Google Scholar] [CrossRef]
- Chou, T.; Orlandi, C. The simplest protocol for oblivious transfer. In Proceedings of the International Conference on Cryptology and Information Security in Latin America, Guadalajara, Mexico, 23–26 August 2015; pp. 40–58. [Google Scholar]
- Comandar, L.; Fröhlich, B.; Lucamarini, M.; Patel, K.; Sharpe, A.; Dynes, J.; Yuan, Z.; Penty, R.; Shields, A. Room temperature single-photon detectors for high bit rate quantum key distribution. Appl. Phys. Lett. 2014, 104, 021101. [Google Scholar] [CrossRef]
- Islam, N.T.; Lim, C.C.W.; Cahall, C.; Kim, J.; Gauthier, D.J. Provably secure and high-rate quantum key distribution with time-bin qudits. Sci. Adv. 2017, 3, e1701491. [Google Scholar] [CrossRef]
- Ko, H.; Choi, B.S.; Choe, J.S.; Kim, K.J.; Kim, J.H.; Youn, C.J. High-speed and high-performance polarization-based quantum key distribution system without side channel effects caused by multiple lasers. Photonics Res. 2018, 6, 214–219. [Google Scholar] [CrossRef]
- Wang, T.; Huang, P.; Zhou, Y.; Liu, W.; Ma, H.; Wang, S.; Zeng, G. High key rate continuous-variable quantum key distribution with a real local oscillator. Opt. Express 2018, 26, 2794–2806. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in Quantum Cryptography. arXiv 2019, arXiv:1906.01645. [Google Scholar] [CrossRef]
- Loura, R.; Arsenović, D.; Paunković, N.; Popović, D.B.; Prvanović, S. Security of two-state and four-state practical quantum bit-commitment protocols. Phys. Rev. A 2016, 94, 062335. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).