Multi-Objective Optimization of Three Different SMA-LRBs for Seismic Protection of a Benchmark Highway Bridge against Real and Synthetic Ground Motions
Abstract
1. Introduction
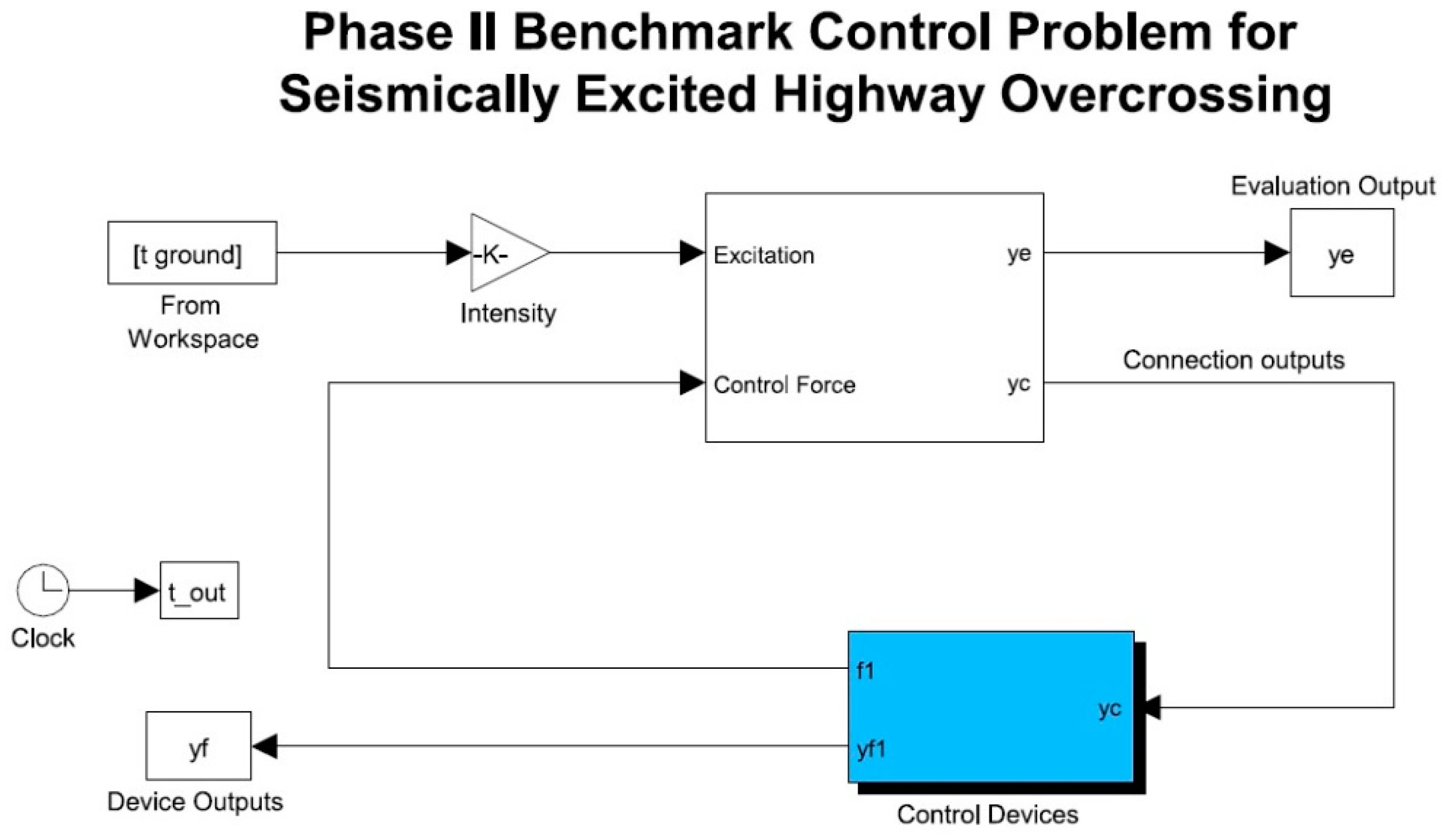
2. Benchmark Highway Bridge
2.1. Structural Model
2.2. Earthquake Excitations
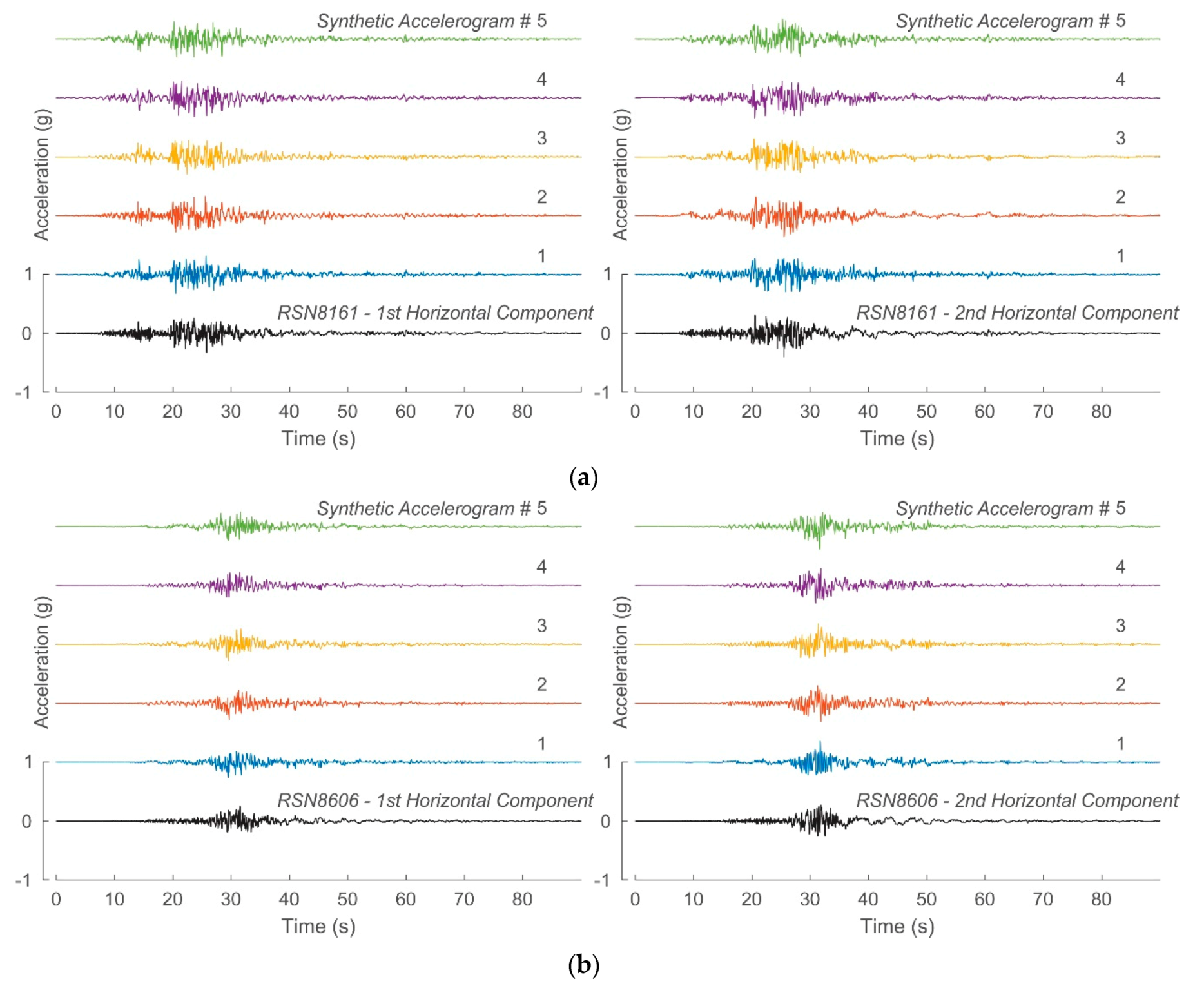
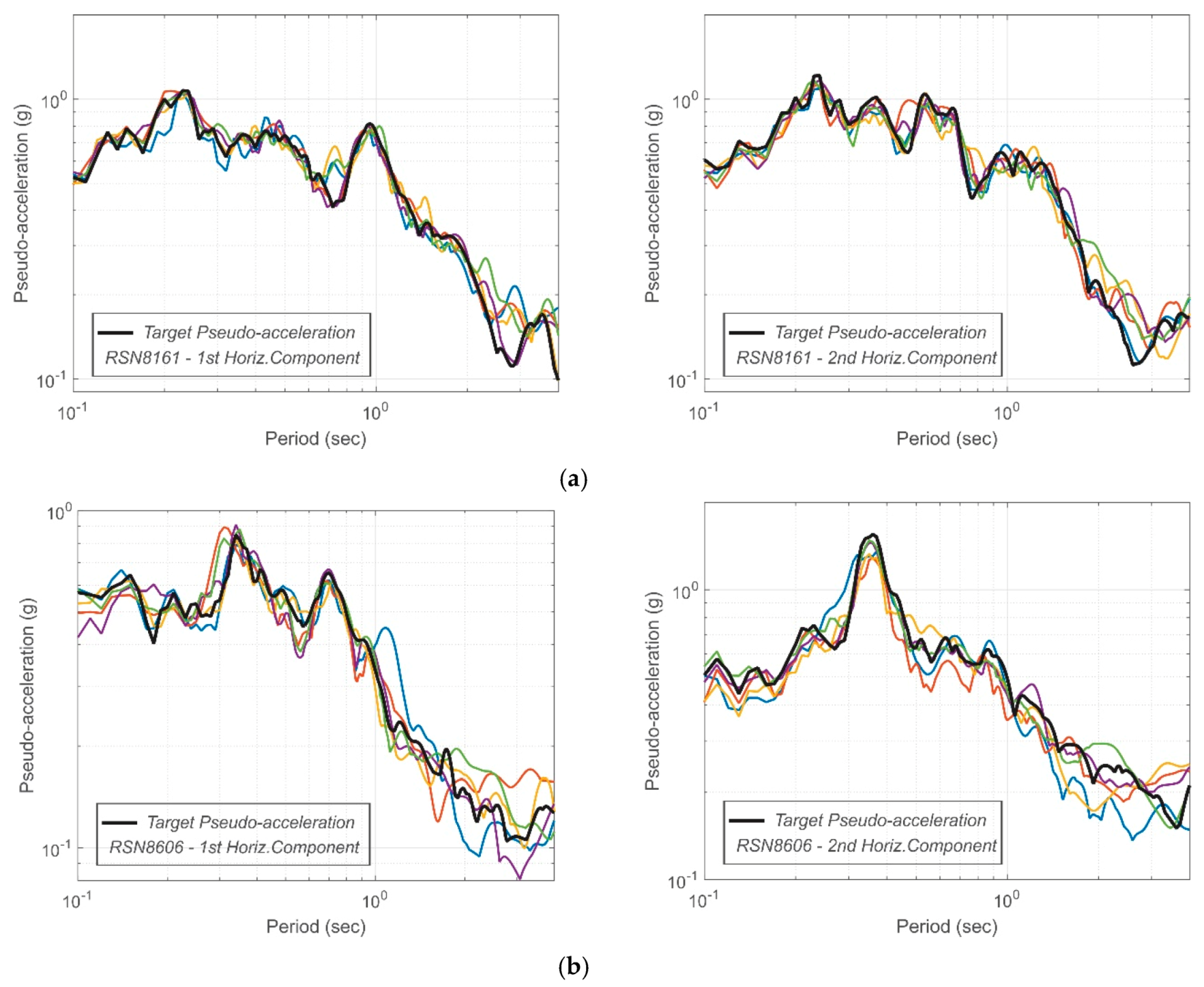
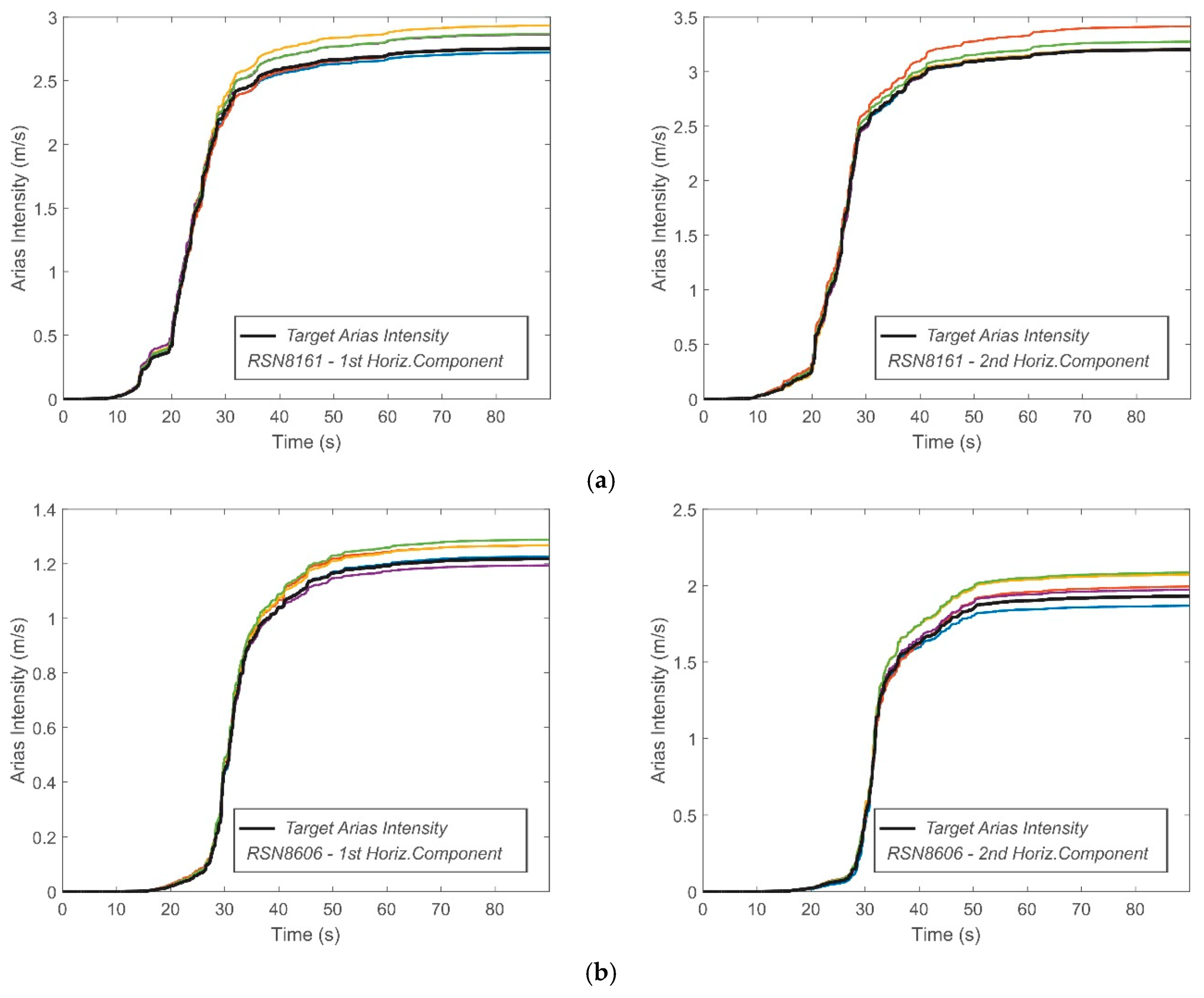
3. Ground Motion Time Histories
- Distance to the causative fault approximately the same as the distance of the bridge to the closest active seismic fault.
- Size of the earthquake equal to the probable maximum magnitude at the closest fault.
- Soil conditions and deeper geological surroundings of the recording station similar to those beneath the bridge.
4. The SMA-LRBs
4.1. The Hysteresis Model of the LRBs
4.2. The Hysteresis Model of SMA Wires
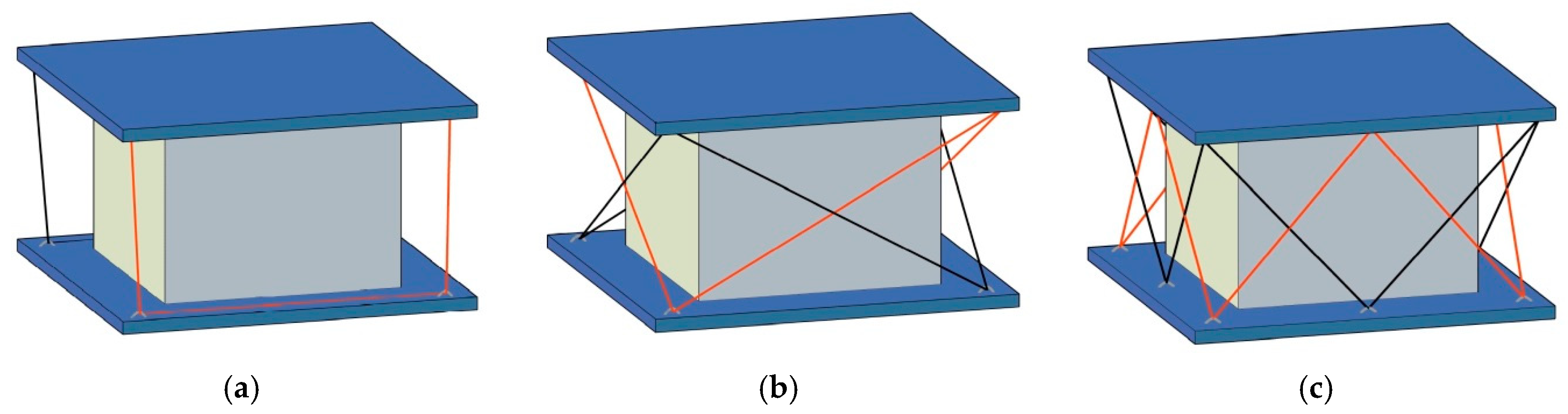
4.2.1. SMA-LRB with Double-Cross Wires
4.2.2. SMA-LRB with Straight Wires
4.2.3. SMA-LRB with Cross Wires
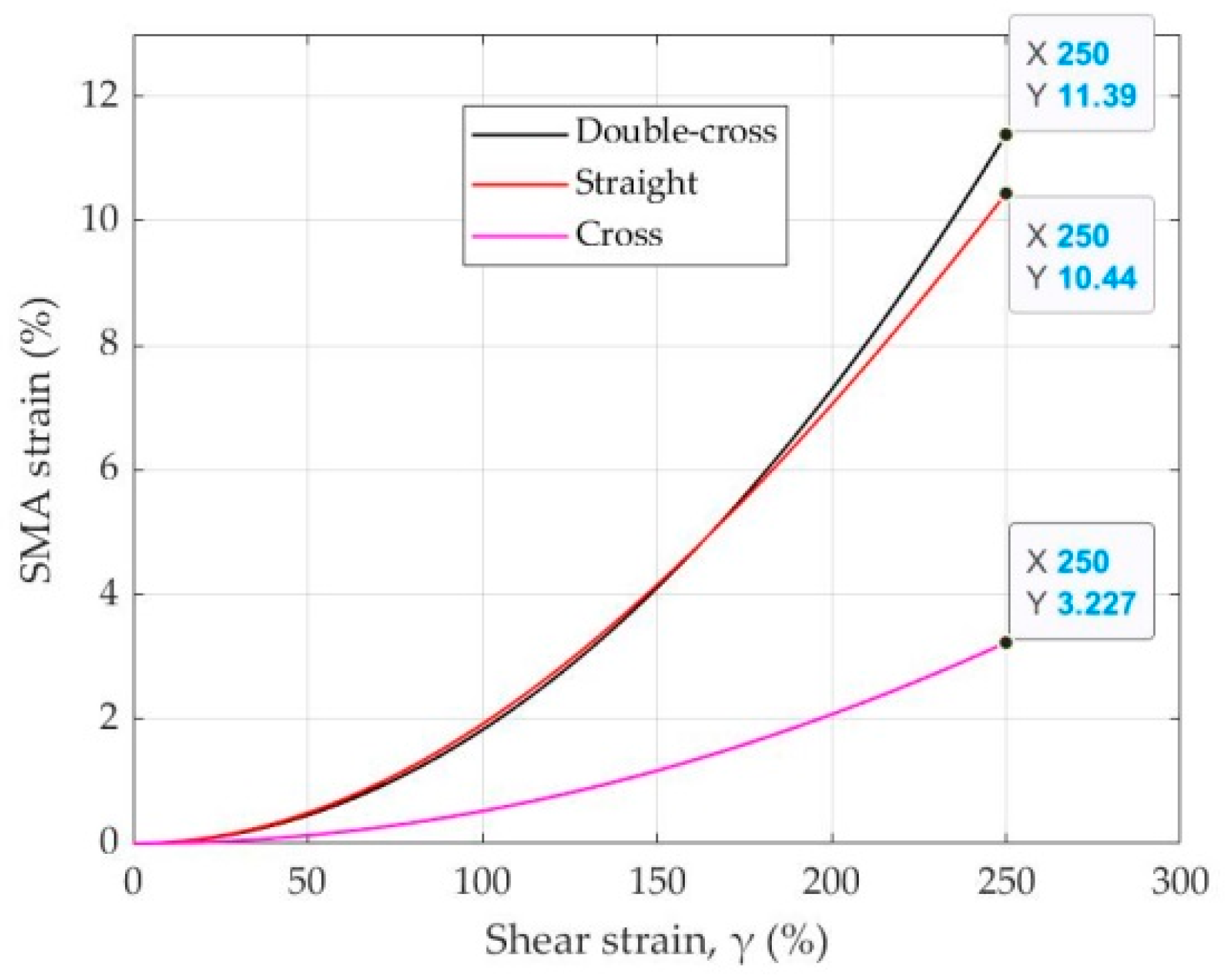
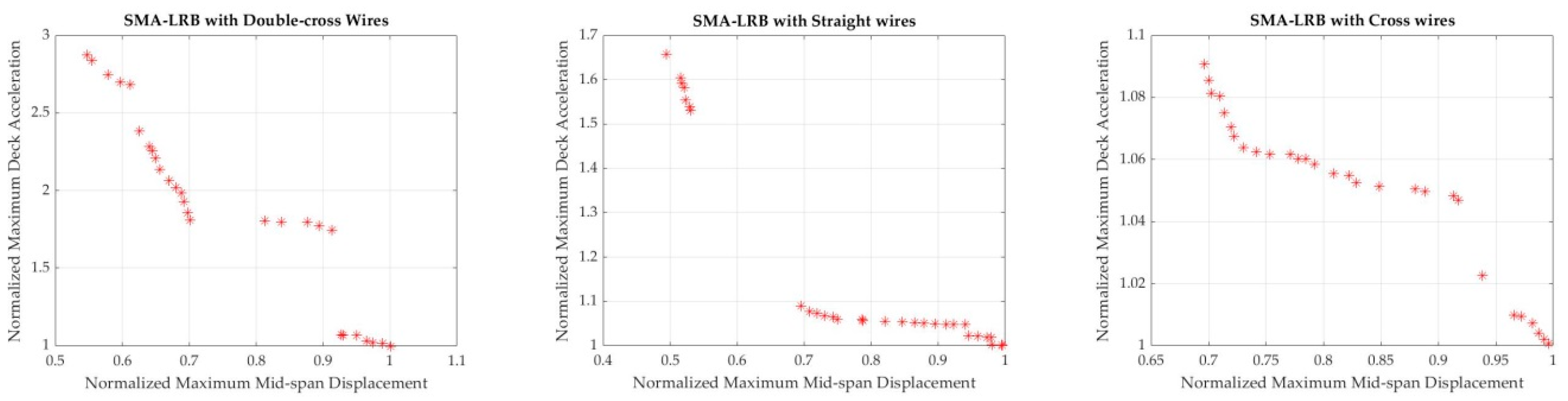
4.2.4. Efficiency of Different Wire Configurations
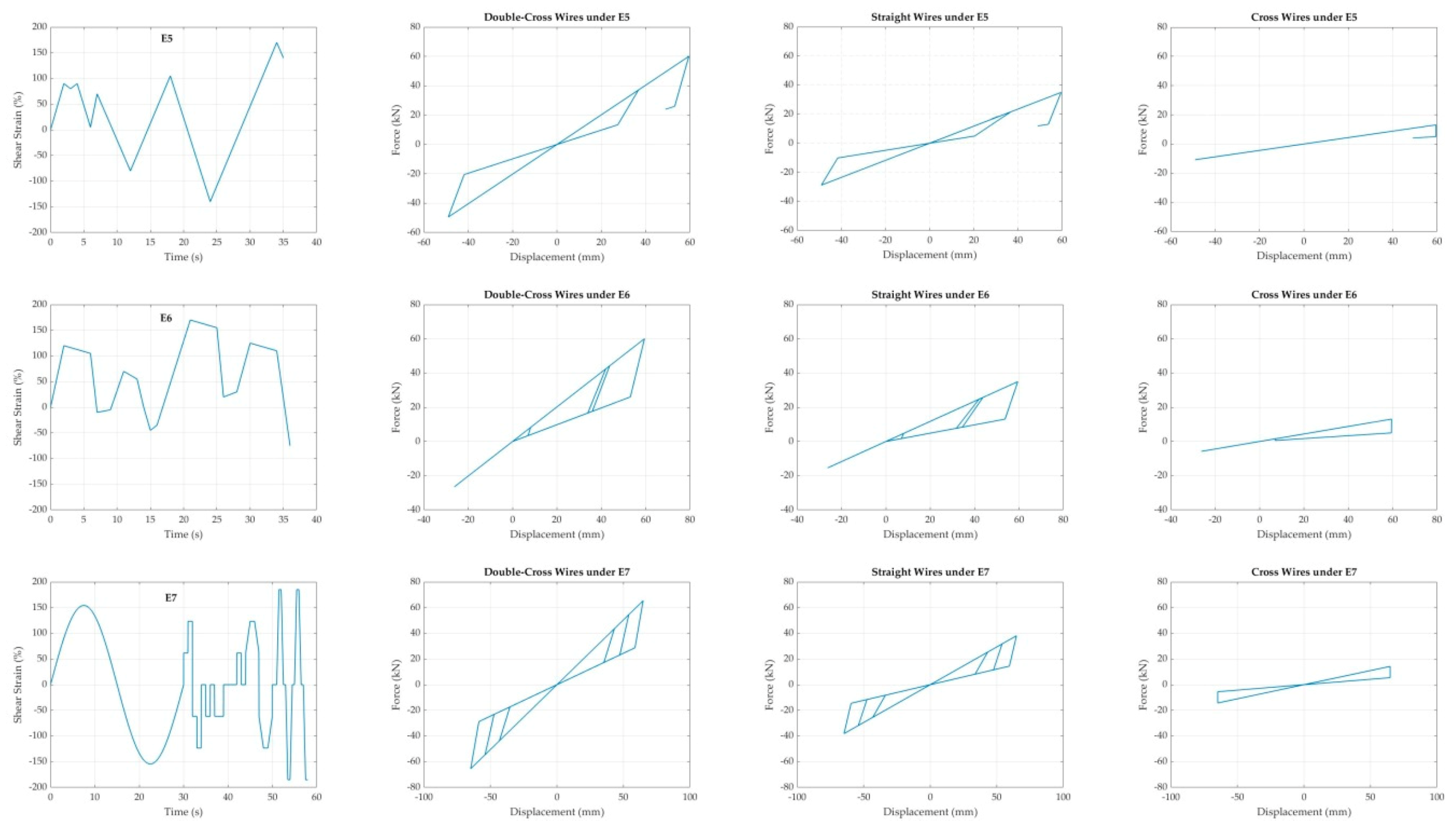
4.2.5. Force–Displacement Curves
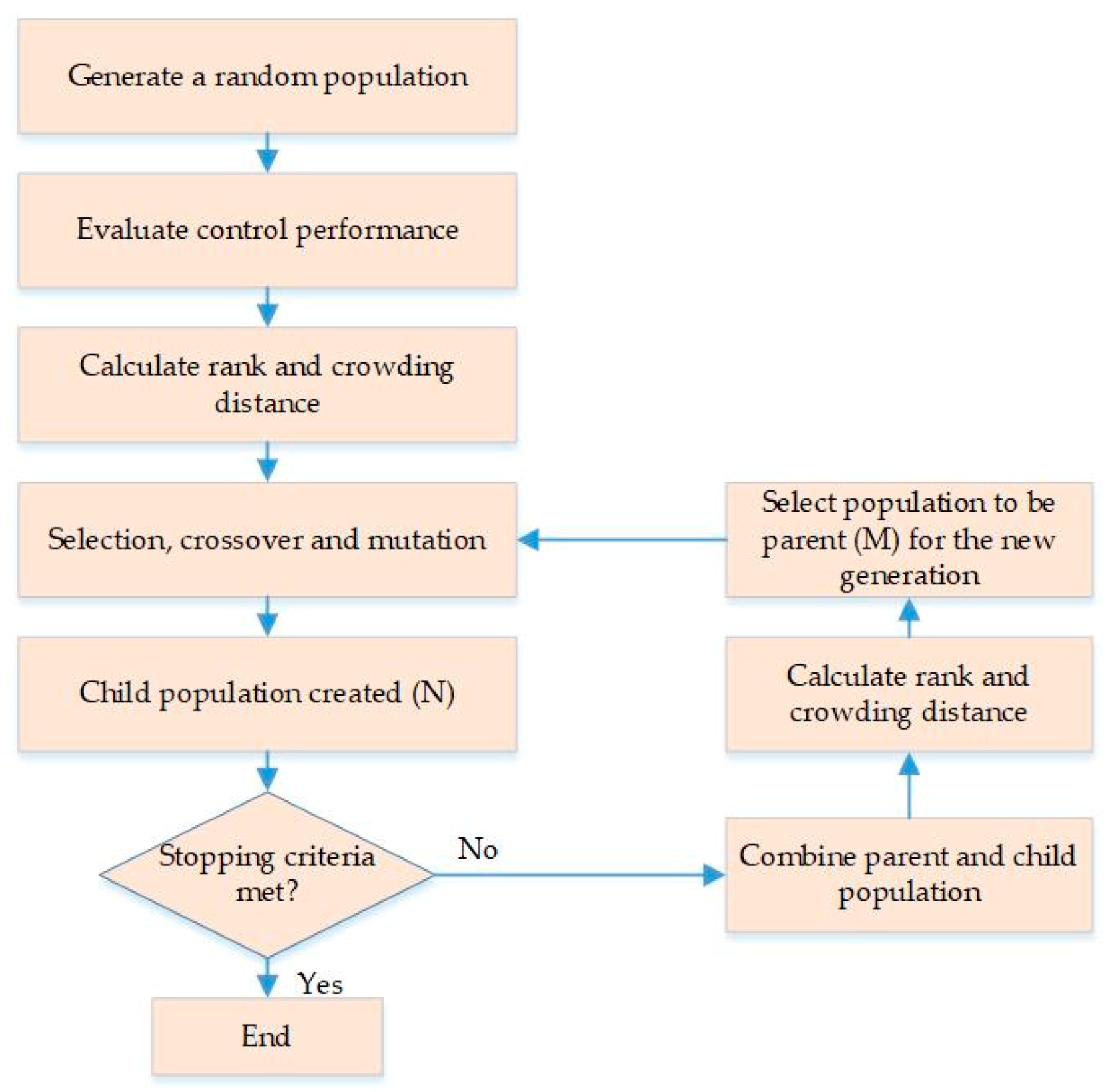
5. Optimizing the SMA-LRBs
6. Numerical Analysis
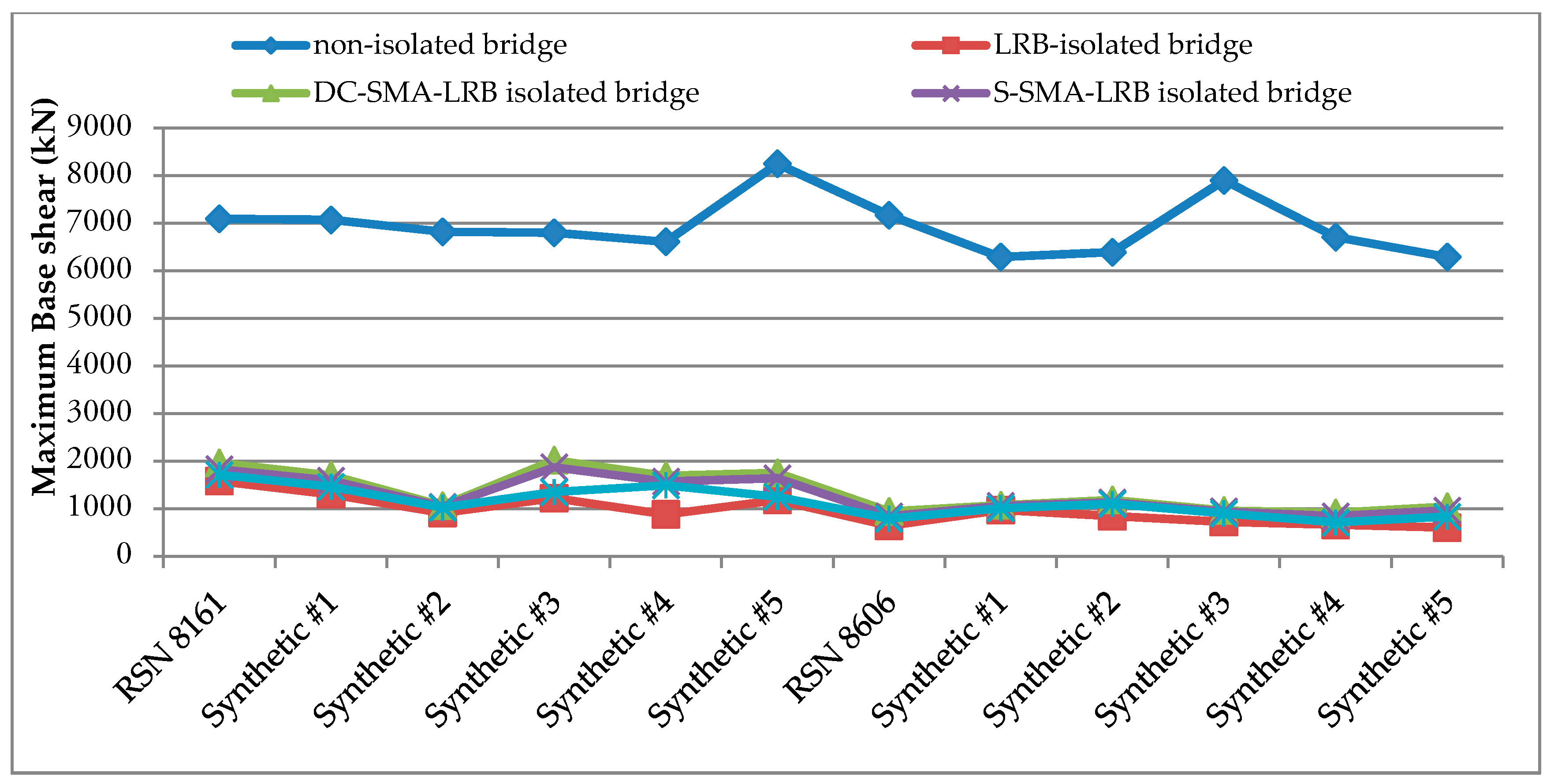
6.1. Base Shear
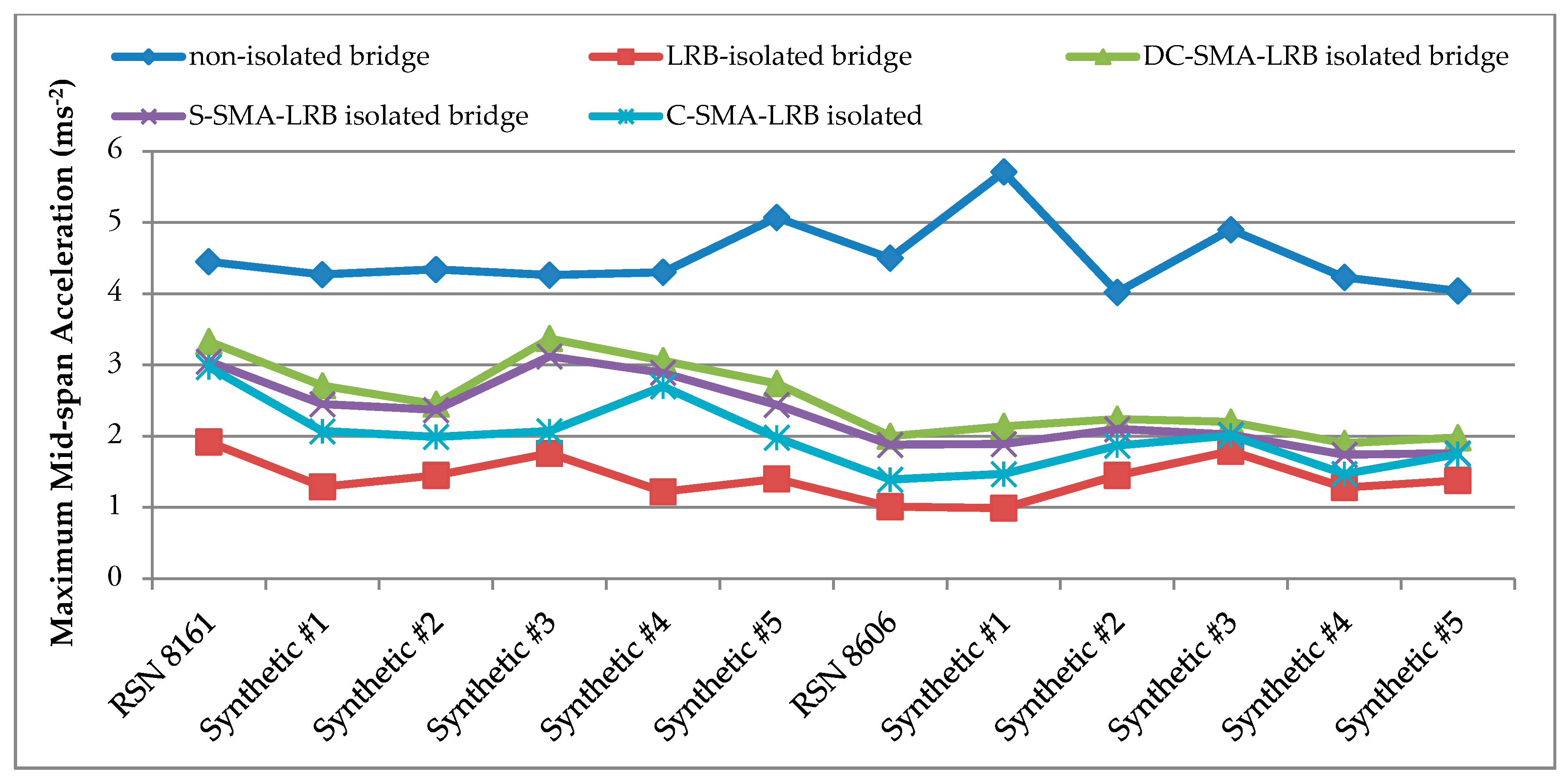
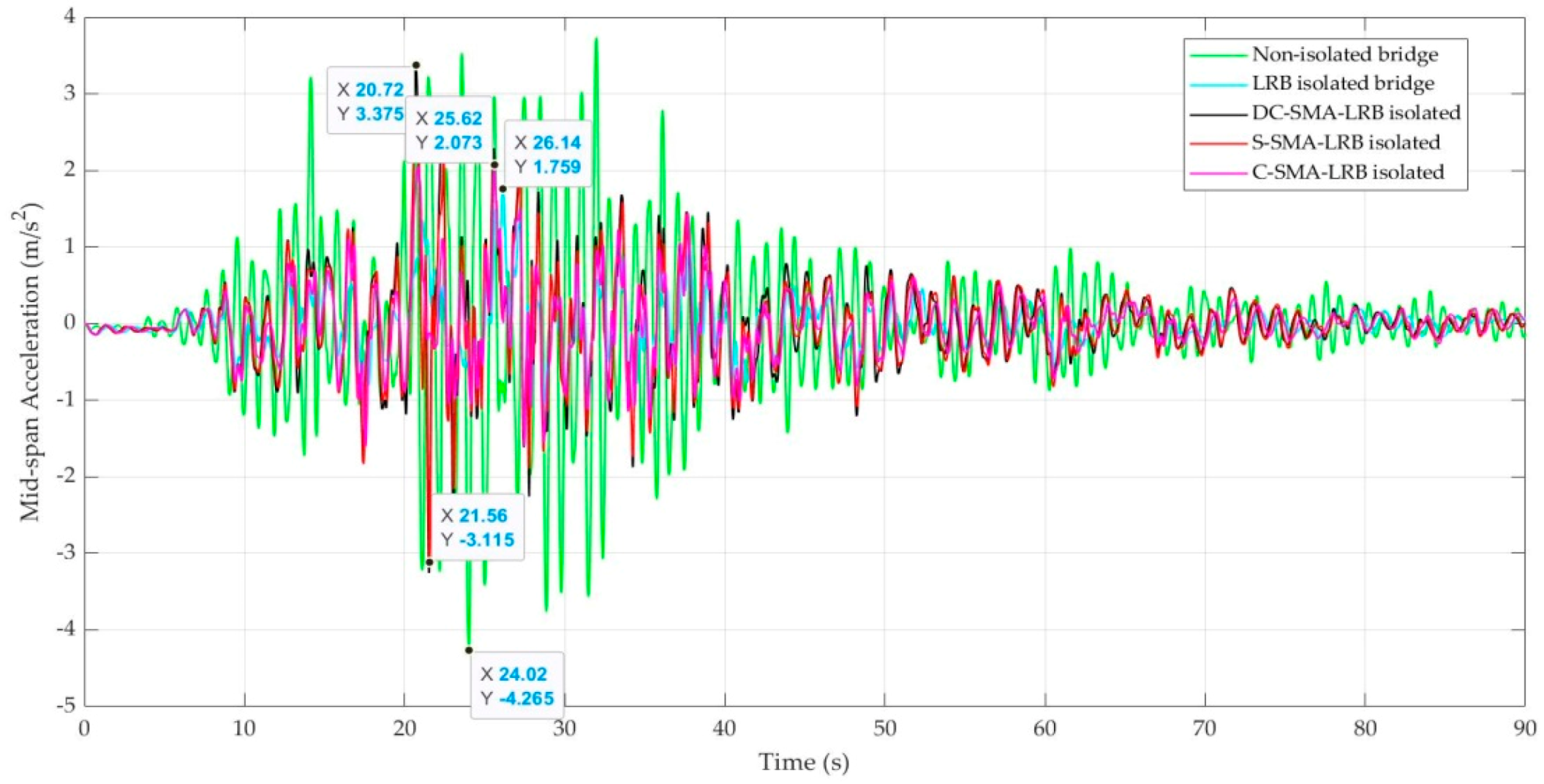
6.2. Mid-Span Acceleration
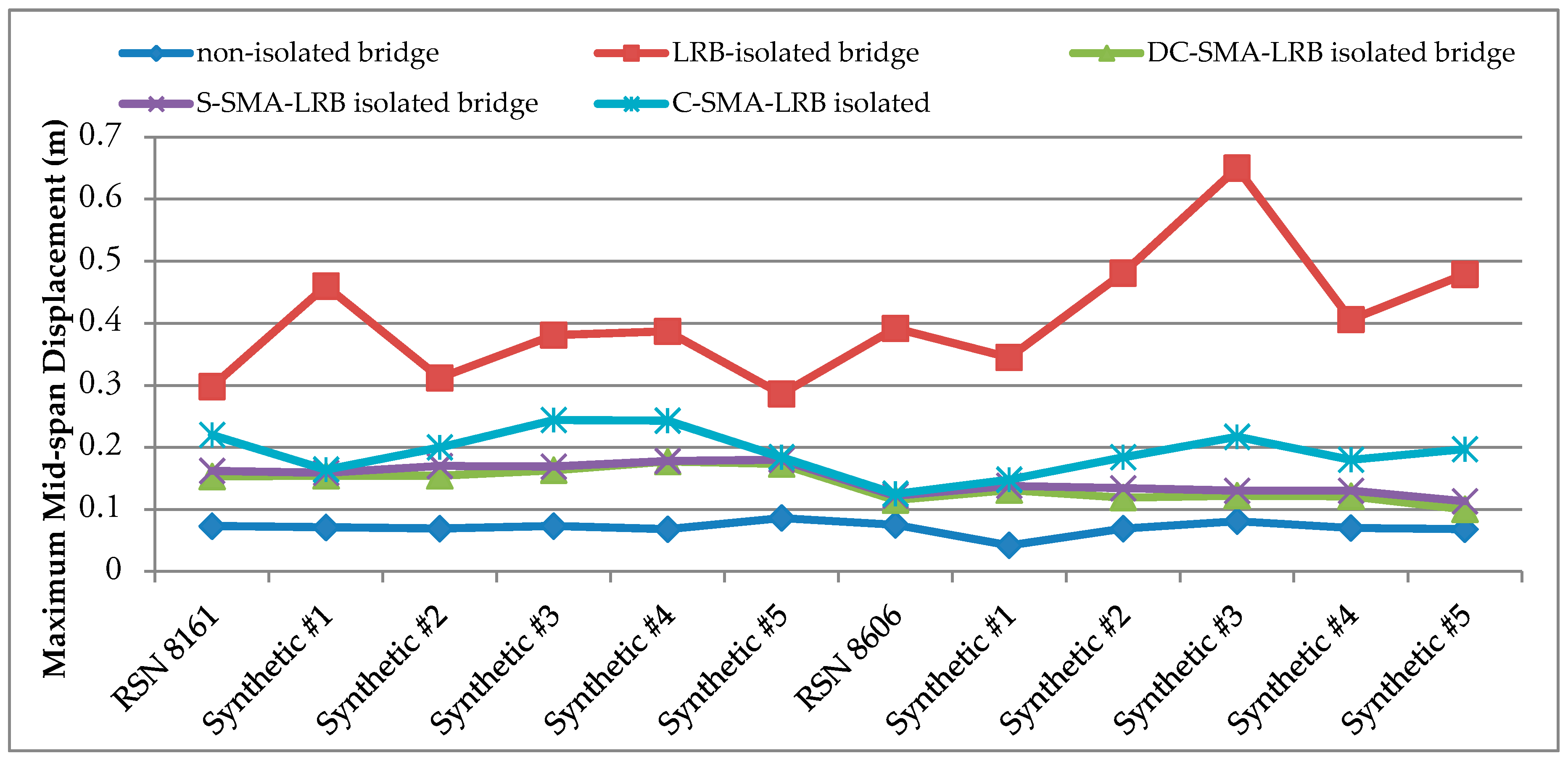
6.3. Mid-Span Displacement
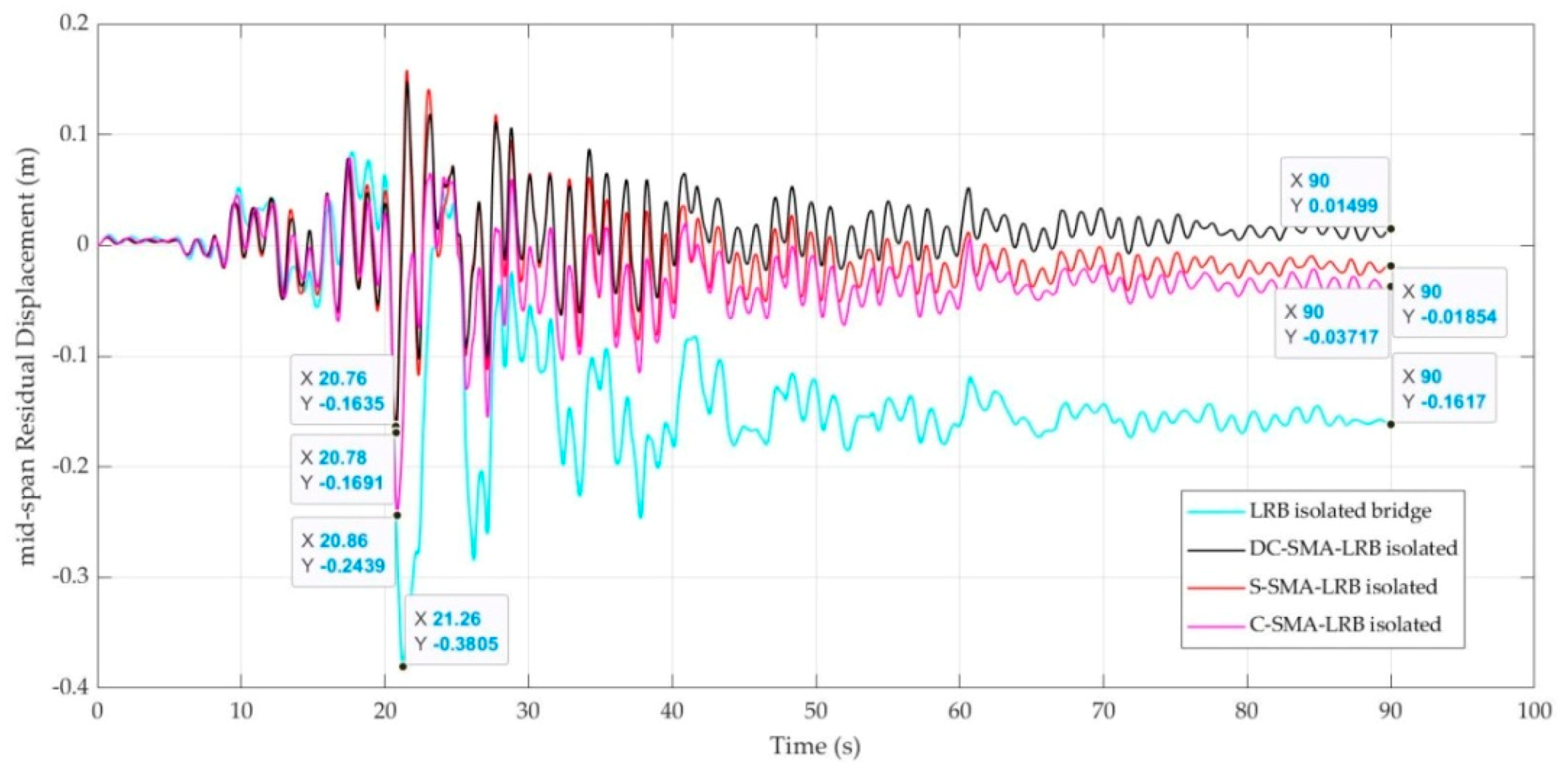
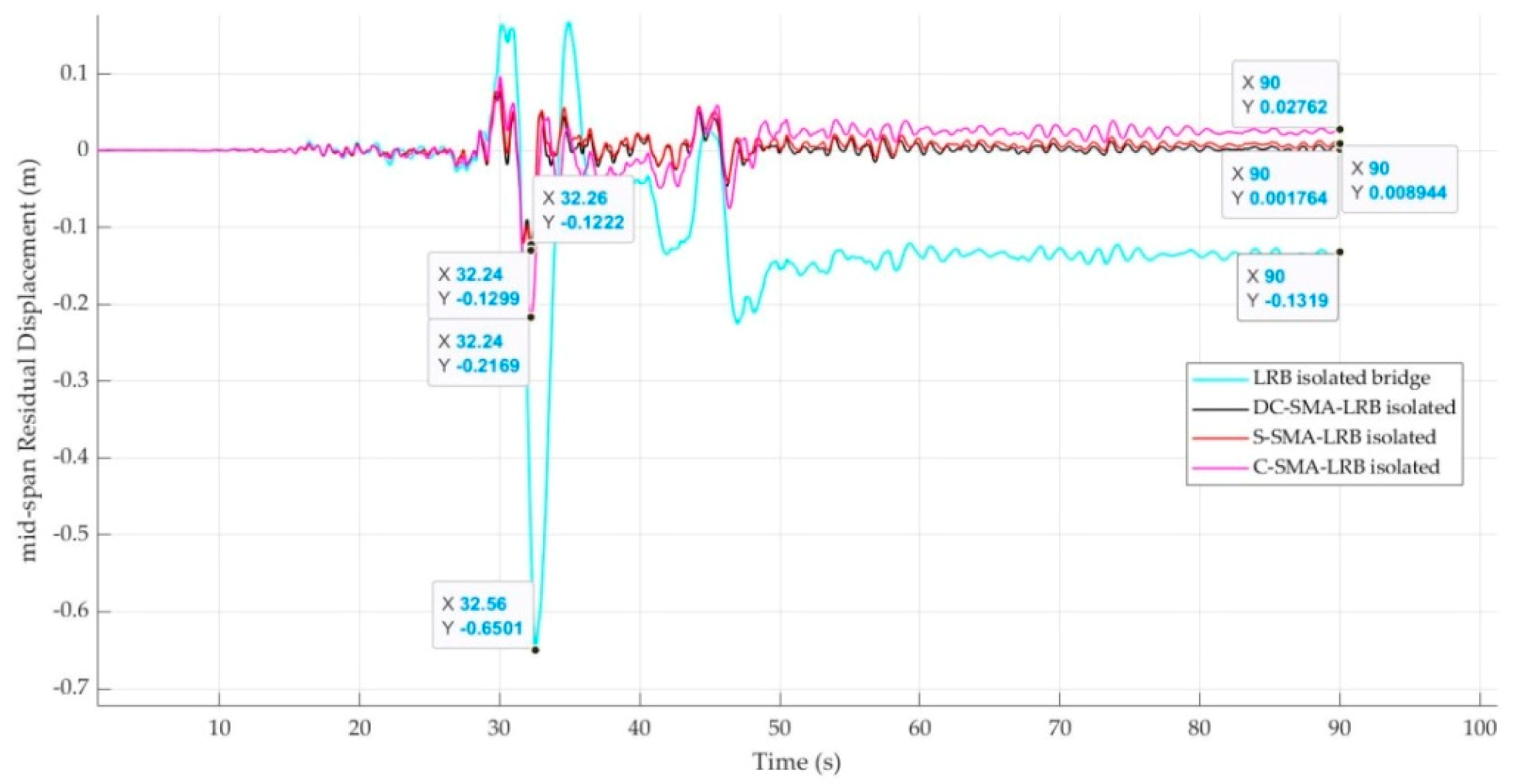
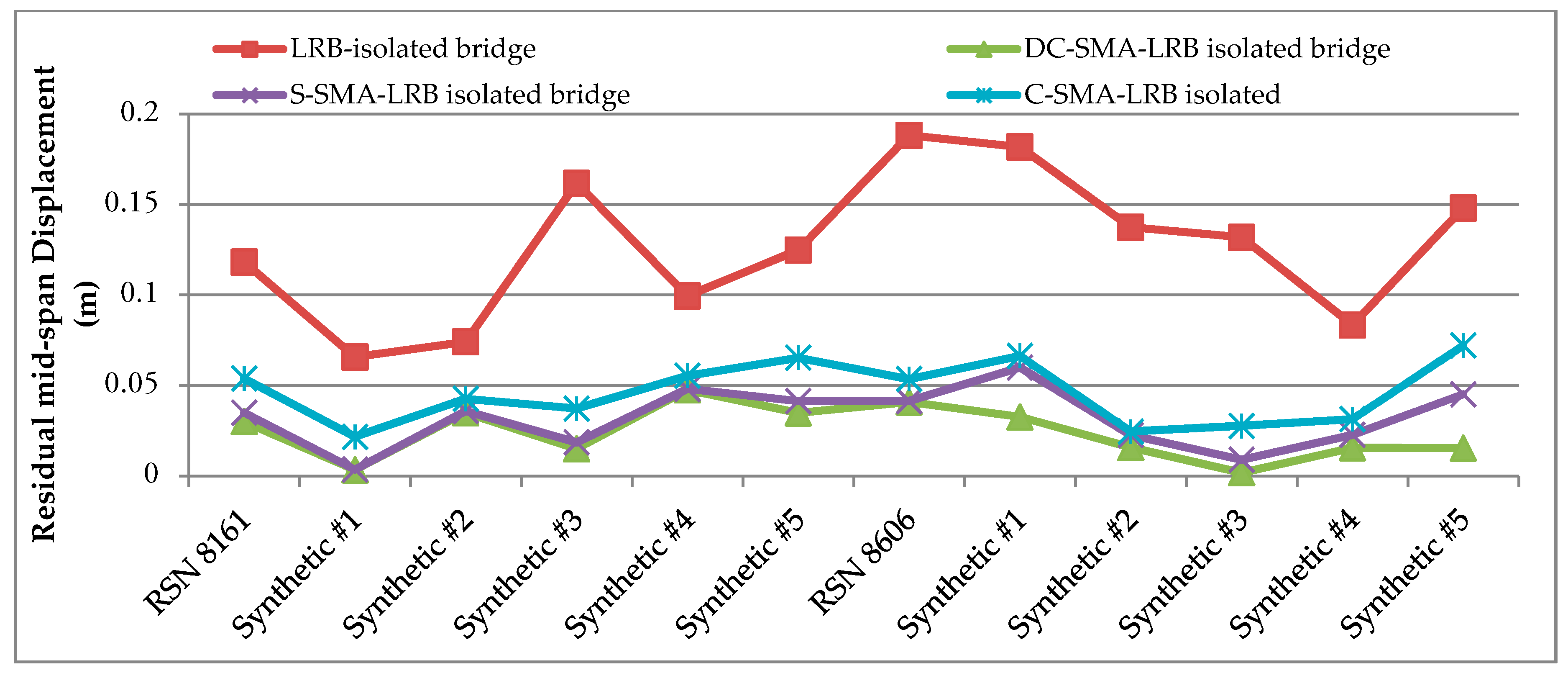
6.4. Residual Mid-Span Displacement
6.5. Comparing the Three SMA-LRBs
7. Conclusions
- As for the optimized double-cross SMA-LRB, this device decreases the maximum base shear and deck acceleration of the isolated bridge from 70.29% to 87.85% and from 20.89% to 62.57%, respectively, under various records compared with the non-isolated bridge. However, LRB still leads to the largest reduction in these figures, from 77.71% to 91.07%, and from 56.85% to 82.66% under various records. Moreover, SMA-LRBs with double-cross wires reduce the maximum mid-span and residual displacements in ranges between 39.51% and 81.23% and from 52.16% to 98.67%, in turn, under different ground motions compared with the LRB isolated bridge. In brief, amongst the three SMA-LRBs, it has the largest shear force and deck acceleration, and needs the longest SMA wire, but leads to the least maximum and residual displacements. Finally, the result of the WSM method indicates that DC-SMA-LRB is the second most successful device.
- Regarding the optimized straight SMA-LRB, it decreases the maximum base shear and deck acceleration of the isolated bridge slightly more than the double-cross SMA-LRBs, from 72.50% to 88.28% and from 26.76% to 66.90%, respectively, under different records, compared with the non-isolated benchmark bridge. Besides, SMA-LRBs with straight wires reduce the maximum and residual mid-span displacement slightly less than the DC-SMA-LRBs, from 37.06% to 80.00% and from 51.55% to 94.67%, in turn, under various excitations, compared with the LRBs. Moreover, the required length of the SMA wire is the least for this configuration. Lastly, the WSM method shows that S-SMA-LRB has the best overall performance.
- As regards the optimized cross SMA-LRB, it results in the reduction of the base shear and deck acceleration more than the other two SMA isolators, compared with the non-isolated bridge. However, it decreases the maximum and residual displacements less than the others and uses rather long SMA wires. Eventually, by conducting WSM, it is ranked as the least successful device.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buckle, I.G. The Northridge, California Earthquake on January 17, 1994: Performance of Highway Bridges; Tech. Rep. NCEER-94-0068; National Center for Earthquake Engineering Research, State University of New York at Buffalo: Buffalo, NY, USA, 1994. [Google Scholar]
- Kawashima, K.; Unjoh, S. The damage of highway bridges in the 1995 Hyogo-ken Nanbu earthquake and its impact on Japanese seismic design. J. Earthq. Eng. 1997, 1, 505–541. [Google Scholar] [CrossRef]
- Hsu, Y.T.; Fu, C.C. Seismic effect on highway bridges in Chi Chi earthquake. J. Perform. Constr. Facil. 2003, 17, 47–53. [Google Scholar] [CrossRef]
- Li, J.; Peng, T.; Xu, Y. Damage investigation of girder bridges under the Wenchuan earthquake and corresponding seismic design recommendations. Earthq. Eng. Eng. Vib. 2008, 7, 337–344. [Google Scholar] [CrossRef]
- Kawashima, K.; Unjoh, S.; Hoshikuma, J.I.; Kosa, K. Damage of bridges due to the 2010 Maule, Chile, earthquake. J. Earthq. Eng. 2011, 15, 1036–1068. [Google Scholar] [CrossRef]
- Buckle, I.; Yen, W.; Marsh, L.; Monzon, E. Implications of Bridge Performance during Great East Japan Earthquake for U.S. Seismic Design Practice. In Proceedings of the International Symposium on Engineering Lessons Learned from the 2011 Great East Japan Earthquake, Tokyo, Japan, 1–4 March 2012; pp. 1363–1374. [Google Scholar]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic response control using shape memory alloys: A review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Roy, B.K.; Chakraborty, S.; Mishra, S.K. Seismic vibration control of bridges with excessive isolator displacement. Earthq. Struct. 2016, 10, 1451–1465. [Google Scholar] [CrossRef]
- Rai, D.C. Future trends in earthquake-resistant design of structures. Curr. Sci. 2000, 79, 1291–1300. [Google Scholar]
- Shinozuka, M.; Chaudhuri, S.R.; Mishra, S.K. Shape-Memory-Alloy supplemented Lead Rubber Bearing (SMA-LRB) for seismic isolation. Probab. Eng. Mech. 2015, 41, 34–45. [Google Scholar] [CrossRef]
- Bhuiyan, A.R.; Alam, M.S. Seismic performance assessment of highway bridges equipped with superelastic shape memory alloy-based laminated rubber isolation bearing. Eng. Struct. 2013, 49, 396–407. [Google Scholar] [CrossRef]
- Paiva, A.; Savi, M.A. An overview of constitutive models for shape memory alloys. Math. Probl. Eng. 2006, 2006, 1–30. [Google Scholar] [CrossRef]
- Lagoudas, D.C. Shape Memory Alloys Modeling and Engineering Applications; Springer: Boston, MA, USA, 2008. [Google Scholar]
- Arghavani, J. Thermo-mechanical Behavior of Shape Memory Alloys under Multiaxial Loading: Constitutive Modeling and Numerical Implementation at Small and Finite Strains. Ph.D. Dissertation, Sharif University of Technology, Tehran, Iran, 2010. [Google Scholar]
- Ozbulut, O.E. Seismic Protection of Bridge Structures Using Shape Memory Alloy-based Isolation Systems against Near-field Earthquakes. Ph.D. Dissertation, Texas A&M University, College Station, TX, USA, 2010. [Google Scholar]
- Hedayati Dezfuli, F.; Alam, M.S. Shape memory alloy wire-based smart natural rubber bearing. Smart Mater. Struct. 2013, 22, 45013–45030. [Google Scholar] [CrossRef]
- Wilde, K.; Gardoni, P.; Fujino, Y. Base isolation system with shape memory alloy device for elevated highway bridges. Eng. Struct. 2000, 22, 222–229. [Google Scholar] [CrossRef]
- Choi, E.; Nam, T.; Cho, B.S. A new concept of isolation bearings for highway steel bridges using shape memory alloys. Can. J. Civ. Eng. 2005, 32, 957–967. [Google Scholar] [CrossRef]
- Andrawes, B.; DesRoches, R. Comparison between Shape Memory Alloy Seismic Restrainers and Other Bridge Retrofit Devices. J. Bridg. Eng. 2007, 12, 700–709. [Google Scholar] [CrossRef]
- Zhu, S.Y.; Qiu, C.X. Incremental Dynamic Analysis of Highway Bridges with Novel Shape Memory Alloy Isolators. Adv. Struct. Eng. 2014, 17, 429–438. [Google Scholar] [CrossRef]
- Hedayati Dezfuli, F.; Alam, M.S. Seismic vulnerability assessment of a steel-girder highway bridge equipped with different {SMA} wire-based smart elastomeric isolators. Smart Mater. Struct. 2016, 25, 75039–75055. [Google Scholar] [CrossRef]
- Xiang, N.; Alam, M.S. Comparative Seismic Fragility Assessment of an Existing Isolated Continuous Bridge Retrofitted with Different Energy Dissipation Devices. J. Bridg. Eng. 2019, 24, 04019070–04019087. [Google Scholar] [CrossRef]
- Hosseini, R.; Rashidi, M.; Hedayati Dezfuli, F.; Karbasi Arani, K.; Samali, B. Seismic Assessment of a Benchmark Highway Bridge Equipped with Optimized Shape Memory Alloy Wire-Based Isolators. Appl. Sci. 2019, 10, 141. [Google Scholar] [CrossRef]
- Hedayati Dezfuli, F.; Alam, M.S. Hysteresis model of shape memory alloy wire-based laminated rubber bearing under compression and unidirectional shear loadings. Smart Mater. Struct. 2015, 24, 065022–065041. [Google Scholar] [CrossRef]
- Hedayati Dezfuli, F.; Alam, M.S. Smart Lead Rubber Bearings Equipped with Ferrous Shape Memory Alloy Wires for Seismically Isolating Highway Bridges. J. Earthq. Eng. 2017, 22, 1042–1067. [Google Scholar] [CrossRef]
- Hedayati Dezfuli, F.; Alam, M.S. Performance-based assessment and design of FRP-based high damping rubber bearing incorporated with shape memory alloy wires. Eng. Struct. 2014, 61, 166–183. [Google Scholar] [CrossRef]
- Agrawal, A.; Tan, P.; Nagarajaiah, S.; Zhang, J. Benchmark structural control problem for a seismically excited highway bridge-Part I: Phase I Problem definition. Struct. Control Health Monit. 2009, 16, 509–529. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Narasimhan, S.; Agrawal, A.; Tan, P. Benchmark structural control problem for a seismically excited highway bridge-Part III: Phase II Sample controller for the fully base-isolated case. Struct. Control Health Monit. 2009, 16, 549–563. [Google Scholar] [CrossRef]
- Tan, P.; Agrawal, A.K. Benchmark structural control problem for a seismically excited highway bridge-part II: Phase I sample control designs. Struct. Control Health Monit. 2009, 16, 530–548. [Google Scholar] [CrossRef]
- Madhekar, S.N.; Jangid, R.S. Variable dampers for earthquake protection of benchmark highway bridges. Smart Mater. Struct. 2009, 18, 115011–115029. [Google Scholar] [CrossRef]
- Madhekar, S.N.; Jangid, R.S. Seismic performance of benchmark highway bridge installed with piezoelectric friction dampers. IES J. Part A Civ. Struct. Eng. 2011, 4, 191–212. [Google Scholar] [CrossRef]
- Madhekar, S.N. Seismic Performance of Benchmark Highway Bridge Installed with Passive Control Devices. Adv. Struct. Eng. 2015, 2, 1377–1390. [Google Scholar]
- Saha, A.; Saha, P.; Patro, S.K. Seismic response control of benchmark highway bridge using non-linear FV spring damper. IES J. Part A Civ. Struct. Eng. 2015, 8, 240–250. [Google Scholar] [CrossRef]
- Saha, A.; Saha, P.; Patro, S.K. Polynomial friction pendulum isolators (PFPIs) for seismic performance control of benchmark highway bridge. Earthq. Eng. Eng. Vib. 2017, 16, 827–840. [Google Scholar] [CrossRef]
- Saha, A.; Saha, P.; Patro, S.K. Seismic protection of the benchmark highway bridge with passive hybrid control system. Earthq. Struct. 2018, 15, 227–241. [Google Scholar]
- Zhang, Y.; Hu, X.; Zhu, S. Seismic performance of benchmark base-isolated bridges with superelastic Cu-Al-Be restraining damping device. Struct. Control Health Monit. 2009, 16, 668–685. [Google Scholar] [CrossRef]
- Casciati, F.; Faravelli, L.; Al Saleh, R. An SMA passive device proposed within the highway bridge benchmark. Struct. Control Health Monit. 2009, 16, 657–667. [Google Scholar] [CrossRef]
- Li, H.N.; Sun, T.; Lai, Z.; Nagarajaiah, S. Effectiveness of Negative Stiffness System in the Benchmark Structural-Control Problem for Seismically Excited Highway Bridges. J. Bridg. Eng. 2018, 23, 04018001. [Google Scholar] [CrossRef]
- Makris, N.; Zhang, J. Seismic Response Analysis of a Highway Overcrossing Equipped with Elastomeric Bearings and Fluid Dampers. J. Struct. Eng. 2004, 130, 830–845. [Google Scholar] [CrossRef]
- Rezaeian, S. Stochastic Modeling and Simulation of Ground Motions for Performance-Based Earthquake Engineering. Ph.D. Dissertation, University of California Berkeley, Berkeley, CA, USA, 2010. [Google Scholar]
- Lee, V.W. Empirical scaling of strong earthquake ground motion: Part III: Synthetic strong motion. ISET J. Earthq. Technol. 2002, 39, 273–310. [Google Scholar]
- Hart, E.W.; Bryant, W.A.; Manson, M.W.; Kahle, J.E. Summary Report: Fault Evaluation Program 1984–1985, South Coast Ranges Region and Other Areas, Calif; Open-File Report 86-3; Depart of Conservation, Division of Mines and Geology: Sacramento, CA, USA, 1986. [Google Scholar]
- Jennings, C.W.; Saucedo, G.J. Fault Activity Map of California and Adjacent Areas, with Locations and Ages of Recent Volcanic Eruptions; California Department of Conservation, Division of Mines and Geology: Sacramento, CA, USA, 1994. [Google Scholar]
- Petersen, M.D.; Wesnousky, S.G. Fault slip rates and earthquake histories for active faults in southern California. Bull. Seismol. Soc. Am. 1994, 84, 1608–1649. [Google Scholar]
- Makris, N.; Zhang, J. Structural Characterization and Seismic Response Analysis of a Highway Overcrossing Equipped with Elastomeric Bearings and Fluid Dampers: A Case Study; PEER Report 2002/17; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2002. [Google Scholar]
- Trifunac, M.D.; Brady, A.G. On the correlation of seismic intensity scales with the peaks of recorded strong ground motion. Bull. Seismol. Soc. Am. 1975, 65, 139–162. [Google Scholar]
- Bulajić, B.; Manić, M.; Lađinović, Đ. Effects of shallow and deep geology on seismic hazard estimates: A case study of pseudo-acceleration response spectra for the northwestern Balkans. Nat. Hazards. 2013, 69, 573–588. [Google Scholar] [CrossRef]
- Bulajić, B.Đ.; Bajić, S.; Stojnić, N. The effects of geological surroundings on earthquake-induced snow avalanche prone areas in the Kopaonik region. Cold Reg. Sci. Technol. 2018, 149, 29–45. [Google Scholar] [CrossRef]
- PEER Center. PEER Ground Motion Database; PEER NGA-West2 Database 2013/03; Pacific Earthquake Engineering Research Center Headquarters at the University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Li, Z.; Kotronis, P.; Wu, H. Simplified approaches for Arias Intensity correction of synthetic accelerograms. Bull. Earthq. Eng. 2017, 15, 4067–4087. [Google Scholar] [CrossRef]
- Gasparini, D.A.; Vanmarcke, E.H. Simulated Earthquake Motions Compatible with Prescribed Response Spectra; Department of Civil Engineering Research Report No. R76-4; Massachusetts Institute of Technology: Cambridge, MA, USA, 1976. [Google Scholar]
- Attanasi, G.; Auricchio, F.; Fenves, G.L. Feasibility Assessment of an Innovative Isolation Bearing System with Shape Memory Alloys. J. Earthq. Eng. 2009, 13, 18–39. [Google Scholar] [CrossRef]
- Mauro, D.; Donatello, C.; Roberto, M. Implementation and testing of passive control devices based on shape memory alloys. Earthq. Eng. Struct. Dyn. 2000, 29, 945–968. [Google Scholar]
- Auricchio, F. A robust integration-algorithm for a finite-strain shape-memory-alloy superelastic model. Int. J. Plast. 2001, 17, 971–990. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Kim, H.; Chang, C.; Kang, J. Evaluation of microvibration control performance of a smart base isolation system. Int. J. Steel Struct. 2015, 15, 1011–1020. [Google Scholar] [CrossRef]
- Tubaldi, E.; Mitoulis, S.A.; Ahmadi, H. Comparison of different models for high damping rubber bearings in seismically isolated bridges. Soil Dyn. Earthq. Eng. 2018, 104, 329–345. [Google Scholar] [CrossRef]
- Rad, A.R.; Banazadeh, M. Probabilistic risk-based performance evaluation of seismically base-isolated steel structures subjected to far-field earthquakes. Buildings 2018, 8, 128. [Google Scholar]
- Chimamphant, S.; Kasai, K. Comparative response and performance of base-isolated and fixed-base structures. Earthq. Eng. Struct. Dyn. 2016, 45, 5–27. [Google Scholar] [CrossRef]

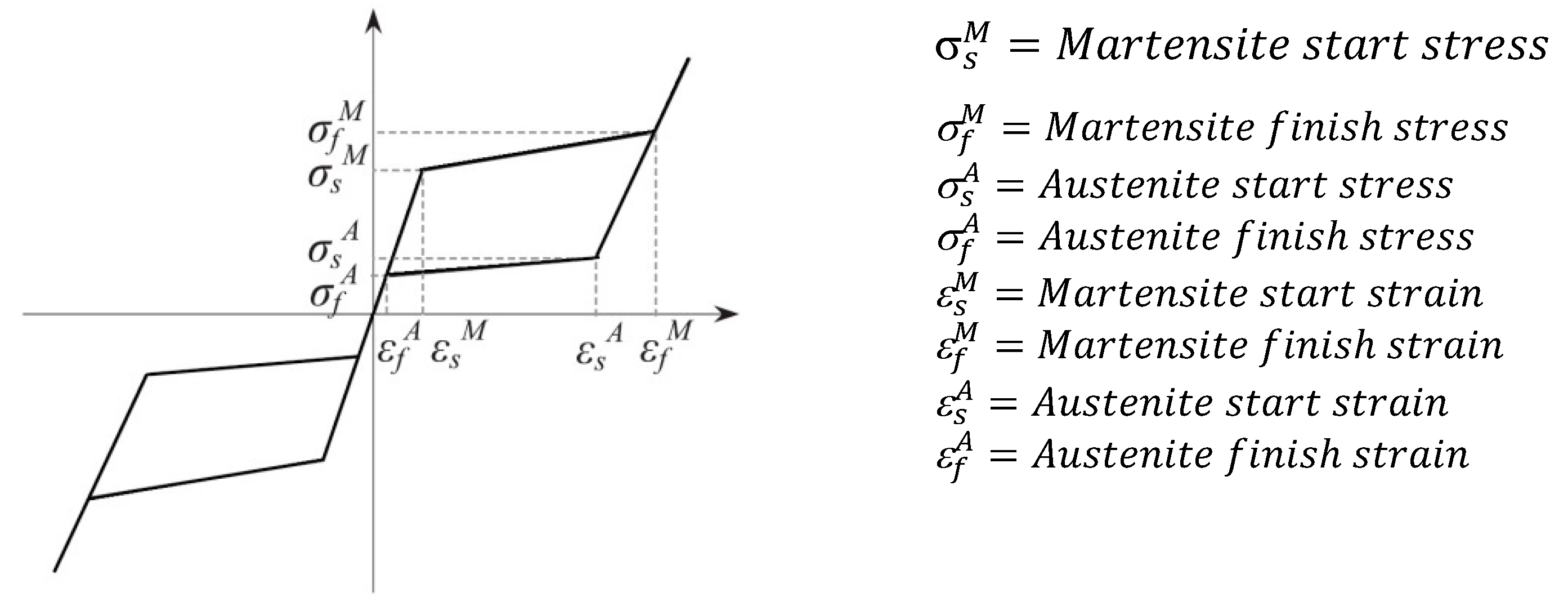
| RSN | Station | Pulse Period (s) | 5–95% Duration (s) | PGA (g) | Earthquake Year and Name | Mw | Mechanism | Rrup (km) | Vs30 (m/s) |
|---|---|---|---|---|---|---|---|---|---|
| 8161 | “El Centro Array #12” | 8.722 | 32.9 | 0.31 | 2010, “El Mayor-Cucapah Mexico” | 7.2 | strike slip | 11.26 | 196.88 |
| 8606 | “Westside Elementary School” | 7.084 | 25.3 | 0.28 | 2010, “El Mayor-Cucapah Mexico” | 7.2 | strike slip | 11.44 | 242 |
| Synthetic Accelerogram # for the station “El Centro Array #12” | 1st Horizontal Component | 2nd Horizontal Component | ||||||
| PGA (g) | Target PGA (g) | AI (m/s) | Target AI (m/s) | PGA (g) | Target PGA (g) | AI (m/s) | Target AI (m/s) | |
| 1 | 0.33 | 0.27 | 2.72 | 2.75 | 0.30 | 0.31 | 3.21 | 3.20 |
| 2 | 0.34 | 2.75 | 0.36 | 3.42 | ||||
| 3 | 0.30 | 2.93 | 0.31 | 3.21 | ||||
| 4 | 0.32 | 2.86 | 0.35 | 3.20 | ||||
| 5 | 0.31 | 2.87 | 0.34 | 3.27 | ||||
| Synthetic Accelerogram # for the station “Westside Elementary School” | 1st Horizontal Component | 2nd Horizontal Component | ||||||
| PGA (g) | Target PGA (g) | AI (m/s) | Target AI (m/s) | PGA (g) | Target PGA (g) | AI (m/s) | Target AI (m/s) | |
| 1 | 0.27 | 0.26 | 1.23 | 1.22 | 0.36 | 0.28 | 1.87 | 1.93 |
| 2 | 0.29 | 1.27 | 0.31 | 1.99 | ||||
| 3 | 0.28 | 1.27 | 0.35 | 2.07 | ||||
| 4 | 0.22 | 1.19 | 0.31 | 1.97 | ||||
| 5 | 0.25 | 1.29 | 0.39 | 2.09 | ||||
| Yield Displacement(m) | Post-Yield Stiffness (kN/mm) | Initial Stiffness (kN/mm) | |
|---|---|---|---|
| Abutment Isolators | 0.015 | 0.6 | 4.8 |
| Mid-pier Isolators | 0.015 | 1.2 | 9.6 |
| Maximum Base Shear (N) | |||||
|---|---|---|---|---|---|
| Earthquake | Non-Isolated | LRB Isolated | DC-SMA-LRB Isolated | S-SMA-LRB Isolated | C-SMA-LRB Isolated |
| RSN 8161 | 7.09 × 106 | 1.58 × 106 | 1.96 × 106 | 1.83 × 106 | 1.71 × 106 |
| Synthetic #1 | 7.07 × 106 | 1.30 × 106 | 1.70 × 106 | 1.59 × 106 | 1.46 × 106 |
| Synthetic #2 | 6.82 × 106 | 0.91 × 106 | 1.06 × 106 | 1.04 × 106 | 1.02 × 106 |
| Synthetic #3 | 6.80 × 106 | 1.22 × 106 | 2.02 × 106 | 1.87 × 106 | 1.35 × 106 |
| Synthetic #4 | 6.61 × 106 | 0.88 × 106 | 1.69 × 106 | 1.57 × 106 | 1.49 × 106 |
| Synthetic #5 | 8.25 × 106 | 1.18 × 106 | 1.75 × 106 | 1.64 × 106 | 1.25 × 106 |
| RSN 8606 | 7.17 × 106 | 0.64 × 106 | 0.94 × 106 | 0.84 × 106 | 0.79 × 106 |
| Synthetic #1 | 6.29 × 106 | 0.97 × 106 | 1.07 × 106 | 1.06 × 106 | 1.01 × 106 |
| Synthetic #2 | 6.39 × 106 | 0.84 × 106 | 1.18 × 106 | 1.13 × 106 | 1.10 × 106 |
| Synthetic #3 | 7.90 × 106 | 0.72 × 106 | 0.96 × 106 | 0.94 × 106 | 0.90 × 106 |
| Synthetic #4 | 6.71 × 106 | 0.66 × 106 | 0.91 × 106 | 0.84 × 106 | 0.71 × 106 |
| Synthetic #5 | 6.29 × 106 | 0.60 × 106 | 1.04 × 106 | 0.96 × 106 | 0.83 × 106 |
| Maximum Mid-span Acceleration (ms−2) | |||||
|---|---|---|---|---|---|
| Earthquake | Non-Isolated | LRB Isolated | DC-SMA-LRB Isolated | S-SMA-LRB Isolated | C-SMA-LRB Isolated |
| RSN 8161 | 4.45 | 1.92 | 3.33 | 3.05 | 2.97 |
| Synthetic #1 | 4.27 | 1.29 | 2.71 | 2.45 | 2.07 |
| Synthetic #2 | 4.34 | 1.45 | 2.45 | 2.37 | 1.99 |
| Synthetic #3 | 4.26 | 1.76 | 3.37 | 3.12 | 2.07 |
| Synthetic #4 | 4.30 | 1.22 | 3.06 | 2.89 | 2.70 |
| Synthetic #5 | 5.07 | 1.40 | 2.74 | 2.44 | 1.98 |
| RSN 8606 | 4.50 | 1.01 | 2.00 | 1.88 | 1.39 |
| Synthetic #1 | 5.71 | 0.99 | 2.14 | 1.89 | 1.47 |
| Synthetic #2 | 4.02 | 1.45 | 2.24 | 2.10 | 1.87 |
| Synthetic #3 | 4.90 | 1.79 | 2.20 | 2.02 | 2.01 |
| Synthetic #4 | 4.23 | 1.28 | 1.90 | 1.74 | 1.47 |
| Synthetic #5 | 4.04 | 1.38 | 1.98 | 1.76 | 1.75 |
| Maximum Mid-Span Displacement (m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Non-ISOLATED | LRB Isolated | DC-SMA-LRB Isolated | S-SMA-LRB Isolated | C-SMA-LRB Isolated | ||||
| Earthquake | Reduction Ratio (%) | Reduction Ratio (%) | Reduction Ratio (%) | |||||
| RSN 8161 | 0.73 × 10−1 | 2.98 × 10−1 | 1.53 × 10−1 | 48.66 | 1.62 × 10−1 | 45.64 | 2.20 × 10−1 | 26.17 |
| Synthetic #1 | 0.71 × 10−1 | 4.60 × 10−1 | 1.54 × 10−1 | 66.52 | 1.59 × 10−1 | 65.43 | 1.64 × 10−1 | 64.35 |
| Synthetic #2 | 0.69 × 10−1 | 3.12 × 10−1 | 1.54 × 10−1 | 50.64 | 1.70 × 10−1 | 45.51 | 2.00 × 10−1 | 35.90 |
| Synthetic #3 | 0.73 × 10−1 | 3.81 × 10−1 | 1.63 × 10−1 | 57.22 | 1.69 × 10−1 | 55.64 | 2.44 × 10−1 | 35.96 |
| Synthetic #4 | 0.68 × 10−1 | 3.87 × 10−1 | 1.77 × 10−1 | 54.26 | 1.78 × 10−1 | 54.01 | 2.43 × 10−1 | 37.21 |
| Synthetic #5 | 0.86 × 10−1 | 2.86 × 10−1 | 1.73 × 10−1 | 39.51 | 1.80 × 10−1 | 37.06 | 1.84 × 10−1 | 35.66 |
| RSN 8606 | 0.75 × 10−1 | 3.92 × 10−1 | 1.15 × 10−1 | 70.66 | 1.22 × 10−1 | 68.88 | 1.25 × 10−1 | 68.11 |
| Synthetic #1 | 0.42 × 10−1 | 3.45 × 10−1 | 1.31 × 10−1 | 62.03 | 1.38 × 10−1 | 60.00 | 1.48 × 10−1 | 57.10 |
| Synthetic #2 | 0.69 × 10−1 | 4.81 × 10−1 | 1.19 × 10−1 | 75.26 | 1.34 × 10−1 | 72.14 | 1.84 × 10−1 | 61.75 |
| Synthetic #3 | 0.81 × 10−1 | 6.50 × 10−1 | 1.22 × 10−1 | 81.23 | 1.30 × 10−1 | 80.00 | 2.17 × 10−1 | 66.62 |
| Synthetic #4 | 0.70 × 10−1 | 4.06 × 10−1 | 1.21 × 10−1 | 70.20 | 1.30 × 10−1 | 67.98 | 1.80 × 10−1 | 55.67 |
| Synthetic #5 | 0.68 × 10−1 | 4.79 × 10−1 | 1.00 × 10−1 | 79.12 | 1.13 × 10−1 | 76.41 | 1.97 × 10−1 | 58.87 |
| Residual Mid-Span Displacement (m) | |||||||
|---|---|---|---|---|---|---|---|
| LRB Isolated | DC-SMA-LRB Isolated | S-SMA-LRB Isolated | C-SMA-LRB Isolated | ||||
| Earthquake | Reduction Ratio (%) | Reduction Ratio (%) | Reduction Ratio (%) | ||||
| RSN 8161 | 0.1182 | 0.0300 | 74.62 | 0.0349 | 70.47 | 0.0538 | 54.48 |
| Synthetic #1 | 0.0657 | 0.0033 | 94.98 | 0.0035 | 94.67 | 0.0216 | 67.12 |
| Synthetic #2 | 0.0741 | 0.0349 | 52.90 | 0.0359 | 51.55 | 0.0426 | 42.51 |
| Synthetic #3 | 0.1617 | 0.0150 | 90.72 | 0.0185 | 88.56 | 0.0372 | 76.99 |
| Synthetic #4 | 0.0995 | 0.0476 | 52.16 | 0.0481 | 51.66 | 0.0553 | 44.42 |
| Synthetic #5 | 0.1248 | 0.0348 | 72.12 | 0.0413 | 66.91 | 0.0653 | 47.68 |
| RSN 8606 | 0.1882 | 0.0408 | 78.32 | 0.0414 | 78.00 | 0.0535 | 71.57 |
| Synthetic #1 | 0.1818 | 0.0326 | 82.07 | 0.0599 | 67.05 | 0.0663 | 63.53 |
| Synthetic #2 | 0.1374 | 0.0157 | 88.57 | 0.0226 | 83.55 | 0.0245 | 82.17 |
| Synthetic #3 | 0.1319 | 0.0018 | 98.67 | 0.0089 | 93.25 | 0.0276 | 79.08 |
| Synthetic #4 | 0.0834 | 0.0155 | 81.41 | 0.0227 | 72.78 | 0.0314 | 62.35 |
| Synthetic #5 | 0.1481 | 0.0153 | 89.67 | 0.0451 | 69.55 | 0.0721 | 51.32 |
| Criteria | Alternatives | Normalized Alternatives | Weights | Weighted Sum Matrix | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DC-SMA-LRB | S-SMA-LRB | C-SMA-LRB | DC-SMA-LRB | S-SMA-LRB | C-SMA-LRB | DC-SMA-LRB | S-SMA-LRB | C-SMA-LRB | ||
| Maximum Base Shear (N) | 1,960,000 | 1,830,000 | 1,710,000 | 0.87 | 0.93 | 1.00 | 0.15 | 0.13 | 0.14 | 0.15 |
| Maximum mid-span Acceleration (ms−2) | 3.33 | 3.05 | 2.97 | 0.89 | 0.97 | 1.00 | 0.15 | 0.13 | 0.15 | 0.15 |
| Maximum mid-span Displacement (m) | 0.153 | 0.162 | 0.22 | 1.00 | 0.94 | 0.70 | 0.3 | 0.30 | 0.28 | 0.21 |
| mid-span Residual Displacement (m) | 0.03 | 0.0349 | 0.0538 | 1.00 | 0.86 | 0.56 | 0.3 | 0.30 | 0.26 | 0.17 |
| Length of the SMA wire (cm) | 242.71 | 133.12 | 205.85 | 0.55 | 1.00 | 0.65 | 0.10 | 0.05 | 0.10 | 0.06 |
| Performance Score | 0.92 | 0.93 | 0.74 | |||||||
| Rank | 2 | 1 | 3 | |||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, R.; Rashidi, M.; Bulajić, B.Đ.; Arani, K.K. Multi-Objective Optimization of Three Different SMA-LRBs for Seismic Protection of a Benchmark Highway Bridge against Real and Synthetic Ground Motions. Appl. Sci. 2020, 10, 4076. https://doi.org/10.3390/app10124076
Hosseini R, Rashidi M, Bulajić BĐ, Arani KK. Multi-Objective Optimization of Three Different SMA-LRBs for Seismic Protection of a Benchmark Highway Bridge against Real and Synthetic Ground Motions. Applied Sciences. 2020; 10(12):4076. https://doi.org/10.3390/app10124076
Chicago/Turabian StyleHosseini, Reyhaneh, Maria Rashidi, Borko Đ. Bulajić, and Kamyar Karbasi Arani. 2020. "Multi-Objective Optimization of Three Different SMA-LRBs for Seismic Protection of a Benchmark Highway Bridge against Real and Synthetic Ground Motions" Applied Sciences 10, no. 12: 4076. https://doi.org/10.3390/app10124076
APA StyleHosseini, R., Rashidi, M., Bulajić, B. Đ., & Arani, K. K. (2020). Multi-Objective Optimization of Three Different SMA-LRBs for Seismic Protection of a Benchmark Highway Bridge against Real and Synthetic Ground Motions. Applied Sciences, 10(12), 4076. https://doi.org/10.3390/app10124076








