A Palm-Jacobaeus Loss Formula for Multi-Service Systems with Separated Resources
Abstract
1. Introduction
2. Model of the Group with Limited Availability
3. Non-Availability Probability of Strictly Defined Resources
4. Results and Discussion
4.1. General Assumptions
4.2. Simulator
- the number k of resources,
- the capacity f of a single resource,
- the number M of traffic stream classes,
- the number of demanded allocation units for a stream of class i (),
- the intensity of a service stream of class i,
- the proportions of offered traffic , i.e., the values of the parameters ,
- the average value a of traffic offered to a single allocation unit in the system, where:
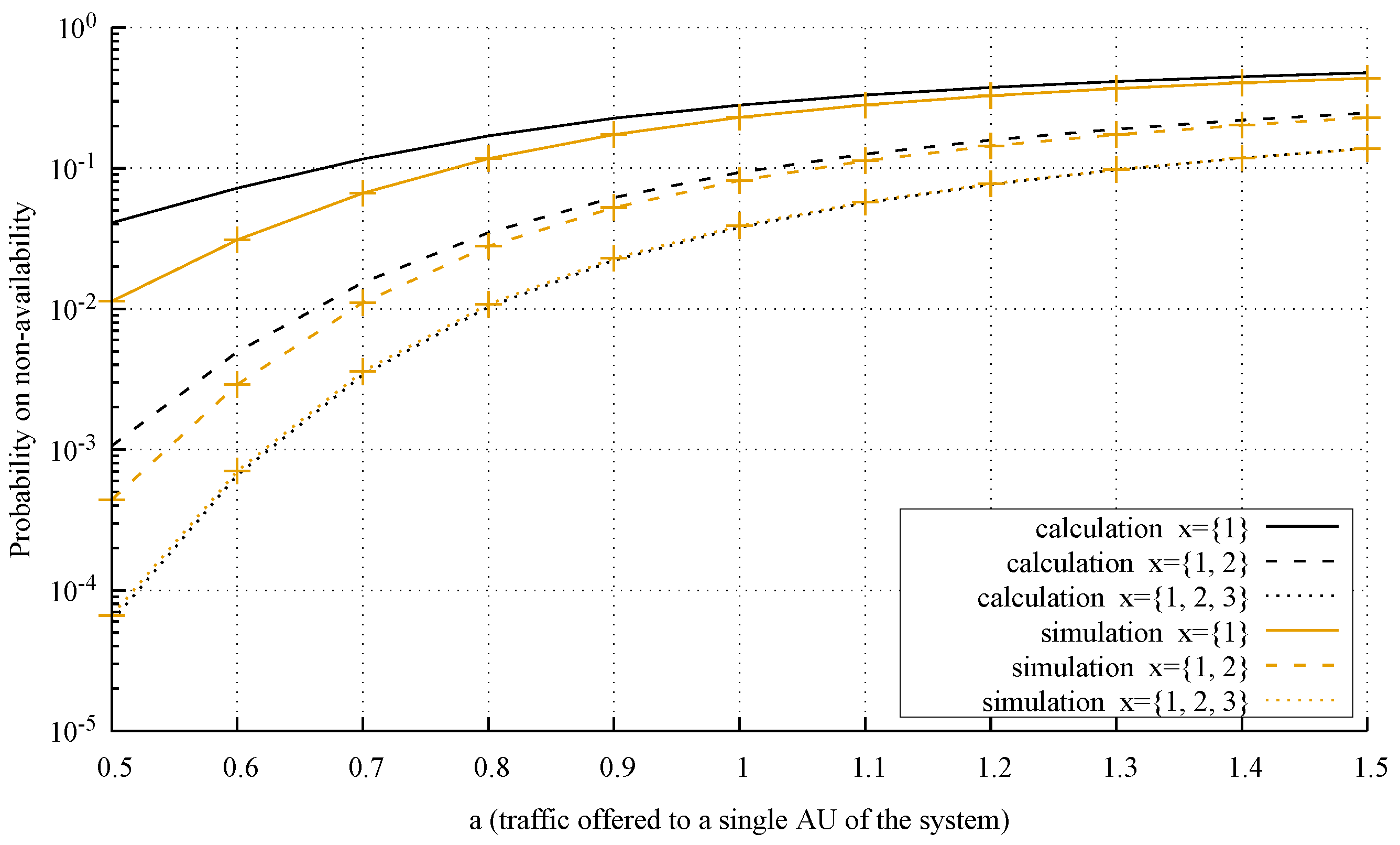
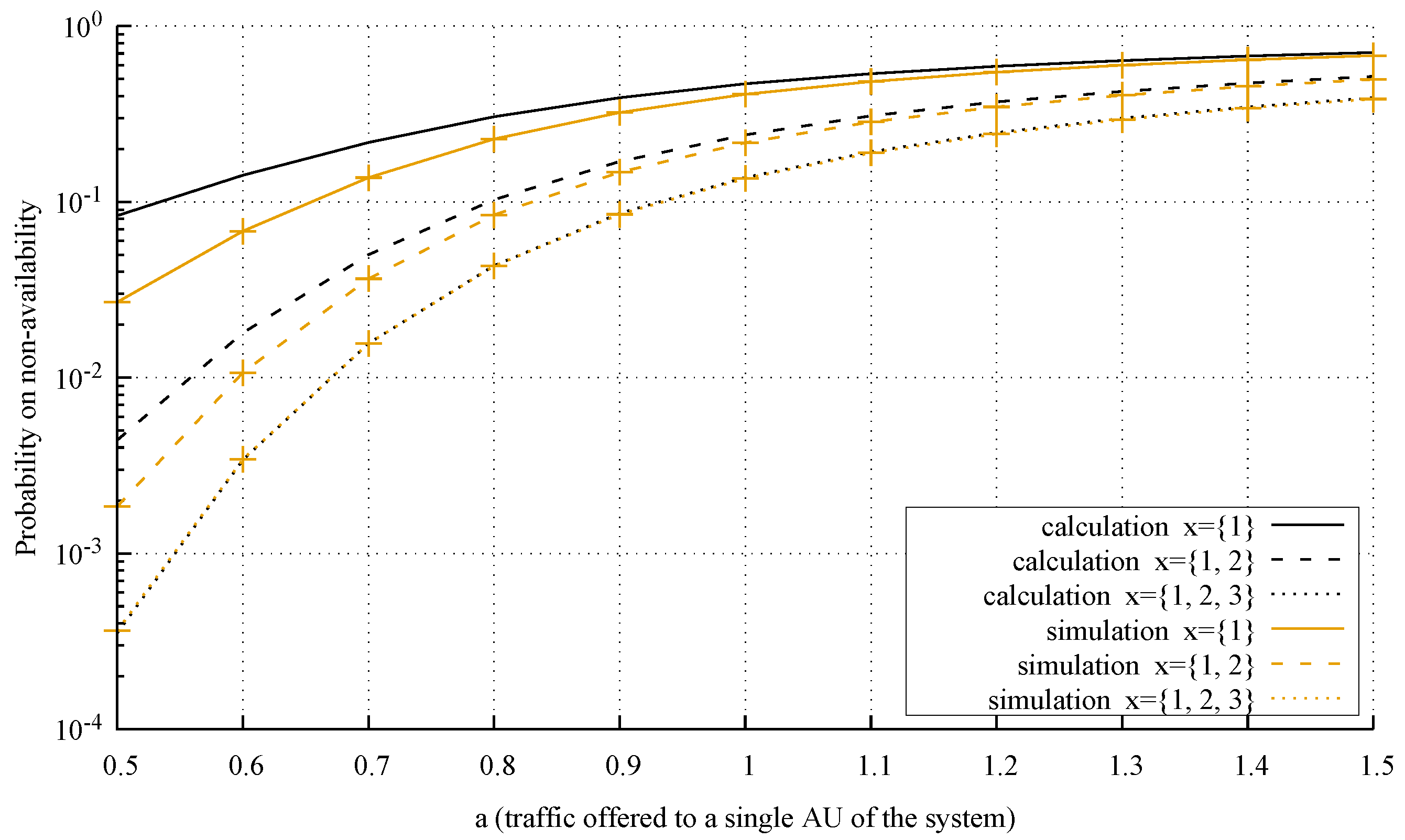
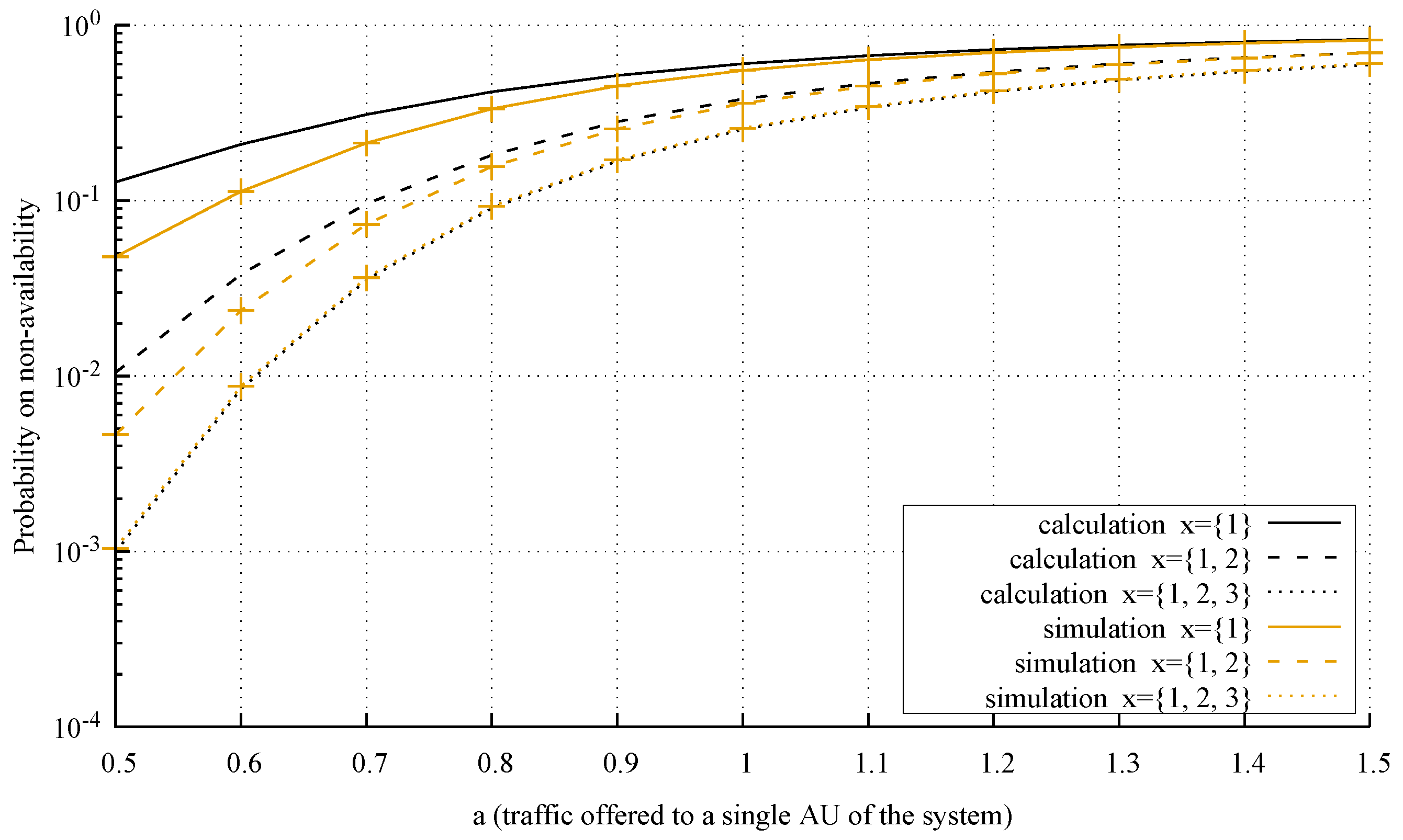
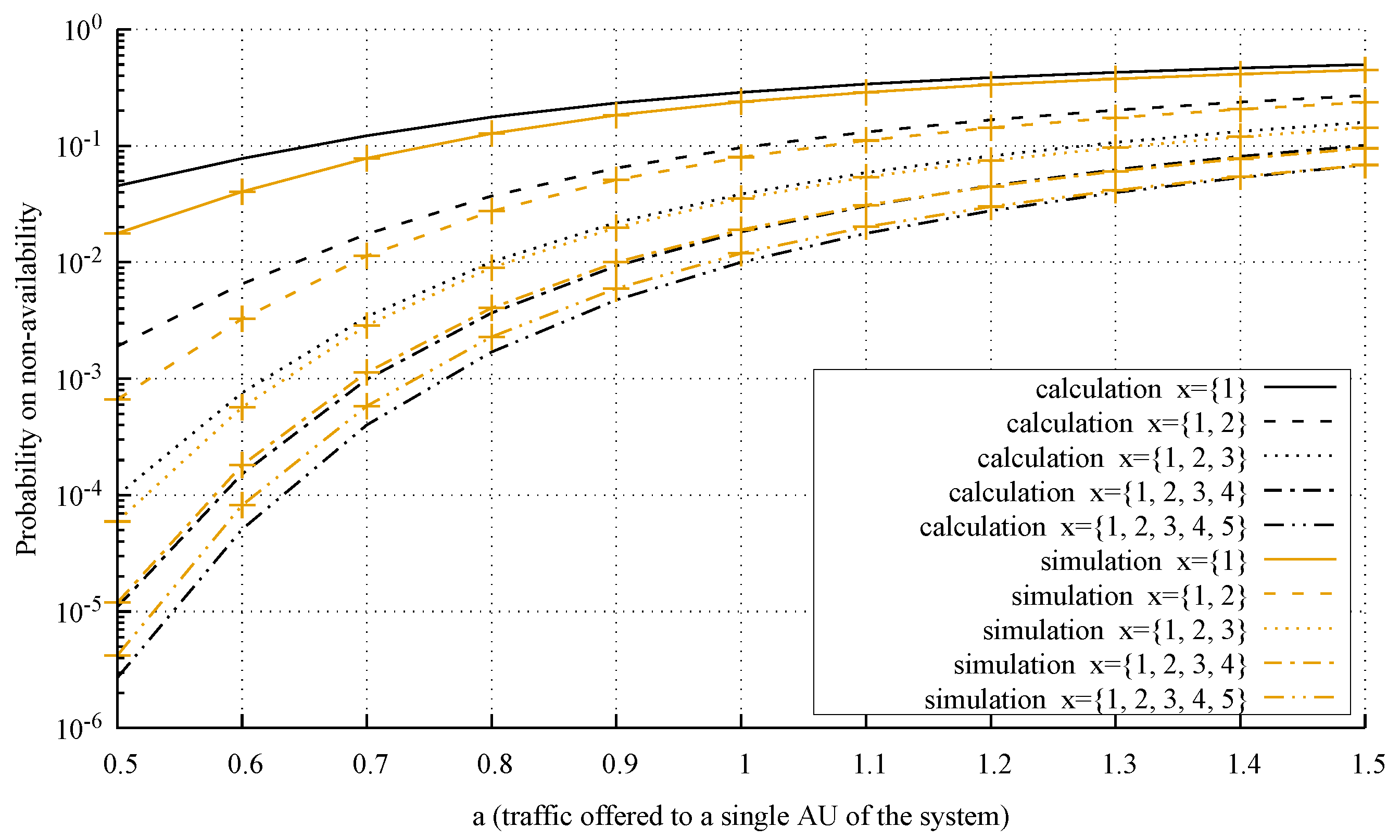
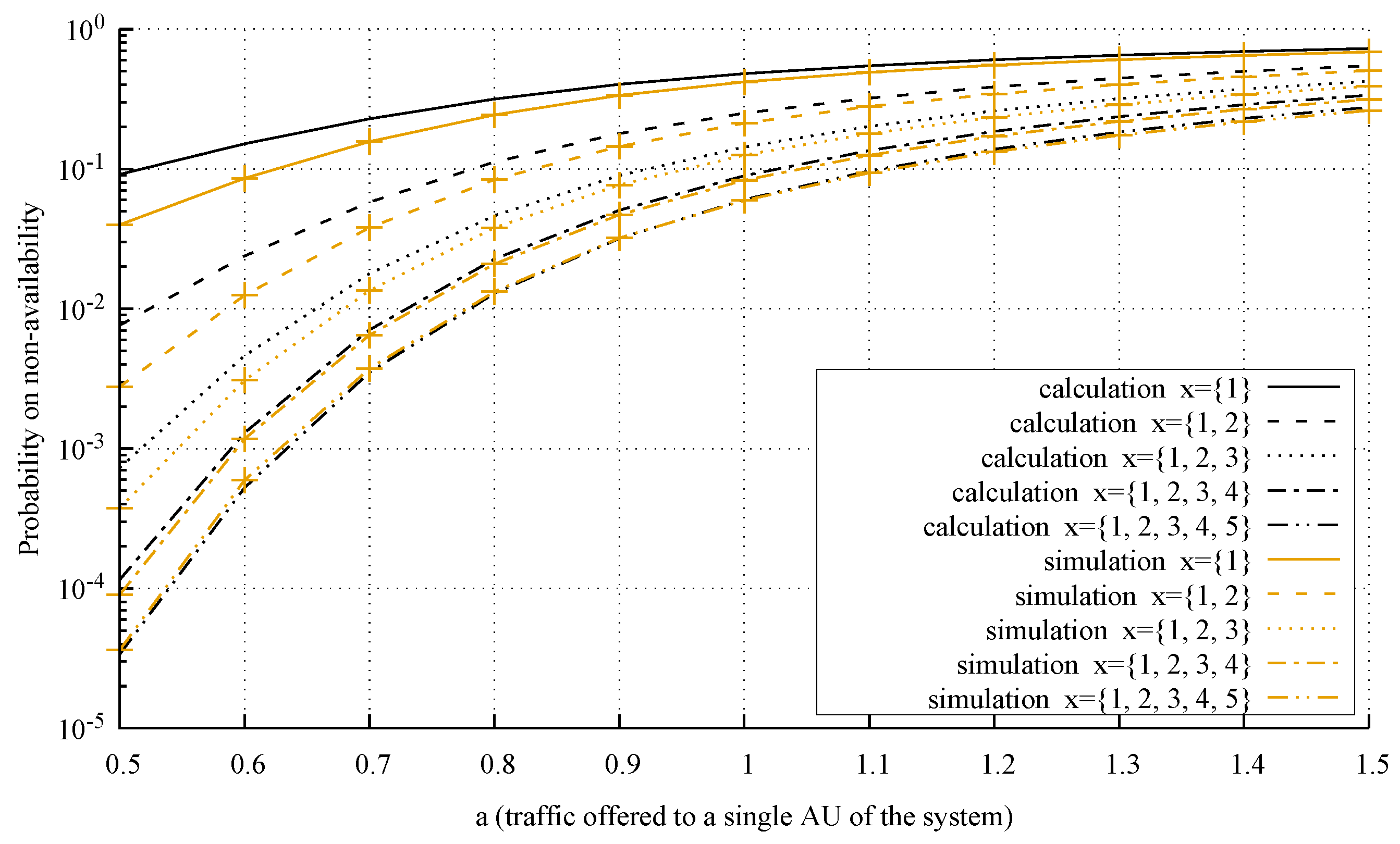
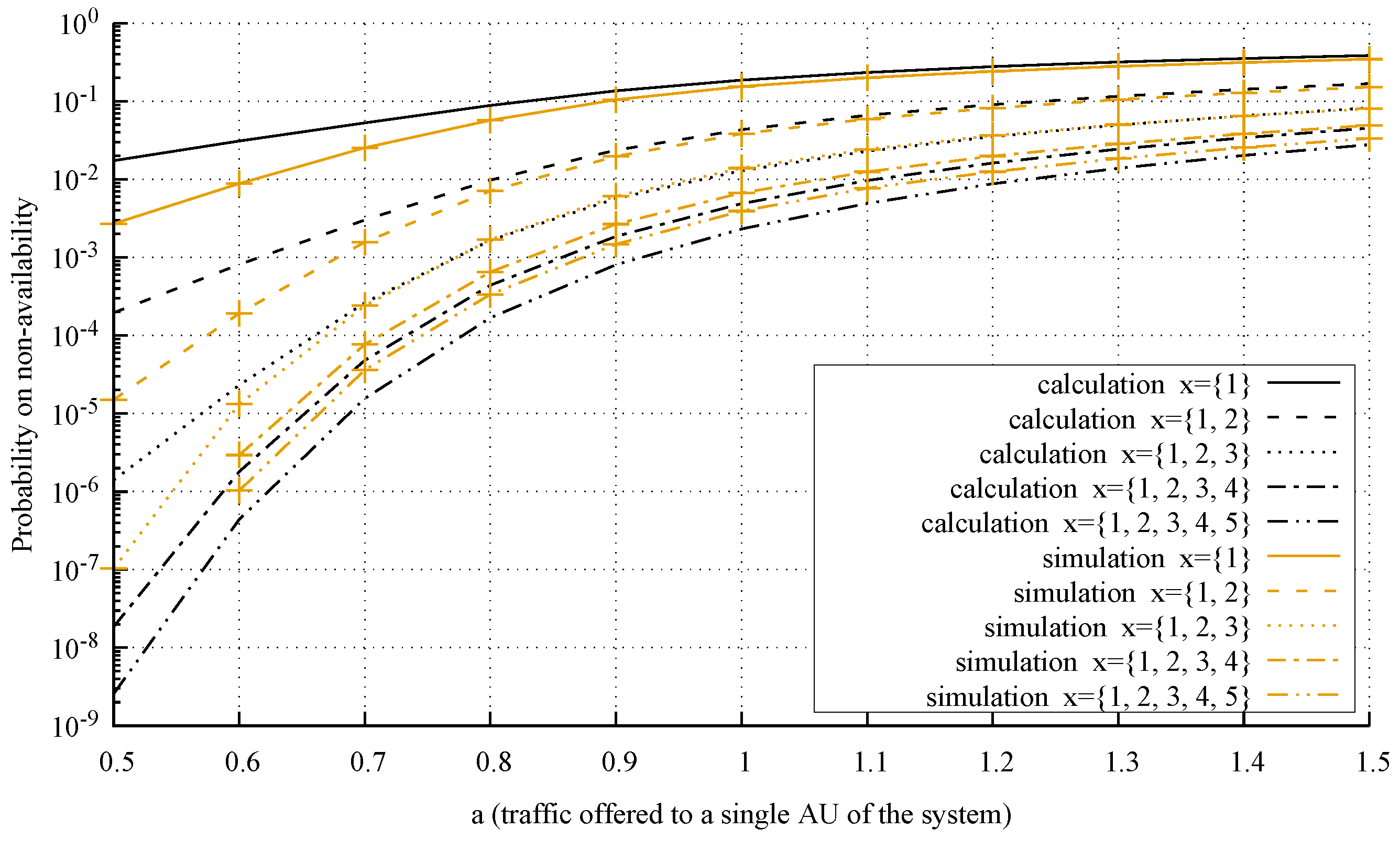
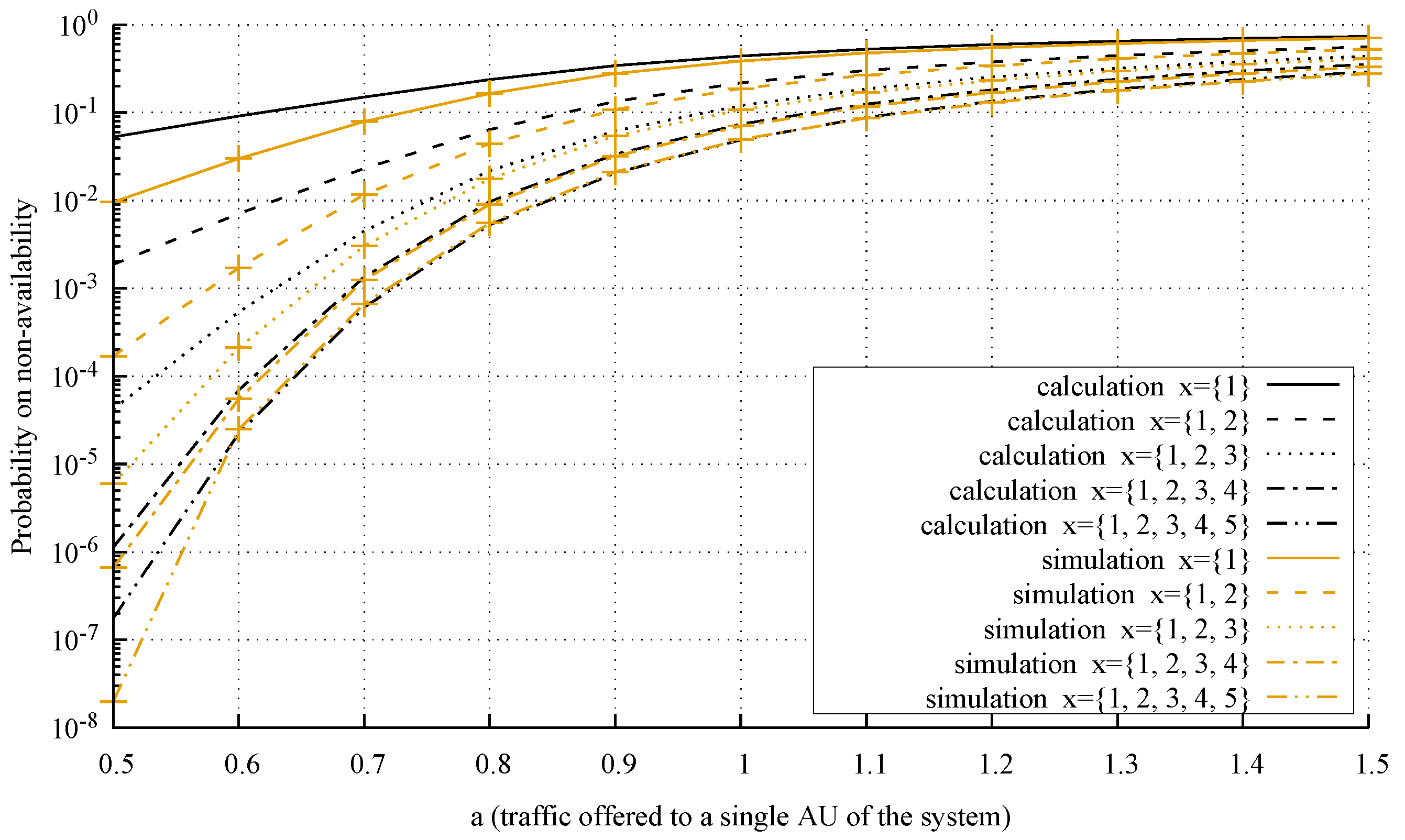
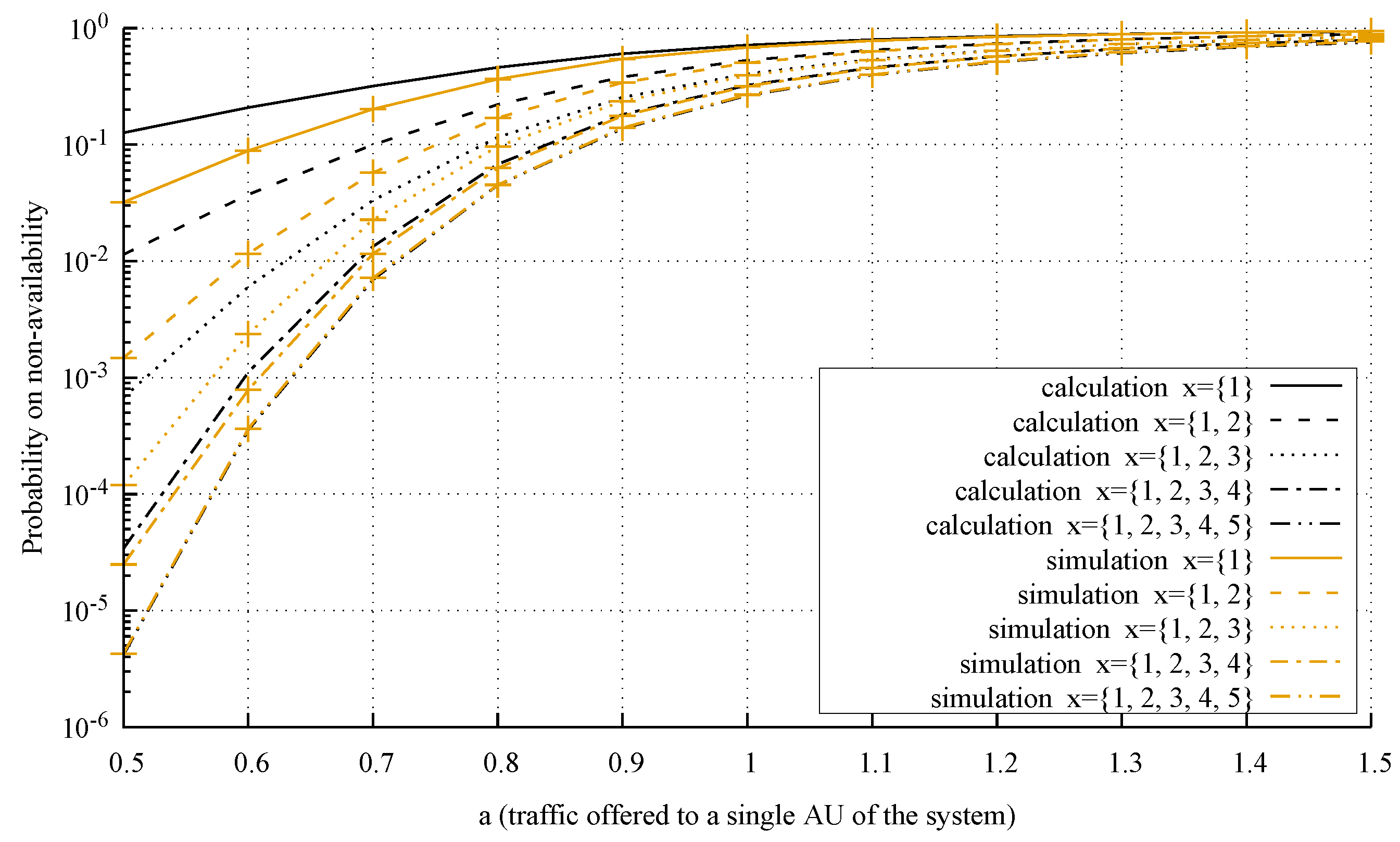
4.3. Accuracy of the Model
- System 1: , AUs, AUs, , AU, AUs, AUs, , ;
- System 2: , AUs, AUs, , AU, AUs, AUs, , ;
- System 3: , AUs, AUs, , AU, AUs, AUs, , .
- The analysis of the considered system is carried out from the microstate level (multi-dimensional Markov process) to the macrostate level (one-dimensional Markov process)—a detailed analysis of this problem is presented in [55].
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oladejo, S.O.; Falowo, O.E. Latency-Aware Dynamic Resource Allocation Scheme for Multi-Tier 5G Network: A Network Slicing-Multitenancy Scenario. IEEE Access 2020, 8, 74834–74852. [Google Scholar] [CrossRef]
- Jian, Z.; Muqing, W.; Ruiqiang, M.; Xiusheng, W. Dynamic Resource Sharing Scheme across Network Slicing for Multi-tenant C-RANs. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Beijing, China, 16–18 August 2018. [Google Scholar] [CrossRef]
- Kazi, B.U.; Wainer, G.A. Next generation wireless cellular networks: Ultra-dense multi-tier and multi-cell cooperation perspective. Wirel. Netw. 2018, 25, 2041–2064. [Google Scholar] [CrossRef]
- Wang, C.X.; Haider, F.; Gao, X.; You, X.H.; Yang, Y.; Yuan, D.; Aggoune, H.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5G wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- Jaber, M.; Imran, M.A.; Tafazolli, R.; Tukmanov, A. 5G Backhaul Challenges and Emerging Research Directions: A Survey. IEEE Access 2016, 4, 1743–1766. [Google Scholar] [CrossRef]
- 3GPP. Self-Configuring and Self-Optimizing Network (Son) Use Cases and Solutions (Rlease 9); Technical Report TR 36.902; 3GPP: Sophia Antipolis Cedex, France, 2010. [Google Scholar]
- 3GPP. TS32.500 V14.0.0: Telecommunication Management; Self-Organizing Networks (SON); Concepts and Requirements; Technical Report; 3GPP: Sophia Antipolis Cedex, France, 2017. [Google Scholar]
- 3GPP. TS32.501 V14.0.0: Telecommunication Management; Self-Configuration of Network Elements; Concepts and Requirements; Technical Report; 3GPP: Sophia Antipolis Cedex, France, 2017. [Google Scholar]
- Bassoy, S.; Jaber, M.; Imran, M.A.; Xiao, P. Load Aware Self-Organising User-Centric Dynamic CoMP Clustering for 5G Networks. IEEE Access 2016, 4, 2895–2906. [Google Scholar] [CrossRef]
- Głąbowski, M.; Hanczewski, S.; Stasiak, M. Modelling Load Balancing Mechanisms in Self-Optimising 4G Mobile Networks with Elastic and Adaptive Traffic. IEICE Trans. Commun. 2016, E99-B, 1718–1726. [Google Scholar]
- Ramirez-Perez, C.; Ramos, V. SDN meets SDR in self-organizing networks: Fitting the pieces of network management. IEEE Commun. Mag. 2016, 54, 48–57. [Google Scholar] [CrossRef]
- Moysen, J.; Giupponi, L. From 4G to 5G: Self-organized network management meets machine learning. Comput. Commun. 2018, 129, 248–268. [Google Scholar] [CrossRef]
- Xu, J.; Yao, J.; Wang, L.; Wu, K.; Chen, L.; Lou, W. Revolution of Self-Organizing Network for 5G MmWave Small Cell Management: From Reactive to Proactive. IEEE Wirel. Commun. 2018, 25, 66–73. [Google Scholar] [CrossRef]
- Paik, C.; Suh, Y.S. Generalized Queueing Model for Call Blocking Probability and Resource Utilization in OFDM Wireless Networks. IEEE Commun. Lett. 2011, 15, 767–769. [Google Scholar] [CrossRef]
- Moscholios, I.D.; Vassilakis, V.G.; Panagoulias, P.I.; Logothetis, M.D. On Call Blocking Probabilities and Resource Utilization in OFDM Wireless Networks. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018; pp. 1–5. [Google Scholar]
- Panagoulias, P.I.; Moscholios, I.D.; Sarigiannidis, P.G.; Logothetis, M.D. Congestion probabilities in OFDM wireless networks with compound Poisson arrivals. IET Commun. 2020, 14, 674–681. [Google Scholar] [CrossRef]
- Efstratiou, P.; Moscholios, I.D. User Mobility in a 5G Cell with Quasi-Random Traffic under the Complete Sharing and Bandwidth Reservation Policies. Autom. Control Comput. Sci. 2019, 53, 376–386. [Google Scholar] [CrossRef]
- Panagoulias, P.I.; Moscholios, I.D. Congestion probabilities in the X2 link of LTE networks. Telecommun. Syst. 2019, 71, 585–599. [Google Scholar] [CrossRef]
- Stasiak, M.; Głąbowski, M.; Wiśniewski, A.; Zwierzykowski, P. Modeling and Dimensioning of Mobile Networks; Wiley: Chichester, UK, 2011. [Google Scholar]
- Chousainov, I.; Moscholios, I.D.; Kaloxylos, A.; Logothetis, M.D. Performance Evaluation of a C-RAN Supporting Quasi-Random Traffic. In Proceedings of the 2019 International Conference on Software, Telecommunications and Computer Networks, SoftCOM 2019, Split, Croatia, 19–21 September 2019; Begusic, D., Rozic, N., Radic, J., Saric, M., Eds.; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, Y.; Chen, H. Queueing analysis for OFDM subcarrier allocation in broadband wireless multiservice networks. IEEE Trans. Wirel. Commun. 2008, 7, 3951–3961. [Google Scholar] [CrossRef]
- Głąbowski, M.; Sobieraj, M.; Stasiak, M. Blocking Probability Calculation in UMTS Networks with Bandwidth Reservation, Handoff Mechanism and Finite Source Population. In Proceedings of the 7th International Symposium on Communications and Information Technologies, Sydney, Australia, 17–19 October 2007; pp. 433–438. [Google Scholar] [CrossRef]
- Palm, C. Nagra foljdsatser urde Erlang’ska formlerna. Tekn. Medd. Kungl. Telegr. 1943. [Google Scholar]
- Jacobaeus, C. A study on congestion in link-systems. Ericsson Tech. 1950, 48, 1–68. [Google Scholar]
- Lotze, A. History and development of grading theory. In Proceedings of the 5th International Teletraffic Congress, New York, NY, USA, 14–20 June 1967; pp. 148–161. [Google Scholar]
- Syski, R. Introduction to Congestion Theory in Telephone Systems; Studies in Telecommunication, North Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Herzog, U. Adaption of the MPJ Loss Formula to Gradings of Various Types (with Special Regard to O’Dell Gradings and Standard Gradings with Slipping)—4. Bericht über verkehrstheoretische Arbeiten; Technical Report; Institut für Nachrichtenvermittlung und Datenverarbeitung, University of Stuttgart: Stuttgart, Germany, 1967. [Google Scholar]
- Binida, N.; Wend, W. Die Effektive Erreichbarkeit für Abnehmerbundel hinter Zwischenleitungsanungen. Nachrichtentechnische Ztg. (NTZ) 1959, 11, 579–585. [Google Scholar]
- Charkiewicz, A. An approximate method for calculating the number of junctions in a crossbar system exchange. Elektrosvyaz 1959, 2, 55–63. [Google Scholar]
- Lotze, A. Bericht uber Verkehrtheoretische Untersuchungen CIRB; Technical Report; Inst. für Nachrichten- Vermittlung und Datenverarbeitung der Technischen Hochschule, University of Stuttgart: Stuttgart, Germany, 1963. [Google Scholar]
- Bazlen, D.; Kampe, G.; Lotze, A. On the Influence of Hunting Mode and Link Wiring on the Loss of Link Systems. In Proceedings of the 7th International Teletraffic Congress, Stockholm, Swedenm, 13–20 June 1973; Organizing Committee: Stockholm, Swedenm, 1973; pp. 232/1–232/12. [Google Scholar]
- Rothmaier, K.; Scheller, R. Design of Economic PCM Arrays with a Prescribed Grade of Service. IEEE Trans. Commun. 1981, 29, 925–935. [Google Scholar] [CrossRef]
- Conradt, J.; Buchheister, A. Considerations on Loss Probability of Multi-Slot Connections. In Proceedings of the 11th International Teletraffic Congress, Kyoto, Japan, 4–11 September 1985; North-Holland: Kyoto, Japan, 1985. [Google Scholar]
- Karlsson, J. Loss performance in trunk groups with different capacity demands. In Proceedings of the 13th International Teletraffic Congress, Copenhagen, Denmark, 19–26 June 1991; North-Holland: Copenhagen, Denmark, 1991. Volume Discussion Circles. pp. 201–212. [Google Scholar]
- Ramaswami, V.; Rao, K. Flexible time slot assignment—A performance study for the integrated services digital network. In Proceedings of the 11th International Teletraffic Congress, Kyoto, Japan, 4–11 September 1985; North-Holland: Kyoto, Japan, 1985. [Google Scholar]
- Stasiak, M. Blocking probability in a limited-availability group carrying mixture of different multichannel traffic streams. Ann. Télécommun. 1993, 48, 71–76. [Google Scholar]
- Głąbowski, M.; Stasiak, M. Multi-rate Model of the Group of Separated Transmission Links of Various Capacities. In Telecommunications and Networking—ICT 2004; Lecture Notes in Computer Science; de Souza, J., Dini, P., Lorenz, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3124, pp. 1101–1106. [Google Scholar] [CrossRef]
- Głąbowski, M.; Stasiak, M.; Stasiak, M.D. QoS Criteria for Energy-Aware Switching Networks. In Quality, Reliability, Security and Robustness in Heterogeneous Systems; Duong, T.Q., Vo, N.S., Phan, V.C., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 137–147. [Google Scholar]
- Głąbowski, M.; Stasiak, M.D. Modelling of Multiservice Switching Networks with Overflow Links for Any Traffic Class. IET Circuits Devices Syst. 2014, 8, 358–366. [Google Scholar] [CrossRef]
- Głąbowski, M.; Stasiak, M.D. Multiservice Switching Networks with Overflow Links and Resource Reservation. Math. Probl. Eng. 2016, 2016, 4090656. [Google Scholar] [CrossRef][Green Version]
- Głąbowski, M.; Sobieraj, M. Analytical modelling of multiservice switching networks with multiservice sources and resource management mechanisms. Telecommun. Syst. 2017, 66, 559–578. [Google Scholar] [CrossRef]
- Panagoulias, P.I.; Moscholios, I.D.; Sarigiannidis, P.G.; Głąbowski, M.; Logothetis, M.D. An Analytical Framework in OFDM Wireless Networks Servicing Random or Quasi-Random Traffic. Appl. Sci. 2019, 9, 5376. [Google Scholar] [CrossRef]
- Roberts, J. (Ed.) Performance Evaluation and Design of Multiservice Networks, Final Report COST 224; Commission of the European Communities: Brussels, Belgium, 1992; pp. 36–44. [Google Scholar]
- Pras, A.; Nieuwenhuis, L.; van de Meent, R.; Mandjes, M. Dimensioning network links: A new look at equivalent bandwidth. IEEE Netw. 2009, 23, 5–10. [Google Scholar] [CrossRef][Green Version]
- Hui, J.Y. Resource Allocation in Broadband Networks. J. Sel. Areas Commun. 1988, 6, 1598–1608. [Google Scholar] [CrossRef]
- Moscholios, I.; Logothetis, M. Efficient Multirate Teletraffic Loss Models Beyond Erlang; Wiley: Chichester, UK, 2019. [Google Scholar]
- Moscholios, I.D.; Logothetis, M.D.; Vardakas, J.S.; Boucouvalas, A.C. Congestion probabilities of elastic and adaptive calls in Erlang-Engset multirate loss models under the threshold and bandwidth reservation policies. Comput. Netw. 2015, 92 Pt 1, 1–23. [Google Scholar] [CrossRef]
- Stasiak, M. Combinatorial considerations for switching systems carrying multi-channel traffic streams. Ann. Télécommun. 1996, 51, 611–625. [Google Scholar]
- Erlang, A. Solution of some problems in the theory of probabilities of significance in automatic telephone exchanges. Elektrotechnikeren 1917, 13, 5. [Google Scholar]
- Roberts, J.; Mocci, V.; Virtamo, I. (Eds.) Broadband Network Teletraffic, Final Report of Action COST 242; Commission of the European Communities; Springer: Berlin, Germany, 1996. [Google Scholar]
- Bonald, T.; Roberts, J.W. Internet and the Erlang Formula. ACM SIGCOMM Comput. Commun. Rev. 2012, 42, 23–30. [Google Scholar] [CrossRef]
- Kelly, F. Effective bandwith at multi-class queues. Queueing Syst. 1991, 9, 5–15. [Google Scholar] [CrossRef]
- Kallos, G.A.; Vassilakis, V.G.; Moscholios, I.D.; Logothetis, M.D. Performance Modelling of W-CDMA Networks supporting Elastic and Adaptive Traffic. In Proceedings of the 4th International Working Conference on Performance Modelling and Evaluation of Heterogeneous Networks (HET-NETs ’06), Ilkley, UK, 11–13 September 2006; Organizing Committee: Ilkley, UK, 2006. [Google Scholar]
- Głąbowski, M.; Kaliszan, A. Simulator of Full-Availability Group with Bandwidth Reservation and Multi-Rate Bernoulli-Poisson-Pascal Traffic Streams. In Proceedings of the Eurocon 2007, Warsaw, Poland, 9–12 September 2007; pp. 2271–2277. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Modeling product-form state-dependent systems with BPP traffic. Perform. Eval. 2010, 67, 174–197. [Google Scholar] [CrossRef]
- Żal, M. Energy-efficient optical switching nodes based on banyan-type switching fabrics. Opt. Switch. Netw. 2019, 33, 95–102. [Google Scholar] [CrossRef]
- Abdulsahib, M.; Michalski, M.; Kabaciński, W. Optimization of wide-sense nonblocking elastic optical switches. Opt. Switch. Netw. 2019, 33, 85–94. [Google Scholar] [CrossRef]
- Hanczewski, S.; Sobieraj, M.; Stasiak, M.D. The Direct Method of Effective Availability for Switching Networks with Multi-Service Traffic. IEICE Trans. Commun. 2016, E99-B, 1291–1301. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, J.; Ji, Y.; Tian, R.; Han, J.; Lee, Y. Performance evaluation of multi-stratum resources integration based on network function virtualization in software defined elastic data center optical interconnect. Opt. Express 2015, 23, 31192–31205. [Google Scholar] [CrossRef] [PubMed]
- Dizaji, L.G.; Rahbar, A.G. PAHON: Power-Aware Hybrid Optical Network. J. Parallel Distrib. Comput. 2018, 117, 1–16. [Google Scholar] [CrossRef]
- Kabaciński, W.; Michalski, M.; Rajewski, R.; Żal, M. Optical datacenter networks with elastic optical switches. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Modelling of Multiservice Networks with Separated Resources and Overflow of Adaptive Traffic. Wirel. Commun. Mob. Comput. 2018, 2018, 7870164. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Overflows in Multiservice Systems. IEICE Trans. Commun. 2019, E102.B, 958–969. [Google Scholar] [CrossRef]
- Głąbowski, M.; Hanczewski, S.; Stasiak, M. Modelling of Cellular Networks with Traffic Overflow. Math. Probl. Eng. 2015, 2015, 286490. [Google Scholar] [CrossRef]
- Keramidi, I.P.; Moscholios, I.D.; Sarigiannidis, P.G.; Logothetis, M.D. Call Blocking Probabilities in a Two-Link Loss Model with Restricted Accessibility. In Proceedings of the 15th International Conference on Telecommunications (ConTEL 2019), Graz, Austria, 3–5 July 2019; pp. 1–7. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Głąbowski, M.; Kaliszan, A.; Stasiak, M. A Palm-Jacobaeus Loss Formula for Multi-Service Systems with Separated Resources. Appl. Sci. 2020, 10, 4019. https://doi.org/10.3390/app10114019
Głąbowski M, Kaliszan A, Stasiak M. A Palm-Jacobaeus Loss Formula for Multi-Service Systems with Separated Resources. Applied Sciences. 2020; 10(11):4019. https://doi.org/10.3390/app10114019
Chicago/Turabian StyleGłąbowski, Mariusz, Adam Kaliszan, and Maciej Stasiak. 2020. "A Palm-Jacobaeus Loss Formula for Multi-Service Systems with Separated Resources" Applied Sciences 10, no. 11: 4019. https://doi.org/10.3390/app10114019
APA StyleGłąbowski, M., Kaliszan, A., & Stasiak, M. (2020). A Palm-Jacobaeus Loss Formula for Multi-Service Systems with Separated Resources. Applied Sciences, 10(11), 4019. https://doi.org/10.3390/app10114019





