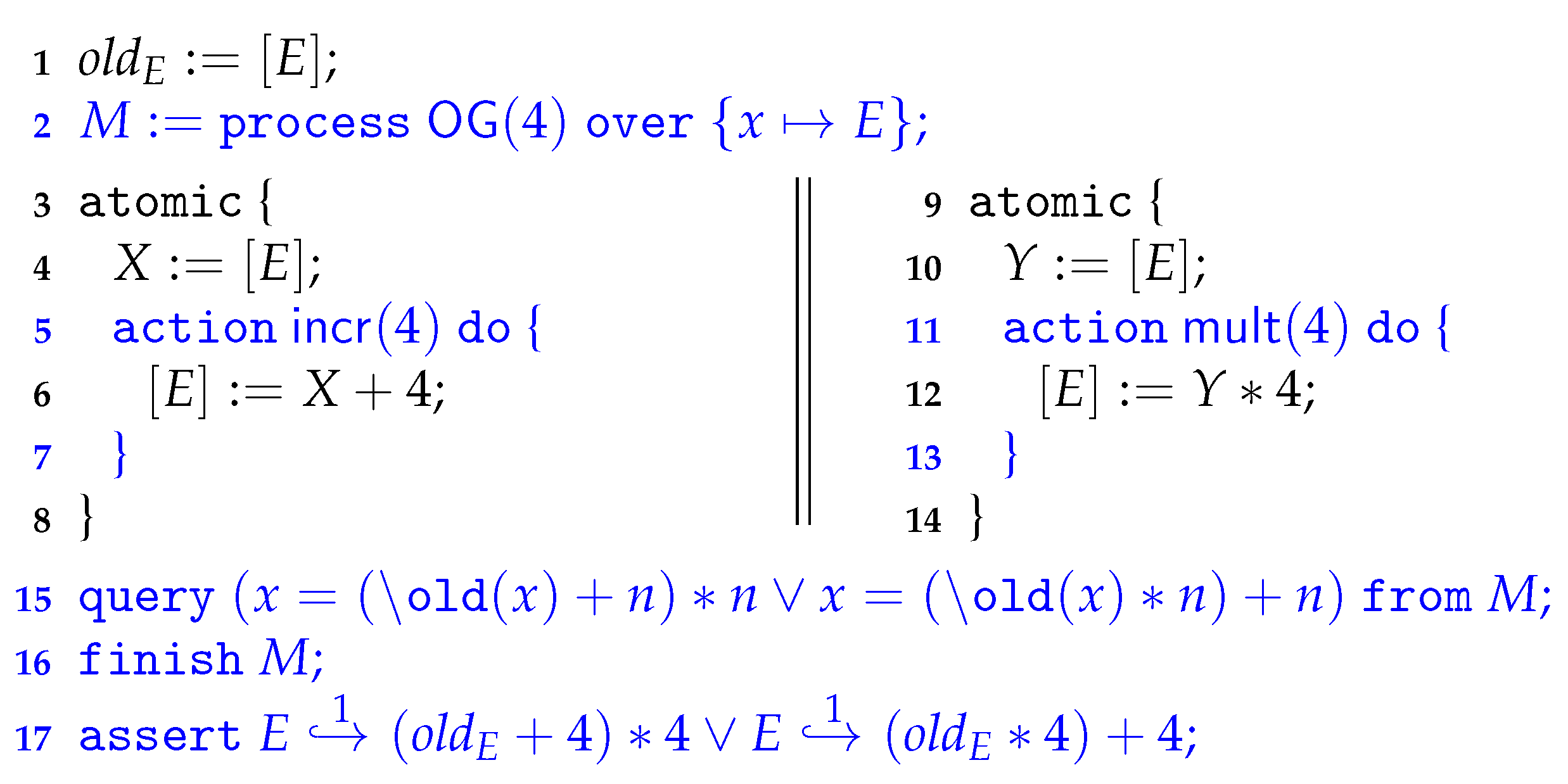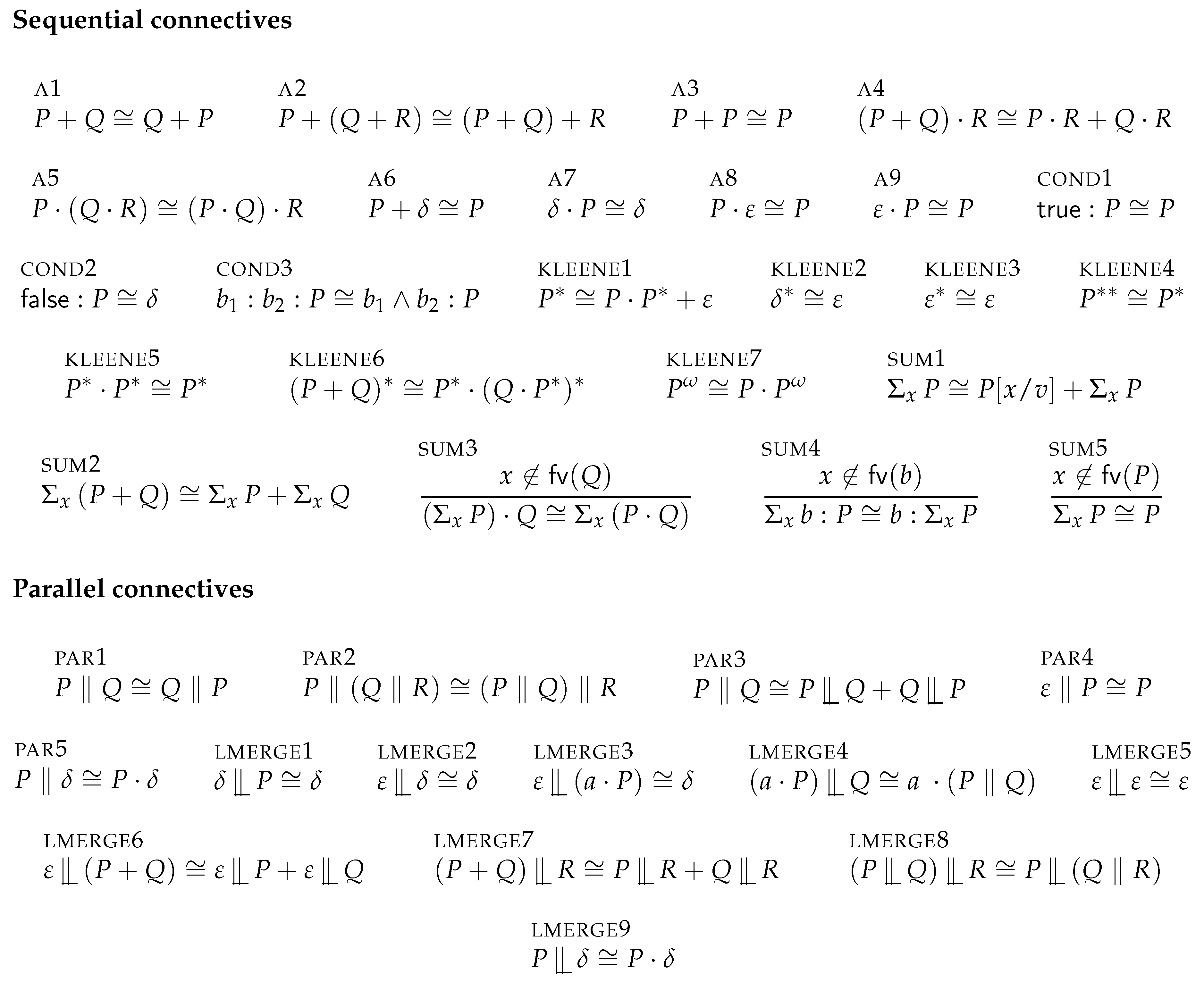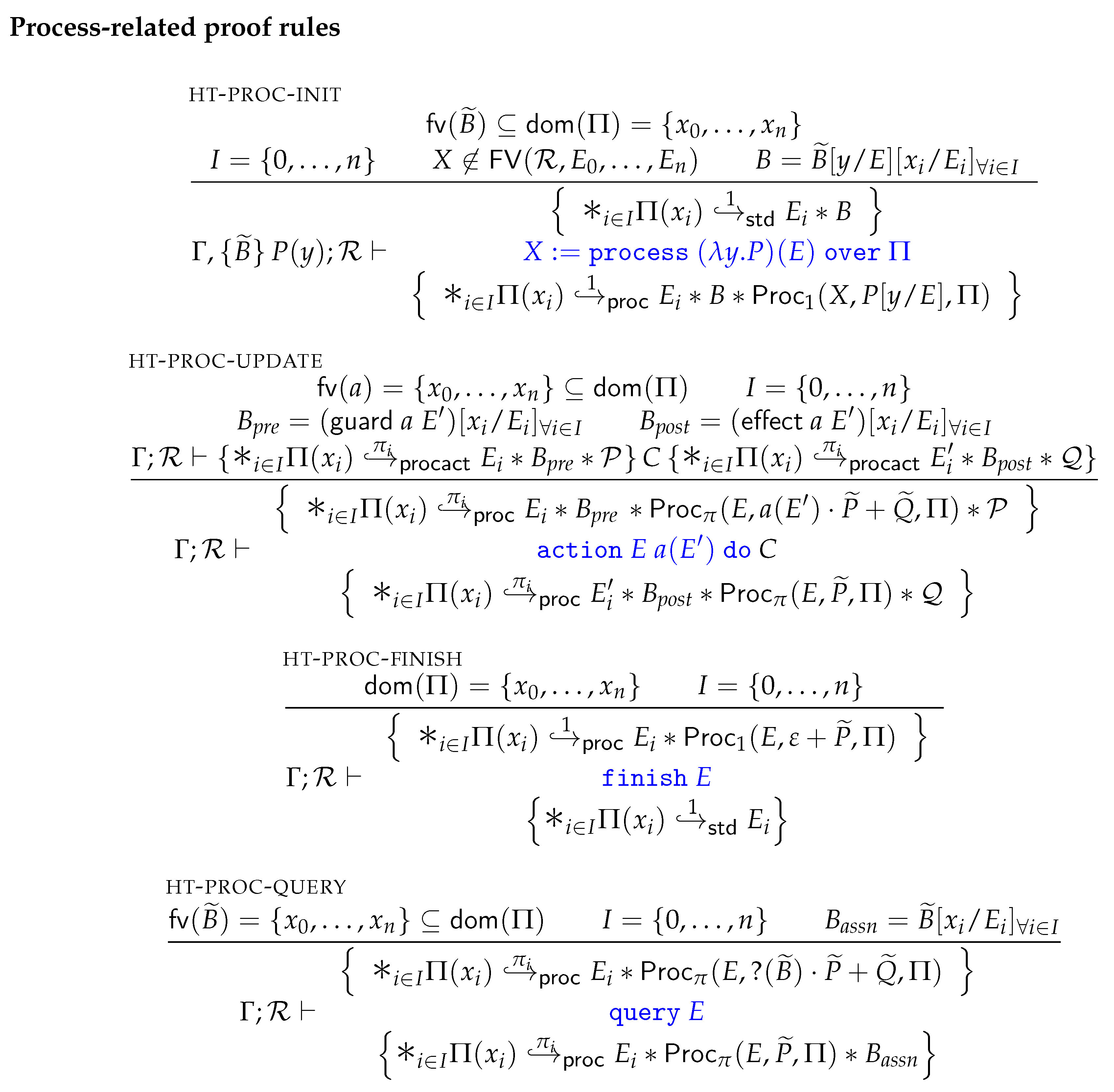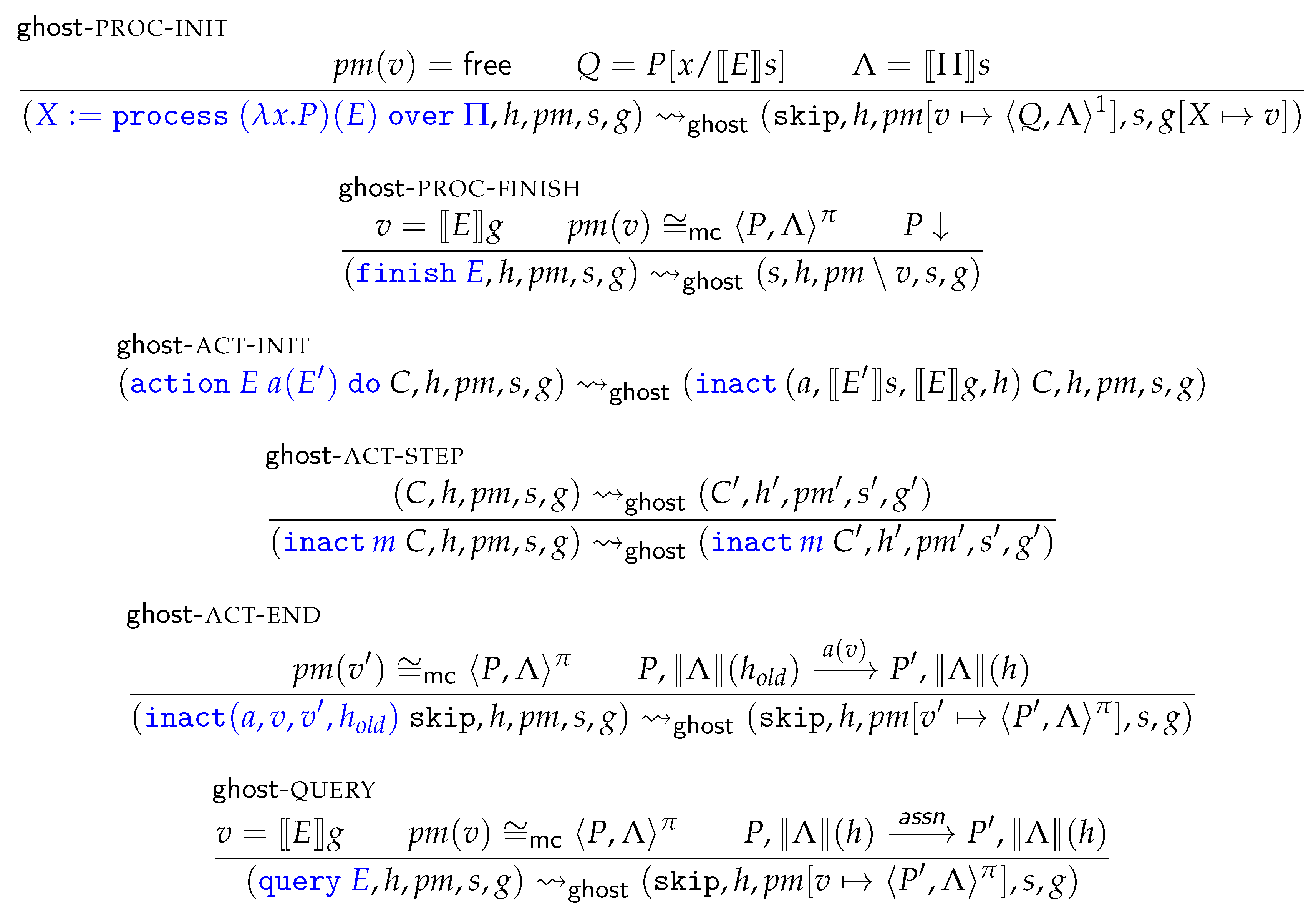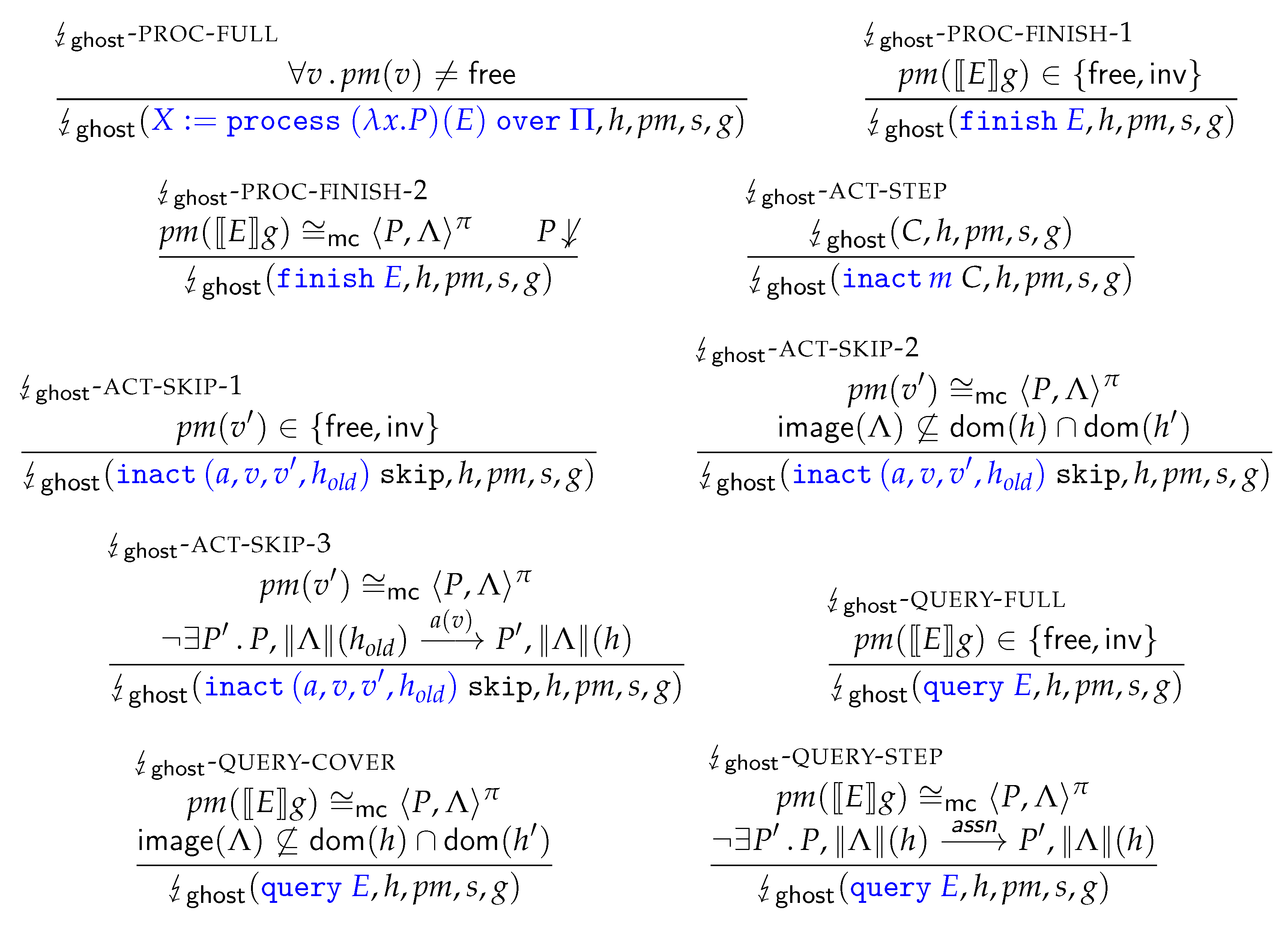3.1. Process-Algebraic Models
Program abstractions are defined using the following ACP-style [
30] process-algebraic specification language, where
are
process-algebraic variables;
are
values from an infinite domain
; and
are
(process-algebraic) actions.
Clarifying the different connectives and constructs,
is the
empty process, which has no behaviour. The
process is the
deadlocked process which neither progresses nor terminates. Processes of the form
are
actions, which model the basic, observable (shared-memory) system behaviours. Actions are parameterised by data, in the form of expressions
e. The process
is the
sequential composition of
P and
Q, whereas
is their non-deterministic
choice. The
parallel composition of processes
P and
Q is written
. The process
P ![Applsci 10 03928 i004 Applsci 10 03928 i004]() Q
Q is the
left-merge of
P and
Q, which is similar in spirit to parallel composition, however
![Applsci 10 03928 i004 Applsci 10 03928 i004]()
insists that the left-most process
P proceeds first. The left-merge is an auxiliary connective commonly used to axiomatise parallel composition [
31], by having
P![Applsci 10 03928 i004 Applsci 10 03928 i004]() Q
Q +
Q![Applsci 10 03928 i004 Applsci 10 03928 i004]() P
P. The process
is the infinite summation
over all values
. Any summation
is a
binder for the summation variable
x. In the remainder we assume without loss of generality that all variables bound by summation are unique (since any such variables can be renamed to unique ones if this is not yet the case). Sometimes
is written to abbreviate
. The conditional (guarded) process
behaves as
P if the Boolean condition
b holds, and otherwise behaves as
. Finally,
is the
repetition, or
iteration of
P, and denotes a sequence of zero or more
P’s. The infinite iteration of
P is derived to be
. Finally,
is the
assertive process, which is very similar to guarded processes:
is behaviourally equivalent to
in case
b does not hold. However, assertive processes have a special role in our approach: they are the main subject of process-algebraic analysis, as they encode the properties
b to verify, as logical assertions. Moreover, they are a key component in connecting process-algebraic reasoning with deductive reasoning, as their properties can be relied upon in the deductive proofs of programs via the
ghost command.
3.1.1. Action Contracts
The presented verification approach uses processes in the presence of data, which is implemented via
action contracts. Action contracts consist of pre- and postconditions which we refer to as
guards and
effects, respectively, that logically describe the state changes that are imposed by the corresponding action. In the remainder of this article, each action is assumed to have an action contract assigned to it. Instead of defining syntax for writing these contracts, the following two functions are assumed for obtaining the pre- and postcondition of an action (from
) and its data parameter (from
), respectively.
Both these conditions are of type , which is the domain of Boolean expressions over process-algebraic variables. Note that, since actions are parameterised by data (see Definition 1), both and take a second argument to account for the input parameter, which is of type —the type of arithmetic expressions over process-algebraic variables.
Here should be read as and interpreted as a function sequence (in the sense of currying). That is, it is the set of functions mapping to the set of functions mapping to .
3.1.2. Free Variables and Substitution
A function
is used to determine the set of free process-algebraic variables in expressions as usual, and likewise for
and
for Boolean expressions
b and processes
P. We often omit the subscripts and simply write
whenever the context allows it. The definitions of
,
and
are mostly standard and thus deferred to [
19]. Noteworthy however are:
Substitution is written (and likewise for Boolean expressions and processes) and has a standard definition: replacing any occurrence of x inside by the expression e. Noteworthy is that substitutions inside action processes do not affect the action contracts: .
3.1.3. Operational Semantics
The denotational semantics of process-algebraic expressions and conditions is defined in the standard way, as total functions that evaluate to and , resp. The set is the domain of process stores, which are used to give an interpretation to all process-algebraic variables. The overloaded notations and are used instead of and wherever the context allows it. Moreover, is sometimes written instead of when e is closed (i.e., when ), and likewise for .
The operational semantics of the process algebra language is expressed as a labelled binary small-step reduction relation over process configurations, defined as —pairs of processes and process stores. The labels of the reduction rules are defined as follows: . Transitions labelled are reductions of actions, whereas indicates reductions of assertions.
Before giving the reduction rules we first define a notion of successful termination of processes P. Successful termination is only defined for processes that are well-formed. Any process P is defined to be well-formed if any action parameters (the e’s in ) and conditions (the b’s in ) occurring inside P are closed.
Definition 2 (Successful termination)
. Intuitively, any process P can terminate successfully if P has the choice to have no further behaviour. This means that can always successfully terminate (↓-EPSILON), as it has no behaviour, while can never successfully terminate. Iteration can always successfully terminate (↓-ITER) as it may choose not to start iterating and thereby to behave as .
The small-step reduction rules of process configurations are given below. Likewise to the definition of successful termination, also these reduction rules require processes to be well-formed.
Definition 3 (Reductions of process configurations)
. Most of the reduction rules are standard in spirit [
32]. However, the handling of actions and their contracts make this process algebra language non-standard. More specifically, the non-standard ⟶-ACT reduction rule for action handling permits the state
to change in any way, as long as these changes comply with the action contract. We will later use the ⟶-ACT rule to connect shared-memory updates in programs, to action contract-complying state changes on the process level.
Moreover, the notion of successful termination is used to define the reduction rule for sequential composition, ⟶-SEQ-R, which is standard in process algebra languages with
[
33]. (An alternative on the explicit use of successful termination is to introduce internal (
-)transitions for the reductions of
. However, this might make the remaining formalisation less elegant, for example by requiring a notion of weak bisimilarity, instead of the notion of strong bisimilarity that is introduced later in this section.)
3.1.4. Process-Algebraic Verification
Process-algebraic verification in our approach amounts to verifying that all reachable assertional processes are always satisfied, which we are interested in so that the program logic can rely on the b’s. Any process configuration fails to verify, or exhibits a fault, which we write , if it can directly violate an assertion. Verifying a process, i.e., checking for fault absence, could for example be reduced to checking the -calculus formula , e.g., using the mCRL2 model checker, where ↯ is modelled as an explicit fault state, meaning “no faults are every reachable”.
Fault exhibition is defined inductively as follows.
Definition 4 (Faulting process configuration)
. Any process configuration is defined to be safe, denoted as , if it can never reach a faulting configuration. More formally:
Definition 5 (Safe process configurations). The predicate is coinductively defined such that, whenever holds, then(1); and (2) for any , and α, if , then .
Definition 6 (Verified processes). Any well-formed process P is defined to be verified with respect to a (pre)condition b, which is written , if .
3.1.5. Bisimulation
Our verification approach allows handling process-algebraic models up to (strong) bisimulation.
Definition 7 (Bisimulation). Any binary relation over processes is defined to be a bisimulation relation if, whenever , then:
- (1)
if and only if .
- (2)
if and only if , for any σ.
- (3)
For any σ, , and α, if , then there exists a such that and .
- (4)
For any σ, , and α, if , then there exists a such that and .
Any two processes P and Q are defined to be bisimilar, or bisimulation equivalent, written , if and only if there exists a bisimulation relation such that . Bisimilarity expresses that both processes exhibit the same behaviour, in the sense that their action sequences describe the same state changes. Any bisimulation relation constitutes an equivalence relation. Furthermore, bisimilarity is a congruence for all process algebraic connectives.
Successful termination can intuitively be understood as P being bisimilar to the process , that is, by having the choice to have no further behaviour.
Proposition 1. If then .
Lemma 1. If and , then .
Figure 2 gives a list of bisimulation equivalences that hold for our process algebra language. Note that the left-merge connective
![Applsci 10 03928 i004 Applsci 10 03928 i004]()
is not strictly needed, in the sense that our approach does not rely on it, but can be used to prove for example that
is bisimilar to
.
3.2. Programs
Our verification approach is formalised on the following simple concurrent pointer language, where are (program) variables.
Definition 8 (Expressions, conditions, conditions, commands)
. This language is a variation of the language proposed by O’Hearn [
24] and Brookes [
23]. In particular, we extend their language with
specification-only commands (code annotations) for handling process-algebraic models. These commands are coloured blue. Note that the blue colourings do not have any semantic meaning; they only indicate which language constructs are specification-only. Moreover, we interchangeably refer to commands also as programs.
3.2.1. Standard Language Constructs
The notation stands for heap dereferencing, where E is an expression whose evaluation determines the heap location to dereference. The commands and denote heap reading and writing: they read from, and write to, the heap at location E, respectively. Moreover, allocates a free heap location and writes the value represented by E to it, whereas deallocates the heap location at E.
Regarding concurrency, the command is the statically-scoped parallel composition of and and expresses their concurrent execution. In the sequel, we sometimes refer to commands that are put in parallel as different threads; for example and in the above. Moreover, expresses a statically-scoped lock: it represents the atomic execution of C, that is, without interference of other threads. The command represents partially executed atomic programs: ones that are currently being executed, where C is the remaining program that still has to be executed atomically. Such commands are sometimes referred to as “runtime syntax”, as they are not written by users of the language, but are instead an artefact of program execution.
3.2.2. Specification-Only Constructs
The instructions that are displayed in blue are the specification-only language constructs, for handling process-algebraic models in the logic. These instructions are ignored during regular program execution and are essentially handled as if they were code comments.
Specification-wise, initialises a new process-algebraic model P in the proof system that takes a single input argument named x, namely (the evaluation of) the expression E. This model is used (1) as a specification of how a particular region of shared memory, specified by , is allowed to evolve over time; and (2) to support reasoning over the model to indirectly prove properties of how the heap evolves. The component is an abstraction binder, which is also defined in Definition 8 and is used to connect process-algebraic variables to heap locations in the program. In particular, the abstraction binders make the connections/links between process-algebraic state and shared-memory program state (that is, heap locations). In the sequel, we often use abstraction binders as if they were finite partial mappings, , from process-algebraic variables to the expressions whose evaluation determine the corresponding heap location. Finally, the variable X identifies the process-algebraic model after initialisation.
The command
is used to
finalise the process-algebraic model identified by
E in the logic, given that it can successfully terminate. Finalisation is later explained in more detail, in
Section 3.4.
The specification command is used to link the execution of programs with the execution of process-algebraic models. More specifically, it executes the program C in the context of the model identified by E, as the process-algebraic action a that takes (the evaluation of) as an input argument. The soundness argument of the program logic establishes a refinement relation between programs and their models, and this relation is established by synchronising program execution with process execution, with help of these action blocks.
The C command denotes a partially executed action program; one that still has to execute C. Likewise to , this command can only occur during runtime and is not written by users.
Lastly,
E is used to connect process-algebraic reasoning to deductive reasoning: it allows the deductive proof of the program to rely on (or
assume) properties that are proven to hold (or
guaranteed) on the process-algebraic model identified by
E, via process-algebraic analysis. These are the properties that are encoded as assertions
in this model. Of course, this would require linking process-algebraic state to program state, which we come to later, in
Section 3.3 and
Section 3.4.
3.2.3. Free Variables and Substitution
We use the standard (overloaded) notations
,
,
and
to refer to the set of free
program variables in the given (Boolean) expression
E and
B, abstraction binder
, and command
C, respectively. Moreover, the notation
denotes the
substitution of the program variable
X for the expression
inside
E; and likewise for Boolean expressions, abstraction binders, and commands. The full definitions of
and
are mostly standard, and therefore deferred to [
19].
3.2.4. User Programs
As just discussed, our simple programming language contains runtime syntax—instructions that are not written by users but are only introduced during runtime. Commands that are free of such runtime constructs are called user commands.
Definition 9 (User commands). Any command C is defined to be a user command, denoted , if C does not contain sub-commands of the forms and , for any command .
3.2.5. Wellformedness
Moreover, our verification approach only applies to well-formed commands. Notably, our technique requires that, for any program of the form and C, the inner action program C only contains a subcategory of commands, excluding atomic commands and specification-only constructs, in particular nested action blocks. The latter is needed since actions must be atomically observable by environmental threads. This restriction is captured by the following definition.
Definition 10 (Basic programs, well-formed programs). Any command C is defined to be basic, denoted , if C does not contain any atomic sub-programs, i.e., or , nor specification-specific language constructs, i.e., , , , , or .
A command C is defined to be well-formed, denoted , if, for any command or C that occurs in C it holds that .
Lemma 2. implies for any command C.
3.2.6. Operational Semantics
The denotational semantics of expressions and conditions are again defined in the standard way, and evaluate to and , respectively, where is a (program) store that gives an interpretation to all program variables.
The operational semantics of programs is defined in terms of a binary small-step reduction relation between program configurations. A program configuration is a triple, consisting of a command C as well as a heap h that models shared memory, and a store that models thread-local memory. Any program configuration of the form is defined to be final or terminated. Heaps are defined to be finite partial mappings from values to values. Heap locations are themselves values, so that they can be assigned to, and read from, local variables, and thus be handled as any value. The function denotes the mapped domain of a given heap, so that .
Definition 11 (Small-step operational semantics of programs)
. Most of the transition rules are standard; see for example [
34]. The
update notation
defines a store that is equal to
s, except that
X is mapped to
v. A similar notation is used for heaps, namely
. Moreover, the notation
denotes the
removal of the entry at
v in
h.
An interesting aspect of the operational semantics is that atomic programs are executed using a small-step reduction strategy (via -INATOM-STEP and -INATOM-SKIP), rather than a big-step execution, which is more customary. This is done for technical reasons: it simplifies the establishment of a simulation/refinement between programs and their models. Consequently, we use a notion of a locked program to define the transition rules for atomic programs. Any command C is said to be (globally) locked if C executes an atomic program, i.e., if C has as a subprogram for some .
Definition 12 (Locked programs)
. Any command C is locked
if holds, where is defined as follows, by structural recursion on C: The rules -PAR-L and -PAR-R for parallel composition allow a thread to make an execution step only if the other thread is not locked, thereby preventing thread interference while executing atomic programs. One might ask whether this handling of locks could not potentially lead to deadlock scenarios, for example by encountering configurations during runtime for which both and hold. However, we will later see and prove that no such deadlocks can be reached, given that one starts with an initial configuration that contains a user program.
Furthermore, the specification-only language constructs do not affect the state of the program (not the heap nor the store) and are essentially handled as if they were comments. Notice however, that commands of the form are first reduced to C before C is being executed. This is done for technical reasons, as this makes it more convenient to later establish a simulation relation between execution steps of programs and processes.
The semantics of programs has the following preservation properties.
Lemma 3. Program execution preserves basicality and wellformedness:
- 1.
If and , then .
- 2.
If and , then .
3.2.7. Fault Semantics
Apart from an operational semantics, we also define a
fault semantics for programs [
35] that classifies runtime errors that may occur during program execution. Its definition uses two auxiliary functions,
and
, for obtaining the set of heap locations that
can be accessed or
written-to, respectively, in a next reduction step of
C. Their definitions are deferred to [
19] as well, as they are quite lengthy and not essential for understanding the definition of the fault semantics.
The fault semantics of program configurations is expressed as a predicate that is inductively defined as follows.
Definition 13 (Fault semantics of programs)
. Intuitively, a program configuration exhibits a fault if it (1) accesses unallocated memory, or (2) is deadlocked, or (3) allows performing a data-race.
More specifically, ↯-READ expresses that heap reading faults if the heap location at E is unoccupied. For the same reason, also heap writing (↯-WRITE) and heap deallocation (↯-DISPOSE) may fault. The ↯-PAR-L rule expresses that any parallel program can fault if can fault, given that is not locked, or the other way around (↯-PAR-R covers the other direction). Program configurations that hold multiple global locks are also considered to be faulting, by ↯-DEADLOCK. Finally, the fault semantics encodes the definition of a data-race, via ↯-RACE-1 and ↯-RACE-2. To clarify, any configuration exhibits a data-race if C has (at least) two threads that can both access a common location in h in the next reduction step, where at least one of these accesses is a write.
We will later see that the soundness argument of our program logic covers that verified programs are free of faults. More specifically, we will prove that, for any program C for which a proof can be derived, we have that C is fault-free with respect to any heap h and store s that satisfy C’s precondition, and moreover, that every configuration that is reachable from is also fault-free.
Finally, to show that the operational semantics of programs is coherent with respect to faults, we prove that the operational semantics is progressive for all non-faulting program configurations.
Theorem 1 (Progress of ). For any program configuration for which holds, either is final, or there exists a configuration such that .
3.3. Assertions
The assertion language of our verification approach is defined by the following grammar.
Assertions can be built from plain Boolean expressions B, and may contain several standard connectives from predicate logic: universal and existential quantifiers, and disjunction. Moreover, logical conjunction (∧) is replaced by the separating conjunction * from Concurrent Separation Logic (CSL). The connective is the iterated separating conjunction, with I a finite set that represents , given that . The connective is known as the magic wand and is used to describe hypothetical judgments, much like the logical implication from predicate logic.
Apart from these standard CSL connectives, the assertion language contains three different heap ownership predicates , with a rational number that represents a fractional permission, and t the heap ownership type, as well as an ownership predicate for program abstractions. Finally intuitively means that and are bisimilar processes with respect to the current state.
The definitions of free variables
of assertions
, and substitution
in
, are the standard ones and are therefore deferred to [
19]. Assertions that are free of
and
predicates are called
pure. Any assertion that is not pure is said to be
spatial.
3.3.1. Heap Ownership
The assertion is the heap ownership assertion and expresses that the heap contains the value represented by the expression at heap location . Moreover, and t together determine the access rights to this heap location. In more detail, depending on the ownership type t, the ownership predicates express different access rights to the associated heap location:
Standard heap ownership. is the standard heap ownership predicate from (intuitionistic) separation logic that provides read-access whenever , and write-access in case . Moreover, the subscript indicates that the associated heap location is not bound to any process-algebraic model. We say that a heap location is bound by, or subject to, a program abstraction, if there is an active program abstraction with a binder that contains a mapping to v, that is, .
Process heap ownership. is the process heap ownership predicate, which indicates that the heap location at E is bound by an active process-algebraic abstraction, but in a purely read-only manner. More precisely, assertions exclusively grant read-access, even in case .
Action heap ownership. is the action heap ownership predicate, which indicates that the heap location E is bound by an active process-algebraic model, and is used in the context of an action block, in a read/write manner.
Observe that action points-to assertions essentially give the same access rights as assertions. Nevertheless, they are both needed, to be able to distinguish between bound and unbound heap locations in the logic. For example, the program logic must not allow to deallocate memory that is currently bound to (protected by) an active process-algebraic model, as this would be unsound.
Moreover, even though predicates never grant write access, we will later see that the proof system allows predicates to be upgraded to inside action blocks, and again provides write access when . More precisely, predicates grant the capability to regain write access to E, in the context of an action program. This system of upgrading enforces that all modifications to E happen in the context of commands, so that the modifications are protected and can be recorded by the program abstraction identified by , as the action a.
In addition to these three heap ownership predicates, we derive a fourth such predicate, called the process–action heap ownership predicate. This ownership predicate is equivalent to only if denotes write access, and otherwise it is equivalent to .
Definition 15 (Process–action heap ownership).
This derived predicate is for later use, in the proof system of our program logic. Finally, the notation is sometimes used as shorthand for , where .
3.3.2. Process Ownership
The assertion expresses ownership of a program abstraction that is identified by E, where the abstraction is represented by the process . Ownership in this sense means that the thread has knowledge of the existence of the process-algebraic model , as well as the right to execute as prescribed by this model. The mapping connects the abstract model to the concrete program by mapping the process-algebraic variables in the abstraction to heap locations in the program, as discussed before. And last, the fractional permission is needed to implement the ownership system of program models. Fractional permissions are only used here to be able to reconstruct the full predicate. We shall later see that predicates can be split and merged along and parallel compositions inside , and be consumed in the proof system by programs.
Even though reasoning about process-algebraic models is done purely on the level of process-algebraic state, in the program logic it is allowed to mix program state with process-algebraic state. This is indicated by the tilde above the , which means that P can have both program variables and process-algebraic variables. Such processes are called hybrid processes and are defined as follows.
Definition 16 (Hybrid expressions, conditions and processes).
These hybrid processes thus allow mixing process-algebraic reasoning with deductive reasoning using our program logic. The function is used for obtaining the set of free process-algebraic variables in , and for obtaining all free program variables in (and likewise for and ).
We shall later see that the program logic allows replaces processes
inside
predicates by bisimilar ones. However, note that one cannot use the standard notion of bisimilarity as defined in Definition 7 for this in case
has any program variables occurring freely in it. To resolve this, we include a relation
in the assertion language, stating that
and
are bisimilar while taking into account any (pure) information that is available from the context. This is further clarified in
Section 3.3.7, after we discussed the models of the logic.
3.3.3. Models of the Program Logic
Before
Section 3.3.7 discusses the semantics of assertions, this section first introduces
permission heaps and
process maps, that form the basis for the models of our concurrent separation logic. Permission heaps extend ordinary program heaps (i.e.,
) to capture the three different types
t of heap ownership, whereas process maps capture the state and ownership of process-algebraic abstractions.
Let us start by introducing fractional permissions, which are used in the definitions of both permission heaps and process maps.
3.3.4. Fractional Permissions
In the assertion language, all heap/process ownership predicates have an associated rational number . There are used to express the “amount” of ownership that is available to the corresponding heap location or program model.
We define a rational number
to be a
(Boyland) fractional permission in case
[
36]. The original work of Boyland uses fractional permissions to distinguish between write access (
) and read access (
) to some shared resource. However, in our work this is slightly different, since the fractional access permissions
annotated to
predicates never provide write access.
To conveniently handle fractional permissions, we define basic notions of validity () and disjointness () of rational numbers, as follows.
Definition 17 (Permission validity, Permission disjointness).
The predicate determines whether the given rational number is within the range , that is, is a valid Boyland fractional permission. (Here is the sort of propositions.) The binary relation determines disjointness of two rationals. Disjoint rational numbers do not overlap, in the sense that both operands are fractional permissions, as well as their addition.
Lemma 4. and satisfy the following properties.
- 1.
If , then , , and .
- 2.
If and , then and .
3.3.5. Permission Heaps
The models of our program logic use permission heaps to give a semantic meaning to heap ownership. Permission heaps and their heap cells are defined as follows, and are slightly richer than ordinary program heaps to be able to administer the access permissions and the different ownership types.
Definition 18 (Permission heap cells, Permission heaps)
. Permission heaps are defined to be total functions from values (representing heap locations) to permission heap cells, , which in turn are inductively defined to be one of the following:
, which is an unoccupied heap cell.
, which is a standard heap cell that stores the value . Standard heap cells are the models of the standard heap ownership predicates, .
, which is a process heap cell that stores the value v. These are used as models of the ownership predicates.
, which is an action heap cell that stores the value . Action heap cells are used as the models for the predicates. Moreover, action heap cells store a second value . This extra value is maintained for technical reasons, to help in establishing soundness of the program logic. The value is referred to as a snapshot value: a copy of the original value stored by the heap cell, that is made when an action block was entered.
, which is an invalid, or corrupted, permission heap cell.
Note that, unlike program heaps, permission heaps are defined to be total functions, where the heap cells have an explicit notion of being . This is done to give permission heaps and their cells nicer algebraic properties. The unit permission heap is defined to be , containing at every entry. Furthermore, permission heap cells also have an explicit notion of being invalid. Invalid heap cells represent the erroneous result of composing two incompatible heap cells.
We now define several operations on permission heaps.
Validity. Any permission heap is defined to be valid if the permissions of all ’s heap cells are valid, where is always valid and is never valid.
Definition 19 (Validity of permission heaps).
A permission heap is defined to be valid
, written , if holds for every , where the predicate is defined as follows. Disjointness. Two permission heaps and are disjoint if all their heap cells are pairwise compatible and their underlying permissions are disjoint.
Definition 20 (Disjointness of permission heaps)
. Two permission heaps, and , are disjoint
, denoted , if holds for every , where the relation is defined as follows. Disjoint union. The following operation defines the disjoint union (i.e., the composition) of two permission heaps.
Definition 21 (Disjoint union of permission heaps)
. The disjoint union of any two permission heaps is defined to be the permission heap , with defined as follows. Note that only gives a non-corrupted entry when applied to two compatible heap cells. Furthermore, is neutral with respect to while is absorbing.
Below are the most important properties of validity, disjointness and disjoint union.
Lemma 5. (The analogous operations on permission heap cells have the exact same properties.)
- 1.
.
- 2.
.
- 3.
If .
- 4.
If , then .
- 5.
If and , then also
- (a)
and
- (b)
.
3.3.6. Process Maps
The models of the logic also use process maps in addition to permission heaps, to give a semantic meaning to process ownership predicates in the logic. Process maps and their entries are defined as follows, where binders are finite partial mappings from process variables to heap locations (i.e., values). These binders are the models for the abstraction binders defined earlier in Definition 8.
Definition 22 (Process map entries, process maps, binders)
. Process maps are total mappings from values (identifying program abstractions) to process map entries, which are, in turn, inductively defined to one of the following three elements:
, which models unoccupied or free entries in .
, which is an occupied process map entry. These are used as models for the assertions, where E identifies the process map entry in , and the binder is a model for .
, which denotes an invalid, or corrupted, process map entry.
Likewise to permission heaps, process maps are defined as total functions with entries that can explicitly be or , as this provides desirable algebraic properties. Corrupted entries represent the erroneous result of taking the disjoint union of two incompatible, non-disjoint entries. The unit process map is defined to be , containing at every entry.
We now define several operations and relations on process maps that are analogous to the operations defined earlier for permission heaps, starting with bisimilarity.
Bisimilarity. Any two process maps are said to be bisimilar, if all their entries are equal point-wise, or contain occupied entries with process components that are bisimilar.
Definition 23 (Process map bisimilarity)
. Two process maps and are defined to be bisimilar, denoted , if for every , with the relation defined as follows. Both and are equivalence relations. A notion of bisimilarity of process maps is needed in addition to ordinary equality, since for example disjoint union of process maps is not associative nor commutative with respect to ordinary equality, as opposed to bisimilarity. Moreover, we will later see that the program logic always allows replacing processes inside predicates by bisimilar ones, as discussed earlier. But to handle such replacements at the semantic level, we allow process maps and their entries to be handled up to and , respectively.
Validity. Any process map is said to be valid intuitively if none of ’s entries are corrupt and all occupied entries of hold a valid associated fractional permission.
Definition 24 (Process map validity)
. Any process map is defined to be valid
, denoted , if holds for every , with the predicate defined as follows. It is not difficult to see that is trivially valid, and that bisimilarity is validity-preserving, i.e., and implies for every and ; and likewise for .
Disjointness. Two process maps are said to be disjoint if none of their entries are corrupt, and all fractional permissions of their entries are point-wise disjoint, as captured by the following definition.
Definition 25 (Process map disjointness)
. Any two process maps and are defined to be disjoint
, denoted , if for every , with the relation defined as follows. The intuition of disjointness is that disjoint process maps can safely be composed without corrupting any of their entries. Disjointness is a symmetric relation and is a congruence with respect to bisimilarity, meaning that and and implies .
Disjoint union. The following operation defines the disjoint union of two process map (entries).
Definition 26 (Disjoint union of process maps)
. The disjoint union
of two process maps and is defined as , with defined as follows. Likewise to disjoint union of permission heaps, the composition of incompatible process map entries produces a corrupted entry. The entry is again neutral, whereas is absorbing (that is, composing with any entry results in ). Disjoint union is a congruence with respect to bisimilarity, so that and implies .
Lemma 6. (The analogous operations on process map entries have the exact same properties.)
- 1.
.
- 2.
.
- 3.
.
- 4.
If , then .
- 5.
If and , then also
- (a)
, and
- (b)
.
3.3.7. Semantics of Assertions
Let us now define the semantic meaning of assertions. The semantics of assertions is defined in terms of a satisfaction relation stating that the assertion is satisfied by the model . Its definition depends on an operation for evaluating abstraction binders , that is defined as follows.
Definition 27 (Abstraction binder evaluation)
. Moreover, recall that hybrid processes may contain both program variables and process-algebraic variables. The semantics of assertions relies on a closure operation for “closing” processes with respect to any program variable occurring in it. More specifically, given any hybrid process and store s, the s-closure of , written , is defined to be , i.e., replacing every free program variable X in by . This operation is “closing” in the sense that and .
Definition 28 (Semantics of assertions)
. The modelling relation is defined by structural recursion on as follows.
As usual, any separating conjunction is satisfied by a model if that model can both be split along and into two disjoint models, such that one satisfies and the other satisfies . The semantic meaning of iterated separating conjunctions can be expressed simply in terms of the interpretation of the binary separating conjunction. Magic wands are satisfied by a model if, for any disjoint extension of that model satisfying , the extended model satisfies .
Moving to the non-standard connectives; heap ownership assertions are satisfied if the permission heap holds an entry at location E that matches with the ownership type t, with an associated fractional permission that is at least . Process ownership assertions are satisfied if the process map holds a matching entry at the position described by E, with a fractional permission at least , and a process that at least includes all the behaviours of the process . Finally, is satisfied if and are bisimilar with respect to the current state. To give an example of the use of ≈, consider the assertion . One might wish to replace with , considering that . But since is a process that includes program variables (namely X), one can not immediately deduce that it is bisimilar to according to Definition 7. However, we do have that , since for every model satisfying this assertion it holds that . We shall later give entailment rules that allow such context-dependent bisimulation equivalences to be used to simplify processes inside ownership predicates.
Lemma 7. The ⊨ modelling relation satisfies the following properties:
- 1.
and implies .
- 2.
If , then for any and such that and it holds that .
Lemma 7.1 is essential for allowing replacing process-algebraic abstractions by bisimilar ones inside the program logic. Lemma 7.2 expresses monotonicity, and states that adding resources does not invalidate the satisfiability of any assertion (i.e., adding more resources makes the assertion “more true”). This is a key property of
intuitionistic separation logic and is necessary for proving soundness of the weakening rule, which we introduce later in
Section 3.4.1.
3.3.8. Semantic Entailment
Let the denotation be the set of all models that are satisfied by the assertion . Given any two assertions and , the assertion is defined to semantically entail , denoted , if every model of is also a model of , that is, . Semantic entailment is thus a preorder and a congruence for all connectives of the assertion language.
3.4. Proof System
This section introduces the proof system of our model-based verification technique, which consists of structural proof rules (
Section 3.4.1) as well as Hoare proof rules (
Section 3.4.2). This proof system essentially extends the CSL of [
34] by adding permission accounting [
36,
37] and machinery for handling process-algebraic program abstractions.
3.4.1. Entailment Rules
Figure 3 presents the structural rules of the program logic. The notation
is a shorthand for both
and
, and indicates that the rule can be used in both directions.
The rules for the standard connectives are mostly as expected. PLAIN-DUPL expresses that plain expressions can freely be duplicated, whereas *-PLAIN shows that * has the same meaning as ∧ in the case of plain assertions. The rule *-WEAK shows that our concurrent separation logic is affine (intuitionistic) by allowing to forget about resources. The rules *-ASSOC and *-COMM express that the separating conjunction is associative and commutative, respectively, whereas *-TRUE allows composing any resource with . The rule TRUE-INTRO is the introduction rule for , while FALSE-ELIM is the elimination rule for stating that anything can be derived from falsehood. The -INTRO and -ELIM rules show that magic wands can be used similarly to the modus ponens inference rule of propositional logic, with respect to *. The rules ∀-INTRO, ∀-ELIM, ∃-INTRO and ∃-ELIM are the standard introduction and elimination rules for universal and existential quantifiers. ITER-SPLIT-MERGE enables splitting and merging iterated separating conjunctions along the associated (finite) index set.
Clarifying the rules for handling heap ownership; -SPLIT-MERGE expresses that heap ownership predicates of any type t may be split (in the left-to-right direction) as well as be merged (right-to-left) along . Note however, that multiple points-to predicates for the same heap location may only co-exist if they have the same ownership type, as indicated by the -INCOMPATIBLE rule. Any heap ownership assertion with an invalid fractional permission associated to it entails by -INVALID Furthermore, the *-PROCACT-SPLIT-MERGE inference rule states that iterated heap ownership predicates can be split into disjoint iterated and predicates, or be merged into one such iteration.
Moving to the entailment rules for handling process-algebraic abstractions; PROC-≅ allows replacing any process by one that is bisimilar in the current context. The rules ≈-REFL, ≈-SYMM and ≈-TRANS show that context-dependent bisimilarity forms an equivalence relation in the logic with respect to separating conjunction, while ≈-CONG-∘, ≈-CONG-SUM, ≈-CONG-COND and ≈-CONG-ITER together show that ≈ is a congruence relation in the logic for all process-algebraic connectives. The rules ≈-COND-TRUE and ≈-COND-FALSE allows eliminating conditionals in any processes (together with the Proc-≅ rule that is). Moreover, ≈-SUM-ALT allows singling out a single choice out of a process-algebraic summation of choices. Notice here that one can pick any arbitrary
program expression for singling out such a choice, which makes this rule particularly useful. Similarly to heap ownership, any process ownership with an invalid fractional permission entails
by Proc-INVALID. The rule ≈-TERM again makes explicit the intuitive meaning of successful termination, matching Proposition 1. Finally, Proc-SPLIT-MERGE allows splitting and merging process ownership predicates in the same style as
, to distribute parallel processes over parallel threads. Notably, by splitting a predicate
into two, both parts can be distributed over different concurrent threads in the program logic, so that thread
i can establish that it executes as prescribed by its part
of the abstract model. Afterwards, when the threads join again the remaining partial abstractions can be merged back into a single
predicate. This system of splitting and merging thus provides a compositional, thread-modular way of verifying that programs meet their abstraction. The logical machinery of this is further discussed in
Section 3.4.2.
Any deduction that can be derived using the rules of
Figure 3 is sound in the standard sense:
Theorem 2 (Soundness of the entailment rules). implies .
3.4.2. Program Judgments
We now define
program judgments and give the Hoare rules of the program logic. Judgments of programs are sequents (quintuples) of the form
. The right-hand side is a traditional Hoare triple, whereas
is a
resource invariant that captures resources available only to atomically executing programs (i.e., in executions that are free of thread interference), and
an environment in the style of interface specifications of [
38]. These
process environments have the following definition.
That is, process environments are comma-separated sequences of pairs of processes P and their precondition , with x a placeholder variable for an input parameter that may occur freely in both P and . Note that processes do not have postconditions here; if desired one could encode process Hoare triples op top of these pairs as —by adding a trailing assertion. Moreover, even though process environments are given as sequences, they are used as if they were (finite) sets, as is customary, in the sense that the order of their pairs is unimportant.
Process environments contain the contracts of the process-algebraic models defined for the program under verification. In particular, they allow for assume-guarantee style reasoning: the proof system may
assume validity of these contracts when dealing with process-algebraic models, since they must be
guaranteed externally, for example via interactive theorem proving or model checking, e.g., using mCRL2 [
25]. Validity of process contracts and process environments is defined as follows.
Definition 30 (Validity of process environments). Any pair of a process P and its precondition is defined to be valid, denoted , if .
Any process environment Γ is defined to be valid
if , which is a judgment inductively defined by the following two rules. Figure 4 and
Figure 5 give the Hoare rules of the logic. The standard structural rules are essentially the same as the ones of classical CSL [
34]. One minor difference is that HT-ATOMIC leaves
instead of “
” after obtaining a resource invariant, since our logic is intuitionistic. (The assertion language of classical CSL contains an extra
construct, for explicitly denoting that the heap is empty. In our intuitionistic version of the logic, resources are allowed to be thrown away using *-WEAK. As a consequence, assertions cannot express “precise” properties about the content of the heap, including emptiness of heaps.) Moreover, our assertion language does not contain the logical conjunction ∧ connective, but has separating conjunction instead.
3.4.3. Heap Ownership
The HT-READ rule states that reading from the heap is allowed with any type t of heap ownership , whereas heap writing (HT-WRITE) is only allowed with ownership predicates of type or . The HT-WRITE rule thus restricts assertions to exclusively grant read-access to the associated location. We will in a moment see that the proof rule for programs can upgrade predicates to to regain write access to the heap location at E. This system of upgrading enforces that all modifications to E are captured by the program abstraction to which the heap location is subject to, inside an action block. The rule HT-ALLOC for heap allocation generates a new points-to predicate of type , indicating that the allocated heap location is not (yet) subject to any program abstraction. Heap deallocation (HT-DISPOSE) requires a full standard ownership predicate for the associated heap location, thereby making sure that the deallocation does not break any bindings of active program abstractions, which would be unsound.
3.4.4. Process Ownership
Figure 5 gives the Hoare rules for introducing, eliminating and updating process-algebraic abstractions. The HT-PROC-INIT rule handles initialisation of an abstract model
P with input parameter
y, over a set of heap locations as specified by
. This rule requires
standard heap write ownership for any heap location that is to be bound by
P according to
, and these are converted to
. Moreover, HT-PROC-INIT requires that the precondition
B of
P holds, which is constructed from
by replacing all process variables
by the values
at the corresponding heap locations as specified by
. (Here we slightly abuse notation for ease of presentation. In the proof rule, we write
for converting a condition
to a condition over only program variables, by substituting all free process variables
occurring in
by a program expression
. However, in our Coq formalisation we of course have a special operation for such conversions.) A
predicate with full permission is ensured, giving the current thread full ownership of the abstraction.
The HT-PROC-UPDATE rule handles updates to program abstractions, by performing an action
in the context of an
program. This rule imposes four preconditions on handling
programs. First, a predicate of the form
is required for some
. In particular, the process component must be of the form
and therewith allow performing the
a action. After performing
a the process will be reduced to
, and
will be discarded as the choice is made not to follow execution as prescribed by
. To get processes in the required format, the entailment rules in
Figure 3 can be used together with the bisimulation equivalences given earlier in
Figure 2. To give an example, processes of the form
can always be rewritten to
to obtain the required choice. Second,
predicates are required for any heap location that is bound by
. These points-to predicates are needed to resolve the guard and effect of
a. Third,
a’s guard must indeed hold. (The notation
is a shorthand for
for some fresh
, and likewise for
.) And last, the remaining resource
must hold as well.
Among the premises of HT-PROC-UPDATE is a proof derivation for the sub-program C, in which all required predicates are “upgraded” to and thereby regain write access when . However, in case the upgrade does not give any additional privileges, since provides read-access just the same. We found that these unnecessary conversions complicate the soundness proof. To avoid unnecessary upgrades, we convert all affected predicates to instead, which simplifies the correctness proof. The HT-PROC-UPDATE rule ensures a process ownership predicate that holds the resulting process after execution of a. In addition, updates to the heap are ensured that comply with the postconditions of the proof derivation of C.
HT-PROC-FINISH handles finalisation of process-algebraic models that can successfully terminate. A predicate with full permission is required, implying that no other thread can have a fragment of the abstract model. The rule converts all bound ownership predicates back to ownerships to indicate that these are no longer subject to the abstract model.
Lastly, HT-PROC-QUERY allows “querying” for properties that are verified on the process algebra level. Recall that the main objective of process-algebraic analysis is to verify that all reachable assertions hold. Observe that in this rule, the assertions may contain program variables in addition to process-algebraic variables, as these may have been introduced via summations (≈-SUM-ALT) or input parameters (HT-PROC-INIT). The soundness argument of the logic makes sure that the process-algebraic analysis can still be done fully on the process level (i.e., without relying on program state), meaning that this rule really makes a fusion between process-algebraic reasoning and deductive reasoning.
3.5. Soundness
This section defines the semantic meaning of program judgments and discuss the soundness proof of the program logic. This soundness proof has been mechanised using Coq, which was non-trivial and required substantial auxiliary definitions. This section discusses the most important auxiliary definitions and explains their use. For further proof details we refer to the Coq development [
19].
The soundness theorem relates program judgments to the operational semantics of programs and boils down to the following: if (1) a proof can be derived for any program C and (2) the contracts in of all abstract models of C are satisfied (proven externally), then C executes safely for any number of computation steps. Execution safety in this sense also includes that C does not fault for any number of reduction steps with respect to the fault semantics of programs; see Definition 13.
Our definition of execution safety extends the well-known inductive definition of configuration safety of Vafeiadis [
34] by adding machinery to handle process-algebraic abstractions. The most important extension is a
simulation argument between concrete program executions (with respect to
) and the executions of all active models (with respect to
). However, as the reduction steps of these two semantics do not directly correspond one-to-one, this simulation is established via an intermediate instrumented semantics referred to as the
ghost operational semantics. This intermediate semantics is defined in
Section 3.5.1 in terms of
ghost transitions that essentially define the lock-step execution of program transitions
and the transitions
of their abstractions. Our definition of “
executing safely for n execution steps” includes that all
steps can be simulated by
steps, and vice versa, for
n execution steps. Thus, the end-result is a
refinement between programs and their abstractions.
In addition to establishing such refinements, our definition of execution safety must ensure that the HT-PROC-QUERY proof rule is sound. In other words, it must allow relying on any assertions embedded in the process-algebraic models in a sound manner, as these are (assumed to be) verified externally. To account for these assertions, the definition of execution safety needs to maintain the invariant that all
active program abstractions
preserve their execution safety as defined in Definition 5 for
n execution steps, with respect to the current state of the program. (Recall that any process
P is said to be
safe according to this definition if
P’s assertions always hold.) The details of maintaining this invariant are discussed further in
Section 3.5.3.
Finally,
Section 3.5.4 formally defines process execution safety—the semantic meaning of program judgments—and presents the exact soundness statement.
3.5.1. Ghost Operational Semantics
To establish the refinements between programs and their abstractions, an intermediate semantics is used that administers the states of all active program abstractions. This intermediate semantics is referred to in the sequel as the ghost operational semantics. The ghost semantics is expressed as a transition relation between ghost configurations , which extend program configurations by two extra components, namely:
A process map that is used to administer the state of all active (initialised, but not yet finalised) process-algebraic abstractions; and
An extra store , referred to as a ghost store, as it is used to map variable names to process identifiers in the context of “ghost” instructions.
The ghost operational semantics uses two stores instead of one, to keep the administration of program data and specification-only (ghost) data strictly separated. Doing so eases establishing that variables referred to in ghost code do not interfere with regular program execution, and vice versa.
Ghost reductions essentially describe the
lock-step execution of concrete programs (
steps) and their abstractions (
steps).
Figure 6 presents an excerpt of the transition rules. This excerpt only contains the reduction rules related to program abstraction; all other rules are essentially the same as those of
, with the two extra configuration components simply carried over and left unchanged. Recall that the blue colourings are merely visual cues and do not have any special semantical meaning.
Clarifying the ghost reduction rules, GHOST-PROC-INIT instantiates a new program abstraction and stores it in a free entry in . GHOST-PROC-FINISH finalises program abstractions that are able to terminate successfully. The rules GHOST-ACT-INIT, GHOST-ACT-STEP and GHOST-ACT-END handle the execution of action blocks. Before discussing these, first observe that the ghost semantics maintains an extra component m in m Ccommands, containing (ghost) metadata: extra runtime information about the process-algebraic model in whose context the program C is being executed. Concretely, ghost metadata m is defined as a quadruple , consisting of:
The label a of the action that is being executed;
The input argument v for this action;
The identifier of the corresponding process-algebraic model in the process map, in which the action a is to be executed; and
A copy h of the heap, made when the program started to execute the action block; that is, when the program was reduced to by .
The ghost-ACT-INIT reduction rule starts executing an block by reducing it to an program, thereby assembling and attaching ghost metadata. In particular, a copy of the heap is made at this point, so that the ghost-ACT-END rule for finalising programs is able to access the original contents of the heap. This is needed to allow the abstraction to make a matching step; in particular to determine the pre-state of such a step. To see how this works, first recall that the process-algebraic state of program abstractions are linked to concrete program state—entries in the heap—via the binders maintained in process maps. Therefore, to be able to make an step, the ghost-ACT-END rule first needs to construct process-algebraic state out of the current program state. This is done using the auxiliary function referred to as the abstract state reification function.
Definition 31 (Abstract state reification)
. The ghost-ACT-STEP rule allows making reductions in the context of programs. Finally ghost-QUERY handles reductions of assertions and synchronises any reductions on the process level with reductions of queries on the program level, with respect to the reified program state.
3.5.2. Faulting Ghost Configurations
In addition to faulting program configurations (Definition 13) we also define a fault semantics for ghost configurations. This
ghost fault semantics is expressed in terms of a predicate
over ghost configurations
.
Figure 7 gives an excerpt of the rules. Only the rules related to specification-only constructs are shown. All other rules are essentially the same as those of Definition 13. We shall later show and prove properties that connect the two faulting semantics.
Clarifying the ghost fault semantics; the initialisation of any process-algebraic model faults if there is no free entry available in (by -PROC-FULL). The finalisation of program abstractions can fault if the corresponding entry in the process map is (1) either unoccupied or invalid (-PROC-FINISH-1), or (2) contains a process-algebraic abstraction that is unable to successfully terminate (by the rule -PROC-FINISH-2). Reductions within action blocks m C may fault if (1) m does not refer to an abstraction (-ACT-SKIP-1), or (2) the abstraction relies on process variables that have an incorrect binding (by the rule -ACT-SKIP-2), or (3) the process is not able to make a matching step (-ACT-SKIP-3), or (4) the subprogram C is able to fault (by -ACT-SKIP). Any program can fault under similar conditions as those of action programs.
The ghost semantics enjoys the same progress property as the standard operational semantics.
Theorem 3 (Progress of ). For any ghost configuration for which holds, either is final, or there exists a such that .
Moreover, it is quite straightforward to establish a
forward simulation between
and
. A matching backward simulation is ensured by the soundness argument of the program logic, as is customary for establishing refinements [
39].
Lemma 8 (Forward simulation). The standard operational semantics and the fault semantics of programs are embeddedin the ghost operational semantics and ghost fault semantics, respectively:
- 1.
If , then .
- 2.
If , then also , for any and g.
The above theorem also shows that the ghost fault semantics extends ↯. The soundness argument of the program logic establishes that verified programs do not fault with respect to , and thus also do not fault with respect to by the above Lemma.
3.5.3. Preservation of Process Execution Safety
As already hinted upon in the preamble of this section, establishing soundness of the program logic requires maintaining an invariant stating that all active program abstractions retain their execution safety throughout program execution, with respect to Definitions 5 and 6. Since process maps are used to administer the status of all active program abstractions, we lift the notion of process configuration safety (Definition 5) to safety of process maps. Process map safety is expressed in terms of judgments of the form stating that is safe if all process-algebraic models stored in execute safely with respect to Definition 5 together with a process store that is constructed (reified) from h.
Definition 32 (Process map safety)
.where is defined by case distinction on , so that Free process cells are always safe whereas corrupted entries are never safe. Moreover, both and are closed under bisimilarity of process maps and their entries, respectively.
Lemma 9. - 1.
If and , then .
- 2.
If and , then .
In a moment we will also define a notion of execution safety for commands. This notion of program execution safety maintains the aforementioned invariant that always holds throughout program execution, where h and are constructed from the current state, at every execution step. This invariant is needed to establish soundness of the HT-PROC-QUERY proof rule.
However, one must be careful on how to exactly state this invariant, to allow re-establishing it after every computation step. In most cases re-establishing the invariant is straightforward. For example, can be re-established after initialising a new program abstraction using the HT-PROC-INIT proof rule, by Definition 6 and by the structure of that proof rule. The invariant can also trivially be re-established after finalising an abstraction using HT-PROC-FINISH, as the abstraction is then no longer active and thereby removed from . However, computation steps that involve heap writing (i.e., handling of programs) may be problematic, as illustrated below.
Technicality 1 (Potential problems due to heap writing)
. To see the potential problem, consider the following code snippet.Suppose that holds on line 5. After computing line 6, the heap h holds the value at location . Moreover, the process map has not been changed, since the action program (lines 5–8) has not fully been executed yet. Nevertheless, may now be violated, as the action can no longer be performed, since after reification, while ’s guard requires x to be positive.
The root of the problem is that the invariant should not necessarily have to hold during intermediate reduction steps while executing programs, but only at the pre- and poststate of such programs. Program execution safety will solve this by making a snapshot of the heap every time an action program is being started on (likewise to ghost-ACT-INIT), and expressing the invariant over these snapshot heaps. Snapshots are recorded at the level of permission heaps, which already have the required structure to do this: action heap cells allow storing snapshot values alongside “concrete” values . These snapshot values are used to construct snapshot heaps.
Definition 33 (Snapshot heaps)
. The
snapshot
of a permission heap is defined in terms of a total function , so that , with The snapshot heap of any permission heap only contains heap cells bound by process-algebraic models, and is constructed by taking the snapshot values of all ’s action heap cells. As we shall see in a moment, the final invariant maintained by program execution safety will be , where and are taken from the models of the program logic and represent the current state of the program. This invariant, combined with establishing a refinement between the program and its abstract models, provide sufficient means for proving soundness of the program logic.
3.5.4. Adequacy
This section defines
program execution safety and uses it to define the semantic meaning of program judgments, from which the soundness theorem (i.e., adequacy of the logic) can be formulated. Program execution safety extends on the well-known notion of
configuration safety of [
34], by adding permission accounting, process-algebraic state, and the machinery introduced earlier in this section.
First, in order to help connect the models of the program logic to concrete program state, we define a concretisation function for permission heaps in the same style as snapshot heaps.
Definition 34 (Concretisation)
. Concretisation
of permission heaps is defined as a total function , so that , with defined as The heap concretisation operator constructs (program) heaps out of permission heaps by simply discarding all internal structure regarding process-algebraic models. Only the information relevant for regular program execution is retained. essentially does the same, but only retains heap cells bound to program abstractions and takes snapshot values whenever possible.
We now have all the ingredients for defining adequacy. Program execution safety is defined in terms of a predicate , stating that C is safe for n reduction steps with respect to a permission heap , process map , two stores s and g, a resource invariant and postcondition .
Definition 35 (Program execution safety). The predicate always holds, whereas holds if and only if the following five conditions hold.
- 1.
If , then .
- 2.
For every and such that and , it holds that .
- 3.
For any it holds that .
- 4.
For any it holds that .
- 5.
For any , , , , , , , and such that, if:
- 5a.
and , and
- 5b.
and , and
- 5c.
implies , and
- 5d.
, and
- 5e.
, and
- 5f.
;
then there exists , , , , , and , such that
- 5g.
and , and
- 5h.
and , and
- 5i.
, and
- 5j.
, and
- 5k.
, and
- 5l.
implies , and
- 5m.
, and
- 5n.
.
Clarifying the above definition, any configuration is safe for steps intuitively if: the postcondition is satisfied if C has terminated (1); the program C does not fault (2); C only accesses heap entries that are allocated (3); C only writes to heap locations for which full permission is available (4); and finally, after making a computation step the program remains safe for another n steps (5). (The predicate is whenever is an occupied heap cell with an associated fractional permission equal to 1.) Condition 2 implies race freedom, while conditions 3 and 4 account for memory safety.
Condition
5 is particularly involved. In particular it encodes the backward simulation: if the program can do a
step (
5f), then it must be able to make a matching
step (by
5m). Moreover, the resource invariant
must remain satisfied (due to
5c and
5l) after making a computation step, whenever the current program is not locked. In addition, the process maps invariably remain safe with respect to the snapshot heap due to
5e and
5k, as discussed in
Section 3.5.3.
Lemma 10. Program execution safety satisfies the following properties.
- 1.
If and , then .
- 2.
If and , then .
- 3.
If and , then .
1 in Lemma 10 states monotonicity in the sense that being safe for n reduction steps implies safety for less than n steps. 2 in Lemma 10 states that process maps can always be replaced by bisimilar ones in safe configurations. Finally, 3 in Lemma 10 states that postconditions may always be weakened.
3.5.5. Semantics of Program Judgments
The semantics of program judgments is defined in terms of a quintuple , expressing that C is safe for any number of reduction steps starting from any state satisfying .
Definition 36 (Semantics of program judgments). holds if and only if:
- (1)
, and
- (2)
If and , then for any such that and and and hold, it holds that:
The underlying idea of the above definition, i.e., having a continuation-passing style definition for program judgments, has first been applied in [
40] and has further been generalised in [
41,
42]. Moreover, the idea of defining execution safety in terms of an inductive predicate originates from [
43]. These two concepts have been reconciled in [
34] into a formalisation for the classical CSL of Brookes [
23], that has been encoded and mechanically been proven in both Isabelle and Coq. Our definition builds on the latter, by having a refinement between programs and abstractions encoded in
.
Observe that only judgments of user programs (i.e., commands free of runtime constructs like and ) have a semantic meaning. Also observe that the semantics of program judgments is conditional on the safety of . It states that C executes safely for any number n of computation steps with respect to any state satisfying , only if is safe—that is, only if all process-algebraic models for C are (assumed to be externally) verified. From the above definition it trivially follows that for any , , and user program C. Notice however that does not hold in general, since C might be able to fault, for example by having data-races.
The following main soundness theorem states that verified programs (i.e., programs for which a proof can be derived according to the proof rules given earlier in
Figure 4 and
Figure 5) are semantically valid (that is, are fault-free, memory-safe, and refine their process-algebraic models).
Theorem 4 (Soundness). .
The soundness proofs of all proof rules have been mechanised using the Coq proof assistant and can be found on the Git repository accompanying this article [
19].
The HT-PROC-UPDATE and HT-PROC-QUERY proof rules were the most difficult to prove sound, as their proofs require, among other things, (1) showing that the abstract model can always match the program with a simulating execution step, as well as (2) maintaining the invariant that any process-algebraic abstraction inside the process map is safe with respect to the reified program state. On top of that, the combination of (1) and (2) requires some extra bookkeeping to ensure that the snapshot heaps stored in ghost metadata agree with the snapshot values stored in permission heaps. This additional bookkeeping has been left out of the formalisation presented so far, but the details of this can be studied in the Coq formalisation.
 Q is the left-merge of P and Q, which is similar in spirit to parallel composition, however
Q is the left-merge of P and Q, which is similar in spirit to parallel composition, however  insists that the left-most process P proceeds first. The left-merge is an auxiliary connective commonly used to axiomatise parallel composition [31], by having P
insists that the left-most process P proceeds first. The left-merge is an auxiliary connective commonly used to axiomatise parallel composition [31], by having P Q + Q
Q + Q P. The process is the infinite summation over all values . Any summation is a binder for the summation variable x. In the remainder we assume without loss of generality that all variables bound by summation are unique (since any such variables can be renamed to unique ones if this is not yet the case). Sometimes is written to abbreviate . The conditional (guarded) process behaves as P if the Boolean condition b holds, and otherwise behaves as . Finally, is the repetition, or iteration of P, and denotes a sequence of zero or more P’s. The infinite iteration of P is derived to be . Finally, is the assertive process, which is very similar to guarded processes: is behaviourally equivalent to in case b does not hold. However, assertive processes have a special role in our approach: they are the main subject of process-algebraic analysis, as they encode the properties b to verify, as logical assertions. Moreover, they are a key component in connecting process-algebraic reasoning with deductive reasoning, as their properties can be relied upon in the deductive proofs of programs via the ghost command.
P. The process is the infinite summation over all values . Any summation is a binder for the summation variable x. In the remainder we assume without loss of generality that all variables bound by summation are unique (since any such variables can be renamed to unique ones if this is not yet the case). Sometimes is written to abbreviate . The conditional (guarded) process behaves as P if the Boolean condition b holds, and otherwise behaves as . Finally, is the repetition, or iteration of P, and denotes a sequence of zero or more P’s. The infinite iteration of P is derived to be . Finally, is the assertive process, which is very similar to guarded processes: is behaviourally equivalent to in case b does not hold. However, assertive processes have a special role in our approach: they are the main subject of process-algebraic analysis, as they encode the properties b to verify, as logical assertions. Moreover, they are a key component in connecting process-algebraic reasoning with deductive reasoning, as their properties can be relied upon in the deductive proofs of programs via the ghost command.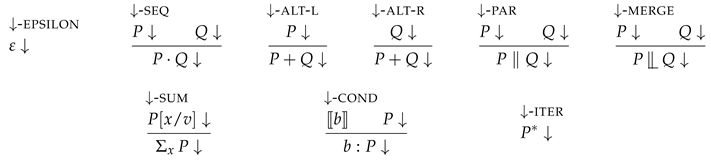
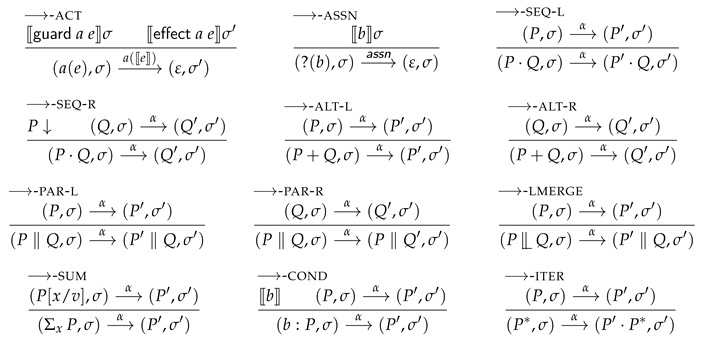
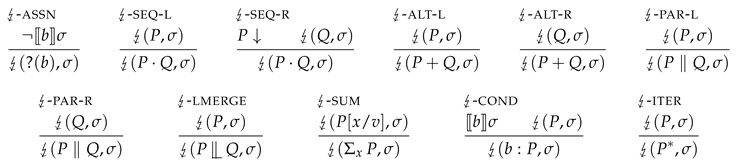
 is not strictly needed, in the sense that our approach does not rely on it, but can be used to prove for example that is bisimilar to .
is not strictly needed, in the sense that our approach does not rely on it, but can be used to prove for example that is bisimilar to .

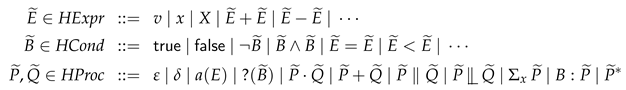

 connectives. Linearisation is a mechanical (automated) procedure based on a rewrite system that uses a subset of the bisimulation equivalences of Figure 2 as rewrite rules [44] (but in one direction only), to try to eliminate parallel connectives. For example, a process term can automatically be linearised to the bisimilar process . Note that linearisation may not always succeed. VerCors outputs a verification error in case linearlisation fails.
connectives. Linearisation is a mechanical (automated) procedure based on a rewrite system that uses a subset of the bisimulation equivalences of Figure 2 as rewrite rules [44] (but in one direction only), to try to eliminate parallel connectives. For example, a process term can automatically be linearised to the bisimilar process . Note that linearisation may not always succeed. VerCors outputs a verification error in case linearlisation fails.